Could CoRoT-7b and Kepler-10b be remnants of evaporated gas or ice giants?

Abstract

We present thermal mass loss calculations over evolutionary time scales for the investigation if the smallest transiting rocky exoplanets CoRoT-7b ($\sim 1.68R_{\mathrm{Earth}}$) and Kepler-10b ($\sim 1.416R_{\mathrm{Earth}}$) could be remnants of an initially more massive hydrogen-rich gas giant or a hot Neptune-class exoplanet. We apply a thermal mass loss formula which yields results that are comparable to hydrodynamic loss models. Our approach considers the effect of the Roche lobe, realistic heating efficiencies and a radius scaling law derived from observations of hot Jupiters. We study the influence of the mean planetary density on the thermal mass loss by placing hypothetical exoplanets with the characteristics of Jupiter, Saturn, Neptune, and Uranus to the orbital location of CoRoT-7b at 0.017 AU and Kepler-10b at 0.01684 AU and assuming that these planets orbit a K- or G-type host star. Our findings indicate that hydrogen-rich gas giants within the mass domain of Saturn or Jupiter cannot thermally lose such an amount of mass that CoRoT-7b and Kepler-10b would result in a rocky residue. Moreover, our calculations show that the present time mass of both rocky exoplanets can be neither a result of evaporation of a hydrogen envelope of a “Hot Neptune” nor a “Hot Uranus”-class object. Depending on the initial density and mass, these planets most likely were always rocky planets which could lose a thin hydrogen envelope, but not cores of thermally evaporated initially much more massive and larger objects.

Highlights

► We model the thermal mass loss of CoRoT-7b and Kepler-10b over their lifetimes. ► Planetary density and orbital distance are key parameters for thermal mass loss. ► CoRoT-7b and Kepler-10b cannot be thermally evaporated remnants of hot gas giants. ► A hot Uranus-type planet as origin of CoRoT-7b and Kepler-10b is very unlikely.

1. Introduction

In spring 2009 the European CoRoT space observatory discovered so far the smallest transiting exoplanet which orbits a G9V star at about 0.017 AU in 0.85 days. CoRoT-7b (Léger et al., 2009) has a size of 1.48–1.68 $R_{\mathrm{Earth}}$ (Bruntt et al., 2010), a mass of $5.5–8.3M_{\mathrm{Earth}}$ (Hatzes et al., 2010), and a density of 9.6±2.7 g/cm³ (Hatzes et al., 2010) and can, therefore, be considered a rocky planet. Pont et al. (2011) suggest an even smaller mass range for CoRoT-7b of $1–4M_{\mathrm{Earth}}$ by modelling the stars activity during the measurements from ESOs High Accuracy Radial velocity Planet Searcher (HARPS), to find the contribution of activity in the radial velocity signal. With the radius range from Bruntt et al. (2010) this gives a lower limit to density of about 1.2 g/cm³. About two years after this pioneering discovery, NASA's Kepler team announced the detection of a more or less similar rocky exoplanet, Kepler-10b (Batalha et al., 2011) with a size of $\sim 1.416R_{\mathrm{Earth}}$ and a mass of $4.{56}_{-1.29}^{+1.17}{M}_{\mathrm{Earth}}$ orbiting a G-type star.

Even more recently the Kepler telescope discovered a six-planet system (Kepler-11b–11f) orbiting also a G-type star, where five of these planets are bodies of the “super-Earth” and sub-Uranus category (Lissauer et al., 2011). However, all planets of the Kepler-11 system orbit at distances $\ge 0.9\mathrm{AU}$ and have much lower densities compared to Kepler-10b. Because of the similarity between Kepler-10b with CoRoT-7b and the much closer orbital location of Kepler-10b compared to the Kepler-11 planets, and the similarity of the planetary parameters we focus here only on Kepler-10b and CoRoT-7b and investigate if these objects could be remaining cores of thermally evaporated hydrogen-rich more massive planets. The determination of the size and mass of CoRoT-7b and Kepler-10b allows to investigate the hypothetical possibility that these planets might be remnants of initially much more massive hydrogen-rich exoplanets. Valencia et al. (2010) studied several questions related to the possible composition, initial mass and origin of CoRoT-7b and concluded that this planet is made only of irons and silicates but its origin remains unknown. These authors suggested that CoRoT-7b may be a remaining small core of a hydrogen-rich gas or ice giant which has lost its hydrogen envelope, or the planet always had a terrestrial composition.

During the past years quite a few mass loss studies of hydrogen-rich “Hot Jupiters” were carried out (Kuchner, 2003; Lammer et al., 2003; Vidal-Madjar et al., 2003; Lecavelier des Etangs et al., 2004; Baraffe et al., 2004; Yelle, 2004, 2006; Tian et al., 2005; Koskinen et al., 2007; Lecavelier des Etangs, 2007; Peng et al., 2008a,b; Penz and Micela, 2008; Davis and Wheatley, 2009; Murray-Clay et al., 2009; Lammer et al., 2009). Some of these studies argued that hydrogen-rich hot gas giants or migrated ice giants might have evaporated down to their cores (e.g. Lammer et al., 2003; Baraffe et al., 2004; Lecavelier des Etangs, 2007; Penz et al., 2008a,b; Davis and Wheatley, 2009).

Lammer et al. (2003) and Baraffe et al. (2004) applied an efficient energy-limited approach of Watson et al. (1981) but used unrealistic input data to study thermal atmospheric loss from hydrogen-rich “Hot Jupiters”. They assumed that a heating efficiency, which is the ratio of the net heating rate to the rate of stellar energy absorption, is 100%. They also assumed that an effective radius where the stellar EUV radiation is absorbed is about $3r_{\mathrm{pl}}$, while in reality this EUV absorbing layer has occurred to be much closer to a planet, as was shown by later studies (Yelle, 2004; García Muñoz, 2007). Lecavelier des Etangs (2007), Davis and Wheatley (2009) and more recently Lissauer et al. (2011) considered a more realistic EUV absorption radius but also assumed unrealistic 100% heating efficiency which resulted in overestimation of the hydrogen escape rate. Recently Murray-Clay et al. (2009) and Lammer et al. (2009) have attempted to reevaluate a heating efficiency in order to obtain correct thermal mass loss rates from hydrogen-rich close-in exoplanets. In their study Murray-Clay et al. (2009) calculated the EUV driven mass loss from a “Hot Jupiter” during the very active pre-main sequence stage of the planet's host star. These authors concluded that the heating efficiency for an EUV irradiated hydrogen atmosphere may be in the range of 25–30% (e.g. Waite et al., 1983; Chassefière, 1996; Lammer et al., 2009) or even as low as 10% if the stellar EUV flux is larger than ${10}^4\mathrm{erg}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$ when $\mathrm{Lyman}\text{-}\alpha$ radiation becomes a dominant cooling process (Murray-Clay et al., 2009). Also recently Cecchi-Pestellini et al. (2009) investigated heating rates and efficiencies of giant exoplanets assuming a monochromatic stellar photon flux. These authors found that for a hydrogen column density of $>{10}^{20}{\mathrm{cm}}^{-2}$ only X-rays are able to heat the gas. For an ionization fraction of 10⁻⁶ heating efficiencies between 12% and 18% (assuming different photon energies of 50, 300, and 1000 eV) have been deduced.

By considering realistic heating efficiencies for EUV exposed hydrogen atmospheres other studies found more moderate loss rates for close-in giant planets (e.g. Tian et al., 2005; Lammer et al., 2009). Lammer et al. (2009) showed that the main escape may happen due to thermal expansion of the thermosphere beyond the Roche lobe region. The evolution of a planet can be split into two main phases: (1), the formation period during which the planet is formed and its mass grows, and (2), the mature period when the planet is detached from the surrounding gas reservoirs and loses its atmosphere owing to the processes driven by its host star. During the formation period the planet is in contact with a mass reservoir of a protoplanetary nebula from which it gains mass. So, the mass evolution of the planet is determined by pressure gradients, as long as there is a nebula surrounding the planet, and by the exosphere and host star properties after the nebula has dissipated.

In the following sections we model the mass loss from hypothetical hydrogen-rich gas or ice giants within an initial density range between 0.2 and 2.0 g cm⁻³ which lies well within the density range of the so far observed exoplanets. The lower density limit corresponds to the lowest gas giants known (e.g. Tres-4b). As thermal escape becomes negligible for high planetary densities (cf. Section 4), we calculate planetary thermal mass loss only for planets with densities of $\le 2.0\mathrm{g}{\mathrm{cm}}^{-3}$. We consider masses of Jupiter, Saturn, Neptune, and Uranus at the orbital location of CoRoT-7b and Kepler-10b around K and G-type host stars. We study the mass loss since the time when the inner part of the nebula has dissipated and detached from the star exposing a newly born planet to extreme XUV-radiation of the star. The main aim of this study is to investigate if giant or Uranus-like planets could lose their huge hydrogen–helium envelopes due to thermal escape so that a core with the mass of CoRoT-7b and Kepler-10b could remain.

2. Planetary formation and atmospheric loss scenarios

The possible origin of CoRoT-7b was the subject of several recent studies. Valencia et al. (2010) (hereafter V2010) investigated the structure, composition and thermal mass loss from CoRoT-7b. The energy-limited formula of Erkaev et al. (2007) was used to determine the thermal mass loss over the CoRoT-7b's evolution. A heating efficiency of 40% was adopted, and the planetary density was assumed to be constant in time. By applying this approach, these authors concluded that CoRoT-7b's origin could be

• •a Jovian-type gas giant with a small core that would have been entirely stripped of its gaseous hydrogen envelope,
• •a remnant of a migrated Uranus-like ice giant,
• •it may have always had a terrestrial composition.

At the same time, Jackson et al. (2010) (hereafter J2010) also investigated the thermal mass loss of CoRoT-7b, but included a possible role of tidal decay of CoRoT-7b's orbit. From their model simulations J2010 suggested that tides generated on the host star by CoRoT-7b may have brought the planet closer to the star, thereby enhancing the mass loss rate. Then they argued that this enhanced mass loss suggested a possibility that CoRoT-7b began its life as a gas giant planet which later completely lost its original hydrogen-helium atmosphere and only its rocky core remained. They estimated that in this case the original mass of CoRoT-7b could have been as large as about 200 Earth masses.

However, first of all one should note that it is impossible for a gas giant planet to form as close to the host star as at about 0.017 AU. The high radiative temperature of the star at this orbital distance would result in rapid evaporation of solid volatile materials and rapid mass loss of light gases from the planet, the rocky core of which was probably melted during the planetary formation phase. Thus, if one assumes that CoRoT-7b originated as a gas giant, one needs also to assume that the planet may have formed farther away from the host star. Then one also needs to invoke a mechanism by which the original gas giant could have been brought to the current close-in orbit at 0.017 AU.

These authors suggested that the mechanism that has brought the gas giant to the present orbit of CoRoT-7b was tidal orbital decay. They used a standard tidal orbital decay model that has been applied in studies of solar and extra-solar systems. However, this model includes a very poorly constrained tidal dissipation parameter $Q{\prime }_{⁎}$ for a star which is uncertain by at least “two orders of magnitude” (between $\sim {10}^5$ and 10⁷ in their model). Simulations by J2010 with $Q{\prime }_{⁎}<{10}^6$ show that the orbit of CoRoT-7b decays so quickly that the planet crashes onto the star and is destroyed in about 2 Gyr. But this time is about the age of the planet and this raises doubts that the orbital decay can indeed be so rapid and the planet could be destroyed instead of being presently observed. Moreover, the recent discovery of Kepler-10b indicates that planets such as CoRoT-7b are no anomaly in planet formation and may occur more frequently. The accompanying orbital evolution for the case when $Q{\prime }_{⁎}<{10}^6$ shows that the initial semi-major axis a could be only about 20% larger than at present (see their Fig. 3). In the opposite case, when the tidal dissipation parameter $Q{\prime }_{⁎}>{10}^6$, the life-time of the planet can be much longer than 2 Gyr, but the increase of the initial orbital radius becomes even less than 20%. Thus, the simulation results by the authors are in contradiction with their main assumption that the planet started as a gas giant far away from the star and then moved much closer to it evaporating along the way its hydrogen–helium envelope. According to their model results, the planet could not have started far away from the star and, as a consequence, it could not have started as a gas giant.

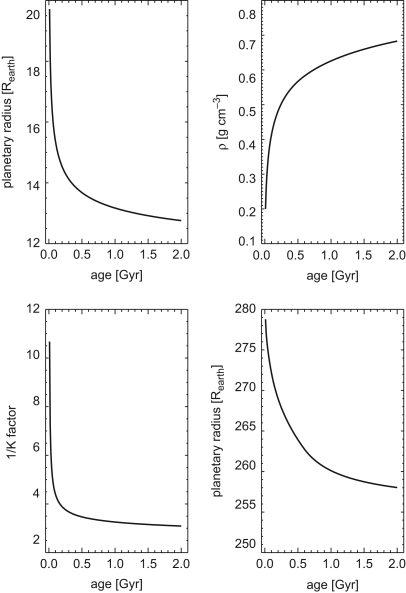
Fig. 3.

Shown is the evolution of planetary parameters (planetary mass, planetary density, planetary, radius, and planetary 1/K mass loss enhancement factor) for an exoplanet with the mass of Tres-4b, which is actually the planet with the lowest density so far detected (0.2 g cm⁻³). We place this planet at a distance of 0.017 AU and let it evolve until it reaches an age of 2 Gyr. In the upper left plot the evolution of planetary thermal mass loss is presented. Within the first Gyr of planetary evolution planetary mass decreases sharply. Planetary radius decreases also sharply (lower left panel) as well as the 1/K mass loss enhancement factor (lower right panel). The only parameter which decreases is planetary density.

Furthermore, both V2010 and J2010 overestimated the mass loss in their models by adopting the scaling law for the stellar EUV flux suggested by Ribas et al. (2005) for the solar analog stars, which are widely different from the host star CoRoT-7. For evaporating Jupiter mass gas giants J2010 assumed unrealistic high heating efficiencies of up to 100%. V2010 used a more moderate heating efficiency of 40%. However, as thoroughly discussed in Lammer et al. (2009), more realistic values for hydrogen thermospheres are 10–25% (Waite et al., 1983; Chassefière, 1996; Murray-Clay et al., 2009; Lammer et al., 2009).

V2010 and J2010 used different integration limits in their mass loss calculations. V2010 integrated down to 0 Gyr, which includes also stages of planetary formation. On the other hand, J2010 stopped their calculations at 100 Myr.

The time when hydrodynamic escape may effectively start is a crucial point in this study, i.e. the time at which processes of mass accretion have ceased and the planetary evolution is dominated by mass loss processes. Generally hydrodynamic escape may start when

• •the circumstellar disk has become optically thin to allow the stellar EUV radiation to heat the planetary atmosphere,
• •the stellar EUV heating is strong enough to drive hydrodynamical escape.

The entire circumstellar disks dissipate in a time range of 1–10 Myr (cf. Hillenbrand, 2005: 3–8 Myr, Haisch et al., 2001: 6 Myr), while for the inner part of the disk the dissipation may finish earlier. According to Hillenbrand (2005) and Lunine et al. (2009) planets form within a time range of 30–100 Myr. After the disks become optically thin which should happen during the first 10 Myr, hydrodynamic escape may start although the planet still accretes mass, resulting in a combined accretion- and mass loss-scenario. After the planet has formed, no mass is accreted anymore and mass loss processes become dominant. To separate these evolutionary stages we compute the thermal mass loss for two phases. Phase 1 corresponds to the phase in which the planet accretes mass until it reaches its maximum and thermal escape may already have started. Phase 2 corresponds to a time at which mass loss dominates the planetary evolution. Here we have adopted time ranges of 10–100 Myr (according to the above stated values of planet formation and disk dissipation time) for phase 1 and greater than 100 Myr for phase 2. As we do not account for mass gain during phase 1 in our calculations, the resulting values are maximum loss rates, whereas the true (net) loss rate could be smaller. Additionally, phase 1 and phase 2 also separate the pre-main sequence from the main-sequence stage of a G-type host star like CoRoT-7 or Kepler 10 as 100 Myr is about the age (Soderblom et al., 1993) when the star entered the zero age main-sequence.

As discussed above, we compute planetary thermal mass loss for phase 1 (10–100 Myr) and phase 2 (100 Myr—till the current age of the planet). For the computation we use initial planetary parameters (mass and density) which we let evolve over CoRoT-7b's and Kepler-10b's ages (see Fig. 4). The choice of a proper combination of planetary mass and density results then in the current upper and lower limits of the mass and densities of both planets.

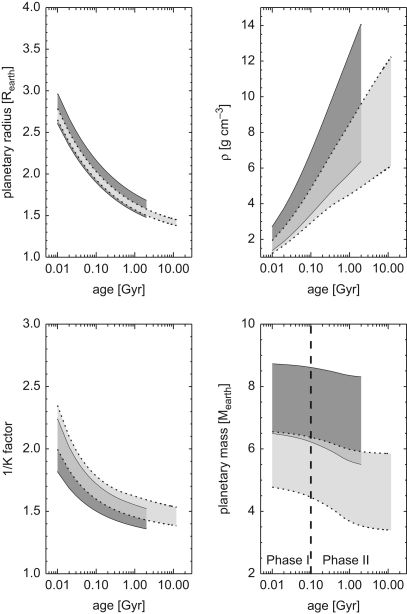
Fig. 4.

Shown is the evolution of radius (upper left panel), density (upper right panel), mass loss enhancement factor (lower left panel), and mass (lower right panel) of the transiting exoplanets CoRoT-7b (dark gray shaded area) and Kepler 10b (light gray shaded area) over their life-time of 2 and 11.9 Gyr, respectively. The shaded areas indicate the range (upper and lower limit) of each parameter. We select proper initial parameters which then result in the currently known parameters of CoRoT-7b and Kepler-10b at the corresponding planetary ages.

3. Atmospheric thermal loss model

While in a number of studies of the thermal atmospheric escape from hot close-in exoplanets a consistent hydrodynamic approach has been applied (Yelle, 2004; Tian et al., 2005; Koskinen et al., 2007; García Muñoz, 2007; Penz et al., 2008a), in the majority of such studies a much simpler but less precise energy-limited approximation has been used, which was first suggested for early Earth by Sekiya et al. (1980a,b) and Watson et al. (1981). According to this approximation the mass loss rate is proportional to the incoming solar EUV-radiation flux. Watson et al. (1981) who applied this approach to study atmospheric escape from a hydrogen-rich early Earth, concluded that the escape flux is limited by the amount of energy conducted downward from where it is absorbed by the thermosphere and that this energy is needed to balance the concomitant adiabatic cooling of the rapidly expanding gas.

From these arguments one may wrongly conclude that the application of the energy-limited approximation can be justified only if thermal conduction plays a role in the thermosphere. However, thermal conduction is negligible for extended hydrogen-rich thermospheres of “Hot Jupiters” (e.g. Yelle, 2004; García Muñoz, 2007; Penz et al., 2008a) and, hence, the energy-limited equation appears to be invalid for hot giant planets. The main source of energy for the part of the atmosphere which is below the thermosphere where the EUV radiation is absorbed is the stellar and atmospheric radiation transfer at longer wavelengths—that is in the visible, near infra-red and infra-red ranges. But Sekiya et al. (1980a,b) showed that hydrodynamic loss of a hydrogen-rich atmosphere does occur under high irradiation when there is no thermal conduction in the thermosphere. These authors solved numerically hydrodynamic equations for spherically-symmetric outflow of molecular hydrogen and atomic helium and obtained supersonic steady-state, equilibrium solutions. In the model atmosphere of Sekiya et al. (1980a,b), in contrast to the simulations of Watson et al. (1981), thermal conduction was completely neglected. By integrating the hydrodynamic equations from the point of the temperature minimum, $r_0$, deep in the atmosphere to the sonic point, $r_{\mathrm{s}}$, in the upper thermosphere they derived an energy-limited equation for the mass loss rate in a general form. In the limiting case where $r_0⪡r_{\mathrm{s}}$ and for relatively low EUV flux, $F_{\mathrm{EUV}}$, Sekiya et al. (1980a) obtained an approximate equation in which the mass loss rate is proportional to the flux, $F_{\mathrm{EUV}}$, irradiating the atmosphere of a planet.

This result indicates that there is no connection between thermal conduction and the condition that the loss rate is or should be proportional to the EUV flux, as supposed by Watson et al. (1981). What may depend on conduction, however, is the column integrated heating rate and the resulting net loss rate. Higher thermal conduction can transfer heat from the upper thermosphere to its lower layers more rapidly where heat is converted to thermal IR-radiation which provides efficient cooling and reduces the supply of energy available to drive atmospheric escape. This effect may be particularly important in a low temperature terrestrial thermosphere which was studied by Watson et al. (1981). But the role of heat conduction in an extended thermosphere of a “Hot Jupiter” is now known to be very small (e.g. Yelle, 2004; García Muñoz, 2007; Penz et al., 2008a) and can, for this reason, be safely neglected.

In this study we apply the energy-limited loss rate equation derived by Erkaev et al. (2007) for hydrogen-rich close-in exoplanets and modified by Lammer et al. (2009) for a mass loss study of recently discovered transiting “Hot Jupiters”. This equation includes the Roche lobe tidal loss effect which is an additional important factor for exoplanets in close orbits. This effect has been ignored in all previous energy-limited calculations (Watson et al., 1981; Sekiya et al., 1980a) except for the study by Lecavelier des Etangs (2007) who was the first to include the Roche lobe effect. However, this author used for the derivation of his mass loss equation a linear perturbation approach which has a limited application range. In contrast, the nonlinear equation derived by Erkaev et al. (2007) is universally applicable and more accurate than the Lecavelier Des Etangs linear formula. A comparison of this approximate formula with the detailed hydrodynamic solutions of Yelle (2004), García Muñoz (2007) and Penz et al. (2008a) shows that, while being much simpler, this formula retains the most essential physics of the hydrodynamic flow under extreme EUV conditions and with properly adjusted input parameters gives practically the same loss rates as much more complex hydrodynamic models, if the EUV flux is strong enough to start hydrodynamic escape. The EUV limit when hydrodynamic escape may start depends mainly on the stellar EUV output, the planetary orbit, planetary mass, and the composition of the planetary atmosphere.

We calculated the current hydrogen loss rate of the hot Jupiter HD209458b (orbiting a solar-like star of spectral type G0 V with an age of $\sim 4\mathrm{Gyr}$) for comparison with the results of the models by Yelle (2004) and Tian et al. (2005). Using the same heating efficiency as Yelle (2004) and Tian et al. (2005) (that is 60%) and three different EUV flux estimates (P2008 mean G-star, P2008 upper limit G-star, and R2005) yields loss rates of 2.2×10¹⁰, 5.2×10¹⁰, and 8.2×10¹⁰ g s⁻¹, similar to the values found by Yelle (2004) (4.7×10¹⁰ g s⁻¹) and Tian et al. (2005) (6.0×10¹⁰ g s⁻¹). We note that this equation was only compared and justified with complex full hydrodynamic flow models for escaping hydrogen atoms. Therefore, the application of this equation to heavy elements which may evaporate from a rocky surface such as applied by Jackson et al. (2010) to so-called core evaporation scenarios is highly questionable.

The thermal mass loss equation, which we use here gives the mass loss rate in g s⁻¹, and has the following form

$$\frac{\mathrm{d}{M}_{\mathrm{th}}}{\mathrm{d}t}=\frac{3\eta F_{\mathrm{EUV}}(t)}{4G{\rho }_{\mathrm{pl}}(t)K(\xi )}\text{,}$$ (1)

where $\eta$ is the heating efficiency of about 10–25% (Chassefière, 1996; Murray-Clay et al., 2009; Cecchi-Pestellini et al., 2009; Lammer et al., 2009); $F_{\mathrm{EUV}}$ is the stellar EUV flux (in erg cm⁻² s⁻¹) at the orbital distance of a planet; G is Newton's gravitational constant (in cgs units), ${\rho }_{\mathrm{pl}}$ is the mean planetary density (in g cm⁻³), and

$$K(\xi )=1-\frac{3}{2\xi }+\frac{1}{2{\xi }^3}\text{,}$$ (2)

is the dimensionless potential energy reduction factor due to the stellar tidal forces (Erkaev et al., 2007). Here $\xi$ is a relative Roche lobe radius,

$$\xi =\frac{r_{\mathrm{rl}}}{r_{\mathrm{pl}}}=d{\left(\frac{4\pi {\rho }_{\mathrm{pl}}}{9M_{⁎}}\right)}^{1/3}\text{,}$$ (3)

where M_⁎ is the mass of the host star (in g) and d is the orbital distance of the planet (in cm). For calculation of the mass loss rate we use a heating efficiency $\eta =25\%$ as an upper limit and 10% as a lower limit. A more detailed description of the model and estimated heating efficiencies $\eta$ are given by Lammer et al. (2009). As one can see the planetary mass loss is a function of stellar EUV flux, mass loss enhancement factor, heating efficiency and planetary density. In Table 1 we list loss rates for Jupiter and Uranus at CoRoT-7b's distance with various initial densities. At the starting time of 0.01 Gyr the loss rates for the given initial densities are the same for Jupiter and Uranus. This is because the loss rate is a function of planetary density. As Jupiter and Uranus evolve with time their densities change different and therefore also their loss rates differ. The evolution of the planetary radius is described by an empirical scaling law taken from Lecavelier des Etangs (2007)

$$r_{\mathrm{pl}}(t)=r_{\infty }(1+\delta t^{-0.3})\text{.}$$ (4)

Table 1.

Shown are loss rates according to Fig. 5 (lower most panels) for the case of Jupiter and Uranus. We apply the lower limit and mean of the P2008 law as XUV flux evolution together with a heating efficiency of 25%. The loss rates are given at times, 0.01, 0.1, 0.5, 1, 2, and 5 Gyr. The first loss rate corresponds to calculations using the lower limit of the P2008 law and the second loss rate corresponds to calculations using the mean P2008 law.

${\rho }_{\mathit{init}}$	${\frac{\mathrm{dM}}{\mathrm{dt}}}_{10\mathrm{Myr}}^{\eta =25\%}$	${\frac{\mathrm{dM}}{\mathrm{dt}}}_{100\mathrm{Myr}}^{\eta =25\%}$	${\frac{\mathrm{dM}}{\mathrm{dt}}}_{500\mathrm{Myr}}^{\eta =25\%}$	${\frac{\mathrm{dM}}{\mathrm{dt}}}_{1\mathrm{Gyr}}^{\eta =25\%}$	${\frac{\mathrm{dM}}{\mathrm{dt}}}_{2\mathrm{Gyr}}^{\eta =25\%}$	${\frac{\mathrm{dM}}{\mathrm{dt}}}_{5\mathrm{Gyr}}^{\eta =25\%}$
[gcm−3]	[10−11gs−1]	[10−11gs−1]	[10−11gs−1]	[10−11gs−1]	[10−11gs−1]	[10−11gs−1]
Jupiter
0.2	140/410	27/83	9/27	2.9/7.6	0.8/2.0	0.13/0.37
0.5	20/58	6/19	2.2/5.7	0.8/1.9	0.2/0.5	0.037/0.095
1	7/20	2.4/7.2	0.9/2.3	0.31/0.76	0.08/0.21	0.015/0.04
1.5	4/11	1.5/4.3	0.6/1.4	0.19/0.47	0.05/0.13	0.009/0.024
2	2.6/7.6	1.0/3.0	0.4/1.0	0.14/0.33	0.037/0.092	0.007/0.07
Uranus
0.2	140/410	25/-	9.9/-	4.3/-	1.4/-	0.30/-
0.5	20/58	5/16	1.6/4.9	0.5/1.7	0.13/0.45	0.024/0.083
1	7/20	1.9/5.7	0.6/1.7	0.20/0.55	0.05/0.15	0.009/0.026
1.5	4/11	1.1/3.4	0.4/1.0	0.13/0.32	0.033/0.087	0.006/0.016
2	2.6/7.6	0.8/2.4	0.28/0.72	0.09/0.23	0.024/0.061	0.004/0.011

Here the time t is taken in Gyr, $\delta =0.3$ for $M_{\mathrm{pl}}\lesssim 0.1M_{\mathrm{Jup}}$, while $\delta =0.2$ for $M_{\mathrm{pl}}\gtrsim 0.3M_{\mathrm{Jup}}$. as originally given in Lecavelier des Etangs (2007). For masses between 0.1 and $0.3{\mathrm{M}}_{\mathrm{Jup}}$ we adopt also a $\delta$ of 0.3. From the mass-density relation we also have an equation for the mean density of a planet

$${\rho }_{\mathrm{pl}}(t)=\frac{3M_{\mathrm{pl}}}{4\pi r_{\mathrm{pl}}^3}\text{.}$$ (5)

Integrating the mass loss equation (1) over time in combination with Eqs. (2)–(5), we calculate the planetary mass, $M_{\mathrm{pl}}$ and density, ${\rho }_{\mathrm{pl}}$ as functions of the EUV photon flux absorbed by the planet, $\eta F_{\mathrm{EUV}}(t)$ at time t.

The masses of CoRoT-7 and Kepler-10 are M_⁎ is $0.93\pm 0.03M_{\mathrm{Sun}}$ (Léger et al., 2009) and M_⁎ is $0.895\pm 0.06M_{\mathrm{Sun}}$, respectively (Batalha et al., 2011). Because the EUV evolution of the host star is unknown, we apply an empirical power law which is inferred from the average observed soft X-ray fluxes (SXR) for K and G-type stars of different age. As shown in Penz et al. (2008b) (P2008 hereafter) and Lammer et al. (2009), the SXR fluxes observed from the ROSAT satellite correlate well with the EUVE satellite observations in the wavelength range of 100–360 Å carried out for solar analogs of different age (Ribas et al., 2005) (R2005 hereafter).

The P2008 power law was derived from the luminosity distributions of the Hyades and the Pleiades, while the R2005 power law was derived by approximating a small sample of solar analogs. Since X-ray luminosities of coeval stars, such as those present in the Hyades or in the Pleiades, show a large spread of about one order of magnitude, we may conclude that there is not a unique law describing the X-ray luminosity evolution but that the evolution of a specific star may depend on initial conditions or on parameters other than age. In this context each star of the R2005 sample represents a “random realization” of the evolution of solar-like coronae at a given age, while cluster stars give the “average” evolution of coronae of stars in a given range of mass. Furthermore the ages of individual stars (as those of R2005 sample) are very uncertain ($\ge 50\%$, see again R2005), while cluster ages are much more precisely determined.

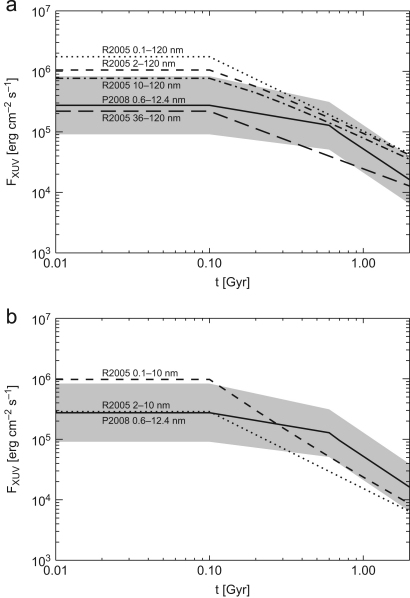
When comparing both power laws one must also consider that the P2008 law was deduced from ROSAT data (6–124 Å), whereas the R2005 law was compiled by summing up several data sets from different wavelength ranges resulting in a total range of 1–1200 Å. However, R2005 gives power laws for smaller wavelength regions which makes it possible to compare them with the power law by P2008. Fig. 1a shows the RoSat SXR distribution for G-stars found by P2008 (shaded area) as the mean relation indicated by a solid line. The dashed line shows the X-ray evolution between 0.1 and 10 nm found by R2005, whereas the dotted line shows the part between 2 and 10 nm only. It can be clearly seen that the R2005 power law for 2–10 nm is about equal to or even below the P2008 0.6–12.4 nm power law. If one extends the wavelength range down to 0.1 nm, the resulting R2005 power law lies slightly above the P2008 upper limit at young ages (up to 0.1 Gyr), but decreases down to the P2008 lower limit later as it evolves. Fig. 1b compares the photon flux over the full XUV range of R2005 (0.1–120 nm, dotted line) with the P2008 SXR flux distribution. This full range flux is significantly above the flux given by the P2008 power law at young ages and approaches later the P2008 upper limit. Removing the short wavelength range (0.1–2 nm, dashed line) reduces the stellar flux at young ages by a factor of $\sim 2$. Comparing the EUV flux of R2005 (10–120 nm, dashed-dotted line) with the P2008 power law shows that the R2005 EUV flux is close to the observed upper limit of the P2008 SXR flux. Therefore, the SXR flux evolution over time can be taken as a good proxy for the EUV flux evolution.

Fig. 1.

Average $F_{\mathrm{SXR}(\mathrm{EUV})}$ flux distribution of G-stars as a function of age at CoRoT-7b's and Kepler-10b's orbital distance (Penz et al., 2008b; Lammer et al., 2009) is shown in both panels (solid line—average G-star flux evolution, shaded area—average G-star flux evolution $\pm 1\sigma$). Upper panel: Comparison with Ribas et al. (2005) X-ray evolution (dashed line: 0.1–10 nm, dotted line: 2–10 nm). Lower panel: Comparison with Ribas et al. (2005) XUV (dotted line: 0.1–120 nm, dashed line: 2–120 nm) and EUV (dash-dotted line: 10–120 nm) evolution. One can see that the EUV evolution for solar-like stars is well approximated by the upper limit of the SXR distribution. Thus, the EUV evolution of cooler G stars, like CoRoT-7, can be approximated by the mean or lower limit G star SXR distribution.

These comparisons clearly demonstrate that the main contribution to the high XUV flux for the R2005 power law (full range) at young ages is the flux at short wavelengths (0.1–2 nm) and partly also the rest of the X-ray region. As R2005 used only solar analogs (i.e. early-type G-stars) for their study, whereas CoRoT-7b is a late-type G-star, it is very likely that its host star's EUV flux evolution can be well approximated by the mean to lower limits of the P2008 SXR flux evolution.

As one can see from Fig. 1a and b the flux below 100 Myr is taken to be constant. The reason for this is that the stellar flux cannot increase to infinity, or in other words the stellar X-ray and EUV flux which is a result of coronal energy generation by magnetically active regions (Güdel, 2007) is limited by the finite surface area of the star which is available for filling with magnetically active regions. A saturation effect occurs which is established by observations of very young pre-main sequence and main-sequence stars. According to Güdel (2007) the X-ray output of a stellar corona depends on the magnetic energy the star holds and is, therefore, a consequence of the dynamo. Stellar magnetic activity is correlated with the rotation period of the star. Due to angular momentum loss the star spins down resulting in a longer rotation period and, therefore, a lower level of magnetic activity. This causes the star to leave the saturation regime.

Davis and Wheatley (2009) computed thermal mass loss rates taking into account the spectral type dependence of the duration of the stellar saturation regime. Their adopted value for the end of the saturation regime was 100 Myr for G-stars, therefore, we will also use this value.

4. Thermal mass loss of hypothetical hydrogen-rich exoplanets at CoRoT-7b's and Kepler-10b's orbital location

In our mass loss model planetary mass, planetary radius, and planetary density vary over time. Fig. 3 shows how these parameters change in response to each other. The calculations shown in these plots are made for the gas giant Tres-4b which is set to 0.017 AU. We use the mean P2008 law corresponding to a G-star evolution and an initial density of 0.2 g cm⁻³, and let evolve this planet over 2 Gyr. Starting at 0.01 Gyr the initial planetary mass decreases sharply within the first Gyr (lower right panel). Also the planetary radius decreases sharply (upper left panel), as well as the mass loss enhancement factor 1/K (lower left panel). In contrast, planetary density increases with evolving time (upper right panel).

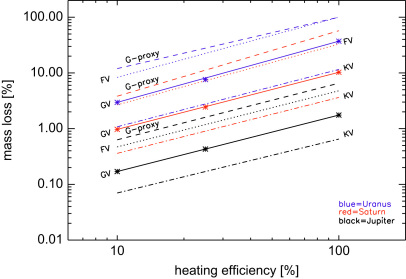
The integrated thermal mass loss (0.01–5 Gyr; upper boundary due to general low level of stellar activity and, therefore, assumed negligible mass loss - see Fig. 5; lower boundary, cf. Section 2) as a function of heating efficiency for hypothetical exoplanets which resemble our hydrogen-rich gas and ice giants like Jupiter (${\rho }_{\mathrm{pl}}=1.326\mathrm{g}{\mathrm{cm}}^{-3}$) (black), Saturn (${\rho }_{\mathrm{pl}}=0.687\mathrm{g}{\mathrm{cm}}^{-3}$) (red), and Uranus (${\rho }_{\mathrm{pl}}=1.27\mathrm{g}{\mathrm{cm}}^{-3}$) (blue) is shown in Fig. 2 for a K (dashed-dotted line), G (solid line), and F-type host star (dotted line). This figure shows that planets with lower initial masses experience enhanced thermal mass loss. If we assume a heating efficiency of 25%, a G-type host star and integrate over 5 Gyr, a Jupiter-like test-planet yields negligible thermal mass loss of only about 0.5% of its initial mass, followed by Saturn ($<3\%$) and Uranus (7.6%). For investigating the influence of the EUV flux on the mass loss rate we model the thermal escape also with the EUV power law given by Ribas et al. (2005) (R2005: dashed lines). One can see that the R2005 power law yields much higher mass loss rates than the P2008 law, but they are still not sufficient to evaporate a Jovian-type or Saturn-type gas giant down to its core. We also note that the test planets lose most of their mass during the first Gyr when the EUV flux of a star is the highest.

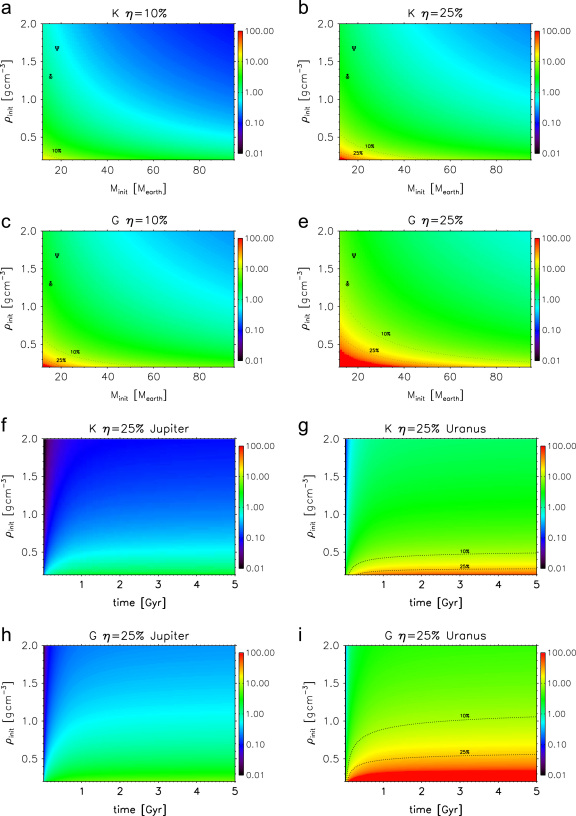
Fig. 5.

Mass loss of exoplanets (four upper panels) ranging from 12 to $95M_{\mathrm{Earth}}$ (initial masses) versus density in the range of 0.2–2 g cm⁻³. All exoplanets are set to an orbital location of 0.017 AU. The integration time of the mass loss calculations is between 10 Myr and 5 Gyr and the heating efficiency is 10 and 25%, respectively. As host stars we consider two cases, namely a $0.93M_{\mathrm{Sun}}$ K-star (corresponding to the lower limit of the P2008 law, cf. 1) and a $0.93M_{\mathrm{Sun}}$ G-star (corresponding to the mean P2008 law, cf. 1). The stellar EUV evolution is described by the P2008 laws. Two Solar System hydrogen-rich ice giants are overplotted (Uranus and Neptune). The four lower panels show the thermal mass loss as a function of time and initial planetary density for a Jupiter- and Uranus-mass exoplanet located at an orbital distance of 0.017 AU and computed for a heating efficiency of 25%. The different colors correspond to different percentages of planetary mass loss. Black: no mass loss (0%), red: a core mass of $5M_{\mathrm{Earth}}$ remains (100%). The black dotted lines correspond to 10 and 25% of thermal planetary mass loss.

Fig. 2.

Shown is the thermal mass loss (in % of the initial planetary mass) integrated between 10 Myr after the planets origin to 5 Gyr for a K-star (dashed-dotted line), G-star (solid line), and F-star scenario for Jupiter (black), Saturn (red), and Uranus (blue) at an orbital distance of 0.017 AU, in dependence of heating efficiency. The effect on the mass loss depending on the R2005 (dashed line) compared to the P2008 EUV evolution power laws is also shown.

From these calculations we can conclude that hydrogen-rich hot gas giants in the Jupiter- and Saturn-size and mass range would have experienced negligible mass loss rates at the orbital distance of CoRoT-7b and Kepler-10b. If we assume that the host star is a K-type star, the EUV driven escape rates would be even lower. None of such planets would evaporate their hydrogen envelopes totally, even if one assumes the improbable upper limit for the energy-limited case of $\eta =100\%$.

Lammer et al. (2009) have shown that the initial planetary density of a hydrogen-rich close-in gas giant combined with the Roche lobe effect (Erkaev et al., 2007) plays an important role in thermal mass loss of “Hot Jupiters”. The gas and ice giants in the Solar System correspond to planets with densities between $\approx 0.7$ and $1.64\mathrm{g}{\mathrm{cm}}^{-3}$. We know from transit and radial velocity observations that low density gas giants like Tres-4b or CoRoT-5b with densities of about 0.2 and 0.27 g cm⁻³ exist. To study the possibility that CoRoT-7b and Kepler-10b could be remnants of more massive gas or ice giants with lower initial densities, we investigate how this parameter influences a hypothetical exoplanet sample within an initial mass range of $12–95M_{\mathrm{Earth}}$ and a density range of 0.2–2.0 g cm⁻³ at the orbital distance of $\sim 0.017\mathrm{AU}$.

The results are shown in Fig. 5 where the different colors correspond to different percentages of planetary mass loss for an integration time of 0.01–5 Gyr, from black (no mass loss: 0%) to red (100%: a core mass of $5M_{\mathrm{Earth}}$ remains). For a heating efficiency of $\eta =25\%$ a higher mass loss occurs for masses below $\sim 15M_{\mathrm{Earth}}$ (K star) and $\sim 20M_{\mathrm{Earth}}$ (G star), for initial planetary densities of $\sim 0.2–0.3\mathrm{g}{\mathrm{cm}}^{-3}$ and $\sim 0.2–0.7\mathrm{g}{\mathrm{cm}}^{-3}$, respectively (see upper panels of Fig. 5). One can see that the most affected planets would be low density “Hot Neptune” or “Hot Uranus”-class objects. For a heating efficiency of $\eta =10\%$ no planet would lose its hydrogen envelope by thermal escape completely if they orbit at 0.017 AU a K star. Only low density “Hot sub-Uranus”-type exoplanets may lose 100% of their initially assumed hydrogen inventories if they orbit a G star.

The tested XUV flux estimations in this study are (a) the lower limit of the P2008 distribution (K-star scenario), (b) the mean P2008 distribution (G-star scenario), (c) the upper limit of the P2008 distribution (F-star scenario), and finally (d) the R2005 law (solar analog scenario). For the case of CoRoT-7b the mean P2008 law fits best to the spectral type of CoRoT-7 (G8 V) as stellar luminosity of K and M-stars is lower than for G-stars (Wood et al., 1994). In Fig. 2 the influence of all these XUV flux estimations on the mass loss can be seen best (see second paragraph of this chapter).

The lower four panels in Fig. 5 show the thermal mass loss as a function of time and initial planetary density for Jupiter- and Uranus-mass planets orbiting K and G-type stars at both planets orbital location and assuming a heating efficiency of $\eta =25\%$. One can see that for a Jupiter-mass planet ($318M_{\mathrm{Earth}}$) and initial density of $\sim 0.5\mathrm{g}{\mathrm{cm}}^{-3}$ the thermal mass loss lies below 1% if the host star is of the K spectral type. The maximum thermal mass loss for a Jupiter-mass planet with the same parameters (for the lowest possible density in the plot of 0.2 g cm⁻³) is $\sim 2.4\%$ or about $8M_{\mathrm{Earth}}$. If we switch from a K to a G star, the maximum loss increases to 6.7% which corresponds to about $21M_{\mathrm{Earth}}$. The maximum thermal mass loss from a Uranus-mass planet with a low initial density of 0.2 g cm⁻³ is 100%, even if we increase the initial density to 0.3 g cm⁻³. When the test planet's initial density reaches 0.34 g cm⁻³, it cannot totally lose its hydrogen envelope ($\mathrm{\Delta }{M}_{\mathrm{pl}}/{M_{\mathrm{pl}}}_{\eta =25\%}$ $\sim 75\%$). In contrast, the maximum thermal mass loss of Uranus with its original density results in 7.6% (see Fig. 2). From these figures one can clearly see that the initial density of a hydrogen-rich hot exoplanet plays a major role in its temporal evolution in accordance with Eq. (1).

In Fig. 4 we show which initial planetary parameters are needed to reach masses and densities of the transiting exoplanets CoRoT-7b and Kepler-10b. For the computation of the thermal hydrodynamic mass loss we use the P2008b G-star law together with a heating efficiency of 25%. The upper left panel shows the evolution of the radii of both planets over the current ages. The differently shaded areas indicate the ranges (upper and lower limits) of the parameters of interest. The range of CoRoT-7b is indicated by dark gray shaded areas (lower and upper limits are indicated by solid lines), whereas the range of Kepler-10b is indicated by light gray shaded areas (lower and upper limits are indicated by dotted lines). The radii of both planets start in the range of $2.6–3.0R_{\mathrm{earth}}$ and reach the approximate current planetary radii after 2 and 11.9 Gyr, respectively.

The upper right panel shows the evolution of planetary density. Our calculations show that the initial densities seem to be much lower at a starting time of 10 Myr (in the range of $\sim 1.2$ and 2.7 g cm⁻³ for both exoplanets) than the current densities of CoRoT-7b and Kepler-10b. The mass loss enhancement factor 1/K, as shown in the lower left panel, is most effective for both exoplanets at small ages corresponding to phase I (10–100 Myr) of our calculations. Planetary density increases during planetary evolution and consequently the 1/K factor decreases (see also Section 5) as it is a function of density.

The lower right panel shows the evolution of the masses of CoRoT-7b and Kepler-10b. For the upper mass limit of CoRoT-7b only $0.4M_{\mathrm{earth}}$ are lost due to thermal hydrodynamic escape and for the lower mass limit the mass loss increases to $\sim 1M_{\mathrm{earth}}$. In case of Kepler-10b, $0.7M_{\mathrm{earth}}$ are lost for the upper mass limit, for the lower mass limit $1.4M_{\mathrm{earth}}$ are lost. As one can see from this comparison, the amount of lost mass of CoRoT-7b and Kepler-10b during their evolution is nearly the same.

The planetary radius decreases with time as planetary atmospheric mass is lost, resulting in an increasing planetary density. Fig. 4 supports the scenario of CoRoT-7b and Kepler-10b having had hydrogen-rich atmospheres (up to $2.6–3.0R_{\mathrm{earth}}$ and initial densities in the range of $\sim 1.2$ and 2.7 g cm⁻³) in their early phases which were evaporated during their evolution, resulting in the currently known parameters of these planets.

5. Discussion

As described in Section 2, V2010 and J2010 investigated the composition and thermal mass loss from CoRoT-7b and obtained according to their rough assumptions much higher mass loss rates compared to our results (Figs. 2 and 5). For evaporating a Jupiter-type gas giant, both studies estimated the thermal mass loss from CoRoT-7b by using the same modified energy-limited approach of Erkaev et al. (2007). J2010 applied higher values for heating efficiency and V2010 used lower integration limits, as well as different evolution of stellar XUV radiation and planetary radius/density. In addition, J2010 considered the influence of tidal evolution on CoRoT-7b's orbit.

Thus both studies do not rule out that CoRoT-7b could be the stripped core of a gas giant.

Comparing the results of their calculations with ours, we may note the following main differences:

• •
  using higher heating efficiencies

  • $○$
    40% (V2010),
  • $○$
    100% (J2010) for their maximum mass loss (200 Earth masses), for heating efficiencies $<25\%$ it is not possible to evaporate a Jovian-type gas giant.
• •
  assuming a different evolution of planetary radius/density

  • $○$
    a constant planetary density (V2010) which results in a constant value of 1/K,
  • $○$
    modelled mass-radius relations (J2010) of Fortney et al. (2007).
• •inclusion of tidal evolution of the orbit (J2010) with a poorly constrained dissipation parameter in the order of at least two magnitudes,
• •assuming a different power law which yields higher fluxes for the EUV flux and which is based on observations of a few solar proxies (Ribas et al., 2005),
• •
  using different lower integration limits for the mass loss,

  • $○$
    0 Gyr (V2010), which includes planetary formation period during the first tens of millions of years,
  • $○$
    100 Myr (J2010).
• •application of the mass loss equation from Erkaev et al. (2007) to the evaporation of rocky materials (J2010).

If we use our approach with the G-star power law of R2005, we can see that the major difference between our results and V2010's comes from their assumption of a constant planetary density. In our calculations the planetary density changes by more than 50% (for Saturn, Uranus, Neptune, and CoRoT-7b), indicating that its temporal evolution cannot be neglected. The difference is related to the mass loss enhancement factor (1/K-factor) due to the tidal forces, which is a function of density and decreases during planetary evolution as the density increases. By assuming a constant planetary density, one keeps the 1/K-factor at an artificially low level during early ages which reduces the resulting mass loss. However, the choice by V2010 of a higher heating efficiency and the R2005 law, combined with the assumption of a lower integration limit of 0 Gyr, results in a net mass loss higher than in our calculations.

J2010 do not exclude that CoRoT-7b could be the remnant of a hot gas giant, but only by using a heating efficiency of 100% and by applying the mass loss equation by Erkaev et al. (2007) to the rocky core, although the equation is only valid for hydrogen-rich atmospheres. However, their results for lower, more realistic heating efficiencies (10% and 25%) would yield mass loss values from which one can draw the conclusion that exoplanets such as CoRoT-7b could only be the remnant of a Uranus-mass planet.

For the estimation of the thermal mass loss of CoRoT-7b one can expect that the P2008 power law suits better due to the origin of the law and due to the fact that the host star of CoRoT-7b was characterized as a late G/early K-star, close to Kepler-10. As expected from Fig. 1, the application of the R2005 power law leads to significantly higher mass loss compared to the results obtained by using the P2008 law (see also Fig. 2). As one can see from Fig. 5, the lower is the initial density, the higher is the mass loss, which is in complete agreement with the mass loss Eq. (1). So, the density variation indeed plays a more important role than the mass of the planet.

By considering appropriate heating efficiencies and EUV flux evolution scenarios, the results of our study indicate that one can most likely exclude a hypothesis that CoRoT-7b Kepler-10b may be remnants of thermally evaporated hydrogen-rich, Jovian-type gas giants. According to our calculations the two other possibilities suggested by V2010 cannot be discarded, but the terrestrial origin of such bodies appears to be the most likely.

Other recent studies also cast doubts on the possibility that CoRoT-7b started out as a Jupiter-like gas giant. Murray-Clay et al. (2009) suggested that complete evaporation of a Jupiter-mass planet's atmosphere may require unrealistically large heating efficiencies. Lammer et al. (2009) suggested that, even if CoRoT-7b could begin with a significant gaseous envelope, its original mass was probably less than Neptune's which could be explained by much lower EUV radiation fluxes used in that study.

The present study investigates the thermal hydrodynamic escape from CoRoT-7b and Kepler-10b but neglects any non-thermal processes. Lammer et al. (2009) have shown that non-thermal stellar plasma induced H⁺ pick-up erosion of a non- or weakly magnetized “Hot Jupiter” is most likely negligible. Due to the high stellar XUV flux, extended ionospheres are produced. The finding of these authors indicate that the ion pressure in these ionospheres is strong enough so that the stellar plasma ram pressure can be balanced at distances of a few planetary radii, resulting in negligible atmospheric erosion rates over evolutionary timescales.

In case of a rocky body which lost its hydrogen envelope such as CoRoT-7b and most likely Kepler-10b a study by Mura et al. (2011) sheds some light on the non-thermal escape of evaporating surface minerals such as Na, Ca⁺, and Mg⁺. These authors found a loss rate in the range of 4.58×10⁵–1.25×10⁶ g s⁻¹ depending on the assumed exospheric temperatures. By comparing these loss rates with hydrogen loss rates modelled for Jovian-type gas giants in the orders of $\ge {10}^{10}\mathrm{g}{\mathrm{s}}^{-1}$ (Yelle, 2004; Penz and Micela, 2008; Lammer et al., 2009) one can clearly see that the loss rate of evaporated heavy surface elements is more than five orders of magnitudes lower.

Observations of CoRoT-7b and Kepler-10b are certainly needed to verify the previously made assumptions. Right after its discovery, CoRoT-7b was observed by ESOs (European Southern Observatory) VLT (Very Large Telescope). Using UVES (Ultraviolet and Visual Echelle Spectrograph), high resolution spectroscopy was performed (Günther et al., 2011) with the aim of detecting for the first time narrow lines in the exosphere which CoRoT-7b is expected to have. Surprisingly, none of the expected exospheric lines like Ca I, Ca II, and Na were detected, only upper limits could be set. As these observations failed to confirm that CoRoT-7b has properties similar to Mercury, any similarities to the solar system planets are questionable.

6. Conclusions

Our results indicate that close-in rocky exoplanets like CoRoT-7b and Kepler-10b cannot be remnants of thermally evaporated hydrogen-rich gas giants. Even Uranus-type ice giants can be excluded (unless an unrealistic heating efficiency of 100% is applied) as progenitors of CoRoT-7b and Kepler-10b. In our view, which is supported by our calculations of the thermal mass loss, it is most likely that CoRoT-7b and Kepler-10b have never been gas or ice giants which have lost their entire hydrogen envelope, but started their evolution as “super-Earths” which may have lost a rather thin hydrogen atmosphere.