Neuromorphic Silicon Neurons and Large-Scale Neural Networks: Challenges and Opportunities

Neuromorphic Silicon Neurons: State of the Art

Complementary metal-oxide-semiconductor (CMOS) transistors are commonly used in very-large-scale-integration (VLSI) digital circuits as a basic binary switch that turns on or off as the transistor gate voltage crosses some threshold. Carver Mead first noted that CMOS transistor circuits operating below this threshold in current mode have strikingly similar sigmoidal current–voltage relationships as do neuronal ion channels and consume little power; hence they are ideal analogs of neuronal function (Mead, 1989). This unique device physics led to the advent of “neuromorphic” silicon neurons (SiNs) which allow neuronal spiking dynamics to be directly emulated on analog VLSI chips without the need for digital software simulation (Mahowald and Douglas, 1991). In the inaugural issue of this Journal, Indiveri et al. (2011) review the current state of the art in CMOS-based neuromorphic neuron circuit designs that have evolved over the past two decades. The comprehensive appraisal delineates and compares the latest SiN design techniques as applied to varying types of spiking neuron models ranging from realistic conductance-based Hodgkin–Huxley models to simple yet versatile integrate-and-fire models. The timely and much needed compendium is a tour de force that will certainly provide a valuable guidepost for future SiN designs and applications.

Neuromorphic Silicon Neurons vs. Digital Neural Simulations

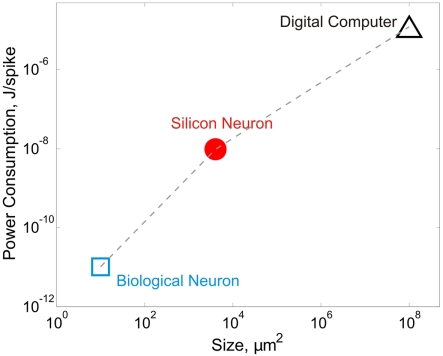
For all the impressive technical feats in neuromorphic engineering, a basic question often from those uninitiated to the field is: why SiN? To be sure, neural modeling “in silico” as practiced today is still largely digital software-based rather than analog silicon chip-based, and for obvious reasons. Digital simulation enjoys double-precision and virtually noise-free numerical outputs that are highly reproducible and readily re-programmable; certainly no way with analog. However, this archetypal reasoning misses the fact that neural computing itself is inherently analog and noisy/variable even though neuron-to-neuron communication is predominantly digital via all-or-none spiking. Computational precision and repeatability are really the least of a neuron's concerns. Instead, biological neural networks excel in performing massive high-speed computations in parallel under noisy and variable environments, all at minute power consumption within a tiny anatomic space. By contrast, even today's most high-power supercomputing clusters cannot simulate neocortical or thalamocortical connectivity in real time (Markram, 2006; Izhikevich and Edelman, 2008; Ananthanarayanan et al., 2009). In comparison, SiNs offer a practical computational medium that is intermediate between biological neurons and digital computers in terms of power and space efficiencies, and is orders of magnitude faster than real neurons in terms of computing speed (Figure 1). Unlike numerical simulation on general-purpose serial computers, computation delay of analog SiN circuits is independent of network size except for signal propagation. SiNs will therefore be most useful when large-scale dedicated neural computing is desired in real time and under stringent power and space/weight constraints, such as in neuroprosthetic, brain–computer interface, or embedded machine intelligence applications.

Figure 1.

Biological and silicon neurons have much better power and space efficiencies than digital computers. A biological neuron consumes approximately 3. 84 × 10⁸ ATP molecules in generating a spike (Attwell and Laughlin, 2001; Lennie, 2003). Assuming 30–45 kJ released per mole of ATP (Berg et al., 2007; or 5–7.5 × 10⁻²⁰ J per ATP molecule), the energy cost of a neuronal spike is in the order of 10⁻¹¹ J. The density of neurons under cortical surface in various mammalian species is ~100,000/mm² (Braitenberg and Schüz, 1998), which translates to a span of ~10 μm² per neuron. Silicon neurons have power consumption in the order of 10⁻⁸ J/spike on a biological timescale. For example, an Integrate-and-Fire neuron circuit consumes 3–15 nJ at 100 Hz (Indiveri, 2003) and a compact neuron model consumes 8.5–9.0 pJ at ~1 MHz (Wijekoon and Dudek, 2008), which translates to 85–90 nJ at 100 Hz. For silicon neurons, the on-chip neuron area is estimated to be ~4,000 μm² (70 μm × 40 μm in Wijekoon and Dudek, 2008, ~3750 μm² in Vogelstein et al., 2007, and 70 μm × 70 μm in Wijekoon and Dudek, 2009). According to Liu and Delbrück (2007), digital computers are 10⁴–10⁸ less efficient than biological neurons. The power efficiency of digital computers is therefore estimated to be 10⁻³–10⁻⁷ J/spike. Most current multi-core digital microprocessor chips have dimensions from 263 to 692 mm². A single core has an average size from ~50 to ~90 mm².

Building Robust Large-Scale Iono-Neuromorphic Silicon Neural Networks

Emulating neuronal spiking on SiNs is only the first step in neuromorphic modeling. Building large-scale SiN networks on VLSI chips to mimic complex brain functions remains a great challenge, not least because subthreshold CMOS circuits are notoriously highly susceptible to mismatch in transistor threshold voltage and current factor caused by fabrication imperfections and temperature variations (Pavasovic et al., 1994; de Gyvez and Tuinhout, 2004; Kinget, 2005; Andricciola and Tuinhout, 2009). The intrinsic VLSI process variability severely limits the scalability of SiN networks since it is not practicable to fine-tune a large number of analog transistor circuits to correct for mismatch on chip after fabrication. Although SiN designs that operate in the above-threshold regime are less sensitive to transistor mismatch (Indiveri et al., 2011), such circuits require much higher currents and power consumption (several orders of magnitude higher), and are non-ideal for VLSI fabrication at a high transistor density.

Another layer of complexity for large-scale neuromorphic modeling is the need for biological realism as constrained by experimental data (Markram, 2006; Djurfeldt et al., 2008). Biological neural networks are not just a large collection of spiking neurons interconnected via plastic chemical synapses or gap junctions (Sporns et al., 2005; DeFelipe, 2010). Instead, neurons and glia cells are endowed with a panoply of membrane and intracellular properties which confer a myriad of complex glial/neuronal, dendritic, axonal, and synaptic dynamics at the cellular level and resultant emergent dynamics at the network level. Such multiscale spatiotemporal dynamics in large-scale SiN networks are difficult to emulate on chip because of inevitable transistor mismatch which may vary across the entire VLSI network. To put this in perspective, traditional subthreshold current-mode differential pair circuits commonly used for emulating the sigmoidal current–voltage relationship of ion channels have a limited input voltage dynamic range of < ±100 mV. Since typical CMOS threshold voltage may vary by ±20 mV (3 standard deviations) or more (ITRS, 2007), the worst-case mismatch errors for single devices could be in excess of 100 mV or 100% across the chip and may be further compounded as network size increases and the temperature varies especially for deep submicron processes. Similar dynamic range limitations also apply to other basis circuits such as transconductance amplifier, translinear multiplier, current mirror, etc. Although integrate-and-fire models of neuronal spiking and bursting behaviors are more amenable to implementation on chip because of their simplicity (Indiveri et al., 2011), these phenomenological SiN models are non-mechanistic and their requisite parameter settings are not readily adjustable en masse post-fabrication or during computation in response to changes in neuronal inputs. Indeed, all subthreshold circuits including phenomenological SiN circuits are subject to similar threshold voltage mismatch limitations regardless of whether they are designed in voltage or current mode, although the sensitivity of phenomenological circuits to mismatch has not been systematically evaluated.

To circumvent these difficulties, a novel subthreshold current-mode circuit design approach has been recently proposed that emphasizes the importance of a wide dynamic range for input voltages in neuromorphic modeling of ion channel and intracellular ionic dynamics (iono-neuromorphic dynamics) in large-scale SiN networks (Rachmuth and Poon, 2008). With judicious circuit designs using source degeneration and other negative feedback techniques, the dynamic range for input voltages of neuromorphic ion channels and other circuits has been extended to >1 V, making them much more robust to mismatch errors. The increased robustness of subthreshold SiNs significantly improves the scalability of iono-neuromorphic networks and allows more faithful reproduction of complex neuronal dynamics, such as chaotic bursting in pacemaker neurons (Rachmuth and Poon, 2008).

Next-Generation Large-Scale Iono-Neuromorphic Silicon Neural Networks

Current subthreshold SiN circuits are susceptible to mismatch because they rely on commercial CMOS processes that are intended for mainstream performance-driven VLSI digital circuits rather than analog or mixed-signal electronics. The good news is that the trend is rapidly changing in recent years due to phenomenal demands for low-power system-on-chip (SoC) applications such as smartphones, wearable electronics, portable medical devices, etc. Processes that are dedicated to low-power subthreshold SoC circuits are already on the horizon. For example, a newly available fully depleted silicon-on-insulator technology optimized for ultra-low-power subthreshold circuit applications allows significant reduction in threshold voltage variation and device capacitance when compared with conventional CMOS transistors (Vitale et al., 2011). This novel subthreshold CMOS technology is already making its way to iono-neuromorphic analog VLSI circuits (Meng et al., 2011).

As the performance of subthreshold SiNs continues to improve, the scale of SiN networks will be ultimately limited at the chip level only by the ever-growing capacity of VLSI technology. The recent introduction of the 22-nm bulk CMOS three-dimensional (non-planar) Tri-Gate process (Intel, 2011) brings a new dimension to VLSI device scaling that is likely to continue to fuel Moore's Law for the next decade. Concurrently, recent advances in three-dimensional integrated circuit technology have made it possible to stack multiple interconnected bulk CMOS dies on top of one another, allowing increased effective VLSI footprint with dramatically shortened interconnect wire lengths (Davis et al., 2005; Mak et al., 2011). These enabling technologies open new and exciting avenues for the next generation of large-scale iono-neuromorphic SiN networks.

Another emerging approach to large-scale neuromorphic modeling employs nanotechnologies such as nanowires, carbon nanotubes, memristors, etc. as the computational analog, either independently or in combination with CMOS technology. For example, memristor-based neuromorphic devices have been recently reported that are capable of emulating spike-timing-dependent synaptic plasticity in a crossbar network with massive connectivity between CMOS-based SiNs (Jo et al., 2010; Zamarreno-Ramos et al., 2011). Despite their promise, these nanocircuits are still fraught with similar (if not greater) problems of non-robustness as CMOS devices, and are less efficient in terms of yields and other performance benchmarks (Chau et al., 2005). From a neuroscience perspective, a fundamental drawback of such nano-sized neuronal analogs is that they are largely phenomenological (artificial) rather than iono-neuromorphic (realistic) models of neuronal function. Future neuromorphic modeling efforts should therefore target not only the integration density and computation and/or power efficiencies of the neuronal analogs (Figure 1) but also their degree of biological realism and robustness, if the full glory of the brain is ever to be captured on chip.