Calcium Cooperativity of Exocytosis as a Measure of Ca²⁺ Channel Domain Overlap

Abstract

The number of Ca²⁺ channels contributing to the exocytosis of a single neurotransmitter vesicle in a presynaptic terminal has been a question of significant interest and debate, and is important for a full understanding of localized Ca²⁺ signaling in general, and synaptic physiology in particular. This is usually estimated by measuring the sensitivity of the neurotransmitter release rate to changes in the synaptic Ca²⁺ current, which is varied using appropriate voltage-clamp protocols or via pharmacological Ca²⁺ channel block under the condition of constant single-channel Ca²⁺ current. The slope of the resulting log-log plot of transmitter release rate versus presynaptic Ca²⁺ current is termed Ca²⁺ current cooperativity of exocytosis, and provides indirect information about the underlying presynaptic morphology. In this review, we discuss the relationship between the Ca²⁺ current cooperativity and the average number of Ca²⁺ channels participating in the exocytosis of a single vesicle, termed the Ca²⁺ channel cooperativity. We relate these quantities to the morphology of the presynaptic active zone. We also review experimental studies of Ca²⁺ current cooperativity and its modulation during development in different classes of synapses.

Introduction

Synaptic neurotransmitter release and endocrine hormone secretion are fundamental physiological processes, and there has been sustained interest and active research aimed at understanding better the steps leading from Ca²⁺ entry to exocytosis. Synaptic transmitter release occurs from active zones, which contain Ca²⁺ channels and transmitter-filled vesicles docked at release sites. The arrangement of channels and vesicles is important in the release process, since exocytosis is evoked by Ca²⁺ that enters the synaptic terminal through voltage-dependent Ca²⁺ channels (Llinás et al., 1981; Stanley, 1993) and remains highly localized to the channels’ Ca²⁺ domains (Augustine et al., 2003; Chad and Eckert, 1984; Fogelson and Zucker, 1985; Neher, 1998a; Simon and Llinas, 1985). However, it is exceedingly difficult to determine active zone morphology due to the small size of the active zone. Even in cases where such morphological information has been determined in detail using freeze-fracture combined with electron or atomic force microscopy, for instance at the frog neuromuscular junction (Ceccarelli et al., 1979; Harlow et al., 2001; Heuser et al., 1979; Pumplin et al., 1981; Stanley et al., 2003), there remains a lack of complete knowledge of the number of functional channels that open per action potential per vesicle, and the contribution of individual channels to vesicle release. Given this limitation in the direct measurement of functional active zone morphology, indirect techniques are used to estimate the number of Ca²⁺ channels contributing to an exocytotic event, which we will refer to below as the Ca²⁺ channel cooperativity. These techniques consist of varying the number of channels that open during a stimulus while measuring both the presynaptic Ca²⁺ current and the release of transmitter through either presynaptic capacitance measurements or postsynaptic measurements. Typically, a log-log plot of the release variable and the presynaptic Ca²⁺ current is made, and the slope of the plot is determined (see e.g. (Bucurenciu et al., 2010; Fedchyshyn and Wang, 2005; Kochubey et al., 2009; Mintz et al., 1995; Quastel et al., 1992; Wu et al., 1999)). This slope, the Ca²⁺ current cooperativity, provides indirect information about the mean number of channels contributing to each exocytotic event and the active zone morphology. A large Ca²⁺ current cooperativity suggests that many channels contribute to exocytotic events, while a small Ca²⁺ current cooperativity is usually understood to mean that release is gated by just a few proximal channels. In particular, a Ca²⁺ current cooperativity near 1 is often taken as an indication that each exocytotic event is gated by the opening of a single channel (reviewed in (Gentile and Stanley, 2005; Schneggenburger and Neher, 2005)).

Measurements of the Ca²⁺ current cooperativity have been used to infer information about synaptic morphology in a wide variety of synapses, including the squid giant synapse (Augustine and Charlton, 1986; Augustine et al., 1991; Llinás et al., 1981), sensory ribbon synapses (Brandt et al., 2005; Coggins and Zenisek, 2009; Jarsky et al., 2010; Johnson et al., 2008; Keen and Hudspeth, 2006; Thoreson et al., 2004), motor nerve terminals (Quastel et al., 1992; Shahrezaei et al., 2006; Yoshikami et al., 1989), the rodent calyx of Held (Borst and Sakmann, 1996; Fedchyshyn and Wang, 2005; Kochubey et al., 2009; Sakaba and Neher, 2001; Wu et al., 1998; Wu et al., 1999) and other central synapses (Bucurenciu et al., 2010; Gentile and Stanley, 2005; Mintz et al., 1995). Theoretical studies have also explored this experimental assay (Bertram et al., 1999; Bucurenciu et al., 2010; Coggins and Zenisek, 2009; Matveev et al., 2009; Meinrenken et al., 2002; Quastel et al., 1992; Shahrezaei et al., 2006; Yoshikami et al., 1989; Zucker and Fogelson, 1986). The first aim of this review is to clarify what information is actually provided by the Ca²⁺ current cooperativity, and to contrast this with the Ca²⁺ channel cooperativity, which is only indirectly inferred from current cooperativity measurements. The second aim is to review Ca²⁺ current cooperativity studies and focus on several cases in which the current cooperativity has been used to obtain important information on active zone morphology or changes in morphology.

Biochemical Ca²⁺ Cooperativity of Exocytosis

Measurements of the Ca²⁺ current cooperativity that reflects active zone morphology first arose in investigating the biochemical (intrinsic) Ca²⁺ cooperativity of release introduced by Dodge and Rahamimoff (Dodge and Rahamimoff, 1967), which is independent of synaptic morphology. The latter measure, which we denote by n, provides a lower bound on the number of Ca²⁺ binding steps required to evoke vesicle fusion (Dodge and Rahamimoff, 1967). The most direct biochemical cooperativity measurement technique uses caged-Ca²⁺ compounds to raise the Ca²⁺ concentration almost uniformly throughout the synaptic terminal and Ca²⁺ imaging to measure the internal Ca²⁺ concentration (Beutner et al., 2001; Bollmann et al., 2000; Kochubey et al., 2009; Lando and Zucker, 1994; Schneggenburger and Neher, 2000). A less direct approach is to vary the extracellular Ca²⁺ concentration [Ca²⁺]_ext, which will affect Ca²⁺ influx through all open Ca²⁺ channels, and increase the intracellular Ca²⁺ concentration (Augustine and Charlton, 1986 ; Borst and Sakmann, 1996; Dodge and Rahamimoff, 1967; Katz and Miledi, 1970; Lester, 1970; Llinás et al., 1981; Mintz et al., 1995; Stanley, 1986). The biochemical cooperativity is then obtained using the log-log slope of the Ca²-secretion curve:

$$n=\frac{\mathit{d}logR}{dlog[Ca]}$$ (1)

where [Ca] represents the concentration of either intracellular or extracellular Ca²⁺, varied in a non-saturating range. Alternatively, some studies define n as the parameter of the Hill-function fit to the entire saturating Ca²⁺-release curve (Jarsky et al., 2010; Sakaba and Neher, 2001). However, in the absence of a biological argument for such a functional relationship, the definition given by Eq. (1) is preferable because it is model-independent (Quastel et al., 1992). The measurement of n does not depend on the number of Ca²⁺ channels that open during the stimulus, so it provides no information on the active zone morphology. Instead, it measures the intrinsic Ca²⁺ sensitivity of transmitter release, and its value ranges from 1 to 5 across different preparations (Augustine et al., 1985; Augustine and Charlton, 1986; Bollmann et al., 2000; Borst and Sakmann, 1996; Brandt et al., 2005; Dodge and Rahamimoff, 1967; Duncan et al., 2010; Llinás et al., 1981; Mintz et al., 1995; Reid et al., 1998; Schneggenburger and Neher, 2000; Stanley, 1986). Values of n greater than one obtained in many synapses suggest that exocytosis requires the binding of several Ca²⁺ ions to proteins gating release, possibly Synaptotagmin, a well-described Ca²⁺ sensing protein that is also a component of the SNARE protein complex, and plays a key role in the gating of transmitter release (Fernandez-Chacon et al., 2001; Geppert et al., 1994; Nagy et al., 2006; Pang et al., 2006; Stevens and Sullivan, 2003; Xu et al., 2007). Isoforms 1, 2, and 9 all have five Ca²⁺ binding sites, with three on the C2A domain and two on the C2B domain of the protein (see (Rizo and Rosenmund, 2008) for review). Note that several studies of sensory ribbon synapses suggest a non-cooperative, linear relationship between release and [Ca²⁺], and suggest an involvement of a different Ca²⁺ release sensor, possibly otoferlin (Dulon et al., 2009; Keen and Hudspeth, 2006; Roux et al., 2006; Thoreson et al., 2004) or non-neuronal synaptotagmin IV (Johnson et al., 2010).

Since transmitter release becomes saturated at high concentrations of internal Ca²⁺, measurements of biochemical cooperativity are made at non-saturating Ca²⁺ levels. It has been shown recently (Lou et al., 2005) that the “intrinsic” biochemical cooperativity may vary with [Ca²⁺] even before saturation is reached, possibly due to an allosteric Ca²⁺ binding mechanism that cannot be approximated as a simple serial or parallel sequence of Ca²⁺ binding steps. It was suggested that this is due to the transition from asynchronous to synchronous release. Another study showed that the biochemical cooperativity for asynchronous release, n=2, is considerably lower than that for synchronous release, n=5, in the calyx of Held synapse (Sun et al., 2007). Studies of asynchronous release in other synapses have found the biochemical cooperativity to be the same as that for synchronous release, but with a lower Ca²⁺ affinity (Goda and Stevens, 1994; Ravin et al., 1997). There is evidence that biochemical cooperativity is not a constant property, but can be lowered by genetically reducing the expression level of the SNARE proteins syntaxin 1A and synaptobrevin (Stewart et al., 2000). It can also be lowered by pharmacologically cleaving SNAP-25 with Botulinum toxin (Cull-Candy et al., 1976) or cleaving VAMP/synaptobrevin with tetanus toxin (Bevan and Wendon, 1984). Finally, it has been proposed that biochemical cooperativity can be dynamically modulated by intracellular kinases such as PKC (Yang et al., 2005)

Ca²⁺ channel cooperativity of exocytosis

An important functional characteristic of the active zone morphology is the mean number of channels that contribute ions to the triggering of a release event. This cannot be measured experimentally because it is impossible to track the paths of individual Ca₂₊ ions to determine their channel source. However, it can and has been estimated using computer simulations (Luo et al., 2008; Shahrezaei et al., 2006). The simulations by Shahrezaei et al., for the frog neuromuscular junction, demonstrated that although there were as many as six Ca²⁺ channel openings per vesicle per action potential, only one or two proximal channels provided the Ca²⁺ ions that evoke release from a nearby release site. This computer simulation suggests that distal channels play little role in gating release from this neuromuscular junction. Since the number of channels contributing to a release event can be no greater than the number of Ca²⁺ binding sites, this measure of the Ca²⁺ channel cooperativity is bounded above by the biochemical cooperativity, n.

The Ca²⁺ channel cooperativity was defined somewhat differently in (Matveev et al., 2009), where m_CH was quantified as the number of channels contributing Ca²⁺ to the local Ca²⁺ domain surrounding the vesicle release sensor. When defined this way, many channels may contribute to the domain, although ions from only a few (at most n) channels actually bind to proteins at the release site. The channel cooperativity m_CH can exceed n but is bounded by M, the number of channels in the vicinity of the release site. The advantage of defining m_CH in this way is that it provides useful information about the extent of overlap of the Ca²⁺ nanodomains of individual open channels, and quantifies the number of channels participating in release over several exocytosis events. In fact, many studies tacitly assume this second Ca²⁺ channel cooperativity definition; for instance, (Borst and Sakmann, 1996) argue for a possibility of dozens of channels being involved in the release of a vesicle in the rodent calyx of Held synapse from immature animals.

For the idealized case in which the channels are equidistant from a release site, channel cooperativity equals the average number of Ca²⁺ channels that open to trigger a release event (i.e., the average number of open channels given that exocytosis takes place). For example, if each release site is surrounded by an average of a dozen equidistant channels, each with open probability of 50% during a stimulus, and assuming for simplicity that exocytosis occurs at every depolarization event, then m_CH=6 since six channels open and provide Ca²⁺ to the local domain at the release site. This number is not limited by the biochemical cooperativity, which would typically be less than six.

Ca²⁺ current cooperativity of exocytosis

Although knowledge of the number of Ca²⁺ channels involved in a single exocytotic event is of significant interest for a full understanding of localized Ca²⁺ signaling in general and synaptic physiology in particular, as pointed out above such a characteristic cannot be measured experimentally. This limitation has led to the use of an indirect measure for the number of channels participating in an exocytotic event. This measure, the Ca²⁺ current cooperativity of exocytosis, m_ICa, was originally introduced in the study of the biochemical Ca²⁺ cooperativity (Augustine et al., 1985; Llinás et al., 1981), and was soon hypothesized to depend on the localization of Ca²⁺ influx (Augustine and Charlton, 1986; Chad and Eckert, 1984; Yoshikami et al., 1989). Current cooperativity was first analyzed with the help of computational modeling by (Zucker and Fogelson, 1986) and analytically by (Yoshikami et al., 1989) and (Quastel et al., 1992). Zucker and Fogelson (1986) showed that m_ICa would increase from 1 to n as the membrane potential increased, which changes the open probability and the driving force. Here we review experiments in which the number of Ca²⁺ channel openings during a stimulus is varied without changing the single-channel current, and both transmitter release and the presynaptic Ca²⁺ current (I_Ca) are measured.

There are two main methods for measuring m_ICa, corresponding to two different ways of modifying the number of open channels without changing the single-channel Ca²⁺ current. One method involves voltage-clamping the pre-synaptic site and administering depolarizations of varying amplitude or duration (Augustine et al., 1985; Llinas et al., 1982). The range of depolarization amplitudes is kept sufficiently narrow to minimize the changes in the driving force for Ca²⁺, ensuring an approximately constant single-channel current (Quastel et al., 1992). Avoiding this complication, a tail current protocol involves a pre-depolarization to near the Ca²⁺ reversal potential, which activates the channels, and is followed by a step to a hyperpolarized voltage, increasing the driving force so that Ca²⁺ floods into the cell through channels opened by the preceding depolarization (Stanley, 1995; Stanley, 2005). In this case the number of open channels is varied by changing the pre-depolarization duration. The second approach uses pharmacological agents to block presynaptic Ca²⁺ channels (Mintz et al., 1995; Wu et al., 1999; Yoshikami et al., 1989). The agent can be specific to a certain type of Ca²⁺ channel (for example, P/Q-type channels can be blocked with ω-agatoxin IVA), or a non-specific agents like Cd²⁺ could be applied to block Ca²⁺ channels of all types. With this approach, the number of channels that open during a stimulus is varied by applying different concentrations of the blocker. In the following we focus on non-specific channel block except where indicated otherwise.

The Ca²⁺ current cooperativity can then be defined as the slope of the log-log plot of the release rate R versus the total Ca²⁺ current, I_Ca (Quastel et al., 1992)

$$m_{\mathit{ICa}}=\frac{\mathit{d}logR}{dlog{I}_{Ca}}=\frac{\mathit{d}logP(R)}{dlog{p}_o},$$ (2)

where P(R) is the probability of release, and p_o is the single-channel open probability. The second equality in Eq. (2) uses the fact that the Ca²⁺ current is proportional to the single-channel open probability, and assumes that the influx is brief (which is true for the tail-current protocol), so that each channel is either in an open or closed configuration (i.e., there is no flickering). As discussed below in more detail, the value of m_ICa is not constant, but initially increases with I_Ca (see Fig. 2) and then decreases as I_Ca approaches saturating levels.

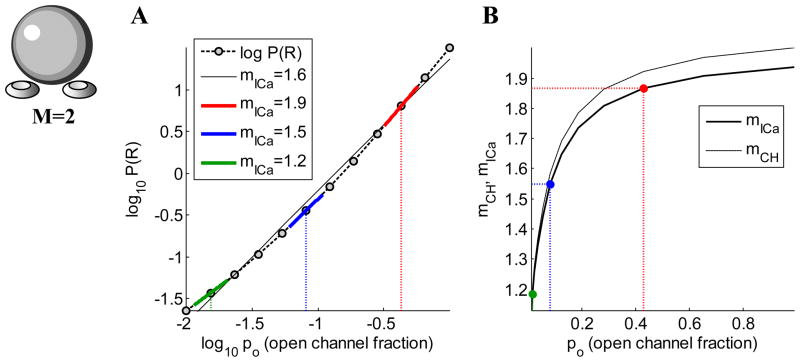
Figure 2.

(A) Log-log plot of release probability vs. open channel probability (computed using Eq. 4), assuming two equidistant channels, and no saturation of release (r=2⁵=32). The value of the slope yields Ca²⁺ current cooperativity of exocytosis, m_ICa, and is different along different parts of the curve. The black curve is a regression line, the slope of which would be the experimentally determined m_ICa. (B) The dependence of both m_ICa and m_CH on p_o. Colors of points correspond to colors of line segments in (A).

Finally, note that the biochemical cooperativity is known to be an upper bound for the Ca²⁺ current cooperativity (Mintz et al., 1995; Quastel et al., 1992; Wu et al., 1999; Zucker and Fogelson, 1986):

$$m_{\mathit{ICa}}\le n$$

That is, m_ICa initially increases with the number of open channels but when there are many channels, the Ca²⁺ concentration approximates a uniform rise owing to extensive domain overlap. For the case of sensory ribbon synapses, the biochemical cooperativity is lower than in many other synapses, with several studies reporting non-cooperative, near-linear relationship between Ca²⁺ and release (Johnson et al., 2008; Keen and Hudspeth, 2006; Thoreson et al., 2004). This constrains the current-release relationship to be linear as well, regardless of the degree of channel domain overlap.

Relationship between current and channel cooperativities: equidistant channel model

What does m_ICa tell us about the number of channels contributing to release, m_CH? If m_CH=1, then each release site has a single proximal channel responsible for gating release, so m_ICa=1 (Augustine, 1990; Bucurenciu et al., 2008; Mintz et al., 1995; Stanley, 1993; Wu et al., 1999; Yoshikami et al., 1989; Zucker and Fogelson, 1986). Thus, if some fraction of presynaptic channels is blocked, then the probability of release from the terminal will be reduced by this same fraction since each release site associated with a blocked channel will be inactive. The relationship between m_ICa and m_CH is more subtle if an exocytotic event is evoked by Ca²⁺ from more than one channel. To illustrate, we examine the case of equidistant channels. While this is a severe geometric constraint, it enables us to derive formulas that provide insight into the relationship between active zone morphology, the actions of Ca²⁺ buffers, and the Ca²⁺ cooperativities we have defined, m_ICa, m_CH, and n.

Starting with the simplest case of two equidistant channels, the probability of release can be expressed in terms of the conditional probabilities of release given that a certain number of channels are open, P(R|1) and P(R|2), and the probabilities that either one or two channels open, P(1) and P(2):

$$P(R)=P(R\mid 1)P(1)+P(R\mid 2)P(2).$$ (3)

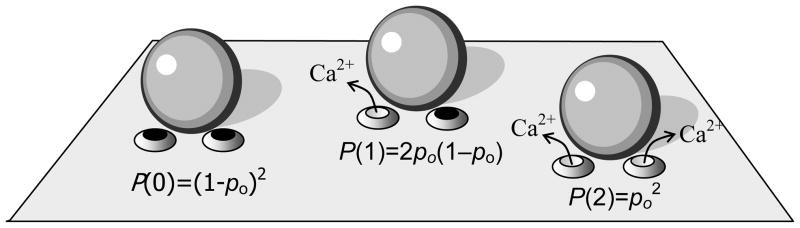
As illustrated in Fig. 1, P(1) = 2p_o (1–p_o) and $P(2)=p_o^2$, where p_o is the probability that a channel is open. We can then rewrite Eq. (3) as

Figure 1.

Probabilities of distinct configurations of the release site with two channels per vesicle. Denoting the open channel probability by p_o, the probability that neither channel is open is P(0)=(1–p_o)², whereas the probability of one open channel is P(1)=2p_o(1– p_o), and the probability of both channels being open is P(2)=p_o². Modified from Matveev et al. (2009).

$$P(R)=P(R\mid 1)(2p_o(1-p_o)+{rp}_o^2)$$ (4)

where

$$r=\frac{P(R\mid 2)}{P(R\mid 1)}$$ (5)

is the ratio of release given that two channels open over that when one channel opens. The release ratio, r, describes the relative contribution that a second open channel makes to release. The advantage of expressing cooperativity measures in terms of r is that it fully quantifies the sensitivity of release to the number of open channels, without need to describe explicitly the details of the underlying Ca²⁺ binding process or [Ca²⁺] diffusion

To fully analyze a particular synaptic release model it is necessary to calculate r, as we do below to examine the effect of channel distribution and buffering, but some simple cases can be understood without calculation. For example, if r=1 then the release site is saturated by the Ca²⁺ from one open channel, and the opening of a second channel makes no contribution. At the other extreme of no saturation, the opening of a second channel doubles the probability that each Ca²⁺ binding site will be occupied. Since there are n such sites (the biochemical cooperativity), r=2ⁿ in this case of no saturation. The Ca²⁺ buffering and the distance of the channels from the release sites also affects the level of saturation. If the channels are close to the vesicle, or buffering is weak, then r is near 1. Conversely, large channel-vesicle separation and/or strong buffering results in a release ratio that is near 2ⁿ. Apart from the release ratio, the only other parameter affecting current and channel cooperativities is the probability that a channel is open, p_o, or equivalently, the fraction of open channels in the terminal.

Equations (2)-(5) can be used to derive relationships between the Ca²⁺ current and channel cooperativities and the two independent parameters r and p_o (see Matveev et al., 2009 for details). In the case of two equidistant channels, these relationships are:

$$m_{CH}=\frac{1+(r-1)p_o}{1+(r-2)\frac{p_o}{2}}$$ (6)

$$m_{\mathit{ICa}}=\frac{1+(r-2)p_o}{1+(r-2)\frac{p_o}{2}}.$$ (7)

where m_ICa is obtained by taking the logarithmic derivative of Eq. (4) with respect to p_o, while m_CH is the average number of open channel given that release has occurred.

While these expressions are similar, there is nevertheless a difference. One can see that, in this case of two equidistant channels,

$$m_{\mathit{ICa}}\le m_{CH}\le 2.$$

Other results can be deduced from Eqs. (6) and (7) by considering some limiting cases. When r = 2, release scales linearly with the number of open channels (there is twice as much release with 2 open channels compared to 1 open channel), so m_ICa is identically 1. In contrast, in this case m_CH depends on the open channel probability, m_CH=1+p_o, linearly increasing from 1 to 2 as p_o is increased from 0 to 1. This is reasonable, since m_CH is conditioned on the fact that release occurs (so at least one channel must open to evoke the release) and in the linear regime (r=2) m_CH reflects the fraction of instances in which the second channel opens. Another instructive case is large r. In this case both channels have to open to trigger release, so m_ICa and m_CH approach their upper bound of 2 (the number of available channels) regardless of the fraction of open channels during the stimulus.

Figure 2 illustrates the definition of m_ICa for two equidistant channels (Eq. (7)), showing its relationship to the experimentally measured value of m_ICa. The experimental value is typically calculated as the slope of the log-log plot of some measure of release versus I_Ca, using linear regression through several data points to construct the curve. The corresponding theoretical definition of m_ICa is demonstrated in Fig. 2A, where P(R) is given by Eq. (4). Here we vary the channel open probability, as would be the case in an experiment using either the tail current or non-specific channel block protocol, and we fix the model active zone morphology. A release mechanism with 5 Ca²⁺ binding sites is assumed, and we consider the case where there is no saturation, so r=2⁵=32. The slope of the black regression line through the points is the Ca²⁺ current cooperativity that would be calculated experimentally if all of the data points in the figure were measured. However, the slope of the Iog(P(R)) vs. log(I_Ca) curve given by Eq. (4) that defines the points in this figure varies with p_o. This is illustrated with the three colored line segments in Fig. 2A. The slopes of these line segments are given by Eq. (7), with r=32 and three different values of p_o. These slopes, m_ICa, are plotted in Fig. 2B as correspondingly colored points. They lie on a curve that is the slope of the log(P(R)) vs. log(I_Ca) curve for p_o ranging from 0 to 1. This m_ICa curve is just the plot of Eq. (7) with r=32 and p_o ranging from 0 to 1.

Given that mICa varies with po, which range of po values is most realistic physiologically? Studies of central synapses found a very high open probability during an action potential, typically between 50% and 70% (Borst and Sakmann, 1998; Li et al., 2007; Sabatini and Regehr, 1997) (but see (Jarsky et al., 2010)). Thus, a value of po=0.5 would be reasonable during an impulse. When mICa is determined through the Ca²⁺ channel block procedure, po may be decreased over 1–2 orders of magnitude, from about 0.5 to about 0.01. Over this range of po values, the slope of the regression line to the points on the dashed theoretical curve in Fig. 2A equals mICa ≈ 1.51, which is close to mICa ≈ 1.55 corresponding to the midpoint of this range (the slope of the blue line segment). (The slopes would differ more if the theoretical curve were not nearly linear.) In contrast, in the tail current protocol, po would be varied from near 1 (functional channels fully activated) to about 0.01. The corresponding full-range mICa slope value would be well matched by the slope of the solid black regression line in Fig. 2A. Figure 2B summarizes how both mICa and mCH vary with the channel opening probability. The two cooperativity measures are both close to one at low po values, since in this case there is usually a single channel opening per each release event. However, mCH and mICa move apart for higher po. Note that they approximate the number of available channels per release site only in the limit of po approaching 1. This implies that the log-log slope of release versus ICa should preferably be measured over the range of po values corresponding to low channel block fraction to determine the number of channels in close proximity to release sites.

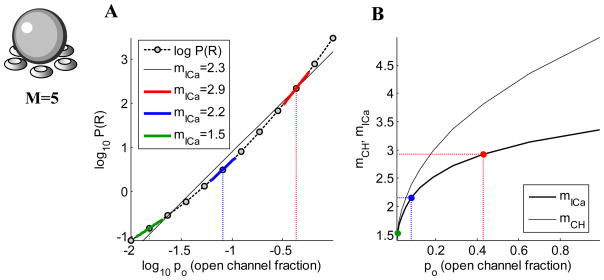
In Fig. 3 the theoretical results given above are generalized to M=5 equidistant channels. In general, we find that

Figure 3.

(A) Log-log plot of the probability of release versus the open channel probability with M=5 equidistant channels and no saturation of release (release is proportional to 5th power of the number of open channels). (B) Ca²⁺ current and channel cooperativities as a function of p_o. Equations for all quantities are given in Matveev et al., 2009. Colors of points correspond to colors of line segments in (A).

$$m_{\mathit{ICa}}\le m_{CH}\le M$$ (8)

regardless of the value of r when the channels are equidistant from the release site. Note that for M = 5 equidistant channels, the separation between m_ICa and m_CH is even greater than with two channels, and m_ICa is far less than the number of equidistant channels. In summary, then, these calculations show that the Ca²⁺ current cooperativity provides only a lower bound on the channel cooperativity and the number of channels proximal to the release site. Thus, whereas low channel cooperativity implies low current cooperativity, low current cooperativity does not imply low channel cooperativity. In general, the estimate of m_CH provided by m_ICa deteriorates as M increases. However, even if M is large, m_ICa is close to m_CH if single-channel opening probability p_o is low and saturation of release is also low (i.e. release ratio r is high). The fact that m_ICa is a strong underestimate of m_CH means that a modest value of m_ICa of about 2 – 3 may imply a fairly large m_CH , at least in the equidistant channel case (see Fig. 4; Coggins and Zenisek, 2010).

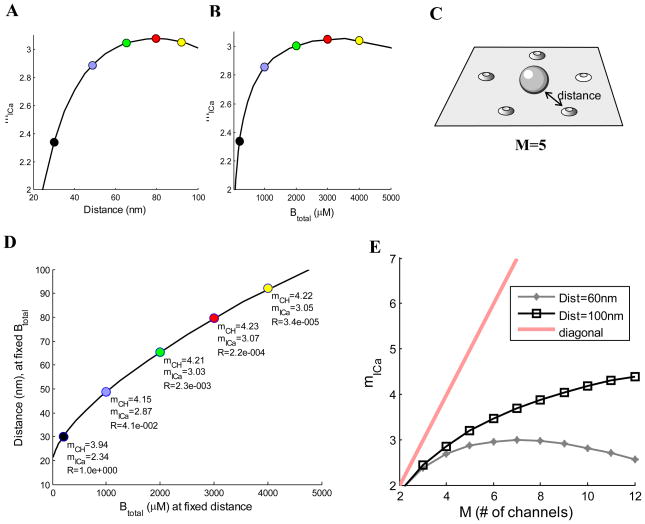
Figure 4.

Dependence of m_ICa on the channel-vesicle distance (A) and buffer concentration, B_total (B), for a ring of 5 equidistant channels (C), with a single-channel current of 0.05 pA and 1 ms duration, with channel open probability of p_o=0.6. In (A), buffer concentration is B_total=200 μM; in (B), channel distance is 30 nm. (D) Correspondence between increasing channel distance and increasing buffering. On x-axis, B_total is varied while keeping channel distance fixed at 30 nm. On y-axis, the channel distance is varied while keeping B_total fixed at 200 μM. (E) Current cooperativity as a function of channel number M, for different channel-vesicle distances, with 200 μM of mobile buffer (D=50 μm²/ms) of 1 μM affinity. Ca²⁺ dynamics is simulated in a 1 μm³ box; a square Ca²⁺ current pulse arrives through each open channel. Open channel probability is varied around the value of p_o=0.6. Release is modeled using the Ca²⁺ binding scheme in (Felmy et al., 2003). Each data point represents a weighted average over all possible open channel configurations. Calcium Calculator modeling software is used for all simulations (Matveev, 2008).

Effects of Ca²⁺ channel distance and buffers on channel and current cooperativity

Endogenous Ca²⁺ buffers, which may be stationary or mobile (Neher, 1998b), trap Ca²⁺ ions that enter through open channels and change their diffusion characteristics. It is therefore expected that buffers may significantly affect the Ca²⁺ channel cooperativity, as confirmed by simulation results illustrated in Fig. 4, which assume 5 equidistant channels per release site. (Ca²⁺ diffusion simulations in the presence of a mobile buffer are performed using standard equations described in Matveev et al., 2009). Figure 4A shows that m_ICa increases as the channels are moved away from the release site, since now more channels must open to gate the release. There is a saturation of m_ICa, and even a slight decrease, far below the upper bound of M=5. At the large distances where this decrease occurs the Ca²⁺ reaching the vesicle location is sufficiently small to become comparable to background Ca²⁺, which will thus play a larger role in gating the release, thereby reducing the current cooperativity.

Figure 4B shows how m_ICa varies with the mobile buffer concentration, with a fixed channel distance of 30 nm. For lower buffer concentrations the current cooperativity increases with increases in the buffer concentration. This is because the buffer’s main effect is to limit the extent of a single channel Ca²⁺ nanodomain, reducing the probability of release when a small number of channels are open, and thus requiring more open channels to supply Ca²⁺ in the local domain at the release site. When the buffer concentration is very large, however, so much of the Ca²⁺ entering through open channels is buffered that the background release rate becomes comparable to the evoked release rate. The primary effect of increasing the buffer concentration under these conditions is to further reduce the contribution of evoked release to the total release, and thus there is a small reduction in m_ICa. Hence, m_ICa first increases, and then decreases slightly as the buffer concentration is increased.

The observation that both channel distance and buffer concentration affect the current cooperativity suggests that the values of m_ICa that can be achieved by changing channel distance can also be achieved by changing the buffer concentration. In fact, Fig. 4D shows that there is indeed an exact correspondence between distance and buffering, so that the same change in release rate and cooperativity is achieved by increasing either the buffering or the distance. The five colored points in Fig. 4D correspond to the five colored points in Figs. 4A and 4B. For example, the black point has m_ICa=2.34. To increase m_ICa to 2.87 (blue point) one could either increase the buffer concentration to 1000 μM while keeping channel distance at 30 nm (x-axis of graph in Fig. 4D), or increase the channel distance to about 50 nm while keeping the buffer concentration constant at 200 μM (y-axis). Each point on the curve in Fig. 4D, then, tells what channel distance (with buffer fixed at 200 μM) provides the same release probability and current cooperativity as would be achieved with the buffer concentration on the x-axis (with channel distance fixed at 30 nm). Panel E shows the effect of distance on m_ICa. At short distances, saturation is significant and m_ICa severely underestimates M, whereas at longer distances the approximation improves somewhat. Similarly, m_ICa gives a better approximation when buffer concentration is large.

Case of non-equidistant channels

While the simplifying assumption of equidistant channels helps in developing intuition about the connection between current and channel cooperativities, in many cases of interest cooperativity depends on the relative contributions of both proximal and distal Ca²⁺ channels. There are a number of experimental studies focused on the effect of channel distance on Ca²⁺ current cooperativity of exocytosis (Fedchyshyn and Wang, 2005; Meinrenken et al., 2002; Shahrezaei et al., 2006). Modeling is useful in analyzing and interpreting the results of such experimental studies, and may make it possible to infer the channel cooperativity values from the measured current cooperativity. This in turn requires a generalization of the channel cooperativity, since this is not a straightforward extension of the definition for equidistant channels. With equidistant channels, each of the channels contributes equally when open, while now some open channels contribute more Ca²⁺ to the local domain of a release site than others. If there are two channels, one distal and one proximal, and both channels open, then both channels contribute to the local domain, but since the proximal channel is closer it will contribute more ions. To determine the contribution made by each, it is therefore reasonable to determine the Ca²⁺ concentration at the release site when either channel opens separately (Ca₁₀ and Ca₀₁, where the first subscript corresponds to the proximal channel and the second to the distal channel and 1 means open). The cooperativity when both channels open can then be defined as $m_{CH}=\frac{{Ca}_{10}+{Ca}_{01}}{{Ca}_{10}}$. This makes intuitive sense, since if the channels are at the Ca10 same distance then Ca01 =Ca10 and mCH ≈ 2. If the distal channel is much further from a release site than the proximal channel, then Ca01 ≪ Ca10 and so mCH ≈ 1. If the proximal channel contributes 4 times as much Ca²⁺ to the local domain as 4 the distal channel, then $m_{CH}=\frac{4+1}{4}=1.25$, which is closer to 1 than to 2, as one 4 would expect. This definition can be generalized naturally to the case of an arbitrary number of non-equidistant channels:

$$m_{CH}=\frac{\sum {Ca}_i}{\underset{i}{max}{Ca}_i}.$$ (9)

where Ca_i is the Ca²⁺ concentration at the release site when the i ^th channel is open and others are closed.

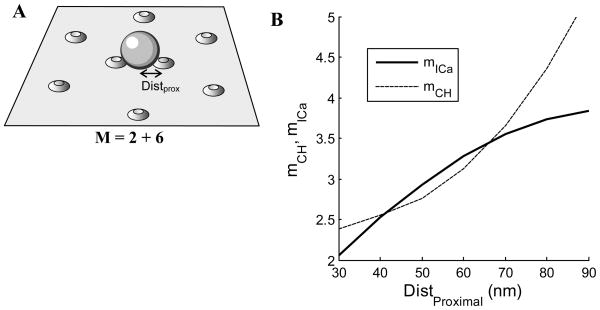
In Fig. 5 we consider a scenario in which there are two proximal Ca²⁺ channels per release site and six distal channels. The distal channels are situated at a distance of 90 nm from a release site, while the location of the proximal channels is varied. When the proximal channels are quite close, 30 nm, they dominate the release. This is reflected in a low current cooperativity of about 2 and a channel cooperativity between 2 and 3. Both forms of cooperativity increase as the proximal channels are moved further from the release site. Note that for a small range of distances m_CH < m_ICa, which would not be possible if channels were equidistant. However, the m_CH curve has upward concavity while the m_ICa curve has downward concavity, so for larger distances the current cooperativity again provides only a lower estimate of the channel cooperativity. When all eight channels are equidistant we know that m_ICa must be less than m_CH, and at 90 nm the current cooperativity is indeed far less than the eight channels available for release.

Figure 5.

Cooperativity and reliability with 2 proximal and 6 distal channels per release site. (A) The distal channels are located at a distance of 90 nm from a release site, while the proximal channel distance is varied. The mobile buffer concentration is 200 μM and the channel opening probability is p_o=0.5. (B) The Ca²⁺ current and channel cooperativities increase as the proximal channels are moved away from the release site.

Selective channel block

Varying the number of open channels using pharmacological channel block rather than a tail current protocol enables one to examine the preferential coupling to exocytosis of specific subtypes of Ca²⁺ channels (Mintz et al., 1995). In this case, larger current cooperativity values suggest closer coupling of the pharmacologically manipulated channel type to exocytosis. Since part of the Ca²⁺ current arrives through channels not affected by a particular blocker, in the case of selective block the relationship between synaptic release and Ca²⁺ current can be much steeper than in the case of non-specific channel block. In fact, the bounds on m_ICa given by Eq. (8) would not hold, and in particular, current cooperativity can in this case easily exceed the number of available channels (Bertram et al., 1999; Matveev et al., 2009; Wu et al., 1999). For example, if a channel blocker preferentially targets channels that are tightly coupled with exocytosis, while the majority of total presynaptic Ca²⁺ influx arrives through channels remote to the vesicles, then the blocker would strongly reduce release with only a minor decrease of presynaptic Ca²⁺ current. This would lead to very large values of current cooperativity. Conversely, if the blocker affects the channels that are remote to the release site and loosely coupled to release, the decrease in I_Ca would greatly exceed the concomitant decrease in release rate, resulting in small values of current cooperativity.

For example, the study of (Wu et al., 1999) found differences in current cooperativity at rat calyx synapses with selective block of three distinct subtypes of Ca² channels: P/Q (Cav2.1, ω-agatoxin IVA-sensitive), N- (Cav2.2, ω-conotoxin GVIA-sensitive) and R-type (Cav2.3) channels. The Ca²⁺ current cooperativity of P/Q channels was higher than the other two subtypes, indicating that a fraction of N- and R-channels were located further away from release sites. Similar studies revealed lower current cooperativity for N-type channels than for P/Q type channels in rat and mouse hippocampal synapses (Qian and Noebels, 2001; Qian and Delaney, 1997), and cerebellar parallel fiber synapses (Mintz et al., 1995), although no difference in m_ICa between channel subtypes was observed in experiments on guinea pig hippocampal cells (Wu and Saggau, 1994) and rat hippocampal autapses (Reid et al., 1998). Further, a study of (Reid et al., 1997) used selective channel block to show that the distribution of specific channel types is not uniform across distinct synaptic terminals, even those efferent from the same cell (see also (Reuter, 1995)). Differences in the exocytotic coupling of distinct channel subtypes using pharmacological channel block were also found in chromaffin cells by (Artalejo et al., 1994)

Functional Implications

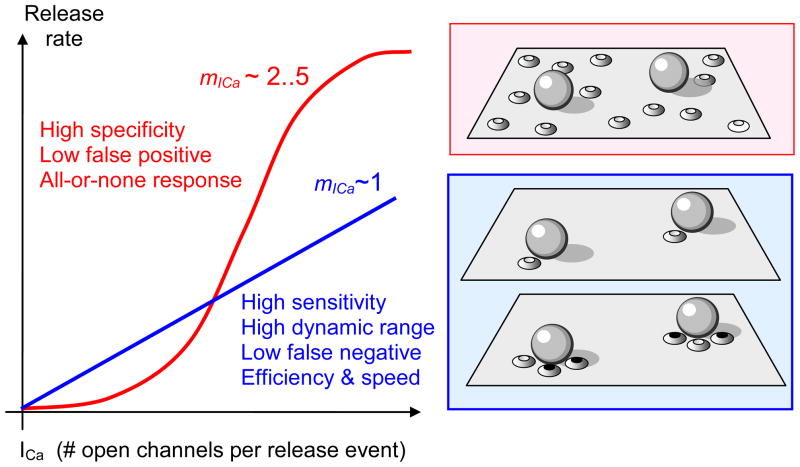
What are the functional implications of having some channels close to release sites and some further away? It has been argued that low values of m_ICa observed for instance in several sensory ribbon synapses contribute to linearity, fidelity and the dynamic range of the sensory response (Brandt et al., 2005; Goutman and Glowatzki, 2007; Jarsky et al., 2010; Johnson et al., 2008; Keen and Hudspeth, 2006; Thoreson et al., 2004). In addition, studies that infer tight vesicle-channel coupling suggest that low current cooperativity is associated with faster and more Ca²⁺ efficient synaptic response (Fedchyshyn and Wang, 2005; Kochubey et al., 2009). In contrast, higher m_ICa values could be required for response specificity, leading to a more all-or-none synaptic transmission profile with lower noise due to fewer false positives (Coggins and Zenisek, 2009). These hypotheses are summarized in Figure 7. As illustrated in this figure, small channel cooperativity can be achieved via two distinct morphological mechanisms: a coupling of a single channel to each vesicle, or the action of several channels with very low release probability, a scenario inferred for instance in mouse retinal ribbon bipolar cell synapses (Jarsky et al., 2010). In turn, higher current cooperativity could either signify a lose association between the spatial vesicle and channel distributions, or a coupling of each vesicle to an array of several proximal channels, each allowing only a non-saturating Ca²⁺ current.

Figure 7.

Possible functional consequences of different Ca²⁺ current cooperativity values. A linear relationship between Ca²⁺ influx and release leads to greater sensitivity and dynamic range of the response, as well as Ca²⁺-efficiency and speed of response due to tighter vesicle-channel coupling. In contrast, high current cooperativity may lead to a more specific, all-or-none response with a lower false-positive rate. High current cooperativity requires an overlap of multiple channel domains (upper-right inset), whereas low current cooperativity can be achieved through either the tight coupling of a single channel to each vesicle (middle-right inset) or low probability of channel opening, whereby only one proximal channel is likely to open with each pulse (lower-right inset; black filled ovals indicate closed channels).

A meta-analysis of several current cooperativity measurements served as the basis for a hypothesis that Ca²⁺ channel domain overlap is adapted to the physiological extracellular Ca²⁺ concentration, so that at lower external Ca²⁺ concentration the synaptic morphology compensates through higher channel clustering (Gentile and Stanley, 2005).

Dynamic and Spatial Modulation of Current Cooperativity

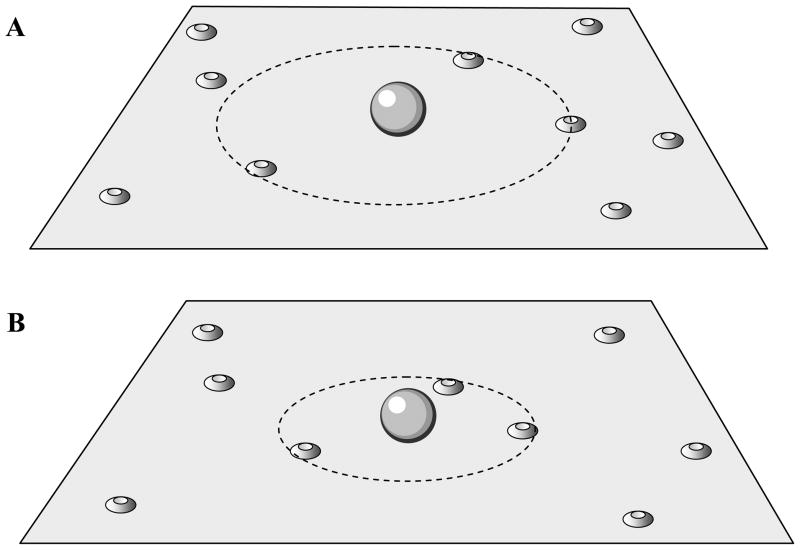
The Ca²⁺ current cooperativity need not be fixed. In fact, there is evidence for developmental changes in m_ICa in synapses. For example, in the rat calyx of Held m_ICa in immature (pre-hearing) calyces was determined to be 4.6 using tail currents (Kochubey et al., 2009), and 4.8 when presynaptic I_Ca was varied by systematically increasing the duration of an action potential waveform that provided the input (Fedchyshyn and Wang, 2005). In mature (post-hearing) calyces the Ca²⁺ current cooperativity was reduced to 3.7 when measured with tail currents and to 2.6 when measured with action potential waveforms. The reduction in m_ICa during development is consistent with a scenario in which there is a tightening of the release site/Ca²⁺ channel complex, so that in mature calyces there are a few proximal channels assisted by more distal channels. The proximal channels could have moved in from more distant locations (Fig. 6), which would reduce m_ICa as in Fig. 5. To test this hypothesis, Fedchyshyn and Wang sealed a patch electrode containing the slow Ca²⁺ chelator EGTA onto mature and immature calyces. Because of its slow binding rate, EGTA can buffer Ca²⁺ from distal channels before it reaches release sites more effectively than Ca²⁺ from proximal channels. In immature calyces exposed to EGTA the quantal output was reduced by ~70%, while in mature calyces the EGTA-mediated reduction was much smaller, only ~20%. In contrast, the fast buffer BAPTA was equally effective in reducing release in both mature and immature calyces. These findings are consistent with the hypothesis that channels are closer to vesicles in the mature case. Distance may not be the only effect; Fedchyshyn and Wang also found that action potentials were wider in the immature calyces, which would further enhance the effectiveness of EGTA relative to mature calyces. In a subsequent study, a synaptic protein, Septin 5, was identified that appears to act as a physical barrier to vesicle docking to release sites (Yang et al., 2010). The data suggest that in the immature calyx, septin 5 proteins block vesicle docking to release sites in the active zone, where most of the Ca²⁺ channels are located. This results in a large distance between channels and vesicles, leading to a relatively large current cooperativity reported in (Fedchyshyn and Wang, 2005). During maturation, the septin 5 proteins move to the active zone periphery, removing the barrier to vesicle docking to active zone release sites. Consequently, docked vesicles are closer to the Ca²⁺ channels, resulting in a lower current cooperativity.

Figure 6.

Hypothesis for the developmental change in vesicle-channel coupling at the calyx of Held. (A) Channels are poorly coupled to release in an immature synapse. (B) With development, a subset of Ca²⁺ channels moves closer to the vesicle location.

Studies using selective blockers of different channel types have shown that N-, P/Q-, and R-type Ca²⁺ channels contribute to transmitter release in calyces from 8–10-day-old rats (Wu et al., 1998), but that P/Q-type channels contribute more to release than the other two types (Wu et al., 1999). This is consistent with imaging using subtype-specific antibodies, which showed that a sizable fraction of the N- and R-type channels are more distant from vesicles than are P/Q-type channels (Wu et al., 1999). A complementary study, again using channel type-specific blockers, found that the contribution to release of P/Q-type channels greatly increased from age 4d to 10d, so that by age 10d release was gated entirely by P/Q-type channels (Iwasaki and Takahashi, 1998). Thus, it seems likely that in the experiments of (Fedchyshyn and Wang, 2005), application of EGTA blocked the contribution of the more distant N- and R-type channels, while the contribution from the closer P/Q-type channels was preserved.

Although the studies above point to a developmental tightening of the release site complex, they do not rule out a parallel developmental change in the biochemical Ca²⁺ cooperativity, n. This possibility was investigated by (Kochubey et al., 2009). They raised the Ca²⁺ concentration throughout the calyx using laser-induced flash photolysis to uncage Ca²⁺ from exogenous chelator. Different flash intensities were used to raise Ca_i to different levels (measured with fura-2), while simultaneously measuring EPSCs in the postsynaptic cells. This approach was used to determine n in immature calyces (from 8d–9d rats) and more mature calyces (from 12d–15d rats). It was found that n was approximately 3.6 in both cases, and thus there was no developmental change in the biochemical cooperativity over the period of time when the current cooperativity declines.

Another example of a developmental change in the Ca²⁺ current cooperativity is the ribbon synapse of the mammalian inner hair cell. These ribbon synapses are specialized to allow sustained release of a large number of vesicles. Cells on the sensory neuroepithelium are tuned to different characteristic frequencies; those in the apical region respond primarily to low-frequency sound, while those in the basal region respond primarily to high-frequency sound (Fettiplace and Fuchs, 1999). Johnson and colleagues studied developmental changes in m_ICa of ribbon synapses in mouse inner hair cells, and in apical and basal cells of the gerbil (Johnson et al., 2008). Using a voltage clamp protocol to vary the number of open Ca²⁺ channels, in the latter study they found m_ICa ≈ 3.8 in immature synapses from both apical and basal cells. In cells from mature gerbils, m_ICa was significantly lower, again showing a developmental reduction in the current cooperativity as in the calyx of Held. However, this reduction was not uniform across the neuroepithelium; synapses from apical (low-frequency) cells had m_ICa ≈ 2.2, while those from basal (high-frequency) cells had m_ICa ≈ 1.

To investigate the origin of the different current cooperativities in the two cells, Johnson et al. (2008) examined the biochemical cooperativity of synapses from each cell type. They determined that n=2.8 for mature apical cells, and n=1.2 for mature basal cell synapses. Hence, the origin of the different current cooperativities in the low-frequency and high-frequency cells of mature animals appears to be at least partially due to differences in the Ca²⁺ trigger for release in the two cells, and may indicate involvement of a distinct Ca²⁺ sensitive proteins, such as otoferlin or non-neuronal synaptotagmins (Duncan et al., 2010; Johnson et al., 2010; Keen and Hudspeth, 2006; Mirghomizadeh et al., 2002). Taken together with studies done in the calyx of Held, it appears that developmental changes in both the structure of the channel/release site complex and the vesicle release mechanism itself can occur so as to reduce m_ICa and increase reliability as the animal matures.

Conclusions

In the absence of a direct way to observe the functional coupling of individual Ca²⁺ channels to neurotransmitter release, measurements of current cooperativity have proved very useful in elucidating the degree of Ca²⁺ channel nanodomain overlap in synaptic vesicle release in a variety of synaptic terminals, from invertebrate neuromuscular junctions to central mammalian synapses. However, care must be taken in interpreting m_ICa measurements, since a given value of current cooperativity does not allow one to directly infer the functional Ca²⁺ channel cooperativity, i.e. the number of Ca²⁺ channels participating on average in the release of a single vesicle. In particular, a small value of m_ICa is not necessarily an indication that a small number of Ca²⁺ channels participates in release. As reviewed above, current cooperativity can provide a good approximation of the underlying channel cooperativity only when the number of channels is very small (2–3), and under further restrictive conditions such as low release saturation or low channel opening probability. Therefore, current cooperativity is not a very sensitive characteristic of synaptic morphology. Still, combined use of experimental and modeling techniques in interpreting m_ICa measurements provide greater insight into functional synaptic morphology (Bucurenciu et al., 2010; Coggins and Zenisek, 2009; Jarsky et al., 2010; Meinrenken et al., 2002; Quastel et al., 1992; Shahrezaei et al., 2006; Yoshikami et al., 1989; Zucker and Fogelson, 1986).

Current cooperativity measurements served a particularly important role in the long-standing argument whether synaptic neurotransmitter release is controlled by the opening of a few channels, or whether an overlap of Ca²⁺ nanodomains of many channels is required to trigger exocytosis (Gentile and Stanley, 2005; Schneggenburger and Neher, 2005). However, recent data strongly suggest that the Ca²⁺ influx varies between different types of synaptic terminals, and can indeed vary with development at each particular synapse (Fedchyshyn and Wang, 2005; Johnson et al., 2005; Johnson et al., 2008; Kochubey et al., 2009; Yang et al., 2010). Further, possible values of current cooperativity are directly dependent on the intrinsic (biochemical) cooperativity, which can also change developmentally, either through modulation of the synaptic machinery or through the presence of heterogeneous pools of vesicles, which may in turn have distinct biochemical cooperativity values under developmental regulation.

It is interesting to speculate on the functional significance of different m_ICa values. It has been suggested that the small values of m_ICa observed in many sensory ribbon synapses are connected to the requirement of linear coding of the sensory signal over a wide dynamic range, while the higher channel cooperativity found in other central synapses may indicate a requirement for an all-or-none response with lower noise due to false positive, spontaneous activity.