Texture analysis methodologies for magnetic resonance imaging

Abstract

Methods for the analysis of digital-image texture are reviewed. The functions of MaZda, a computer program for quantitative texture analysis developed within the framework of the European COST (Cooperation in the Field of Scientific and Technical Research) B11 program, are introduced. Examples of texture analysis in magnetic resonance images are discussed.

Magnetic resonance imaging (MRI) is a unique and powerful tool for medical diagnosis, in that it is a noninvasive technique that allows visualization of soft tissues. There is an increasingly growing interest in using MRI for early detection of many diseases, such as brain tumors, multiple sclerosis, and others. The diagnostic information is often included in the image texture.^1,2 In such cases, it is not sufficient to analyze image properties on the basis of point-wise brightness only; higher-order statistics of the image must be taken into account. Texture quantitation, ie, its description by precisely defined parameters (features) is then needed to extract information about tissue properties. Numerical values of texture parameters can be used for classification of different regions in the image, eg, representing either tissues of different origin or normal and abnormal tissues of a given kind. Changes of properly selected texture parameters in time can quantitatively reflect, changes in tissue physical structure, eg, to monitor progress in healing.

A European research project COST (Cooperation in the Field of Scientific and Technical Research) B11 was performed between 1998 and 2002 by institutions from 13 European countries, aimed at. development of quantitative methods of MRI texture analysis.³ It gathered experts of complementary fields (physics, medicine, and computer science) to seek MRI acquisition and processing techniques that would make medical diagnoses more precise and repetitive. One of the unique outcomes of this project is MaZda/⁴ a package of computer programs that allows interactive definition of regions of interest. (ROIs) in images, computation of a variety of texture parameters for each ROI, selection of most informative parameters, exploratory analysis of the texture data obtained, and automatic classification of ROIs on the basis of their texture.

The MaZda software has been designed and implemented as a package of two MS Windows®, PC applications: MaZda.exe and B11.exe⁴ Its functionality extends beyond the needs of analysis of MRI, and applies to the investigation of digital images of any kind, where information is carried in texture. The essential properties of the MaZda package is described in this report, illustrated by examples of its application to selected MRI texture analysis.

Texture analysis methods

Although there is no strict definition of the image texture, it. is easily perceived by humans and is believed to be a rich source of visual information about the internal structure and three-dimensional (3D) shape of physical objects. Generally speaking, textures are complex visual patterns composed of entities or subpatterns that have characteristic brightness, color, slope, size, etc. Thus, texture can be regarded as a similarity grouping in an image.⁵ The local subpattern properties give rise to the perceived lightness, uniformity, density, roughness, regularity, linearity, frequency, phase, directionality, coarseness, randomness, fineness, smoothness, granulation, etc, of the texture as a whole.⁶ A large collection of examples of natural textures is contained in the album by Brodatz.⁷

There are four major issues in texture analysis:

• Feature extraction: To compute a characteristic of a digital image that can numerically describe its texture properties.

• Texture discriminatiorr. To partition a textured image into regions, each corresponding to a perceptually homogeneous texture (leading to image segmentation).

• Texture classification: To determine to which of a finite number of physically defined classes a homogeneous texture region belongs (eg, normal or abnormal tissue).

• Shape from texture: To reconstruct 3D surface geometry from texture information.

Feature extraction is the first stage of image texture analysis. The results obtained from this stage are used for texture discrimination, texture classification, or object shape determination.

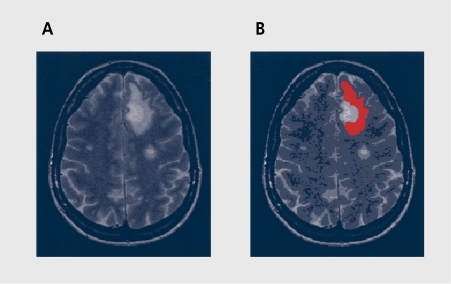
Consider an MRI cross-section of human skull (Figure 1a) in which an elongated, kidney-shape bright object in the upper-right quadrant, of the image is needed to be numerically characterized. This object is our ROT in this example, and is marked in red in Figure 1b For a population of images, the subimagc covered by ROI is a random variable. Assuming that, texture is homogeneous within the ROI and that the area of the ROI is sufficiently large, one can compute a number, say N, of statistical parameters based on image points contained in the ROI. Depending on definition of these statistics, different properties of the ROI texture can be highlighted; these parameters are called texture features. In the example illustrated, the calculated parameters can be arranged to form a feature vector [p₁, p₂, ..., pN]. Such a vector is a compact description of the image texture. Comparison of vectors computed for images measured for different patients indicates whether the texture covered by ROI represents normal or abnormal tissue.

Figure 1. A cross-section of human skull (A), with the region of interest (ROI) marked in red (B).

Feature vectors can be applied to the input of a device called a classifier. On the basis of its input, the classifier takes the decision as to which predefined texture classes its input represents. Consider a population of K images, each showing a different, instance of texture A. A feature vector is computed for each image, and applied to the input of the classifier. In an ideal case, “seeing” a vector drawn from texture of class A, the classifier responds with the information “class A” at its output. Similarly, for a population of K images, K feature vectors can be computed. Any of these could be applied to the input of the classifier. In an ideal case, the response of the classifier to a feature vector computed for texture class B is “class B.” (Sometimes a classifier cannot make a correct decision; in such cases, it wrongly recognizes a texture class different, from the one represented at the input, or it is unable to make a choice between assumed texture classes.)

The concept of textured image segmentation is illustrated in Figure 2 The left and right halves of the image in Figure 2a have different textures. In the process of image segmentation, the two regions are automatically identified and marked in different colors, eg, orange and blue in Figure 2b. (Some parts of the image are wrongly recognized as regions of yet other texture types, though.) There are two main techniques of image segmentation: supervised, where texture classes are known in advance; and unsupervised, where they arc unknown, and so the segmenting device has to identify not. only the texture classes, but. also their number. There exist, a variety of different, texture segmentation methods, such as region growing, maximum likelihood, split-and-merge algorithms, Bayesian classification, probabilistic relaxation, clustering, and neural networks.² All of these are based on feature extraction, which is the initial step and is necessary to describe (measure and analyze) the texture properties.

Figure 2. Textured image segmentation.

This paper is confined mainly to feature extraction and texture classification techniques, which are typically the basic steps performed to support medical diagnosis. Approaches to texture analysis are usually categorized into structural, statistical, model-based, and transform methods.

Structural approaches

Structural approaches^6,8 represent texture by well-defined primitives (microtexture) and a hierarchy of spatial arrangements (macrotexture) of those primitives. To describe the texture, one must define the primitives and the placement rules. The choice of a primitive (from a set of primitives) and the probability of the chosen primitive to be placed at a particular location can be a function of location or the primitives near the location. The advantage of the structural approach is that it provides a good symbolic description of the image; however, this property is more useful for texture synthesis than analysis tasks. The abstract descriptions can be ill defined for natural textures because of the variability of both micro- and macrostructure and no clear distinction between them. A powerful tool for structural texture analysis is provided by mathematical morphology.^9,10 This may prove to be useful for bone image analysis, eg, for the detection of changes in bone microstructure.

Statistical approaches

In contrast to structural methods, statistical approaches do not attempt to explicitly understand the hierarchical structure of the texture. Instead, they represent the texture indirectly by the nondeterministic properties that govern the distributions and relationships between the gray levels of an image. Methods based on second-order statistics (ie, statistics given by pairs of pixels) have been shown to achieve higher discrimination rates than the power spectrum (transform-based) and structural methods¹¹. Human texture discrimination in terms of the statistical properties of texture is investigated in reference 12. Accordingly, the textures in gray-level images are discriminated spontaneously only if they differ in second-order moments. Equal second-order moments, but. different, third-order moments, require deliberate cognitive effort. This may be an indication that, for automatic processing, statistics up to the second order may be the most important.¹³ The most, popular second-order statistical features for texture analysis are derived from the so-called co-occurrence matrix.⁸ These have been demonstrated to feature a potential for effective texture discrimination in biomedical images.^1,14

Model-based approaches

Model-based texture analysis^15-20 using fractal and stochastic models attempts to interpret an image texture by use of a generative image model and a stochastic model, respectively. The parameters of the model are estimated and then used for image analysis. In practice, the computational complexity arising in the estimation of stochastic model parameters is the primary problem. The fractal model has been shown to be useful for modeling some natural textures. It can be used also for texture

Transform methods

Transform methods of texture analysis, such as Fourier^24-26 and wavelet^27-29 transforms, produce an image in a space whose coordinate system has an interpretation that is closely related to the characteristics of a texture (such as frequency or size). Methods based on the Fourier transform perform poorly in practice, due to lack of spatial localization. Gabor filters provide means for better spatial localization; however, their usefulness is limited in practice because there is usually no single filter resolution at which one can localize a spatial structure in natural textures.

Compared with the Gabor transform, the wavelet transform have several advantages:

• Varying the spatial resolution allows it to represent textures at. the most, appropriate scale.

• There is a wide range of choices for the wavelet function, and so the best-suited wavelets for texture analysis can be chosen a specific application.

Wavelet transform is thus attractive for texture segmentation. The problem with wavelet transform is that it. is not translation-invariant.^30,31

Regardless of their definition and underlying approach to texture analysis, texture features should allow good discrimination between texture classes, show weak mutual correlation, preferably allow linear class separability, and demonstrate good correlation with physical structure properties. For a more detailed review of basic techniques of quantitative texture analysis, the reader is referred to reference 2. In this paper, we will discuss practical implementation of these techniques, in the form of MaZda computer program.

MaZda: a software package for quantitative texture analysis

The main steps of the intended image texture analysis are illustrated in Figure 3. First, the image is acquired by means of a suitable scanner. The ROIs are defined using the interactive graphics user interface of the MaZda program. (The name “MaZda” is an acronym derived from “Macierz Zdarzen,' which is Polish for ”co-occurrence matrix.“ Thus, MaZda has no connection with the Japanese car manufacturer.) Up to 16 ROIs can be defined for an image; they may overlap each other. Once ROIs are established, MaZda allows calculation of texture parameters available from a list of about 300 different definitions that cover most of the features proposed in the known literature. The parameters can be stored in text files.

Figure 3. Main steps of digital image texture analysis.

One can demonstrate using properly designed test images that some of the higher-order texture parameters, especially those derived from the co-occurrence matrix, show correlation to first-order parameters, such as the image mean or variance. To avoid this unwanted phenomenon, prior to feature extraction, image normalization is preferably performed.

Typically, the features computed by MaZda are mutually correlated. Morover, not all of them are equally useful for classification of given texture classes or to measure properties of the underlying physical object, structure. Thus, there is a need for feature selection. To do that, a subset of the computed parameters can be selected manually. MaZda also offers the possibility of selecting the best 10 features automatically following two different selection criteria. One criterion maximizes the ratio of between-class to within-class variance, which resembles the Fisher coefficient.^32,33 TTic second minimizes a combined measure of probability of classification error and correlation between features.³³

The selected best 10 parameters can be used for texture classification. Still, it is too difficult for a human operator to imagine and understand relationships between parameter vectors in the 10-dimensional data space. The B11 program of the MaZda package allows further data processing to transform them to a new, lower-dimension data space. The data preprocessing employs linear transforms, such as principal component, analysis (PCA)³⁴ and linear discriminant analysis (LDA),³² as well as nonlinear operations leading to artificial neural network (ANN)-based nonlinear discriminant analysis (NDA).³⁵The B11 program displays both input and transformed data in a form of a scatter-plot graph.

B11 allows also raw and transformed data vectors classification, and evaluation of the usefulness of texture features calculated using MaZda to classification of different texture classes present in image regions. For data classification, the nearest-neighbor classifier (k-NN)³⁶ and ANN classifiers^33,37,38 are implemented. Neural networks of the architecture defined during training can be tested using data sets composed of feature vectors calculated for images not used for the training.

At the time of writing this paper, MaZda version 3.20 was available. It implements procedures which allow⁴:

• Loading image files in most popular MRI scanner standards (such as Siemens, Picker, Brucker, and others). MaZda can also load images in the form of Windows Bitmap files, DICOM files, and unformatted gray-scale image files (raw images) with pixel intensity encoded with 8 or 16 bits. Additionally, details of image acquisition protocol can be extracted from the image information header.

• Image normalization. .There are three options: default (analysis is made for original image); ±3σ (image mean m value and standard deviation a is computed, then analysis is performed for gray scale range between m-3σ and m+3σ); or 1 % -99 % (gray-scale range between 1% and 99% of cumulated image histogram is taken into consideration during analysis).

• Definition of ROIs. The analysis is performed within these regions. Up to 16 regions of any shape can be defined; they can be also edited, loaded, and saved as disk files. A histogram of defined ROIs may be visualized and stored.

• Image analysis, which is computation of texture feature values within defined ROIs. The feature set (almost 300 parameters) is divided into following groups: histogram, co-occurrence matrix, run-length matrix, gradient, autoregressive model, and Haar wavelet-derived features. Detailed description of feature definitions can be found in reference 33.

• Computation of feature maps that represent distribution of a given feature over an analyzed image. It is possible to save or load feature maps into a special floating-point file format or into Windows Bitmap file.

• Display of image analysis reports, saving, and loading reports into disk files.

• Feature reduction and selection, in order to find a small subset, of features that, allows minimum error classification of analyzed image textures. This is performed by means of two criteria, as explained above. Selected features can be transferred to B11 program for further processing and/or classification.

• Image analysis automation by means of text scripts containing MaZda language commands. Scripts allow loading analyzed images and their ROI files, running the analysis, and saving report files on disk.

The number of features computed by MaZda is still increasing. New feature groups are added according to suggestions of the project members and other MaZda users. Also, new procedures for data processing are being appended.

MaZda module

MaZda generates windows and selected window elements when the program main functions are invoked. The report window contains list of numerical values of all parameters computed by MaZda for defined ROIs. The selection of texture parameters that are actually computed is made using appropriate options window. Once computed, the reports can be stored as text files. There is a possibility of manual and automatic feature selection that gives lists of 10 parameters maximizing selection criteria. These lists can be stored as text files.

Texture parameters can also be computed by MaZda in a rectangular ROI moved automatically around the analyzed image. Parameter values calculated for each ROI position can be arranged to form a new image, a so-called feature map. Options of feature maps calculations (ROI size and step size of ROI movement) can be selected using appropriate window tools.

B11 module

This program can either be called from the MaZda windows or run as a separate MS Windows application. Input to this program is a file containing data vectors corresponding to selected texture parameters. TTic content of this file is displayed in the left panel of B11 window. The results of data transformation and classification are shown in the right panel of the window. The input data preprocessing and classification options can be selected in the options window.

Nonlinear transforms and classifiers implemented in B11 employ feedforward ANNs. Training techniques of these networks are described in the User's Manual of MaZda.³³ The clusters formed in the transform data spaces can be visualized in the form of 2D or 3D scatter plots, which are generated by B11 program and discussed in the next section.

Application example 1

Figure 4a shows an MRI image that contains regions of different texture, and its respective ROIs are illustrated in Figure 4b Each circular region in Figure 4a represents a cross-section through a tube filled with polystyrene spheres of different diameters, which were test objects manufactured in the Institute of Clinical and Experimental Medicine in Prague. The example experiment described here was made to verify whether texture classes represented in the image in Figure 4a could be classified based on some selected texture parameters computed using the MaZda software.

Figure 4. Magnetic resonance image cross-section of four test objects of different texture. B. Four regions of interest (four texture classes) defined for the image in A.

There were 22 images showing different cross-sections of the test objects, leading to 22 examples of texture of each class. Numerical values of about. 300 texture statistical parameters were computed using MaZda module. This step produced eighty-eight 300-dimensional data vectors. A list of 10 best, features was then automatically generated based on Fisher coefficient criterion (maximization of the ratio F of between-class to within-class variance). The best parameters were then passed to the B11 module. Thus, the input to B11 was made of eighty-eight 10-dimensional data vectors, with 22 vectors for each texture class.

A scatter plot of the input data in the 3D data space was made of first three best texture features. The raw data were transformed to lower-dimensional spaces, using the PCA, LDA, and NDA projections. In each case, the Fisher coefficient F was calculated for the obtained data vectors. They were also classified using a 1-NN classifier, and tested using a leave-one-out technique.³⁶

The PCA projection to a lower-dimensionality data space does not improve the classification accuracy. This can be explained by the fact that PCA is optimized for representation of data variability, which is not the same as data suitability for class discrimination (which is the case of LDA). Although the LDA gives lower value of the .Fisher coefficient F, it eliminates the classification errors. Thus, the lower F coefficient, does not necessarily indicate worse classification. Extremely large F can be obtained using NDA; however, one should verify (using a separate test, dataset) whether the ANN does not suffer from the overtraining problem.³⁸ An overtrained network does not. generalize the training data well and, consequently, it may wrongly classify unseen data points.

Application example 2

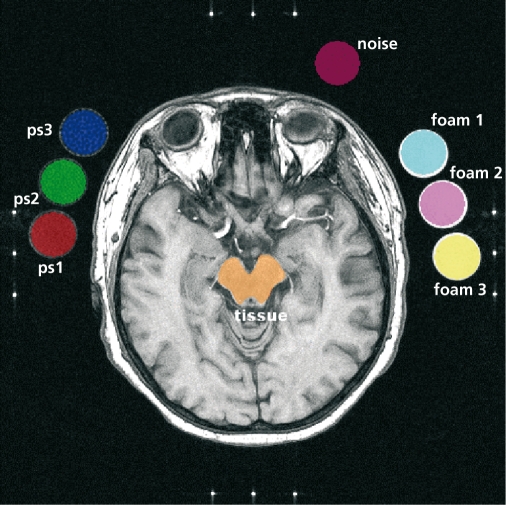
Figure 5 shows an MRI image that contains cross-section of human scull, along with cross-section of six artificial test objects (phantoms designed and manufactured to generate standard texture patterns), three on each side of the scull. There are altogether eight ROIs defined for this image, each marked with a different color. The numerical experiment carried out. on seven images of the described category aimed to verify whether one can find features able to separate mixed, artificial, and natural textures.

Figure 5. Magnetic resonance image with eight regions of interest (ROIs) marked with different colors. ps1, ps2, ps3, foam 1, foam 2, and foam 3 are test objects.

The experiment was performed in three parts. First, higherorder features were considered only. Those were co-occurrence matrix, run-length matrix, gradient, and autoregressive model-derived parameters. The best of these were automatically selected by MaZda. Using the Bll program, the two sets of best, features were transformed (PCA and LDA) and the transform data were used as new features for classification (by means of a 1-NN classifier tested using the “leave-one-out” technique). The results are shown in Table I, which indicates, that lowest error figure (3/56) was obtained for the LDA data, with no possibility of perfect classification.

In the second part of the experiment, histogram-based features were added to the higher-order ones used in the first part. Table I shows significance of these parameters in region discrimination. Perfect classification was achieved for LDA- transformed data. One can notice that even if histogram data do not represent texture, they are significant to ROI classification.

In the third part, wavelet-based features only were used. Table I shows that perfect ROI discrimination is possible even in the raw data space. This family of features seems to describe texture for classification purposes extremely well. The results collected (Table I) indicate that one cannot specify in advance which particular texture features will be useful for discrimination of texture classes, and that raw-data texture features usually do not allow perfect discrimination - some pre-processing is necessary, eg, by means of linear or nonlinear discriminant transforms.

Table I. Number of classification errors (out of 56 samples) for higher-order features (histogram and wavelet-based features excluded; wavelet-based features excludes; and wavelet-based features only). POE, probability of classification error; AC, average correlation coefficient; PCA, principal component analysis; LDA, linear discriminant analysis.

	“As computed” data			Standardized data
	Raw	PCA	LDA	RAW	PCA	LDA
Best higher-order features (histogram and wavelet-based features excluded)
Fisher	22	31	19	22	31	19
POE+ACC	26	28	3	6	4	4
Best higher-order features (wavelet-based features excluded)
Fisher	1	1	1	9	9	1
POE+ACC	24	24	0	4	3	2
Best higher-order features (wavelet-based features only)
Fisher	3	4	0	0	0	0
POE + ACC	3	6	0	0	0	0

Summary

Texture analysis applied to MRI (and other modalities) is one of the methods that provide quantitative information about internal structure of physical objects (eg, human body tissue) visualized in images. TTiis information can be used to enhance medical diagnosis by making it more accurate and objective. Within the framework of a European COST B11 action, a unique package of computer programs has been developed for texture quantitative analysis in digital images. The package consists of two modules: MaZda.exe and B11.exe.The modules are seamlessly integrated, and each of the modules can be run as a separate application. Using the package, one can compute a large variety of different texture features and use them for classification of regions in the image. Moreover, MaZda allows generation of feature map images that can be used for visual analysis of image content in a new feature space, highlighting some image properties. The package has already been used for quantitative analysis of MRI images of different kinds,³⁹ such as images of human liver'¹⁰ and computed tomography images for early detection of osteoporosis.²³ The program appears to be a useful research tool in a PhD student laboratory.⁴¹

The MaZda package is available on the Internet.³³ So far more than 300 researchers from all over the world have downloaded it onto their computers.

Selected abbreviations and acronyms

ANN

artificial neural network

LDA

linear discriminant analysis

NDA

nonlinear discriminant analysis

PCA

principal component analysis

ROI

region of interest

This article is published following the 14th Biological Interface Conference held in Rouffach, France, between October 1 and 5, 2002, on the theme of “Drug Development.” Other articles from this meeting can be found in Dialogues in Clinical Neuroscience (2002, Vol 4, No 4).

Delivery of MRI images by Dr Richard Lerski of Dundee University and Hospital (Figure 2a), Prof Milan Hajek of the Institute of Clinical and Experimental Medicine in Prague (Figure 4), Prof Lothar Schad of German

Cancer Research Centre in Heidelberg (Figures 1 and 5), and Dr Michal Strzelecki (Figure 2) is very much appreciated.