Pairwise additivity of energy components in protein-ligand binding: The HIV II protease-Indinavir case

Abstract

An energy expansion (binding energy decomposition into n-body interaction terms for n ≥ 2) to express the receptor-ligand binding energy for the fragmented HIV II protease-Indinavir system is described to address the role of cooperativity in ligand binding. The outcome of this energy expansion is compared to the total receptor-ligand binding energy at the Hartree-Fock, density functional theory, and semiempirical levels of theory. We find that the sum of the pairwise interaction energies approximates the total binding energy to ∼82% for HF and to >95% for both the M06-L density functional and PM6-DH2 semiempirical method. The contribution of the three-body interactions amounts to 18.7%, 3.8%, and 1.4% for HF, M06-L, and PM6-DH2, respectively. We find that the expansion can be safely truncated after n = 3. That is, the contribution of the interactions involving more than three parties to the total binding energy of Indinavir to the HIV II protease receptor is negligible. Overall, we find that the two-body terms represent a good approximation to the total binding energy of the system, which points to pairwise additivity in the present case. This basic principle of pairwise additivity is utilized in fragment-based drug design approaches and our results support its continued use. The present results can also aid in the validation of non-bonded terms contained within common force fields and in the correction of systematic errors in physics-based score functions.

INTRODUCTION

Fragment-based drug design (FBDD), which focuses on using small molecular “fragments” to form larger molecules,¹ has gained considerable popularity over the past decade and forms a complementary approach to methods such as high throughput screening of drug-like molecules.² Many academic institutions and major pharmaceutical and biotechnology companies have put an emphasis on FBDD with their efforts placing drug candidates into clinical trials.³ FBDD scans small molecule libraries for activity using biophysical techniques such as surface plasmon resonance, protein-ligand NMR spectroscopy, isothermal titration calorimetry, x-ray crystallography, or with bioassays.² In addition, technological advancements have allowed for the development of various computational tools, which aid in different phases of a FBDD effort such as the generation of fragment libraries and in silico screening of these libraries against targets to identify potential hits. The hope that successful binding mode prediction would facilitate the evolution of a hit to a potent lead molecule underscores the need for molecular docking studies^{4, 5, 6, 7, 8} and this has given rise to the use of computational screening as a starting point in FBDD.⁹

The underlying assumption in FBDD is an additive (or nearly-additive) enhancement of binding affinity from each of the fragment molecules constituting the fully assembled inhibitor. Our study assesses the validity of this assumption in a realistic model by exploring the additivity of quantum mechanics-derived fragment energies relative to interaction energies computed for an entire protein-ligand complex. The model system is the active site of the human immunodeficiency virus (HIV) II protease bound to the commercially available drug Indinavir,^{10, 11, 12} which has been isolated from the rest of the enzyme and abstracted into a series of representative protein-ligand fragments. The interaction energy expansion functional adopted from Xantheas's study of water clusters¹³ has been utilized to compute the n-body corrections for the interaction energy of the fragment model of the binding pocket with the inhibitor and these have been compared to the binding energy of the ligand to the pocket as a whole. Although we anticipated a non-additivity level of up to 30% of the total binding energy as observed in Xantheas's water cluster studies, we found largely an additive interaction pattern for the protein-ligand model system we studied.

Before proceeding, the definition for additivity and non-additivity must be established. Benos and co-workers expressed additivity as the independent contribution of fragments to binding.¹⁴ Thus, the total interaction energy would equal to the sum of the energies of the individual contacts. The simplest unit of a contact involves two bodies, where only one interaction is present between the fragment pairs. Hence, the real simplifying assumption for combinatorial purposes would involve pairwise additivity, which ignores n-body interactions with n > 2 because of their (presumed) very low contribution to the total interaction energy. However, in the case of water clusters Xantheas found contributions as high as 30% for three-body interactions.¹³ Shimizu and Chan emphasize the pairwise character of additivity by comparing the total free energy of association among a set of N solutes to the sum of free energies of all two-body combinations of these N solutes, specifically to the N(N-1)/2 possible pairings of the solutes calculated one pair at a time for two solutes while the effects of the remaining N-2 solutes were ignored.¹⁵ Here, we should make a distinction between our work and this approach – we do not predict anything specifically about free energies but only electronic energies, which is further discussed in the “Theory” section. Nonetheless, this study constitutes a validation of pairwise additivity of interaction energies computed in FBDD studies.

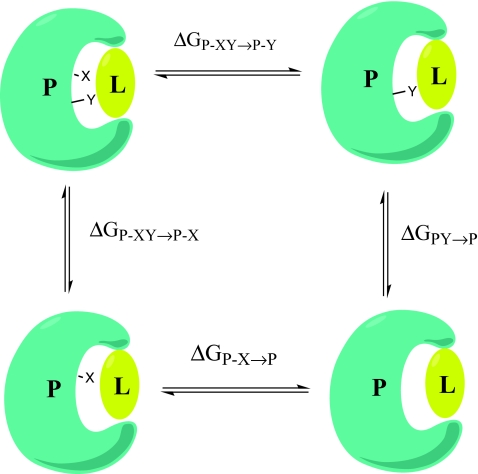
Biochemists examine additivity concepts through double mutant cycles.¹⁶ Basically, constructing a double mutant cycle corresponds to constructing a thermodynamic cycle involving the wild-type protein, the protein with a particular point mutation in the region of interest, the protein with a different point mutation again in the region of interest and the protein with both single mutations applied simultaneously as shown in Figure 1. Thus, if free energy additivity holds true, the impact of the double mutation should be equal to the sum of the two single mutations which allows for the prediction of the free energy associated with a certain functionality or structural element of any protein in the cycle from measurements of the other three proteins in the cycle. This practice resembles our strategy, whereby the ligand is kept intact and the binding pocket of the protein is varied, but has focused on addressing the (non)-additivity of free energies. Free energy additivity of point mutations has been observed at enzyme-substrate interfaces in several studies.^{17, 18, 19} However, the observed additivity was largely traced back to the remoteness of the point mutation sites, which implies no interaction between the two sites. Any means of interaction between the two mutated residues, both via direct contact and indirect electrostatic interactions were described by Wells as factors which would cause the simple additivity model to collapse.¹⁹ Schreiber and Fersht examined coupling free energies between two mutated sites, ΔΔG_int, which correspond to non-additivity in the thermodynamic cycle of singly- and doubly-mutated proteins.²⁰ They found that residues separated by less than 7 Å showed non-additivity and this non-additive behavior was interpreted to imply cooperativity between those residues. It was concluded that at greater separations the effects of the point mutations were additive implying that the mutual interaction between these point mutations was minimal. In contrast, our studies have explored the additivity of interaction energies beyond these distance boundaries. Some fragments that we examined were separated by less than 7 Å, but only had interaction energies of a few hundredths of a kcal/mol. Nevertheless, the observed free energy additivity behavior of fragment energies located in close proximity can be complex, as demonstrated by Wells.¹⁹ Establishment of an inverse correlation between additivity and cooperativity is a very common conclusion. That is, most studies connect the non-additivity to cooperativity among the examined fragments.^{15, 19, 20} Accordingly a non-zero coupling energy, which is accepted to be the measure of the cooperativity between interacting fragments, implies either a direct interplay mediated by steric, electrostatic, hydrogen-bonding, or hydrophobic interactions, or an indirect interplay through structural changes in the protein or solvent shell. The non-additive character of free energies associated with fragments is largely the result of the non-additivity of entropic terms. However, for enthalpies or energies, in addition to being theoretically justified,²¹ additivity has been observed in, for example, the isothermal calorimetry experiments of Baum et al. and Olejniczak et al.^{22, 23} Geometrical changes induced by point mutations can contribute to the non-additivity of observed free energies, but this point is not a major concern in the present work because of the fixed geometry we are using and due to the additivity of enthalpies experimentally observed in Refs. ²² and ²³.

Figure 1.

A representative double mutant cycle involving protein (P)-ligand (L) interactions. X and Y stand for two residues, which are mutated individually and together in the wild type protein (P-XY). The free energy change associated with each mutation is inserted into the following equations in order to obtain the free energy of coupling, ΔΔG_int: ΔΔG _int =ΔG_{P− XY →P−X}−ΔG_P−Y→P=ΔG_{P− XY →P−Y}−ΔG_P−X→P.

In order to understand the role additivity plays, it is important to select the appropriate computational model. The method to be employed should have a good balance between accuracy, cost-efficiency, and feasibility in terms of memory and computer time requirements. Recent work examining the accuracy of several computational methods when compared to complete basis set (CBS) results acquired at the coupled-cluster single double (triple) (CCSD(T)) level of theory suggested that the M06-L (Ref. ²⁴) meta-GGA (generalized gradient approximation) functional is such an appropriate level of theory.²⁵ Even in conjunction with the 6-31G* basis set²⁶ it yielded a narrow error distribution for the bound Indinavir system. We note that in spite of its relative accuracy and speed the M06-L functional has difficulty with convergence for charged systems.²⁷ Thus, substantial effort was expended to deal with convergence problems for fragments containing acetate and methyl guanidinium. For comparison purposes HF/6-31G* and PM6-DH2 calculations were performed as well.

The present work is organized as follows: first, the model system and the computational details are reviewed. Next, the justification for using the computed energies as a measure of additivity validation is presented. The energy decomposition scheme for the cluster analysis of the binding site of the enzyme complexed with its inhibitor is then introduced. Then the contributions of the n-body interactions to the total energy of the system are evaluated at different levels of theory and the conclusions are given. Finally, the ramifications of our work on FBDD and force fields are discussed.

METHODS

The protein-ligand model system is based on the crystal structure of the HIV II protease obtained from Protein Data Bank at 1.9 Å resolution (PDB ID:1HSG).¹⁰ The binding pocket was decomposed previously into a total of 21 fragments by Faver et al. in their recent study,²⁵ for which the enzyme-ligand complex structure was obtained from the PDB, hydrogen atoms were added to the structure with the program Reduce²⁸ and were subsequently optimized with the AMBER FF99SB force field.²⁹ These 21 receptor fragments and the ligand were combined to model the binding site. Overlapping receptor fragments were joined to yield a total of 18 fragments from the original 21 fragments. The resultant cluster structure was retained for all subsequent calculations. The final model contained short aliphatic alkanes including ethane, propane, isobutane, and butane along with polar species consisting of acetate, acetic acid, methyl guanidinium, and four peptide chains containing up to 35 atoms. Two tightly coordinated water molecules in the crystal structure were retained and treated as two distinct fragments. The ligand L-735 524,^{11, 12} an orally bio-available inhibitor of HIV proteases with the commercial name Indinavir, was kept intact in all calculations.

Single point calculations were carried out at the HF, density functional theory (DFT), and semiempirical levels. The 6-31G* Pople type basis set²⁶ was used throughout. The M06-L/6-31G* combination of level of theory was chosen because of its narrow systematic and random error distribution with respect to a CCSD(T)/CBS reference. Moreover, through its parameterization the M06-L functional gives a good account of intermolecular interactions as evidenced by the low systematic error associated with the polar and non-polar interactions relative to CCSD(T)/CBS reference calculations. On the other hand, HF/6-31G* calculations represent another extreme in that this method has both large random and systematic errors largely due to the incorrect treatment of dispersion.²⁵ The large size of the quantum region was the major obstacle to upgrading to much larger basis sets and prompted our choice of the 6-31G* basis set. In order to examine higher order multi-body interaction energies the semiempirical PM6-DH2 (Ref. ³⁰) level of theory was employed due to its accurate performance with regards to the CCSD(T)/CBS results and its fast computational speed. Considering the individual accuracies for polar and non-polar interactions gave us further confidence in the use of PM6-DH2 method in our calculations.²⁵

Convergence problems were encountered for some of the acetate and methyl guanidinium containing systems, which were addressed by using quadratic convergence methods,³¹ Fermi temperature broadening,³² and shifting of orbital energies. In order to correct for the basis set superposition error the counterpoise method was applied.³³ In each calculation the nuclei of the atoms which did not belong to that particular calculation were deleted while their basis functions were retained.

The DFT and HF calculations were performed with the GAUSSIAN 09 (Ref. ³⁴) suite of programs, while MOPAC2009^TM,³⁵ was used for the semiempirical computations. Visualizations were done using the Visual Molecular Dynamics (VMD) (Ref. ³⁶) program, while the density plots were obtained using the statistical software package R.³⁷

THEORY

The process of partitioning a larger molecule into constituent fragments and treating those fragments as unique bonding units within the framework of the larger system formally splits the Hamiltonian of the larger molecule into individual fragment Hamiltonians. The total binding energy is given by the ensemble average of the Hamiltonian H of the full ligand containing N particles, at a volume V and at a temperature T:²¹

$$E\left(N,V,T\right)={〈H〉}_{N,V,T}.$$ (1a)

Now, let us assume that the Hamiltonians associated with the distinct fragments sum to model the Hamiltonian of the full protein-ligand system. Thus, for a system of n fragments,

$$H=\sum _{i=1}^n{H}_i.$$ (1b)

By combining Eq. 1a and Eq. 1b, we can define an energy expression:

$$E=〈H〉=〈\sum _{i=1}^n{H}_i〉=\sum _{i=1}^n{E}_i,$$ (1c)

suggesting that the energy and enthalpy of the system is additive as long as the Hamiltonian is additive.

The additivity of enthalpies was experimentally studied by Baum et al. using isothermal titration calorimetry for a series of thrombin inhibitors.²² Incorporation of a particular functionality into the inhibitor always corresponded to a specific ΔΔH, which underlines the independent (additive) behavior of the enthalpy component, whereas the free energies and the entropy components for the same structural changes were much more variable suggesting non-additivity. Furthermore, this finding also supports the idea of associating a functional group present within a molecule with a given enthalpy change, which bolsters the notion of attributing certain energies or enthalpies to fragments of a larger molecule.

In this study we employ an approximation for the energy decomposition of the binding pocket of HIV II protease bound to the ligand Indinavir.^{10, 11, 12} The decomposition scheme we used was adopted from Xantheas's formulation for water clusters.¹³ The total energy E_n of an n-body cluster can be expanded into one-, two-, three-, four-, …, n-body terms via the formula below

$$\begin{array}{ccc}\hfill E_n& =& E\left(1234...n\right)\hfill \\ & \equiv & \sum _{i=1}^{n}E\left(i\right)+\sum _{i=1}^{n-1}\sum _{j>i}^n{\Delta }^{2}E\left(ij\right)\hfill \\ & & +\sum _{i=1}^{n-2}\sum _{j>i}^{n-1}\sum _{k>j}^n{\Delta }^{3}E\left(ijk\right)\hfill \\ & & +\sum _{i=1}^{n-3}\sum _{j>i}^{n-2}\sum _{k>j}^{n-1}\sum _{l>k}^n{\Delta }^{4}E\left(ijkl\right)\hfill \\ & & +...+{\Delta }^{n}E\left(1234...n\right).\hfill \end{array}$$ (2)

Here, the first term corresponds to the one-body term, the second to the two-body, the third to the three-body, … and eventually the last term to the n-body term. E(i) denotes the energies of the single fragments or the ligand, E(ij) represents the energies of all possible combinations involving two bodies out of the pool of fragments and the ligand and E(ijk), E(ijkl) describe the energies of the multi-body combinations out of the same pool.

The total binding energy of the Indinavir ligand to the HIV II protease binding pocket, which was split into 18 fragments, was first calculated using Eq. 3,

$$E_{bind}=E_{l+bp}-E_l-E_{bp},$$ (3)

where E_bind stands for the total binding energy, E_{l + bp} is the energy of the entire system consisting of the ligand and the fragmented binding pocket, E_l indicates the energy of the ligand, and E_bp refers to the energy of the binding pocket comprising its 18 fragments. The total binding energy E_bind is compared to the binding energy $E_{bind}^{\prime }$, which was obtained from the expansion 2 for the same system. If we write $E_{bind}^{\prime }$ explicitly using Eq. 2 and label the ligand as the 19th fragment, we arrive at

$$\begin{array}{ccc}\hfill E_{bind}^{\prime }& =& \sum _{i=1}^{19}E\left(i\right)+\sum _{i=1}^{18}\sum _{j>i}^{19}{\Delta }^{2}E\left(ij\right)+\sum _{i=1}^{17}\sum _{j>i}^{18}\sum _{k>j}^{19}{\Delta }^{3}E\left(ijk\right)\hfill \\ & & +\sum _{i=1}^{16}\sum _{j>i}^{17}\sum _{k>j}^{18}\sum _{l>k}^{19}{\Delta }^{4}E\left(ijkl\right)+...\hfill \\ & & +{\Delta }^{19}E(1234...19)-E\left(19\right)\hfill \\ & & -\left(\sum _{i=1}^{18}E\left(i\right)+\sum _{i=1}^{17}\sum _{j>i}^{18}{\Delta }^{2}E\left(ij\right)\right.\hfill \\ & & +\sum _{i=1}^{16}\sum _{j>i}^{17}\sum _{k>j}^{18}{\Delta }^{3}E\left(ijk\right)\hfill \\ & & +\sum _{i=1}^{15}\sum _{j>i}^{16}\sum _{k>j}^{17}\sum _{l>k}^{18}{\Delta }^{4}E\left(ijkl\right)+...\hfill \\ & & \left.+{\Delta }^{18}E(1234...18)\right).\hfill \end{array}$$ (4)

The collection of terms in the first row of the expansion 4 corresponds to E_{l + bp} in Eq. 3, E(19) is equivalent to E_l and the expression in the third row excludes the 19th fragment, namely, the ligand, leaving the energy of the whole binding pocket composed of 18 fragments (n = 1–18) in the absence of the ligand. The difference between E_bind and $E_{bind}^{\prime }$ will help us address the issue of additivity or non-additivity of the interaction energy. As more terms in Eq. 4 are considered, the difference between $E_{bind}^{\prime }$ and E_bind will approach zero. Truncation at lower order terms (e.g., two-body) will allow us to investigate the contribution of the higher order multi-body terms to E_bind.

Let us turn our attention to the individual n-body terms. The two-, three-, four-, and … n-body terms are defined as follows:

$$\begin{array}{ccc}\hfill {\Delta }^{2}E\left(ij\right)& =& E\left(ij\right)-\left\{E\left(i\right)+E\left(j\right)\right\}\hfill \\ \hfill {\Delta }^{3}E\left(ijk\right)& =& E\left(ijk\right)-\left\{E\left(i\right)+E\left(j\right)+E\left(k\right)\right\}\hfill \\ & & -\left\{{\Delta }^{2}E\left(ij\right)+{\Delta }^{2}E\left(ik\right)+{\Delta }^{2}E\left(jk\right)\right\}\hfill \\ \hfill {\Delta }^{4}E\left(ijkl\right)& =& E\left(ijkl\right)-\left\{E\left(i\right)+E\left(j\right)+E\left(k\right)+E\left(l\right)\right\}\hfill \\ & & -\{{\Delta }^{2}E\left(ij\right)+{\Delta }^{2}E\left(ik\right)\hfill \\ & & +{\Delta }^{2}E\left(il\right)+{\Delta }^{2}E\left(jk\right)+{\Delta }^{2}E\left(jl\right)+{\Delta }^{2}E\left(kl\right)\}\hfill \\ & & -\{{\Delta }^{3}E\left(ijk\right)+{\Delta }^{3}E\left(ikl\right)+{\Delta }^{3}E\left(jkl\right)\hfill \\ & & +{\Delta }^{3}E\left(ijl\right)\}....\hfill \end{array}$$ (5)

The number of m-body terms out of a system of n bodies, where m ≠ n, is simply given by the number of m-combinations out of a set of n bodies. Thus, for our cluster with 19 bodies, there are $\left(\begin{array}{c}19\\ 2\end{array}\right)=\frac{19!}{2!*17!}=171$E(ij) values. However, using Eq. 4 and noting that the 18 receptor fragments are common to both expansions in the first and the third rows, we observe that only the E(ij) values involving the ligand, the 19th fragment, will survive. Thus, the total two-body term ∑Δ²E(ij) encountered in Eq. 4 involves $\left(\begin{array}{c}19\\ 2\end{array}\right)-\left(\begin{array}{c}18\\ 2\end{array}\right)=18$ Δ²E(ij) values, which is actually obvious from the fact that there exist 18 fragments to pair with the ligand. The same logic applies to the Δ³E(ijk), Δ⁴E(ijkl), … terms, which will be referred to as n-body correction terms in the sense that these terms supplement the total ∑Δ²E(ij) term in converging to E_bind. In other words, they correct $E_{bind}^{\prime }$ to approach E_bind. Hence, 153 Δ³E(ijk) values are required to calculate the total three-body correction term, while 816 and 3060 and Δ⁴E(ijkl)’s and Δ⁵E(ijklm)’s compose the total four-body and five-body correction terms, respectively. As indicated above, the many-body energy values in the correction terms always involve the ligand since the interactions among only the receptor fragments are cancelled in the total decomposition scheme.

The sum of the two-body terms, namely, the ∑Δ²E(ij) is defined as the additive part of the binding energy decomposition, while the higher multi-body correction terms represent the non-additive part. According to this definition, the neglect of higher order multi-body corrections might be expected to produce a significant difference between $E_{bind}^{\prime }$ and E_bind demonstrating the importance of non-additivity. This is what was observed in the work of Xantheas for water clusters, where the three-body terms and above represented 30% of the total binding energy. On the other hand, for the energy decomposition scheme given by Eq. 1c, the additive part must be much bigger than the non-additive many-body correction terms. This manuscript aims to elucidate the extent of non-additivity for protein-ligand binding clusters.

Having chosen our cluster we need to address the basis set superposition error (BSSE) because we will employ finite basis sets for our calculations. We applied the counterpoise method to account for BSSE.³³ Accordingly, the energies of the many-body subsystems, e.g., E(ijk) for the subsystem (ijk), at the cluster geometry were calculated in the full basis of the entire system, which was denoted by E(ijk|ijk…n). That is, in all the multi-body energy calculations, the basis functions centered on each of the 323 nuclei were kept, while the nuclei, which do not participate in that particular calculation were deleted. The inclusion of these so-called “ghost” orbitals removes the effects of BSSE. This approach completes the formulation of the individual many-body correction terms given in Eq. 5 by converting the expressions into Eq. 6,

$$\begin{array}{ccc}\hfill {\Delta }^{2}E\left(ij\left|ijkl...n\right.\right)& =& E\left(ij\left|ijkl...n\right.\right)-\left\{E\left(i\left|ijkl...n\right.\right)+E\left(j\left|ijkl...n\right.\right)\right\}\hfill \\ \hfill {\Delta }^{3}E\left(ijk\left|ijkl...n\right.\right)& =& E\left(ijk\left|ijkl...n\right.\right)-\left\{E\left(i\left|ijkl...n\right.\right)+E\left(j\left|ijkl...n\right.\right)+E\left(k\left|ijkl...n\right.\right)\right\}\hfill \\ & & -\{{\Delta }^{2}E\left(ij\right|ijkl...n)+{\Delta }^{2}E\left(ik\right|ijkl...n)+{\Delta }^{2}E\left(jk\right|ijkl...n)\}\hfill \\ \hfill {\Delta }^{4}E\left(ijkl\left|ijkl...n\right.\right)& =& E\left(ijkl\left|ijkl...n\right.\right)-\left\{E\left(i\left|ijkl...n\right.\right)+E\left(j\left|ijkl...n\right.\right)+E\left(k\left|ijkl...n\right.\right)+E\left(l\left|ijkl...n\right.\right)\right\}\hfill \\ & & -\left\{\begin{array}{c}{\Delta }^{2}E\left(ij\left|ijkl...n\right.\right)+{\Delta }^{2}E\left(ik\left|ijkl...n\right.\right)+{\Delta }^{2}E\left(il\left|ijkl...n\right.\right)+\hfill \\ {\Delta }^{2}E\left(jk\left|ijkl...n\right.\right)+{\Delta }^{2}E\left(jl\left|ijkl...n\right.\right)+{\Delta }^{2}E\left(kl\left|ijkl...n\right.\right)\hfill \end{array}\right\}\hfill \\ & & -\{{\Delta }^{3}E\left(ijk\right|ijkl...n)+{\Delta }^{3}E\left(ikl\right|ijkl...n)+{\Delta }^{3}E\left(jkl\right|ijkl...n)+{\Delta }^{3}E\left(ijl\right|ijkl...n)\}\hfill \\ & & ....\hfill \end{array}$$ (6)

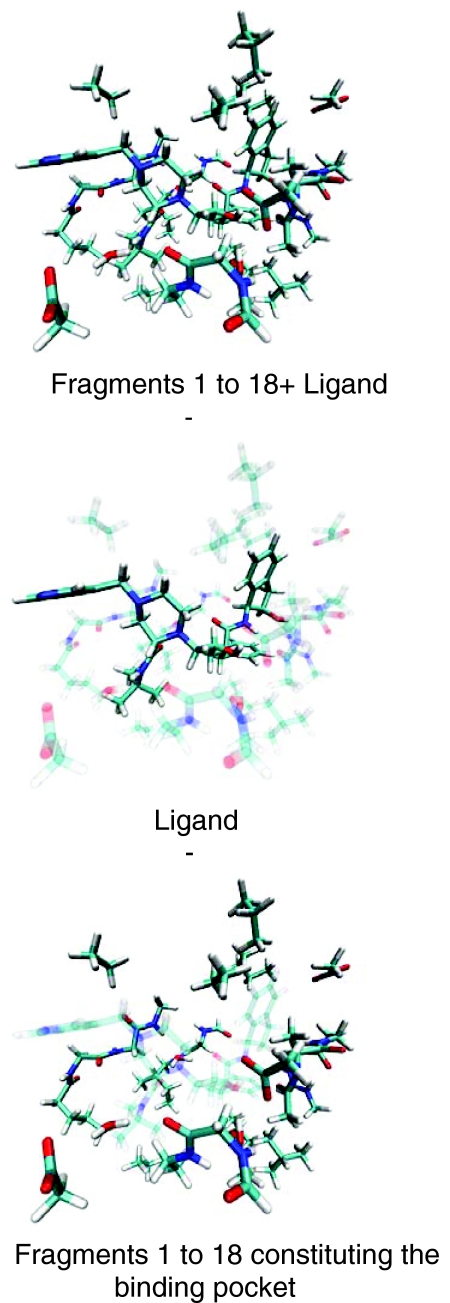
Figures 23 visually demonstrate the procedure used to obtain the binding energies $E_{bind}^{\prime }$ and E_bind. Insertion of the individual correction terms given in Eq. 6 into Eq. 4 yields the terms that must be computed to obtain the two binding energies. In Figure 2, Eq. 3 is visualized for the HIV II protease-ligand system. The atoms containing ghost orbitals are transparent, while the darker atoms designate the nuclei present in that particular calculation.

Figure 2.

Visualization of the components of Eq. 3: Upper panel shows the whole system with all the 18 fragments of the binding pocket and the Indinavir ligand. The middle panel displays the Indinavir ligand with the “ghosted” binding pocket. The lower panel shows the entire binding pocket with Indinavir in the “ghosted” state. All figures were created using the VMD package (see Ref. 36).

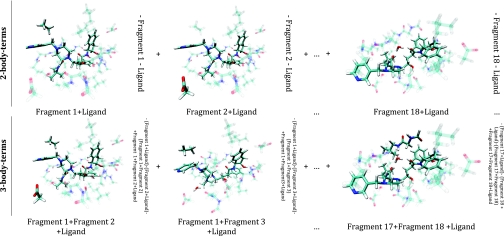
Figure 3.

Visualization of the components summing up to total correction terms given in Eq. 4. The panels display the ligand and the particular fragments’ nuclei participating in the calculations. Transparent atoms are the “ghosted” ones, while the solid atoms are the ones whose nuclei take part in that particular calculation. All figures were created using the VMD package (see Ref. 36).

In Figure 3, the components of the energy decomposition scheme given by Eq. 4 producing $E_{bind}^{\prime }$ are represented. The same color-coding scheme used for Figure 2 applies to Figure 3.

RESULTS AND DISCUSSION

First, the total binding energy E_bind of the HIV II protease to the Indinavir ligand was computed according to Eq. 3 with the constituent terms shown in Figure 1. It was found to amount to −23.57 kcal/mol, −111.60 kcal/mol, and −131.68 kcal/mol for the HF/6-31G*, M06-L/6-31G*, and PM6-DH2 levels of theory, respectively, as shown in Table 1. Next, the correction terms ∑ΔⁿE(ij…n) given by Eq. 6 were obtained. The large jump in the number of the energy values needed to generate the total many-body correction terms set the limit to where we truncated Eq. 6. The limit is mostly forced by the computational expense of the various methods.

Table 1.

E_bind, $E_{bind}^{\prime }$ and the total correction terms for various orders of correction estimated using M06-L, HF, and PM6-DH2. For HF and M06-L, the calculations were completed up to 3° (n = 3), while with PM6-DH2, terms up to 5° were (n = 5) achieved. All energy value entries are in kcal/mol.

Level of theory	Total interaction energy for the order n				$E_{bind}^{\prime }$ up to n (kcal/mol)
	n = 2	n = 3	n = 4	n = 5	n = 3	n = 5	Ebind
HF/6-31G*	−26.86	4.24	…	…	−22.62	…	−23.57
M06-L/6-31G*	−111.49	−4.45	…	…	−115.94	…	−111.60
PM6-DH2	−132.86	1.92	−0.76	0.08	−130.94	−131.62	−131.68

Table 1 shows the individual total correction terms for the three levels of theory, HF, M06-L, and PM6-DH2. The first point to note about these total correction terms is that as n increases, the absolute value of the total correction term associated with n, ∑ΔⁿE(ij…n), decreases. That is, the magnitude of the contributions of the total correction terms associated with that particular n to $E_{bind}^{\prime }$ diminishes as n rises. For HF, it dropped from |−26.86| kcal/mol to |4.24| kcal/mol, which corresponds to a fall of 84.2%. Thus, the three-body total correction produces 18.7% of the $E_{bind}^{\prime }$. At the M06-L level, this decline is much sharper: the total two-body correction term was |−111.49| kcal/mol, while the total three-body correction equaled |−4.45| kcal/mol, which yielded a reduction of 96.0%. The ∑Δ³E(ijk) correction contributed 3.84% to the overall $E_{bind}^{\prime }$. The semiempirical PM6-DH2 level was found to show an even sharper drop of 98.6%, from |−132.86| kcal/mol to |1.92| kcal/mol. The contribution of the three-body correction terms to $E_{bind}^{\prime }$ was 1.46%. Due to the speed of semiempirical methods higher order correction terms up to n = 5 were included in the computed $E_{bind}^{\prime }$ for PM6-DH2 and were found to make small contributions. The four-body corrections add up to |−0.76| kcal/mol, which corresponds to 0.58% of the total $E_{bind}^{\prime }$ and 0.57% of the total two-body correction. The total five-body correction term is |0.08| kcal/mol, or 0.06% of the total $E_{bind}^{\prime }$ and 0.06% of the overall two-body correction. This equality of percentages in the presence or absence of the higher order correction terms ∑ΔⁿE(ij…n) with n > 2 demonstrates that their effect on the energetics within the active site of the HIV II protease bound to Indinavir is negligible. In other words, the energetics of this model system is additive. In contrast to the present cluster, Xantheas observed a non-additivity of the order of 30% for small water clusters.¹³ This finding suggested that pairwise additive potentials (e.g., MCY,³⁸ TIP3P,³⁹ etc.) of water may be less accurate than previously thought (previously it was claimed to be ∼10% (Ref. ⁴⁰)). In our case, the pairwise additivity corresponds to 86.0% of the total E_bind at the HF level, to 99.9% at the M06-L level and to 99.1% at the PM6-DH2 level of theory where the numbers were calculated by the following formula: $\left[1-|\frac{\sum {\Delta }^{2}E\left(ij\right)-E_{bind}}{E_{bind}}|\right]\times 100\%$.

Thus, in the case of the present protein ligand system pairwise additivity appears to be a realistic model.

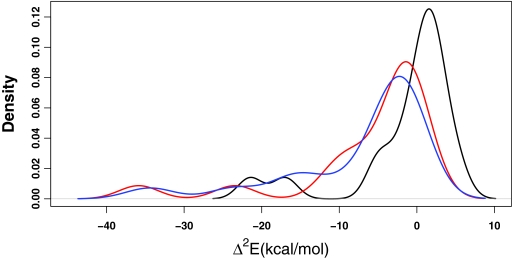
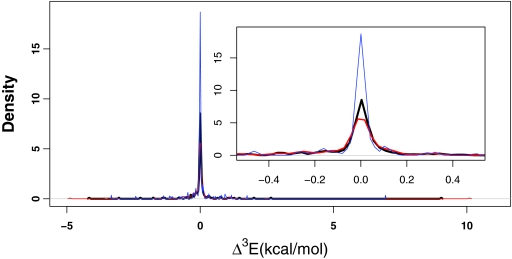
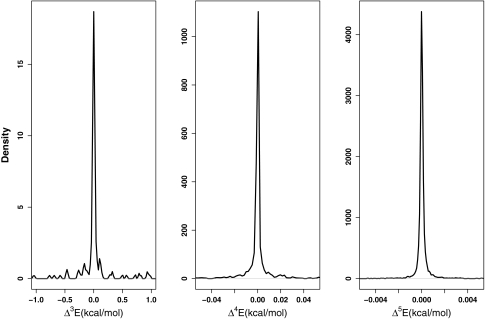
Having analyzed the cumulative effect of the total n-body correction terms with n ≥ 2, let us turn our attention to a deeper analysis of the individual multi-body correction terms. The distributions of individual correction terms for both ligand-binding pocket interactions and for the interactions among the fragments forming the binding pocket were examined. First of all, they reveal again an n-dependent behavior similar to the magnitudes of the total correction terms. As n rises, the number of terms included in the expansion jumps very rapidly, as mentioned previously and thus the populations of the distributions increase very rapidly as well. However, as one goes to higher n, the distribution gets consistently narrower. At all three levels of theory, for the ligand-binding pocket interactions, the majority of the eighteen two-body corrections have magnitudes falling into the [0.00–20.00] kcal/mol range. This range shrinks for all the methods when the three-body corrections to the ligand-binding pocket interactions are considered. At the M06-L level, the majority of the terms lie in the [−0.52:0.16] kcal/mol range at 80% confidence level, while at the HF level this range is [−0.34:0.23] kcal/mol. The PM6-DH2 level had the narrowest distribution for these interactions with a range of [−0.25:0.13] kcal/mol. For higher order n-body corrections to the ligand-binding pocket interactions, where n equals 4 and 5, only the semiempirical PM6-DH2 results are available for assessment. For the four-body corrections to the ligand-binding pocket the range is [−0.007:0.004] kcal/mol, while the range for the five-body corrections is [−0.0002:0.0003] kcal/mol. Thus, even with the large number of terms for n > 3 the sum does not yield a significant impact on the total energy $E_{bind}^{\prime }$. Figures 456 summarize these observations.

Figure 4.

The distribution of the two-body corrections to the ligand-binding pocket interaction energies at the HF level (black), M06-L level (red), and PM6-DH2 level (blue). The y axis denotes the density for all three plots (the AUC = 1). Most pairwise interactions fall into a range of [−5.06:2.70] kcal/mol for HF, [−11.10:−0.31] kcal/mol for M06-L, and [−16.00:−1.08] kcal/mol for PM6-DH2 level.

Figure 5.

The distribution of the three-body correction terms to the ligand-binding pocket interactions at M06-L, HF, and PM6-DH2 levels are given in panels (red), (black), and (blue), respectively. The inset shows the peak region in more detail, where the y axis is the density (the AUC = 1).

Figure 6.

The distributions of the n-body terms for n = 3 (left), n = 4 (middle), and n = 5 (right) at the PM6-DH2 level. These distributions apply to ligand-receptor interactions.

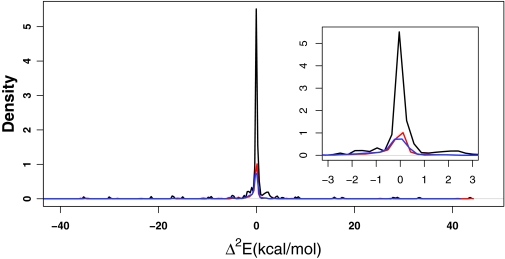
When we expand the examination of these ranges over the entire collection of interactions within the binding pocket, that is, over all the interactions among the eighteen fragments making up the binding pocket and those between the ligand and the binding pocket, the same observation is made: As n rises, the range for the magnitudes of the interaction energy corrections shrinks. By looking at the distributions shown in Figure 7 we see the majority of the pairwise interactions, that is for n = 2, fall into the range of [−1.00:1.00] kcal/mol for the HF, M06-L, and PM6-DH2 levels of theory. It should be kept in mind that the interactions between the binding pocket fragments cancel out in the overall energy decomposition scheme upon subtraction of the third row from the first in Eq. 4 when considering a particular nth total correction term, ∑ΔⁿE(ij…n). However, these interactions between the binding pocket fragments survive in the subsequent higher order correction terms and thus, their magnitudes affect the value of $E_{bind}^{\prime }$.

Figure 7.

The distributions of the pairwise corrections to all the interactions present within the Indinavir-binding pocket complex at the (black) HF level, (red) M06-L level, and (blue) PM6-DH2 level. One interaction lies around −110 kcal/mol at both HF and M06-L levels, which involved adjacent opposite charges and has been omitted for the purpose of visual clarity. The detailed peak region is shown in the inset.

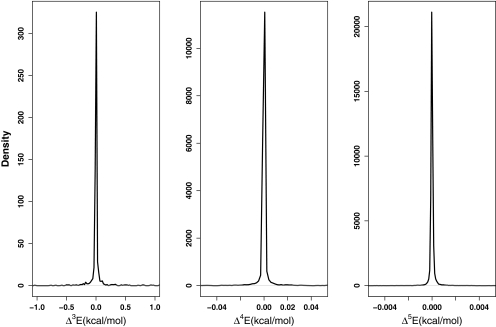
As we have seen, the energy ranges including the majority of the n-body corrections for n = 2–5 of all the interactions arising within Indinavir-binding pocket complex narrow down as n increases. For n = 2, the range of the magnitudes containing most of the interactions is [0.00:1.00] kcal/mol (Figure 7), while this range loses one order of magnitude for n = 3 (see Figure 8). For n = 4 and n = 5, the corresponding range decreases one and three orders of magnitude further relative to the three-body correction terms, respectively. Hence, there is an overall decline in the magnitudes of the interactions as more “parties” are involved in one particular interaction. To reframe the picture, in spite of the higher number of interaction terms involving increasing number of parties, the cumulative energy correction arising from the entire group of interactions among n bodies shows such a strong decay that at cases for n ≥ 4, it reaches below the limits of accurate computation.

Figure 8.

The distributions of n-body correction terms for n = 3 (left), n = 4 (middle), and n = 5 (right) at the PM6-DH2 level of theory. These correction terms apply to all the interactions involving 3- to 5-parties out of the members of the Indinavir-binding pocket complex system, including all the 18 fragments constituting the binding pocket and the Indinavir ligand.

Having discussed the limits of accuracy, it is necessary to acknowledge the uncertainty within the consecutive correction terms. Revisiting Eq. 5, the (n + 1)th total correction term of the energy decomposition scheme given in Eq. 4, ∑Δ^{n + 1}E(ijk..), includes the lower nth, (n − 1)th, (n − 2)th, … and eventually first order correction terms. At this point, any nth order correction term with n > 1 would have some level of uncertainty. The number of lower order terms contributing to the nth order correction term rises with increasing n, which results in accumulation of uncertainty within the n-body total correction term. Hence, although the decreasing magnitudes of the nth order corrections with increasing n has been confirmed by three different levels of theory, we do not claim that the numbers presented for higher n-body corrections are free of uncertainty. What is certain here is that the contribution of corrections to the total energy expansion yielding $E_{bind}^{\prime }$ decreases as one includes higher terms in the expansion given in Eq. 4.

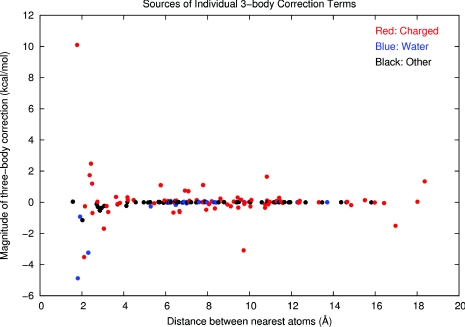
Although it was found that the pairwise interactions represent the full interaction energy E_bind to 86.0% at the HF level, to 99.9% at the M06-L level, and to 99.1% at the PM6-DH2 level of theory, the slight contribution of the higher order corrections was another point of interest. The cumulative impact of the three-body corrections was very little. However, the individual Δ³E(ijk) values associated with some of the receptor fragments and the ligand had magnitudes of several kcal/mol. In order to understand whether the magnitudes of these individual three-body corrections could be categorized according to the proximity of the two receptor fragments interacting with the ligand, the distance between the nearest atoms of the non-ligand fragments has been plotted against the corresponding three-body correction at the M06-L level of theory as shown in Figure 9. These data reveal that the significant three-body corrections stem from interactions involving polarization of the ligand or the surrounding receptor fragments. The red data points symbolize the charged fragments, whereas the blue data points stand for the two water fragments and the black data points represent the remaining peptide and hydrocarbon fragments. The charged and hydrogen-bonding fragments significantly polarize their environment including both the ligand and the non-ligand parties involved in the three-body interaction. Each polarizing entity affects the electron densities on the remaining parties involved in that particular interaction which evokes a larger magnitude for the individual three-body correction. At distances <4 Å, the impacts of polarization are stronger due to the proximity of the receptor fragments. Only the charged fragments are capable of polarizing the remaining interacting parties over greater distances (>4 Å) and influence the interaction to result in a considerable three-body correction.

Figure 9.

Magnitude of individual three-body corrections vs. the distance between the nearest atoms of the two-receptor fragments involved in the three-body interaction. Interactions involving charged fragments are color-coded with red, water fragments with blue, and other fragments with black. The plot has been obtained by using GNUPLOT 4.2.

Taken altogether, we conclude that to a good approximation, the protein-ligand complex studied herein behaves additively. This observation supports the use of pairwise additive force fields and enthalpy computation in fragment-based drug design. Most force fields define non-bonded interactions as a double summation, which can be decomposed into van der Waals and electrostatic energies over all interacting atom pairs.^{41, 42} This pairwise treatment of non-bonded interactions in protein-ligand complexes is supported by the enormous drop of contributions from the n-body correction terms, where n > 2, at multiple levels of theory. Second, as mentioned in the “Introduction,” the observed additivity for the ligand-binding pocket energetics provides a powerful approximation for the potential additivity of the binding enthalpies of the fragments when they are unified into a larger molecule.

This observed additivity has another significant application for the improvement of scoring algorithms based on energy. Faver et al.²⁵ have recently suggested that systematic errors propagate as a simple sum of the errors contained within the individual interactions associated with each fragment pair. Thus, if the sum of the energies of the fragment pairs approximates the total binding energy well enough, then the error propagation formula of Error_Systematic=Err₁+Err₂+Err₃+... represents the total systematic error to a considerable accuracy. This finding confirms the proposed idea of accounting for the systematic errors in a physics-based score function by constructing a reference library composed of numerous unique interacting fragments and developing accurate error probability density functions based on those interaction libraries. The effective application of a systematic error correction scheme is facilitated through additivity with respect to the fragment energies.

CONCLUSIONS

In this work we aimed to show that additivity principles are applicable to electronic interaction energies of fragments making up a larger molecular entity. We employed an energy expansion, which decomposes protein-ligand interaction energies into n terms where each term designates the contributions originating from m interacting fragments with m ≤ n. In our scenario involving the HIV II protease active site complexed to the inhibitor Indinavir, m ranged from 2 to 5. The reliability of this decomposition scheme was confirmed at the HF, M06-L, and PM6-DH2 levels of theory. For all three levels, inclusion of higher order terms with m > 2 brought the interaction energy expansion closer to the exact binding energy of the system, which was obtained by subtraction of energies of the ligand and the binding pocket from that of the full complex (E_bind).

Additivity is theoretically and experimentally unsupported in the literature with regards to free energies.^{21, 22, 23} However, for enthalpies and electronic energies, additivity is largely supported in the case studied herein. The narrowing of the distributions for higher order interactions (for m > 2) supports additivity for energies and enthalpies. The energy ranges encompassing the mth order corrections become consistently narrower with increasing m. Moreover, the ranges get exceedingly narrow such that they cannot be accurately detected with the present computational methods. Although the number of correction terms summing up to the total m-body correction term increases very rapidly and amounts to thousands at m = 4, the magnitudes of these corrections are so small, that they do not accumulate to significant values. In other words, the quick decrease in the magnitudes of the correction terms with rising m overwhelms the increase in the number of single correction terms to be added to yield the total m-body correction term for a particular m. This observation is advantageous from a computational perspective, since the thousands of terms in the m > 3 corrections may safely be neglected in the energy expansion for analogous systems.

From the present work we can arrive at three main conclusions. First, many force fields evaluate non-bonded interactions in a pairwise fashion for protein-ligand systems. Now, having confirmed that the two-body corrections to the overall energy expansion constitute more than 95% of the total protein-ligand interaction energy, the use of pairwise potentials in drug design applications is supported. Second, our results place fragment-based drug design on a firmer footing especially with regards to interaction energy computation. Finally, if the additive model provides a good approximation for the total binding energy of the ligand to the receptor, then the systematic errors in each of the receptor-ligand fragment interactions accumulate as a simple sum, which accurately reveals the total systematic error for the whole binding event. Thus, the observed additivity of fragment energies supports the idea of the post-hoc correction of systematic errors in physics-based score functions.