Electrostatics and aggregation: How charge can turn a crystal into a gel

Abstract

The crystallization of proteins or colloids is often hindered by the appearance of aggregates of low fractal dimension called gels. Here we study the effect of electrostatics upon crystal and gel formation using an analytic model of hard spheres bearing point charges and short range attractive interactions. We find that the chief electrostatic free energy cost of forming assemblies comes from the entropic loss of counterions that render assemblies charge-neutral. Because there exists more accessible volume for these counterions around an open gel than a dense crystal, there exists an electrostatic entropic driving force favoring the gel over the crystal. This driving force increases with increasing sphere charge, but can be counteracted by increasing counterion concentration. We show that these effects cannot be fully captured by pairwise-additive macroion interactions of the kind often used in simulations, and we show where on the phase diagram to go in order to suppress gel formation.

INTRODUCTION

Crystallizing proteins or colloids is difficult in part because the growth of kinetic aggregates called gels can compete with crystal nucleation.^{1, 2, 3} Considerable insight into the competition between crystallization and gelation has been obtained from models of spherical particles in implicit solvent with pairwise-additive interactions, modeling both the forces (hydrogen bonds, hydrophobic effects, etc.) that drive association, and the electrostatic repulsions⁴ that act to suppress association.^{5, 6, 7, 8, 9} Such models have shown how the phase diagram varies with interaction strength and range, and have revealed the presence of kinetically-arrested gels and glasses.¹⁰ While pairwise-additive “screened” potentials capture much of the important physics of electrostatics, they neglect explicit counterion degrees of freedom. Here we show that accounting for counterion entropies reveals that electrostatics does more than simply prevent association: it can induce a thermodynamic driving force that favors a gel over a crystal.

MODEL

We consider a collection of hard spheres (macroions) of radius a in aqueous solution with added salt (we set a = 1.6 nm, appropriate for a small protein). Spheres carry a point charge q at their centers, and interact with square-well attractions of depth −ε and range 2a(λ − 1). We are interested in three phases: the solution phase of dissociated spheres, a close-packed three-dimensional crystal, and a kinetically stabilized gel that we model as a one-dimensional rod of associated spheres. We describe a crystallization window that is bounded on one side by the thermodynamic stability of the crystal, and on the other by the appearance of the kinetically favored gel. We approximate the kinetic threshold for gelation as the regime in which the chemical potential of a linear aggregate drops below that of the solution; since one-dimensional objects lack a nucleation barrier, we expect gelation to pre-empt crystallization in this regime.³¹ This threshold reproduces qualitatively the gelation boundaries determined from numerical and experimental studies of colloids and proteins^{3, 7, 11, 12, 13} while allowing efficient computation of electrostatics.

We write the chemical potentials of the zero-, one-, and three-dimensional phases (shown in Fig. 1) as

$$\begin{array}{ccc}\hfill {\mu }_0=\ln \rho +\rho (4-3\rho ){(1-\rho )}^{-2}& & \mathrm{solution},\hfill \\ \hfill {\mu }_1=-\epsilon -k_{\mathrm{B}}T\ln ({\lambda }^3-1)+\Delta f_1^{\mathrm{es}}& & \mathrm{gel},\hfill \\ \hfill {\mu }_3=-z\epsilon ∕2-3k_{\mathrm{B}}T\ln (\lambda -1)+\Delta f_3^{\mathrm{es}}& & \mathrm{crystal}.\hfill \end{array}$$ (1)

These expressions account for free energies of binding and electrostatic free energies $\Delta f_d^{\mathrm{es}}$ associated with each d −dimensional assembly (d = 0 refers to solution-phase monomers, d = 1 refers to chain-like aggregates and d = 3 describes the crystal phase). The chemical potential μ₀ for the solution phase contains the Carnahan-Starling expression for the free energy of hard spheres as a function of ρ, the volume fraction of spheres in solution.¹⁴ The expression μ₁ for the rod phase accounts for the fact that each particle makes two pairwise contacts of energy −ε. It also contains an entropic term that accounts for the fact that a new particle can add to the end of a rod anywhere within a shell of volume ∼(2aλ)³ − (2a)³ around the existing end particle. This contribution accounts for both bending and vibrational entropies (we neglect unimportant constant terms). We also neglect rod branching,¹⁵ which at the level of electrostatics amounts to assuming the characteristic linear extent of a gel is long compared to the Debye length. The chemical potential μ₃ of the close-packed crystal accounts for the energetic contacts between each particle and its z nearest neighbors (we set z = 12), and the fact that each particle can vibrate a distance of order 2a (λ − 1) in each direction.⁶ We set λ = 1.2 in our calculations, motivated by the recognition that proteins typically possess interactions of short range.^{6, 16, 17, 18}

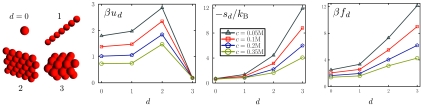
Figure 1.

Counterion entropies dominate the electrostatic free energies of d-dimensional assemblies. We plot per-particle electrostatic energies, u_d, entropies, s_d, and free energies, f_d, for each d-dimensional assembly (pictured left; the case d = 2 is included for comparison only). We have assumed a macroion charge q = 5e and have considered four different salt concentrations c. The electrostatic free energy cost for establishing each assembly is dominated by the entropy loss upon counterion confinement, and not by macroion-macroion repulsion energies.

To these expressions we add the electrostatic free energies $\Delta f_d^{\mathrm{es}}$ of each d-dimensional assembly. We calculated these free energies using the Poisson-Boltzmann (PB) equation,

$${\nabla }_{\mathbf{x}}^2{\Phi }_d=\sinh \left({\Phi }_d\right),$$ (2)

which we have written in terms of scaled spatial coordinates x≡κr and a dimensionless potential Φ_d ≡ eψ_d/k_BT. κ⁻¹ is the Debye length, given by κ² ≡ 2e²c/(εk_BT), where c is the concentration of ions in a reservoir of solvent in osmotic equilibrium with the system. We assume our charged particles to be in aqueous solution with positive and negative salt ions of local concentration $c_d^{\pm }\left(\mathbf{r}\right)\equiv c{e}^{\mp {\Phi }_d\left(\mathbf{r}\right)}$. To determine the potential Φ_d we solved Eq. 2 for given assembly geometry. To simplify the solution of the PB equation we approximated the rod as a smooth cylinder. For the crystal we used a cell model.^{16, 19, 20} We have also considered a two-dimensional assembly to gain insight into the scaling behavior of the electrostatics, although we stress that one would need to consider an anisotropic particle-particle interaction to stabilize such a structure (see, e.g., Refs. ²¹ and ²²). The electrostatic calculations are presented in detail in the Appendix.

We then computed the electrostatic energy U_d and entropy S_d associated with each assembly. The energy U_d stored in the electric field is

$$U_d=\frac{\epsilon }{2}\int d^3\mathbf{r}{\left({\nabla }_{\mathbf{r}}{\psi }_d\right)}^2,$$ (3)

where ε ≡ 80ε₀ is the permittivity of water (ε₀ is that of free space). The entropy S_d quantifies the cost of confining counterions and excluding coions from the screening layer associated with a d-dimensional assembly.²³ The entropy cost per unit volume of maintaining a screening layer of ion concentration c_s in thermal contact with a reservoir of ions at concentration c is

$$\begin{array}{ccc}\hfill -S∕k_{\mathrm{B}}& =& {\int }_c^{c_{\mathrm{s}}}\mathrm{d}{c}^{\prime }\ln (c^{\prime }∕c)\hfill \\ & =& c_{\mathrm{s}}\ln (c_{\mathrm{s}}∕c)-c_{\mathrm{s}}+c.\hfill \end{array}$$ (4)

The electrostatic free energy can then be written F_d=U_d−TS_d=∫d³rF_d, where the free energy density is

$$\begin{array}{ccc}\hfill {\mathcal{F}}_d& =& \frac{\epsilon }{2}{\left({\nabla }_{\mathbf{r}}{\psi }_d\right)}^2+k_{\mathrm{B}}T\left\{c_d^{+}\ln (c_d^{+}∕c)\right.\hfill \\ & & \left.+c_d^{-}\ln (c_d^{-}∕c)-c_d^{+}-c_d^{-}+2c\right\}.\hfill \end{array}$$ (5)

Note that the minimization of Eq. 5 with respect to ionic concentration results in Eq. 2.²⁴

Finally, to compute the electrostatic free energy cost of assembling spheres into each d −dimensional structure, we computed the free energy per particle in the assembly, f_d = F_d/N, and subtracted from this the electrostatic free energy of the monomeric building blocks in solution (determined by solving the PB equation for an isolated sphere). The result is $\Delta f_d^{\mathrm{es}}$.

RESULTS

Counterion entropy dominates the electrostatic free energy of assembly

Figure 1 shows the electrostatic free energy f_d of a d-dimensional assembly, and its components, the electrostatic energy u_d, and entropy s_d (the case d = 2 is included for comparison, but it will not appear in our phase diagram). We see that the energy per particle is non-monotonic in aggregate dimensionality: the energy change upon condensation from the free particle state to the crystalline state is negative, because the macroion-macroion repulsion is overcome by the attraction between macroions and the counterions confined within the crystal's cavities (assumed to be small compared to the Debye length). By contrast, the electrostatic entropy cost increases monotonically with aggregate dimensionality. Furthermore, these entropies are much larger in magnitude than their energetic counterparts, and so the electrostatic free energy cost becomes larger as the structure increases in dimensionality. Although it seems intuitively obvious that assembling charged spheres into a crystal should meet with an electrostatic free energy cost, it is not obvious, a priori, that the origin of this cost is entropic, and not energetic.²⁵

Figure 1 reveals that the electrostatic entropy alone is a reasonable approximation of the electrostatic free energy cost of assembly, a fact that has been long appreciated in polymeric systems.^{26, 27} The behavior of the entropy with d can be understood from the following simple argument. Electroneutrality requires that q counterions be confined near each macroion. Counterions are free to extend a distance κ⁻¹ in each of the 3 − d dimensions extending away from the assembly, but are confined within a distance of order the particle size a in each of the d dimensions of the assembly. Thus the volume v_localize within which q counterions must be localized scales as v_localize ∼ a^dκ^{d − 3}, and so the entropic cost per macroion of building the screening layer scales as −s_d/k ∼ qln (c(aκ)^d/qκ³), or

$$-s_d∕k\sim qd\ln \left(a\kappa \right).$$ (6)

This cost increases with d.

Electrostatic interactions are not pairwise additive

One immediate consequence of the fact that counterion entropies dominate the free energy cost for assembling charged particles is that effective macroion interactions are not in general pairwise-additive: the free energy difference $\Delta f_d^{\mathrm{es}}$ depends on the volume of space accessible to counterions, but does not necessarily vary linearly with the number of contacts made by particles in each assembly. We can define ${\Delta }_{31}\equiv z\Delta f_1^{\mathrm{es}}$∕2$\Delta f_3^{\mathrm{es}}$ as a measure of the relative electrostatic cost of making a macroion-macroion contact in a gel versus a crystal. When Δ₃₁ is unity there is no difference in this cost, the electrostatic effects can be absorbed into an effective pairwise interaction, such as a Yukawa potential.²⁸ However, when Δ₃₁ ≠ 1 the electrostatic free energy is non-additive, rendered so by counterion degrees of freedom.

In Fig. 2 we plot Δ₃₁ as a function of salt concentration c and particle charge q. Δ₃₁ is in general less than unity, indicating that it is easier, per macroion contact, to fit counterions around a gel than within a crystal. Δ₃₁ is also non-monotonic: in principle, at large salt concentration strong electrostatic screening will ensure that macroion sites are independent, with electrostatic free energies becoming pairwise-additive (as seen in the plot, though such concentrations can be unattainably high). At low salt concentration Δ₃₁ again approaches unity. This can be understood by considering Eq. 6 for a cubic packing arrangement. In this case d is proportional to the number of nearest neighbors and each additional pair of neighbors reduces the volume accessible to the counterions by a factor κa. This results in an electrostatic free energy linear in the number of nearest neighbors. However, at finite salt concentration the volume occluded by the macroion (neglected in Eq. 6) becomes a significant perturbation to v_localize, and the approximation of pairwise additivity fails.

Figure 2.

Relative electrostatic cost of making a macroion-macroion contact in a gel versus a crystal, Δ₃₁, as a function of salt concentration c and macroion charge q. Only when Δ₃₁ is unity is the electrostatics of assembly effectively pairwise-additive, which in general is not the case.

Model phase diagram: How does one avoid gelation?

We turn now to calculation of the model's phase diagram. We found the solution-crystal coexistence line by setting μ₀ = μ₃, and estimated the nonequilibrium solution-gel coexistence line by setting μ₀ = μ₁. This line does not describe an equilibrium coexistence: what we mean by it is the location at which there exists a driving force for monomers to aggregate in a disordered way. The crystal may be thermodynamically stable, but at moderate degrees of supercooling or supersaturation it is separated from the solution phase by a free energy barrier, and may require considerable time to appear. By contrast, there exists no free energy barrier to the formation of a linear aggregate, and so we expect a gel to form readily below the nonequilibrium solution-gel coexistence line.

Our phase diagram in the temperature-density plane is shown in Fig. 3a, for fixed salt concentration and for two macroion charges. The close-packed crystal is stable below the gray solution-crystal coexistence lines, but we expect a driving force for gelation below the red solution-gel coexistence lines. This behavior is similar to that seen in simulations of spheres with short range attractions.¹² The resulting “window” of crystal stability and accessibility (shaded region between the red and blue lines) is narrow, and becomes narrower as macroion charge increases. This is a key finding of our study. As noted before, the reason for this narrowing is the increasing cost of confining counterions within a close-packed crystal relative to around an open gel.

Figure 3.

(a) Phase diagram in the temperature-density plane showing solution-gel (red) and crystal-solution (gray) coexistence lines, for macroion charges q = 0 (solid), and q = 6e (dotted) for salt concentration 0.1 M. As macroion charge increases the crystal can be rendered stable by decreasing temperature, but counterion entropy increasingly favors the gel over the crystal. The “window” (shaded) within which the crystal is stable and the solution is stable against gelation therefore shrinks as charge increases. (b) Phase diagram in the charge-salt concentration plane for two bond strengths ε/k_BT. As charge increases, adding salt lessens the entropic difference between gel and crystal, widening the desired shaded region between the sol-gel and sol-crystal lines. Note that this region narrows as bond strength increases.

High salt concentrations promote crystallization

We have seen that there are two consequences of increasing macroion charge: the crystallization window narrows, and it shifts to smaller values of k_BT/ε. This latter effect is useful for protein crystallization where we might not have the freedom to raise temperature (lest it lead to denaturation): increasing protein charge might be one way to move the crystallization window into the region of k_BT/ε accessible experimentally. The tradeoff is that adding charge causes the window to narrow, but this can be counteracted by adding salt. Figure 3b shows how, for two fixed bond strengths ε/k_BT, one can alter charge and salt concentration to widen the crystallization window. Note that this window narrows as bond strength increases.

The shrinking of the crystallization window with the bond strength can be understood by writing the net interaction between the particles in terms of the attractive and repulsive components ε_net = −ε + ε_rep, where ${\epsilon }_{\mathrm{rep}}=2\Delta f_3^{\mathrm{es}}∕z$ is the electrostatic repulsion energy per crystal contact. In terms of these variables we can express the solution-crystal coexistence line, given by μ₀ = μ₃, as

$${\epsilon }_{\mathrm{rep}}=\epsilon +\frac{2}{z}(3k_{\mathrm{B}}T\ln (\lambda -1)+{\mu }_0).$$ (7)

Similarly, we can express the solution-gel coexistence line as

$${\epsilon }_{\mathrm{rep}}=\frac{\epsilon }{{\Delta }_{31}}+\frac{1}{{\Delta }_{31}}(k_{\mathrm{B}}T\ln ({\lambda }^3-1)+{\mu }_0),$$ (8)

where we have used Δ₃₁ to write the electrostatic free energy of the gel in terms of ε_rep.

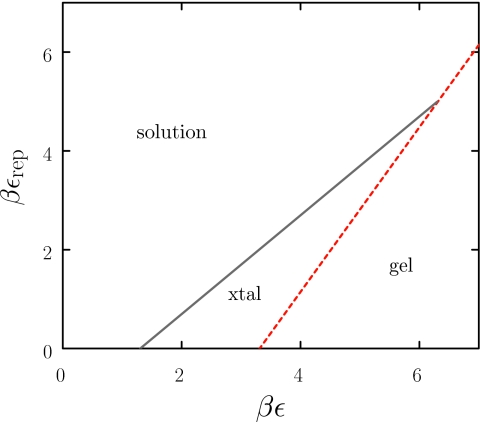
Equations 7, 8 are plotted in Fig. 4. We see that strongly attractive particles (large ε) can be brought within the crystallization window by increasing ε_rep. However, this window becomes narrower with increasing ε, and above a critical attraction vanishes entirely. This happens because strongly attractive particles require large charges to weaken particle-particle interactions enough to destabilize the gel, but large charges in turn recruit dense screening layers which act to favor the gel over the crystal. This effect can be mitigated by working under conditions for which electrostatic interactions are approximately pairwise-additive (large Δ₃₁). Increasing the value of Δ₃₁ decreases the slope of the solution-gel coexistence line (dotted line in Fig. 4). This widens the crystallization window and increases the critical value of ε at which the solution-gel line overtakes the solution-crystal line. In practice, Δ₃₁ can be increased by simultaneously increasing salt concentration and particle charge. For example, within our model system a macroion charge q = 2.8 in 100 mM salt, or a charge of q = 8.1 in 800 mM salt, both destabilize crystal bonds by 0.5 k_BT. However, the former condition destabilizes bonds in the gel phase by only 0.17 k_BT, while the latter condition destabilizes bonds by 0.25 k_BT. Thus, high salt∕high charge conditions are more conducive to crystallization than low salt∕low charge conditions. We speculate that the addition of multi-valent counterions may further reduce the entropic cost of neutralizing the crystal, although a quantitative analysis of this scenario is beyond the limitations of our PB model.

Figure 4.

Phase diagram showing the lines μ₀ = μ₁ (dotted) and μ₀ = μ₃ (solid) as a function of the attractive and repulsive contributions to the net interaction (here Δ₃₁ = 0.6 and c = 0.04).

CONCLUSION

We have studied a minimal model of the crystallization and gelation of charged attractive spheres in aqueous salt solution. We find that there exists an electrostatic driving force that favors the gel over the crystal, because there exists more ion-accessible volume for confined counterions around a gel than within a crystal. This effect renders the effective interactions between macroions non-pairwise-additive, and is responsible for a narrowing of the crystallization window as macroion charge is increased.

APPENDIX: POISSON-BOLTZMANN FREE ENERGIES

For the environmental conditions considered in this paper we find that solutions Φ_d of the Poisson-Boltzmann equation [Eq. 2 in the main text] are closely approximated by solutions ${\Phi }_d^{\mathrm{lin}}$ of its linearized counterpart, the Debye-Huckel (DH) equation. We present numerical results derived from the PB equation, but also present, for the reader's convenience, the well-known analytic solutions of the DH equation. For completeness, we also consider a 2d membrane (in 2d the PB equation has an analytic solution). We draw the same qualitative conclusions from both levels of theory.

To compute the electrostatic free energy cost of assembling the building blocks into each d-dimensional structure, we compute the free energy per particle in the assembly, f_d = F_d/N and subtract from this the electrostatic free energy of the monomeric building blocks in solution. The per-particle electrostatic free energy of assembly is then Δf_d = f_d − f₀. To determine f₀ we solve the PB equation for the potential of an isolated sphere of radius a carrying charge q. The corresponding solution of the DH equation is

$${\Phi }_0^{\mathrm{lin}}\left(x\right)=\frac{\kappa {\ell }_{\mathrm{B}}{e}^{\kappa a}}{1+\kappa a}\frac{e^{-x}}{x}.$$ (A1)

Here ℓ_B ≡ e²/(4πεk_BT) is the Bjerrum length.

1D assembly

We treat the 1D assembly as an infinitely long cylinder of radius a and linear charge density ρ = q/2a, and obtain Φ₁ from the PB equation in plane polar coordinates. The corresponding solution of the DH equation is²⁹

$${\Phi }_1^{\mathrm{lin}}\left(x\right)=\frac{e}{k_{\mathrm{B}}T}\frac{q}{4\pi a^2\epsilon \kappa {\mathrm{K}}_1\left(\kappa a\right)}{\mathrm{K}}_0\left(x\right).$$ (A2)

Here x is the scaled distance from the cylinder center and K_n is the nth order modified Bessel function of the second kind.

2D assembly

We treat each surface of the 2D assembly as an infinitely extended plane carrying areal charge density σ=qA₂∕2πa². Here A₂≃0.91 is the area occupied by close-packed spheres in a sheet. The exact solution of the PB equation in planar geometry at a scaled distance x from the plane surface is

$${\Phi }_2\left(x\right)=2\ln \left(\frac{1+e^{-x}\tanh ({\phi }_0∕4)}{1-e^{-x}\tanh ({\phi }_0∕4)}\right),$$ (A3)

where ϕ₀ ≡ 2sinh ⁻¹[2πℓ_Bσ/(κe)] is the electrostatic potential at the plane surface. From Eqs. 3 and (4) in the main text we find

$$U_2=A_{\mathrm{sheet}}\frac{\kappa k_{\mathrm{B}}T}{\pi {\ell }_{\mathrm{B}}}\frac{{\lambda }^2}{1-{\lambda }^2},$$ (A4)

and

$$S_2∕k_{\mathrm{B}}=A_{\mathrm{sheet}}\frac{8c_0}{\kappa }\frac{3{\lambda }^2-2\lambda \ln \left(\frac{1+\lambda }{1-\lambda }\right)}{1-{\lambda }^2},$$ (A5)

where λ ≡ tanh (ϕ₀/4) and A_sheet is the area of the sheet.

3D assembly

Following previous work on colloidal systems¹⁶, ¹⁹, ²⁰ we treat the 3D assembly as a collection of spherical macroions of radius a, each of which is surrounded by a spherical aqueous cavity of radius b. We assume that macroions are close-packed at volume fraction A₃=(a∕b)³≃0.74. To calculate the electrostatic free energy of this assembly we assume that the electric field on the surface of each aqueous cavity vanishes²⁰ (valid for assemblies whose characteristic linear size is much greater than the Debye length). We also assume that the field at the macroion surface is unaffected by the presence of salt and counterions. We find the potential Φ₃ from the appropriate PB equation. This solution is closely approximated by linearizing the PB equation around the average potential between macroions. By writing ${\Phi }_3\left(x\right)={\Phi }_3^{\mathrm{lin}}\left(x\right)+\overline{\phi }$, where x is the scaled distance from the macroion center, and the mean potential,

$$\overline{\phi }\equiv {\sinh }^{-1}\left(\frac{3q{\mathcal{A}}_3}{8\pi c_0{a}^3(1-{\mathcal{A}}_3)}\right),$$ (A6)

is given by a jellium model,²⁰, ²⁵ we impose the boundary conditions described above and find, after some algebra,

$$\begin{array}{ccc}\hfill {\Phi }_3^{\mathrm{lin}}\left(y\right)& =& \frac{{\alpha }^2{E}_0}{e^{-\alpha +\beta }(\alpha +1)(\beta -1)-e^{\alpha -\beta }(\alpha -1)(\beta +1)}\hfill \\ & & \times \left(\frac{e^{\beta -y}(\beta -1)}{y}+\frac{e^{y-\beta }(\beta +1)}{y}\right)-\tanh \overline{\phi }.\hfill \end{array}$$ (A7)

Here $E_0\equiv qe\kappa {\left(\cosh \overline{\phi }\right)}^{1∕2}∕\left(4\pi \epsilon k_{\mathrm{B}}T\right)$; $y\equiv {\left(\cosh \overline{\phi }\right)}^{1∕2}\kappa r$; $\alpha \equiv {\left(\cosh \overline{\phi }\right)}^{1∕2}\kappa a$; and $\beta \equiv {\left(\cosh \overline{\phi }\right)}^{1∕2}\kappa b$.

Our model is likely to become unreliable at high salt concentrations and at low values of the packing fractions A_2,3. Under such conditions the approximation of taking filament and sheet surfaces to be smooth becomes unrealistic because the aqueous volume of surface corrugations becomes comparable to the total volume of the screening layer (accounting for steric corrections to the PB equation³⁰ then becomes necessary). In order to neglect these corrugations, it is necessary that both the Debye length and the Gouy-Chapman length, ℓ_GC = e/2πℓ_Bσ, exceed the characteristic length scale of the surface cavities. For this reason we restrict our analysis to salt concentrations below c = 0.5 M and q = 10, for our chosen macroion radius a = 1.6 nm.