Mechanisms producing coordinated function across the breadth of a large biarticular thigh muscle

SUMMARY

We examined the hypothesis that structural features of the iliotibialis lateralis pars postacetabularis (ILPO) in guinea fowl allow this large muscle to maintain equivalent function along its anterior–posterior axis. The ILPO, the largest muscle in the hindlimb of the guinea fowl, is a hip and knee extensor. The fascicles of the ILPO originate across a broad region of the ilium and ischium posterior to the hip. Its long posterior fascicles span the length of the thigh and insert directly on the patellar tendon complex. However, its anterior fascicles are shorter and insert on a narrow aponeurosis that forms a tendinous band along the anterior edge of the muscle and is connected distally to the patellar tendon. The biarticular ILPO is actively lengthened and then actively shortened during stance. The moment arm of the fascicles at the hip increases along the anterior to posterior axis, whereas the moment arm at the knee is constant for all fascicles. Using electromyography and sonomicrometry, we examined the activity and strain of posterior and anterior fascicles of the ILPO. The activation was not significantly different in the anterior and posterior fascicles. Although we found significant differences in active lengthening and shortening strain between the anterior and posterior fascicles, the differences were small. The majority of shortening strain is caused by hip extension and the inverse relationship between hip moment arm and fascicle length along the anterior–posterior axis was found to have a major role in ensuring similar shortening strain. However, because the knee moment arm is the same for all fascicles, knee flexion in early stance was predicted to produce much larger lengthening strains in the short anterior fascicles than our measured values at this location. We propose that active lengthening of the anterior fascicles was lower than predicted because the aponeurotic tendon of insertion of the anterior fascicles was stretched and only a portion of the lengthening had to be accommodated by the active muscle fascicles.

INTRODUCTION

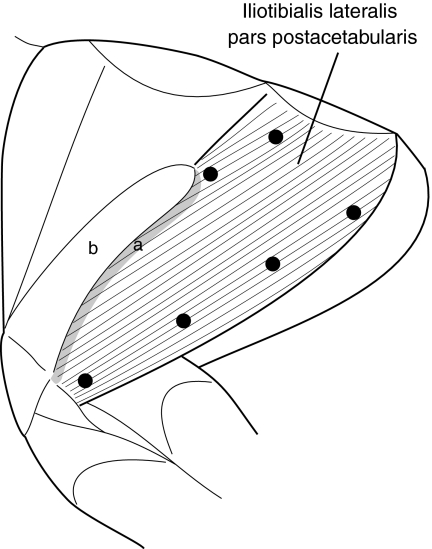
In vivo measurements of strain and activity in the ILPO may provide insight into the evolution of the locomotor system to provide stable, economical locomotion. The possibility of regional differences in function both along the axis of long muscle fascicles and in parallel fascicles across the breadth of a muscle can limit the extent to which the function of large architecturally complex muscles can be inferred from localized measurements or modeled predictions. For example, in a companion study to the work presented here (Carr et al., 2011a), strain in-series along the posterior fascicles in the iliotibialis lateralis pars postacetabularis (ILPO) of guinea fowl was examined. During active lengthening, the distal portion of the posterior fascicles experiences the most strain. It lengthens farther and faster because it begins activity at shorter sarcomere lengths on the ascending limb of the length–tension curve. Because of the self-stabilizing effects of operating on the ascending limb, the segments reached the end of lengthening and started shortening at the same sarcomere length. The ILPO has a broad origin from near the dorsal margin of the pelvis posterior to the hip (Fig. 1), and the possibility of variation in function along the anterior–posterior axis also needs to be examined.

Fig. 1.

Anatomy of the iliotibialis lateralis pars postacetabularis (ILPO) in the guinea fowl. The aponeurotic tendon of insertion of the anterior fascicles is indicated by the gray band (a). Superficially, this tendinous band is contiguous with the posterior edge of the superficial aponeurosis of the femerotibialis muscle (b) and extends medially to the depth of the ILPO. Black circles indicate the position of the sonomicrometry crystals. Electromyographic (EMG) electrodes were also placed along the fascicles at the midpoint between each pair of crystals. Figure drawn by Dr David Ellerby.

Assuming simultaneous activation of the fascicles in a muscle during locomotion, possibly the most straightforward hypothesis is that the architectural features of the musculoskeletal system have evolved to assure functional equivalence, i.e. equal strain, stress and shortening velocity at the sarcomere level resulting from excursion of a joint (Gans et al., 1985; Gans and de Vree, 1987). This hypothesis would appear to be the unstated alterative hypothesis in studies that have documented compartmental function of various muscles. Maintaining similar strain and shortening velocity may be particularly important for muscles that are active while undergoing substantial changes in length, because the length–tension and force–velocity properties of the fibers have substantial effects on performance. In terms of hip function, the architecture of the ILPO appears to be consistent with this hypothesis. The parallel fascicles of this muscle have an obvious anterior to posterior gradient of increasing extensor moment arm at the hip. Corresponding to this gradient, fascicle length increases from 30 mm near the hip joint to more than 80 mm near the posterior edge. This variation in length could compensate for the increasing hip moment arm resulting in similar strain induced by angular excursion at the hip. However, the ILPO is also a knee extensor and a substantial change in knee angle occurs during stance (Gatesy, 1999a). The insertions of all fascicles converge on the patellar tendon complex at the knee, and, therefore, are predicted to have a similar knee extensor moment arm. Thus, in the absence of other compensatory mechanisms, angular excursion at the knee would be expected to cause differential strain in the fascicles because of the variation in fascicle length. Therefore, considering both angular changes at the hip and the knee, functional equivalency of muscle strain could only be maintained if other structural features compensate for the effects of knee angle.

Alternatively, the parallel fascicles in the ILPO may show regional differences in function, possibly because of differences in muscle innervation and activation (English, 1984). Although these compartments have been most extensively studied using activation patterns, in some thigh muscles with broad origins or insertions, compartmental organization clearly allows partitioning of mechanical function, e.g. the cat sartorius, biceps femoris and tensor fasciae latae (English and Weeks, 1987; Chanaud et al., 1991), and the avian iliofibularis (Johnston and Bekoff, 1992; Hoogendyk, 2005). However, compartmental organization does not necessarily lead to differences in mechanical function, e.g. the cat semitendinosus (Bodine et al., 1982; Hutchinson et al., 1989; Chanaud et al., 1991). Regional differences in strain may also occur in the presence of similar activation across the muscle (Pappas et al., 2002; Higham and Biewener, 2009). Note that the stance active ILPO can itself be considered a neuromuscular compartment of the iliotibialis lateralis because in most species it is contiguous with the iliotibialis lateralis preacetabularis, which is active during swing phase (Gatesy, 1999b). Whether further differences in function occur along the anterior–posterior axis within the ILPO has not been revealed in previous studies (Buchanan, 1999; McGowan et al., 2006; Roberts et al., 2007).

In the present study, we tested the hypothesis of functional equivalency along the anterior and posterior axis of the ILPO. We examined the activation and strain in the anterior and posterior regions of the ILPO during walking and running. To elucidate whether the strains in the anterior and posterior regions were determined solely by muscle moment arms and the joint angular excursions, the measured strains were compared with muscle–tendon unit strains calculated from a model using the in vivo angular excursions at the hip and knee and post-mortem measurements of the instantaneous effective muscle moment arms of the anterior and posterior fascicles at these joints.

MATERIALS AND METHODS

Animals and training

Four guinea fowl [Numida meleagris (Linnaeus 1758)], averaging 1.59±0.1 kg body mass were used for this experiment. The guinea fowl were housed in individual cages at the Northeastern University Animal Care Facility, with food and water provided ad libitum on a 10 h:14 h light:dark cycle. Before surgery and experimental recordings, the birds were trained to run inside a three-sided box on a motorized treadmill. The birds were trained for 3–5 days per week for a minimum of 5 weeks. Each training session lasted for 30 min. Once trained the birds could, in an individual session, maintain level speeds of 2.5 m s^–1 for 15 min, 2.78 m s^–1 for 3 min and 3.0 m s^–1 for 3 min. When a bird was sufficiently trained, surgery was performed to insert sonomicrometry and electromyographic (EMG) sensors. After surgery, birds were allowed to recover in individual cages for at least 40 h prior to the experimental recordings. After recovery, birds were run on the treadmill and experimental recordings were taken as described below. During experimental recordings, birds were run at speeds of 0.5, 1.0, 1.5, 2.0, 2.5, 2.78 and 3.0 m s^–1 on a level treadmill for at least 30 s per speed. All procedures involving work with live animals were approved by the Northeastern University Animal Care and Use Committee. Animals were killed with 150 mg kg^–1 intravenous Euthasol® (pentobarbital and phenytoin).

Sonomicrometry and electromyography

More detailed descriptions of sonomicrometry and electromyography surgical techniques, sarcomere measurements, and calculations of length and velocity are given by Carr et al. (Carr et al., 2011a).

The anterior fascicles of the ILPO were implanted with two sonomicrometry transducers that spanned the majority of the length of the fascicle (Fig. 1). The posterior fascicle was too long to be spanned by a single set of sonomicrometry transducers and instead was implanted with four transducers that measured length change in the proximal, central and distal segments of the posterior fascicle (Fig. 1). The length change that occurred in each individual segment along the posterior fascicle were summed to determine the overall length change of the much longer posterior fascicle. Two fine-wire bipolar EMG electrodes were implanted into each segment of the fascicles to measure muscle activity. Sonomicrometry signals were acquired digitally with a sampling frequency of 613 Hz using Sonoview software and a Sonometrics TRX Series 8 interface (Sonometrics Corp., London, ON, Canada). Digital signals were transferred to the application IGOR Pro (Wavemetrics, Inc., Portland, OR, USA) and processed using custom-written functions. The EMG signals were amplified by WPI model DAM-50 preamplifiers (World Precision Instruments, Sarasota, FL, USA) with analog high- and low-pass filters set at 10 and 3000 Hz, respectively. The signals were digitized at frequency of 10 kHz using an ADInstruments Power Lab 16 bit A-D converter (Model 16SP, ADInstruments, Colorado Springs, CO, USA) controlled by a Macintosh computer using the application Chart from ADInstruments. The data were then filtered (finite impulse response band-pass filter, 90–1000 Hz) and rectified using IGOR Pro (Wavemetrics). The mean rectified value was calculated both for duration of the burst and the duration of the stride. As described by Carr et al. (Carr et al., 2011a), we standardized the mean amplitude values by dividing the mean amplitude measured for each electrode by the mean amplitude measured when the animals were running uphill at 2.0 m s^–1 (Carr et al., 2011b).

In vivo segment lengths measured by sonomicrometry (L_so) were converted to sarcomere lengths using reference sonomicrometer lengths (L_so,ref) and sarcomere lengths (L_sc,ref) measured in rigor. After the experimental measurements the animals were killed, allowed to go into rigor, and L_so,ref measured. Portions of the muscle from each segment were then removed, frozen and sectioned to measure mean L_sc,ref. The in vivo sarcomere length (L_sc) was then calculated using the equation:

(1)

The sarcomere length was then converted to fractions of optimal length (L₀) by dividing by 2.36, which is the sarcomere length expected in the center of the plateau of the length–tension curve determined according to the filament lengths (Carr et al., 2011a). Fascicle strains are similarly given as ΔL_sc divided by 2.36.

In vivo joint angles

Prior to the experimental recordings, the birds were marked using either white paint or reflective tape. Markers were placed above the caudal and cranial pelvis; on the hip, ankle, tarsometatarsal–phalangeal and interphalangeal joints; and the end of digit III. The knee was not marked because skin movement makes surface markers less reliable for locating this joint (Rubenson and Marsh, 2009). Instead, the knee position was calculated from the measured hip and ankle positions and the distance from the hip to the knee and knee to the ankle, which were measured post-mortem. Video footage of animals walking and running on the treadmill was recorded to VHS tape with a NAC HV-1000 high-speed video camera (NAC Image Technology, Sim Valley, CA, USA) operating at 500 fields s^–1. We synchronized the EMG and sonomicrometry traces with the video recordings using a square-wave voltage pulse generated by the data acquisition system that was recorded on the video fields with a NAC wave inserter. The video was digitized and imported in DV format into a Macintosh computer. The digital video was then imported into NIH ImageJ (NIH Image J version 1.38, Wayne Rasband; http://rsb.info.nih.gov/nih-image/). In ImageJ, the video was rescaled to correct for the non-square aspect ratio of the DV format, and the positions of the reflective markers were either manually tracked or auto-tracked using the plugin MTrack2 (Nico Sturrman, Leiden University, Institute of Molecular Plant Sciences, The Netherlands). Angles at the hip, knee and ankle were calculated from the marker positions with custom MATLAB scripts and expressed using the same coordinate system used by Gatesy (Gatesy, 1999a). Data were collected for ten constant-speed strides at each speed for each bird.

Moment arm measurements

Post-mortem measurements of moment arm were made using the ‘tendon excursion’ method (Spoor and van Leeuwen, 1992) using simultaneous continuous measurements of the change in joint angle and excursion. The limb was moved through angular excursions at either the hip or knee joint while videos and length measurements were recorded. To avoid undesirable end effects when subsequently calculating the moment arms, the angular excursions used were always greater than the maximum in vivo excursion during locomotion. To measure angular change, we tracked reflective markers using video taken at a field rate of 60 Hz using a digital video camera (JVC model #GR-DVL9800; JVC, Wayne, NJ, USA). The excursions resulting from the joint rotation were measured with a Harvard Bioscience length transducer (Model 52-9511, Harvard Bioscience, Holliston, MA, USA) and recorded at 1000 Hz on a Macintosh computer using the A-D system described for recording EMG signals. The video was synchronized with length measurements using a voltage pulse that activated an LED in the field of view of the camera.

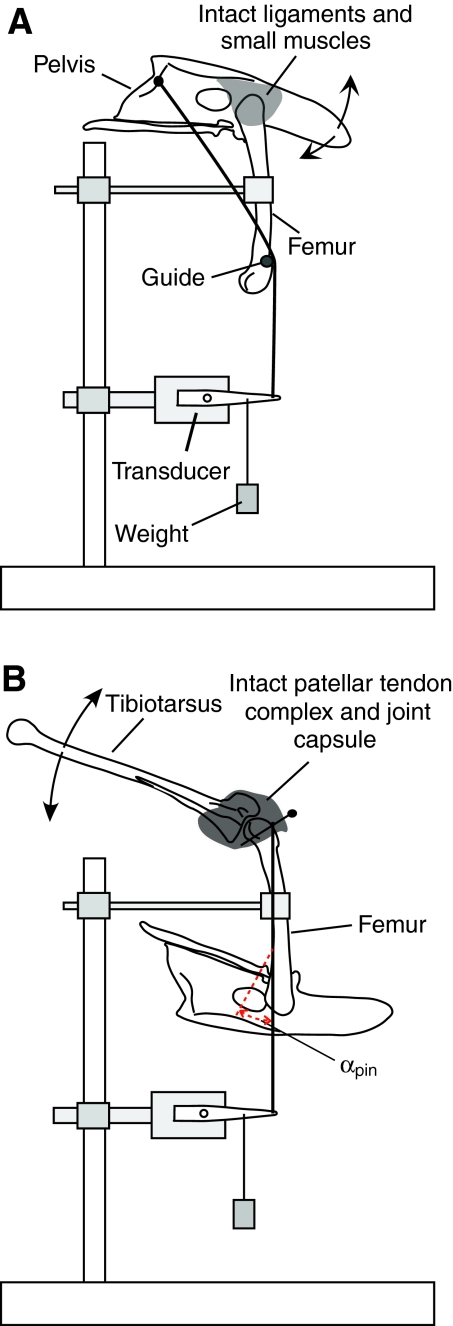
To measure the moment arms of the anterior and posterior fascicles at the hip, the femur was fixed in place using a bone clamp, and the pelvis was rotated (Fig. 2A). Reflective markers were placed cranially and caudally on the pelvis and proximally and distally on the femur, with the proximal marker over the center of rotation of the hip joint. The origins on the pelvis of the anterior and posterior fascicles that had been monitored in vivo by sonomicrometry were marked. All the large muscles were removed from the pelvis, but the hip articulation was preserved. For each fascicle, a hole was drilled through the pelvis at the origin and silk thread was attached at this point. The thread was then placed around a guide glued to the femur at a position chosen to keep the thread in the same orientation as the fascicle relative to the femur. The end of the thread was connected to the counterweighted length transducer such that the thread remained perpendicular to the lever arm of the transducer.

Fig. 2.

Experimental set up for measuring moment arm at the hip (A) and knee (B). The skeletal elements are drawn to scale, but other features are diagrammatic including the tissues at the knee and hip. Figure drawn by Dr Richard Marsh.

To measure moment arm at the knee, the femur was fixed in place using a bone clamp and the tibiotarsus was rotated (Fig. 2B). Almost all the muscle was removed from the femur, but the knee joint capsule and patellar tendon complex at the knee was left intact. Because the insertion for the ILPO is a fairly broad piece of connective tissue, stainless steel insect pins were threaded perpendicularly across the tendon to maintain the tendon shape across the knee. The tendon (via the insect pin) was then attached to a silk thread that was in turn attached to the length transducer so that the thread was parallel to the long axis of the femur and perpendicular to the arm of the length transducer. Reflective markers were used to mark the center of rotation of the hip, knee and ankle. The long axis of the femur was considered to be the axis of the tendon of insertion. Our subsequent calculations of fascicle strain resulting from angular excursion at the knee corrected for the pinnation angle between this axis and the axis of the fascicles.

The video was transferred from DV-tape to a computer, deinterlaced and imported into NIH ImageJ. Subsequent processing and calculation of angles were done as for the high-speed video, except that the marked center of rotation for the knee was used in calculating knee angle. Using the application IGOR Pro the length signals were downsampled to 60 Hz to match the video field rate. The data on length excursion as a function of the joint angle in radians were fitted to polynomial equations using least squares regression analysis, with the order of the equation determined by stepwise addition of higher order terms. Two criteria were used for inclusion of higher order terms. The first was a P-value for the added term of <0.05. The second was an approximately uniform distribution of the residuals across the range of angles examined. In all cases the hip data were described with a third-order polynomial. The knee data were described by either a fourth- or fifth-order polynomial. In all cases the fitted equations described the length change extremely well, the lowest R² value was 0.93 and most were greater than 0.98. The resulting polynomial equations were analytically differentiated to derive a polynomial equation (second-order for hip and third or fourth for the knee) to predict the instantaneous moment arm as a function of angle.

Predicted strains

The equations for instantaneous moment arm versus angle at the hip and knee were used along with joint angles measured from guinea fowl running at 0.5, 1.5 and 2.5 m s^–1 to calculate the changes in fascicle length predicted from moment arm and angle measurements. Fascicle strain was calculated from the predicted change in length using the estimated optimal length of the fascicles, which was derived from the fascicle length measured with the animals in rigor and corrected to optimal length using the rigor measurements of sarcomere length. Our model made certain simplifying assumptions, which we think are justifiable. (1) We assumed the angular change and moment arms measured in the sagittal plane accounted for all the length change in the ILPO. This assumption seems reasonable because the degree of adduction of the femur and tibiotarsus is relatively constant during stance (Gatesy, 1999a). (2) Our method for measuring the moment arm at the hip assumed that the position relative to the long axis of the femur of the distal end of the fascicles was constant. This assumption ignores any movement of the insertion along the femur due to angular changes at the knee. Given the predicted length changes due to knee rotation, these effects are expected to be very small. (3) We assumed that the tendinous band forming the tendon of insertion of the fascicles was constrained to movements along the long axis of the femur, i.e. the tendon axis. This assumption seems reasonable because of connections to the superficial aponeurosis of the femerotibialis muscle (Fig. 1). Assumption 3 results in the prediction that length change in the fascicle due to knee rotation will be smaller than the length change along the tendon axis, which was predicted from our measured knee moment arm (Fig. 2). The length change in the fascicle is expected to be equal to the length change along the tendon axis times the cosine of the pinnation angle between the fascicle and the tendon axis, α_pin (Fig. 2). Using a planar geometric model the value of α_pin was found to change linearly with changing hip extension. For the maximum range of hip angles found in vivo the pinnation angle was between 14 and 30 deg for the posterior fascicle and 13 and 38 deg for the anterior fascicles. The variation in pinnation angle was incorporated into our model, but it only has a small effect on the results.

Fascicle strain in % L₀ was calculated as:

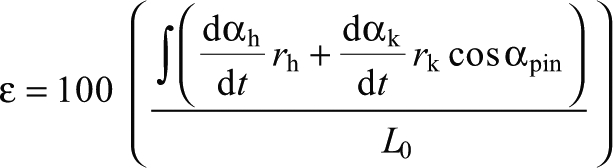(2)

where, ε is strain, α_h and α_k are hip and knee angles in radians, r_h and r_k are hip and knee instantaneous moment arms at the respective values of α_h and α_k, L₀ is optimal length and α_pin is the pinnation angle as a function of hip angle.

Statistical analyses

ANOVA was conducted using the general linear model in the application SPSS (version 18.0 for Mac OS, SPSS Inc., Chicago, IL, USA). In the comparisons of the standardized EMG amplitude, EMG duration, active strain or shortening velocity between the anterior and posterior fascicles the ANOVA models included: animal identifier as a random factor, fascicle location (anterior and posterior) as a fixed factor, and speed as a fixed factor. In the comparisons of modeled and measured strain the ANOVA models included: animal identifier as a random factor, method for deriving strain (modeled and measured) as a fixed factor, and speed as a fixed factor. Paired t-tests were used to compare predicted and modeled strains for each speed. Results of all statistical tests were considered significant if the P-values were less than 0.05. Results are reported as means ± 1 standard error of the mean (s.e.m.).

RESULTS

Activation and measured values of strain

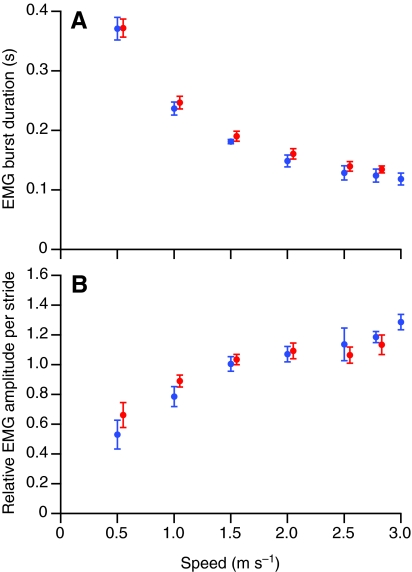
Both the anterior and posterior regions of the ILPO were activated shortly before the beginning of stance (Fig. 3). The duration of activity in the two regions (Fig. 4A) was statistically indistinguishable (d.f.=1,45, F=3.74, P=0.07). Similarly, no significant difference was found between the anterior and posterior fascicle in either the standardized EMG amplitude per stride (Fig. 4B; F=0.06, P=0.81) or per burst (not shown; F=0.425, P=0.518).

Fig. 3.

Mean lengths (% L₀) and representative traces of electromyographic activity in the anterior (red) and posterior (blue) fascicles of the ILPO of guinea fowl walking at 0.5 m s^–1 (A), and running at 2.5 m s^–1 (B). Traces are plotted for an average stride from foot-down to foot-down with toe-off indicated with a black arrow. Shaded bands indicate ±1 s.e.m.

Fig. 4.

Mean EMG burst duration (A) and average EMG amplitude per stride (B) in the anterior (red) and posterior (blue) regions of the ILPO of guinea fowl as a function of speed. Anterior values are offset slightly on the speed axis for clarity. Error bars indicate ±1 s.e.m.

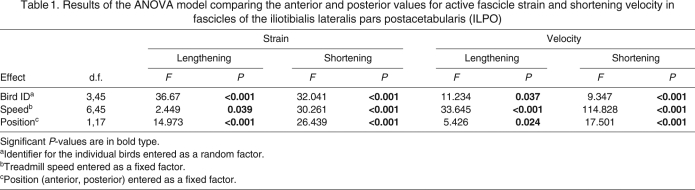
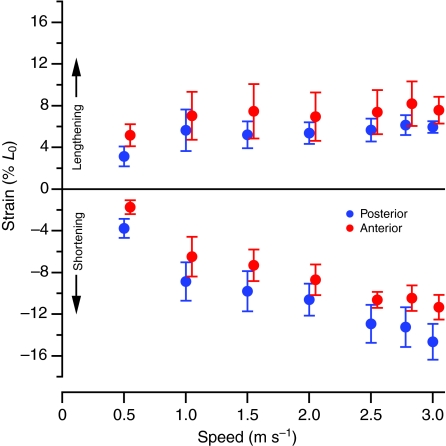
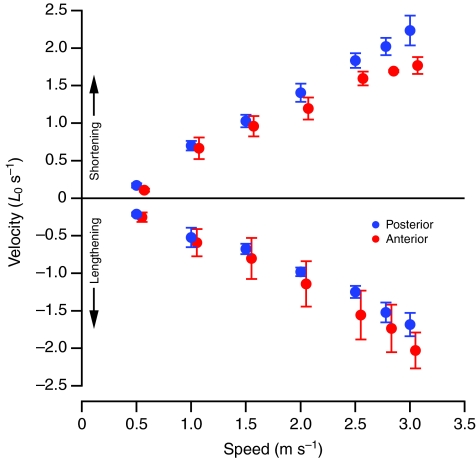
The anterior and posterior fascicles both initially lengthened while active and then actively shortened in the latter part of stance (Fig. 3). Small but significant differences in strain were found between the two locations for both shortening and lengthening (Table 1; Fig. 5). The mean difference amounted to 2% of L₀ and was not significantly correlated with speed (R²<0.4, P>0.12). Average shortening velocity also showed small, but significant differences between the anterior and posterior sites (Table 1; Fig. 6). For both lengthening and shortening velocities this absolute difference increased significantly with speed (R²=0.85, P=0.003), reaching a maximum of 0.35 and 0.46 L₀ s^–1 at a speed of 3.0 m s^–1 for lengthening and shortening, respectively.

Table 1.

Results of the ANOVA model comparing the anterior and posterior values for active fascicle strain and shortening velocity in fascicles of the iliotibialis lateralis pars postacetabularis (ILPO)

Fig. 5.

Mean fascicle strain expressed as a % L₀ during active lengthening and active shortening in the anterior (red) and posterior (blue) ILPO as a function of speed. Positive strain indicates lengthening. Anterior values are offset slightly on the speed axis for clarity. Error bars indicate ±1 s.e.m.

Fig. 6.

Mean active shortening velocity (positive values) and active lengthening velocity (negative values) in the anterior (red) and posterior (blue) ILPO expressed as lengths per second. Anterior values are offset slightly on the speed axis for clarity. Error bars indicate ±1 s.e.m.

Moment arms

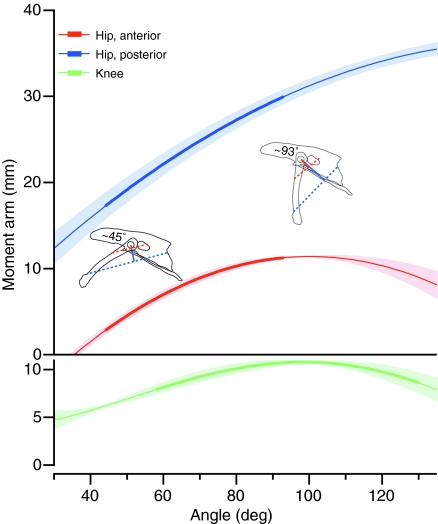
The average moment arm of the ILPO at the hip for both anterior and posterior fascicles increased with increasing joint angle throughout the range of hip angles found in vivo (Fig. 7). The hip moment arm of the posterior fascicles was ∼3.5 times the value found for the anterior fascicles. Because the origin of the anterior fascicles was dorsal to the center of rotation of the hip, the moment arm for these fascicles drops to zero at very flexed hip angles.

Fig. 7.

Upper panel: mean moment arm of the anterior (red) and posterior (blue) fascicles of the ILPO at the hip, as a function of the hip joint angle. Lower panel: moment arm of the patellar tendon complex at the knee. The range of angles measured in vivo is indicated by the thicker part of the trace for each curve. Shaded bands indicate ±1 s.e.m.

The moment arm of the patellar tendon complex at the knee varied ∼20% over the range of knee angle found in vivo with a peak value at ∼95 deg and was approximately the same magnitude as that found for the moment arm of the anterior fascicles at the hip (Fig. 7).

Modeled versus measured fascicle strain

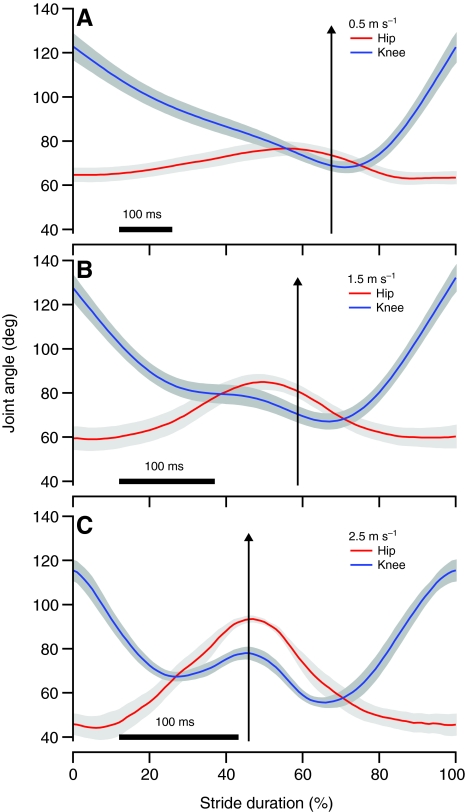
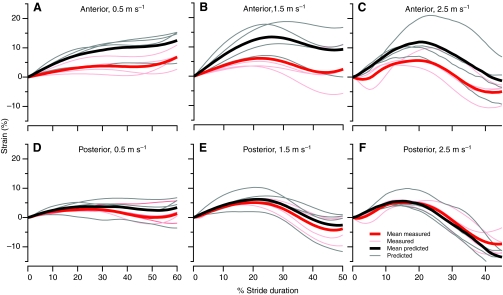
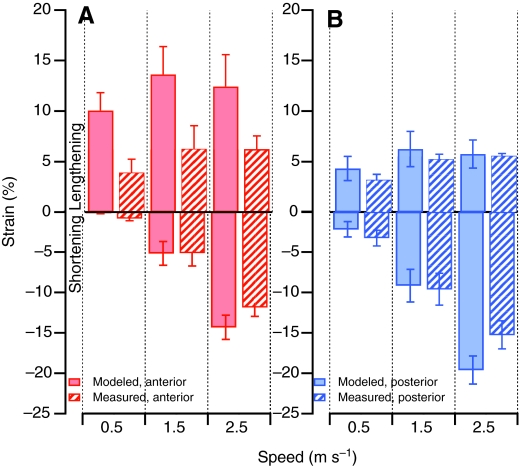
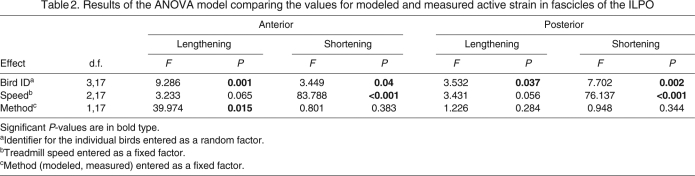
For each bird the angular excursions at the knee and hip (Fig. 8) instantaneous moment arm as a function of angle, were used to calculate the predicted active strain at 0.5, 1.5 and 2.5 m s^–1 (Figs 9 and 10). In the posterior ILPO fascicles, no significant differences were found between calculated and measured active lengthening or shortening (P>0.28; Table 2). In the anterior ILPO fascicles, our model predicted values of active shortening that were not significantly different from the measured values (P>0.38; Table 2). However, the predicted and measured values for active lengthening in the anterior fascicles were significantly different (P=0.015; Table 2).

Fig. 8.

Mean knee (blue) and hip (red) joint angles in the guinea fowl during running on the level at 0.5 (A), 1.5 (B) and 2.5 m s^–1 (C) as a function of stride duration (foot-down to foot-down) with toe-off indicated by black arrows. Gray bands indicate ±1 s.e.m.

Fig. 9.

Mean predicted (thick black lines) and measured (thick red lines) active strain in the anterior (A–C) and posterior (D–F) ILPO during running at 0.5 m s^–1 (A,D); 1.5 m s^–1 (B,E); and 2.5 m s^–1 (C,F). The thin lines indicate the individual predicted (gray) and measured (pink) curves for each animal. The curves for the modeled and measured strain were aligned at 0 strain at the beginning of the stride. The curves for the modeled and measured strain in the anterior fascicles diverge during active lengthening; however, modeled and measured active shortening are similar.

Fig. 10.

Mean measured (hatched bars) and predicted (solid bars) maximal strains in anterior (A) and posterior (B) fascicles of the ILPO. Positive strain indicates lengthening. Error bars indicate ±1 s.e.m.

Table 2.

Results of the ANOVA model comparing the values for modeled and measured active strain in fascicles of the ILPO

DISCUSSION

The hypothesis of functional equivalence of sarcomere function stems from a consideration of musculoskeletal architecture and muscle physiology (Gans et al., 1985). The architecture of limb muscles and the skeletal elements to which they attach is diverse and appears to have resulted from natural selection that has operated to adapt the locomotor system to the functional demands of locomotion, although this selection need not have produced optimal solutions (Lauder, 1982). Many considerations of architecture have focused on features within muscles that affect their mechanical output (Otten, 1988; Van Leeuwen and Spoor, 1992; Lieber and Fridèn, 2000). However, the muscle architecture must also be considered in the context of the position and geometry of the muscle relative to the rotating joints. Basically, this issue is one of ‘packaging’ a specific muscle volume within the constraints of the co-evolving skeletal architecture. In proposing the hypothesis of functional equivalence, Gans and colleagues specifically considered muscles with broad origins and/or insertions that are part of the complex architecture of jaw muscles, but the hypothesis can be applied also to the limb muscles (Gans et al., 1985; Gans and de Vree, 1987). The hypothesis states that, for a muscle that exhibits nearly simultaneous activation throughout, its internal architecture and position in relation to the joint center of rotation should allow the sarcomeres throughout the muscle to contribute equally to force and work output. This equivalence stems from the corollary assumptions that the sarcomeres will operate in the same regions of their force–velocity and length–tension curves when active. The extent to which functional equivalence is obtained in various muscles has been sparsely documented, with recent studies instead emphasizing differential function in different muscle regions resulting from neuromuscular compartmentalization or other factors. Because many factors can produce localized differences in mechanical function, it is probably unlikely that in any large muscle all muscle fibers have precisely identical mechanical function. Nevertheless natural selection may have favored structural features that minimize large regional differences in mechanical function because these differences may produce suboptimal force and work output.

Our results are consistent with the hypothesis of functional equivalence in the anterior and posterior regions of the ILPO. Although the strains during shortening and lengthening are significantly different between the anterior and posterior fascicles, the differences are relatively small and result in small differences in shortening velocity as a fraction of maximum shortening velocity (V_max). Based on the V_max found for leg muscles in turkeys (Nelson et al., 2004) and adjusting for body size, the V_max of the ILPO is expected to be ∼15 L₀ s^–1. Given this value, the maximum differences in velocity between the anterior and posterior regions represent only 2–3% of V_max.

We found that similar active shortening strain in the anterior and posterior fascicles of the ILPO is predicted because most of the active shortening results from hip extension and the increasing moment arm at the hip from the anterior to posterior fascicles is matched by an increasing fascicle length. During active shortening, which occurs in the latter half of stance, the hip and knee both extended, but the knee had a much smaller angular change than the hip. The anterior fascicles have a smaller moment arm at the hip and experience a smaller absolute change in length as a function of angle compared with the length change in the posterior fascicles. Even though the anterior fascicles go through less absolute length change, as a function of angle they are shorter, resulting in a similar strain in both the anterior and posterior ILPO during this period of the stride.

In contrast to the predictions for active shortening, the musculoskeletal model predicted a significantly larger strain during active lengthening in the anterior fascicles compared with that predicted in the posterior fascicles at all speeds (Figs 9 and 10). Active lengthening in the ILPO occurred during the first half of stance and the predicted strain was primarily driven by the large knee flexion occurring during this period. Because the anterior and posterior ILPO share the same moment arm at the knee joint, our model predicted similar changes in length, and, therefore, larger strains in the shorter anterior fascicles. The amount of active lengthening in the anterior ILPO was predicted to be considerably larger than the lengthening measured by sonomicrometry (Table 2; Fig. 10). In contrast, the values for measured and predicted active lengthening in the posterior ILPO were not significantly different. We are left with the question of what mechanisms account for the difference between predicted and measured active lengthening in the anterior and posterior ILPO. Although we cannot rule out entirely potential errors in our predicted strain resulting from the assumptions of our musculoskeletal model (see Materials and methods), we consider it unlikely that these assumptions account for the difference in predicted and measured strain. For example, using a constant pinnation angle would result in predicting greater stretch than allowing the pinnation angle to increase with increasing hip angle.

One possible mechanism that could reduce active lengthening of the anterior fascicles is differential stretch of the tendon of insertion at the knee. The more anterior fascicles of the ILPO insert on a tendinous band that is parallel with and medial to the posterior edge of the superficial aponeurosis that forms the insertion of the some of the fascicles of the femerotibialis muscle (Fig. 1). This architecture results in a gradient of distal tendon length, with the more anterior fascicles having a longer tendon of insertion. A stretch of 4.5% in the tendon of insertion of the anterior fascicles could account for the difference we observed between the predicted and measured fascicle lengths. This tendon strain is well below the 8–10% strain at which tendon failure occurs (Biewener, 2003). Because the posterior fascicles insert almost directly onto the stout patellar tendon, they have very little tendon available for stretch. This short posterior tendon length probably explains why we were able to accurately predict length changes in the posterior fascicles based on moment arm and joint kinematics at all speeds.

However, if forces in the anterior ILPO were causing stretch of the tendon one might predict that the tendon stretch would be greater at the faster speeds when a greater cross-sectional area of muscle is active, as indicated by the increase in EMG amplitude (Carr et al., 2011b). However, the difference between the predicted and measured strains is similar across the different speeds (Fig. 9). Tendon stretch could only account for the observed data if the active muscle fibers (fascicles) transmitted force through separate elements of the tendon. Although measurements of force transmission in the tendon of the cat soleus suggested that it acts as a bulk structure (Proske and Morgan, 1984), more recent structural analyses have suggested that force could be transmitted along individual collagen fibrils or fascicles (Provenzano and Vanderby, 2006; Haraldsson et al., 2008). An interesting feature of the tendinous band along the anterior edge of the ILPO is that even without magnification the band appears to consist of separate collagen strands running parallel to its long axis. The presence of these separate strands raises the possibility that the structure of this tendinous band facilitates localized force transmission, allowing substantial tendon stretch at low forces. A small portion of the fibers of the femerotibialis muscle also insert on the same band and could influence tendon stretch as well.

Conclusions

Despite its architectural complexity, the ILPO undergoes similar active lengthening and shortening along its anterior–posterior axis. The direct relationship between hip moment arm and fascicle length allows similar active shortening under the influence of hip extension. However, active lengthening in early stance is driven by knee flexion and, because all fascicles have the same knee moment arm, the shorter anterior fascicles are predicted to have more than twice the lengthening strain of the posterior fascicles. Despite this predicted difference, the measured differences in strain were minimal (∼2% of L₀). We hypothesize that a portion of lengthening induced by knee flexion is taken up by stretching the long tendinous band that forms the tendon of insertion of the anterior fascicles. In the ILPO, muscle, tendon and joint architectures appear to have evolved to maintain similar function across the breadth of the muscle.

LIST OF SYMBOLS AND ABBREVIATIONS

ILPO

iliotibialis lateralis pars postacetabularis

L_so

in vivo segment lengths measured by sonomicrometry

L_sc

in vivo sarcomere length

L_sc,ref

reference sarcomere length

L_so,ref

sonomicrometer length

L₀

length at the middle of the plateau region of the length–tension curve (optimal length)