Kinetics of Hole Nucleation in Biomembrane Rupture

Abstract

The core component of a biological membrane is a fluid-lipid bilayer held together by interfacial-hydrophobic and van der Waals interactions, which are balanced for the most part by acyl chain entropy confinement. If biomembranes are subjected to persistent tensions, an unstable (nanoscale) hole will emerge at some time to cause rupture. Because of the large energy required to create a hole, thermal activation appears to be requisite for initiating a hole and the activation energy is expected to depend significantly on mechanical tension. Although models exist for the kinetic process of hole nucleation in tense membranes, studies of membrane survival have failed to cover the ranges of tension and lifetime needed to critically examine nucleation theory. Hence, rupturing giant (~20 μm) membrane vesicles ultra-slowly to ultra-quickly with slow to fast ramps of tension, we demonstrate a method to directly quantify kinetic rates at which unstable holes form in fluid membranes, at the same time providing a range of kinetic rates from < 0.01 s⁻¹ to > 100 s⁻¹. Measuring lifetimes of many hundreds of vesicles, each tensed by precision control of micropipet suction, we have determined the rates of failure for vesicles made from several synthetic phospholipids plus 1:1 mixtures of phospho- and sphingo-lipids with cholesterol, all of which represent prominent constituents of eukaryotic cell membranes. Plotted on a logarithmic scale, the failure rates for vesicles are found to rise dramatically with increase of tension. Converting the experimental profiles of kinetic rates into changes of activation energy versus tension, we show that the results closely match expressions for thermal activation derived from a combination of meso-scale theory and molecular-scale simulations of hole formation. Moreover, we demonstrate a generic approach to transform analytical fits of activation energies obtained from rupture experiments into energy landscapes characterizing the process hole nucleation along the reaction coordinate defined by hole size.

1. Introduction

Nearly a century ago, physiologists found that cells rupture quickly (lyse) when subjected to large osmotic pressure differences yet remain sealed much longer before rupturing when subjected to smaller osmotic stresses (cf. classic book on red blood cell hemolysis by Ponder [1]). Similarly, fifty years ago, Deryagin and Gutop [2] observed that supported surfactant membranes (films) survive for variable periods of time and that the times diminish with increase in film tension. Building on earlier concepts in phase nucleation (Zeldovich [3]), Deryagin and Gutop proposed that membrane rupture originates from thermal activation of a unstable hole (pore) and introduced what is now the paradigmatic theory for hole nucleation in tense membranes [2]. Shortly after this seminal proposition, experimenters shifted their focus to measuring permeability and charge conductance through supported membrane films, exploring the impact of voltage up to the limit of capacitive breakdown (cf. examples in [4-9]). Particularly relevant to thermal activation, fluctuations in conductance across membranes under low voltages reveal frequent transient-permeating defects that quickly vanish without becoming metastable or even forming open nanopores [9]. Yet, in the same tests at high voltage, catastrophic holes open in the membrane that cause capacitive breakdown. In most studies of membrane conductance and capacitive breakdown, the events have been too fast and too small to capture by visible light microscopy. However, innovative approaches have been devised to briefly stabilize macroscopic holes in weakly-tensed membranes, enabling quantitative study of the fluid dynamics of holes and providing an assay of the “edge energies” ε (i.e. line tensions) for large holes [10-12].

In contrast to transient permeation and conductance in supported membranes, studies of cell and vesicle membrane poration have for the most part been focussed on the measuring the stresses (lateral tension or electro-compression) needed to break the membranes, yet neglecting the time dependence of membrane survival on the history of stress. For this reason, a few years ago we developed an approach called dynamic tension spectroscopy (DTS, [13]) to quantify the most frequent tensions σ* at which giant (~20 μm) membrane vesicles rupture when subjected to ramps of tension, σ(t) = r_σ t, and thus, the most frequent membrane lifetimes under increasing tension, t*. While DTS exposes the inherent trade off between membrane strength and survival, it does not directly assay the kinetic rates of failure, which must be derived from the ramp speed dependence of the data using parametric or model-dependent fits. Postulating kinetic rates to be continuous functions of tension, the criterion for most frequent rupture (*) is specified by the crossover where reduction in the “time” needed to open an unstable hole (1/k_hole) under rising tension surpasses the reciprocal ramp speed [13], - [∂(1/k_hole)/∂σ]* = 1/r_σ. To circumvent this approach, yet utilizing the four orders in magnitude range of vesicle lifetimes obtained from DTS, we will demonstrate how the methodology can be modified to directly assay kinetic rates of vesicle failure at several times t_k over the course of a repeated tension ramp experiment. Invoking Arrhenius phenomenology for thermally-activated kinetics, ~ exp(−E_b/k_BT), we convert the measurements of kinetic rates k_hole(t_k) on a logarithmic scale to relative changes in activation energy ΔE_b (scaled by thermal energy, k_BT ≈ 4.08 × 10⁻²¹ J), which become related to membrane tension through the product of ramp speed and time, i.e. σ(t_k) = r_σ t_k. The measured dependencies of energy barriers on tension are then correlated with expressions for thermal activation derived from meso-scale theory and molecular-scale simulations of hole formation. Using these correlations as examples, we end by demonstrating how analytical fits to the measured dependencies of barrier energy on tension can be transformed into quantitative images of the energy landscapes governing thermal activation along a scalar reaction coordinate defined by hole size.

2. Stochastic process of unstable hole formation in tense membranes

When external stresses creating membrane tensions persist, as in pipet aspiration of vesicles (Fig. 1) or in mechanical stretch of cells, a mesoscopic hole will eventually arise that has no possibility of closing. Hence, the random process describing formation of unstable holes can be formulated as a two-state kinetic transition between an intact and ruptured membrane. Assuming that molecular-scale dynamics in nucleation are much faster than frequencies for appearance of unstable holes, k_hole(t), we use a single Markov equation to characterize the diminishing probability S(t) of membrane survival, i.e.

$$\mathrm{dS}\left(t\right)∕\mathrm{d}t=-{\mathrm{k}}_{hole}\left(t\right)\mathrm{S}\left(t\right)$$ (1)

The number of failure events per increment of time defines the probability density of rupture, p(t) = − dS(t)/dt. Hence, by establishing experimental estimators for the probability density and probability of survival, then taking their ratios at common sample times t_k, we acquire a direct method to assay the kinetic rates for forming unstable holes in membranes, i.e.

$${\mathrm{k}}_{hole}\left(t_{\mathrm{k}}\right)=\mathrm{p}\left(t_{\mathrm{k}}\right)∕\mathrm{S}\left(t_{\mathrm{k}}\right)$$ (2)

Of particular significance, this method of assay yields several values of the kinetic rate throughout the course of any deterministic history of tension when applied to a large population of vesicles. Dependence of the kinetic rate on tension is then established independently using the tension history, i.e. σ(t_k) = ∫ _o→tk r_σ(t’) dt’, set by the programmed changes in tension r_σ(t).

Figure 1.

Top: video microscope image of ~20 μm bilayer vesicle aspirated into a micropipet. Bottom: intensity scans taken along the axis of symmetry before (solid curve) and one video frame later (~ 0.01 s) after vesicle rupture (dotted curve).

2.1 Experimental estimators for statistics of biomembrane survival

For the tests reported here (described in Appendix I), the experimental approach has been to pressurize 50-100 individual membrane vesicles using micropipet aspiration to create a steady ramp of tension (Δσ/Δt = constant r_σ). This test was repeated with 4-6 ramps for each membrane composition selected in a range from 0.01 to 100 mN/m/s. During the course of pressurization, the vesicle was monitored by ultrafast video image processing to accurately determine its increase in surface area and its lifetime up to the moment of rupture. As the estimator for probability S(t) of survival, the vesicle lifetimes t_i in a particular test were arranged into an indexed array N(t_i) of ascending order in time beginning with N_total at the shortest time and ending with one at the longest time (cf. examples in Figs. 2a-b). At the same time, the statistics of failure events were organized into a discrete histogram of values ΔN_k per time interval Δt, thereby providing the estimator for probability density of rupture p(t_k) and the (negative) coarse-grained derivative of the survival probability at the sampling times t_k (cf. Figs. 2c-d).

Figure 2.

a) Sample test of 1:1 SOPC:Ch vesicles ruptured by a common tension ramp of 10 mN/m/s. Open black circles represent lifetimes of all (60) vesicles. A small number (4) of apparent multi-bilayer structures is evidenced by the deviant branch highlighted at the terminus (crossed open black circles connected by dotted lines). b) Sample test of SOPC vesicles ruptured by a common tension ramp of 0.07 mN/m/s. Open black circles represent lifetimes of all (80) vesicles and a few (6) apparent multi-bilayer structures are highlighted at the terminus. c-d) Histograms showing the numbers of failure events ΔN_k per fixed time increments in a-b. White patterned bins identify the few events (putative multi-bilayer vesicles) truncated from the “raw data” to establish the un-normalized estimator N(t_i) for probability S(t) of “single” bilayer survival (open blue circles in a-b). The frequencies of membrane failure shown in subsequent figures were obtained from ratios of the bin contents ΔN_k to values for N(t_k) found by interpolation at bin sampling times t_k (solid yellow circles superposed on the lifetime arrays).

The “raw” data of lifetimes N(t_i) from rupture experiments characterize the survival of all vesicles tested with a ramp. However, especially when made from neutral-uncharged lipids, a small percentage (< 10%) of the vesicles were likely to be double- (or multi-) walled structures. Although nearly impossible to identify optically when filled with a higher refractive-index medium, we found many years ago that multi-walled vesicles are more resistant to stretch than single-walled vesicles. However, elastic moduli of multi-walled vesicles do not partition into precisely quantized groups since the outer-most lamellae support more stress – and displace further into a suction pipet – than the inner lamellae. Providing better discrimination, multi-walled vesicles live much longer than single-walled vesicles before rupture creating a marked deviation in the lifetime data at its terminus (cf. the black crosses superposed on open black circles in Figs. 2a-b). Thus, when clearly evident, we truncated these short deviant tails to better represent the actual population of single bilayer vesicles (N_uni) experiencing a common well-defined tension history (cf. blue open circles in Figs. 2a-b). The few events associated with the deviant branches in Figs. 2a-b are also shown highlighted by white patterned bins in the corresponding histograms of Figs. 2c-d.

2.2 Experimental assay for kinetic rates of forming unstable holes in biomembranes

After constructing the histogram estimator for probability density of failure, p(t_k) ≈ [ΔN_k/Δt]/N_uni, we then interpolated amongst the array of vesicle lifetimes to acquire estimators, N(t_k)/N_uni, for survival probabilities at the histogram sampling times t_k. As developed above, the ratios of probability densities to probabilities provided direct assays of the kinetic rates, i.e. k_hole(t_k) ≈ [ΔN_k/ N(t_k)]/Δt, at the sampling times. Formulated in this way, the assay is independent of sample size and remains valid when transition rates vary over time as when a tension history involves increases, decreases, or rapid steps to constant levels of tension. In the paragraphs that follow, we demonstrate the assay with results from tests of giant vesicles composed of single component phospholipids and 1:1 mixtures of phospho- or sphingo lipids with cholesterol. We begin by describing results for vesicle compositions where the kinetic rates depend only on levels of tension. Then, we present results for vesicle compositions where the kinetic rates depend not only on levels of tension but also on speed of tension application. Although yet to be explained, we will show that the unexpected behaviour can be attributed to differences in the frequencies for nucleating initial symmetry breaks (i.e. “zero-size” pores).

2.3 Kinetic rates of unstable hole formation in strong biomembranes

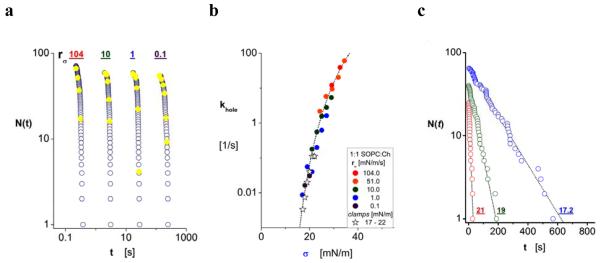
Recognized to be important constituents of eukaryotic cell membranes, we begin with the results obtained from experiments on mixtures of phospho-and-sphingolipids plus cholesterol, which are known to create very strong membranes [14-17]. The experimental data will show that these bilayers survive for long periods (> hrs) under low tensions (< 10 mN/m), yet withstand large tensions (< 20-30 mN/m or more) for short periods (0.1 s or less). As the first demonstration of the assay for kinetic rates (k_hole), we will focus on the tests of vesicles made from 1:1 mixtures of C18:0/1 PC plus cholesterol (1:1 SOPC:Ch). Compiled from rupture of ~60 vesicles using a 10 mN/m/s tension ramp, a sample of the lifetime data is shown above in Fig. 2a along with its corresponding histogram in Fig. 2c. In order to best summarize the full span of data obtained from tests with the various membrane compositions, we will present cumulative log plots of the un-normalized probabilities for bilayer survival versus log time as shown for 1:1 SOPC:Ch vesicles in Fig. 3a. Likewise, instead of plotting histograms of the data from each ramp test, we have superposed solid yellow circles on each lifetime array at the interpolation points corresponding to the histogram bin centers (cf. Fig. 3a); note, the bin content ΔN_k local to each yellow point is the difference between numbers of lifetimes starting from the previous time midpoint (t_k - ½ Δt) to the following time midpoint (t_k + ½ Δt). Determining the ratios of these bin contents to interpolated values for lifetimes, we obtain the kinetic rates, k_hole(t_k) = [ΔN_k/N(t_k)]/Δt. Establishing the levels of tension at each sampling time, σ(t_k) = r_σ t_k, we have then plotted the rates from all ramp tests on a common log scale versus tension as shown in Fig. 3b for 1:1 SOPC:Ch vesicles. With each ramp test labelled by a particular solid-coloured symbol, we see in Fig. 3b that the kinetic rates of membrane failure rise continuously upward with each faster ramp speed. To confirm that the continuous progression in kinetic rates represents an explicit dependence on tension, independent of ramp speed, we have also plotted the kinetic frequencies obtained from tests using tension clamps between 17 and 21 mN/m (open stars) in Fig. 3b. The tension clamps were created by brief periods of rapid vesicle pressurization, stopped abruptly to set a specific level of tension and held fixed until rupture. For clamps, the kinetic rates were derived from linear regression fits to the lifetime data plotted on a log scale versus time as illustrated in Fig. 3c. Unfortunately tension clamps have a limited range of usefulness, on the one hand because vesicles survive for long periods of time at modest tensions, and on the other hand because vesicles cannot be pressurized fast enough to reach large tensions before rupture.

Figure 3.

a) Data for log N(t_i) versus log t_i (lifetime) encompassing the full span of tension ramps applied to vesicles formed from 1:1 mixtures of SOPC with cholesterol (Ch). Yellow solid circles identify histogram sample times at which kinetic rates of failure were determined during each ramp. [Note: for clarity, we show only 4 of the 6 ramp tests in order that each is spaced by ~1 decade in time scale from the next.] b) Kinetic rates of failure plotted on a log scale versus the tensions corresponding to sample times in rupture histograms (solid coloured circles). c) Lifetimes of 1:1 SOPC:Ch vesicles obtained with three tension clamps (17.2, 19, and 21 mN/m). The single exponential decays superposed on the data were used to determine the kinetic rates plotted as open stars in b). Fit by variation of pre-exponential frequency scale, the continuous blue-dashed curve underlying the kinetic rates follows the dependence of activation energy on tension predicted by equation (3) in the text using the parameters appearing in Table 1a. [Note: r_δ = 0 to reflect lack of evidence for precursor dynamics.]

Even stronger and longer lived than 1:1 SOPC:Ch vesicles, the data for survival probabilities of vesicles made from 1:1 mixtures of brain sphingomyelin (SM) and cholesterol in Fig. 4A are seen to be shifted to much longer times when compared at similar ramp speeds. Again determined at the sample times in histograms and plotted on a log scale, the kinetic rates of failure in Fig. 4b exhibit a nonlinear dependence of failure rate on tension similar in form to that for 1:1 SOPC:Ch vesicles, yet shifted to significantly higher tension. Interestingly, although not as strong or long lived at any level of tension as the cholesterol-containing vesicles, the survival statistics (Fig. 5a) for single component diC22:1 PC vesicles yield kinetic rates of failure that also seem to exhibit a similar functional dependence on tension (Fig. 5b), albeit shifted to lower tensions. Certainly relevant to the high strengths and longevities under stress, all three of these lipid compositions form thick membranes as indicated by their average peak-peak headgroup distances obtained from x-ray scattering using multibilayer preparations at the room temperature, i.e. ~4.24 nm for SOPC:Ch [17], ~4.37 nm for diC22:1 PC [18], and ~4.55 nm for 1:1 SM:Ch [17].

Figure 4.

a) Data for log N(t_i) versus log t_i (lifetime) encompassing the full span of tension ramps applied to vesicles formed from 1:1 mixtures of sphingomyelin with cholesterol. Yellow solid circles identify histogram sample times at which kinetic rates of failure were determined during each ramp. b) Kinetic rates of failure plotted on a log scale versus the tensions corresponding to sample times in ramp-test histograms (solid coloured circles). Fit by variation of pre-exponential frequency scale, the continuous blue-dashed curve underlying the kinetic rates follows the dependence of activation energy on tension predicted by equation (3) in the text using the parameters appearing in Table 1a. [Note: r_δ = 0 to reflect lack of evidence for precursor dynamics.]

Figure 5.

a) Data for log N(t_i) versus log t_i (lifetime) encompassing the full span of tension ramps applied to vesicles formed from diC22:1 PC. Yellow solid circles identify histogram sample times at which kinetic rates of failure were determined during each ramp. b) Kinetic rates of failure plotted on a log scale versus the tensions corresponding to sample times in ramp-test histograms (solid coloured circles). Fit by variation of pre-exponential frequency scale, the continuous-dashed curve underlying the kinetic rates follows the dependence of activation energy on tension predicted by equation (3) in the text using the parameters appearing in Table 1b. Evidence for precursor dynamics is highlighted by data points correlating with the short solid-red line (defined by r_δ = 0.67 nm) vis a vis deviation of the continuous blue-dashed curve.

2.4 Kinetic rates of unstable hole formation in weak biomembranes

In marked contrast to the thick-strong membranes just described, bilayers made from diC13:0 PC are thin (~3.41 nm [18]) and weak, failing in less than a minute at 1 mN/m and surviving no more than ~10 ms at 4 mN/m. Figure 6a shows the cumulative log plot of survival statistics versus log time for the tension ramps applied to diC13:0 PC vesicles. Best demonstrating the fragility of diC13:0 PC bilayers, the kinetic rates of failure plotted in Fig. 6b are seen to be very fast even at low levels of tension. However, the rapid initial rise in kinetic rates follows a weakly curved form somewhat like that exhibited by strong biomembranes even though at ten-fold lower tensions. Most striking, in contrast to the data for strong membranes, the kinetic rates for diC13:0 PC bilayers exhibit a marked cross over to a single exponential dependence on tension above ~1.6 mN/m (highlighted by the red solid line in Fig. 6b). As discussed later, the cross over in dependence of kinetic rate on tension implies a switch in dominance between two activation barriers that exist along the thermodynamic pathway governing kinetics.

Figure 6.

a) Data for log N(t_i) versus log t_i (lifetime) encompassing the full span of tension ramps applied to vesicles formed from diC13:0 PC. Yellow solid circles identify histogram sample times at which kinetic rates of failure were determined during each ramp. b) Kinetic rates of failure plotted on a log scale versus the tensions corresponding to sample times in ramp-test histograms (solid coloured circles). Fit by variation of pre-exponential frequency scale, the continuous-dashed curve underlying the kinetic rates follows the dependence of activation energy on tension predicted by equation (3) in the text using the parameters appearing in Table 1b. Evidence for precursor dynamics is highlighted by data points correlating with the long solid red line (defined by r_δ = 1.48 nm).

2.4 Kinetics of unstable hole formation in intermediate-strength biomembranes

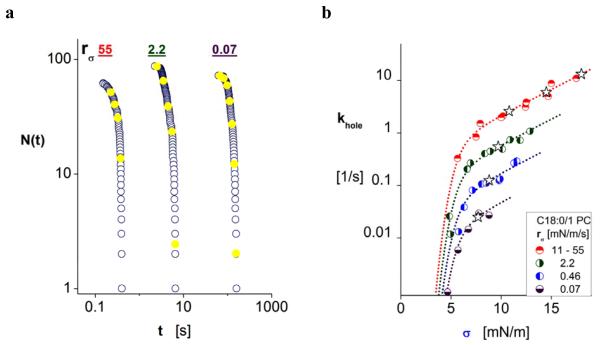
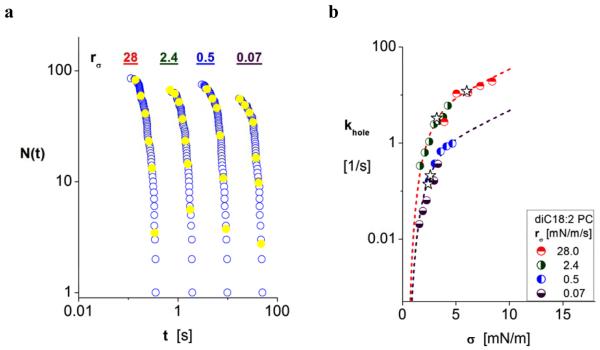
Intermediate in strength and longevity between thin diC13:0 PC bilayers and thick diC22:1 PC bilayers, single-component vesicles formed from C18:0/1 PC lipid (SOPC) were found to survive for long times (~hr) at tensions below 5 mN/m and less than ~0.1 s above 15 mN/m. Figure 7a shows the cumulative log plot of survival statistics versus log time for tension ramps used in the experiments. Plotting the statistics on a log-log scale again shows decade reductions in vesicle lifetimes with ten-fold increases in tension ramps as seen for weak and strong biomembranes (cf. Figs. 3a, 4a,5a, 6a). Surprisingly, however, the kinetic rates of failure (Fig. 7b) obtained from the lifetime statistics are dramatically different. We see that the rates shift upward with increase in ramp speed until the speeds exceed 10 mN/m/s. Completely puzzling, the kinetics depend on speed of tension application – as well as tension level – suggesting that some dissipative mechanism plays a role in the process of opening a hole at the molecular scale. Moreover, we have found the same effect in all of our tests of single component diacyl 18-carbon PC vesicles (C18:0/1, diC18:1, diC18:2, diC18:3), although the results for each lipid differ in quantitative details (cf. Fig. 8 for diC18:2). By comparison, the data plotted in Figs. 5b and 6b for other single component PC vesicles (diC22:1, diC13:0) seem to correlate explicitly with tension – not ramp speed – as do vesicles made from a 1:1 mixtures of PC or SM with cholesterol (cf. Figs. 3b and 4b). Even though we have no explanation for the unusual ramp speed dependence at the present time, we show next that all of the kinetic rates for these PC bilayers correlate with a generic dependence on level of tension merely by rescaling each set of data at the different ramp speeds by a pre-exponential constant.

Figure 7.

a) Data for log N(t_i) versus log t_i (lifetime) encompassing the full span of tension ramps applied to vesicles formed from C18:0/1 PC. Yellow solid circles identify histogram sample times at which kinetic rates of failure were determined during each ramp. b) Kinetic rates of failure plotted on a log scale versus the tensions corresponding to sample times in ramp-test histograms (solid coloured circles). As discussed in the text, the failure kinetics surprisingly shift upward with increase in ramp speed until the speeds exceed 10 mN/m/s (i.e.half solid-red circles represent data cumulated from tests at 11, 25, and 55 mN/m/s). Fit separately to data for kinetic rates at each ramp speed data by variation of pre-exponential frequency scale, the continuous-dashed curves underlying the kinetic rates follow the dependence of activation energy on tension predicted by equation (4) in the text using the parameters appearing in Table 1b. For comparison to our previous work [13], we have plotted the most frequent kinetic rates (open stars) predicted for each ramp speed by the relation, − [∂(1/k_hole)/∂σ]* = 1/r_σ.

Figure 8.

a) Data for log N(t_i) versus log t_i (lifetime) encompassing the full span of tension ramps applied to vesicles formed from diC18:1 PC. Yellow solid circles identify histogram sample times at which kinetic rates of failure were determined during each ramp. b) Kinetic rates of failure plotted on a log scale versus the tensions corresponding to sample times in ramp-test histograms (solid coloured circles). Similar to Fig. 7b, the failure kinetics shift upward with increase in ramp speed until the speeds exceed 2 mN/m/s. Fit separately to data for kinetic rates at each ramp speed by variation of pre-exponential frequency scale, the continuous-dashed curves underlying the kinetic rates follow the dependence of activation energy on tension predicted by equation (3) in the text using the parameters appearing in Table 1b. Again for comparison to our previous work [13], we have plotted the most frequent kinetic rates (open stars) predicted for each ramp speed by the relation, − [∂(1/k_hole)/∂σ]* = 1/r_σ.

3. Correlations of activation energy to mesoscopic models and molecular simulations

Employing Arrhenius phenomenology and treating pre-exponential factors as constants (see Appendix AII.3), we have converted all of the kinetic rates to increases in activation energy ΔE_b measured relative to the fastest kinetic rate k_max, i.e. ln(k_max/k_hole) ≡ ΔE_b/k_BT. [Even though meso-scale models for rates involve pre-exponential dependences on tension (cf. Appendix II), the impact on correlations with the data is imperceptible in accuracy of fit; however, the pre-exponential scale for frequency changes by a numerical factor in the range of 1 to 3.] Treated in this way, the kinetic measurements presented in Figs. 3-8 provide the experimental profiles for changes of activation energy appearing in Figs. 9. Illustrated by the continuous curves underlying the measures of activation energy in Fig. 9 and the kinetic rates in Figs. 3-8, we will show that the experimental data agree well with the expressions for thermal activation derived from a combination of meso-scale theory and molecular-scale simulations of hole formation. Although highlighted in the following paragraphs, formal details of the developments are to be found in Appendix II.

Figure 9.

Data for kinetic rates of hole formation measured in vesicle rupture experiments converted to increases in activation energy ΔE_b relative to the fastest kinetic rate k_max employing Arrhenius phenomenology, i.e. ln(k_max/k_hole) ≡ ΔE_b/k_BT. a-d) Changes in activation energy obtained in this way directly from measurements presented in Figs. 4b,3b,5b, and 6b respectively. e-f) Changes in activation energy obtained from the measurements presented in Figs. 8b and 7b respectively following shifts of the slow ramp speed data upward to merge with the fast ramp speed plateaux. The shifts involved optimal choices of constants x k_max leading to the pre-exponential frequency scales listed in Table 1b. Regimes dominated by precursor dynamics are highlighted by data points correlating solid red lines where slopes are defined by, πr_δ²/k_BT. As shown by optimal fits underlying data for each bilayer composition, the experimental measures of activation energy agree well with the expressions for thermal activation [equations (3) and (4)] described in the text. [Note: even though nontrivial pre-exponential factors are expected from theory, variations in correlations with the data are imperceptible in the accuracy of fits.]

3.1. Mesoscopic models and molecular-scale simulations

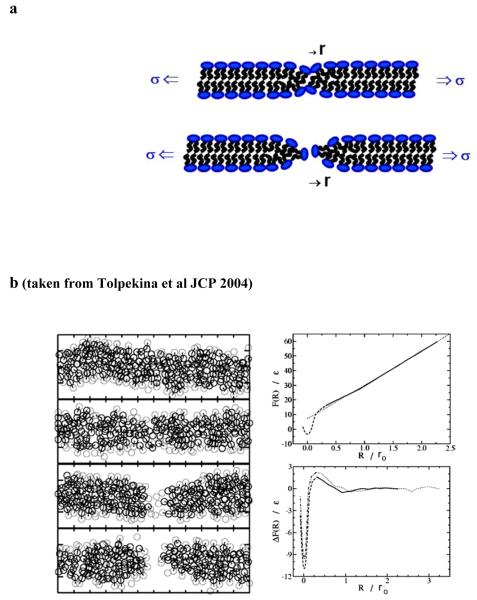
While transient permeation and opening of holes in fluid-lipid membranes have been studied with many careful experiments [4-12], the collective model usually employed to explain the results is based on the mesoscopic theory first described by Deryagin and Gutop [1], then subsequently reintroduced in more contemporary forms by Helfrich [19] and Litster [20]. In the D-G model, membrane holes are treated as circular defects (radius r) in a 2-d incompressible fluid (cf. bottom sketch in Fig. 10a), contributing an excess energy proportional to the hole perimeter (i.e. 2πr ε). The material property characterizing hole energy is the edge energy/length or line tension, ε. When subjected to lateral tension, the membrane free energy is lowered by mechanical work of dilation as the hole opens [i.e. E(r) = 2πr ε - πr² σ]. Well known from idealized models of cavity formation in 3-d fluids, excess energy of the cavity dominates at small radii yet is overwhelmed by work of mechanical tension at large radii. In the cavitation model, the transition to an unstable hole is marked by passing the barrier, E_c = πε²/σ, positioned at a critical radius defined by, r_c = ε/σ. Thus, mediated by thermal activation, the likelihood of forming an unstable hole is characterized by an activation barrier, E_b ~ σ_β/σ, that increases dramatically under tension on a scale set by edge energy and temperature [13], σ_β = (πε²/k_BT). However, completely absent from this model are the dynamics nucleating the initial symmetry break that initiates a “zero-size” pore.

Figure 10.

a) Schematic illustrations of collective membrane “conformers”. Top: activated pre-pore state. Bottom: symmetry break initiating an aqueous pore. [Note: fluctuations that thin a membrane prior to the symmetry break move material centrifugally outward as if created by a “positive” radius hole. In contrast, collective fluctuations that thicken the membrane draw material centripetally inward as if created by a “negative” radius hole without changing thickness.] b) Data and images replotted from [21] with permission. Left panels: cross sections of amphiphilic bilayers computed in coarse-grained molecular dynamics simulations. For clarity, only the particles (size r_o) within a distance of 1 r_o normal to the planes of each cross section appear in the plots. Head-group particles in gray and tail particles in black together depict the final configurations obtained for the particular values of reaction coordinate defined by, ζ = 0, 0.37, 0.80, and 0.92 (top to bottom). Based on a particle insertion criterion, no pore was detected in the top two cross sections, whereas pores of radii R = 0.95r_o and 1.48r_o respectively were found for the bottom two panels. The circles represent the molecular-size scale; solvent particles were omitted for clarity. Right top: Free energies computed in simulations of a tensionless bilayer plotted as a function of the pore radii R. The solid line denotes states with a detectable pore (ζ > 0.5). The dotted portion for R(ζ) in the range ζ = 0 → 0.5 was derived using an extrapolation based on the requirement that R effectively measures the excess particle density. The dotted line represents a fit to the hole perimeter energy as idealized in the mesoscopic theory for cavitation. Right bottom: Differences ΔF(R) between the free energy functions computed in the simulations and hole energy for zero tension (~solid and dashed) and for a tension producing 3.5% membrane stretch (dotted and dash-dotted). (Note, in the simulations [20], the size scale r_o = 1/3 nm, the energy scale ε ≈ ¾ k_BT (3.3 × 10⁻²¹ J at 325 ^oK). Thus, the linear regime of free energy (R/r_o >1) divided by 2πR, yields an edge energy, ε = 3.7 ε/r_o ≈ 37 pN.)>

Extending the mesoscopic paradigm, recent studies of fluctuations in membrane conductance [9] indicate that collective defects of some type exist prior to opening an open hole (cf. top panel in Fig. 9). Labelled “prepores” [9], these ephemeral precursors most often vanish and, based on dynamic studies of vesicle rupture [13], seem to only rarely initiate pores (cf. bottom panel in Fig. 9). Supporting these experimental perceptions, recent coarse-grained molecular dynamics simulations of hole formation [21-22] have revealed energy landscapes that commence from a deep energy well prior to symmetry breaks opening nascent pores (cf. panels in Fig. 10b taken from reference [21] with permission of the authors). Once a pore opens (lower-left panels in Fig. 10b), the free energies computed in the simulations were found to increase linearly with the mean-hole radius as idealized in the cavitation theory (cf. top-right panel in Fig. 10b). Although values we present for edge energies and the length scales describing precursor structures will differ significantly from the simulation results, the models used to correlate the experimental data for activation energies in Fig. 9 will mirror the shapes of energy landscapes obtained in the coarse-grained molecular dynamics and illustrated by the right panels in Fig. 10b. [Note: distinct from pore size, the apparent hole radius begins with the outward/inward radial displacements of material due to thinning/thickening of the membrane at the site of pore nucleation, which is then followed by opening of the pore lumen.]

3.2. Correlations of models for activated kinetics to changes in barrier energies with tension

Applying Kramers Brownian-kinetic theory [23-24] to minimal representations of the energy landscapes just described, we have developed analytical expressions for the dependence of activation energy on tension and thereby kinetic rates when given a pre-exponential scale for frequency. As shown in Appendix II, full treatment of even a minimal landscape like that found in the simulations (Fig. 10b) can involve many parameters, six or more in this case, creating a challenge to correlations with experiments. Fortunately, several of the parameters appear as pre-exponential factors scaling the paramount Arrhenius-like exponential dependence on activation energy. Hence, over the range of experimental data, the analytical expressions for kinetic rates are found to be well approximated by the product of a pre-exponential constant (frequency scale) and the exponential weight describing activation, i.e. ~ k_o exp(−E_b/k_BT). Most important is that the pre-exponential frequency reflects the large energy barrier governing precursor dynamics and symmetry breaks (cf. illustrations in Fig. 11). Moreover, since creating a symmetry break, as well as opening a pore, causes radial expansion of the membrane, application of membrane tension acts to lower both (precursor and mesoscopic) barriers, yet impacts the exponential weight exp(−E_b/k_BT) in very different ways. Correlating analytical models for kinetics to our experimental results, we will emphasize how these two barriers can be distinguished and how their properties depend on membrane composition.

Figure 11.

Illustrations of minimal energy landscapes in hole-radius space used to model Brownian kinetics of membrane failure. a) Energy landscape dominated by cavity formation (i.e. large edge energy ε) and hiding a deep-harmonic well (−E_o) that governs nucleation of “zero-size” pores. Mechanical work of tension, −πr² σ, configures an activation barrier, E_b = πε²/σ, which decreases inversely with tension and moves inward toward a cusp at the periphery of the deep well. b) Energy landscape for cavity formation with small edge energy. When subjected to large tensions, the cavitation barrier moves through the symmetry break at radius r_* exposing a precursor barrier. c) Energy landscape for cavity formation with intermediate-strength edge energy and punctuated by a weak-metastable depression local to the symmetry break. When subjected to large tensions, the energy depression deepens and the cavitation barrier falls below the precursor barrier before reaching the symmetry break.

Figures 11a-b represent the simplest energy landscape that approximates the simulation results appearing in the top-right panel of Fig. 10b. Differing only in their range of precursor dynamics, the free energies in Figs. 11a-b emerge from deep wells and cross over monotonically to a linear energy dependence on hole perimeter without the small energy bump indicted in the bottom-right panel of Fig. 10b. For this case, the relation describing dependence of activation energy on tension (cf. eqn AII.3.7) involves only three parameters: 1) a frequency scale k_δ^o for escape from the deep well to initiate symmetry breaks, 2) a thermal tension scale, σ_δ = π r_δ²/k_BT, for reduction of the precursor barrier set by mean radius r_δ of symmetry breaks, and 3) a thermal tension scale, σ_β = πε²/k_BT, for reduction of the cavitation barrier set by pore edge energy ε, i.e.

$${\mathrm{E}}_{\mathrm{b}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}+\ln \left({{\mathrm{k}}_{\delta }}^{\mathrm{o}}\right)\approx -\sigma ∕{\sigma }_{\delta }+({\sigma }_{\beta }∕\sigma ){(1-\sigma r_{\delta }∕\epsilon )}^2$$ (3)

In this model, tensions greater than σ_⊗ = ε/r_δ cause the cavitation barrier E_c to “sunset” below the energy cusp E_δ that characterizes the precursor barrier, thereby defining a cross over between kinetics limited by the cavitation barrier and kinetics limited by nucleation of a symmetry break. The signature for this cross over is a switch in form of the barrier energy from a curved regime ~ σ⁻¹ at low tensions to a linear regime ~ σ at high tensions. An important experimental caveat is that the cross over tension σ_⊗ may be inaccessible due to very small defect size r_δ and large edge energies ε as discoverd when correlating equation (3) with the activation energies plotted in Figs. 9a-b for 1:1 SM:Ch and 1:1 SOPC:Ch vesicles. Failing to detect a cross over to linear dependence on tension for these very strong membrane materials, we can only establish upper bounds for the sizes of symmetry breaks as listed in Table 1a. Completing the analysis, activation energy correlations are then matched to the kinetic rates (as shown in Figs. 3b and 4b) to obtain the pre-exponential scales for frequency. Again, lacking evidence for symmetry breaks, these frequency scales represent attempt rates for forming unstable holes starting from the deep-ground state and are thus very fast (cf. k_*^o in Table 1a) .

Table 1.

Parameters for energy landscapes that best match the data for kinetic rates

a)cavitation no evidence of pre-pore dynamics
	k*o [1/s]	rδ [nm]	ε [pN]	σβ [mNm]
1:1 SM:Ch	1.6×105	< 0.47	23	407
1:1 SOPC:Ch	7×105	< 0.59	20.5	324

b)cavitation nucleated by pre-pore dynamics
	kδo [1/s]	rδ [nm]	ε [pN]	σβ [mN/m]	ΔE*app [kBT]	r⊗ [nm]
diC22:1 PC	0.006	0.67	15	173	--	0.67
diC13:0 PC	0.04	1.48	3.1	7.4	--	1.48
C18:0/1 PC
11-55 mN/m/s	0.24	0.54	8.6	57	3.6	1.41
2.2 mN/m/s	0.065	’ ’	’ ’	’ ’	’ ’	’ ’
0.46 mN/m/s	0.019	’ ’	’ ’	’ ’	’ ’	’ ’
0.07 mN/m/s	0.005	’ ’	’ ’	’ ’	’ ’	’ ’
diC18:2 PC
28 mN/m/s	3.8	0.51	3.25	8.1	--	0.51
2.4 mN/m/s	2.7	’ ’	’ ’	’ ’	’ ’	’ ’
0.5 mN/m/s	0.45	’ ’	’ ’	’ ’	’ ’	’ ’
0.07 mN/m/s	0.26	’ ’	’ ’	’ ’	’ ’	’ ’

By comparison, the highest rupture tensions attained for strong diC22:1 PC vesicles appeared to be just sufficient to reveal a cross over in the activation energies as demonstrated by a short deviation of the cavitation regime from the few red data points for high tensions in Fig. 9c. Even though short, the linear regime in equation 3 (highlighted in red) at high tensions provides a good estimate of the mean size for symmetry breaks (r_δ in Table 1b). Yet matched to the curved regime ~ σ⁻¹ over most of the tension range, the barrier energies yield an accurate measure of the hole-edge energy (also in Table 1b). At the same time, even though much weaker materials, the activation energies obtained from kinetic rates for diC13:0 PC vesicles are seen in Fig. 9d to also match the tension dependence given by equation (3), revealing a pronounced cross over to an extended linear regime. Here spanning more than half of the accessible experimental range of tensions, the linear regime yields a much larger size for symmetry breaks (cf. Table 1b), which seem to dominate the kinetics of failure except at very low tensions. Final fits of the activation energy correlations to both sets of kinetic rates (shown in Figs. 5b and 6b) have provided the pre-exponential frequency scales characterizing frequencies of symmetry breaks defined by k_δ^o (Table 1b).

Turning to the intriguing experiments in which kinetic rates were found to depend on ramp speed as well as tension, we have found that the activation energies obtained from logarithms of kinetic rates for rupture of diC18:2 PC and C18:0/1 PC vesicles at the various ramp speeds can be collapsed to generic dependences on tension (cf. Figs. 9e-f) simply by shifting slower ramp speed data upward to match the data for the fastest ramp speeds. The shifts were accomplished through fits of each pre-exponential frequency scale as give in Table 1b. Treated in this way, the data for each type of membrane can be seen to follow the same linear regime characterizing symmetry breaks and the same cavitation regime, albeit with composition-specific parameters like edge energy and radius scale of the symmetry break. Most simple, we find that the activation energies for diC18:2 PC bilayers correlate well with the relation given by equation (3) as evidenced by the continuous blue-dashed curve and solid red line appearing in Fig. 9e. While yielding a comparable low value for edge energy like diC13:0 PC, the radius scale for symmetry breaks in diC18:2 PC bilayers is found to be nearly three-fold shorter (cf. Table 1b).

In contrast to the other PC bilayers, the activation energies in Fig. 9f can only be fit by postulating a weak depression in the free energy landscape, ΔE_*^app , local to the symmetry break after the precursor barrier at r_δ (cf. Fig. 11c and lower-right panel in Fig. 10b). As developed in Appendix II, the relation describing dependence of activation energy on tension (cf. eqn AII.3.6) involves the same three parameters in equation (3) plus the possibility of weak confinement represented by the parameter, ΔE_*^app , i.e.

$${\mathrm{E}}_{\mathrm{b}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}+\ln \left({{\mathrm{k}}_{\delta }}^{\mathrm{o}}\right)\approx -\sigma ∕{\sigma }_{\delta }+\ln \{1+\exp [({\sigma }_{\beta }∕\sigma ){(1-\sigma r_{\delta }∕\epsilon )}^2-\Delta {{\mathrm{E}}_{\ast }}^{\mathrm{app}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}]\}$$ (4)

Unlike the simpler landscape with no overshoot in energy at the precursor barrier, the energy depression, ΔE_*^app , following the barrier causes the cavitation barrier to “sunset” below the precursor barrier at a tension σ_⊗ greater than σ_δ as predicted by, ΔE_* = (π ε² /σ_⊗) (1 - σ_⊗ r_δ/ε)². Moreover, lacking explicit local details of the energy landscape, this condition only provides bounds on the location r_* of a symmetry break, i.e. r_δ < r_* < r_⊗ = ε/σ_⊗ (see equation AII.3.5 for the analytical expression specifying r_⊗).

Correlated to the activation energies for C18:0/1 PC bilayers, equation (4) is found to closely match the superposed ramp data given a common energy depression of ΔE_* ~ 3.6 k_BT. Similar to the bump in energy appearing in the simulation results, this value for ΔE_* would only produce very brief weak confinement – if at all – near the symmetry break. Still, a small energy depression is needed to achieve the quality of fit shown by the continuous blue-dashed curve and solid red line underlying the data in Fig. 9f. Here, the red line yields nearly the same radius scale for location of the precursor barrier as found for diC18:2 PC bilayers, yet the energy depression results in a low cross over tension σ_⊗ (i.e. large radius r_⊗, Table 1b). The correlation in Fig. 9f for tensions less than σ_⊗ yields a value for edge energy of C18:0/1 PC bilayers intermediate between the values for diC18:2 PC and diC22:1 PC. Using the correlations to activation energies defined by parameters in Table 1b, the apparent frequency scales characterizing symmetry breaks in C18:0/1 PC and diC18:0/1 PC bilayers have been derived from fits to each ramp speed data set for kinetic rates as shown by the curves underlying data in Figs. 7b and 8b. Listed in Table 1b, the apparent frequency scales increase with ramp speeds for both bilayer systems and appear to reach a plateaux when speeds exceed 10 mN/m/s, suggesting that fast ramps prevent relaxation to deeper ground states. While the 10-50 fold changes in frequency scale appear striking, the ranges would likely only represent about 10-15% variation in depths of the ground states as sketched in Fig. 11c.

4. Conclusions and Discussion

In our previous DTS tests of diacyl PCs [13], we concluded that the most frequent tensions for membrane failure (strengths) under slow and fast tension ramps revealed a sequence of two kinetic events. When tested with slow tension ramps, the most frequent rupture tensions increased weakly with ramp speed as predicted by the mesoscopic theory for cavitation and the relation connecting kinetic rates to most frequent rupture, − [∂(1/k_hole)/∂σ]* = 1/r_σ. On the other hand, when tested with fast tension ramps, a second regime emerged at high tensions where the most frequent rupture tensions increased exponentially with ramp speed indicating a switch of activation barrier to some type of defect nucleation process. However, fitting the cross over between the two ramp-speed regimes was often difficult and inconclusive. Hence, we set out in this work to establish a direct assay for kinetic rates of failure. Taking advantage of the ten-thousand fold span in vesicle lifetimes attainable with tension ramps, we have demonstrated the efficacy of this assay with results from tests of the same membrane compositions examined previously with DTS. Now, the measurements of kinetic rates plotted on a log scale directly reveal the changes in activation energies corresponding to the levels of applied tension, enabling critical comparisons to energy landscapes for thermal activation. Following the formal approach to Brownian kinetics introduced by Kramers [23], we have developed relations for activation energies and rates of unstable hole formation utilizing minimal representations of energy landscapes that capture the essential features expected from a long history of mesosopic theory [2, 19-20] and membrane experimentation [4-13] as well as recent molecular dynamics simulations [21-22]. The close fits between these expressions and our measurements provide direct support for the postulated sequence of kinetic transitions, the first leading to symmetry breaks that initiate “zero-size” pores and the second producing unstable cavities that cause membrane failure. Moreover, the correlations yield key nanoscale parameters that govern mechanical strength and survival of biomembranes.

When first applying the experimental assay, we expected to obtain kinetic rates consistent with the values derived indirectly in the original DTS experiments. This expectation turned out to be correct for the data obtained in tests of SOPC:Ch, SM:Ch, diC22:1 PC, and diC13:0 PC vesicles. On the other hand, completely unexpected, the kinetic rates measured in tests of C18:0/1 PC (SOPC) and diC18:2 PC bilayers (as well as results not shown for other unsaturated diacyl PC bilayers) exposed a ramp speed dependence that was not perceived in DTS experiments with the same compositions. Interestingly, even though dependent on ramp speeds, we have shown that logarithms of these kinetic rates collapse to common dependences on tension simply by shifting slower ramp speed data upward to match the data for the fastest ramp speeds. In this way, the activation energies governing cavitation after symmetry breaks, as well as the apparent size of the nucleating defects, are found to be independent of ramp speed. Yet, for some reason still to be determined, the frequency scales for precursor nucleation increase almost exponentially with slow ramp speeds as if nucleated from shallower ground states and then become independent of ramp speed above a few mN/m/s.

In correlating the data for activation energies, we have used the dependences of barrier energies on tension derived from models of free energy landscapes formulated in terms of apparent-hole radius. However, alternatively, we could have performed generic fits to the data for activation energies to establish the dependences on tension, ΔE_b(σ), even choosing piece-wise continuous relations when needed to match a cross over from a steep-curved regime at low tensions to a linear-like regime at high tension (see note below). Given the thermodynamic principles governing activation, the apparent-hole size is defined by the scalar area a_b that couples with tension to lower the energy barrier as prescribed by the derivative, a_b = − (∂E_b/∂σ)_T. Transformed in this way to functions of apparent-hole area, ΔE_b(a_b), the changes in barrier energy obtained with any analytical fit can be used to map the corresponding segment of the energy landscape along a scalar reaction coordinate defined by area, i.e. ΔE(a_b) = ΔE_b + σ a_b. As a simple demonstration, we have illustrated the generic approach in Fig. 12 using the model fits obtained with activation energies measured in tests of diC13:0 PC, C18:0/1 PC, and 1:1 SM:Ch vesicles. To distinguish the thermodynamic measure of hole size from the cylindrical radius characterizing physical models and simulations, we have used an apparent diameter D_hole = (4a_b/π)^1/2 to represent the apparent-hole area [= − (∂ΔE_b/∂σ), which is plotted as a function of tension in Fig. 12a. The size scale D_hole provides easy comparison to the average cross sections of phospholipids in bilayers (~ 1 nm). Figure 12b shows the barrier energy fits transformed to functions of the apparent-hole diameter. Finally, adding the mechanical potential, σ a_b, the corresponding energy landscape segments appear in Fig. 12c. As a simple confirmation of validity, application of the approach to data for 1:1 SM:Ch bilayers reproduces the expected theoretical behaviour for idealized cavitation: i.e. D_hole (= 2ε/σ) is inversely proportional to tension in Fig. 12a; barrier energy, ΔE_b/k_BT [= (πε/2k_BT) Δ(D_hole)], rises in linearl proportion to D_hole in Fig. 12b; and ΔE [= 2ΔE_b], also rises linearly in linear proportion to D_hole at twice the slope in Fig. 12c. Nontrivial by comparison, and unique to this treatment, the energy landscape for C18:0/1 PC bilayers reveals a non-linear dependence on hole diameter at the onset of the cavitation regime following the symmetry break (red stars in Fig. 12c). [Note: the series expression, C_o - σ/σ_δ + ∑_n≥2 C_n Φ(σ)ⁿ, involving powers of an order-parameter like function, Φ(σ) ≡ (1- σ/σ_⊗) for σ ≤ σ_⊗ and Φ(σ) ≡ 0 for σ > σ_⊗, provides equally as good fits to the data for activation energies as found with the model-based equations (3-4) in Figs. 9a-f .]

Figure 12.

Analytical fits of changes in activation energy ΔE_b versus tension transformed into energy landscapes characterizing hole nucleation along a reaction coordinate defined by hole size. Representing weak to strong fluid membranes, the generic approach is illustrated by transformations of the fits appearing in Figs. 9a,c,d,f. a) Step 1: determination of hole size as a function of tension, i.e. area a_b = − (∂E_b/∂σ). [Plotted on a scale reflecting molecular cross section (~ 1nm), we have used the apparent diameter, D_hole = (4 a_b/π)^1/2, to characterize hole size.] b) Step 2: changes in activation energies transformed to functions of hole size. c) Step 3: energy landscapes [i.e. ΔE = ΔE_b + σ a_b] for hole nucleation mapped as functions of hole size.

Quantified by the approach just described, our experiments show that the sizes of rupture pores in biomembranes appear to be small, remaining molecular in scale even for the lowest rupture tensions (except for perhaps very weak bilayers like diC13:0 PC). As such, the results can be compared directly to the molecular scale simulations of hole formation [21-22]. First, although small, the length scales derived from the precursor regimes appearing in Figs. 9d-f (cf. r_δ inTable 1) for single-component PC bilayers seem to be significantly larger than those revealed in coarse-grained molecular dynamics simulations of diC16:0 PC lipids [22] which, in turn, are comparable to simulations of structure-less particles [21]. However, of greater concern, much larger edge energies (30-40 pN) are obtained from simulations [21-22, 25] than derived here from the fits to the data for activation energies. Given a range from 30-40 pN, the thermal tension scales predicted to characterize activated hole formation would be so large, σ_β ~ 700-1200 mN/m, that membrane rates of rupture would be expected to rise by three-four orders of magnitude over a mere 10% increase in applied tension. The dramatic increase in barrier energy for small change in tension would make membranes appear “brittle” and require extreme frequency scales for thermal excitations driven by “sonic” transport (as in fracture of solids). By comparison, the span of kinetic rates obtained over a large range of tension in experiments reveals the role of overdamped-Brownian excitations in failure of fluid biomembranes. Further supporting this view, it is important note that edge energies derived from hydrodynamic responses of micron-size holes in similar bilayers [11-12] lie in the mid-range of ε values listed in Table 1. A possible reason for the significant difference between edge energies of molecular simulations and vesicle experiments could be that membrane configurations in simulations only have enough time to equilibrate through local molecular extension and density relaxation. Perhaps to fully equilibrate, collective excitations on much longer time scales may be needed that move (shear) molecules relative to one another with almost no change in density yet create significant viscous dissipation [cf. 11-12].

Appendix I. Experimental materials and methods

AI.1. Lipids and preparation of giant unilamellar vesicles

For the sample experiments described in this article, fluid membrane vesicles were made from five types of diacyl phosphocholine (PC) lipids: saturated 1,2-tridecanoyl-sn-glycero-3 phosphocholine (diC13:0 PC); cis unsaturated 1-stearoyl-2-oleoyl-sn-glycero-3 phosphocholine (C18:0/1 PC, “SOPC”); 1,2-dioleoyl-sn-glycero-3 phosphocholine (diC18:1 PC, “DOPC”); and 1,2-dierucoyl-sn-glycero-3 phosphocholine (diC22:1 PC). A complete set of experiments was performed using each vesicle preparation, four with single component phospholipids and two with 1:1 mixtures of a single phospholipid component C18:0/1 PC, diC18:1 PC, or brain sphingomyelin (SM, a natural product) plus cholesterol (Ch). All of the materials were purchased from Avanti Polar Lipids (Alabaster, AL) and used without further purification. The gel to liquid crystalline transition temperatures for diC13:0 PC, C18:0/1 PC, diC18:1 PC, and SM are reported to be 15 °C, 6 °C, −20 °C, and ~40 °C (broad) respectively (see Avanti Polar Lipids catalog). The giant unilamellar vesicles (GUVs) were formed well above each lipid phase transition temperature by slow hydration of multibilayer films following their evaporation from organic solvent onto a teflon disk as described previously [17-18]. The final step in swelling involved soaking the hydrated multibilayer films in 200 mM sucrose overnight to establish a large osmotic potential inside the vesicles. Prior to each experiment, the vesicle suspension was equilibrated at the room temperature (~ 22-23 °C) for 2 - 3 hrs and then an aliquot of the vesicle suspension was diluted many-fold in a buffer containing glucose at just slightly higher osmolarity. The difference of index of refraction between inside-outside solutes was used to produce excellent image contrast with Hoffman phase optics as demonstrated by Fig.1a.

AI.2. Tension history and measurement of vesicle lifetime

Micropipet pressurization was used to set the membrane tension of individual vesicles. Positions of the vesicle boundaries were monitored along the axis of symmetry by high speed video-image processing at a scan speed of ~1500/s as shown by intensity profile below the image in Fig. A1. Programmed by computer software, the time course for pipet suction ΔP(t) was implemented by a motorized ground-glass syringe pump connected to the micropipet assembly. The value of tension at each video time point was calculated from the programmed suction pressure P(t) using the simple relation, σ(t) = ΔP(t) R_p/2(1 - R_p/R_v), for mechanical equilibrium of a fluid membrane vesicle in which the pipet radius R_p and radius R_v of the vesicle segment exterior to the pipet describe the two unsupported membrane geometries. Produced either by steady ramps or steps in suction, the tension rate r_σ(t) describing the stress history experienced by a vesicle was calculated directly from the change of tension with time. Measured relative to the first application of stress, each vesicle lifetime was determined by the time span up to its moment of disappearance. Compiled from ~50-100 vesicle ruptures, the data for lifetimes at a particular tension history were arranged into an ascending array of lifetimes beginning with N_total vesicles surviving to the shortest lifetime and ending with 1 vesicle surviving at the longest lifetime (see examples in Figs. 2a and 2c).

Appendix II. Kinetic models and molecular simulations of hole formation in membranes

AII.1. Kramers-Smoluchowski theory

Here, we outline Kramers theory for (Brownian) escape from a deeply bound state to formally connect energy landscapes for hole nucleation with kinetic rates. As described in the main text, we will focus on two related energy landscapes, the first being the paradigmatic theory for “2-d cavitation” introduced fifty years ago by Deryagin and Gutop [1], and the second being the same cavitation landscape modified to reflect nucleation of a precursor defect (initial symmetry break).

In its over-damped limit, Kramers (Smoluchowski) theory models diffusive transport of states over an energy landscape that commences from a deep initial well, then rises to a prominent energy barrier, and subsequently drops to a much deeper second well [23]. The essence of the approximation is that the density of states local to the initial ground state equilibrates rapidly and changes little shape over time, yet diminishes in total content as a steady flux of states slowly diffuses past the barrier (labelled transition state). For kinetic transport in hole-radius space, the steady 1-d flux defines the rate of forming unstable holes. In the absence of intervening metastable states, Kramers theory reduces to a deceptively simple Arrhenius-like expression that describes the forward transition rate, i.e. k_→ = (D/l_ol_ts) exp[−E_b/k_BT]. The diffusive dynamics are embodied in an attempt-frequency (pre-exponential factor), D/l_ol_ts, defined by a viscous coefficient for damping ζ (≡ k_BT/D) and the product of two length scales l_ol_ts. Typically evaluated using asymptotic approximations, these two lengths represent integrals of Boltzmann-weighted changes in energy, ∫ exp[−ΔE(r)/k_BT] dr, the first local to the ground state (deep well) and the second local to the transition state (barrier). Hence, the length l_o describes confinement of states local to the initial minimum and 1/l_o approximates the density of states ρ_o at r =0. The length l_ts represents the thermal width of the transition state local to the activation barrier as determined by fall off of energy away from the peak. Clearly, the paramount factor in kinetic rate is the exponential (Arrhenius) dependence on height of the barrier E_b. Except for the damping coefficient ζ, all of parameters (E_b, l_o, l_ts) in the expression for kinetic rate are determined by the free energy landscape. (Note, within factors of order unity, Kramers approximation applied to the 1-d energy landscapes modelling hole formation provides the same outcome as an analysis of “mean first passage times” [24].)

AII.2. Rates of forming unstable holes predicted by idealized cavitation

In the cavitation-based theory, thermal fluctuations δr/δt in hole radius space are confined relative to a steric barrier at zero radius by the linear rise in hole energy, 2πε r, as set by the material “edge energy” ε. At low-to-modest tensions, the thermal spread in states near r =0 is little affected by the applied tension and can be approximated by, l_o = l_ε ≈ k_BT/(2πε). Yet, the added mechanical potential, −π r² σ, overcomes the hole energy at large distance to produce a finite energy barrier at a critical radius r_c = ε/σ. When normalized by thermal energy, the energy barrier, E_c = πε²/σ, leads to a generic Arrhenius factor, exp(−σ_β/σ), that describes the mechanical susceptibility of kinetics to tension as set by the thermal scale for tension, σ_β = πε²/k_BT. Since curvature of the energy landscape │∂²E/∂r²│ is proportional to tension, the asymptotic (Gaussian) integral for thermal width local to the transition state is approximated to first order by, l_ts = l_c ≈ (k_BT/σ)^1/2, when σ_β >> σ. Hence, ignoring the nontrivial dynamics creating incipient holes and symmetry breaks local to the origin, we obtain a compact-generic expression for kinetic rate of hole formation predicted by the idealized energy landscape for cavitation [13],

$${\mathrm{k}}_{hole}={{\mathrm{k}}_{\ast }}^{\mathrm{o}}{(\sigma ∕{\sigma }_{\beta })}^{1∕2}\exp (-{\sigma }_{\beta }∕\sigma )$$ (AII.2.1)

In this case, the attempt frequency k_*^o scaling the rate is simply given by the ratio of thermal tension to the viscous coefficient that damps the thermal fluctuations, i.e. k_*^o=(σ_β/ζ). [Note: for 2-d incompressible membranes, fluctuations in hole radius r drive radially-divergent collective flows impeded by a surface-shear viscosity η and locally characterized by the energy dissipation per area, ∂e/∂t = 4πη [∂ln(r)/∂t]².. When integrated over the entire membrane, it follows [13] that the coefficient of damping fluctuations in hole radius becomes, ζ= 4πη.]

AII.3. Kinetic rates of forming unstable holes seeded by precursor nucleation

Requiring many more parameters, we now apply Kramers theory to an energy landscape for hole opening that involves two regimes of nucleation, perhaps even punctuated by a weak metastable intermediate. As evidenced in earlier experiments [9,13] and supported by recent molecular-scale simulations [21-22], collective precursor excitations seem to precede symmetry breaks that initiate an incipient pore, thereby seeding the process of unstable cavity formation. Even when closed, these excitations act to locally thin/thicken the membrane introducing small area expansions/condensations that can couple with tension to lower the activation barrier governing hole opening. Although seeming to be dominated by the energetics of cavity formation, nucleation of the symmetry break can become the rate-limiting process at high levels of tension.

Snapshots from molecular-scale simulations (left panels in Fig. 10 taken from [21]) suggest that collective “pinches” and “bulges” of the membrane structure seem to occur local to the symmetry break that creates an incipient pore. Concomitant to these precursor excitations, the simulation reveals a free energy landscape that commences from a deep well rising by ~15 - 20 k_BT to terminate in a “cusp” at a very small radius r_δ. Beyond the cusp (r > r_δ), the free energy appears to increase in proportion to the pore perimeter [~2π r] with no perceptible effect of the applied tension, yielding an apparent edge energy ε ~ 9 k_BT/nm (upper-right panel in Fig. 10 taken from [21]). However, subtracting out the linear increase (i.e. as if subjected to very large tension σ ≈ ε / r_δ), the authors exposed a small excess (~2-3 k_BT) in the free energy just beyond the cusp (lower-right panel in Fig. 10 taken from [21]). The actual break in symmetry creating a pore seems to follow the small energy bump at a radius r_*, which is much larger than r_δ. Even though small and imperceptible at low tension, the excess in energy suggests a possibility that a weak metastable intermediate could exist at the symmetry break. Interestingly, in related coarse-grained simulations using detailed chemical models of phosholipid molecules [22], the results indicate a similar excess in free energy relative to a linear open-pore regime characterized by nearly the same edge energy. Motivated by these features, we will apply Kramers theory to a modified energy landscape that commences with a precursor regime nucleating symmetry breaks and initiating “zero-size” pores.

AII.3.1 Modelling an energy landscape punctuated by weak metastable confinement

Lacking specific details of the free energy contour in radius space, we can only crudely characterize the energy barriers and minima that describe the sequence of two kinetic regimes. Guided by the discussion above, we begin by defining a “cusp” energy E_δ° at the terminus r_δ of a deep-initial well, which represents the precursor dynamics seeding symmetry breaks. Next, we assume that the symmetry break arises at a position r_* beyond the cusp. The energy level at the symmetry break is defined relative to the continuation of an apparent hole-perimeter energy profile mapped outward from the cusp, E_δ° + 2π( r_* - r_δ) ε, yet reduced locally by a small energy, − ΔE_*, possibly leading to weak confinement, i.e. E_*^o = E_δ^o + 2π( r_* - r_δ ) ε - ΔE_*. Although shifted downward by ΔE_* at r_*, the linear hole-perimeter energy then continues to rise indefinitely upward as, E_*^o + 2π(r - r_*) ε, characterizing larger hole radii, r > r_*. Taking mechanical tension into consideration, we lower the energy everywhere along the contour by the area-dependent potential, −πr² σ. Thus, eventually the linear rise in hole-perimeter energy will be overcome by the mechanical potential to establish a transition state at the radius r_c beyond which holes are unstable. When described relative to the symmetry break, E_*= E_*^o - π r_*² σ, the height of the energy barrier for cavitation is given by,

$$\Delta {\mathrm{E}}_{\mathrm{c}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}=({\sigma }_{\beta }∕\sigma ){(1-\sigma r_{\ast }∕\epsilon )}^2$$ (AII.3.1)

At the same time, the mechanical potential will also lower the cusp energy in proportion to a local area (neglecting higher order contributions), i.e. E_δ ≈ E_δ° - π r_δ² σ. Hence, the energy difference, E_δ - E_* ≈ ΔE_* - 2π ( r_* - r_δ ) ε + πσ (r_*² - rδ²), characterizes the possibility of weak confinement. Notably, E_δ - E_*, has to be greater than zero for confinement; hence, at zero tension, ΔE_* must exceed 2π (r_* - r_δ) ε. At the same time, this simple model predicts that increasing tension enhances weak confinement at the symmetry break.

Turning now to the Kramers stationary-flux approximation, we represent the ground state and intermediate state densities [ρ(0), ρ(r_*)] as probabilities for being in the vicinity of each position divided by length scales [l_o, l_*] that characterize local confinement, i.e. ρ(0) = P_o/l_o and ρ(r_*) = P_*/l_*, recognizing, P_o + P_* = 1. Hence, given a constant flux over the 1-d landscape,

$$\mathit{constant}=({\mathrm{k}}_{\mathrm{B}}\mathrm{T}∕\zeta )\exp [-\mathrm{E}\left(r\right)∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}]\partial \left\{\rho \left(r\right)\exp [\mathrm{E}\left(r\right)∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}]\right\}∕\partial r\equiv {\mathrm{k}}_{hole}$$

we establish the two probabilities by integrating the energy weighted flux { k_hole exp[E(r)/k_BT] } first from the ground state to the symmetry break, i.e.

$${\mathrm{k}}_{hole}(\zeta l_{\delta }∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T})\exp ({\mathrm{E}}_{\delta }∕{\mathrm{k}}_{\mathrm{B}}T)\approx ({\mathrm{P}}_{\mathrm{o}}∕l_{\mathrm{o}})-({\mathrm{P}}_{\ast }∕l_{\ast })\exp ({\mathrm{E}}_{\ast }∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T})$$

and then integrating from the symmetry break to the adsorbing-end state,

$${\mathrm{k}}_{hole}(\zeta l_{\mathrm{c}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T})\exp (\Delta {\mathrm{E}}_{\mathrm{c}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T})\approx ({\mathrm{P}}_{\ast }∕l_{\ast })$$

Implicit in each step, integration over an energy weight becomes the product of a Boltzmann weight for the transition-state energy multiplied by a thermal-length scale, i.e. one [l_δ] local to the cusp and the other local to the hole transition [l_c]. Along with the confinement lengths [l_o, l_*], these four length scales would in principle be evaluated using detailed models of the energy landscape in the Boltzmann-weighted integrals. However, since these parameters appear in pre-exponential coefficients, we will ignore details of their computation and show where they become embedded in phenomenological parameters scaling frequency.

Rearranging the integration results, we obtain the kinetic rate for opening unstable holes in terms of activation over two barriers given the probability of being in the ground state,

$${\mathrm{k}}_{hole}=[{\mathrm{k}}_{\mathrm{B}}\mathrm{T}∕\left(\zeta l_{\mathrm{o}}{l}_{\delta }\right)]\exp (-{\mathrm{E}}_{\delta }∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}){\mathrm{P}}_{\mathrm{o}}∕\{1+(l_{\mathrm{c}}∕l_{\delta })\exp [(\Delta {\mathrm{E}}_{\mathrm{c}}+{\mathrm{E}}_{\ast }-{\mathrm{E}}_{\delta })∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}]\}$$ (AII.3.2)

and determine the ratio of probabilities,

$${\mathrm{P}}_{\ast }∕{\mathrm{P}}_{\mathrm{o}}\approx (l_{\ast }∕l_{\mathrm{o}})\exp (-{\mathrm{E}}_{\delta }∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T})∕\{(l_{\delta }∕l_{\mathrm{c}})\exp (-\Delta {\mathrm{E}}_{\mathrm{c}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T})+\exp [({\mathrm{E}}_{\ast }-{\mathrm{E}}_{\delta })∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}]\}$$ (AII.3.3)

In the case of large barrier energies and weak metastable confinement, the ratio of probabilities is extremely small, P_*/ P_o << 1. Thus, we can use equation AII.3.2 with P_o ≈ 1 to approximate the kinetic rate. Although the energy barriers impeding each transition are the primary factors governing kinetics in AII.3.2, we will see that weak metastable confinement can also have a significant effect.

Incorporating all exponential dependences on tension in equation AII.3.2, we acquire an expression that predicts the kinetic rate for forming unstable holes nucleated by precursor excitations and the subsequent transition to a symmetry break,

$${\mathrm{k}}_{hole}\approx {{\mathrm{k}}_{\delta }}^{\mathrm{o}}\exp (\sigma ∕{\sigma }_{\delta })∕\{1+(l_{\mathrm{c}}∕l_{\delta })\exp [({\sigma }_{\beta }∕\sigma ){(1-\sigma r_{\delta }∕\epsilon )}^2-\Delta {\mathrm{E}}_{\ast }∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}]\}$$ (AII.3.4)

where there are now two thermal tension scales, σ_β ≡ πε²/k_BT, σ_δ ≡ k_BT/(πr_δ)², and a frequency scale, k_δ^o ≡ [k_BT/(ζ l_ol_δ)] exp(−E_δ^o/k_BT), for escape from the deep well, τ_δ = 1/k_δ^o. We see that the effect of an energy depression at the symmetry break, ΔE_*, is to cause the cavitation barrier to “sunset” below the cusp energy [E_c < E_δ] when tension reaches a value σ_⊗ determined by, ΔE_* = (π ε²/σ_⊗) (1 - σ_⊗ r_δ/ε)₂, thereby establishing the cross over between kinetics limited by passing the cavitation barrier and kinetics limited by nucleation of a symmetry break. However, at this level of approximation, there is no explicit dependence on location r_* of the symmetry break, other than it lies between, r_δ < r_* < r_⊗ = ε/σ_⊗, i.e.

$$r_{\delta }<r_{\ast }<r_{\delta }[1+e_{\ast }+{(2e_{\ast }+{e_{\ast }}^2)}^{1∕2}]$$ (AII.3.5)

as defined by the parameter, e_* = ΔE_*/(2π r_δ ε). [Note: the pre-exponential dependence on ratio of lengths (l_c/l_δ) in equation (AII.3.4) can be incorporated as a hidden contribution to the apparent energy depression at the symmetry break, ΔE_*^app/k_BT = ΔE_*/k_BT - ln(l_c/l_δ)

Viewed in the context of Arrhenius phenomenology, − ln(k_hole) ≈ E_b/k_BT, we will use the kinetic rate in equation (AII.3.4) to define the effective barrier energy for opening unstable holes,

$${\mathrm{E}}_{\mathrm{b}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}+\ln \left({{\mathrm{k}}_{\delta }}^{\mathrm{o}}\right)\approx -\sigma ∕{\sigma }_{\delta }+\ln \{1+\exp [({\sigma }_{\beta }∕\sigma ){(1-\sigma r_{\delta }∕\epsilon )}^2-\Delta {E_{\ast }}^{\mathrm{app}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}]\}$$ (AII.3.6)

By comparison, in the absence of an intermediate state, we obtain a simpler relation for the effective activation barrier characterized by the dynamical cross over, σ_⊗ = ε/r_δ,

$${\mathrm{E}}_{\mathrm{b}}∕{\mathrm{k}}_{\mathrm{B}}\mathrm{T}+\ln \left({{\mathrm{k}}_{\delta }}^{\mathrm{o}}\right)\approx -\sigma ∕{\sigma }_{\delta }+({\sigma }_{\beta }∕\sigma ){(1-\sigma r_{\delta }∕\epsilon )}^2$$ (AII.3.7)

As r_δ → 0, and ignoring pre-exponential factors, equation (AII.3.7) approaches the classical expression in equation (AII.2.1) for idealized cavitation, E_b/k_BT + ln(k_δ^o) ≈ σ_β/σ.

AII.4. Comments regarding the coarse-grained molecular-dynamics simulations in [21-22]

Treating the evolution of bilayer structure and metastable prepore as states in an activated reaction process, the authors in references [21-22] have computed a free energy landscape for the process using a method called the potential of mean constraint force (PMCF). The following quote nicely summarizes the coarse-grained approach in the first paper [21]: “The amphiphiles consist of one head particle and four tail particles, the latter representing three to four CH₂ groups each. The solvent particles, representing two water molecules, are identical to the head particles. Most non-bonded interactions are modeled by the usual Lennard-Jones potential Φ_LJ(r) = 4 ε [(r/r_o)⁻¹² - (r/r_o)⁻⁶], with r_o = 1/3 nm and ε = 2 kJ/mol ≈ ¾k_BT. Exceptions are the hydrophobic interactions between tail particles and head or water particles, which are mimicked by a purely repulsive soft core potential Φ_sc(r) = ε (r/r_sc)⁻⁹, with r_sc = 1.05 r_o. … The initial simulation boxes were created by constructing two parallel square lattice layers holding 24×24 straight amphiphilic molecules each, with their heads pointing outward, and by randomly adding 10,800 solvent particles. The bilayers were oriented parallel to the square xy face of the box. In the first box the sides of this face were matched to produce a tensionless state, which for the current model amounts to an area of A_o = 1218 r_o².” (Note: to avoid confusion with the variable “σ” we use for tension, we have replaced the same variable used by the authors to define molecular length scale by r_o and the scale for figure abscissas.)

When equilibrating the free energy at positions constrained along a specialized reaction coordinate ζ, the authors used a particle insertion routine to determine when a pore opened and to provide a measure of its radius R. Evaluated in this way, open holes were established for values, ζ > 0.5. Yet, the particle insertion routine yielded spurious-negative radii at reaction coordinates of ζ < 0.5. To circumvent the anomaly, the authors used linear extrapolation to determine the radius as ζ → 0 from the last detectable positive radius. Interestingly, the extrapolated regime (R < 0.25 r_o) encompassed a deep minimum in the free energy. In Fig. 10b left taken from [21], we see examples of bilayer cross sections obtained along the reaction coordinate in the vicinity of the symmetry break opening a hole. Adjacent in Fig. 10b right (top), we see that free energies rise rapidly from the minimum up to ~15 k_BT at R = 0.25r_o. As noted by the authors, the tail particles were gradually expelled from the center of the bilayer, reducing the thickness of the bilayer at the origin, and increasing values of R even before the hole opens. When pushing the tail particles away from the center, the molecular directors tilt in order to minimize contact between the remaining tail particles and the solvent. Then, at R > 0.75r_o, the symmetry break occurs and the diametrically opposed head-group particles lose contact. At this stage, the free energy has risen by some 25∈, or 18 k_BT, making pore formation a rare, activated process. The linear rise in free energy divided by 2πR yields an edge energy, ε = 3.7 ε/r_o. Given k_BT ≈ 4.49 × 10⁻²¹ J and r_o =1/3 nm in the simulations, the edge energy is quite large, ≈ 37 pN. As noted above, similar values for edge energy have been obtained in coarse-grained simulations using detailed chemical models of phospholipid molecules [22].