A Bayesian hierarchical nonlinear mixture model in the presence of artifactual outliers in a population pharmacokinetic study

Abstract

The purpose of this study is to develop a statistical methodology to handle a large proportion of artifactual outliers in a population pharmacokinetic (PK) modeling. The motivating PK data were obtained from a population PK study to examine associations between PK parameters such as clearance of dexmedetomidine and cytochrome P450 2A6 phenotypes. The blood samples were sparsely sampled from patients in intensive care units (ICUs) while different doses of dexmedetomidine were continuously infused. Conventional population PK analysis of these data revealed several challenges and intricacies. Especially, there was strong evidence that some plasma drug concentrations were artifactually high and likely contaminated with the infused drug due to blood sampling processes that are sometimes unavoidable in an ICU setting. If not addressed, or if arbitrarily excluded, these outlying values could lead to biased estimates of PK parameters and miss important relationships between PK parameters and covariates due to increased variability. We propose a novel population PK model, a Bayesian hierarchical nonlinear mixture model, to accommodate the artifactual outliers using a finite mixture as the residual error model. Our results showed that the proposed model handles the outliers well. We also conducted simulation studies with a varying proportion of the outliers. These simulation results showed that the proposed model can accommodate the outliers well so that the estimated PK parameters are less biased.

1 Introduction

Recently research groups have shown that exposure to widely-used sedatives and analgesics for relief of suffering in critically ill patients in intensive care units (ICUs) may be a major risk factor for poor clinical outcomes such as delirium and coma. Several studies have set out to define the factors that contribute to the risk of these adverse outcomes; one key risk factor is the intensity of exposure to drugs. The dose of drug administered has most often been used as a measure of the intensity of exposure to sedatives and analgesics due to difficulty of measuring plasma drug concentrations in ICU patients. These patients are critically ill and usually only a small number of blood samples can be obtained. A common problem that arises with data obtained from complex clinical situations such as ICUs is the finding of unexpectedly discrepant high or low values (outliers). In the extreme examples, when biologically implausible, these outlier values are clearly due to error. For example, extremely high concentrations can occur in samples drawn from an intravenous (IV) line that was also used to infuse the drug. However, considering the rapidly changing and complex clinical environment in the ICU, for many outlier values it is difficult to determine which are artifactual and which represent true biological variability.

In a recent study, we analyzed the pharmacokinetic (PK) data of a sedative, dexmedetomidine (DEX), using a population PK modeling to estimate drug exposure and examine source of variability in drug kinetics in ICU patients. The DEX PK data, however, posed statistical challenges to a conventional population PK modeling approach. A major obstacle was the large number of outliers that were too numerous to be ignored (9% of the weighted residuals had an absolute value of greater than 3 and this percentage may under-represent the actual number of outliers due to an increased residual variability driven by the outliers), as we will discuss later.

This problem is not unique. In clinical studies that measure drug concentrations, there often is a proportion of outliers that could be artifactual due to assay or sampling problems, or incorrect recording of the time after administration of drug, or could be due to biological variability. Some outlier values in our DEX data resulted from errors in the blood sampling process. Specifically, many ICU patients have two IV lines, one for drug infusion and the other for blood sampling, and if possible, blood for drug concentrations is not drawn from the line used for infusion. Other patients have multi-lumen central venous catheters that are used for both drug infusion and blood sampling. Although the first portion of the blood sample drawn to clear the dead space was discarded, there was always a potential for the samples to be contaminated with a high concentration of the infused drug if the portion drawn and discarded was insufficient or if this important step was inadvertently omitted. Even for the patients with two IV lines, if the blood samples were drawn proximal of the infusion site, i.e., further down along the venous drainage towards the heart, then blood samples for analysis could be contaminated with the infused drug.

However, some outlier values may not be artifactual but rather represent individuals with truly high drug concentrations due to biological variability - a problem relevant to the ICU where the clinical status of patients can change rapidly, potentially affecting drug elimination. Thus, in all patients with extreme outlying values, we first examined the patients’ charts to check for changes in renal or hepatic function; however, outlying values were not associated with obvious clinical deterioration in renal or hepatic function. Thus, our problem remained to distinguish how likely it was that any particular drug concentration value was artifactual or due to biological variability.

We use a term “artifactual” to mean outlier values seen in the DEX PK data that were likely due to error and not biological variability. In contrast, the other conventional outliers would be generated from a variety of unknown sources of errors. Their overall effects would be a random fluctuation around the residual error of mean 0, and could be reasonably well modeled by a typical residual error model.

In the presence of these artifactual outliers, the standard assumptions on residual errors in conventional population PK models may not be valid. If not addressed, estimates of PK parameters would be biased, and the factors altering kinetics may not be detected as a result of inflated variances.

Many statistical methods have been developed for handling outliers [1, 2, 3] in general settings, including the applications of robust methods [4] in univariate [5, 6, 7, 8, 9] and multivariate samples [10, 11, 12, 13], and Bayesian methods [14, 15, 16, 17, 18]. Methods for dealing with outliers in population PK analysis have been also proposed: finding appropriate residual error models [19, 20, 21] including a mixture of two normal distributions investigated in a simulation setting [22], and robust methods on distributional assumption of random effects PK parameters, such as nonparametric [23, 24], semiparametric [25, 26] and Bayesian robust methods [27, 28].

These existing methods for dealing with outliers may not be directly applicable to a complicated real life population PK data with a large proportion of artifactual outliers. These methods have been developed to handle single or few outliers in simpler settings or developed to make robust inferences on outlying individuals in hierarchical models. Thus, a statistical methodology is needed to analyze population PK data with a substantial proportion of outlying observations.

Depending on how we perceive outliers to have been generated, contaminant (outlier)-generating alternative models [5, 13, 29, 30] may be considered. We consider a mixture model as a contaminant-generating model, since the artifactual outliers in our PK data can be reasonably assumed to come from a population different from that of the main body of data; i.e. our data consist of a mixture of two different populations: valid and invalid concentrations. We propose a novel population PK model with a mixture model as the residual error model to accommodate the artifactual outliers. In order to classify which ones are more likely to be the artifactual outliers, as opposed to an empirical statistical model, our model uses a PK model’s predictive ability as a structural model to predict an individual drug concentration-time trajectory even with frequent change of doses. The proposed model is implemented within a Bayesian framework and compared with the conventional population PK analysis. The model is also evaluated using simulation studies.

The manuscript outline is as follows. Section 2 describes the motivating data and presents a conventional population PK analysis. Section 3 presents the evidence of artifactual outliers. In Section 4, we propose a Bayesian hierarchical nonlinear mixture model to accommodate the artifactual outliers. Section 5 discusses model checking and makes inferences based on the results from the proposed model while Section 6 presents simulation results. A summary and discussion follows in Section 7.

2 Data and Conventional Population PK Analysis

2.1 The data

The motivating PK data consist of DEX plasma concentrations (ng/mL) with 1 to 15 measurements per patient obtained over a time interval that ranges from 13 hours to 5 days, with a total of 247 measurements from 43 patients in the ICU at Vanderbilt University Medical Center, Nashville, Tennessee, and Washington Hospital Center, Washington, DC [31]. The data are sparse: 13 patients (30%) of the 43 patients have three or fewer measurements; the median number of measurements per patient is five.

The study drug, DEX was titrated continuously by the bedside nurse from a starting dose of 0.15 μg/kg/hr to a maximum of 1.5 μg/kg/hr to achieve the sedation goal set by the patient’s medical team using the Richmond Agitation-Sedation Scale (RASS). Thus, the sedation goals were individualized for every patient, and the severity of illness and the time course of critical illness determined the depth of sedation. For example, patients who were critically ill and had significant ventilator-patient dyssynchrony required a higher sedation level; others who were improving clinically often required lighter sedation.

Blood samples were collected at 3 predefined time points each day during continuous DEX infusion: at 05:00 ± 2 hr by the bedside nurse, at 10:00 ± 2 hr by the investigators during the morning sedation level assessment, and at 16:00 ± 2 hr with the evening sedation level evaluation. Thus, every attempt was made to standardize blood draw times. Differences in the number of samples among patients were due to a variety of reasons, including patients being in procedures during the planned blood draw or a lack of adequate access sites (e.g., central lines). Thus, missing blood draws were not necessarily related to the severity of illness, and hence there was little chance of sampling bias. While collected at two sites, the data were well standardized. Each patient’s blood was collected and processed in a similar fashion from the time it was drawn to the point at which it was stored in the freezer at −80 °C and then assayed.

Five covariates were considered: age, gender, smoking status, weight, and P450 2A6 (CYP2A6) phenotypes. The major interest of the DEX PK study is to characterize the genetic factors which could alter the pharmacokinetics of DEX, particularly the associations between cytochrome CYP2A6 phenotypes and a PK parameter, clearance.

2.2 Conventional population PK analysis

We define the notation for general population PK models. Suppose that drug plasma concentration, y_ij, is measured on individual i, i = 1, …, N, at the j^th time t_ij, j = 1, …, n_i. The drug plasma concentration-time profile for each individual i is predicted by a nonlinear function f(θ_i, t_ij) characterized by the i^th individual parameters θ_i = (θ_1i, θ_2i, …, θ_pi). Let Z_i be a design matrix which may include the i^th individual’s covariates. The most commonly used distributional assumption for PK parameters is a multivariate lognormal distribution, θ_i = Z_iθ + b_i, b_i ~ MVN(0, Ω), where θ_i are a p–vector of logarithmic transformed PK parameters specific to the individual i, θ are a p–vector of fixed parameters, and b_i is a p–vector of random effects. The MVN stands for a multivariate normal with mean vector 0 and a covariance matrix Ω. Let e_ij denote the intra-individual errors associated with the measurement y_ij, and assume the following regression model y_ij = f (θ_i, t_ij) + e_ij.

We analyzed the DEX PK data using a conventional population PK model implemented in NONMEM [32] that uses maximum likelihood methods to estimate PK parameters in population PK models [33]. We fit model candidates using first order conditional estimation methods.

Since DEX was intravenously infused with constant rate multiple times, we considered a multiple-infusions model [34] as f(θ_i, t_ij). We tried both one- and two-compartment models, and the one-compartment model was chosen as the final model since the latter did not improve the fit. The model has two PK parameters, clearance (Cl), the key parameter of interest, and volume of distribution (V). This final model was used in the conventional PK analysis and our proposed model.

We tried several residual errors models, such as lognormal and normal models. For normal residual error models, (a) additive (e_ij = ε_ij), (b) proportional [e_ij = f (θ_i, t_ij) ε_ij], (c) combined proportional and additive [e_ij = f (θ_i, t_ij) ε_1ij + ε_2ij], and (d) power models [e_ij = f (θ_i, t_ij)^α ε_ij] were considered, where ε_ij are independently and normally distributed with mean zero. For the the random effects PK parameters, a multivariate lognormal distribution was assumed; θ_i = (log Cl_i, log V_i). We also included patients covariates, Z_i, such as age, gender, smoking status and weight in addition to CYP2A6 phenotypes to adjust for other covariates altering kinetics; however, these time-invariant covariates did not explain much of the between-subject variability, and hence their inclusion did not improve the fit.

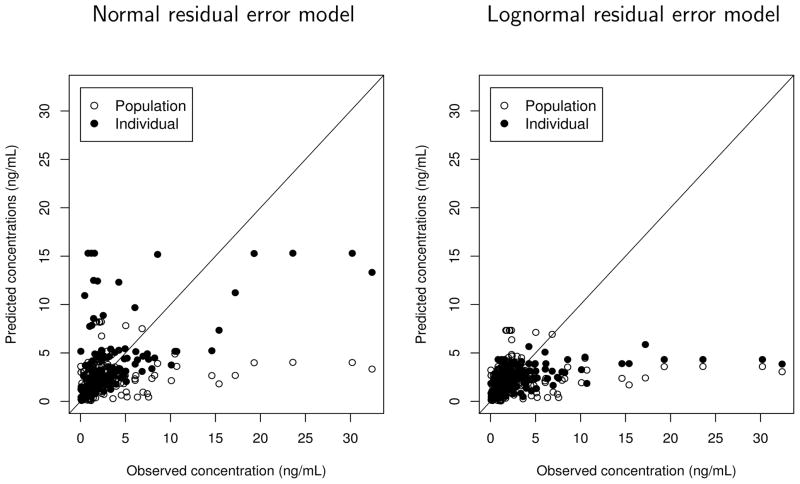
The final estimates of PK parameters and the predicted concentrations from the best model without covariates are presented in Table 1 and Figure 1. For comparison purposes, the results from both the normal proportional error model and the lognormal model are presented. As a model check, the observed DEX concentrations versus the predicted ones are also shown for both models. Many of the predicted concentrations are severely underestimated compared to the observed ones. This suggests that the distribution of drug concentrations is highly skewed to the right, probably due to the unusual number of outliers. The difference in the estimates of PK parameters from the two models in Table 1 is minimal. The estimate of Cl (32.5 L hr⁻¹) is much smaller, and the estimate of V (190 L) is larger, when compared to the systemic clearance and the central volume of distribution reported in literature, also suggesting that they may be biased due to the artifactual outliers. For example, Venn et al. [35] estimated Cl = 49.2 L hr⁻¹ and V = 44.1 L for critically sick ICU patients, a population similar to ours, and Petroz et al. [36] reported Cl = 54.6 L hr ⁻¹/70 kg and V = 56.7 L/70 kg for children aged in 2 – 12 years (the estimates were converted to 70 kg unit). This leads us to conclude that the commonly used residual error models are not appropriate to fit the DEX data.

Table 1.

The estimates of model parameters.

	Bayesian mixture	Conventional lognormal	Conventional normal
	posterior mean (s.d.)	mean (s.e.)	mean (s.e.)
Cl	49.1 (4.1)	32.5 (4.2)	29.0 (3.7)
V	100.3 (32.5)	190 (38.6)	199 (37.5)
${\mathrm{\Omega }}_{Cl}({\sigma }_{Cl}^2)$	0.22 (0.06)	0.43 (0.16)	0.73 (0.17)
${\mathrm{\Omega }}_V({\sigma }_V^2)$	0.29 (0.24)	0.62 (0.22)	0.87 (0.20)
σ2	0.10 (0.002)	0.63 (0.15)	0.35 (0.06)
w1	0.69 (0.05)	–	–
w2	0.29 (0.04)	–	–
w3	0.02 (0.02)	–	–
a	1.07 (0.07)	–	–
b	0.25 (0.03)	–	–
c	5.82 (2.56)	–	–
d	3.31 (1.11)	–	–

Figure 1.

The observed dexmedetomidine (DEX) plasma concentrations versus the predicted ones (empty circles: population fitted values based on the fixed-effects estimates and the random effects being equal to their mean value 0; filled circles: the conditional expectation of DEX concentrations given the estimates of random effects) obtained from the conventional population PK analysis implemented by NONMEM using the normal proportional residual error model (left panel) and lognormal residual error model (right panel).

3 Evidence of Artifactual Outliers

The poor fit from the conventional population PK analysis suggested plotting individual PK data fits. When investigating potential outliers, we considered a feasible range of DEX concentrations. The maximum tolerated plasma concentration of DEX in humans described in the literature is 16 ng/mL during continuous infusion at stepwise increasing dose rates [37]. The dose rates at which these concentrations were reached in 2 subjects were not reported. An earlier study reported peak plasma concentration was about 10 ng/mL at the end of a 5-min infusion of DEX (2 μg/kg) [38]. The average plasma concentrations for healthy Caucasians receiving low doses of DEX in a study conducted by the authors [39, 40] was 0.14 ng/mL after three 10-min infusions of DEX (at 0.1, 0.15, and 0.15 μg/kg; cumulative dose, 0.4 μg/kg) over 90 minutes. This information and the distribution of drug concentrations suggested that some of the extreme outliers were obviously artifactual.

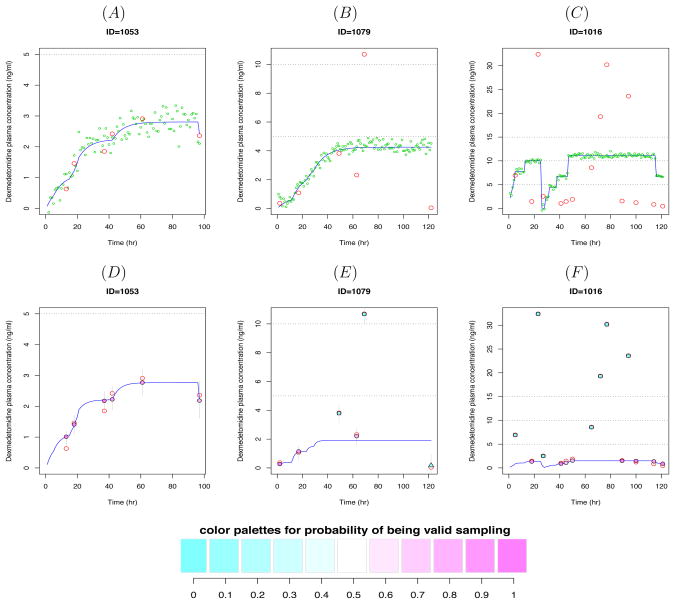
Figure 2 shows DEX plasma concentrations-time profiles for three patients who had diverse DEX dose histories. In the upper panel of Figure 2, along with the observed concentrations (red empty circles), the blue solid lines are drawn to distinguish the high values due to high doses from outliers. The lines are the predicted concentrations from individual fits. The green dots are simulated values from the estimated PK parameters with standard deviation of 0.3 to present uncertainty around the predicted lines. Figure 2(A) shows that all the DEX plasma concentrations lie within the feasible range and the envelope of predicted line, supporting that they are all valid measurements. On the other hand, the measurements in Figure 2(B) appear to be a mixture of valid and invalid values based on the predicted line, although all of them lie within the described range. Note that the data point at around 120 min is close to zero (0.04 ng/mL) although the infusion was continuously given, implying that it may be a data entry error. In Figure 2(C), the values greater than 16 ng/mL are likely to be contaminants, and also some values between 5–15 ng/mL may be artifactual if the first set of detected contaminants is removed (based on new predicted line which will be downward after the first set is removed).

Figure 2.

Dexmedetomidine (DEX) plasma concentration-time profiles for 3 subjects. The red empty circles represent the observed DEX concentrations. Upper panel: The blue solid lines represent the predicted concentrations from individual PK data fits by NONMEM and the green dots are simulated values from the estimated model. Lower panel: The solid circles, squares and triangles represent the posterior means of the individual predicted concentrations obtained from Bayesian hierarchical nonlinear mixture model. The circles represent data points classified as valid whereas the squares and triangles are classified as artifactual outliers (the second and third component, respectively). Each point is filled with color in proportion to the w₁, the probability of being a valid concentration. The blue solid lines represent the predicted concentrations from the model given the posterior means of individual PK parameters. The 95% credible intervals are represented by thin gray vertical lines.

Notice that the predicted lines in Figures 2(B) and (C) are biased upward, driven by the outliers. This demonstrates how the large outlying values could markedly affect the estimates of the PK parameters, resulting in overestimation of the plasma concentrations and underestimation of Cl. Although we could remove some of the extreme outliers by visual inspection or some other relatively arbitrary criterion based on the distribution of the data before performing the PK analysis, it would be problematic for the following reasons. First, there were too many potentially problematic values similar to the ones shown in these plots. Second, many suspect values were not very far from the boundaries of the expected range and thus were not totally improbable. Third, the uncertainty in regard to these high values being contaminants would not be taken into account. Alternatively, we have also seen that ignoring these outliers is not viable. The individual plots, along with the blood sampling process, provide strong evidence that some of the blood samples were contaminated with high concentrations of the infused drug and thus the estimated PK parameters would be seriously biased, if the outliers are not accommodated.

4 A Bayesian Hierarchical Nonlinear Mixture Model

We propose a Bayesian hierarchical mixture PK model to accommodate the artifactual outliers observed in the motivating PK data. Bayesian hierarchical models are well suited to population PK models [28, 41, 42, 43] with one more level defining priors. We will use the same model for inter-individual variation as in the conventional population PK analysis. The key component of our new model is the model for the intra-individual variation at the first stage. Specifically, we propose a finite mixture model as the residual error model to accommodate the outliers. Such a mixture model assumes that the contaminants are generated from a population (high concentration of the infused drug) different from the main population (valid plasma drug concentrations).

At the first stage, we specify the following nonlinear regression model for y_ij with a mixture error distribution as follows:

$$\begin{array}{l}{y}_{ij}=f({\mathit{\theta }}_{\mathit{i}},x_{ij})+e_{ij}\\ e_{ij}\mid {\mathit{\psi }}_{\mathit{q}}\sim \sum _{q=1}^Q{w}_q{d}_q({\mathit{\psi }}_{\mathit{q}}),\end{array}$$

where d_q is a distribution with parameters ψ_q and w = (w₁, …, w_Q) is an unknown vector of mixing weights. We assume that the number of components Q is fixed. We have found that setting Q = 3 appears to be adequate to accommodate the outliers in our motivating data.

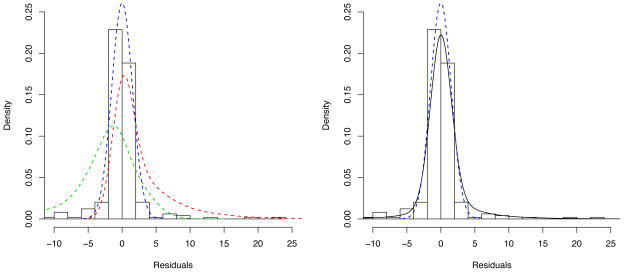
We performed a residual analysis that could be helpful in choosing the number of components in the mixture model and candidate distributions. The distribution of residuals obtained from the conventional population PK analysis is overlaid by a normal density curve (blue dashed line) in Figure 3. The figure clearly shows that the residual error distribution is highly skewed in both tails, more skewed to the right (due to a high proportion of large values of outliers), suggesting that a three-component mixture would be a good choice. A three-component mixture described below is shown on the right panel (black solid line), and the components are separately presented on the left panel with a fixed set of parameters shown in the figure. This figure suggests that each component could appropriately model the heavy-tailed residuals in both tails while still adequately modeling the bulk of the data. That is, the three-component mixture appears to fit the whole residuals reasonably well. Although not necessary for a similar type of data, this empirical approach would be especially useful when a dataset does not provide enough information for a certain parameter in the model, for example, due to a limited population size, so that we need to fix some parameters.

Figure 3.

A distribution of residuals obtained from the conventional population PK analysis with the normal proportional residual error model is overlaid by a normal density curve (blue dashed line). A three-component mixture density curve is represented by black solid line on the right panel, which is defined by ${\sum }_{q=1}^Q{w}_q{d}_q({\mathit{\psi }}_{\mathit{q}})$, where Q = 3, d₁ = N(0, τ₁), d₂ = N(0, τ₂) * Ga(a, b), d₃ = N(0, τ₃) * NGa(c, d), w₁ = 0.66, w₂ = 0.24, w₃ = 0.10, τ₁ = τ₂ = 0.09, τ₃ = 9, a = c = 1, and b = d = 0.2. These three components are separately presented by blue (d₁), red (d₂) and green (d₃) dashed lines, respectively, on the left panel.

For the DEX data, we consider the following: d₁ is a normal (N) with mean 0 and variance τ₁, N(0, τ₁), d₂ is the convolution of a N(0, τ₂) and a Gamma (Ga) with shape a and rate parameter b, and d₃ is the convolution of a N(0, τ₃) and the distribution of the negative of a gamma random variable (henceforth referred to as the negative gamma, NGa) with shape c and rate d. To elaborate, if X ~ Ga(c, d) then − X ~ NGa(c, d) and our residual error distribution is e_ij ~ w₁N(0, τ₁)+w₂N(0, τ₂)*Ga(a, b)+w₃N(0, τ₃)*NGa(c, d), where an * denotes distributional convolution. Instead of Ga and NGa, a lognormal, and the distribution of the negative of a lognormal random variable, may be used as alternative distributions when the distribution of artifactual concentrations would be expected to be less skewed.

The rationale behind this distribution is as follows. We presume that w₁ is large; hence most of the data are assumed to have normally-distributed errors (e.g. the normal density represented by blue dashed line in Figure 3). The second component is the convolution of a N(0, τ₂) and Ga(a, b), which accommodates large values of contaminants close to the boundary of the valid concentrations as well as more obviously large outliers (e.g. the density represented by red dashed line). The third component, a convolution of a N(0, τ₃) and NGa(c, d), is for small values of artifactual concentrations (hence large negative residuals), which will be likely due to dilution of the sample with saline flush or discontinuation of the infusion which had not been recorded. This term is also for accommodating the outliers close to the boundary and the more obviously small ones (e.g. the density represented by green dashed line).

Though we presented the full model above, a useful submodel fits the data well and presents a parsimonious and interpretable subclass. Specifically, consider a case where τ₁ = τ₂ = τ₃ = τ. Then the model is specified as

$$\begin{array}{l}{e}_{ij}\sim w_1\text{N}(0,\tau )+w_2\text{N}(0,\tau )\ast \text{Ga}(a,b)+w_3\text{N}(0,\tau )\ast \text{NGa}(c,d)\\ \sim w_1\text{N}(0,\tau )\ast \delta (0)+w_2\text{N}(0,\tau )\ast \text{Ga}(a,b)+w_3\text{N}(0,\tau )\ast \text{NGa}(c,d),\end{array}$$

where δ(0) is a distribution that is degenerate at 0. It is informative to note that this distribution arises from the equation e_ij = ε_ij + ξ_ij where ε_ij is a N(0, τ) random variable and ξ_ij is a mixture of a distribution degenerate at 0, a Ga(a, b) and a NGa(c, d) with probabilities w₁, w₂ and w₃, respectively.

Represented in this form, the error model is uniquely interpretable. Specifically, ε_ij can be thought of as representing natural residual error, while ξ_ij represents the outlier shift. Here, the outlier shift process, ξ_ij, is degenerate at 0 with probability w₁, is positive with probability w₂ and is negative with probability w₃. To reiterate, the model is:

$$\begin{array}{l}{y}_{ij}=f({\mathit{\theta }}_{\mathit{i}},x_{ij})+{\epsilon }_{ij}+{\xi }_{ij}\\ {\epsilon }_{ij}\sim \text{N}(0,\tau )\\ {\xi }_{ij}\sim \{\begin{array}{ll}\text{Degenerate}\text{at}0\hfill & \text{w}.\text{p}.w_1\hfill \\ \text{Ga}(a,b)\hfill & \text{w}.\text{p}.w_2\hfill \\ \text{NGa}(c,d)\hfill & \text{w}.\text{p}.w_3,\hfill \end{array}\end{array}$$

where w.p. stands for ‘with probability’. This parsimonious approach worked well as discussed in Section 5 and was implemented using Markov chain Monte Carlo (MCMC) methods in WinBUGS [44] and PKBugs [45, 46].

Notice that our model specification naturally produce an ordering constraint in the components means that would avoid the label switching problems, a well known problem in a mixture modeling [47, 48]. This problem is due to the invariance of likelihood for re-labeling of the mixture components (this means the likelihood is the same for all permutations of the components’ indices of the mixture). A commonly used solution is to impose an identifiability constraint by ordering the components means or the mixture weights [47].

In addition, the model allows the probability of being valid or an outlier for each point depending on how far the data point is from the expected range by taking advantage of the predictive ability of a PK model. Although we do not expect that the amount of shift from the PK model would be systemic, the direction of outliers can be expected, either much larger or smaller than the predicted at each point. The greater the deviation from the prediction, the higher the chance of being contaminated; this is incorporated as a probability weight. Although some covariates could be helpful to better model contaminants, they were not collected in this study; in fact, it may not even be feasible to collect them in a ICU setting.

As a note, a normal proportional error model would not be a good choice for the valid population, since it would compete with the Gamma component of the model to model outliers, making the MCMC sampling for posterior distributions difficult. Even if the valid population follows a normal proportional error model, the use of a normal additive error model would result in little bias in the estimates for PK parameters, since some skewed valid concentrations on the boundary of the invalid would be categorized as the valid in many MCMC iterations (so still high probability of being valid, although not 1), allowing them to contribute in estimating the PK parameters most of times. Our simulation results below also support this.

At the third stage, we define priors as follows. We use vague priors for fixed effects θ, normal distributions with zero means and very small precision 10⁻⁴ (i.e. very large variance). We use the conjugate prior for the inverse of the normal variance, τ ~ Ga(0.1, 0.1) (i.e. τ has a prior mean of 1 and a prior variance of 10). The inverse of Ω is assigned the conjugate prior, a Wishart prior W(R, ρ) with a scale matrix R of order 2 × 2 for which diagonal elements set about 0.18 (i.e. the 2 × 2 mean of the Wishart distribution is ρR⁻¹; the precision of each element is approximately 11 ≈1/0.3²), corresponding to 30% CV for inter-individual variability of PK parameters and off-diagonals set to 0. The degrees of freedom ρ is set 2 which allows the least informative proper Wishart prior for the inverse of Ω (ρ must be equal to or greater than 2 for the prior to be proper, and the larger ρ represents stronger belief in the prior guess on R). We use the conjugate prior probabilities of group membership, a Dirichlet distribution for the mixing weights, w ~ Dirichlet(α₁, α₂, α₃), with a common default set for a vague prior, α₁ = α₂ = α₃ = 1, which assigns equal prior masses on each group membership and is equivalent to a prior sample size of 3. Finally, the priors for a and c are assumed to be a uniform (Unif) with boundaries of 1 and 10, Unif(1, 10), and those for b and d to be Unif(0, 10), based on the shape of residual distribution and a plausible range of the parameters.

5 Model Checking and Inferences

5.1 Goodness-of-fitness

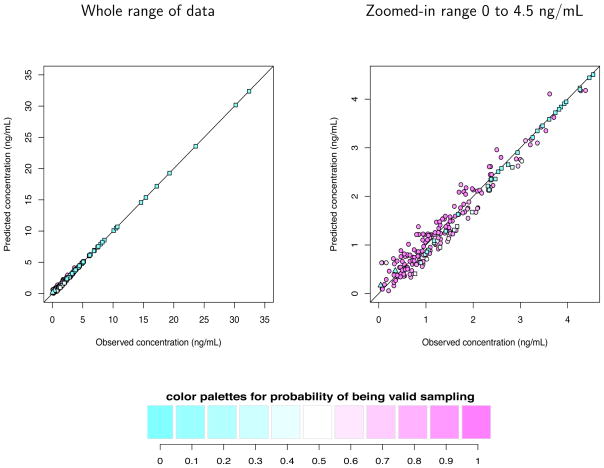
The observed DEX concentrations versus the posterior means of the predicted ones obtained from Bayesian hierarchical nonlinear mixture model are shown in Figure 4 for the whole range (left panel), and for the zoomed-in range of 0 – 4.5 ng/mL where the majority of data lie (right panel). The circles represent data points classified as valid whereas the squares and triangles are classified as artifactual outliers (the second and third component, respectively) on at least half of the MCMC iterations. Each point is filled with color in proportion to the w₁ (the color coding is shown below the figure); the darker the pink color, the higher the probability of being a valid concentration, and the darker the blue, the higher the probability of being an outlier. The white represents an estimated 50% chance of being valid or an outlier. Each data point was weighted by its corresponding the posterior probability of w₁ (probability of being valid) in estimating PK parameters. Notice that the data points with dark blue color (w₁ ≈ 0) have little influence on estimating PK parameters, so that they are practically removed in the estimation procedure. All the posterior means of the predicted concentrations are in good agreements with the observed concentrations.

Figure 4.

The observed dexmedetomidine plasma concentrations versus the posterior means of the predicted ones from Bayesian hierarchical nonlinear mixture model for the whole range (left panel), and for the zoomed-in range of 0 – 4.5 ng/mL (right panel). The circles represent data points classified as valid whereas the squares and triangles are classified as artifactual outliers (the second and third component, respectively). Each point is filled with color in proportion to the w₁, the probability of being a valid concentration.

The lower panel of Figure 2 shows the posterior means of the individual predicted concentrations and 95% credible intervals obtained from Bayesian hierarchical nonlinear mixture model overlaid with the observed drug plasma concentrations represented by red empty circles for the same three subjects discussed in Section 4. The interpretation of the color is the same as the one in Figure 4. The blue solid lines represent the predicted concentrations from the model given the posterior means of individual PK parameters. All the data points from the individual in Figure 2(D) were fully counted in estimating PK parameters as valid data (w₁ ≈ 1). The two large data points and the one very small value from the individual in Figure 2(E) almost did not contribute in estimating PK parameters (w₁ ≈ 0) whereas the rest of data points did fully contribute (w₁ ≈ 1). Notice that in contrast to the predicted line in Figure 2(B), the one in Figure 2(E) closely passes through these valid data points. In addition, the predicted line in Figure 2(E) is downward compared to the one in Figure 2(B), suggesting the bias in the estimates of PK parameters obtained from the conventional analysis was reduced. We can observe the same phenomena in comparison of Figure 2(C) and (F).

A brief explanation of estimation procedure would be informative to understand how the classified outliers are discounted disproportional to w₁. At each MCMC iteration, the model classifies each data point as valid or an outlier depending on how far the point is from expected values for valid data given the uncertainty in the data. After the classification, the PK parameter will be estimated using the main population classified as valid concentrations. If a data point is on the boundary of valid, it will be classified as valid for some MCMC iterations and as invalid for other iterations. The data point will be included in the estimation of PK parameters only if it is classified as valid. For example, see the dark blue squares in the right tail of x-axis in Figure 4. If the concentration is unexpectedly large (so very likely an artifactual outlier), then this data point will be classified as an outlier at almost all MCMC iterations and excluded at the corresponding estimation stage. The proportion of MCMC iterations for which it is classified to the second component is the estimate of w₂; in this example, w₂ ≈ 1, hence this data point will be almost entirely predicted by the normal-gamma convolution, in no relationship with other data points and the PK parameters. As such, the posterior mean of this point will be very close to the observed one if the second component fits the outlier well. For light blue squares, the proportion of MCMC iterations for its being valid would be 0 < w₁ < 0.5. Thus, they will be sometimes included in the estimation at 100w₁% of MCMC iterations, during which their prediction is in connection with other data points, and hence the posterior means would not be perfectly matched with the observed ones.

5.2 Posterior predictive assessment

We performed a posterior predictive model check [49] which requires simulating replicated data (y^rep) from the posterior predictive distribution. Using the replicated data, we can measure discrepancy between data and the proposed model for any aspect of the model by comparing a discrepancy measure based on the replicated data T(y^rep) to the one based on the observed data T(y). Common choices of discrepancy measure are sample quantiles, the mean and the standard deviation [50]. A posterior predictive P–value is defined by the probability that the T(y^rep) is more extreme than the T(y) and can be computed by the proportion of draws such that T(y^rep) > T(y). A P–value close to 0 or 1 indicates lack of fit.

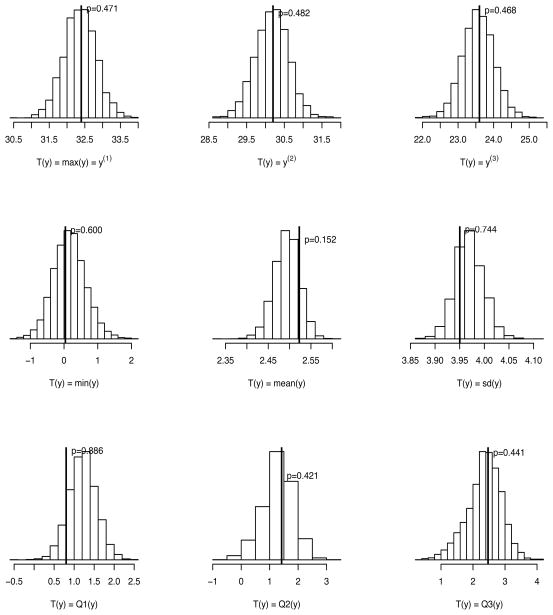
Since we also want to explore whether the proposed model could model extreme outliers well, we choose the first three largest order statistics as well as the minimum, the three quartiles (Q1, Q2, and Q3), the mean and the standard deviation as the discrepancy measures. The posterior predictive distributions of T(y^rep) are displayed in Figure 5 along with T(y) represented by vertical lines and the corresponding posterior predictive P–values. The model-generated results are similar to the observed one, supporting the model fits well.

Figure 5.

The posterior predictive distributions of T(y^rep) along with T(y) represented by vertical lines and the corresponding posterior predictive P–values. The discrepancy measures T(y) are the first three largest order statistics (y⁽¹⁾, y⁽²⁾, y⁽³⁾), the minimum (min(y)), the mean (mean(y)), the standard deviation (sd(y)), and the three quartiles (Q1(y), Q2(y), Q3(y)).

5.3 Model comparison

We compared the proposed model with traditional models. Although a deviance information criterion (DIC, [51]) is useful for comparing many Bayesian models, it has been proposed that DIC may not be a good measure for assessing mixture models [44, 52]. Since the deviance (−2 log likelihood) is the key element of many model comparison criteria such as AIC, BIC and DIC, we examined the posterior mean of the deviance defined by E[−2 log p(y|θ)]; a large reduction in the deviance would be good indication of model improvement. The posterior mean deviance of normal additive and proportional error models were 1282 and 722, respectively, whereas the posterior mean deviance of our proposed model was 126. This large reduction provides strong evidence in favor of our proposed model.

In addition, we performed the model comparison using posterior predictive loss approach developed by Gelfand and Ghosh [53] in a decision theoretic setting, which can be considered as a generalization of the work by Laud and Ibrahim [54]. For a replicated data $y_{ij}^{\mathbf{rep}}$, the observed data y_ij and the assumed model M, we choose the model minimizing the following loss function:

$$D_k(M)=\sum _{i,j}\left\{\frac{k}{k+1}{({\mu }_{ij}^M-y_{ij})}^2+V_{ij}^M\right\},$$

where ${\mu }_{ij}^M=\mathbf{E}[y_{ij}^{\mathbf{rep}}\mid y_{ij},M]$ and $V_{ij}^M=\mathbf{E}[y_{ij}^{\mathbf{rep}}\mid y_{ij},M]$. The first term measures goodness-of-fit for the replicated data if the experiment is repeated tomorrow and the second term can be considered as a penalty term for model complexity. Often k = 1, 10, 100, 000 are considered and D(k) of our model was much smaller than the normal proportional error model for all k (e.g. 2120 vs. 3494 for k=1, and 4199 vs. 5106 for k = 100,000).

The large reduction in the posterior mean deviance and the smaller D(k) along with the goodness-of-fit plots and the posterior predictive checking, all suggest that the proposed model greatly improves the fit and is preferable. Although a reduced model by fixing the shape parameters to 1 had a slightly smaller deviance (97), we present a more general form of the model with the shape parameters being free, since the major goal is to propose a general model which could be also useful for other dataset having more information for the outlier distributions.

5.4 Inferences

The posterior means and standard deviations of PK parameters and the mixing weights obtained from the Bayesian hierarchical nonlinear mixture model are presented in Table 1. The Cl is greater and V is smaller then those estimated from the conventional population PK analysis. They are in a similar range of the published values [36, 35], supporting the estimates of PK parameters obtained from our proposed PK model may be less biased. For this comparison, the covariates were not included. The posterior means of the mixing weights are 0.69, 0.29 and 0.02, respectively, which are reasonable estimates for this data.

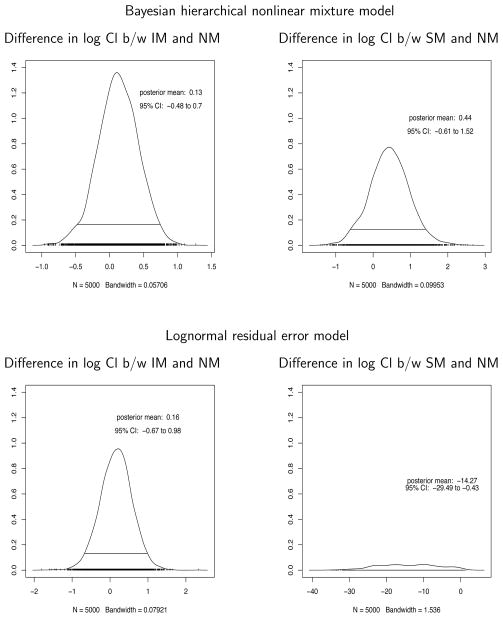
Figure 6 shows the posterior distributions of the difference in logarithm of clearances between intermediate metabolizers (IM) and normal metabolizers (NM), and that between slow metabolizers (SM) and NM from Bayesian hierarchical nonlinear mixture model (upper panel). The posterior means and 95% credible intervals are also presented, providing little evidence that CYP2A6 phenotypes are associated with Cl and could alter the DEX kinetics. The plots for a lognormal residual error model implemented in Bayesian framework are also presented on the lower panel where the posterior distributions of the difference are wider than the ones from our proposed model, suggesting a potential power gain when an appropriate residual error model is used.

Figure 6.

The posterior distributions of the difference in log clearances (log Cl) between intermediate metabolizers (IM) and normal metabolizers (NM), and that between slow metabolizers (SM) and NM from Bayesian hierarchical nonlinear mixture model (upper panel) and from lognormal residual error model implemented in Bayesian framework (lower panel). The posterior means and 95% credible intervals (CI) are also presented.

6 Simulation Studies

Simulation studies were conducted in a variety of scenarios to evaluate our proposed model. Especially, we considered several outlier-generating mechanisms for the large outliers: normal-gamma convolution, lognormal, and dose-dependent models. In addition, both normal additive and proportional residual error models were considered for the main population (valid concentrations) for each outlier-generating model. The simulated data from the combination of the outliers and the main population models were fit to evaluate a sensitivity of modeling assumption for our proposed model. They serve one correct model, and five incorrect models. Among the five incorrect models, either the assumption for the outliers or the main population is incorrect in three models, and both are incorrect in two models which would serve as one of the worst scenarios. From each outlier-generating model, a proportion of the large outliers was simulated in a range of 10 – 30%, which in our experience are reasonably supported values for clinical data.

The true population values of Cl and V were 50 and 70, respectively, and lognormals with about 20–30% of CV (σ_CL and σ_V equal to 0.2 or 0.3) were assumed for the random effects PK parameters. The residual error standard deviation for the main population, σ, was 0.2 or 0.3. The proportion of the large values of outliers, w₂, was 0.1, 0.2 or 0.3 whereas the proportion of the small values of outliers, w₃, was fixed to 0.05 since a proportion for the small values of outliers in clinical data is not likely to be greater than 5%. The sampling times were at 1, 2, 4, 12, 24, 48, and 72, and the rate of infusion, R_i, was chosen among 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100, a similar dose range as the DEX data. A one-compartment infusion model was used as the structural model. Five subjects per each dose, a total of 50 subjects for each replicated dataset and 500 replicate datasets were simulated. The outlier-generating model specific parameters were defined as follows.

1. Normal-gamma convolution

   $${\xi }_{ij}\sim \{\begin{array}{ll}\mathbf{Ga}(1,0.25)\hfill & \mathbf{wp}{w}_2\hfill \\ \mathbf{NGa}(6,3)\hfill & \mathbf{wp}{w}_3.\hfill \end{array}$$
2. Lognormal

   $$\begin{array}{l}{y}_{2ij}\sim \mathbf{lnN}(log5,{0.8}^2)\mathbf{wp}{w}_2\\ y_{3ij}\sim \mathbf{lnN}(log0.01,{0.2}^2)\mathbf{wp}{w}_3,\end{array}$$

   where lnN(p, q) stands for a lognormal distribution with the logarithm of the mean, p, and the variance, q.

3. Dose dependent model

   $$\begin{array}{l}{y}_{2ij}\sim \mathbf{lnN}(log(0.3R_i),{0.3}^2)\mathbf{wp}{w}_2\\ y_{3ij}\sim \mathbf{lnN}(log0.01,{0.2}^2)\mathbf{wp}{w}_3.\end{array}$$

Tables 2 – 4 summarize the medians and the 2.5^th and 97.5^th percentiles in parentheses for the estimates of parameters from our proposed model under three major conditions: (1) moderate variability (σ_Cl = σ_V = σ = 0.2) with small proportion of outliers (w₂ = 0.1); (2) moderate variability (σ_Cl = σ_V = σ = 0.2) with moderate proportion of outliers (w₂ = 0.2); and large variability (σ_Cl = σ_V = σ = 0.3) with large proportion of outliers (w₂ = 0.3).

Table 2.

The results for simulation studies (σ_Cl = σ_V = σ = 0.2 and w₂ = 0.1).

Parameters	Gamma		Lognormal		Dose dependent
	Normal	Normal prop.	Normal	Normal prop.	Normal	Normal prop.
Cl (50)	49.9 (46.8, 53.1)	50 (46.4, 53.6)	50.2 (46.9, 53.9)	49.4 (45.5, 53.3)	50.1 (45, 53.9)	48.6 (43.4, 52.8)
V (70)	69.2 (61.2, 79.7)	69.2 (61.2, 78.7)	70.5 (61.7, 79.5)	70 (61.9, 78.4)	70 (61.1, 80.3)	70.5 (61.4, 79.5)
σCl (0.2)	0.21 (0.17, 0.27)	0.22 (0.17, 0.27)	0.22 (0.17, 0.27)	0.22 (0.17, 0.28)	0.22 (0.17, 0.71)	0.23 (0.18, 0.74)
σV (0.2)	0.25 (0.2, 0.36)	0.26 (0.2, 0.36)	0.25 (0.2, 0.38)	0.26 (0.19, 0.37)	0.26 (0.2, 0.41)	0.26 (0.2, 0.4)
σ (0.2)	0.2 (0.18, 0.22)	0.17 (0.13, 0.21)	0.2 (0.18, 0.23)	0.15 (0.12, 0.19)	0.2 (0.18, 0.22)	0.16 (0.12, 0.2)
w1 (0.85)	0.85 (0.83, 0.87)	0.8 (0.74, 0.85)	0.85 (0.81, 0.87)	0.76 (0.65, 0.83)	0.85 (0.81, 0.87)	0.77 (0.67, 0.83)
w2 (0.1)	0.09 (0.08, 0.11)	0.11 (0.08, 0.16)	0.1 (0.09, 0.11)	0.12 (0.1, 0.15)	0.1 (0.09, 0.1)	0.11 (0.1, 0.13)
w3 (0.05)	0.06 (0.05, 0.07)	0.08 (0.05, 0.14)	0.05 (0.03, 0.09)	0.12 (0.06, 0.23)	0.05 (0.03, 0.09)	0.12 (0.06, 0.22)
Ma (100)	98 (96, 99.1)	92 (86.3, 95.4)	96.3 (93.3, 98)	88.6 (77.1, 94.9)	97.1 (92.8, 98.9)	90.1 (78.7, 96)

^aM: Percent of correctly classified membership.

Table 4.

The results for simulation studies (σ_Cl = σ_V = σ = 0.3 and w₂ = 0.3).

Parameters	Gamma		Lognormal		Dose dependent
	Normal	Normal prop.	Normal	Normal prop.	Normal	Normal prop.
Cl (50)	49.4 (44.5, 55.4)	51 (44.8, 58.2)	50.9 (45.3, 57.2)	52.2 (45.9, 59.5)	50.1 (41.9, 56.7)	49 (37.7, 56.2)
V (70)	67.9 (50.4, 89)	66.4 (49.4, 85.5)	70.1 (50.8, 91.1)	69.9 (51.9, 86.5)	70.1 (36.9, 91.8)	68.7 (37.1, 88.2)
σCl (0.3)	0.3 (0.23, 0.41)	0.32 (0.23, 0.61)	0.31 (0.23, 0.44)	0.32 (0.24, 0.42)	0.34 (0.24, 1.01)	0.36 (0.25, 1.02)
σV (0.3)	0.37 (0.26, 0.59)	0.4 (0.26, 0.71)	0.36 (0.27, 0.73)	0.38 (0.25, 0.72)	0.37 (0.26, 1.07)	0.4 (0.26, 1.07)
σ (0.3)	0.31 (0.27, 0.35)	0.23 (0.16, 0.32)	0.31 (0.26, 0.35)	0.18 (0.13, 0.24)	0.3 (0.26, 0.35)	0.21 (0.15, 0.28)
w1 (0.65)	0.66 (0.62, 0.7)	0.62 (0.54, 0.7)	0.64 (0.56, 0.69)	0.55 (0.48, 0.61)	0.65 (0.56, 0.68)	0.57 (0.48, 0.64)
w2 (0.3)	0.28 (0.25, 0.32)	0.3 (0.24, 0.36)	0.3 (0.27, 0.33)	0.35 (0.3, 0.39)	0.3 (0.27, 0.31)	0.32 (0.28, 0.35)
w3 (0.05)	0.06 (0.04, 0.08)	0.07 (0.04, 0.13)	0.06 (0.03, 0.15)	0.11 (0.05, 0.17)	0.05 (0.02, 0.14)	0.11 (0.05, 0.2)
Ma (100)	92.6 (89.1, 95.1)	85.1 (79, 89.1)	91.1 (81.5, 94)	84.3 (76.8, 89.7)	95.1 (85.4, 97.1)	88.4 (79.3, 94.3)

^aM: Percent of correctly classified membership.

The estimates of PK parameters including the proportions of mixture components were close to the true values for all scenarios, even for the incorrect models. The percents of correct classification to the membership were also reported since we know the true membership to the main or the outlier population, and all these estimates were reasonably high.

As expected, the results from the correct model were the best, and ones from incorrect models for both the main and outliers populations were the worst. Although the model misspecification for the main population results in more bias in general than the misspecification of the outlier-generating mechanism, the maximum bias in the estimates of Cl and V was at most 5% across all models in this simulation study. The most affected parameters by the model misspecification were the variance components. For example, the σ_CL and σ_V were overestimated since incorrect use of normal model would underestimate σ when a normal proportional model is correct and the unexplained variability would get absorbed to σ_CL and σ_V. Also the proportions of outliers were slightly overestimated since some skewed valid observations following a normal proportional model were incorrectly classified as outliers, which would have been classified as valid if the normal proportion model were used instead. In conclusion, our simulation results support that our proposed model can well accommodate the outliers even generated from incorrect models in a reasonable range of proportions and variability of data.

7 Summary and Discussion

In a motivating PK dataset with a large non-ignorable proportion of artifactual outliers, we present strong evidence that conventional PK/PD models are unsatisfactory. Model checking revealed that the commonly used residual error models in conventional population PK analysis cannot handle this large proportion of outliers and lead to biased estimates.

We proposed a novel population PK model to accommodate the artifactual outliers using a mixture distribution as the residual error model within a Bayesian framework. A normal-gamma convolution mixture model was successfully applied to the motivating PK data. A residual analysis would be helpful to choose starting candidates for the specific components in the mixture error model. Our model checking supported the ability of our model to accommodate the large proportion of artifactual outliers well compared to conventional population PK analysis. We also conducted simulation studies with a reasonable range of proportions of the outliers. The results showed that our proposed model can accommodate the outliers well, with small to large proportion of outliers, findings which are relevant to most observational PK studies.

The proposed modeling approach would be most useful when we suspect systemic outliers for either known or unknown reason. However, we would not recommend using this approach as a panacea for handling outliers when conventional error models could perform reasonably well.

Although outlying individuals were not evidenced in the motivating data, there might be outlying individuals in the other similar ongoing studies. For such cases, our future work would be to develop an extended PK model to accommodate both the artifactual outlying observations and outlying individuals.

Table 3.

The results for simulation studies (σ_Cl = σ_V = σ = 0.2 and w₂ = 0.2).

Parameters	Gamma		Lognormal		Dose dependent
	Normal	Normal prop.	Normal	Normal prop.	Normal	Normal prop.
Cl (50)	49.6 (46.6, 53.4)	50.2 (46.4, 54.2)	50.5 (46.9, 54.2)	50 (46.1, 54.2)	49.6 (41.4, 53.7)	48.3 (39.2, 53.1)
V (70)	68.2 (59.8, 79.3)	67.9 (58.1, 78.5)	70 (60.8, 80.5)	69.5 (60.1, 77.8)	69.6 (60.3, 79.6)	69.8 (59.7, 79)
σCl (0.2)	0.21 (0.17, 0.27)	0.22 (0.17, 0.27)	0.22 (0.18, 0.28)	0.22 (0.18, 0.31)	0.23 (0.18, 0.89)	0.24 (0.18, 0.91)
σV (0.2)	0.26 (0.21, 0.38)	0.27 (0.21, 0.39)	0.27 (0.21, 0.38)	0.27 (0.2, 0.39)	0.27 (0.21, 0.76)	0.28 (0.2, 0.61)
σ (0.2)	0.2 (0.18, 0.23)	0.17 (0.13, 0.21)	0.2 (0.18, 0.23)	0.15 (0.11, 0.18)	0.2 (0.18, 0.23)	0.16 (0.12, 0.2)
w1 (0.75)	0.76 (0.73, 0.78)	0.72 (0.65, 0.77)	0.75 (0.71, 0.77)	0.67 (0.59, 0.73)	0.75 (0.7, 0.77)	0.68 (0.59, 0.74)
w2 (0.2)	0.19 (0.17, 0.21)	0.21 (0.17, 0.25)	0.2 (0.18, 0.21)	0.22 (0.2, 0.25)	0.2 (0.18, 0.2)	0.21 (0.18, 0.23)
w3 (0.05)	0.06 (0.05, 0.06)	0.07 (0.05, 0.12)	0.05 (0.03, 0.09)	0.11 (0.06, 0.19)	0.05 (0.03, 0.1)	0.11 (0.06, 0.2)
Ma (100)	96.3 (94.3, 98.3)	90.3 (85.7, 93.7)	95.4 (92.6, 97.4)	89.1 (80.1, 93.7)	97 (91.6, 98.6)	91.1 (82, 96.3)

^aM: Percent of correctly classified membership.