Abstract
Principal component regression is a multivariate data analysis approach routinely used to predict neurochemical concentrations from in vivo fast-scan cyclic voltammetry measurements. This mathematical procedure can rapidly be employed with present day computer programming languages. Here, we evaluate several methods that can be used to evaluate and improve multivariate concentration determination. The cyclic voltammetric representation of the calculated regression vector is shown to be a valuable tool in determining whether the calculated multivariate model is chemically appropriate. The use of Cook’s distance successfully identified outliers contained within in vivo fast-scan cyclic voltammetry training sets. This work also presents the first direct interpretation of a residual color plot and demonstrated the effect of peak shifts on predicted dopamine concentrations. Finally, separate analyses of smaller increments of a single continuous measurement could not be concatenated without substantial error in the predicted neurochemical concentrations due to electrode drift. Taken together, these tools allow for the construction of more robust multivariate calibration models and provide the first approach to assess the predictive ability of a procedure that is inherently impossible to validate because of the lack of in vivo standards.
Keywords: Principal component regression, residual analysis, fast-scan cyclic voltammetry, dopamine, in vivo voltammetry
Fast-scan cyclic voltammetry (FSCV) is an electroanalytical technique used to measure real time neurochemical signaling dynamics in vivo of electroactive biomolecules including catecholamines.1 FSCV used with carbon-fiber microelectrodes offers several advantages including subsecond temporal resolution, excellent sensitivity, micrometer spatial resolution, and minimal damage in vivo.2,3 FSCV is also one of the most selective electrochemical approaches because FSCV is a multivariate technique. The shape of the characteristic cyclic voltammogram for most neurochemicals is unique and can be used as a fingerprint identifier for measured analyte.4,5
Mathematical programming software packages, such as Matlab, have become widely available throughout the scientific community, and they enable the use of sophisticated mathematical tools developed in the 1970s.6 One of these methods, principal component regression (PCR), is a chemometric technique that combines principal component analysis with inverse least-squares regression.7−9 In PCR, a training set containing reference voltammograms at known concentrations is assembled. Abstract representations of the training set voltammograms called principal components (PCs) are calculated. PCs that describe relevant information necessary for concentration prediction are retained, and PCs that describe noise are discarded. The projection of the training set voltammograms onto the relevant PCs (called scores) are calibrated to the reference concentration values through regression analysis. Finally, concentration values of unknown voltammograms are predicted by calculating their relevant scores and using the calibration determined from the training set. Incorporation of PCR into the analysis of in vivo FSCV measurements improved neurochemical concentration determination of analytes with overlapping cyclic voltammograms in single cells, brain slices, and awake behaving rats.4,7,8,10−12
The applicability of calibration models to the unknown data sets being predicted should be properly characterized before concentration prediction of unknown samples.13 A residual analysis procedure developed by Jackson and Mudholkar14 has been incorporated into the PCR analysis of in vivo FSCV data to address this concern.7,8,10 If the extraneous variance in the unknown measurement (denoted as Q) is greater than a calculated tolerance level (denoted as Qα) the multivariate calibration is insufficient to predict neurochemical concentration values in the unknown measurement. However, this procedure is not perfect and has been shown to fail.12
The accuracy of multivariate calibration models should also be verified before concentration prediction and is addressed in a process called validation.9,13 One disadvantage to the current PCR analysis of in vivo FSCV data is that, unlike in vitro measurements, there is no independent method to calculate the “true” concentration of the species being measured. The reference concentration values of in vivo training sets are determined empirically by dividing the measured peak current by an in vitro calibration factor so any validation procedure may not be of much use. In vitro standards cannot be used because of differences in peak shapes and peak potentials between in vitro and in vivo cyclic voltammograms. Therefore, qualitative information concerning the identity of the species detected is of prime importance. If there existed an approach to assess the predictive ability of multivariate models without using standards, an indirect “pseudovalidation” method could be incorporated into the PCR analysis. The validity of constructed in vivo calibration models would then be judged on the ability of models to properly identify the characteristic voltammetric shapes and sensitivities associated with the analytes being studied, rather than properly predicting specified concentration values as is traditionally done with in vitro measurements.
The goal of this work was to improve the PCR prediction of neurochemical concentrations detected by FSCV in vivo by using examples that demonstrate the pitfalls associated with the approach. In addition, other diagnostic tools are applied here to characterize the overall multivariate calibration model. As suggested in the literature,15 these diagnostics should be simple, graphical, and give specific guidance of how to improve the calibration methodology. We qualitatively evaluate an estimation of pure analyte cyclic voltammograms determined from the PCR calibration relationship, incorporate Cook’s distance to successfully identify and remove standards classified as outliers in the training set, and describe the first interpretation of a residual color plot. In addition, PCR prediction of in vivo FSCV data was previously limited to 90 s because the presence of electrode drift caused Q to cross the Qα tolerance level.10 One way to circumvent this problem would be to break up a long continuous measurement into smaller epochs, perform PCR with residual analysis on each epoch, and concatenate the results into one concentration trace for each analyte. However, this approach has not been evaluated. This work presents these tools in a simplified manner such that users may recognize their importance without complicated mathematical manipulations.
Theory
Throughout the paper, uppercase bold letters represent matrices, lowercase bold letters represent vectors, and normal notation represents scalar values.
PCR and K Generation
PCR prediction of unknown neurochemical concentrations (Cunk) can be described according to
| 1 |
where Aunk contains the unknown cyclic voltammograms to be predicted, Vc contains the relevant PCs of rank r (the superscript T represents the matrix transpose), and F contains the regression coefficients that relate unknown concentrations of each analyte to the scores of the relevant PCs.9 The regression coefficients in F are calculated using the training set according to
| 2 |
where CTS are the training set reference concentration values and AprojTS are the relevant PC scores of the training set cyclic voltammograms.9 Here we define CTS as being size j × m, where j is the number of analytes and m is the number of training set samples. The training set voltammetric matrix (ATS) is size n × m, where n is the number potential steps in the cyclic voltammetric waveform.
Ignoring error, the relevant currents of any unknown data set can be predicted if pure analyte cyclic voltammograms are known according to
| 3 |
where K is a matrix containing cyclic voltammograms of each analyte j in units of current per concentration change. Substituting eq 3 into eq 1 shows that K is the inverse of the quantity FVCT calculated during the PCR procedure. However, since the quantity FVCT is not square, K can be calculated by taking the pseudoinverse of FVCT.16 We have previously used the calculation of K to compare the specific current contributions of dopamine, pH change, and electrode drift after an intravenous infusion of cocaine in a freely moving rat.17
Each column of K, kj, can be thought of as a cyclic voltammetric representation of the regression vector for each analyte in the relevant multivariate calibration space of the training set. Stated another way, each kj vector can be thought of as the PCR interpretation of sensitivity at each potential for a specific analyte j based on the training set cyclic voltammograms, reference concentration values, and the relevant PCs of the multivariate model. Therefore, the shape of each kj vector could be used as an overall qualitative measure to assess whether constructed PCR calibration models are chemically appropriate.
Leverage
Several statistics exist for the evaluation and optimization of multivariate calibration models.18 Leverage (hi) is a measure of uniqueness and describes how far away the ith sample is away from the other m – 1 training set samples in the calibration space. While there are multiple ways to calculate hi, if singular value decomposition is used to decompose the n × m training set voltammetric matrix,7,8,16 then each hi value is easily calculated as the ith diagonal element of the following multiplication
| 4 |
where Vr is the m × r subset that spans the relevant row information of the training set voltammetric matrix.19hi is a scalar that takes on values between 0 and 1, with samples of higher leverage having greater potential to influence the calculation of the regression vector. A good rule of thumb in for eliminating high leverage samples is to delete those that have hi values higher than 2r/m or 3r/m.18,19
While conservative, eliminating samples based on leverage is not always ideal. First, multiple outliers make the identification of truly high leverage outliers difficult.20 It is also possible that a sample with high leverage may have an extreme composition relative to other samples in the training set, which may occur at either the low or high end of a calibration. These regions are usually of great interest to the user during the analysis. Leverage does not take into account accuracy so samples could be eliminated based on the possibility of harm, rather than the actual error.
Practically, in vivo FSCV training sets can be inherently high leverage. In vivo FSCV training samples are generated by stimulating the freely moving rat to elicit neurochemical release of varying amplitudes. Stimulations are given to encompass a wide range of responses, but they do not always evenly span the calibration space. In addition, only five cyclic voltammograms per analyte are traditionally incorporated into a training set.7,8,12 Therefore, excluding samples with hi > 3r/m is not ideal in practice.
Studentized Residual
Another figure of merit that can be used to evaluate multivariate calibrations is termed studentized residual and has the notation ti. If ei is the difference between the estimated and reference concentration values, ti can be calculated as
| 5 |
where SEC is the standard error of the calibration.18 Pure concentration prediction error cannot be used to evaluate fit because of hi. Samples with high leverage tend to determine the overall multivariate calibration model, which would tilt the regression vector toward them, and would as such have a lower overall prediction error.18,21 Because studentized residuals should be normally distributed with common variance, a statistical test can be used to determine if the ith sample is a potential outlier.18,19 However, a significant value of ti may also sometimes be indicative of an imprecise estimate of the reference concentration. Deletion of this sample may cause an underestimation of the PRESS statistic that is sometimes used for rank estimation.19
Cook’s Distance
Cook’s distance22 (Di) combines hi and ti, and is a measure of the effect of the ith sample on the overall multivariate calibration. In PCR, Di is calculated as (without mean centering of the training set voltammetric matrix)
| 6 |
where r is the number of retained PCs.19Di is a measure of the distance that the regression vector moves within the calibration space if the ith sample is removed from the training set.19,22,23Di takes into account the overall extent to which a sample can be considered an outlier (ti) and the sensitivity of the regression vector to outliers at each data point [hi/(1 – hi)].22 Large values of Di indicate that the ith sample is highly influential in the calculation of the regression coefficients and deletion of the ith sample would cause a dramatic difference in their values.22−25
Calculated Di values can be compared to the F-distribution to determine the extent to which the removal of the ith sample changes the calculation of the regression coefficients greater than a user-defined tolerance. In PCR, the tabulated F-value used is F1−γ(r, m – r – 1) where γ is the significance level.25 However, in this case, γ is a descriptive significance level and does not take the familiar p-value interpretation.23,26,27 Specifically, a Di value that equals F1−γ(r, m – r – 1) means that deletion of the ith sample moves the regression vector to the distance away corresponding to the edge of a γ confidence ellipsoid around the original regression vector. Di is not distributed as F, and therefore, Di is not a true test statistic. Instead, Di is an indicator of how close the regression vectors are with and without the ith sample (for further review, see refs (23), (26), and (27)).
Di values that are greater than the tabulated F1−γ(r, m – r – 1) mean that deletion of the ith sample causes the regression vector to move farther than a tolerable amount in the relevant multivariate calibration space. It is incorrect to state that one is (1 – γ)% confident a particular sample is an outlier if its Di value is greater than the tabulated F1−γ(r, m – r – 1) value. Instead, the ith sample is said to be very influential in calculating the regression vector because its deletion grossly repositions the regression vector greater than a predefined amount.24 Such samples should be removed from the training set because of their adverse influence on the overall regression model.19 Cook’s distance has been used successively with multivariate calibration to remove outliers in training sets and should serve as excellent assessment of the prediction model.19,25,28,29Di is more powerful than either hi or ti alone because Di simultaneously reflects error of prediction and uniqueness of spectral information.29 Unfortunately, because hi is used in the calculation of Di, Di suffers from the disadvantage that multiple outliers may not be detected.30
Results and Discussion
The Use of K as a Qualitative Diagnostic Tool
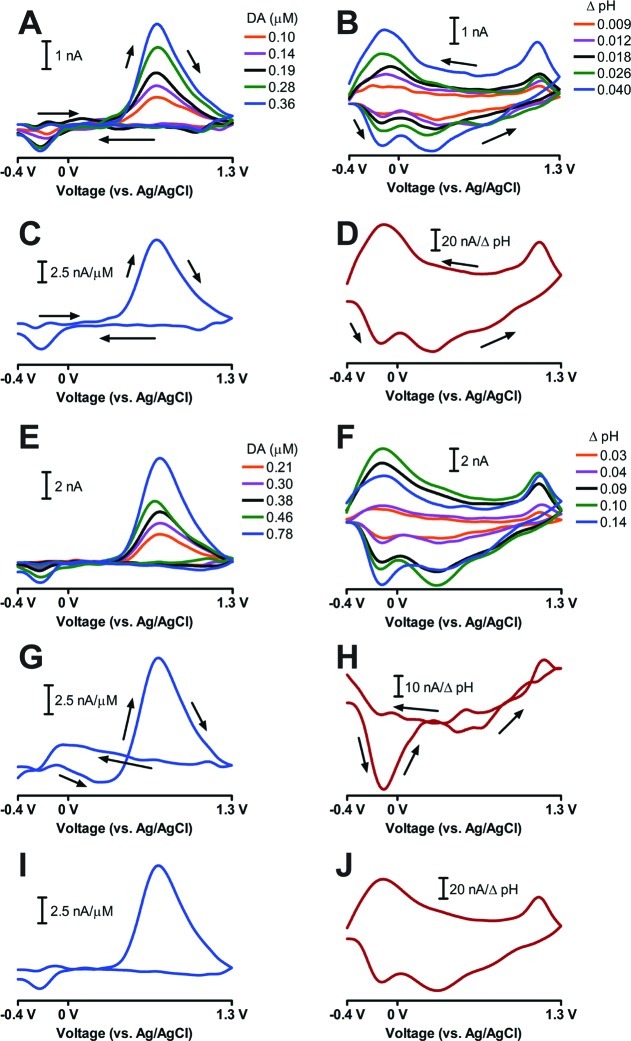
Because of ineffective validation, there is a need for a rapid, simple diagnostic criterion that can be used to verify that the PCR model correctly identified the characteristic voltammetric pattern and sensitivity associated with each neurochemical of interest. In a qualitative way, the kj vector provides this information as illustrated by the following two data sets. Figure 1A and B shows an example of a proper training set consisting of five dopamine cyclic voltammograms and five pH change cyclic voltammograms. The cyclic voltammograms for each species had a consistent shape and spanned the calibration space well with an estimated rank of two. The calculated values of kj for dopamine (kDA) and pH change (kpH) are shown in Figure 1C and D, respectively. These cyclic voltammetric representations are consistent with those of the training set and the known cyclic voltammograms of these two neurochemicals.4,31 The sensitivity at the peak potentials of dopamine and pH change were also consistent with values reported in the literature.1,4,31
Figure 1.
K representations of a proper and a questionable training set. (A) Dopamine cyclic voltammograms of the proper training set. (B) pH change cyclic voltammograms of the proper training set. (C) kDA for the proper training set shown in (A) and (B). (D) kpH for the proper training set shown in (A) and (B). (E) Dopamine cyclic voltammograms of the questionable training set. (F) pH change cyclic voltammograms of the questionable training set. (G) kDA for the questionable training set shown in (E) and (F). (H) kpH for the questionable training set shown in (E) and (F). (I) and (J) show the recalculated kDA and kpH vectors, respectively, for the questionable training set shown in (E) and (F) if the QH-peak is used for pH change quantitation rather than the C-peak. The arrows in (A), (B), (C), (D), (G), and (H) indicate the direction of the voltammetric sweep.
Figure 1E and F shows an example of a questionable training set with an estimated rank of three (the rank of in vivo FSCV training sets varies with signal-to-noise ratio and is not a diagnostic criterion for an invalid training set12). The dopamine cyclic voltammograms showed a consistent shape that spanned a wide concentration range. However, the 0.14 basic pH change cyclic voltammogram was inconsistent with the rest of the pH change cyclic voltammograms. The pH change cyclic voltammogram normally has three peaks known as the C-peak at approximately −0.2 V on the oxidative sweep, the QH-peak at approximately 0.3 V on the oxidative sweep, and the Q-peak at approximately −0.3 V on the reductive sweep.31 Using the other pH change cyclic voltammograms for comparison, the peak current of the C-peak for the 0.14 basic pH change was much too large given (a) the peak currents for the QH- and Q-peaks and (b) the overall shape for reasons that are not understood. The C-peak has been shown to be highly dependent on the extracellular environment, so possible variations in the local extracellular environment could alter the ratio of the measured currents of the C-, Q-, and QH-peaks.31 Since the C-peak was used for quantitation, the 0.14 basic pH change reference value was also likely incorrect.
Figure 1G and H shows the calculated kDA and kpH vectors for the poor training set. Even though the dopamine cyclic voltammograms of the poor training set were of good quality, the shape of kDA was distorted. Moreover, the shape of kpH was even worse with only the C-peak was apparent. The broad shape of the pH change cyclic voltammogram was incorporated into kDA rather than kpH, as well as most of the QH- and Q-peaks. In fact, the sensitivity of dopamine at the reduction potential was a positive value.
Since K is calculated from the inverse of FVcT, there are three reasons that would cause kj vectors to deviate from ideal behavior. First, the number of relevant PCs chosen during factor selection could be incorrect. This was unlikely because factor selection has been previously evaluated for in vivo FSCV training sets.12 Second, the reference concentration values could be incorrect, leading to erroneous relationships between the projections onto the regression vectors and predicted concentrations. To illustrate this point, the QH-peak was used instead of the C-peak to determine the amplitude of the basic pH shifts from the questionable training set in Figure 1F. kDA and kpH were recalculated and are shown in Figures 1I and J. These values were consistent with the known cyclic voltammograms.4 This result showed that the reference pH changes determined using the QH-peak were more appropriate, given the shapes of the pH change cyclic voltammograms of the questionable training set.
PCR assumes that the amplitude of the entire cyclic voltammogram linearly increases with concentration so the choice of which of the C-, QH-, or Q-peaks is used for quantitation should be irrelevant because their relative ratios should remain constant. However, the amplitude of the C-peak has been shown to vary depending on the extracellular environment meaning that the C-peak is more susceptible to voltammetric inconsistencies and overall error.31 In that work, it was suggested that a current versus time trace taken at the C-peak was unsuitable for quantitation of pH changes in vitro or in vivo. The results here provide clear evidence that extends this conclusion to multivariate analysis of in vivo FSCV data. Instead, the QH- or Q-peak should be used to determine the value of the reference pH changes for in vivo FSCV training sets.
A third possibility for improper kDA or kpH values is that inconsistent cyclic voltammograms could be included in the training set that drastically alter the multivariate calibration space. Such samples could unduly influence the position of the regression vector and thus K. While the K approach can be used as a simple, rapid, qualitative graphical diagnostic tool to assess model construction, another criterion should be included to identify any cyclic voltammograms of the training set that act as outliers, unduly influencing the position of the regression vectors and the relevant calibration space.
Identifying and Removing Training Set Outliers Using Cook’s Distance
If there is a significant change in a calibration model upon the deletion of one sample, the sample is likely an outlier and should not be included in the training set. Mathematically, if Di is larger than a tabulated F-value, that sample should be considered for rejection. Originally, Cook suggested that a value of 0.1 be used for γ, but this selection was arbitrary.22 Using a value of 0.1 for γ determined that 31 out of a library of the 119 training sets contained at least one poor standard. The shapes and corresponding concentration values for the poor cyclic voltammograms were qualitatively evaluated by careful visual inspection to verify the presence of outliers for these questionable training sets. Several of these questionable training sets did not contain poor standards, indicating that a γ value of 0.1 was too sensitive (data not shown). A γ value of 0.1 led to the calculation of tolerable distance shifts that were too small for the high leverage FSCV data (see Theory). Instead, a γ value of 0.05 was used here that yielded satisfactory results, as shown below.
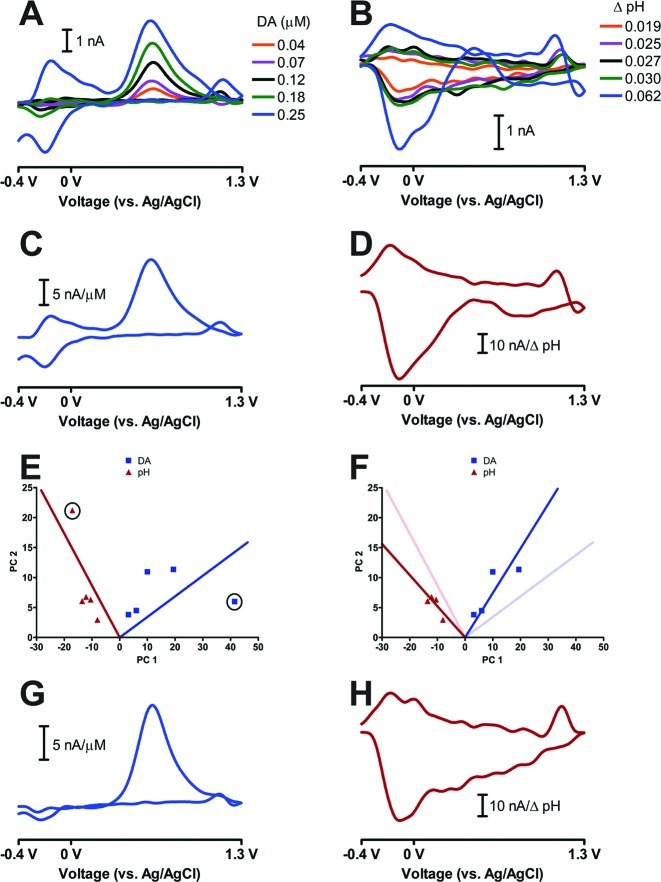
Figure 2 shows how Cook’s distance can be used to improve the PCR analysis of in vivo FSCV data. Figure 2A and B shows the dopamine and pH change cyclic voltammograms, respectively, for a poor training set. The 0.25 μM dopamine and 0.062 basic pH change samples were clearly uncharacteristic of the other neurochemical cyclic voltammograms. The estimated rank of this training set was two. The 0.25 μM dopamine cyclic voltammogram had an extra peak at −0.2 V on the forward sweep, and the 0.062 basic pH shift had a positive current deflection at 0.4 V on the forward sweep.
Figure 2.
Use of Cook’s distance to improve PCR calibration. (A) and (B) show the dopamine and pH change cyclic voltammograms (respectively) of a poor training set. (C) and (D) show kDA and kpH, respectively, for the poor training set shown in (A) and (B). (E) Score plot showing both the dopamine (blue squares) and pH change (red triangles) cyclic voltammograms of the training set in (A) and (B). The solid lines represent the calculated regression vectors for both dopamine (blue) and pH change (red). The circled points represent the 0.25 μM dopamine and 0.062 basic pH change standards. (F) Score plot as in (E) with the 0.25 μM dopamine and 0.062 basic pH change standards removed. The regression vectors without these standards were recalculated and are plotted. The original regression vectors in (E) are also shown as faded solid lines. (G) and (H) show the recalculated kDA and kpH vectors, respectfully, after the removal of the 0.25 μM dopamine and 0.062 basic pH change standards.
The cause for the uncharacteristic shapes of these cyclic voltammograms was unknown but could have been due to improper stimulation parameters (magnitude and/or location within the brain), deterioration of the glass seal of the carbon-fiber microelectrode, or possible biofouling of the sensor. The extraneous peak at −0.2 V on the forward sweep on the 0.25 μM dopamine cyclic voltammogram was at the same potential as the C-peak of the pH change cyclic voltammogram. The C-peak is associated with changes in electrode capacitance and is not restricted to only pH change cyclic voltammograms.31 This extraneous peak in the 0.25 μM dopamine cyclic voltammogram suggests that there may have been adsorption or desorption of electrochemically inert species on the surface of the carbon-fiber microelectrode31 coincident with dopamine release during the stimulation event that generated this cyclic voltammogram.
kDA and kpH for this poor training set are shown in Figure 2C and D, respectively. The inclusion of the questionable standards negatively affected the interpretation of pure analyte voltammograms by the PCR model, especially for pH change. Figure 2E shows the score plot for the poor training set from Figure 2A and B. Visually, the 0.25 μM dopamine and the 0.062 basic pH shift samples resemble possible outliers in the relevant calibration space. hi of the questionable dopamine and pH change standards were calculated to be 0.61 and 0.60, respectively, higher than all the other samples, indicating that these two samples had moderate potential to influence the multivariate calibration. Indeed, the position of the regression vectors appear tilted toward these outliers and away from the other analyte standards.
The calculated Di values for these questionable dopamine and pH standards were 5.49 and 5.01, respectively, which were significantly higher than the tablulated F-value of 4.74. The significant Di values indicate that these two samples were outliers and should not have been included in the calibration model because of their overall adverse impact on the regression vectors. The regression vectors were recalculated with the outliers removed from this training set and are plotted in Figure 2F. There was a dramatic shift in the position of the regression vectors for each neurochemical. Without the outliers, the regression vectors more accurately spanned the remaining training set samples for both dopamine and pH change.
kDA and kpH were also recalculated without the outliers and are shown in Figure 2G and H, respectively. kDA and kpH differed in shape from the proper training set shown in Figure 1, but they were consistent with the remaining neurochemical cyclic voltammograms of this training set. The shape of a pH change cyclic voltammogram depends on both the extracellular environment and carbon surface chemistry,31 and has been published with varying C-/QH-/Q-peak ratios.10,17,32,33
Di was also used to evaluate the poor training set shown in Figure 1E and F. hi was calculated to be 0.86 for the questionable pH change cyclic voltammogram labeled as a 0.14 basic pH shift. Such a large hi indicates that this sample had a large potential to influence the calculation of the regression vectors. Calibrating with the pH change, cyclic voltammograms with the C-peak gave a Di value of 6.65 and calibrating with the QH-peak gave a Di value of 11.42. Since both of these values were larger than the tabulated F-value of 4.76, this standard was considered an outlier no matter how the reference pH change value was determined. The removal of this questionable cyclic voltammogram generated new kDA and kpH vectors that were consistent with those shown in Figure 1C and D.
Cook’s distance may also likely improve model selection. Recently, it was shown that Malinowski’s F-test improved factor selection for in vivo FSCV training sets.12 This approach estimates rank by identifying PCs that contain statistically more variance than PCs that span noise. While the ideal rank of a training set containing only dopamine and pH is two, many training sets had an estimated rank higher than two. One reason for a large estimated rank is that inconsistencies were present in the cyclic voltammograms that were significantly larger than the noise. For these training sets, Malinowski’s F-test could retain more PCs to span inconsistencies in outlier cyclic voltammograms rather than only the relevant calibration space.
Cook’s distance was used to test this hypothesis. Of the 119 training sets analyzed, 15 were identified to contain outliers based on Cook’s distance. Interestingly, Malinowski’s F-test estimated the rank to be larger than two for 13 of the 15 training sets. Upon removal of the identified outliers, the estimated rank decreased for 10 of those 13 training sets. This result shows that the estimated rank increased for some training sets only to span samples that would adversely impact the overall prediction of the multivariate calibration model. Therefore, Cook’s distance can be used to improve both the prediction ability and selection of the relevant factor space of multivariate in vivo FSCV calibration models.
While discarding data is not ideal, in vivo measurements are considerably more difficult than in vitro measurements and require more experimental flexibility. Since only 15 out of 119 training sets contained outlier cyclic voltammograms, this occurrence is not an overwhelming concern. Furthermore, the residual analysis procedure can be used as a check to determine if any of these outlier cyclic voltammograms of the training set are contained within the unknown data being predicted. The residual analysis procedure identifies all sources of variance not accounted for by the relevant principal components of the training set. If the distortions of measured data existed, they would show up as artifacts in the residual color plot and residual Q-plot, informing the user that discarded cyclic voltammograms of the training set are representative of the unknown data and the training set should be reconstructed.
Interpretation of Residual Color Plots for the Identification of Deterministic Error
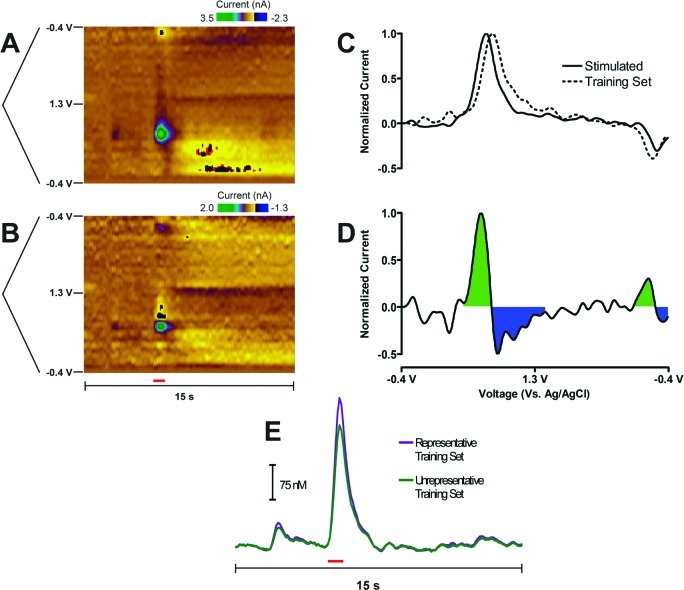
A residual color plot7,8 provides extra information to the Q-plot for assessing training set augmentation; the specific peak potentials causing the error can quickly be identified, but this has not been widely reported in the literature. Figure 3A shows a representative color plot of stimulated neurochemical release measured in the nucleus accumbens of a freely moving rat. At the time of the stimulation (as indicated by the red bar), dopamine was released, followed by a basic pH change that lasted for approximately 7 s. There was also a transient increase in dopamine before the stimulation was given.
Figure 3.
Interpretation of a residual color plot when an unrepresentative training set is used for concentration prediction. (A) Color plot representation of stimulated dopamine release in the nucleus accumbens of a freely moving rat. The voltammetric sweep is plotted to the left of the color plot. (B) Residual color plot after an unrepresentative training set was used for concentration prediction. (A) and (B) share the time axis below (B), with the red bar indicating a stimulation given to the animal (60 Hz, 24 pulses, 125 μA). (C) Unfolded normalized dopamine cyclic voltammograms for the stimulated dopamine release in (A) (solid line) and a dopamine cyclic voltammogram from the unrepresentative training set (dashed line). (D) Unfolded cyclic voltammogram representing the subtraction of the improper training set dopamine cyclic voltammogram from the stimulated dopamine release shown in (C). The green and blue shadings are shown to highlight differences at the oxidation and reduction peaks, with the color scheme mimicking that of the residual color plot shown in (B). (E) Concentration prediction comparison between the proper representative and improper unrepresentative training sets.
An unrepresentative training set was generated by exchanging representative dopamine cyclic voltammograms for those taken from a different animal to illustrate how the residual color plot can be used to improve the multivariate calibration and to show why training sets generated in one animal is risky for concentration prediction in another animal. Both the dopamine calibration factor and the pH change cyclic voltammograms remained consistent. After concentration prediction using the unrepresentative training set, the residual color plot was calculated and is shown in Figure 3B. There was considerable deterministic error that was only present during the prediction of dopamine events. Specifically, positive-negative current deflections at the oxidation and reduction peak positions were calculated.
The origin of the residual color plot can be explained by the unfolded cyclic voltammograms shown in Figure 3C. The unfolded cyclic voltammogram of dopamine taken at maximal release from Figure 3A is shown as the solid black trace in Figure 3C, and one of the dopamine cyclic voltammograms of the unrepresentative training set used for the prediction is shown as the dashed trace in Figure 3C. There was a difference in peak separation (ΔEp) of approximately 130 mV between dopamine from the measured stimulation and the dopamine cyclic voltammograms of the training set. Such shifts in ΔEp can arise from differences in electron transfer kinetics or resistance differences between carbon-fiber microelectrodes.34
Subtracting training set dopamine from stimulated dopamine release gives the pattern shown in Figure 3D that arises from the differences in ΔEp. This difference shows positive–negative current deflections at the oxidation and reduction peak potentials apparent in the color representation (Figure 3B). Ideally, the residual color plot should contain only random noise. Deterministic error will arise if the training set is not representative of the unknown data set either because of differences in the in the shapes of analyte cyclic voltammograms or because of the presence of an interfering species. Theoretically, these should cause the Q-plot to cross the Qα threshold, but this does not always occur. To minimize the possibility of such errors, training sets should be collected within the same animal at the same location of the unknown measurement.
Small differences in ΔEp values occurred even though the exact same type of carbon-fiber microelectrodes was used for all experiments. This effect has been shown before35 and is likely due to a combination of slight differences in electron transfer properties of the carbon-fiber and possible fouling in vivo. The ratio of oxidative to reductive peak current of in vivo dopamine cyclic voltammograms is also known to vary between electrodes35 which would likely alter predicted concentrations if they were included in training sets from other electrodes.
The predicted stimulated dopamine release differed by approximately 50 nM or 18% between the two training sets (Figure 3E), but the same general trend was measured. This difference in predicted dopamine concentrations arose even though the difference in ΔEp values was only 3.8% of the total cyclic voltammetric waveform (two 1.7 V sweeps). Therefore, slight variations in peak shapes may yield qualitative information on neurochemical changes, but neurochemical quantitation will likely be inaccurate. However, if events are detected near the limit of detection, small peak shifts can deteriorate even qualitative information. Therefore, the creation of a standard training set of in vivo cyclic voltammograms applicable to all experiments36 is risky. Moreover, if the residual analysis procedure was to be used, a standardized training assumes that the noise level of all electrodes in all animals performing all types of behavioral tasks is constant. It was previously hypothesized that the noise level of in vivo FSCV measurements was correlated to animal movement,12 so tasks that involve more motor movements would likely contain an overall larger noise level. Therefore, standard training sets may also invalidate the proper application of the residual analysis procedure.
This example used unrepresentative training set cyclic voltammograms from a different animal to illustrate the use of the residual color plot, but the residual color plot can also be used to identify prediction errors within the same animal. The same positive-negative current deflections may be represented in a residual color plot if analyte cyclic voltammograms in the training set have different peak potentials from those present in the unknown data within the same animal. This would indicate to the user that an electrochemiocal shift has occurred (possibly due to electrode deterioration) and the training set must be augmented before neurochemical concentration prediction by PCR.
Transformation of the Qα Value
The residual error in the Q-plot at time t, Qt, describes the amount of residual error contained in a specific cyclic voltammogram. Qt is calculated by summing the squared residual current in the data not included in the retained PCs of the training set. Qα represents a tolerable noise level based on the discarded noise of the training set and is calculated independently of Qt.7,8 Because each Qt value is calculated by summing the square residual current between the original data and the data described by the primary PCs at each point of the cyclic voltammogram, an approximate noise threshold in units of current can be calculated as
| 7 |
where iTH could be either positive or negative. The quantity iTH represents a current value that 1 – α% of currents due to random noise would be below based on the amount of random noise discarded during PC selection. Stated another way, iTH is the (1 – α) percentile of random noise currents.
The value of iTH can give a user an approximation of tolerable noise in units that have physical significance, rather than being an abstract transformation representing the sum of squared currents. The analysis of all 119 library training sets taken from two laboratories gave an average iTH value of 0.41 ± 0.17 nA, but this value will vary based on several factors including the signal-to-noise ratio of the training set cyclic voltammograms, the quality of the carbon-fiber microelectrode, the activity level of the animal, and the level of environmental noise.12 Users should be familiar with the noise level during their experiments so an uncharacteristically large value of iTH would indicate too large of an amount of information being discarded during factor selection and could alert the user that Qα is too high to be of practical use.
Analysis of Continuous Multiple Minute Data Sets
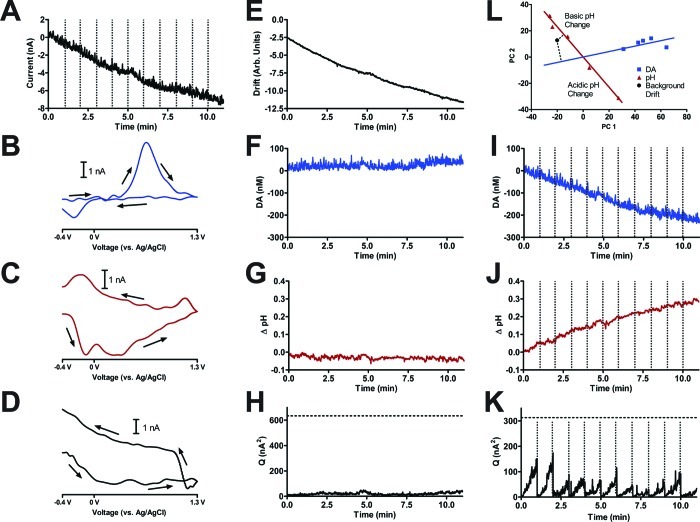
Figure 4 describes the effect of electrode drift in the analysis of in vivo FSCV data. A carbon-fiber microelectrode was lowered into the nucleus accumbens of an awake rat, and 11 min of continuous data was recorded in the absence of stimulation or any behavioral event. Digital background subtraction can be used to eliminate the large charging current associated with FSCV, but the presence of any electrode drift will still be visualized.
Figure 4.
Neurochemical prediction by PCR with and without electrode drift in the training set. The carbon-fiber microelectrode was located in the nucleus accumbens of a freely moving rat. (A) Concatenated digital background subtracted current versus time traces at the oxidation potential of dopamine. The vertical dotted lines in (A) represent the start of a new 60 s data epoch. (B) Dopamine and (C) basic pH change cyclic voltammograms from this animal. (D) Digital background-subtracted cyclic voltammogram taken at 60 s. (E) Electrode drift predicted by PCR. (F) Dopamine concentration predicted with electrode drift in the training set. (G) pH change predicted with electrode drift in the training set. (H) Q-plot for the data predicted in (E) through (G). The horizontal dashed line represents Qα. (I) (Second row, third column) Concatenated dopamine concentrations predicted without electrode drift in the training set. (J) Concatenated pH changes predicted without electrode drift in the training set. (K) Concatenated Q-plots for the data predicted in (I) and (J). The horizontal dashed line represents Qα. The vertical dotted lines in (I), (J), and (K) represent the start of a new 60 s data epoch. (L) (First row, third column) Score plots and regression vectors for the training set without background drift. Blue squares represent the dopamine cyclic voltammograms, and red triangles represent pH change cyclic voltammograms. Acidic and basic pH change cyclic voltammograms are noted. The black circle represents the background drift cyclic voltammogram in (D), and its projections onto the dopamine regression vector (blue) and pH regression vector (red) are plotted.
Figure 4A shows a concatenated current versus time trace from the eleven consecutive 60 s data epochs at the oxidation potential of dopamine. This trace was made by digitally background subtracting five cyclic voltammograms recorded at the beginning of each epoch and concatenating current values, using the last current value of the previous epoch as the new baseline for the next epoch, rather than again starting at zero which is normal for digitally subtracted data. Clearly, there is a large change in the recording, but this information is insufficient to discern whether this change is due to dopamine (Figure 4B), pH change (Figure 4C), or another species. In fact, a cyclic voltammogram taken at 60 s (after digital background subtraction of the first epoch) shown in Figure 4D did not correspond to that of dopamine or pH change and had a shape consistent with electrode drift.17
Because electrode drift was present in the measurement, it should be included as an analyte in the training set. When background drift was included in the training set, analog background subtraction was used to remove the charging current of the electrode rather than digital subtraction.17 PCR predicted that the magnitude of electrode drift increased with time (Figure 4E), with only minimal changes in dopamine (Figure 4F) or pH change levels (Figure 4G). The Q-plot was below the Qα threshold throughout the entire trace, verifying that the training set accounted for all significant variance in the measured data (Figure 4H). These predictions were expected because the animal neither was performing a behavioral task nor was under the effect of any pharmacological agents (including anesthesia), and the carbon-fiber microelectrode is known to cause minimal damage in vivo.3
There is an inappropriate way to analyze these data sets that we have seen investigators employ, attempting to circumvent the effect of electrode drift. The data were analyzed in consecutive 60 s epochs, each of which were digitally background subtracted using five cyclic voltammograms recorded at the beginning of each epoch so the carbon-fiber microelectrode did not appear to significantly drift over the course of the unknown measurement epoch being predicted. The predicted concentration values were concatenated using the last concentration value of the previous epoch as the baseline for the next epoch. This procedure predicted an approximate 200 nM decrease in dopamine (Figure 4I, located on the second row and third column of the figure) and a 0.3 basic pH shift (Figure 4J), both of which were uncharacteristic given the animal was idle during the course of the measurement. The Q-plot was below the Qα threshold throughout the unknown measurement (Figure 4K). However, the cyclic voltammogram at 60 s (Figure 4D) verifies that the concentrations predicted in this manner must be incorrect. The electrode drift cyclic voltammogram shown in Figure 4D had a projection onto the analyte regression vectors corresponding to a decrease in dopamine concentration and a basic pH shift (Figure 4L, located on the first row and third column of the figure), leading to the erroneous concentration values in Figure 4I and J.
Although the Q-plot was below the Qα threshold for each epoch, the Q-plot exhibited unusual discontinuities upon concatenating the data. Values increased as time progressed during the duration of each 60 s epoch as shown in Figure 4K. The limiting duration of analysis of in vivo FSCV by PCR was determined by the magnitude of electrode drift that caused the Q-plot to cross the Qα threshold.10 Here, incorrect concentrations were predicted even though the Q-plot was below the Qα threshold throughout the entire trace meaning that electrode drift was statistically insignificant, but dramatically influenced the predicted concentration values. Ideally, the Q-plot should have no structure (only random variations such as that shown in Figure 4H) so a pattern such as that shown in Figure 4K could illustrate the presence of another analyte in the unknown data set not present in the training set.
It is not advisible to use linear/polynomial fits to remove electrode drift. The temporal behavior of electrode drift has been shown to be nonlinear and unpredictable.17 PCR also offers two other advantages in the removal of electrode drift. First, in PCR, the current values at all potentials are taken into account during prediction rather than relying on information at one specific potential which could bias the prediction of electrode drift. Second, the shape of electrode drift is specific so the presence of noise and even other analytes in the measurement are completely ignored will not bias the fit of the final prediction. Therefore, it is best that electrode drift should be incorporated into the training set of multiple minute data sets rather than using risky analysis “tricks” to circumvent the problem.
Concluding Remarks
This work presents examples of several vital improvements in the multivarate prediction of neurochemicals detected with FSCV using PCR with residual analysis in a simple, straightforward manner without complicated mathematical manipulations. An approach based on the pseudoinverse of the PCR calibration matrix allowed for a simple, straightforward, rapid graphical way to qualitatively assess whether multivariate prediction models were chemically appropriate. Using this approach, it was shown that the C-peak of the pH cyclic voltammogram should not be used to determine the reference pH change values of in vivo FSCV training sets. The incorporation of Cook’s distance successfully demonstrated how outliers could be removed from the training set before unknown concentrations are predicted. The residual color plot was shown to be effective in identifying specific differences between training set cyclic voltammograms and the unknown data being predicted, giving specific information regarding how training sets can be augmented to be more representative of the unknown data to be predicted. Finally, the presence of electrode drift can introduce significant error in the prediction of dopamine and pH change for multiminute recordings, even if the continuous data set was analyzed in smaller segments.
This work has two important conclusions. First, we give concrete examples of errors that arise when PCR is performed inappropriately with in vivo FSCV data. PCR should only be performed in an animal where a training set can be properly constructed from consistent data measured within the same animal with the same carbon-fiber microelectrode to prevent prediction errors. This may limit the utility of PCR, but it will prevent incorrect biological conclusions from being reached that may only arise from erroneous data analysis. Second, while the accuracy of neurochemical concentration data obtained from PCR is impossible to determine due to the lack of in vivo standards, the K-matrix approach can provide a simple, graphical, and qualitative assessment of the ability of PCR to recognize the characteristic voltammetric shape and sensitivitities associated with a particular neurochemical, thereby generating neurochemical concentration information that makes chemical sense. The incorporation of several tools, including the K-matrix approach, Cook’s distance, the residual color plot, and proper accounting of electrode drift is crucial in providing more precise, valid, and robust information regarding neurochemical signaling dynamics in vivo.
Methods
Electrochemical and Animal Experimentation
FSCV data was collected with cylindrical, T-650 type (Thornel, Amoco Corporation, Greenville, SC) carbon-fiber microelectrodes prepared as described elsewhere.17,37 Voltages are reported versus a Ag/AgCl reference electrode. The voltammetric waveform used was a triangular excursion at 400 V/s from −0.4 to 1.3 to −0.4 V. Data was acquired and collected as described previously.38 Animal experimentation was conducted on male Sprague–Dawley rats (Charles River Laboratory, Willmington, MA) weighing approximately 300 g in accordance with the University of North Carolina Institutional Animal Care and Use Committee. Surgical protocols and freely moving experimental procedures used to generate the data analyzed here were carried out as described elsewhere.10,39,40
Data Analysis
Data analysis was carried out using locally written software in the MATLAB (Mathworks, Natick, MA) and LabVIEW (National Instruments, Austin, TX) programming environments. Voltammetric data was filtered at 2 kHz. PCR was performed as described previously, using singular value decomposition to decompose the training set voltammetric matrix.7,8,12,16 Rank was estimated using Malinowski’s F-test.12,41,42 Score plots and analyte regression vectors were calculated from theory.9,43,44
Data was taken from experiments performed using analog background subtraction17 in the nucleus accumbens to determine the effect of electrode drift on predicted neurochemical concentrations. The output was initially zero, with only analyte electrochemistry and electrode drift being detected. The data was collected continuously but was broken up into 11 separate consecutive 60 s epochs.
Neurochemical concentrations were predicted both with and without electrode drift in the training set. If electrode drift was to be accounted for, electrode drift training set cyclic voltammograms were collected at various times before and after the measurement. Because the unit for quantitation of electrode drift was arbitrary, reference values were taken to be the measured current at the peak at −0.3 V on the forward sweep. Because the analog background subtraction reduced the amplitude of the background, digital background subtraction45 was unnecessary.
When electrode drift was not accounted for, a training set was created using only dopamine and pH change cyclic voltammograms. Although the data was collected using analog background subtraction, digital background subtraction can still be performed on analog background subtracted data. Each of the 11 consecutive, 60 s data epochs were digitally background subtracted using an average of five cyclic voltammograms collected at the beginning of the data epoch, and neurochemical levels were predicted using PCR. The resulting traces were concatenated together to create analyte predictions over 11 min, where the last concentration value of the previous epoch was taken as the baseline value for the next file being predicted.
In Vivo FSCV Training Sets
The training sets used in this work were taken from a library of 119 in vivo training sets measured in freely moving rats.12 The cyclic voltammograms were taken from stimulated neurochemical release measured in the dorsal and ventral striatum, but the location in the brain where the training sets were generated was irrelevant for the analyses. Unless noted, training sets were used without modification.
Each training set consisted of five dopamine and five pH change cyclic voltammograms. The reference concentration values reported in the library were determined by dividing peak current by a calibration factor determined using flow injection analysis46 after the experiment was performed.40 The oxidation potential for dopamine (approximately 0.6 V on the positive sweep) and the C-peak of pH change (approximately −0.2 V on the positive sweep)31 were chosen for determining library reference concentrations of the training set, by convention. In this work, the QH-peak (approximately 0.3 V on the positive sweep) was also used for pH change quantitation to compare to the values calculated with the C-peak from the library.
Acknowledgments
The authors thank Professor Regina M. Carelli for the use of her data.
Glossary
Abbreviations
- Di
Cook’s distance
- FSCV
fast-scan cyclic voltammetry
- hi
leverage
- K
matrix containing cyclic voltammograms of each analyte in units of current per concentration change
- kDA
dopamine K vector
- kpH
pH change K vector
- PC
principal component
- PCR
principal component regression
- Qα
Residual error tolerance level
Author Contributions
R.B.K. performed all calculations, experiments, and literature searches. R.M.W. provided overall guidance and direction.
This work was supported by the National Institutes of Health (DA 10900).
Funding Statement
National Institutes of Health, United States
References
- Heien M. L.; Phillips P. E.; Stuber G. D.; Seipel A. T.; Wightman R. M. (2003) Overoxidation of carbon-fiber microelectrodes enhances dopamine adsorption and increases sensitivity. Analyst 128, 1413–1419. [DOI] [PubMed] [Google Scholar]
- Robinson D. L., and Wightman R. M. (2007) Rapid dopamine release in freely moving rats. In Electrochemical Methods for Neuroscience (Michael A. C., and Borland L. M., Eds.), pp 17–36, CRC Press, Boca Raton, FL. [PubMed] [Google Scholar]
- Jaquins-Gerstl A.; Michael A. C. (2009) Comparison of the brain penetration injury associated with microdialysis and voltammetry. J. Neurosci. Methods 183, 127–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heien M. L.; Johnson M. A.; Wightman R. M. (2004) Resolving neurotransmitters detected by fast-scan cyclic voltammetry. Anal. Chem. 76, 5697–5704. [DOI] [PubMed] [Google Scholar]
- Phillips P. E. M.; Wightman R. M. (2003) Critical guidelines for validation of the selectivity of in-vivo chemical microsensors. TrAC, Trends Anal. Chem. 22, 509–514. [Google Scholar]
- Lavine B.; Workman J. (2010) Chemometrics. Anal. Chem. 82, 4699–4711. [DOI] [PubMed] [Google Scholar]
- Keithley R. B.; Wightman R. M.; Heien M. L. (2009) Multivariate concentration determination using principal component regression with residual analysis. TrAC, Trends Anal. Chem. 28, 1127–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keithley R. B.; Wightman R. M.; Heien M. L. (2010) Multivariate concentration determination using principal component regression with residual analysis: Erratum. TrAC, Trends Anal. Chem. 29, 110–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer R. (1998) Chemometric Techniques for Quantitative Analysis, Marcel Dekker, Inc., New York. [Google Scholar]
- Heien M.; Khan A. S.; Ariansen J. L.; Cheer J. F.; Phillips P. E. M.; Wassum K. M.; Wightman R. M. (2005) Real-time measurement of dopamine fluctuations after cocaine in the brain of behaving rats. Proc. Natl. Acad. Sci. U.S.A. 102, 10023–10028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wightman R. M.; Heien M. L.; Wassum K. M.; Sombers L. A.; Aragona B. J.; Khan A. S.; Ariansen J. L.; Cheer J. F.; Phillips P. E.; Carelli R. M. (2007) Dopamine release is heterogeneous within microenvironments of the rat nucleus accumbens. Eur. J. Neurosci. 26, 2046–2054. [DOI] [PubMed] [Google Scholar]
- Keithley R. B.; Carelli R. M.; Wightman R. M. (2010) Rank Estimation and the Multivariate Analysis of in Vivo Fast-Scan Cyclic Voltammetric Data. Anal. Chem. 82, 5541–5551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daszykowski M.; Walczak B. (2006) Use and abuse of chemometrics in chromatography. TrAC, Trends Anal. Chem. 25, 1081–1096. [Google Scholar]
- Jackson J. E.; Mudholkar G. S. (1979) Control Procedures for Residuals Associated with Principal Component Analysis. Technometrics 21, 341–349. [Google Scholar]
- Weisberg S. (1983) Discussion: Some Principles for Regression Diagnostics and Influence Analysis. Technometrics 25, 240–244. [Google Scholar]
- Hendler R. W.; Shrager R. I. (1994) Deconvolutions Based on Singular-Value Decomposition and the Pseudoinverse - a Guide for Beginners. J. Biochem. Biophys. Methods 28, 1–33. [DOI] [PubMed] [Google Scholar]
- Hermans A.; Keithley R. B.; Kita J. M.; Sombers L. A.; Wightman R. M. (2008) Dopamine detection with fast-scan cyclic voltammetry used with analog background subtraction. Anal. Chem. 80, 4040–4048. [DOI] [PubMed] [Google Scholar]
- ASTM International (2000) ASTM Standard E1655, “Standard Practices for Infrared Multivariate Quantitative Analysis”, Vol. 03.06, ASTM International, West Conshohocken, PA. [Google Scholar]
- Marbach R.; Heise H. M. (1990) Calibration Modeling by Partial Least-Squares and Principal Component Regression and Its Optimization Using an Improved Leverage Correction for Prediction Testing. Chemom. Intell. Lab. Syst. 9, 45–63. [Google Scholar]
- Zhang M. H.; Xu Q. S.; Massart D. L. (2003) Robust principal components regression based on principal sensitivity vectors. Chemom. Intell. Lab. Syst. 67, 175–185. [Google Scholar]
- Stevens J. (2002) Applied multivariate statistics for the social sciences, Lawrence Erlbaum Associates, Mahwah, NJ. [Google Scholar]
- Cook R. D. (1977) Detection of Influential Observation in Linear-Regression. Technometrics 19, 15–18. [Google Scholar]
- Gunst R. F., and Mason R. L. (1980) Regression analysis and its application: a data-oriented approach, M. Dekker, New York. [Google Scholar]
- Cook R. D.; Weisberg S. (1980) Characterizations of an Empirical Influence Function for Detecting Influential Cases in Regression. Technometrics 22, 495–508. [Google Scholar]
- Naes T. (1989) Leverage and Influence Measures for Principal Component Regression. Chemom. Intell. Lab. Syst. 5, 155–168. [Google Scholar]
- Obenchain R. L. (1977) Letters to the Editor. Technometrics 19, 348–349. [Google Scholar]
- Cook R. D. (1977) Letters to the Editor. Technometrics 19, 349–350. [Google Scholar]
- Hawkins D. M.; Yin X. (2002) A faster algorithm for ridge regression of reduced rank data. Comput. Stat. Data Anal. 40, 253–262. [Google Scholar]
- Walczak B.; Massart D. L. (1995) Robust principal components regression as a detection tool for outliers. Chemom. Intell. Lab. Syst. 27, 41–54. [Google Scholar]
- Lawrence A. J. (1995) Deletion Influence and Masking in Regression. J. R. Stat. Soc. B 57, 181–189. [Google Scholar]
- Takmakov P.; Zachek M. K.; Keithley R. B.; Bucher E. S.; McCarty G. S.; Wightman R. M. (2010) Characterization of Local pH Changes in Brain Using Fast-Scan Cyclic Voltammetry with Carbon Microelectrodes. Anal. Chem. 82, 9892–9900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roitman M. F.; Stuber G. D.; Phillips P. E. M.; Wightman R. M.; Carelli R. M. (2004) Dopamine operates as a subsecond modulator of food seeking. J. Neurosci. 24, 1265–1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuber G. D.; Roitman M. F.; Phillips P. E. M.; Carelli R. M.; Wightman R. M. (2005) Rapid dopamine signaling in the nucleus accumbens during contingent and noncontingent cocaine administration. Neuropsychopharmacology 30, 853–863. [DOI] [PubMed] [Google Scholar]
- Wipf D. O.; Kristensen E. W.; Deakin M. R.; Wightman R. M. (1988) Fast-Scan Cyclic Voltammetry as a Method to Measure Rapid, Heterogeneous Electron-Transfer Kinetics. Anal. Chem. 60, 306–310. [Google Scholar]
- Clark J. J.; Sandberg S. G.; Wanat M. J.; Gan J. O.; Horne E. A.; Hart A. S.; Akers C. A.; Parker J. G.; Willuhn I.; Martinez V.; Evans S. B.; Stella N.; Phillips P. E. M. (2009) Chronic microsensors for longitudinal, subsecond dopamine detection in behaving animals. Nat. Methods 7, 126–129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flagel S. B.; Clark J. J.; Robinson T. E.; Mayo L.; Czuj A.; Willuhn I.; Akers C. A.; Clinton S. M.; Phillips P. E. M.; Akil H. (2010) A selective role for dopamine in stimulus-reward learning. Nature 469, 53–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawagoe K. T.; Zimmerman J. B.; Wightman R. M. (1993) Principles of voltammetry and microelectrode surface states. J. Neurosci. Methods 48, 225–240. [DOI] [PubMed] [Google Scholar]
- Michael D. J.; Joseph J. D.; Kilpatrick M. R.; Travis E. R.; Wightman R. M. (1999) Improving Data Acquisition for Fast-Scan Cyclic Voltammetry. Anal. Chem. 71, 3941–3947. [DOI] [PubMed] [Google Scholar]
- Day J. J.; Roitman M. F.; Wightman R. M.; Carelli R. M. (2007) Associative learning mediates dynamic shifts in dopamine signaling in the nucleus accumbens. Nat. Neurosci. 10, 1020–1028. [DOI] [PubMed] [Google Scholar]
- Owesson-White C. A.; Cheer J. F.; Beyene M.; Carelli R. M.; Wightman R. M. (2008) Dynamic changes in accumbens dopamine correlate with learning during intracranial self-stimulation. Proc. Natl. Acad. Sci. U.S.A. 105, 11957–11962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malinowski E. R. (1988) Statistical F-tests for abstract factor analysis and target testing. J. Chemom. 3, 49–60. [Google Scholar]
- Malinowski E. R. (1990) Erratum to Statistical F-tests for abstract factor analysis and target testing. J. Chemom. 4, 102. [Google Scholar]
- Jolliffe I. T. (2002) Principal Component Analysis, Springer-Verlag, New York. [Google Scholar]
- Jackson J. E. (1991) A User’s Guide to Principal Components, Wiley, New York. [Google Scholar]
- Howell J. O.; Kuhr W. G.; Ensman R. E.; Wightman R. M. (1986) Background Subtraction for Rapid Scan Voltammetry. J. Electroanal. Chem. 209, 77–90. [Google Scholar]
- Kristensen E. W.; Wilson R. L.; Wightman R. M. (1986) Dispersion in flow injection analysis measured with microvoltammetric electrodes. Anal. Chem. 58, 986–988. [Google Scholar]