Abstract
Na (and Li) currents and fluorescence transients were recorded simultaneously under voltage-clamp conditions from mouse flexor digitorum brevis fibers stained with the potentiometric dye di-8-ANEPPS to investigate the distribution of Na channels between the surface and transverse tubular system (TTS) membranes. In fibers rendered electrically passive, voltage pulses resulted in step-like fluorescence changes that were used to calibrate the dye response. The effects of Na channel activation on the TTS voltage were investigated using Li, instead of Na, because di-8-ANEPPS transients show anomalies in the presence of the latter. Na and Li inward currents (INa, ILi; using half of the physiological ion concentration) showed very steep voltage dependences, with no reversal for depolarizations beyond the calculated equilibrium potential, suggesting that most of the current originates from a noncontrolled membrane compartment. Maximum peak ILi was ∼30% smaller than for INa, suggesting a Li-blocking effect. ILi activation resulted in the appearance of overshoots in otherwise step-like di-8-ANEPPS transients. Overshoots had comparable durations and voltage dependence as those of ILi. Simultaneously measured maximal overshoot and peak ILi were 54 ± 5% and 773 ± 53 µA/cm2, respectively. Radial cable model simulations predicted the properties of ILi and di-8-ANEPPS transients when TTS access resistances of 10–20 Ωcm2, and TTS-to-surface Na permeability density ratios in the range of 40:60 to 70:30, were used. Formamide-based osmotic shock resulted in incomplete detubulation. However, results from a subpopulation of treated fibers (low capacitance) provide confirmatory evidence that a significant proportion of ILi, and the overshoot in the optical signals, arises from the TTS in normal fibers. The quantitative evaluation of the distribution of Na channels between the sarcolemma and the TTS membranes, as provided here, is crucial for the understanding of the radial and longitudinal propagation of the action potential, which ultimately govern the mechanical activation of muscle in normal and diseased conditions.
INTRODUCTION
The central role that the transverse tubular system (TTS) plays in skeletal muscle physiology has been recognized since the pioneering experiments of Huxley and Taylor (1958) demonstrating that localized current stimulation elicited sarcomeric contraction only when a stimulation pipette was placed at the Z-lines. This is where the openings of the transverse tubules (T-tubules) were later confirmed to be located in amphibian muscle fibers (Peachey, 1965; Franzini-Armstrong et al., 1975; Zampighi et al., 1975). Notable progress was made later when scientists showed that the TTS can be envisioned as a distributed cable network (Falk and Fatt, 1964; Falk, 1968; Schneider, 1970), which is responsible for the inward (radial) spread of the depolarization in the muscle fiber, and that the fibers’ passive electrical properties are well accounted for by a radial cable equivalent circuit (Adrian et al., 1969; Falk, 1968). In this model of the TTS, the transmembrane voltage across each patch of membrane with a defined radial coordinate is predicted by the integration of a partial differential equation that takes into account the cylindrical geometry of the fiber, the structural properties of the TTS, the lumen conductivity of the T-tubules, and the passive resistance of each membrane patch (Adrian et al., 1969). Additional evidence, obtained in amphibian muscle fibers, suggested that the TTS is an active membrane network with Na and K conductances contributing to the radial propagation of an action potential (AP) toward the center of the fiber (Adrian and Peachey, 1973). These latter authors proposed that, in this preparation, Na and K conductances in the TTS needed to be scaled down to 1/20th with respect to that at the sarcolemma (while sharing the same kinetics), and that an access resistance (Rs), in series with the TTS, of ∼150 Ωcm2 was necessary to be included to prevent unrealistic secondary notches in the modeled AP (Adrian and Peachey, 1973).
Because the membrane potential across the TTS membranes cannot be measured directly by electrical methods, the experimental confirmation of the existence of a so-called “T-tubular AP” required the application of optical methods. This endeavor was made possible by the development of dye molecules capable of tracking fast voltage changes (within a few microseconds) when they stain biological membranes (Salzberg et al., 1973; Ross et al., 1977). The first report demonstrating the existence of a T-tubular AP was done in bundles of frog muscle fibers stained with the fluorescent potentiometric indicator Merocyanine 540 (Vergara and Bezanilla, 1976). These were later extended to single fiber measurements with the use of more efficient absorbance- and fluorescence-type indicators such as NK2367, WW781, and, more recently, di-8-ANEPPS (Kim and Vergara, 1998; DiFranco et al., 2005). The importance of using potentiometric dyes for the characterization of TTS conductances was fully realized in voltage-clamp studies of the inward rectifier K conductance (Kir) in amphibian muscle fibers (Heiny et al., 1983; Ashcroft et al., 1985). By contrasting optical data (representing average TTS voltage changes) with model predictions from the radial cable model expanded to include the electrical properties of this conductive pathway, these authors were able to obtain accurate parameter values for its relative distribution in the TTS and sarcolemma (Heiny et al., 1983; Vergara et al., 1983; Ashcroft et al., 1985). Similarly, in frog muscle fibers where the Na conductance was intact, as indicated by the presence of prominent Na currents, it was observed that a significant acceleration of the TTS depolarization (or “escape of voltage control”) is suggestive of the presence of a prominent nonlinear Na conductance in the TTS (Vergara and Bezanilla, 1981; Heiny and Vergara, 1982). An important corollary of these studies, which has been confirmed with further experimentation using fluorescent electrochromic indicators of high efficiency and low toxicity (Bedlack et al., 1992; Tsau et al., 1996; Obaid et al., 1999), is that although potentiometric dye signals represent average measurements of voltage changes occurring in radial cable elements of the TTS, they provide the necessary constraints for the quantitative analysis of the electrical properties of the TTS, including the actual value of the access resistance Rs (Kim and Vergara, 1998).
Mostly because of limitations encountered in dissecting intact single mammalian fibers and mounting them in experimental setups designed to acquire sophisticated electrophysiological and optical data, studies comparable to those described above have been lacking in mammalian muscle fibers. In recent years our laboratory has demonstrated the feasibility of performing combined electrical and optical studies in enzymatically dissociated flexor digitorum brevis (FDB) muscle fibers and reported specifically the use of di-8-ANEPPS to demonstrate, using two-photon laser scanning imaging microscopy, that the TTS is structurally organized in a distinctive pattern of double columns per sarcomere (DiFranco et al., 2005, 2007, 2009), which contrasts with the single row distribution observed in frog fibers (Escobar et al., 1994; DiFranco et al., 2002).
The work reported in this paper is part of a long-term project aiming to determine the ion channel endowment of both the surface and TTS membranes, as this knowledge is crucial for a thorough understanding of the electrophysiological behavior of mammalian muscle fibers. This, in turn, will be required to understand the mechanisms underlying diseases associated with altered ion conductances in various channelopathies (Cannon, 2006). We have recently addressed the long-standing question of the relative distribution of ClC-1 in FDB fibers (DiFranco et al., 2011a) using an approach similar to that used to quantify the fraction of gKir present in the TTS of amphibian fibers (Heiny et al., 1983; Ashcroft et al., 1985). In this paper, we focus on the Na channel of mammalian skeletal muscle fibers (NaV1.4) that, in spite of the general consensus that it plays a central role in the excitability of muscle fibers, and that it is likely to be responsible for the active radial propagation of the APs in the TTS, has not been characterized in sufficient detail in intact mammalian fibers. A major outstanding question, for example, is the relative distribution of the Na permeability between the TTS and the sarcolemma. We report our successful attempts to answer this question, comparing experimental data obtained using mouse FDB muscle fibers bathed in a reduced external Na (and Li) concentration with the predictions of an extended version of the radial cable model that includes a Hodgkin–Huxley representation (Hodgkin and Huxley, 1952b) of the Na channel. We also provide an independent assessment of the presence of a large Na conductance in the TTS with experiments in partially detubulated fibers after osmotic shock treatment with formamide (del Castillo and Escalona de Motta, 1978; Lueck et al., 2010).
MATERIALS AND METHODS
Biological preparation
Animals were handled according to the guidelines of the UCLA Animal Care Committee. FDB and interossei muscles from 14–15-wk-old C57BL mice were used. Fibers were enzymatically dissociated as described previously (Woods et al., 2004; DiFranco et al., 2011a). The diameter and length of the fibers were 49.5 ± 1.2 and 438 ± 12 µm, respectively (n = 30).
Solutions
External solutions (composition in mM).
Tyrode: 156 NaCl, 10 MOPS, 2 CaCl2, 10 dextrose, 1 MgCl2, and 2.5 KCl, pH adjusted with NaOH. Li-Tyrode: 156 LiCl, 10 MOPS, 2 CaCl2, 10 dextrose, 1 MgCl2, and 2.5 KCl, pH adjusted with LiOH. TEA-Cl: 145 TEA-OH, 10 MOPS, 10 CsOH, 2 Ca(OH)2, 1 Mg(OH)2, 5 dextrose, 2 × 10−5 verapamil, 2 × 10−5 nifedipine, and 0.4 9-anthacene carboxylic acid (9-ACA), pH adjusted with HCl. Solutions containing half-Na or half-Li concentrations (hereafter denoted as 1/2Na and 1/2Li external solutions) were prepared by mixing equal volumes of TEA-Cl and Tyrode (or Li-Tyrode). The final concentration of Cs, verapamil, nifedipine, and 9-ACA in these external solutions was the same as in TEA-Cl.
Internal solution (composition in mM).
Cs-internal: 80 aspartic acid, 20 MOPS, 50 EGTA, 5 ATP-Mg, 5 Na2-creatine phosphate, and 5 reduced glutathione, pH adjusted with CsOH. The high EGTA concentration in the internal solution was used to arrest fiber contraction to avoid movement artifacts in the optical records.
All solutions were adjusted to pH 7.2, and osmolarity was 300 ± 5 mOsmol/kg H2O. All chemicals were from Sigma-Aldrich.
Detubulation procedures
The detubulation method was based on the use of formamide (del Castillo and Escalona de Motta, 1978) and modified from that described elsewhere (Lueck et al., 2010) for enzymatically dissociated mouse FDB fibers. After enzymatic digestion and dissociation, muscle fibers were transferred to a 50-ml glass beaker in which the Tyrode solution was reduced to ∼0.5 ml; then, 10 ml of 1.5 M formamide was added. After 10 min, the external volume was reduced again to ∼0.5 ml, and 40 ml Tyrode was quickly added. Approximately 10 min after the osmotic shock, the excess external solution was reduced and the fibers were stained with di-8-ANEPPS as described above. Two criteria were used to evaluate the extent of detubulation: (1) reduction of membrane capacitance, measured after rendering the fiber electrically passive (see below); and (2) di-8-ANEPPS fluorescence imaging, using a 100× 1.4-NA objective. In some experiments, the detubulation was acutely performed in a single fiber while voltage clamped.
Electrophysiology
Experiments were performed under voltage-clamp conditions using a two-microelectrode high voltage amplifier (TEV-200A; Dagan Corporation) as described previously (Woods et al., 2004; DiFranco et al., 2005). Two identical electrodes filled with internal solution were used. To increase the frequency response of the voltage-clamp amplifier, electrodes were drawn to the largest possible tip size compatible with the preservation of the fibers’ integrity; also, the electrodes’ capacitance was maximally compensated. The electrodes had resistances in the range of 6–12 MΩ when filled with internal solution and were impaled approximately midway along the longitudinal axis of the fiber, and ∼10 µm apart. In general, experiments with detubulated fibers required the use of electrodes with low resistances to improve voltage-clamp stability. The maximal feedback gain of the voltage-clamp amplifier was used. To minimize the presence of oscillations at the pulses’ edges, command pulses were digitally prefiltered at 50 kHz (τ of ∼20 µs).
Muscle fibers were first impaled under current-clamp conditions. After a period of ∼20 min, which allowed for the equilibration of the pipette solution and the myoplasm (Woods et al., 2004), fibers were voltage clamped at a holding potential (VH) of −90 mV. Fibers requiring more than 12 nA to maintain VH were discarded. Membrane currents were typically recorded in the presence of 1/2Na or 1/2Li external solutions. To prevent ionic currents other than those flowing through Na channels, the internal solution contained >80 mM Cs (instead of K), and the external solution contained TEA (>72 mM) and 10 mM Cs; furthermore, 9-ACA and nifedipine and verapamil were used to block the chloride (ClC-1) and calcium (DHPR) channels, respectively. To block currents through the sodium channels (INa or ILi), 1 µM tetrodotoxin (TTX) was added to the external solution.
To eliminate the linear capacitive components from membrane current records, a two-pulse protocol was used: depolarizing pulses (20–25 ms in duration) were followed after a 40–100-ms interval by hyperpolarizing pulses of the same duration. To avoid membrane damage, hyperpolarizing pulses of the same amplitude were applied for depolarizing pulses up to 90 mV; for larger depolarizations, the amplitude of the hyperpolarizing pulse was one half that of the depolarizing pulse. To obtain undistorted Na (Li) currents, nonlinear charge movement currents were further subtracted from current records. Charge movement current records were typically obtained at the end of the experiments in TEA-Cl with TTX as described elsewhere (DiFranco et al., 2011b).
The capacitance of every fiber was measured by integrating linear capacitive currents during small voltage pulses once the fibers were rendered electrically passive at the end of the experiments (DiFranco et al., 2007, 2011a,b). In normal fibers, the average capacitance per unit surface membrane area was 4.93 ± 0.1 µF/cm2 (n = 29). Sodium currents were expressed in µA/cm2; conversion to A/F can be readily made using the average specific capacitance. All experiments were performed at room temperature (20–22°C).
Optical setup for the recording of di-8-ANEPPS signals
The optical methodology used in these experiments is essentially the same as described elsewhere (DiFranco et al., 2005, 2011b). In brief, dissociated fibers stained with di-8-ANEPPS (Invitrogen or Biotium) were placed on 3.5-mm coverslip-bottomed Petri dishes sitting on the stage of an inverted microscope (IX-71; Olympus) equipped with a standard epifluorescence attachment, a cooled CCD camera (ST-402ME; Santa Barbara Instrument Group, Inc.), and a photo detector consisting of a photodiode (UV-001; OSI Optoelectronics) connected to a patch-clamp amplifier (Axopatch 2A; Molecular Devices). Only fibers displaying a sharp sarcomere banding and the distinctive double row pattern of di-8-ANEPPS fluorescence bands, which is typical of TTS staining (DiFranco et al., 2005, 2007, 2009, 2011b), were used for the experiments. In addition, for detubulated fibers, only those displaying predominant peripheral di-8-ANEPPS staining were selected. For normal fibers, the illumination spot was normally adjusted to form a disc ∼25 µm in diameter, which was focused (using a 100× 1.4-NA objective) at the center of the x, y, and z axes of the fiber. In detubulated fibers, the spot was widened (∼25% more than the fiber’s diameter) to deliberately include the peripheral di-8-ANEPPS fluorescence. In either case, the illumination spot was centered at the site where the voltage microelectrode was impaled. Optical signals were low-pass–filtered (2-kHz) single sweeps. Optical data are presented as normalized fluorescence changes (ΔF/F) as defined elsewhere (Vergara et al., 1978; DiFranco et al., 2005, 2011a,b).
Radial cable model simulations
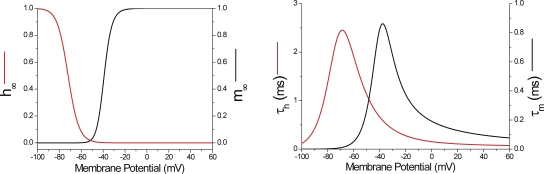
The radial cable model is described in the Appendix. Sodium (lithium) currents at the surface and TTS and TTS membrane potential were simulated with a radial cable model similar to that published previously (DiFranco et al., 2011a) but lacking the chloride conductance and incorporating an H–H formalism for the Na (or Li) permeability (PNa or PLi; see Appendix). Kinetic and voltage-dependent parameters are presented in Table A1. Channels at the surface and TTS membranes were assumed to behave equally.
TABLE A1.
Specific parameter values for passive radial cable
| Parameter | Symbol | Value | Dimension |
| Radius | a | 20–30 | µm |
| Specific capacitance TTS wall | CW | 0.9 | µF/cm2 |
| TTS lumen conductivity | GL | 11.3 | mS/cm |
| TTS access resistance | Rs | 10-40 | Ωcm2 |
| Fraction of fiber volume occupied by the TTS | ρ | 0.004 | |
| Volume to surface ratio of the TTS | ς | 1.1 × 10−6 | cm |
| Tortuosity factor on the TTS | σ | 0.32 | |
| Na diffusion coefficient | DNa | 10−5 | cm2/sec |
Data acquisition and statistical analysis
Voltage, current, and fluorescence records were filtered at 10, 5, and 2 kHz, respectively, using multiple-pole analogue Bessel filters. Data points were sampled every 30 µs using a data-acquisition interface (PCI-6221; National Instruments) and custom software written in LabView (National Instruments).
Unless otherwise stated, pooled data are expressed as mean ± SEM. Significance was set at P < 0.05.
Online supplemental material
Fig. S1 shows the voltage dependence of steady-state and undershoot distortions in di-8-ANEPPS transients in 1/2Na, and how they are corrected when TEA replaces Na in the external solution. Fig. S2 shows comparisons of data and model predictions for Li currents in a detubulated fiber. Fig. S3 illustrates the effects that the value of Rs has on the predictions (by model simulations) of ILi, and of the voltage dependence of peak ILi and the overshoot. Figs. S1–S3 are available at http://www.jgp.org/cgi/content/full/jgp.201110682/DC1.
RESULTS
Di-8-ANEPPS signals recorded from electrically passive fibers
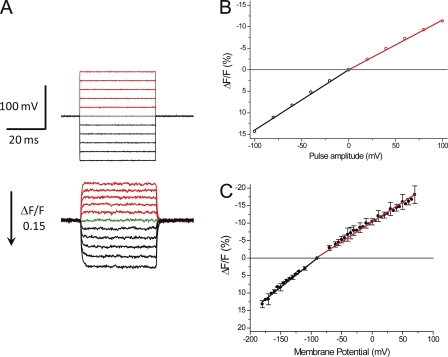
The main goal of this work is to assess the characteristics and distribution of Na channels between the surface and TTS membranes of skeletal muscle fibers. As it will become clear later in the paper, this goal requires that we are able to establish comparisons between average membrane potential changes in the TTS, as reported by the potentiometric indicator di-8-ANEPPS, and corresponding radial cable model predictions. To make this comparison possible, potentiometric signals from the TTS must be reliably calibrated in terms of membrane potential changes. We do this at the end of each experiment by rendering the fibers electrically passive (i.e., blocking all the ionic currents) in the TEA-Cl–TTX solution. A typical result of this calibration procedure is shown in Fig. 1. Fig. 1 A compares actual membrane potential changes as reported by the voltage electrode (top records) and simultaneously recorded potentiometric signals (bottom records). It should be noted that to facilitate the comparison between membrane potential changes and optical signals, the latter are shown inverted; i.e., the reduction in fluorescence in response to depolarizing pulses is shown upwards. It can be observed in Fig. 1 A that although the voltage-clamp steps are established within a settling time of <60 µs (top records), the kinetics of di-8-ANEPPS transients report the quasi-exponential slower charging process (τ of ∼0.5 ms) of the TTS membrane capacitance (bottom records). In response to either depolarizing or hyperpolarizing pulses, the potentiometric signals acquired from electrically passive fibers display two important features: (1) the fluorescence is stable for the duration of the pulses, indicating that the membrane potential at the TTS attains a steady-state value in which bleaching, or other decay processes, are not significant; and (2) at the end of the pulses, the fluorescence decays to the baseline with a similar time constant as for the onset. Thus, in passive fibers, di-8-ANEPPS responses to step voltage pulses maintain the step-like appearance without obvious overshoots or decays.
Figure 1.
Calibration of di-8-ANEPPS transients in electrically passive fibers (TEA-Cl + TTX). (A; top) Voltage records, acquired from a fiber clamped at −90 mV, in response to step pulses of amplitudes ranging from −100 to +100 mV in 20-mV increments. Depolarizing and hyperpolarizing pulses are shown in red and black, respectively. The baseline (0 mV) is shown in green. (Bottom) Di-8-ANEPPS transients (single sweeps) acquired in response to the voltage-clamp pulses shown in the top panel. Transients elicited in response to depolarizing pulses are shown in red, and those elicited in response to hyperpolarizing pulses are shown in black. The green trace shows the baseline noise (0-mV pulse). The arrow indicates the magnitude and direction of positive ΔF/F changes. Fiber parameters: radius, 23 µm; length, 490 µm; capacitance, 4.9 µF/cm2. (B) Steady-state amplitude of di-8-ANEPPS transients shown in A plotted as a function of the pulse amplitude. The linear regression fits to the data for hyperpolarizing and depolarizing pulses are shown as solid black and red lines (slopes are 14 and −11 [%/100 mV], respectively). (C). Voltage dependence of the amplitude of di-8-ANEPPS transients recorded from fibers (n = 6) clamped at −90 mV (filled symbols; mean ± SD). The slopes of the linear regressions through the symbols (in [%/100 mV]) are (mean ± SD) 14.3 ± 1.1 (black line) and −11.5 ± 1.2 (red line) for hyperpolarizing and depolarizing pulses, respectively.
The voltage dependence of the steady-state amplitude of the di-8-ANEPPS transients in Fig. 1 A is shown in Fig. 1 B. As reported previously for other VHs (DiFranco et al., 2011a), the fluorescence of this dye changes linearly with the pulse amplitude, but the slope in response to hyperpolarizing pulses is steeper (14%/100 mV) than to depolarizing pulses (−11%/100 mV). It is important to note that calibration curves, such as that in Fig. 1 B, are used to convert the ΔF/F of fluorescence signals into TTS membrane potential values while recognizing the actual sign of the membrane potential change. The average voltage dependence of di-8-ANEPPS signals for a population of fibers (n = 6) is shown in Fig. 1 C. The relatively small error bars, which in this case are the SDs of the measurements at every voltage, suggest that the average slope values for the calibration of optical signals (0.143 ± 0.011 and −0.115 ± 0.012 [%mV−1] for hyperpolarizing and depolarizing pulses, respectively) are representative of the overall voltage dependence of di-8-ANEPPS in skeletal muscle fibers under our experimental conditions.
Sodium currents from muscle fibers bathed in 1/2Na Tyrode
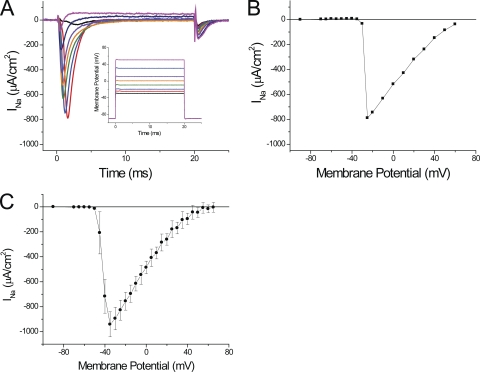
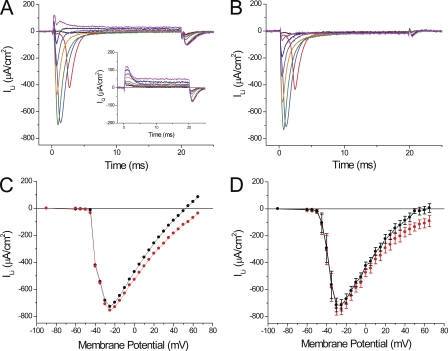
We first attempted to record sodium currents in fibers bathed in Tyrode solution that contains a typical Na concentration of ∼150 mM. We found that, under these conditions, the maximal peak current exceeded 2 mA/cm2, but also noted that the voltage-clamp amplifier was not capable of maintaining adequate control because the voltage electrode displayed gross deviations from the step command pulses (unpublished data). To avoid these problems, and to assure adequate space-clamp conditions at the surface membrane of the short fiber preparation (Bezanilla et al., 1982), we previously measured currents in fibers bathed in extracellular solutions containing reduced monovalent cation (Na or Li) concentrations. As illustrated in the inset of Fig. 2 A, a reduction to half the [Na] in the Tyrode solution (i.e., to 78 mM) was sufficient to ensure that the transmembrane potential measured by the voltage electrode lacked significant deviations with respect to the command pulses. Fig. 2 A shows the current records obtained under these conditions, after removing the linear components, in response to various depolarizations. As expected for INa, fast inactivating inward currents are seen briefly after the pulses’ onset. The magnitude of the currents abruptly increases for small depolarizations (to −30 and −25 mV; Fig. 2 A, black and red traces) while becoming faster and smaller for larger depolarizations (green to magenta traces). An outward current is observed for depolarizations to membrane potentials larger than +60 mV (not depicted). It is important to note that, as stated above, peak currents up to ∼1 mA/cm2 do not result in prominent current-dependent distortions of membrane potential as recorded by the voltage electrode (see inset in Fig. 2 A). Only records in response to depolarizations to −25 and −20 mV show small (∼1-mV) glitches that occur at the time that INa reaches its peak. Consequently, the relative abruptness in the voltage dependence of activation of INa, by which increases in the magnitude of the depolarization as small as 5 mV result in an almost all-or-none appearance of ionic current (as illustrated by comparing the magnitude of the black and red traces in Fig. 2 A), suggests that a membrane compartment other than the surface membrane (which is under voltage-clamp control) may be the main source of the current, at least for these small depolarizations.
Figure 2.
Sodium currents recorded in 1/2Na external solution. (A) Currents obtained after the subtraction of linear components from records obtained in response to step depolarizations to −30, −25, −20, −10, 0, 10, 30, and 50 mV (black, red, blue, green, orange, purple, dark blue, and magenta, respectively). The membrane potentials recorded by the voltage electrode are shown in the inset (same color code). Fiber parameters: radius, 28 µm; length, 410 µm; capacitance, 5 µF/cm2. (B) Voltage dependence of the peak sodium currents (INa) for the same fiber as in A. (C) Average peak INa plotted as a function of the membrane potential. Data were obtained from eight fibers in 1/2Na external solutions. In B and C, the symbols are connected with straight lines.
The abruptness in the voltage dependence of peak INa is further illustrated in the I-V plot of the peak inward current shown Fig. 2 B, where an ∼800-µA/cm2 jump in current is observed to occur between −25 and −20 mV; this is followed by a progressive decrease in magnitude for further depolarizations. The average voltage dependence of the peak INa, obtained from nine fibers in 1/2Na external solutions, is illustrated in Fig. 2 C. The average maximal peak INa, recorded at −35 mV, was 941 ± 100 µA/cm2. It can be observed in Fig. 2 C that, similarly to the results from the individual fiber in Fig. 2 (A and B), the average peak INa calculated from data from a population of fibers also reports an abrupt voltage dependence that seems to be incompatible with the smooth voltage dependence of NaV1.4 currents reported from heterologous expression systems (Takahashi and Cannon, 2001; Wu et al., 2005), and recently from detubulated mammalian skeletal muscle fibers (Fu et al., 2011).
Effects of sodium ions and sodium currents on di-8-ANEPPS signals
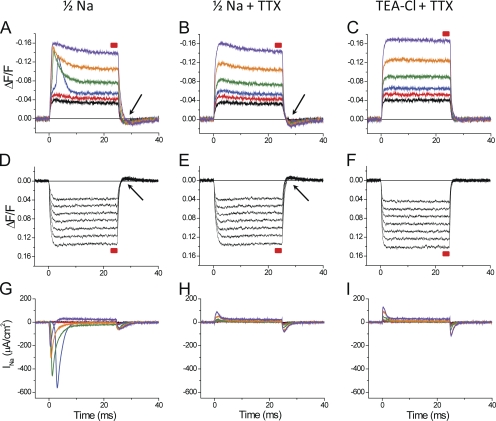
We have demonstrated previously that potentiometric dye signals from the TTS provide a means to quantitatively assess the relative contribution of the inward rectifier potassium current and the chloride current arising from the surface and TTS membranes to the total current recorded from muscle fibers (Heiny and Vergara, 1982; Heiny et al., 1983; Ashcroft et al., 1985; DiFranco et al., 2011a). To extend this approach to the investigation of the Na conductance in mammalian skeletal muscle fibers, optical data obtained before and after blocking INa with TTX must be compared. Fig. 3 shows the results of an experiment exploring the effects of INa on di-8-ANEPPS transients. Data were obtained from the same fiber sequentially exposed to three external solutions: (1) 1/2Na, which allows for the recording of a sizable INa (Fig. 3, A and G); (2) 1/2Na plus TTX, in which INa was blocked (Fig. 3, B and H); and (3) TEA-Cl + TTX in which sodium channels were blocked in the absence of external Na (Fig. 3, C and F). It must be noted that minimal currents are detected in response to hyperpolarizing pulses; thus, they are not shown. The most striking difference between di-8-ANEPPS transients recorded in 1/2Na with and without TTX (Fig. 3, B and A, respectively), especially in response to moderate size–depolarizing pulses, is the appearance of early fast components that ride on top of step-like responses (compare, for example, the blue, green, and orange traces in Fig. 3, A and B). Although we will carefully characterize (later in this paper) this extra component in the optical traces (overshoot), suffice it to say now that it is most prominent for depolarizations above 50–55 mV, which is precisely the voltage range where INa starts being activated (Fig. 3 G) and becomes less notorious for very large depolarizations (e.g., to +50 mV; purple trace in Fig. 3, A and B). It is also quite obvious that the kinetics of the overshoot components in di-8-ANEPPS transients are broadly correlated with those of INa (Fig. 3 G). Nevertheless, the data in Fig. 3 illustrate that aside from the overshoot, there are two issues with the optical signals recorded in 1/2Na that are apparent in the presence or absence of TTX, but that are more evident when TTX eliminates the overshoot. First, there are slow decays during the transients that become quite pronounced for large depolarizations (e.g., orange and purple traces in Fig. 3, A and B). This decay is also less apparent for hyperpolarizing than for depolarizing pulses (compare traces in Fig. 3, B, D, and E). Another issue is that, after the end of the pulses, di-8-ANEPPS signals show undershoots, which are more pronounced after depolarizing than after hyperpolarizing pulses (see arrowheads in Fig. 3 A, B, D, and E). Interestingly, these undershoots are almost identical in 1/2Na with or without TTX (Fig. 3, B and A, respectively).
Figure 3.
Effects of external Na on di-8-ANEPPS transients. (A–C) Di-8-ANEPPS transients elicited by depolarizing pulses of 30, 40, 50, 70, 100, and 140 mV (black, red, blue, green, orange, and purple traces, respectively). The red boxes above each optical trace indicate the period during which measurements of steady-state ΔF/F (for Fig. 4 A) were made. (D–F) Di-8-ANEPPS transients elicited by hyperpolarizing pulses of −30, −40, −50, −60, −70, −80, and −90 mV (all traces in black). The arrows indicate the presence of undershoots in the optical records. (G–I) Current records for depolarizing pulses used in A–C, respectively (same color code as in A–C). The current records obtained with hyperpolarizing pulses are not shown. The data in A, D, and G were obtained in 1/2Na external solutions. The data in B, E, and H were obtained in 1/2Na + TTX. The data in C, F, and I were obtained in TEA-Cl external solution + TTX. Fiber parameters: radius, 22 µm; length, 416 µm; capacitance, 5.5 µF/cm2.
Because none of these latter anomalies in the di-8-ANEPPS transients were observed in Fig. 1, when the transients were recorded in TEA-Cl + TTX, we decided to assess in the same fiber of Fig. 3 whether the replacement of the 1/2Na + TTX external solution by TEA-Cl (with TTX) corrected the issues. The results are shown in Fig. 3 (C and F). It can be observed that, as expected, the slow decay and undershoot in the di-8-ANEPPS transients disappeared in the TEA-Cl external solutions, yielding clean step-like transients very similar as those shown in Fig. 1. Furthermore, the residual charge movement current records in TTX containing 1/2Na and TEA-Cl external solutions are quite similar (Fig. 3, H and I, respectively). Thus, they are not able to explain the presence or absence of the anomalies in the optical records observed when comparing B and C, respectively, in Fig. 3.
A quantitative assessment of the anomalies of di-8-ANEPPS signals recorded in the 1/2Na solutions, and how they are corrected by the replacement of external Na by TEA, is presented in Fig. S1. Fig. S1 A plots the voltage dependence of steady-state ΔF/F measurements (made just before the end of the pulse, as indicated by the red boxes in Fig. 3) of di-8-ANEPPS transients in the three solutions (1/2Na, 1/2 + TTX, and TEA-Cl + TTX). It can be observed in Fig. S1 A that the steady-state values of transients recorded in 1/2Na solution (black symbols) are indistinguishable from those recorded in the presence of TTX (red symbols). However, both datasets are smaller than those obtained when Na was exchanged for TEA (Fig. S1 A, green symbols). Also, these differences are less prominent for hyperpolarizing pulses. Fig. S1 B demonstrates the actual magnitude (∼1–2%) of the ΔF/F undershoots, measured after the end of pulses, for transients recorded in the presence of external Na. These undershoots are not observable in TEA-Cl + TTX; consequently, they were not shown. It should also be noted in Fig. S1 B that the ΔF/F undershoots observed in 1/2Na solutions have a very weak voltage dependence and are not affected by the presence or absence of TTX, as opposite to the case for the overshoot.
Although we do not have a mechanistic explanation for the anomalies in the di-8-ANEPPS transients described above, a practical (and perhaps tantalizing) conclusion that can be posed is that the presence of Na ions in the external solution is the only factor responsible for them.
Replacement of sodium by lithium corrects the anomalies in di-8-ANEPPS transients
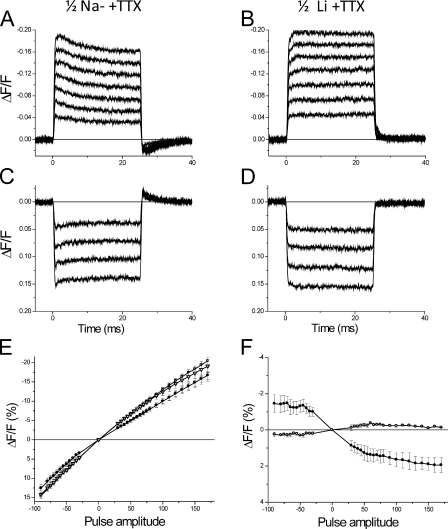
From a practical point of view, the apparent effects of external Na on the optical signals hinder the possibility of investigating the effects of INa on the TTS membrane potential, and hence the prospect of assessing the distribution of Na channels between TTS and surface membranes. In our attempt to circumvent these problems, we reasoned that because the permeability of Na channels for Li ions is close to that for Na ions (Hille, 1972; Campbell, 1976), it was worth first attempting the replacement of Na for Li in the external solution in the presence of TTX to investigate whether external Li does not have deleterious effects on di-8-ANEPPS transients. The results of such experiments are shown in Fig. 4. The comparison in Fig. 4 of the di-8-ANEPPS transients in B and D, with respect to those in A and C, demonstrates that the replacement of Na by Li actually eliminates the anomalies virtually the same way that TEA replacement did it in the case of Fig. 3. The effects of exchanging Na by Li (and later by TEA) on the voltage dependence of di-8-ANEPPS signals, as observed in three fibers, are summarized in Fig. 4 (E and F). Fig. 4 E shows that the steady-state amplitude the signals recorded in 1/2Na (filled circles) is smaller than that in both Li (open triangles) and TEA (open squares), whereas the two latter are significantly different from each other. Fig. 4 F also demonstrates that the undershoots observed after the end of the pulses in 1/2Na solution (filled circles) are virtually eliminated by the replacement of Na by Li. Collectively, these findings strengthen the idea that the anomalous features of di-8-ANEPPS signals recorded in the presence of Na are peculiar for this ion. More importantly, they provide the means to accurately investigate the effects that currents carried by Li ions through the skeletal muscle NaV1.4 channel have on TTS signals, while eliminating the secondary effects of Na on the potentiometric dye signals.
Figure 4.
Sodium replacement by lithium eliminates anomalies in di-8-ANEPPS transients. (A and B) Di-8-ANEPPS transients elicited by depolarizing pulses of 30, 50, 70, 90, 110, and 140 mV recorded in 1/2Na + TTX and 1/2Li + TTX external solutions, respectively. (C and D) Transients recorded under the same conditions as in A and B, respectively, but in response to hyperpolarizing pulses (−30, −50, −70, and −90 mV). Fiber parameters: radius, 26 µm; length, 365 µm; capacitance, 5.3 µF/cm2. (E) Average steady-state ΔF/F values of di-8-ANEPPS transients recorded in 1/2Na + TTX (filled circles), 1/2Li + TTX (open triangles), and TEA-Cl + TTX (open squares). (F) Average undershoot ΔF/F values of di-8-ANEPPS transients recorded in 1/2Na (black circles) and 1/2Li (open circles). For E and F, the fibers (n = 3) were bathed sequentially, first with 1/2Na + TTX, then with 1/2Li + TTX, and finally with TEA-Cl + TTX.
Lithium currents (ILi) in fibers bathed in 1/2Li external solutions
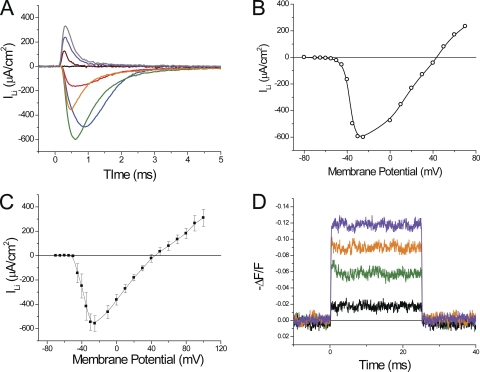
It is well known that Li ions can effectively replace Na ions as charge carriers through the Na channel in a variety of excitable cells, including amphibian nodes of Ranvier and skeletal muscle fibers (Hille, 1972; Campbell, 1976). To our knowledge, this has not been reported previously for skeletal mammalian fibers. Fig. 5 shows our results demonstrating that Li currents (ILi), similar to those carried by Na ions (Fig. 2), are recorded in 1/2Li external solution. The family of raw ILi traces shown in Fig. 5 A illustrates that the kinetics and voltage dependence of large inactivating currents display the same characteristics described for INa in Fig. 2. Namely, ILi activates abruptly with voltage (compare black and red traces in response to pulses differing only by 5 mV in Fig. 5 A), increases with the depolarization up to a maximum (green trace), becomes smaller and faster with stronger depolarizations (orange, purple, and dark blue traces), and finally reverts in sign for very large depolarizations (magenta trace). The majority of the current in Fig. 5 A corresponds to Li current through Na channels because they are completely removed by TTX (not depicted), or, as shown in the inset of Fig. 5 A, by the replacement of external Li by TEA + TTX. However, the residual charge movement/gating currents (IQ) shown in the inset, although significantly smaller than those before blockage, have a significant impact in two aspects of the current records: (1) at the onset of the pulses, particularly for large depolarizations (e.g., dark blue and magenta traces in Fig. 5 A); and (2) after the end of the pulses where they are responsible for the majority of the tail currents at every voltage, but mostly for large depolarizations (Fig. 5 A). Consequently, to obtain a more accurate depiction of the actual ionic currents through the Na channels, we subtracted (one by one) the records in the inset from those in Fig. 5 A and obtained the corrected records shown in Fig. 5 B. As expected, corrected ILi records are broadly similar to raw ILi, except that outward and tail currents have been mostly removed. The almost perfect removal of tail currents in corrected ILi records indicates that, in mammalian skeletal muscle fibers, the fast inactivation of Na channels is mostly complete ∼10 ms after the onset of depolarizing pulses. Although the effects of the corrections in ILi records are quite notorious for large depolarizations, they affect (in variable proportions) the peak currents at every voltage, as illustrated in the I-V curve of peak ILi shown in Fig. 5 C. It can be seen that both the uncorrected I-V (Fig. 5 C, black squares) and corrected (red circles) datasets are similar for small depolarizations, but they differ significantly for larger membrane potentials.
Figure 5.
Currents recorded from fibers bathed in 1/2Li external solution. (A) Current records elicited by depolarizing pulses to −45, −40, −30, −20, 0, +20, +40, and +60 mV. The inset shows (in an expanded ordinate scale) the nonlinear charge movement/gating currents recorded in TEA-Cl + TTX. (B) Corrected ILi records once the charge movement/gating currents have been subtracted from the records in A. (C) Voltage dependence of the peak current in A before (black circles) and after correction by charge movement/gating subtraction (red circles). Fiber parameters: radius, 23 µm; length, 491 µm; capacitance, 4.9 µF/cm2. (D) Voltage dependence of the average peak ILi before (black circles) and after correction (red circles), measured in nine FDB fibers.
Fig. 5 D shows I-V plots of the average raw and corrected peak ILi (black and red circles, respectively) obtained from nine fibers in 1/2Li external solution. It should be noted that the I-V curve for the raw data (Fig. 5 D, black circles) is very similar to that shown for uncorrected INa I-V curve in Fig. 2 C. The only differences are that the maximal average ILi (716 ± 42 µA/cm2) occurs at −30 mV (instead of −25 mV for INa) and is ∼24% smaller (P < 0.05) than that observed in fibers bathed in 1/2Na solution (Fig. 2 C). As it will be discussed later, the fact that maximal ILi was detected at a more positive potential than for INa is probably related to differences in magnitudes between the averages of ILi and INa. It can also be observed in Fig. 5 D that, once corrected, ILi approaches asymptotically the abscissa, rather than showing a distinct reversal potential. Although we did not show it in Fig. 2 C, the correction of INa records, by subtraction of charge movement/gating currents, yields very similar results as those shown in Fig. 5 D. In principle, the asymptotic behavior of the corrected ion currents is a surprising result because the experiments were performed using an internal [Na] of 10 mM, which results (assuming a permeability ratio of ∼1 for Na and Li) in an estimated ENa of 52 mV, a value more negative than the largest membrane potential (65 mV) shown in the I-V plot. Thus, a reversal of the currents should have been observed at very large depolarizations. The rest of this paper will be devoted to finding explanations for this behavior in the I-V curves.
Di-8-ANEPPS transients in fibers bathed in 1/2Li external solutions
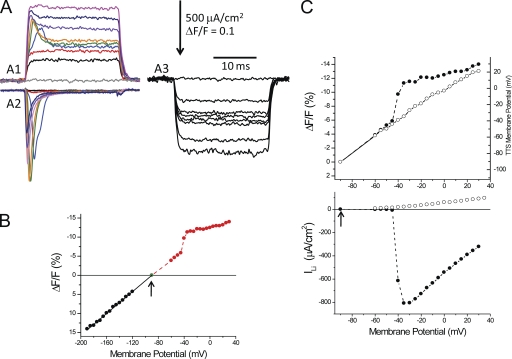
As briefly described above for the case of INa (Fig. 3; but also see Heiny and Vergara, 1982), in contrast with what happens with the activation of IKir and ICl (Heiny et al., 1983; Ashcroft et al., 1985; DiFranco et al., 2011a), the activation of ILi results in an excessive depolarization of the TTS, which is observed as an overshoot in di-8-ANEPPS signals from the TTS. This is illustrated in Fig. 6 A, where simultaneous records of di-8-ANEPPS transients and ILi allow for a comparative assessment of the interrelationship between both processes (Fig. 6 A, A1 and A2). For small depolarizations (e.g., up to −40 mV), which do not elicit significant ILis (Fig. 6 A, A2, black and red traces), the optical signals have step-like time courses similar to those observed with hyperpolarizing pulses of the same amplitude (Fig. 6 A, A3). However, for slightly larger depolarizations (only 5 mV larger), the significant ILi record (Fig. 6 A, A2, blue trace) is associated with a large overshoot in the corresponding di-8-ANEPPS transient (Fig. 6 A, A1, blue trace); this is not seen for a hyperpolarization of the same amplitude (Fig. 6 A, A3). Similar to ILi, the overshoot in the optical signals apparently increases to a maximum for a pulse to −35 mV (Fig. 6 A, A1 and A2, green traces). Beyond those voltages, both currents and overshoots become smaller (Fig. 6 A, A1 and A2, purple, dark blue, and magenta traces). In contrast, hyperpolarizing pulses only result in monotonically increasing step-like optical transients (Fig. 6 A, A3), similar to those reported previously for electrically passive fibers (Figs. 1 A and 4 D). To explore the impact that the activation of ILi has on the optical signals, we measured the peak amplitude of the latter (or when overshoots were absent, their steady-state amplitude) and plotted them as a function of membrane potential (Fig. 6 B). It can be observed that for membrane potentials more negative than the activation of ILi, the magnitude of the optical signals depended linearly on the membrane potential, but that there was an abrupt jump in magnitude when the membrane potential exceeded −35 mV. Finally, for very large depolarizations, the amplitude of di-8-ANEPPS transients seemingly resumes its linear dependence on the membrane potential. The tight correlation between the peak amplitude of the optical transients and the magnitude of peak ILi is further illustrated in Fig. 6 C. It can be seen that the supralinear behavior in the optical signals (Fig. 6 C, top, filled circles) approximately mirrors the voltage dependence of ILi (Fig. 6 C, bottom, filled symbols). Clearly, after blocking ILi (Fig. 6 C, bottom, open symbols), the optical signals are linearized (Fig. 6 C, top, open symbols). As explained previously, the linearization of the di-8-ANEPPS transients after blocking all conductances allowed us to calibrate (in the same fiber) the fluorescence changes in terms of the underlying polarization of the TTS. The right axis of the top panel in Fig. 6 C represents the outcome of this calibration. Consequently, by extrapolation to the data before the blockage of ILi, we can estimate, for example, that for a voltage clamp to −30 mV, the average TTS membrane potential reached a peak at ∼6 mV; this implies an ∼36-mV “escape of control” for this membrane compartment. In all likelihood, this depolarization is transient because the currents quickly inactivate.
Figure 6.
Di-8-ANEPPS signals and ILi in a fiber bathed in 1/2Li. (A; A1) Family of di-8-ANEPPS fluorescence transients recorded in response to depolarizing pulses to −90 (0-mV pulse), −60, −45, −40, −35, −30, −10, +10, and +30 mV (gray, black, red, blue, green, orange, purple, dark blue, and magenta traces, respectively). (A2) Family of corrected ILi records in response to the same pulses as in A1. (A3) Family of di-8-ANEPPS fluorescence transients recorded in response to hyperpolarizations to −90 (0-mV pulse), −120, −135, −140, −145, −150, −170, and −180 mV. (B) Voltage dependence of the magnitude (at the peak or steady state) of di-8-ANEPPS transients elicited by depolarizing (red symbols) and hyperpolarizing (black symbols) pulses for the same fiber as in A. The arrow indicates VH. (C; top) Voltage dependence of the magnitude of di-8-ANEPPS transients elicited in response to depolarizing pulses in 1/2Li (peak values, filled circles) and in TEA-Cl + TTX (steady-state values, open circles) external solutions. The right ordinate was the calibration of the TTS membrane potential obtained from steady-state values of di-8-ANEPPS transients in TEA-Cl + TTX. The deconvolution of ΔF/F into membrane potential (right vertical axis) was done according to the formula: (in mV). (Bottom) I-V plot of the peak ILi (filled circles) and residual current after blockage with TEA-Cl + TTX (open circles). Fiber parameters: radius, 28 µm; length, 470 µm; capacitance, 5.3 µF/cm2.
Lithium currents and di-8-ANEPPS transients in detubulated fibers
We have already suggested that two characteristic features of ILi (i.e., the abrupt voltage dependence of peak I-V plots, and the absence of a distinct reversal potential), together with the presence of overshoots in di-8-ANEPPS transients, are demonstrations that the membrane potential in the TTS “escapes” the voltage-clamp control because of the presence of Na channels in the TTS membranes. To evaluate this hypothesis, we measured ILi and di-8-ANEPPS signals in detubulated fibers. From a population of 20 fibers subjected to osmotic shock (16 batch and 4 acute treatments), we found a broadly variable reduction in specific fiber capacitance. The range went from fibers that showed no change in capacitance to fibers displaying values as low as 2 µF/cm2. The average capacitance after treatment was 3.3 ± 1.2 µF/cm2 (mean ± SD; n = 20); these values are significantly smaller than those from normal fibers (4.93 ± 0.55 µF/cm2; mean ± SD; n = 29). From this population, we selected fibers with the lowest specific capacitances (2.5 ± 0.28 µF/cm2; n = 4). Epifluorescence images (100×, 1.4 NA) demonstrated that, in these fibers, di-8-ANEPPS staining was restricted to the periphery, including not only the surface membrane but (to a variable extent) also the outermost regions of the TTS. These observations were confirmed with two-photon laser scanning microscopy (not depicted).
The main results in detubulated fibers are summarized in Fig. 7. Fig. 7 A shows a family of ILi traces obtained after subtraction of linear and nonlinear current components. There are two notorious differences between these records and those obtained in normal fibers (e.g., Fig. 5 B). ILi records reflect a more gradual voltage dependence of ILi activation up to the largest current (Fig. 7 A, black, red, blue, and green traces). In addition, well-defined outward currents with fast kinetics are observed at large depolarizations (Fig. 7 A, brown, violet, and gray traces). These features are manifested in the voltage dependence of the peak ILi for this detubulated fiber, as shown in Fig. 7 B. It can be observed that, although the negative slope region of the I-V plot is still quite steep, it shows the typical concavity expected for a relatively well-controlled current at very small depolarizations. This is in notorious contrast with equivalent plots in normal fibers (Fig. 5 C). Also, the I-V plot in Fig. 7 B shows a reversal potential of approximately −40 mV for ILi, which is in contrast with the absence of reversal potentials in I-V plots from normal fibers (e.g., Fig. 5 C). The voltage dependence of average peak ILi from detubulated fibers (n = 4) is shown in Fig. 7 C. It is clear that the relative smoothness of the I-V plot for very small depolarizations is lost in the average population, but that a distinct reversal potential is observed (46 ± 5 mV). This value is close to the one predicted by the Nernst equation (52 mV), assuming complete equilibration between the myoplasm and the pipette solution. The maximum peak ILi recorded from these fibers was −556 ± 64 µA/cm2, which is ∼22% smaller (P < 0.05) than that from nontreated (normal) fibers. In one successful acute experiment, we demonstrated a reduction in capacitance of ∼50%, which was associated with an ∼22% reduction in peak ILi.
Figure 7.
Lithium currents and di-8-ANEPPS signals from detubulated fibers. (A) ILi records elicited by 25-ms depolarizations to −70-, −50-, −45-, −40-, −35-, 0-, 20-, 40-, 60-, and 80-mV pulses (black, blue, red, green, orange, brown, cyan, magenta, gray, and purple traces, respectively). Only the first 5 ms are shown. No currents were seen at the pulse off (not depicted). Fiber parameters: radius, 23 µm; length, 329 µm; capacitance, 2 µF/cm2. (B) Voltage dependence of peak ILi for the fiber in A. (C) Voltage dependence of the average peak ILi (n = 4). Symbols and bars are the average and SEM. Fiber parameters: radius, 25.7 ± 1.1 µm; length, 421.2 ± 40.3 µm; capacitance, 2.5 ± 0.28 µF/cm2. (D) Di-8-ANEPPS transients elicited by 20-ms depolarizing pulses of 20, 60, 100, and 140 mV. Spot illumination was 50 µm. Data are from the same fiber as in A.
Because ILi records from detubulated fibers are expected to better represent the actual properties of the Na channels under improved voltage-clamp control, traces like those shown in Fig. 7 B were used to calculate the voltage dependence of the characteristic Na channel kinetic parameters (αm, βm, αh, and βh), which were incorporated in the radial model to predict the experimental data (see below and Appendix). A comparison of the simulated currents (for simplicity, assuming only surface membrane contributions) and experimental ILi records for the fiber in Fig. 7 A are presented in Fig. S2. It can be seen that the model predictions reproduce the main kinetic features of the experimental currents. In addition, the peak I-V plot compares well with the experimental data in Fig. 7 B, except for the remaining abruptness in voltage dependence, which we believe reflects contributions from still-present peripheral TTS segments.
Di-8-ANEPPS transients recorded from detubulated fibers also provide interesting information for understanding the impact that Na channels have in the physiological properties of the TTS. Optical records from the same fiber as in Fig. 7 A are shown in Fig. 7 D. The fiber was stained after the osmotic shock. Although there is a marked reduction in the signal-to-noise, as a result of the reduced membrane area stained, these records illustrate remarkable differences with respect to di-8-ANEPPS transients recorded in normal fibers (Figs. 3 A and 6 A). The most obvious are their faster kinetics and the marked reduction in the overshoot. An ∼15% overshoot is observed for the 60-mV depolarization (Fig. 7 D, brown trace), which activated a relatively large ILi (∼600 µA/cm2). Also, the rising and falling phases of the optical signals are greatly accelerated, with time constants of ∼100 µs. Collectively, the observations from fibers treated with the formamide osmotic shock suggest that both the optical and current records arise from membrane areas whose voltage is much better controlled by the surface membrane voltage clamp. We infer from these results and from the reduction in fiber capacitance that both the presence of large overshoots in the TTS signals and the peculiar behavior of the ILi currents observed in normal fibers are significantly contributed by a large proportion of the Na conductance localized in the TTS membranes.
Quantitative calculation of the overshoot
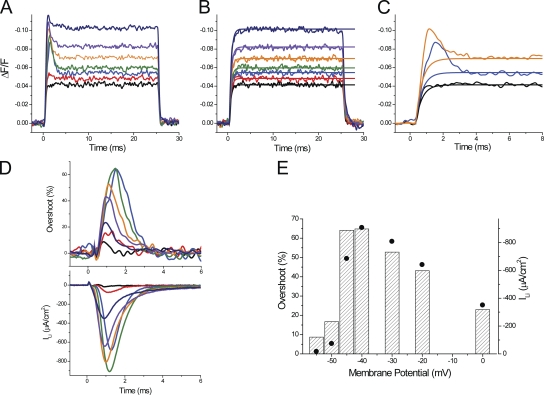
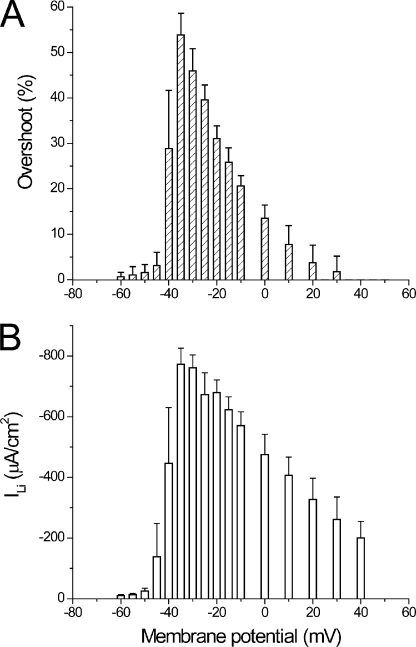
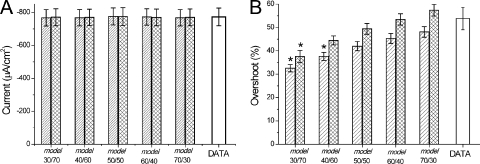
To allow for a quantitative comparison between experimental transients and current and model predictions, we needed to develop a method to quantitatively assess the magnitude of the overshoot component in di-8-ANEPPS transients. This is outlined in Fig. 8 for a fiber in 1/2Li external solution. The method is based on the finding that di-8-ANEPPS transients recorded in the presence of TTX can be used as a reference for the passive polarization of the TTS membranes (in the absence of active conductances). If this is the case, for every voltage, the net effect of the activation of the Li current on the TTS membrane potential can be assessed by subtracting the optical signals recorded after blocking ILi (Fig. 8 B) from those obtained under control conditions (Fig. 8 A). However, to avoid the excessive noise that the subtraction process would entail, we chose to fit the optical transients recorded under passive conditions to single-exponential functions as illustrated in Fig. 8 B. For example, Fig. 8 C shows the superimposition of the fitted and control signals obtained in response to pulses of 35, 45, and 60 mV. The overshoot, calculated as the percentage difference between the signals in Fig. 8 A and the corresponding fitted traces in Fig. 8 B, is shown in the top panel of Fig. 8 D. The bottom panel of Fig. 8 D shows the ILi in the same expanded timescale. It can be seen that although the kinetics of the calculated overshoot traces match closely those of the ILi records, their peak magnitude differs slightly as a result of the normalization process. But in general, as illustrated in Fig. 8 D, these short-living components of the optical signals have durations that are not too different to that of their corresponding ILi records. Fig. 8 E shows that the voltage dependence of the peak amplitude of the overshoot (dashed bars), although not identical, bears a resemblance to that of the peak ILi (filled circles). A more careful comparison between both measurements, but now obtained from multiple fibers (n = 6), is shown in Fig. 9. The average maximal peak ILi for this set of measurements was 773 ± 53 µA/cm2 (not significantly different from the average shown in Fig. 6; P > 0.4), and it was also obtained at −30 mV. The maximal overshoot calculated from the optical data was 54 ± 5% at −35 mV. It is likely that the slight mismatch (of 5 mV) between the voltages at which the maxima occur in both datasets occurs because overshoot calculations involve a normalization process that tends to magnify changes obtained at smaller depolarizations. This normalization in the calculation of the overshoot is also responsible for the steep reduction in its magnitude as a function of the membrane potential for depolarizations beyond −35 mV (Fig. 9 A). The corresponding decrement is significantly less steep in the I-V plot of the peak ILi (Fig. 9 B). Nonetheless, there is a similarity between the bar graphs in Fig. 9 (A and B) that clearly indicates the tight correlation between the escape of control of the membrane potential of the TTS and magnitude of ILi.
Figure 8.
Quantitative evaluation of the overshoot in di-8-ANEPPS transients recorded in 1/2Li external solutions. (A) Family of di-8-ANEPPS fluorescence transients recorded, in 1/2Li external solution, in response to depolarizing pulses to −55, −50, −45, −40, −30, −20, and 0 mV (black, red, blue, green, orange, purple, and dark blue, respectively). (B) Family of di-8-ANEPPS fluorescence transients (noisy traces) recorded in response to the same pulses as in A, but when the external solution was changed to TEA-Cl + TTX. The smooth lines correspond to single-exponential fits to each of the optical records. (C) Superposition (in an expanded time scale) of selected traces from A, black (−55 mV), blue (−45 mV), and orange (−30 mV), with the corresponding exponential fits from B. (D) Time course of the overshoots (in percentage) calculated from the traces in A and B (top), and the simultaneously acquired ILi records (bottom). The same color code was used for A–D. (E) Comparison of the voltage dependence of the magnitude of the overshoot of di-8-ANEPPS transients (dashed bars) and the peak ILi (filled circles). Fiber parameters: radius, 22 µm; length, 413 µm; capacitance, 4.6 µF/cm2.
Figure 9.
Comparison of the voltage dependence of average overshoot and peak ILi. (A) Voltage dependence of the average overshoot calculated from data obtained in six fibers bathed in 1/2Li external solutions. (B) Voltage dependence of the average peak ILi in the same fibers as in A.
Radial cable model simulation predicts the features of di-8-ANEPPS transients, provided that a significant fraction of the Na channels is in the TTS
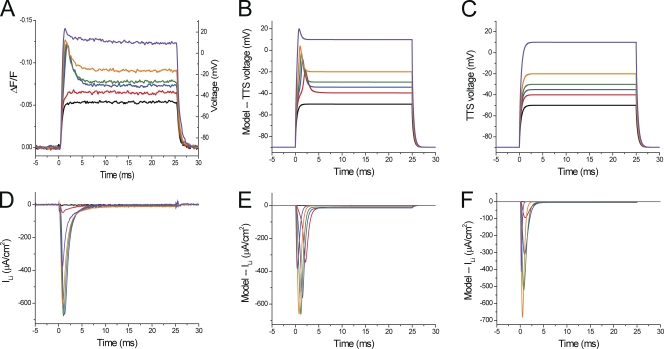
The results described previously demonstrate that the properties of di-8-ANEPPS transients, in particular early after the onset of small depolarizing pulses, depend crucially on the presence or absence of INa or ILi. As illustrated elsewhere for other conductances of amphibian (Heiny and Vergara, 1982; Heiny et al., 1983; Ashcroft et al., 1985) or mammalian (DiFranco et al., 2011a) muscle fibers, an accurate way to test the dependence of the TTS voltage changes on the presence of an intrinsic conductance is to: (a) predict these changes using a realistic model of the voltage propagation in the TTS; and (b) compare the optical data with the model predictions of the optical signals, all while taking into account the well-documented assumption that the optical signals represent a weighted average of the TTS voltage changes (Heiny et al., 1983; Ashcroft et al., 1985; Kim and Vergara, 1998; DiFranco et al., 2011a). A detailed description on how step (a) is fulfilled in the current work, including a model for the Na conductance capable of predicting the properties of INa (or ILi) records, is provided in the Appendix. Fig. 10 illustrates our attempts to explain the results obtained from a fiber in 1/2Li external solution. Fig. 10 A shows the di-8-ANEPPS transients recorded in response to 40-, 50-, 55-, 60-, 70-, and 100-mV voltage-clamp pulses. Fig. 10 D displays the corresponding ionic current records. The most relevant features of these experimental records resemble those described previously for Fig. 8 (A and D). Namely, the relatively large transient inward currents elicited by depolarizing pulses to −35 and −30 mV (Fig. 10 D, blue and green traces) are associated with early overshoots in the di-8-ANEPPS signals (Fig. 10 A, blue and green traces), which are not present for di-8-ANEPPS transients associated with smaller pulses (e.g., to −50 to −40 mV; Fig. 10 A, black and red traces) or with hyperpolarizing pulses of any magnitude (not depicted, but see Fig. 6). As illustrated for Fig. 6, to allow for a comparison with model predictions of average TTS voltage changes, ΔF/F values of di-8-ANEPPS signals were converted into membrane potential (Fig. 10 A, right axis) by using the calibration once the fiber was rendered electrically passive at the end of the experiment.
Figure 10.
Comparison between experimental data and radial cable model predictions. (A) Di-8-ANEPPS transients recorded in response to 0-, 50-, 55-, 60-, 70-, and 100-mV depolarizing pulses (black, red, blue, green, orange, and purple traces, respectively). The deconvolution of ΔF/F (left vertical axis) into membrane potential (right vertical axis) was done according to the regression formula: (in mV). (B) Model predictions of the TTS membrane potential assuming that the Na channel permeability density is 5.64 × 10−4 cm/s at the TTS membranes (-TTS) and 3.76 × 10−4 cm/s at the surface membrane (PNa-S). The access resistance for the TTS (Rs) was 10 Ωcm2. Other model parameters are listed in Table A1. (C) Model predictions of the TTS membrane potentials assuming that ILi is only generated at in the surface membrane (-TTS = 0 and -S = 11.1 × 10−4). (D) Experimental ionic currents corresponding to the optical records in A. (E and F) The predicted ionic currents associated with the simulated traces in B and C, respectively. The same color code was used in A–F. Fiber parameters: radius, 30 µm; length, 572 µm; capacitance, 4.9 µF/cm2.
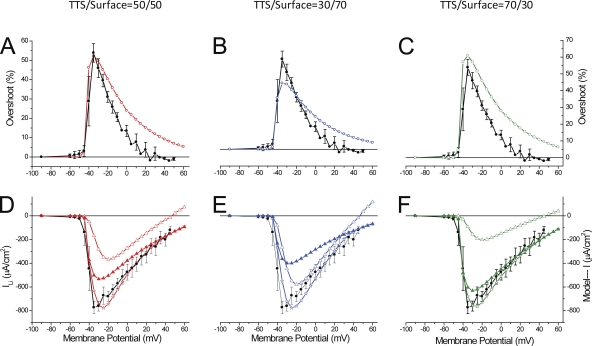
Fig. 10 (B and E) illustrates the radial cable model predictions (of the TTS membrane potential and ILi, respectively) while assuming, for this particular fiber, an Rs value of 10 Ωcm2 and a 60:40 relative distribution of the Na channel permeability density in the TTS with respect to the surface membrane (-TTS/-S). It can be seen that the most salient features of ILi and di-8-ANEPPS transients (Fig. 10, A and D, respectively) are reproduced by the model predictions (Fig. 10, B and E, respectively). In particular, the model predicts the abruptness of the appearance of ILi for depolarizations to −35 and −30 mV (Fig. 10 E, blue and green traces) and, quite remarkably, the existence of current-dependent overshoots in the TTS membrane potential at these depolarizations (Fig. 10 B, blue and green traces). The overall kinetics of the overshoots and the membrane potentials reached at the steady state during the pulses are also well predicted by the model. In addition (not depicted), the model predicts accurately the linear behavior of the TTS voltage changes for hyperpolarizing pulses.
The results shown in Fig. 10 (B and E) are not fortuitous. We found that the set of parameters required to faithfully reproduce the experimental data was unique for this fiber, particularly the -TTS/-S ratio. Assigning all the Na (or Li) permeability to the TTS yielded unstable and unrealistic results (not depicted). Alternatively, Fig. 10 (C and F) shows the results of model simulations, assuming that the TTS lacks Na channels and that all the Na permeability is at the surface membrane. Note that in this case, the absolute value of -S (11.1 × 10−4 cm/s) was larger than the total permeability in the previous simulations (9.4 × 10−4 cm/s) to compensate for the absence of PNa in the TTS. The most evident results of these simulations is that, as illustrated in Fig. 10 F, current records of the same magnitude of those in Fig. 10 (D and E), are not associated with overshoots in the simulated TTS voltage records. Interestingly, the simulated TTS voltage changes in this case predict instead the properties of di-8-ANEPPS transients that would be obtained in electrically passive fibers (e.g., Fig. 8 B).
Voltage dependence of model-predicted overshoots and ILi
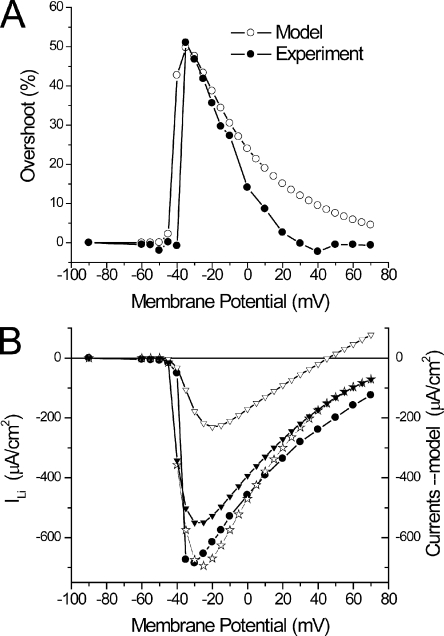
Because the comparison between model predictions and experimental data will ultimately set the basis for a quantitative assessment of the actual distribution of Na channels between the surface and TTS membranes, it is important to specifically examine salient features of model-predicted overshoots and I-V curves. The experimental and predicted di-8-ANEPPS transients presented in Fig. 10 (A and B, respectively) were used to calculate overshoot traces (not depicted) as illustrated in Fig. 8; their peaks are superimposed and plotted as a function of the membrane potential in Fig. 11 A (filled and open circles, respectively). It can be observed that the magnitude and voltage dependence of overshoots predicted by model simulations, while using the same parameters as in Fig. 10, which in turn were specifically tuned to simultaneously predict the magnitude and voltage dependence of ILi (Fig. 11 B, filled circles and open stars), are quite comparable to those calculated from the experimental data (Fig. 11 A). Both plots display an abrupt jump, for an ∼10-mV voltage change, to a maximum (Fig. 11 A, filled and open circles, ∼51 and 50%, respectively) and become progressively smaller in magnitude thereafter for larger depolarizations.
Figure 11.
Voltage dependence of experimental and predicted overshoots and peak ILi for the experiment in Fig. 10. (A) Overshoots calculated from the transients in Fig. 10 A (filled circles) and from the predicted TTS voltage transients in Fig. 10 B (open circles). Model overshoot values were calculated from the peaks of the normalized subtraction (at every voltage) of TTS transients with and without ILi. (B) I-V curves of the experimental data (filled circles) and model-predicted total (open stars), surface (open triangles), and TTS (filled triangles) currents.
The voltage dependence of the peak values of experimental and simulated current records, as is shown in Fig. 10 (D and F, respectively), is shown with filled circles and open stars in Fig. 11 B. It is important to note that the I-V plot of simulated currents (Fig. 11 B, open stars) to a great extent shares the initial abruptness observed in the experimental data (filled circles). Thus, in a span of ∼15 mV, the currents jump from undetectable values to ∼700 µA/cm2. Furthermore, for depolarizations beyond −30 mV, the I-V of both datasets (experimental and simulated) display significantly less steep voltage dependences. Most importantly, for membrane potentials close to (or more positive than) calculated ELi (∼45 or 52 mV for 13 and 10 mM [Na]i, respectively), both the experimental and predicted currents do not show a reversal but instead approach asymptotically the abscissa. We must highlight that the ability of the model to predict not only the properties of the TTS optical records but also this peculiar feature of experimentally recorded ILi strongly suggests a link between the two processes. Namely, as shown by the open triangles in Fig. 11 B, the current from the surface membrane (in this case, a small component that peaks at ∼220 µA/cm2) displays a clear reversal potential (ELi). This is an intrinsic property of the Na permeability for every membrane patch in the model, as described in the Appendix; because the surface membrane is under voltage-clamp control, the I-V shows the intrinsic properties of the Na permeability. In contrast, the model simulations illustrate that the current component arising from the TTS (Fig. 11 B, filled triangles), which represents the majority of the current at every membrane potential, never reaches a reversal potential. More importantly, it can be observed in Fig. 11 B that this current component displays almost a discontinuous jump in voltage dependence, which is responsible for the abruptness in the I-V of the total current (open stars). In summary, model simulations demonstrate that the presence of a substantive Na conductance in the TTS affords an escape of control of the TTS membrane voltage that can be optically measured quantitatively by recording of di-8-ANEPPS transients, and which is responsible for the peculiar abruptness observed at small depolarizations and the lack of reversal potential (and asymptotic approach to the abscissa) typically observed in peak I-V plots.
In Fig. S3 we present a comprehensive comparison of model simulations for Rs = 10, 20, and 40 Ωcm2 with the experimental data. The model simulations were obtained using specific -TTS/-S ratios that uniquely predicted the maximal peak ILi and the 50% overshoot of the data, as shown in Figs. 10 and 11 for Rs = 10 Ωcm2. It can be observed that for Rs = 10 and 20 Ωcm2, the model predicts current traces (Fig. S3, A and B) with voltage-dependent kinetic features that are compatible with those observed experimentally in Fig. 10 D. In contrast, it is apparent from Fig. S3 C that for 40 Ωcm2, the predicted traces show exaggeratedly slow and prominent secondary current components (at every voltage, but particularly observable at small depolarizations), which are not only incompatible with the experimental traces shown Fig. 10 but also with all ILi records obtained in 1/2Li external solution. Furthermore, although the peak I-V plots predicted for Rs = 10 and 20 Ωcm2 (Fig. S3, D and E, red circles) show a reasonable resemblance to the experimental I-V plot (black circles), the one corresponding to 40 Ωcm2 shows a right-shifted maximal peak (as a result of the dominance of the surface membrane component; not depicted) and a peculiar bending for larger depolarizations. The features of the I-V plots of model predictions using a value of 40 Ωcm2 for Rs are not only unlike the data for this experiment but also for the average I-V plots shown in Figs. 5 and 9.
Effects of the Na channel inactivation on di-8-ANEPPS transients
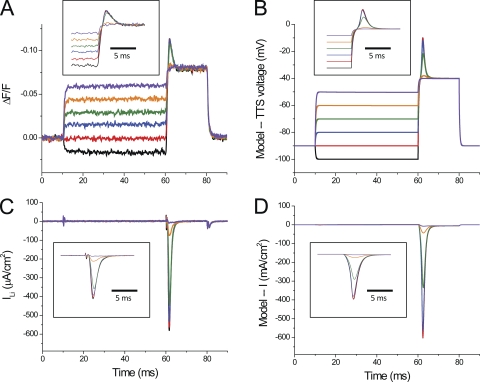
The correlation between the amplitude of ILi and the overshoot observed in optical data can be readily demonstrated by taking advantage of the inactivation properties of Na channels. Fig. 12 shows di-8-ANEPPS transients (Fig. 12 A) and current records (Fig. 12 C) obtained from a fiber stimulated with a two-pulse protocol in which a test pulse to −30 mV (10 ms in duration) was preceded by conditioning prepulses of variable amplitudes (50 ms in duration). It can be observed that conditioning pulses that change the membrane potential from −95 to −70 mV, in 5-mV steps (Fig. 12, black, red, blue, green, orange, and purple traces) did not result in detectable currents (Fig. 12 C) and elicited step-like di-8-ANEPPS transients (Fig. 12 A). These prepulse responses were followed by signals with significant overshoots only for prepulse to −95, −90, −85, and −80 mV (Fig. 12, black, red, blue, and green traces). Prepulses to −75 and −70 mV abruptly eliminated the overshoot components during the test pulses. It can be seen in Fig. 12 C that these two prepulses effectively reduced ILi, whereas smaller prepulses afforded less effective reductions in ILi. The currents and the optical signals shown in expanded time scale in the insets of Fig. 12 (A and C) allow for a better visualization of these effects. Fig. 12 (B and D) demonstrates that model simulations, using parameters similar to those used in Figs. 10 and 11, reproduce the simultaneous effects that Na inactivation has on the overshoot component of TTS voltage changes (Fig. 12 B) and total current predicted.
Figure 12.
Effect of steady-state inactivation of ILi on di-8-ANEPPS transients. (A) Di-8-ANEPPS recorded in response to a two-pulse protocol in which the test pulse was to −30 mV and prepulses were from −95 mV (black trace) to −70 (purple trace) in 5-mV steps. The inset shows the transients in an expanded time scale. (B) Predicted average TTS voltage traces for the same pulses as in A. The inset is equivalent to the one in A. (C and D) Experimental ILi and simulated current records for the same pulses in A, respectively. Fiber parameters: radius, 28 µm; length, 413 µm; capacitance, 5 µF/cm2. The fiber radius used in model simulations was the same as the fiber. Rs = 10 Ωcm2; -TTS = -S = 5.5 × 10−4 cm/s. The rest of the model’s parameters are listed in Tables I and II.
DISCUSSION
In this paper we present a direct quantitative assessment of the overall properties of the Na conductance in intact adult mammalian skeletal muscle fibers. We used an approach comparable to the one recently reported to determine the fraction of ClC-1 conductance present in the TTS of this preparation (DiFranco et al., 2011a). In short, Na (or Li) currents, and changes in TTS membrane potential, measured using the fluorescent potentiometric probe di-8-ANEPPS (Fluhler et al., 1985; Rohr and Salzberg, 1994; Kim and Vergara, 1998; DiFranco et al., 2005, 2011a), were recorded from voltage-clamped muscle fibers bathed in 1/2Na and 1/2Li external solutions. These data were compared with predictions from a model of the TTS that includes voltage- and time-dependent Na channels (see Appendix) to decide how the presence of Na channels in the TTS membranes affects the overall properties of electrical and optical signals. Overall, we demonstrated that the main features of di-8-ANEPPS transients and current records are only predicted by model simulations in which the relative distribution of Na channels between the surface and TTS membranes is restricted within a range that always indicates the substantial presence of Na channels in the TTS membranes.
Measurement and calibration of TTS membrane potentials
As stated previously, to validate model predictions on kinetic changes in the average TTS membrane potential, we rely on indirect measurements of this parameter using optical methods. In the past, our laboratory has extensively developed this approach in both amphibian and mammalian skeletal muscle fibers. Two properties of the potentiometric indicator di-8-ANEPPS, its rapid response time (<120 µs), as measured with total internal refraction microscopy in intact fibers (Capote et al., 2011) and in detubulated fibers (this work), and its adequate linearity (DiFranco et al., 2005, 2011a), are fundamental for our approach. Thus, calibration curves constructed from data at steady-state conditions (as illustrated in Fig. 1) can be readily applied to dynamic changes in membrane potential. We have recently reported the steady-state properties of di-8-ANEPPS at two VHs of −40 and −20 mV (DiFranco et al., 2011a). However, because changes in the hyperpolarizing direction are slightly larger than those in the depolarizing direction, we measured its voltage dependence at −90 mV (Fig. 1). Although the calibration data presented in Fig. 1 are useful to illustrate the relatively narrow dispersion in the optical data (mainly a result of noise) from fiber to fiber, we actually calibrated that optical data for every fiber determined at the end of the experiment.
An obstacle, which potentially could have majorly impaired our ability to complete the assessment of the role of the Na channels in mammalian muscle fibers, was the discovery that in this preparation, Na ions alter (seemingly per se) the linear properties of di-8-ANEPPS. By rendering fibers electrically passive in 1/2Na solution (by the addition of TTX), we unveiled a nonlinear behavior in di-8-ANEPPS transients in response to both depolarizing and hyperpolarizing pulses. Although out of the scope of the present work, understanding the detailed mechanism for the intriguing effect of Na ions on di-8-ANEPPS optical signals from the TTS in muscle fibers may be worth future efforts by our laboratory. However, because the anomaly is seen in response to hyperpolarizing pulses, and disappears upon Na ion removal, it seems unlikely that it arises from surface potential changes as a result of charge movement/gating of ion channels (Jong et al., 1997).
The discovery that Na replacement by Li overcomes the distortion in passive di-8-ANEPPS transients is of paramount importance because it actually enabled the straightforward investigation of the role of Na channels in the TTS, with, of course, the caveat that muscle Na channels are almost equally permeable to Na and Li ions (Campbell, 1976). We do not have an explanation for the differential effects of Na and Li on di-8-ANEPPS transients, nor have we explored whether other alkali metals share the effects of Li, but it is well know that Na and Li have differential interactions with membrane proteins such as the Na/Ca exchanger and the Na,K ATPase, which are both expressed in skeletal muscle fibers. Targets like these proteins may prove important for the effects of Na; however, a direct interaction between the dye molecules and Na cannot be discarded.
Na and Li currents in intact mammalian muscle fibers
Previous studies on the effects of nonregenerative conductances (e.g., ClC-1 and gKir) on the TTS membrane potentials were made under experimental conditions designed to optimize the magnitude of the currents within a range not exceeding ∼1 mA/cm2 (Heiny et al., 1983; Ashcroft et al., 1985; DiFranco et al., 2011a). Larger currents can introduce space-clamp deviations that result in significant errors in the voltages and currents recorded (Bezanilla et al., 1982). For the case of the of the Na conductance, we have found that currents >2 mA/cm2 can be measured in the presence of physiological extracellular Na concentration (not depicted). Accordingly, to preserve adequate space-clamp conditions, we performed all the experiments in this paper using 1/2Na and 1/2Li external solutions, a strategy previously used to demonstrate the presence of Na conductance in the TTS of amphibian fibers (Heiny and Vergara, 1982). In the current work, we demonstrate that INa of ∼900 µA/cm2 can be measured in mammalian muscle fibers without significantly distorting the controlled surface membrane potential (Fig. 2 A, inset). In spite of this, as it will be discussed below, INa (or ILi) records and peak I-V plots suggest that abrupt jumps in voltage dependence at small depolarizations are likely consequences of the fact that, although the surface membrane potential is adequately space clamped and controlled by the voltage-clamp circuitry, the TTS membrane potential escapes from this control. We already described this phenomenon in mammalian muscle fibers bathed in normal Tyrode (DiFranco et al., 2005), but we noted that adequacy of the voltage control of the surface membrane under these conditions was not optimal. In this paper, we exploited the same situation to evaluate the relative Na permeability density in the surface and TTS membrane compartments under unquestionably controlled conditions.
Because of the anomaly introduced by external Na on di-8-ANEPPS transients, most of the emphasis in this paper was put in the description of currents carried by Li ions through the Na channel (ILi). As expected, we found that the properties of ILi are almost identical to those of INa, except that they are ∼30% smaller (compare results in Figs. 2 and 6). This is consistent with results previously reported for amphibian myelinated nerve (Hille, 1972) and skeletal muscle fibers (Campbell, 1976). Both in the case of INa and ILi, the amplitude of the currents jumped abruptly from barely detectable to maximum values within 5–10 mV of membrane depolarizations (Figs. 2, A and C, and 6). As proved by the optical records, this behavior is suggestive of a regenerative process in the TTS being responsible for the abrupt contribution to the recorded current. Furthermore, we found that after correcting for the contributions that charge movement/gating currents (Fig. 6, A and B), peak I-V plots of ILi approached asymptotically the abscissa without reaching a distinct reversal potential (Fig. 6, C and D). This apparently surprising result can also be explained by the presence, in intact muscle fibers, of a substantial inward current contribution from the TTS, as the membrane potential of this compartment can hardly reach (let alone exceed) the Na (or Li) reversal potentials. The results of model simulations in Fig. 11 provide a clear depiction of this phenomenon.
To our knowledge, there are no previous reports in the literature of Na currents recorded from intact mammalian muscle fibers under experimental conditions comparable to ours. Nevertheless, another laboratory recently reported (Fu et al., 2011), using detubulated FDB fibers and very low extracellular Na concentrations, Na currents that have a relatively smooth voltage dependence and a well-defined reversal potential, unlike those shown here for INa and ILi in Figs. 2 and 6, respectively. These differences are precisely what would be predicted if the regenerative contributions from the TTS membrane, present in intact fibers, are (at least partially) eliminated by detubulation.
Detubulation experiments
We observed that treatment of enzymatically dissociated FDB fibers with the formamide osmotic shock resulted in cells with widely dispersed characteristics. Although, on average, their capacitance was significantly reduced (∼67%) with respect to that of normal fibers, the electrical (maximal peak ILi) and optical properties (double-banded fluorescence TTS pattern and overshoot in optical records) of the majority of them were not sufficiently different from those in intact fibers to be considered as a distinct population. Nevertheless, we found that a small subpopulation of the treated fibers (n = 4), with an average capacitance of ∼2.5 µF/cm2, still approximately threefold the capacitance of 0.9 µF/cm2 assumed for the sarcolemma in model simulations, was suitable to address questions regarding the effects of detubulation. These fibers, when stained with di-8-ANEPPS, reported the existence of TTS remnants in the periphery, which are open to the extracellular space. Our observations are compatible with electron microscopic measurements in detubulated frog fibers, suggesting that the remnant TTS segments open to the extracellular space are contained in a peripheral ring of ∼1/5 to 1/10 of the radius (Franzini-Armstrong et al., 1973).
We believe that incomplete detubulation, even in the selected population with the lowest measured capacitance, provides a reasonable explanation for our results. The “stumps” of the TTS network open to the external solution remaining after osmotic shock likely constitute a “truncated peripheral network.” We propose that the voltage distribution in this truncated network, still electrically coupled to the sarcolemma in so-called detubulated fibers, is responsible for most of the optical and electrical properties observed under these experimental conditions. Interestingly, we observed in these fibers a significant reduction in the maximum peak ILi with respect not only to the overall population of intact fibers (∼20%) but also to the rest of treated fibers (not depicted). But how can ∼50% reductions in capacitance result in ∼20% reductions in the average maximum peak ILi? Although the quantitative answer to this question necessitates illustration with model simulations that go beyond the scope of this paper (and that we intend to extensively report in a future publication), suffice it to say that the model predicts that, even when PNa is approximately equally distributed between the sarcolemma and the TTS, the majority of the ILi arises from peripheral segments of the TTS that remain connected after partial detubulation. The reason for this is that these TTS peripheral segments, undergoing voltage changes more similar to the voltage-clamp pulses at the surface membrane, contribute in larger proportions to ILi than those of more internal segments of the radial network whose voltage changes “escaped” control and reached peak amplitudes closer to the Na equilibrium potential. Di-8-ANEPPS transients recorded from optimally “detubulated” fibers indicate that voltage changes in peripheral TTS remnants, together with the sarcolemma, show up to 15% deviations from those commanded by the voltage clamp (Fig. 7 D). This is significantly less than what was observed for the entire TTS network in normal fibers (∼54%) but more than what is expected for the sarcolemma itself. This is in contrast with the membrane capacitance that, being measured under passive conditions, reflects more precisely the proportion of the TTS that remains connected. Collectively, the presence of a still significant membrane compartment (in addition to the sarcolemma) with an improved voltage control with respect to that of the entire TTS network present in intact fibers reasonably explains why the total ILi in treated fibers is still quite large, while showing evidence of a distinct reversal potential, as illustrated in Figs. 7 C and S2 C.
Our findings about the limited effects of detubulation have some additional implications. On the one hand, they provide an independent confirmation that a measurable fraction of ILi (particularly that observed at small depolarizations) is contributed by portions of the TTS that are effectively disconnected from the surface membrane by the treatment. This is only possible if a relatively large proportion of NaV1.4 channels are in the TTS membranes. On the other hand, based on the fact that detubulation is likely to be incomplete, and that peripheral remnants of the TTS membrane area may represent an active fraction of the total TTS membranes, caution has to be exercised with the approach by itself, as it may lead to unrealistic estimates of the relative distribution of ion channels between the surface and the TTS. Interestingly, though, when used in conjunction with optical methods (as done here), osmotic shock treatments may become a useful tool to assess both the properties of muscle conductances in their natural environment (under adequate voltage control) and to confirm the relative distribution between the surface and TTS membranes of endogenous muscle conductances.
Di-8-ANEPPS transients in 1/2Li external solutions
As for INa (Fig. 3), depolarizations able to activate ILi are associated with the appearance of prominent overshoots in di-8-ANEPPS transients (Fig. 7). Once converted into voltage, the overshoots in optical signals demonstrate that, in general, the average TTS membrane potential exceeds that imposed by the voltage clamp at the surface membrane. Because the magnitude of these TTS potential changes are current dependent, they are in turn determined by the magnitude of the Na permeability density in the TTS. Similar effects were found in amphibian muscle fibers (Heiny and Vergara, 1982), except that the optical signals associated with INa in this preparation were qualitatively different from those reported here. Although in mammalian fibers the overshoots are short spike-like components of the optical signals with durations not too different from those of the underlying current records, in frog fibers these components are significantly longer lasting (Heiny and Vergara, 1982). These differences probably stem from differences in fiber radii, permeability densities in the TTS, and access resistance (Rs) to the TTS, between both preparations. Regarding the latter, it should be noted that mammalian fibers were obtained by enzymatic digestion of FDB muscles, whereas amphibian fibers were mechanically dissected from frog semitendinosus muscles. In any case, the model parameters used in this paper (see Appendix) have been tailored to reproduce the main features of the current records, I-V curves, and TTS transients recorded from mammalian muscle fibers, and they differ significantly from those reported for amphibian fibers (Heiny et al., 1983; Ashcroft et al., 1985; Kim and Vergara, 1998).
Quantitative evaluation of the relationship between overshoots and currents
Similar to our analysis of the attenuation of di-8-ANEPPS in the presence of large ClC-1 chloride currents (DiFranco et al., 2011a), we developed in this paper a method to quantitatively assess the properties of the overshoot in di-8-ANEPPS transient recorded in the presence of relative large Li currents (Figs. 8, 9, and 11). As mentioned above, the accuracy of this procedure was ascertained when using Li, instead of Na, in the external solution because, in this case, the reference signals when the Li conductance is blocked by TTX are indistinguishable from those recorded under passive conditions. Consequently, model predictions of the average TTS potential can be quantitatively compared with experimental measurements of the TTS potential once the optical data are converted into voltage, as was done in Fig. 11 A.
Probably the most important finding of the present work is precisely that, as illustrated in Fig. 10, the overall properties of di-8-ANEPPS transients, and their overshoot in particular (Fig. 11 A), can only be predicted by model simulations if a large fraction of the Na permeability density is in the TTS membranes. As shown in the Appendix, the radial cable model equations, stipulating the existence of an access resistance (Rs) in series with the TTS, were modified from the original equations of Adrian and collaborators (Adrian et al., 1969; Adrian and Peachey, 1973) to include time- and voltage-dependent Na channels similarly to what was done previously with nonregenerative ionic conductances (Heiny et al., 1983; Ashcroft et al., 1985; DiFranco et al., 2011a). In the Appendix, we explain how the radial cable elements of the TTS include Na channels characterized by a maximal permeability density ( in cm/s) and typical Hodgkin–Huxley gating characteristics (Hodgkin and Huxley, 1952b), and they are conditioned to take into account concentration-dependent fluxes assuming that the independence principle is obeyed (Hodgkin and Huxley, 1952a). In addition, the model contemplates a diffusion equation, modified from Barry and Adrian (1973; Friedrich et al., 2001), to calculate Na (or Li) concentration changes in the lumen of the T-tubules resulting from fluxes through the Na channel at each radial segment of the TTS. Both the radial cable model and diffusion equations were integrated simultaneously using conventional numerical methods (see Appendix). It is important to mention that the changes in external [Na] computed in the model presented here amount for a few millimolars and do not affect significantly the results, even for fibers equilibrated with 1/2Na and 1/2Li external solutions.
There is a question that has yet to be addressed: What are the respective contributions of the sarcolemma and the TTS membrane Na (or Li) currents to the total INa (or ILi) records that would still explain the optical data? Although the question is complex, we already ruled out the possibility that all of the Na channels are in the sarcolemma, as it is generally incompatible with the optical data presented throughout the paper and also reinforced by detubulation experiments. The other extreme case, that all of the Na channels are in the TTS, seems unrealistic because it is unlikely that the sarcolemma is entirely deprived of excitability, and because model simulations suggest extreme instability if this was the case (not depicted). It might seem that the excellent predictions by model simulations of ∼51% overshoot in the case of the fiber in Fig. 10, which yielded a large TTS/surface current ratio for the 60:40 -TTS/-S ratio, have already provided a definite answer about the issue of permeability distribution. However, this is not necessarily the case, as we should explore other possibilities to encompass possible fiber-to-fiber variability of the data. Fortunately, our simultaneous measurements of the voltage dependence of peak overshoots, and peak I-V curves, from multiple fibers (Fig. 9) allow us to complete the task. Fig. 13 shows the results from model simulations using various -TTS/-S ratios and an Rs of 20 Ωcm2 to generate a range of overshoot profiles while constraining the maximal peak ILi to be constant. The resulting simulated I-V plots are superimposed (Fig. 13, D–F, open stars) with the average experimental data (Fig. 13, D–F, filled black circles) for comparison. Fig. 13 A shows the superposition of the experimental peak overshoot (black circles) with the one predicted by model simulation assuming a 50:50 -TTS/-S ratio (Fig. 13 A, red open circles). It can be seen that this assumption provides a very adequate prediction of the maximum overshoot (∼54%) and of the maximal peak ILi (∼775 µA/cm2) obtained from the population of fibers. Notably, because the TTS represents the largest of the two-membrane compartments in the muscle fiber, an equal distribution between the TTS and surface membranes results in a predicted maximal ILi arising from the TTS of ∼530 µA/cm2 (at −30 mV and ∼0.8 ms after the onset of the pulse). This represents ∼70% of the total current at this membrane potential and time, while the surface membrane contributes the other ∼30% (∼226 µA/cm2). Fig. 13 (B and E) shows the results of simulations in which we deliberately limited the density of Na channels in the TTS membranes to be ∼43% of that at the surface membrane (30:70 ratio). It can be seen that this ratio predicts that the maximal TTS voltage overshoot (Fig. 13 B, blue open circles) is ∼41% smaller than the one observed experimentally. Thus, although the peak I-V plot of the total current (Fig. 13 E, open blue stars) was not too dissimilar to the one shown in Fig. 13 D, the TTS component (Fig. 13 E, filled blue triangles) with a maximum of ∼400 µA/cm2 (at −30 mV) seems to be too small to explain the observed overshoot in the average population of fibers. In spite of this, this current component would still contribute a substantial proportion (∼50%) to the total current recorded at the same membrane potential. This type of comparison illustrates the great sensitivity afforded by the optical measurements to discriminate between channel distributions that would give the same total current but have very different balance between the surface and TTS current contributions. Without the information provided by the potentiometric dye records about the associated changes in TTS membrane potential, it would be impossible to decide upon which is the correct one. Likewise, a 70:30 -TTS/-S ratio (Fig. 13, C and F) predicts a peak overshoot of ∼63%, which is larger than those recorded. In this case, the current component arising from the TTS (Fig. 13 F, filled green triangles) has a maximum of ∼631 µA/cm2 at −30 mV, which not only seems to be too large to explain the optical data, but would also account for >82% of the total current at that potential. This might possibly lead to electrical instability of the fiber under normal conditions, but the point needs to be investigated in greater detail. The suggestion from this analysis comparing experimental data and model simulations at a fixed total current in 1/2Li external solutions is that the distribution of Na channels between the surface and TTS of mammalian skeletal muscle fibers is probably constrained to -TTS/-S ratios in the range between 40:60 and 60:40.
Figure 13.
Model predictions of overshoot and currents for various PNa distributions in the surface and TTS membranes. (A–C) Voltage-dependent overshoots calculated (see Fig. 11 A) using the following -TTS/-S ratios: 1 (or 50:50) in A; 0.429 (or 30:70) in B; and 2.333 (or 70:30) in C. The total values of were 12 × 10−4 cm/s, 13.5 × 10−4, and 11 × 10−4 for the calculations of the overshoot in A, B, and C, respectively. In every panel, the filled black symbols are the average values shown in Fig. 9 A; the superimposed open symbols were obtained with 50:50 (A, red), 70:30 (B, blue), and 30:70 (C, green) S/PNa-TTS, respectively. (D–F) Average peak I-V plots of ILi as shown Fig. 9 B (black symbols) are superimposed with model predictions for 50:50 (A, red symbols), 30:70 (B, blue symbols), and 70:30 (C, green symbols) -TTS/-S ratios, respectively. In every panel, open stars represent the total current, filled triangles represent the TTS current component, and open triangles represent the surface membrane current component. The fiber radius used in model simulations was the average for all the experiments (25 µm), and Rs was 20 Ωcm2. The rest of the model’s parameters are listed in Tables I and II.
To further analyze the statistical significance of the comparison between model predictions and experimental data, we considered the possibility that the variability in the overshoot optical data may arise principally from the dispersion in the peak ILi. Thus, we tested the effects of a range of currents encompassing the dispersion in the maximal peak ILi of the experiments, and asked the model to predict the overshoot for these currents at various -TTS/-S ratios and Rs values of 10 and 20 Ωcm2. The results are shown in Fig. 14. Fig. 14 A shows that the actual maximum peak ILi simulated with the model for the various distribution scenarios has been maintained to the same average and SEM values as the data (Fig. 14 A, open bar). Fig. 14 B shows the overshoot predicted from simulations using Rs = 10 Ωcm2 (diagonally hatched bars) and 20 Ωcm2 (cross-hatched bars). It can be seen in Fig. 14 B that for simulations generated using Rs = 10 Ωcm2, -TTS/-S ratios of 40:60 and 30:70 would predict significantly smaller overshoots than those recorded experimentally. Alternatively, if we assume that Rs = 20 Ωcm2, then a -TTS/-S ratio of 40:60 would still be compatible with the optical data, but a 30:70 ratio would not. Interestingly, for both Rs values, simulations using larger than 50:50 ratios do not result in overshoot predictions significantly larger than the experimental data. Collectively, the theoretical predictions shown in Fig. 14 suggest that the magnitude of the overshoots observed in experiments using 1/2Li external solution are only compatible with the presence of a significant Na permeability density (most likely centered around an equal distribution of Na channels) in the TTS with respect to that at the surface membrane. Whichever the case may be, and this should be further evaluated in future experiments, the TTS contribution will seemingly exceed 50% of the total Na current recorded in intact muscle fibers. Importantly, this TTS contribution manifests itself most significantly at small depolarizations, thus explaining the abruptness in the I-V plots, regardless of the value of Rs or of other fiber parameters such as diameter, capacitance, etc.
Figure 14.
Statistical analysis of model predictions of the overshoot at various distributions and Rs values. (A) Maximum peak ILi predictions assuming various -TTS/-S ratios and Rs = 10 (diagonally hatched bars) and 20 Ωcm2 (cross-hatched bars). (B) Model predictions of the maximum overshoot assuming the same conditions as in A. The empty bars represent the experimental maximum peak ILi (A) and overshoot (B). -TTS/-S ratios are indicated in the plots. The asterisks indicate statistical significance (P < 0.05).
The values -TTS/-S that are compatible with the optical and electrical data reported in this paper for mammalian fibers are, in general, extremely high when compared with values of ∼1/20, as suggested on theoretical grounds and AP model simulations, for frog skeletal muscle fibers (Adrian and Peachey, 1973). There are significant differences in the geometrical and passive electrical properties between both types of fibers that must be taken into account for the understanding of their respective overall electrical characteristics. For example, we recently reported a value of 40 Ωcm2 for the access resistance to the TTS (Rs) in enzymatically dissociated mammalian fibers (DiFranco et al., 2011a). This value is significantly smaller than the 120–150 Ωcm2 suggested for mechanically isolated amphibian fibers (Adrian and Peachey, 1973; Kim and Vergara, 1998). As shown in Figs. 10 and S3, only small Rs values (10–20 Ωcm2) permit to predict simultaneously the overall kinetics and I-V characteristics of ILi, and an overshoot of ∼50%. Furthermore, as illustrated in Fig. S3, even 40 Ωcm2 predicts the existence of exaggerated dual peaks in the ILi records and odd I-V plots, which are not observed under our working conditions. We believe that the new estimates of Rs are more accurate than previous values (for approximately the same lumen conductivity GL); apparently, the rapid kinetics and peculiar voltage dependence of Li currents are excellent tests for the adequate estimation of this parameter in model predictions. Although further testing will be necessary in the future, the possibility that Rs values are lower than the previously reported 40 Ωcm2 would reinforce the concept (DiFranco et al., 2011a) that a large proportion ClC-1 channels are in the TTS of normal mammalian muscle fibers (not depicted). In addition, the combined effect of large in the TTS with small Rs values may explain our finding that, under current clamp conditions, optically recorded APs in mouse FDB fibers are almost identical to the electrically recorded ones (DiFranco et al., 2005).
In summary, although several model parameters were adjusted in this paper to explain the various features of the experimental data, the one that needed the most critical attention to predict simultaneously the properties of INa and the optical data is the relative partitioning of Na permeability density between surface and TTS membranes. An important merit of the current work is precisely that we succeeded in providing a quantitative assessment of the narrow range in the relative distributions of Na channels between these two membrane compartments that can explain the experimental data. This is a fundamental contribution for the future assessment of the electrical properties of skeletal muscle fibers in normal and diseased animals.
APPENDIX
Radial cable model equations for the TTS of mammalian skeletal muscle fibers, including sodium permeability and ion diffusion
The radial cable model equations are essentially the same as those described in detail in the Appendix of DiFranco et al. (2011a), which in turn followed the nomenclature reported previously (Ashcroft et al., 1985; Kim and Vergara, 1998; DiFranco et al., 2007) and the assumption (Adrian and Peachey, 1973) that the lumen of the TTS is separated from the extracellular fluid by an access resistance (Rs, in Ωcm2).
The partial differential equation that governs the radial (r) and time (t)-dependent changes in T-tubule membrane potential (u(r,t)) in response to voltage changes at the external boundary is (Adrian et al., 1969):
| (A1) |
where, a is the radius of the muscle fiber, and In these equations, the parameters and are the capacitance (in µF/cm3) and conductance (in S/cm3) of the tubular membrane per unit volume of muscle fiber, respectively ( and ). Also, is the effective radial conductivity ( in S/cm). As noted elsewhere, numerical integration methods are necessary to solve Eq. A1, and to predict the voltage of TTS cable elements, when nonlinear conductances are assumed to be in parallel with capacitive elements (Adrian and Peachey, 1973; Heiny et al., 1983; Ashcroft et al., 1985; DiFranco et al., 2011a). To this end, we replace the term in Eq. A1 with the more general term
where is a generalized current normalized per volume of fiber. Keeping the same definitions for R and T, Eq. A1 is transformed into:
| (A2) |
For the simulations in this paper, we assumed that is contributed by a small residual leak current, akin to the chloride permeability described in DiFranco et al. (2011a), but primarily by the flow of Na ions across the TTS walls through Na channels characterized by a prominent permeability (PNa; see below).
Thus,
| (A3) |
where ICl(u,R,T) and INa(u,R,T) are the chloride and sodium current per cm2 of TTS membrane.
Our approach to simulate the voltage-dependent kinetics of INa at each radial cable element was to use the classical Hodgkin and Huxley (HH) m3h approach (Hodgkin and Huxley, 1952b), while also assuming the independence principle to account for the effect of external sodium concentration on the ion flow through the sodium channels (Hodgkin and Huxley, 1952a).
These two conditions are accounted for by the use of the following equations:
| (A4) |
where m and h are the traditional HH activation and inactivation gates, respectively, and
| (A5) |
in which represents the maximal sodium permeability (in cm/sec), V is the membrane potential at which each current calculation is made, [Na]o and [Na]i are the external and internal sodium concentrations, respectively, and F, R, and T are the common gas constants (note that these R and T constants must be distinguished from the variables R and T of the radial cable model).
As usual, m and h are calculated from the differential equations:
| (A6) |
| (A7) |
The variables αm, βm, αh, and βh are voltage-dependent kinetic rate constants for the state variables m and h, respectively; they are characterized by equations with a similar structure of those reported recently by other authors (Fu et al., 2011):
| (A8) |
| (A9) |
Typical values of the parameters used in the model are included in Table A2. Fig. A1 illustrates the voltage dependence of the steady-state values of m and h (m∞ and h∞) and of their characteristic time constants (τm and τh) when the parameter values listed in Table A2 are used.
TABLE A2.
Typical parameter values for muscle sodium channels
| Parameter | Value | Dimension |
| PCl | (1 − 5) × 10−6 | cm/sec |
| 2 × 10−4 − 2 × 10−3 | cm/sec | |
| 0.13 | ms−1 | |
| −40 | mV | |
| 4 | mV | |
| 0.7 | ms−1 | |
| 6 | mV | |
| 2 × 10−4 | ms−1 | |
| −19 | mV | |
| 7.6 | mV | |
| 9 | ms−1 | |
| 0.08 | (mV × ms)−1 | |
| 20 | mV | |
| [Na]o | 78 | mM |
| [Na]i | 13 | mM |
See Results for specific deviations from these values.
Figure A1.
Voltage dependence of m∞, h∞, τm, and τh using characteristic model parameters for INa.
Sodium diffusion in the TTS lumen
Changes in luminal sodium concentration in the TTS ([Na]o) occurring in response to the current flow across the T-tubule walls were calculated from simultaneous integration of the diffusion equation (Barry and Adrian, 1973; Friedrich et al., 2001):
| (A10) |
where DNa is the diffusion coefficient of Na (or Li) ions in the lumen of the TTS (in cm2/sec), F is the Faraday constant, and INa is the sodium current per cm2 of TTS membranes. Using the dimensionless variables R = r/a and τ = σDNa t/a2, this equation becomes:
| (A11) |
Numerical integration of model equations
TTS voltage.
The TTS cable is assumed to be made of n = 60 radial shells sealed at the center of the muscle fiber. As described previously (Kim and Vergara, 1998; DiFranco et al., 2007, 2011a), at a given time j, the finite differences approximation of the partial differential equation of the T-tubular voltage (Eq. A2), while using an implicit Crank-Nicolson algorithm (Crank, 1975; Gerald, 1978), yields the following equation for an arbitrary annulus i:
| (A12) |
where is the current per unit fiber volume (calculated from Eqs. A3 and A4) flowing through the T-tubular element at shell i and at the time interval j during the numerical integration process. Eq. A12 is a recursive formula allowing for the calculation of at a time interval while knowing The system of tridiagonal coefficient matrices was solved using an LU decomposition algorithm (Gerald, 1978). The integration of Eqs. A6 and A7, updating the value of INa for every cable element and for the surface membrane, was performed with a second-order Runge–Kutta algorithm at every time step. The values of the general cable parameters used for the simulations shown in the paper are summarized in Table A1. Specific permeability parameters are given in the figure legends.
Sodium concentration in the lumen of the TTS.
The finite difference approximation and Crank–Nicolson algorithm used for the integration of Eq. A11 to calculate the luminal sodium concentration () at every shell i and at time interval j followed an equivalent rationale previously reported for chloride ions in the Appendix of DiFranco et al. (2011a). In brief, at a given time j, the finite differences approximation of the partial differential equation for [Na]o in the TTS (Eq. A11) yields the recurrence formula:
| (A13) |
At the outside boundary (i = n) we apply Fick’s law to the T-tubule’s opening:
and at the inside (closed) boundary (i = 0):
Total current and optical signals
The total ionic currents calculated from the integration of the radial cable equations, including the independence principle/HH model of INa at each radial cable element of the TTS, was the sum of two contributions: (1) a surface membrane component calculated from the direct temporal integration of Eq. A4 in response to VCOM; and (2) a TTS component, which encompasses the effective sum of currents originated in this membrane compartment; this was calculated from the application of Kirchhoff laws at the external opening of the TTS (Ashcroft et al., 1985; Kim and Vergara, 1998), as:
| (A14) |
where is the voltage across the outermost segment of the TTS at time interval j.
Under the assumption that di-8-ANEPPS optical signals occur homogenously at superficial and deep regions of the TTS, and that changes in its optical properties with the membrane voltage occur identically at every submicroscopic region of the TTS, the optical signal obtained within our illumination disk is expected to represent an ensemble average of the voltage contributed by every cable element in the TTS () weighted by the radius of each annulus (Heiny et al., 1983; Ashcroft et al., 1985; Kim and Vergara, 1998; DiFranco et al., 2011a). This is calculated, for each successive time step, using a numerical trapezoidal integration algorithm based on Simpson’s rule (Gerald, 1978) from the formula:
This assumption was used to calculate the predicted optical signals (for comparison with the data) in Figs. 4 and 8.
Acknowledgments
The authors also thank Mr. R. Serrano for technical support.
This work was supported by National Institutes of Health/National Institute of Arthritis and Musculoskeletal and Skin Diseases grants AR047664 and AR54816 (to J.L. Vergara), and the multi-PI grant AR041802 (PI: Susan Hamilton, Baylor College of Medicine, Houston, TX).
Richard L. Moss served as editor.
Footnotes
Abbreviations used in this paper:
- AP
- action potential
- FDB
- flexor digitorum brevis
- TTS
- transverse tubular system
- TTX
- tetrodotoxin
References
- Adrian R.H., Peachey L.D. 1973. Reconstruction of the action potential of frog sartorius muscle. J. Physiol. 235:103–131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adrian R.H., Chandler W.K., Hodgkin A.L. 1969. The kinetics of mechanical activation in frog muscle. J. Physiol. 204:207–230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashcroft F.M., Heiny J.A., Vergara J. 1985. Inward rectification in the transverse tubular system of frog skeletal muscle studied with potentiometric dyes. J. Physiol. 359:269–291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barry P.H., Adrian R.H. 1973. Slow conductance changes due to potassium depletion in the transverse tubules of frog muscle fibers during hyperpolarizing pulses. J. Membr. Biol. 14:243–292 10.1007/BF01868081 [DOI] [PubMed] [Google Scholar]
- Bedlack R.S., Jr, Wei M., Loew L.M. 1992. Localized membrane depolarizations and localized calcium influx during electric field-guided neurite growth. Neuron. 9:393–403 10.1016/0896-6273(92)90178-G [DOI] [PubMed] [Google Scholar]
- Bezanilla F., Vergara J., Taylor R.E. 1982. Voltage clamping of excitable membranes. Methods of Experimental Physics. Volume 20. Ehrenstein G., Lecar H., Academic Press, New York: 445–511 [Google Scholar]
- Campbell D.T. 1976. Ionic selectivity of the sodium channel of frog skeletal muscle. J. Gen. Physiol. 67:295–307 10.1085/jgp.67.3.295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannon S.C. 2006. Pathomechanisms in channelopathies of skeletal muscle and brain. Annu. Rev. Neurosci. 29:387–415 10.1146/annurev.neuro.29.051605.112815 [DOI] [PubMed] [Google Scholar]
- Capote J.C., DiFranco M., Vergara J.L. 2011. Differential recording of voltage changes at the surface and transverse tubular system membranes of mammalian skeletal muscle fibers using di-8-ANEPPS and global and TIRFM. Biophys. J. 100:590a 10.1016/j.bpj.2010.12.3404 [DOI] [Google Scholar]
- Crank J. 1975. The Mathematics of Diffusion. Oxford University Press, Oxford: 414 pp [Google Scholar]
- del Castillo J., Escalona de Motta G. 1978. A new method for excitation-contraction uncoupling in frog skeletal muscle. J. Cell Biol. 78:782–784 10.1083/jcb.78.3.782 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiFranco M., Novo D., Vergara J.L. 2002. Characterization of the calcium release domains during excitation-contraction coupling in skeletal muscle fibres. Pflugers Arch. 443:508–519 10.1007/s004240100719 [DOI] [PubMed] [Google Scholar]
- DiFranco M., Capote J., Vergara J.L. 2005. Optical imaging and functional characterization of the transverse tubular system of mammalian muscle fibers using the potentiometric indicator di-8-ANEPPS. J. Membr. Biol. 208:141–153 10.1007/s00232-005-0825-9 [DOI] [PubMed] [Google Scholar]
- DiFranco M., Capote J., Quiñonez M., Vergara J.L. 2007. Voltage-dependent dynamic FRET signals from the transverse tubules in mammalian skeletal muscle fibers. J. Gen. Physiol. 130:581–600 10.1085/jgp.200709831 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiFranco M., Quinonez M., Capote J., Vergara J. 2009. DNA transfection of mammalian skeletal muscles using in vivo electroporation. J. Vis. Exp. 32:1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiFranco M., Herrera A., Vergara J.L. 2011a. Chloride currents from the transverse tubular system in adult mammalian skeletal muscle fibers. J. Gen. Physiol. 137:21–41 10.1085/jgp.201010496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiFranco M., Tran P., Quiñonez M., Vergara J.L. 2011b. Functional expression of transgenic α1sDHPR channels in adult mammalian skeletal muscle fibres. J. Physiol. 589:1421–1442 10.1113/jphysiol.2010.202804 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escobar A.L., Monck J.R., Fernandez J.M., Vergara J.L. 1994. Localization of the site of Ca2+ release at the level of a single sarcomere in skeletal muscle fibres. Nature. 367:739–741 10.1038/367739a0 [DOI] [PubMed] [Google Scholar]
- Falk G. 1968. Predicted delays in the activation of the contractile system. Biophys. J. 8:608–625 10.1016/S0006-3495(68)86511-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falk G., Fatt P. 1964. Linear electrical properties of striated muscle fibres observed with intracellular electrodes. Proc. R. Soc. Lond. B Biol. Sci. 160:69–123 10.1098/rspb.1964.0030 [DOI] [PubMed] [Google Scholar]
- Fluhler E., Burnham V.G., Loew L.M. 1985. Spectra, membrane binding, and potentiometric responses of new charge shift probes. Biochemistry. 24:5749–5755 10.1021/bi00342a010 [DOI] [PubMed] [Google Scholar]
- Franzini-Armstrong C., Venosa R.A., Horowicz P. 1973. Morphology and accessibility of the ‘transverse’ tubular system in frog sartorius muscle after glycerol treatment. J. Membr. Biol. 14:197–212 10.1007/BF01868078 [DOI] [PubMed] [Google Scholar]
- Franzini-Armstrong C., Landmesser L., Pilar G. 1975. Size and shape of transverse tubule openings in frog twitch muscle fibers. J. Cell Biol. 64:493–497 10.1083/jcb.64.2.493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedrich O., Ehmer T., Uttenweiler D., Vogel M., Barry P.H., Fink R.H. 2001. Numerical analysis of Ca2+ depletion in the transverse tubular system of mammalian muscle. Biophys. J. 80:2046–2055 10.1016/S0006-3495(01)76178-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y., Struyk A., Markin V., Cannon S. 2011. Gating behaviour of sodium currents in adult mouse muscle recorded with an improved two-electrode voltage clamp. J. Physiol. 589:525–546 10.1113/jphysiol.2010.199430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerald C.F. 1978. Applied Numerical Analysis. Addison-Wesley Publishing Company, Boston: 518 pp [Google Scholar]
- Heiny J.A., Vergara J. 1982. Optical signals from surface and T system membranes in skeletal muscle fibers. Experiments with the potentiometric dye NK2367. J. Gen. Physiol. 80:203–230 10.1085/jgp.80.2.203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heiny J.A., Ashcroft F.M., Vergara J. 1983. T-system optical signals associated with inward rectification in skeletal muscle. Nature. 301:164–166 10.1038/301164a0 [DOI] [PubMed] [Google Scholar]
- Hille B. 1972. The permeability of the sodium channel to metal cations in myelinated nerve. J. Gen. Physiol. 59:637–658 10.1085/jgp.59.6.637 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin A.L., Huxley A.F. 1952a. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 116:449–472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin A.L., Huxley A.F. 1952b. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500–544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley A.F., Taylor R.E. 1958. Local activation of striated muscle fibres. J. Physiol. 144:426–441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jong D.S., Stroffekova K., Heiny J.A. 1997. A surface potential change in the membranes of frog skeletal muscle is associated with excitation-contraction coupling. J. Physiol. 499:787–808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim A.M., Vergara J.L. 1998. Supercharging accelerates T-tubule membrane potential changes in voltage clamped frog skeletal muscle fibers. Biophys. J. 75:2098–2116 10.1016/S0006-3495(98)77652-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lueck J.D., Rossi A.E., Thornton C.A., Campbell K.P., Dirksen R.T. 2010. Sarcolemmal-restricted localization of functional ClC-1 channels in mouse skeletal muscle. J. Gen. Physiol. 136:597–613 10.1085/jgp.201010526 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obaid A.L., Koyano T., Lindstrom J., Sakai T., Salzberg B.M. 1999. Spatiotemporal patterns of activity in an intact mammalian network with single-cell resolution: optical studies of nicotinic activity in an enteric plexus. J. Neurosci. 19:3073–3093 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peachey L.D. 1965. Transverse tubules in excitation-contraction coupling. Fed. Proc. 24:1124–1134 [PubMed] [Google Scholar]
- Rohr S., Salzberg B.M. 1994. Multiple site optical recording of transmembrane voltage (MSORTV) in patterned growth heart cell cultures: assessing electrical behavior, with microsecond resolution, on a cellular and subcellular scale. Biophys. J. 67:1301–1315 10.1016/S0006-3495(94)80602-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross W.N., Salzberg B.M., Cohen L.B., Grinvald A., Davila H.V., Waggoner A.S., Wang C.H. 1977. Changes in absorption, fluorescence, dichroism, and birefringence in stained giant axons: optical measurement of membrane potential. J. Membr. Biol. 33:141–183 10.1007/BF01869514 [DOI] [PubMed] [Google Scholar]
- Salzberg B.M., Davila H.V., Cohen L.B. 1973. Optical recording of impulses in individual neurones of an invertebrate central nervous system. Nature. 246:508–509 10.1038/246508a0 [DOI] [PubMed] [Google Scholar]
- Schneider M.F. 1970. Linear electrical properties of the transverse tubules and surface membrane of skeletal muscle fibers. J. Gen. Physiol. 56:640–671 10.1085/jgp.56.5.640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi M.P., Cannon S.C. 2001. Mexiletine block of disease-associated mutations in S6 segments of the human skeletal muscle Na(+) channel. J. Physiol. 537:701–714 10.1113/jphysiol.2001.012541 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsau Y., Wenner P., O’Donovan M.J., Cohen L.B., Loew L.M., Wuskell J.P. 1996. Dye screening and signal-to-noise ratio for retrogradely transported voltage-sensitive dyes. J. Neurosci. Methods. 70:121–129 10.1016/S0165-0270(96)00109-4 [DOI] [PubMed] [Google Scholar]
- Vergara J., Bezanilla F. 1976. Fluorescence changes during electrical activity in frog muscle stained with merocyanine. Nature. 259:684–686 10.1038/259684a0 [DOI] [PubMed] [Google Scholar]
- Vergara J.L., Bezanilla F. 1981. Optical studies of E-C coupling with potentiometric dyes. The Regulation of Muscle Contraction: Excitation-Contraction Coupling. Brazier A.G.M., editor Academic Press, New York: 66–77 [Google Scholar]
- Vergara J., Bezanilla F., Salzberg B.M. 1978. Nile blue fluorescence signals from cut single muscle fibers under voltage or current clamp conditions. J. Gen. Physiol. 72:775–800 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergara J.L., Delay M., Heiny J.A., Ribalet B. 1983. Optical studies of T-system potential and calcium release in skeletal muscle fibers. The Physiology of Excitable Cells. Moody A.D., editor Alan R. Liss, Inc., New York: 343–355 [Google Scholar]
- Woods C.E., Novo D., DiFranco M., Vergara J.L. 2004. The action potential-evoked sarcoplasmic reticulum calcium release is impaired in mdx mouse muscle fibres. J. Physiol. 557:59–75 10.1113/jphysiol.2004.061291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu F.F., Gordon E., Hoffman E.P., Cannon S.C. 2005. A C-terminal skeletal muscle sodium channel mutation associated with myotonia disrupts fast inactivation. J. Physiol. 565:371–380 10.1113/jphysiol.2005.082909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zampighi G., Vergara J., Ramón F. 1975. On the connection between the transverse tubules and the plasma membrane in frog semitendinosus skeletal muscle. Are caveolae the mouths of the transverse tubule system? J. Cell Biol. 64:734–740 10.1083/jcb.64.3.734 [DOI] [PMC free article] [PubMed] [Google Scholar]