Elevated intracellular Ca²⁺ reveals a functional membrane nucleotide pool in intact human red blood cells

Abstract

Elevated intracellular calcium generates rapid, profound, and irreversible changes in the nucleotide metabolism of human red blood cells (RBCs), triggered by the adenosine triphosphatase (ATPase) activity of the powerful plasma membrane calcium pump (PMCA). In the absence of glycolytic substrates, Ca²⁺-induced nucleotide changes are thought to be determined by the interaction between PMCA ATPase, adenylate kinase, and AMP-deaminase enzymes, but the extent to which this three-enzyme system can account for the Ca²⁺-induced effects has not been investigated in detail before. Such a study requires the formulation of a model incorporating the known kinetics of the three-enzyme system and a direct comparison between its predictions and precise measurements of the Ca²⁺-induced nucleotide changes, a precision not available from earlier studies. Using state-of-the-art high-performance liquid chromatography, we measured the changes in the RBC contents of ATP, ADP, AMP, and IMP during the first 35 min after ionophore-induced pump-saturating Ca²⁺ loads in the absence of glycolytic substrates. Comparison between measured and model-predicted changes revealed that for good fits it was necessary to assume mean ATPase V_max values much higher than those ever measured by PMCA-mediated Ca²⁺ extrusion. These results suggest that the local nucleotide concentrations generated by ATPase activity at the inner membrane surface differed substantially from those measured in bulk cell extracts, supporting previous evidence for the existence of a submembrane microdomain with a distinct nucleotide metabolism.

INTRODUCTION

Elevated intracellular [Ca²⁺]_i in human red blood cells (RBCs) causes ATP depletion by the irreversible conversion of adenine nucleotides to IMP (Lew, 1971; Almaraz et al., 1988; Almaraz and García-Sancho, 1989). The extent and kinetics of ATP depletion depend on the magnitude and duration of the [Ca²⁺]_i increase, the absence or presence of metabolic substrates, and on a multiplicity of other factors (Lew, 1971; Arese et al., 1981; Till et al., 1981; Almaraz et al., 1988; Dagher and Lew, 1988; Almaraz and García-Sancho, 1989). ATP depletion is triggered by the ATPase activity of the plasma membrane calcium pump (PMCA; Schatzmann, 1966; Adunyah et al., 1982; Schatzmann, 1983; Kosk-Kosicka and Bzdega, 1988; Carafoli, 1992; Reusch et al., 1997); inhibition of the pump by vanadate prevents ATP depletion and IMP formation (Tiffert and Lew, 2001). Also, rapid calcium extraction by the addition of a calcium chelator to a suspension of Ca²⁺-loaded cells in the presence of ionophore instantly reverts the rate of ATP fall to that of precalcium load levels (Dagher and Lew, 1988). With the application of properly combined ionophore and Ca²⁺ concentrations in the medium, Ca²⁺ influx can be set so high that it overcomes the Ca²⁺ extrusion capacity of all RBCs in any given sample, thus loading the cells uniformly with pump-saturating [Ca²⁺]_i levels at an ionophore-determined equilibrium defined by [Ca²⁺]_i/[Ca²⁺]_o = ([H⁺]_i/[H⁺]_o)² (Ferreira and Lew, 1976; Pressman, 1976; Dagher and Lew, 1988; Lew and García-Sancho, 1989). Ionophore-mediated Ca²⁺ transport can be instantly blocked by the addition of cobalt in excess of Ca²⁺ in the medium, allowing the mean rate of pump-mediated Ca²⁺ extrusion to be directly measured (Dagher and Lew, 1988). The mean Ca²⁺ extrusion V_max of the PMCA was found to be highly variable, generally within the range of 8 to 20 mmol per liter of packed red cells per hour (mmol/Lch). Applying the cobalt method in combination with special experimental designs, it was shown that RBCs from single donors differed by over an order of magnitude in PMCA V_max activity (Lew et al., 2003). The coefficient of variation in V_max among cells from a single donor was ∼50%, largely caused by an age-related decline in pump activity by unknown mechanisms (García-Sancho and Lew, 1988; Romero and Romero, 1997, 1999; Raftos et al., 2001; Lew et al., 2007; Bookchin et al., 2009). Saturated Ca²⁺ extrusion rates may thus vary from >60 mmol/Lch in young RBCs to <4 mmol/Lch in aged RBCs. With a Ca²⁺/ATP stoichiometry of 1:1, the age-related V_max variation applies equally to PMCA-mediated Ca²⁺ extrusion and Ca²⁺ ATPase activity.

Besides the PMCA ATPase, the nucleotide changes induced by elevated [Ca²⁺]_i in RBCs are strongly influenced by two other enzymes: the adenylate kinase (AK), which buffers the reduction in ATP levels generated by ATPase activity, and the AMP-deaminase (AMPDA), which catalyzes the irreversible conversion of AMP to IMP. The combined set of reactions mediated by this three-enzyme system is

$$\begin{array}{l}\mathrm{C}{\mathrm{a}}^{2+}\mathrm{ATPase}:\mathrm{ATP}\to \mathrm{ADP}+{\mathrm{P}}_{\mathrm{i}},\\ \mathrm{AK}:2\mathrm{ADP}\leftrightarrow \mathrm{ATP}+\mathrm{AMP},\hspace{0.17em}\mathrm{and}\\ \mathrm{AMPDA}:\mathrm{AMP}\to \mathrm{IMP}.\end{array}$$

In human RBCs, AK and AMPDA have maximal activities in the order of 1–2 mol/Lch, over two orders of magnitude higher than the Ca²⁺ ATPase. Thus, AK activity maintains the distribution of [ATP], [ADP], and [AMP] within RBCs at levels determined by its equilibrium dissociation constant, K^AK = [ATP] × [AMP]/[ADP]² = ∼0.9 (Whittam, 1964). AMPDA, on the other hand, is a highly regulated enzyme, and although its V_max in RBCs is comparable with that of the AK, its actual activity level is far lower in most conditions, essentially nil in physiological conditions, because of the powerful inhibitory effects of 2,3-diphosphoglyceric acid (DPG), the normal low [Ca²⁺]_i (a powerful stimulator at higher concentrations; Almaraz et al., 1988), and the normal low concentration of its substrate, AMP (Askari, 1966; Askari and Rao, 1968; Almaraz et al., 1988; Almaraz and García-Sancho, 1989). AMPDA is activated by AMP following a sigmoid activation kinetics best fitted with a cubic power function with three hypothetical sites of equal affinity (K_AMP = ∼50 µM). 2,3-DPG is the main allosteric inhibitor of AMPDA; ATP competes with 2,3-DPG, relieving this inhibition with sigmoid kinetics. Because in the substrate-free conditions analyzed here, 2,3-DPG remained essentially constant for the brief duration of the experiments (Alvarez et al., 1988), ATP may be effectively described as an allosteric activator of the enzyme. When RBCs undergo rapid ATP depletion in the combined presence of a metabolic substrate and a glycolytic inhibitor (inosine and iodoacetamide, for instance; Lew, 1971), ATP is stoichiometrically converted to IMP, even in the absence of Ca²⁺ (Lew, 1971; Plagemann et al., 1985). In this condition, although the inhibitory effect of 2,3-DPG persists, the inhibition-relieving effects of ATP, while ATP was declining, proved sufficient to allow AMPDA-mediated IMP formation. Calcium was shown to be a powerful but indirect activator of AMPDA, effective after a small delay, by antagonizing an as yet unidentified endogenous inhibitor (Almaraz and García-Sancho, 1989).

Although ATP depletion and IMP accumulation have been well documented in the past, the precise time course of the Ca²⁺-induced nucleotide changes and the extent to which the three-enzyme system can account for them remain to be determined. This is the aim of the present study. We investigated the Ca²⁺-induced changes in ATP, ADP, AMP, and IMP in human RBCs using a state-of-the-art photodiode array detector HPLC system that provides the full absorbance spectrum of each peak, thus allowing its instant identification. The observed nucleotide changes were compared with those predicted by a model incorporating our knowledge of the kinetic behavior of the three-enzyme system. The comparison brought to light unexpected insights on possible dynamic differences between nucleotide concentrations in cell cytoplasm and in submembrane microdomains, supporting earlier proposals by Hoffman and co-workers (Parker and Hoffman, 1967; Proverbio and Hoffman, 1977; Hoffman, 1997; Hoffman et al., 2009).

MATERIALS AND METHODS

Preparation of cells

Venous blood from healthy volunteers was drawn into heparinized syringes after informed written consent. The cells were immediately washed four times by centrifugation (2,000 g for 5 min) and resuspension in ∼5 vol of solution A containing 90 mM KCl, 60 mM NaCl, 10 mM HEPES-Na, pH 7.5 at 37°C, 0.2 mM MgCl₂, and 0.1 mM Na-EGTA. The reason for the high K⁺ concentration in solution A was to prevent significant volume changes in the Ca²⁺-loaded RBCs after activation of the Ca²⁺-sensitive K⁺ channels (Kcnn4, Gardos channels; Gardos, 1958; Ferreira and Lew, 1976; Lew and García-Sancho, 1989; Tiffert et al., 2005); the high K⁺ concentration in the medium sets the K⁺ concentration gradient across the RBC membrane very near the equilibrium potential for K⁺, preventing net KCl and water shifts in the K⁺-permeabilized cells. After each spin, the supernatant and top cell layer containing white cells and platelets were removed. For nucleotide measurements, the washed cells were suspended at 20% hematocrit in solution A. CaCl₂ was added from a concentrated stock to a final concentration of 120 µM in the cell suspension. The suspension was incubated at 37°C with continuous magnetic stirring. At t = 0, the ionophore A23187 was added to this suspension, to a final concentration of 20 µM (to give 100 µmol/liter of cells assuming full partition in the cells; Simonsen and Lew, 1980; Simonsen et al., 1982). Samples for nucleotide measurements by HPLC were taken before and after ionophore addition, at the times indicated in the figures.

Processing of samples for nucleotide measurements

Using plastic-tip dispensers, 0.8-ml samples from the 20% hematocrit cell suspension were delivered deep into a microcentrifuge tube of 1.5-ml nominal capacity containing 0.3 ml of ice-cold 15% perchloric acid (PCA). The sample was mixed by sucking and delivering once or twice and was kept in the ice bath until convenient to spin. After a 2-min spin at 14,000 rpm in a refrigerated microfuge (model 5402; Eppendorf) set at 4°C, the tube was transferred back to the ice bath for further processing at convenient times. 0.8 ml PCA supernatant was transferred to a second ice-cold microfuge tube containing a 40-µl aqueous solution of methyl orange 0.05% (rose color). 100 µl of ice-cold 3 M K₂CO₃ was then added to neutralize the PCA and mixed over vortex (yellow color), and CO₂ was allowed to be released before closing the tube. The tube was centrifuged for 4 min at 14,000 rpm in the refrigerated microfuge and kept on ice. About 0.8 ml perchlorate supernatant was aspirated into a syringe using a thin needle, the needle was exchanged for a 0.2-µm filter (Millipore), the syringe contents were delivered through the filter into a new microfuge tube, and the neutralized, filtered sample was kept frozen until injected into the HPLC chromatography column. To test whether all the nucleotides had been extracted in the supernatant, dried PCA and perchlorate pellets from original cell samples were washed in minimal volumes. The optical densities at 250 nm (inosine peak) and 259 nm (adenine peak) in the wash supernatants were negligible, confirming optimal extraction in the original supernatants.

Calculation of the nucleotide content of cells

The nucleotide content of the cells, in micromoles/liter of cells (µmol/Lc), was estimated from the dilution factors during sample processing, from the recorded area under the chromatographic peaks, and from the slope of the calibration curves obtained as reported for Fig. 2. For an approximate estimate of the concentration of nucleotides in cell water (µmol/Lcw), the mean water content of the cells was assumed to be 0.75 Lcw/Lc (Lew and Bookchin, 1986; Lew et al., 1991). For model experiment comparisons, it is the pattern of nucleotide concentration changes that counts, not the precise value of the nucleotide concentrations, which can vary by as much as 30% in RBC samples from different healthy donors.

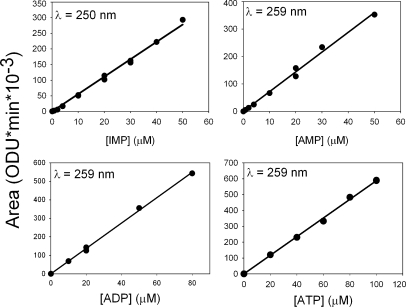
Figure 2.

Calibration curves of ATP, ADP, AMP, and IMP. The recorded peak area values (in ODUs × minutes × 10⁻³) at 259 nm for adenine nucleotides and at 250 nm for IMP are plotted as a function of nucleotide concentrations dissolved in solution A. The range of concentrations covered matched those in the RBC samples. Data are from 13 experiments, like that illustrated in Fig. 1, with different nucleotide additions.

Photodiode array detector HPLC settings

The system used comprised a photodiode array detector (model 990; Waters), a solvent delivery system (model 501; Waters), and an automated gradient controller (model 680; Waters). The eluent from the chromatography column (Partisil SAX Radial-PAK cartridge, 8 mm × 10 cm; Waters) flowed through a quartz cell of 8-µl vol and 10-mm path length, driven by a pressure gradient of 150 psi. Incident white light from a deuterium lamp, transmitted through the flow cell, was focused onto a diffraction grating, separating wavelengths from 190 to 600 nm with 2-nm resolution. The photodiode discharge was proportional to the intensity of the transmitted light. The collective diode recharge currents at each wavelength were converted into light absorption spectra identifying the nucleotide in each detected peak. Operation of the system was fully automated and software controlled, recording absorbance values (in ODU) at set wavelengths (250 and 259 nm), peak areas (in ODU × minutes × 10⁻³), and absorbance spectra for each peak set between wavelengths of 220 and 300 nm.

The three-enzyme model

Modeling was required to test whether our current understanding of the Ca²⁺ effects on red cell nucleotide metabolism was sufficient to account for the experimentally observed behavior. The model was designed to optimize comparison between predicted and observed changes in cell ATP, ADP, AMP, and IMP concentrations after Ca²⁺ loads in the absence of glycolysis. It encodes our current knowledge of the kinetics of the three relevant enzymes and the known effects of Ca²⁺ on the PMCA ATPase and AMPDA, as briefly reviewed in the Introduction. In the model, the only ATPase activity considered is that mediated by the PMCA. ATPase contributions from the Na pump or other sources were neglected because within the short duration of the present experiments, the measured decline in ATP in Ca²⁺-free cells was minimal (Dagher and Lew, 1988), Ca²⁺ loads like those imposed here cause substantial Na pump inhibition (Brown and Lew, 1983), and because in preliminary experiments, ouabain failed to elicit a detectable change in Ca²⁺-induced ATP decline, even at the saturating external K⁺ levels for the Na pump applied in these experiments. The model equations and the numerical computations are detailed in the Appendix.

RESULTS

Nucleotide measurements

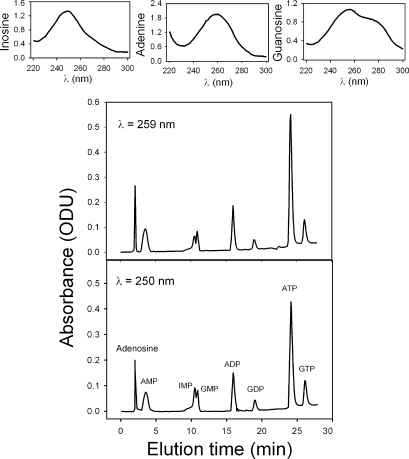
Fig. 1 reports the optical absorbance of nucleotides dissolved in medium A at 250- and 259-nm wavelengths as a function of elution time. The top panel of Fig. 1 shows the typical spectra obtained for each of the three types of nucleotides tested in this run: inosine, adenosine, and guanosine nucleotides.

Figure 1.

Elution times and UV absorption spectra of inosine, adenosine, and guanosine nucleotides in the diode array HPLC system used for the current experiments. The optical absorbance at 250- and 259-nm wavelengths is reported as a function of elution time. The nucleotides were dissolved in medium A, at concentrations within the ranges shown on the x axis of Fig. 2, to match those extracted from the RBC samples. Typical spectra obtained for each of the three types of nucleotides tested in this run are shown at the top of the figure. Results are typical of 13 similar experiments with different nucleotide additions.

Fig. 2 shows the calibration curves derived from the measurements illustrated in Fig. 1 for the four relevant nucleotides in this study. The recorded peak area values at 259 nm for adenine nucleotides and at 250 nm for IMP are plotted as a function of nucleotide concentrations. The range of concentrations covered matched those in the RBC samples, and it can be seen that linear regressions adequately fit the experimental points over such ranges.

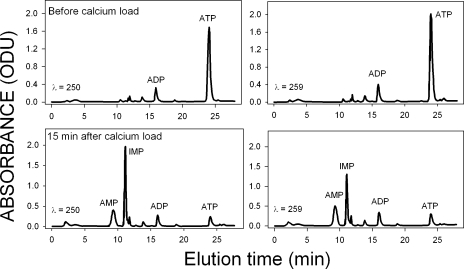
Fig. 3 shows representative chromatograms at 250 nm (left) and 259 nm (right) of nucleotides from RBC samples. Peak identities were determined by elution times and spectral characteristics. The figure illustrates the rapid and dramatic changes induced by Ca²⁺ loads on cell nucleotides in the absence of metabolic substrates. Before the Ca²⁺ load (Fig. 3, top), AK-imposed equilibrium is with a distribution following ATP >> ADP >> AMP; the AMP peak was hardly visible on this scale, although with an area clearly detectable above background, and the IMP peak area was near zero in all the samples before Ca²⁺ loading. 15 min after the onset of the Ca²⁺ load, much of the ATP had been converted to AMP and IMP, with a slight increase in ADP concentration.

Figure 3.

Nucleotide chromatograms at 250 nm and 259 nm from RBC samples, before and 15 min after a sustained PMCA-saturating calcium load. Left, 250 nm; right, 259 nm; top, before calcium load; bottom, 15 min after calcium load. RBCs were incubated in the absence of metabolic substrates. Results are representative of three identical experiments with blood from two donors.

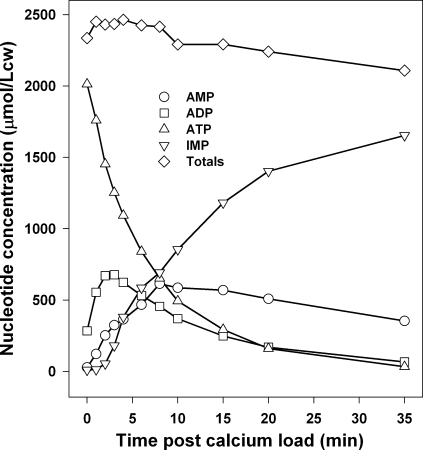
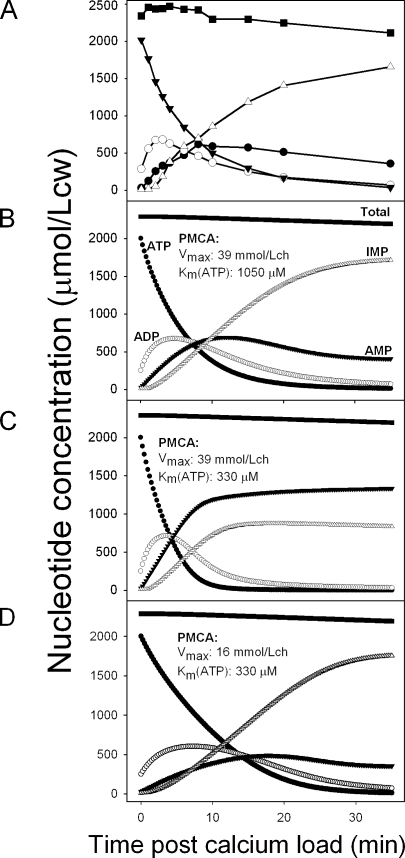
Fig. 4 shows the detailed time course of the Ca²⁺-induced nucleotide concentration changes in RBCs suspended in substrate-free medium A. This result was typical of three identical experiments with RBCs from two donors. Although the initial ATP concentration varied slightly in the three experiments, the pattern of variation was identical for all three samples and also to that recorded with lower time resolution and precision in earlier work (Arese et al., 1981; Till et al., 1981; Almaraz et al., 1988). It is important to stress that for valid comparisons with model predictions, pattern conservation is the relevant condition, irrespective of the minor differences in initial ATP levels among RBC samples.

Figure 4.

Time course of Ca²⁺-induced nucleotide concentration changes in RBCs suspended in substrate-free media. Results are representative of three identical experiments with RBCs from two donors containing slightly different initial ATP concentrations (donor 1, 2.01 and 2.11 mmol/Lcw; donor 2, 1.73 mmol/Lcw). The decline in the total nucleotide concentration is attributed to the breakdown of IMP to hypoxanthine at a rate of ∼0.2 mmol/Lch in the present experimental conditions.

It can be seen (Fig. 4) that Ca²⁺ entry initially caused a rapid fall in ATP, a rapid but limited accumulation of ADP, a slower increase in AMP, and a delayed, large, and progressive accumulation of IMP. Whereas the fall in ATP and the rise in IMP were monotonic throughout, the changes in ADP and AMP were biphasic, slow reductions after the large initial increases.

This general pattern can be interpreted as follows. The sudden Ca²⁺ load has two major effects: it activates the Ca²⁺ ATPase to Ca²⁺-saturating levels and sets the Ca²⁺-dependent component of AMPDA activity to the [Ca²⁺]_i level applied in these experimental conditions (Almaraz et al., 1988; Almaraz and García-Sancho, 1989). The initial high ATP concentration exerts its maximal antagonistic effect on the inhibition of AMPDA by 2,3-DPG, which remains fairly steady at its normal high physiological level of ∼5 mmol/Lc (Askari and Rao, 1968; Alvarez et al., 1988). However, the low initial AMP concentration keeps the initial AMPDA activity to a minimum. ATPase activity initiates a steep reduction in ATP. In the absence of AK activity, all ATP would be converted to ADP. AK activity sharply limits this conversion and transfers much of the ADP back to ATP and AMP to comply with the instant validity of the AK-imposed equilibrium [ATP] × [AMP]/[ADP]² = 0.9 throughout the experiment. The resulting increase in AMP concentration activates AMPDA, leading to a slightly delayed increase in IMP concentration. The subsequent time course of the AMP and IMP concentration changes is determined by the opposing effects on AMPDA activity of AMP accumulation (stimulatory) and ATP decline (inhibitory), by the fall in ATP on the activity of the Ca²⁺ ATPase, and by the instant buffering effects of AK on the adenine nucleotides. It is this complex and delicate balance that requires modeling to understand its mechanism, as its complexity is beyond intuitive grasp.

The three-enzyme model: Search for best-fit parameters

In its simplest formulation, the model interprets the Ca²⁺-induced nucleotide concentration changes as if taking place in a single cell, equivalent to the condition of a perfectly uniform cell population. We consider first the assumptions required to fit the experimental results for the perfect homogeneity case. The effect of the well-documented age heterogeneity of PMCA V_max is considered next.

Homogeneity.

Simulations were systematically performed to explore a wide range of parameter values for the Ca²⁺ ATPase and AMPDA, within and outside measured ranges (unpublished data). Comparisons between the experimental results and model simulations are shown in Fig. 5. The observed pattern of Ca²⁺-induced nucleotide changes is reproduced in Fig. 5 A for easy comparison. Only those results with PMCA Km(ATP) and V_max values close to those in Fig. 5 B approximated the experimentally observed pattern of Ca²⁺-induced nucleotide variation. No other combination of parameter values of ATPase and AMPDA under AK-controlled equilibrium provided satisfactory fits. Best fits were obtained with a Km(ATP) of the ATPase of >1 mM, at least threefold higher than that measured for the isolated calcium ATPase (Garrahan and Rega, 1978; Mualem and Karlish, 1979; Muallem and Karlish, 1981, 1983; Garrahan et al., 1982), and with a mean ATPase V_max of ∼40 mmol/Lch, about twice the highest mean Ca²⁺ extrusion rates measured in intact RBCs (Dagher and Lew, 1988; Lew et al., 2003). Selected misfit examples are shown in Fig. 5 (C and D) to illustrate the effects of different combinations of previously measured (V_max = ∼16 mmol/Lch and Km(ATP) = ∼0.3 mM) and best-fit parameter values (V_max = ∼39 mmol/Lch and Km(ATP) = ∼1.05 mM) and to aid in the analysis and interpretation of the results (see Discussion).

Figure 5.

Comparison between patterns of calcium-induced nucleotide changes observed experimentally and predicted by the three-enzyme-model. (A) The experimentally observed pattern shown in Fig. 4 is reproduced to aid direct visual comparisons. (B–D) Selected model-derived patterns using the Ca²⁺ ATPase V_max and Km(ATP) parameter values shown in the figures and the default values reported in the Appendix for all the other parameters of the system. The rate of IMP breakdown to hypoxanthine, which is responsible for the decline in total nucleotide concentration, was set at 0.2 mmol/Lch in all simulations. (B) Best-fit parameter values for pattern reproduction. (C) Pattern rendered when using experimentally determined Km(ATP) values at high V_max. (D) Pattern rendered when using V_max–Km(ATP) values within measured ranges.

Heterogeneity.

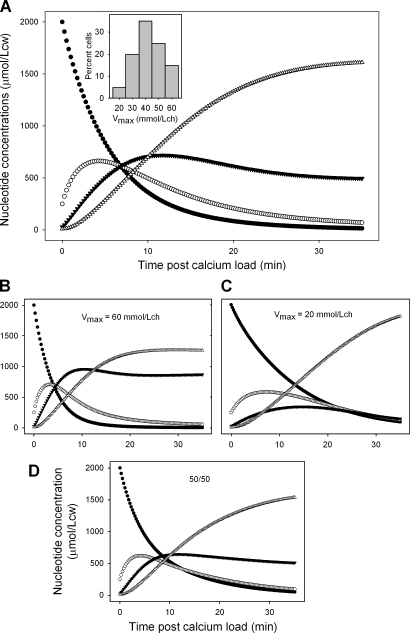
Preliminary simulations exploring distributions of different parameters indicated that the only ones that yielded patterns of nucleotide change approximating the one observed were those in which the single distributed parameter was the V_max of the PMCA ATPase at a Km(ATP) ≥1 mM (Fig. 6). The V_max distribution illustrated in Fig. 6 A (inset) follows the slightly skewed pattern that was previously described (Lew et al., 2003). However, the simulations in Fig. 6 (B–D) provide an example of extreme heterogeneity, with one half of the cells having a V_max of 60 mmol/Lch and the other half having a V_max of 20 mmol/Lch. It illustrates how very different patterns of nucleotide change in each subpopulation (Fig. 6, B and C) can deliver the observed pattern for the mean (Fig. 6 D) as long as the only parameter varied in the RBC population is the V_max of the ATPase (at Km(ATP) = 1.0 mM), with the mean V_max kept at ∼40 mmol/Lch.

Figure 6.

Predicted patterns of mean nucleotide changes in RBCs with distributed values of the Ca²⁺ ATPase V^P_max, at Km(ATP) = 1.05 mM. (A) Mean pattern obtained with the V^P_max distribution shown in the inset. (B) Pattern corresponding to a V^P_max of 60 mmol/Lch. (C) Pattern corresponding to a V^P_max of 20 mmol/Lch. (D) Mean pattern resulting from an equal mix (50/50) of the patterns in B and C. The mean V^P_max in both A and D is 40 mmol/Lch. Closed circles, ATP; open circles, ADP; closed triangles, AMP; open triangles, IMP.

The conclusion from the results in Figs. 5 and 6 is that for both homogeneous and heterogeneous conditions, good fits with the three-enzyme model require PMCA V_max–Km(ATP) values substantially above previously measured ranges for these parameters.

DISCUSSION

The aim of the current investigation was to explore the extent to which the effects of elevated intracellular Ca²⁺ on the nucleotide metabolism of human RBCs in the absence of glycolysis could be accounted for by a model of the three-enzyme system, which incorporates our current understanding of the mechanism behind these effects. Although the overall pattern of Ca²⁺-induced nucleotide changes has been described before, the lower precision of the nucleotide-measuring methods used and the lower sampling frequency in the earlier measurements were not adequate for a proper comparison between experimental results and model predictions. The HPLC measurements reported here in Fig. 4 allowed this comparison and also confirmed the general pattern described in earlier work (Arese et al., 1981; Till et al., 1981; Almaraz et al., 1988).

Simulations with the three-enzyme model consistently showed that the experimentally observed time course of nucleotide changes can only be reproduced when using unrealistically high parameters of PMCA function, 1 mM or higher for the Km(ATP) instead of the measured 0.33 mM (Mualem and Karlish, 1979; Muallem and Karlish, 1981; Rega and Garrahan, 1986) and ∼40 mmol/Lch for the mean Ca²⁺-saturated V_max of the ATPase instead of measured values from ∼8 to 20 mmol/Lch (Dagher and Lew, 1988). To seek an understanding of how measured parameters fail to explain the data, it is necessary to analyze the model predictions for the activities of the enzymes that determine the time course and magnitude of the nucleotide changes.

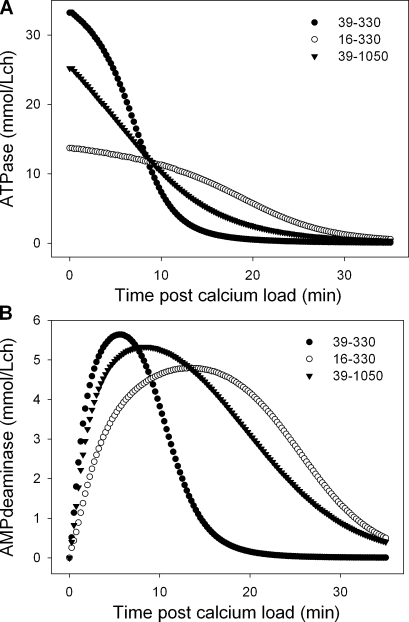
The time course of changes in ATPase and AMPDA activities predicted by the model in the conditions of Fig. 5 (B–D) is shown in Fig. 7. The analysis focuses on the V_max and Km(ATP) of the Ca²⁺ ATPase. The V_max–Km(ATP) pairs corresponding to each of the curves are indicated in the figures. It can be seen that for all parameter combinations, the Ca²⁺ ATPase activity declines with time (Fig. 7 A), as the ATP concentration falls (Fig. 4), and that the AMPDA activity changes along a biphasic pattern, early stimulation followed by late decline (Fig. 7 B).

Figure 7.

Predicted changes in Ca²⁺ ATPase and AMPDA activities as a function of time after calcium load for different values of paired V_max–Km(ATP) parameters. (A) Ca²⁺ ATPase. (B) AMPDA. The paired V_max–Km(ATP) values corresponding to each symbol (curve) are indicated in each panel.

Let us consider first the two conditions with an identical V_max of 39 mmol/Lch and different Km(ATP) values of 0.33 and 1.05 mM. The Km(ATP) influences the initial ATPase activity. At an initial ATP concentration of ∼2 mmol/Lcw and a Km(ATP) of 1.05 mM, the ATPase is only at a 64% saturation level with ATP, setting the initial ATPase activity level at 25 mmol/Lch (Fig. 7 A, triangles). With a Km(ATP) of 0.33 mM, saturation reaches 85%, and initial ATPase activity is 33 mmol/Lch (Fig. 7 A, closed circles). The higher ATPase activity at a Km(ATP) of 0.33 mM causes ATP to fall faster than with a Km(ATP) of 1.05 mM (compare ATP curves in Fig. 5, B and C). Deaminase activity, which is dependent on the inhibition-relieving effect of ATP, declines faster the faster the fall in ATP (Fig. 7 B). The time course and pattern of decline in deaminase activity is also powerfully influenced by the rate of AMP formation, which is in turn controlled by AK and ATPase activities. The combined effects on deaminase activity decline result in reduced IMP formation and a higher accumulation of AMP (Fig. 5 C) relative to the best-fit pattern (Fig. 5 B), yielding patterns of nucleotide change at variance with those observed.

In the simulation with a realistic V_max–Km(ATP) pair (16–330; Figs. 5 D and 7), the low ATPase activity (Fig. 7 A) causes a more gradual decline in ATP than in the other two conditions (Fig. 5, compare D with B and C), allowing deaminase activity to be sustained for longer (Fig. 7 B) with slower ADP formation, delayed and reduced AMP accumulation, and sustained IMP production relative to the observed pattern, resulting in a striking mismatch with the data.

This analysis shows that fitting the documented pattern of Ca²⁺-induced nucleotide changes with a model incorporating the known kinetics of the three-enzyme system imposes a restricted choice on the value of the two relevant parameters of PMCA function, well outside the range of experimentally determined values. The conclusion is that, as formulated, the model fails to account for the experimental results. It may be possible that the Km(ATP) of the Ca²⁺ ATPase in intact RBCs is indeed higher than that measured in isolated membrane preparations or resealed ghosts, but no such doubts can be entertained about the V_max discrepancy, which was directly measured in intact RBCs (Dagher and Lew, 1988). Is there a way by which an ATPase with realistic Km(ATP)–V_max values can be interpreted by the model as if operating with the elevated Km(ATP)–V_max parameter values required for good fits?

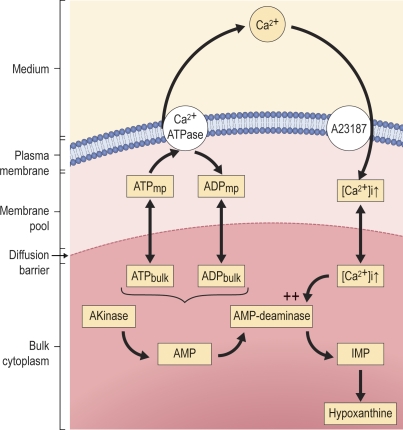
After the seminal observations of Parker and Hoffman (1967), a large body of evidence accumulated in support of the existence in human RBCs of a membrane compartment with a distinct ATP pool (perhaps ATP + ADP pool), diffusionally restricted from bulk cell nucleotides (Parker and Hoffman, 1967; Proverbio and Hoffman, 1977; Mercer and Dunham, 1981; Low et al., 1993; Hoffman, 1997; Hoffman et al., 2009). The membrane ATP pool, sustained by membrane-bound glycolytic enzymes, is considered the immediate source of energy for the sodium and calcium pumps. When depleted by pump activity, the membrane ATP pools can be refilled by glycolytic flow from membrane-bound glycolytic enzymes or by diffusion from the bulk cytoplasmic ATP pool. In the microdomain of the membrane nucleotide pool (mp), which is inaccessible to AK and to other soluble enzymes, Ca²⁺ ATPase activity would generate local concentrations of ADP and ATP such that (ADP/ATP)mp >> (ADP/ATP)bulk, as illustrated in Fig. 8 A (blue curves) for an imaginary isolated pool. The [ATP]mp/[ATP]bulk and [ADP]mp/[ADP]bulk concentration gradients would drive net diffusional flows of ATP into the pool and of ADP out of the pool. The three-enzyme model, as currently designed (see Appendix), ignores the two compartments and reads the resulting kinetics as if generated by a high V_max–Km(ATP) ATPase (Fig. 5 B and Fig. 6). A proper test of the membrane pool interpretation of the current results requires extension of the three-enzyme model to incorporate the diffusion dynamics of the membrane and cytoplasmic nucleotide pools, for which much additional experimental information would be required, extensions beyond the scope of the present study.

Figure 8.

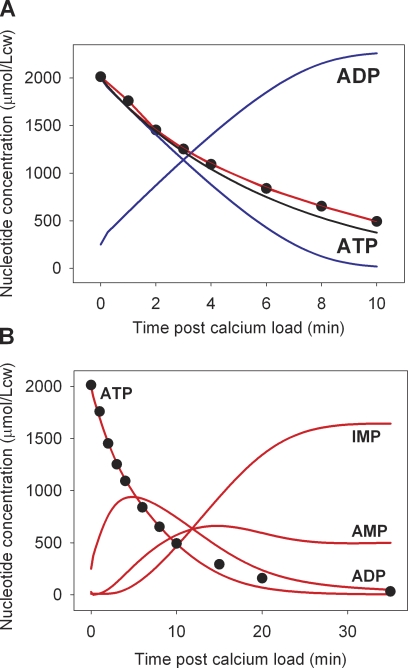
Model tests of the membrane pool interpretation of the data using ATPase parameters within measured ranges. Note the different timescales of the x axes in A and B. Red curves report the result of model simulations run with the introduction of delay factors of the form K^AK(t) = K^AK × (1 − exp[−k × t]) and V^DA(t) = V^DA × (1 − exp[−k × t]) for access of pool ATP and ADP to AK and AMPDA activities, respectively. Allowed ATPase V^P_max values were ≤20 mmol/Lch, and allowed K^P_ATP values were between 0.2 and 0.4 mM. The simulations sought values of V^P_max, K^P_ATP, and k that would provide a good fit to the measured Ca²⁺-induced ATP decline as reported in Fig. 4 (reproduced as closed circles here). The values of V^P_max, K^P_ATP, and k offering the fit shown by the red curves were 20 mmol/Lch, 0.3 mM, and 0.17 min⁻¹, respectively. (A) Comparison of model-estimated ATP decline rates with experimentally measured points (closed circles). The blue curves report the ATP and ADP concentration changes that would be generated within an isolated pool by an ATPase with the 20–0.3-V^P_max–K^P_ATP parameter values. The black curve reproduces the best fit to the ATP decline rendered by the original three-enzyme model, as shown in Fig. 5 B. (B) Overall nucleotide concentration change pattern predicted by the delay-extended three-enzyme model with the given ATPase parameters.

However, a proof of principle of the viability of the membrane pool interpretation of the current results may be obtained from a rudimentary model analysis of global delay times that may be expected for ATP and ADP equilibration between membrane pool and bulk cell cytoplasm. The question may be formulated as follows: if we assume that the ATPase activity is restricted to a membrane pool inaccessible to AK and AMPDA activities, could the incorporation of delayed access of pool ATP and ADP to cytoplasmic AK and AMPDA in the three-enzyme model allow a Ca²⁺ ATPase operating within the range of experimentally determined mean values of V^P_max and K^P_ATP account for the measured Ca²⁺-induced ATP fall and for the overall pattern of nucleotide concentration changes? To answer this question, we incorporated in the model exponential delay factors of the form K^AK(t) = K^AK × (1 − exp[−k × t]) and V^DA(t) = V^DA × (1 − exp[−k × t]) for the pool nucleotides to access AK and AMPDA activities, respectively, and explored whether acceptable parameter values for ATPase and k could be found that would provide good fits to the observed rate of Ca²⁺-induced ATP decline (Fig. 8 A) and to the overall nucleotide change pattern (Fig. 8 B).

With the search restricted to V^P_max values ≤20 mmol/Lch, a good fit to the measured ATP decline rate was obtained with a V^P_max of 20 mmol/Lch, a K^P_ATP of 0.3 mM, and a k value of 0.17 min⁻¹, equivalent to a t_1/2 of 0.693/0.17 ∼4 min (Fig. 8, closed circles and red curves). This fit compares well with the best fit obtained for the single compartment model with the 39-V^P_max, 1.0-K^P_ATP ATPase (Fig. 8 A, black curve). The delay correction, with realistic pump parameters, also provided an acceptable approximation to the observed nucleotide change pattern (Fig. 8 B). The surprisingly long half-time delay of ∼4 min, several orders of magnitude longer than that expected from unrestricted diffusion in water, suggests that the putative nucleotide pool serving the membrane transporters is somehow physically fenced off from the bulk cytoplasm, severely restricting the rate of nucleotide equilibration between the two compartments. A representation of the pool properties suggested by the analysis of the present results and by previous results in the literature (Hoffman, 1997; Hoffman et al., 2009) is shown in Fig. 9. This crude analysis then supports the plausibility of a pool explanation of the current results and prompts a search for additional intact-cell responses that could be reinterpreted as resulting from membrane pool function.

Figure 9.

A model of the membrane pool interpretation of the effects of elevated [Ca²⁺]_i on the nucleotide metabolism of RBCs in the absence of glycolytic substrates. The model portrays events related to the specific experimental protocol applied in this study. Addition of a high concentration of the Ca²⁺ ionophore A23187 established rapid Ca²⁺ equilibration across the RBC membrane, with saturating [Ca²⁺]_i levels for the PMCA. The nucleotide pool available to the Ca²⁺ ATPase is diffusionally restricted from the bulk cell cytoplasm so that Ca²⁺ ATPase activity generated a sustained [ADP]/[ATP] concentration ratio that was higher within the membrane pool than in the bulk cell cytoplasm. The AK and AMPDA enzymes are assumed to be excluded from the membrane pool and confined to the cytoplasm. AMPDA activity is highly stimulated by elevated [Ca²⁺]_i. The combined activity of the three enzymes (Ca²⁺ ATPase within the membrane pool and AK and AMPDA within the cytoplasmic compartment) generates ADP, AMP, and IMP at the expense of declining ATP along the time course and pattern documented in Fig. 4, with the minor decline in the total nucleotide content of the cells attributed to irreversible hypoxanthine formation from IMP. The likely physical localization of the functionally defined diffusion barrier in the space between inner membrane surface and cytoskeletal mesh, as suggested in previous depictions of the membrane pool (Hoffman, 1997), was left out of the diagram because the present results do not contribute any additional information on this point.

The response of intact red cells to Ca²⁺ permeabilization stress is one possible example. When a small Ca²⁺ influx is suddenly set up by addition of Ca²⁺ ionophores to RBCs suspended in a medium containing Ca²⁺, a Ca²⁺ uptake peak is generated; the sharp initial increase in Ca²⁺ content is followed by an exponential decline to a new pump–leak steady state with half-times of ∼3 min (Ferreira and Lew, 1976; Scharff et al., 1983; Scharff and Foder, 1986; García-Sancho and Lew, 1988). Further additions of ionophore or Ca²⁺ elicit further peaks until the set Ca²⁺ influx overcomes the pump capacity of all the cells. Although the peaks were shown to occur with a marked heterogeneity of Ca²⁺ content among the cells (García-Sancho and Lew, 1988), a subpopulation of cells always exhibited a biphasic response, consisting of an initial rapid but limited net Ca²⁺ uptake followed by slow Ca²⁺ extrusion. One rather elegant explanation advanced for this phenomenon was based on the kinetics of Ca²⁺-dependent calmodulin binding and activation of the pump (Scharff et al., 1983; Scharff and Foder, 1986). However, this explanation was at variance with subsequent findings that the native configuration of the pump in the membrane was dimeric (Cavieres, 1984) and that in such a configuration pump kinetics conformed to that of a calmodulin-bound pump even in the absence of calmodulin (Kosk-Kosicka and Bzdega, 1988; Kosk-Kosicka and Bzdega, 1990; Kosk-Kosicka et al., 1990). The monomers were shown to be joined through the calmodulin binding site, functioning with the kinetics of a high-V_max, high-Ca²⁺ affinity pump (Carafoli, 1994). The submembrane ATP pool offers an alternative to the calmodulin interpretation of the peak response: pump activation by the sudden increase in Ca²⁺ influx depletes the membrane ATP pool, momentarily and partially, allowing a reduced net Ca²⁺ gain. As the pool is replenished by ATP diffusion from the cytoplasm, the pump regains the extrusion capacity of a fully ATP-supplied pump capable of sustaining an increased pump–leak balance. Although the time resolution of the early measured peak responses was poor (Ferreira and Lew, 1976), peak decline half-times were clearly within the time domain of ∼4 min found for the t_1/2 of pool-bulk equilibration. Thus, as pointed out by Hoffman (1997), ATP pools in intact RBCs may function as an energy reserve for sustained ion pumping during periods of transient stress.

APPENDIX

The three-enzyme model, equations, and numerical computations

The equations and equation parameter values determine the behavior of the system in time. Its initial state is defined by the values of the nucleotide concentrations at t = 0. Initial inputs therefore require entry of parameter values and initial nucleotide concentrations. The system parameters are listed as follows, with default values corresponding to those providing the best fit of the pattern observed for the experimental protocol investigated here: V^P_max: Ca²⁺-saturated maximal mean ATPase activity, 39 mmol/Loc; K^P_ATP: Km for ATP on the ATPase, 1.05 mM; V^DA: maximal AMPDA activity set by the prevailing 2,3-DPG and [Ca²⁺]_i levels, 8 mmol/Lch; K^DA_ATP: effective Km for ATP on the AMPDA at physiological 2,3-DPG levels, 25 µM; K^DA_AMP: Km for AMP on AMPDA, 50 µM; V^H: rate of IMP to hypoxanthine conversion, responsible for total nucleotide decline, set to match the observed decline rate (Fig. 4), 0.2 mmol/Lch; and K^AK: AK equilibrium dissociation constant, 0.9.

After a sudden increase in RBC [Ca²⁺]_i (t = 0) to saturating PMCA levels, the model computes the evolution in time of the nucleotide concentrations. In the numerical computations, iteration time intervals, Δt, of between 0.2 and 1 s rendered results differing by <0.1%.

Model equations

Ca²⁺ ATPase (P).

For [ATP] and [ADP] at t = t − Δt:

$${(\Delta \left[\mathit{ATP}\right])}^P=V_{\max }^P\left(\frac{\left[\mathit{ATP}\right]}{K_{\mathit{ATP}}^P+\left[\mathit{ATP}\right]}\right)\Delta t$$

and (Δ[ADP])^P = −(Δ[ATP])^P. Then, [ATP]^t = ${\left[ATP\right]}^{t-\Delta t}$ + (Δ[ATP])^P and${\left[ADP\right]}^t={\left[ADP\right]}^{t-\Delta t}+{\left(\Delta \right[ADP\left]\right)}^P\text{.}$

AMPDA (DA).

For [ATP] and [AMP] at t = t − Δt, neglecting basal activity when [ATP] → 0 at physiological 2,3-DPG levels (Almaraz and García-Sancho, 1989) gives

$$\begin{array}{l}{(\Delta [\mathit{IMP}\left]\right)}^{DA}=\\ V^{DA}{\left(\frac{\left[ATP\right]}{K_{ATP}^{DA}+\left[ATP\right]}\right)}^2\times {\left(\frac{\left[AMP\right]}{K_{AMP}^{DA}+\left[AMP\right]}\right)}^3\Delta t\end{array}$$

and (Δ[AMP])^DA = −(Δ[IMP])^DA. Then, [AMP]^t = ${\left[AMP\right]}^{t-\Delta t}$ + (Δ[AMP])^DA and [IMP]^t = ${\left[IMP\right]}^{t-\Delta t}$ + (Δ[IMP])^DA. Total nucleotide decline through IMP → hypoxanthine conversion (H) gives (Δ[IMP])^H = −V^HΔt. The new IMP concentration at t = t is now [IMP]^t = [IMP]^t + (Δ[IMP])^H.

AK equilibrium (AK).

In each Δt interval, AK equilibrium imposes a change in adenine nucleotide concentration, z, such that 2([ADP] − z) ↔ ([ATP] + z) + ([AMP] + z). The quantity z can be computed from the equilibrium condition

$$\frac{({\left[ATP\right]}^t+z)\times ({\left[AMP\right]}^t+z)}{{({\left[ADP\right]}^t-z)}^2}=K^{AK}$$

by solving the quadratic equation in z:

$$z^2+bz+c=0\text{,}$$

$$b=\frac{{\left[AMP\right]}^t+{\left[ATP\right]}^t+2K^{AK}{\left[ADP\right]}^t}{(1-K^{AK})}\text{, and}$$

$$c=\frac{{\left[AMP\right]}^t{\left[ADP\right]}^t-K^{AK}{\left({\left[ADP\right]}^t\right)}^2}{(1-K^{AK})}$$

using the temporary concentrations for [ATP]^t, [ADP]^t, and [AMP]^t defined above and the solution z = −b/2 + ([b/2]² − c)^0.5.

The new adenine nucleotide concentrations at t = t are now given by [ATP]^t = [ATP]^t + z, [ADP]^t = [ADP]^t − 2z, and [AMP]^t = [AMP]^t + z. Total nucleotide concentration at t = t is [N]^t = [ATP]^t + [ADP]^t + [AMP]^t + [IMP]^t. This completes the computations within each Δt, ready for the next iteration step. The frequency of data outputs is set to optimize model experiment comparisons.