A Novel Approach to Dual Excitation Ratiometric Optical Mapping of Cardiac Action Potentials with Di-4-ANEPPS using Pulsed LED Excitation

Abstract

We developed a new method for ratiometric optical mapping of transmembrane potential (V_m) in cardiac preparations stained with di-4-ANEPPS. V_m-dependent shifts of excitation and emission spectra establish two excitation bands (<481 and >481 nm) that produce fluorescence changes of opposite polarity within a single emission band (575–620 nm). The ratio of these positive and negative fluorescence signals (excitation ratiometry) increases V_m sensitivity and removes artifacts common to both signals. We pulsed blue (450±10 nm) and cyan (505±15 nm) light emitting diodes (LEDs) at 375 Hz in alternating phase synchronized to a camera (750 frames-per-second). Fluorescence was bandpass filtered (585±20 nm). This produced signals with upright (blue) and inverted (cyan) action potentials (APs) interleaved in sequential frames. In 4 whole swine hearts with motion chemically arrested, fractional fluorescence for blue, cyan, and ratio signals was 1.2±0.3%, 1.2±0.3%, and 2.4±0.6%, respectively. Signal-to-noise ratios were 4.3±1.4, 4.0±1.2, and 5.8±1.9, respectively. After washing out the electromechanical uncoupling agent, we characterized motion artifact by cross-correlating blue, cyan, and ratio signals with a signal with normal AP morphology. Ratiometry improved cross-correlation coefficients from 0.50±0.48 to 0.81±0.25, but did not cancel all motion artifacts. These findings demonstrate the feasibility of pulsed LED excitation ratiometry in myocardium.

I. Introduction

Optical mapping is a well-established technique for studying the electrical and chemical dynamics of excitable tissue with high spatial and/or temporal resolution. It can be applied to scales ranging from single cells to the whole organ. It is in wide use in cardiac electrophysiology where it has provided important insights into the mechanisms of arrhythmias in normal and diseased preparations. Optical mapping utilizes optical probes, or fluorophores, that exhibit changes in fluorescence (ΔF) that correspond with changes in physiologically relevant parameters such as transmembrane potential (V_m). Fluorescence can be recorded from the surface of tissue preparations or from three dimensional arrays when excitation and emission light is delivered through optical fibers inserted in the tissue [1].

Conventional optical mapping uses single wavelength bands for both excitation and fluorescence emission. A drawback to this approach is that the signal acquired from a site is proportional not only to the parameter of interest, but to local effective dye concentration and local excitation light intensity. Dye loading is not spatially uniform and also changes in time because of compartmentalization, washout, and bleaching. Likewise, illumination intensity is likely to vary spatially. Consequently, conventional optical mapping is inappropriate for comparing parameter levels from site-to-site or for tracking slow temporal changes. In addition, in tissue such as cardiac muscle that can move, the correspondence between a photodetector pixel and the tissue it images is not constant, which results in motion artifact [2].

Ratiometric optical mapping addresses these limitations using a form of common mode rejection [3]. In ratiometry, two fluorescence signals are collected that exhibit different (usually opposing) ΔF with respect to the parameter under study. Artifacts due to the above factors are common to both signals and are therefore attenuated when the ratio of the two signals is taken. At the same time, if ΔF changes have opposite sign, parameter sensitivity is amplified. Ratiometry also allows optical signals to be calibrated to physical units. This approach is widely used in measuring intracellular calcium concentration ([Ca²⁺]_i) [4, 5] and has been reported in optical mapping of V_m in neurons [6].

The most common types of ratiometry are emission ratiometry and excitation ratiometry. In emission ratiometry, tissue is excited with a single wavelength band while two emission bands are recorded. This typically requires two photodetectors that are carefully aligned so that corresponding pixels image the same tissue. Excitation ratiometry uses two excitation bands, typically interleaved in time, but records only a single emission band. Excitation ratiometry reduces both the cost and complexity of the photodetector setup relative to emission ratiometry. However, it poses a significant technical challenge in that the excitation sources must be rapidly switched in synchrony with the photodetector. In previous studies, this has been done mechanically with such devices as filter wheels and light choppers, which limit the switching rate [6, 7].

Commercially available high-power light emitting diodes (LEDs) have recently come into use as excitation light sources. For example, they have been used with constant illumination in guinea pig auditory cortex neurons [8], swine ventricles [9] and cultured monolayers of neonatal rat ventricular myocytes [10, 11]. LEDs can be electrically pulsed at much higher speeds than traditional light sources can be switched mechanically, and therefore provide an attractive and low cost solution to implement excitation ratiometry. Pulsed LEDs in non-ratiometric mode have been used to measure V_m in cultured monolayers of neonatal rat ventricular myocytes [11] and [Ca²⁺]_i transients in human sperm [12]. Excitation ratiometry with pulsed LEDs has been used to measure [Ca²⁺]_i in cultured rat cardiac myocytes [4, 13] and spider VS-3 neurons [5]. However, a recent study that used pulsed LEDs for performing excitation ratiometry to measure V_m in cultured monolayers of neonatal rat ventricular myocytes suggested that viable ratio signals were difficult to achieve using ANEP dyes [11].

In this paper, we present the first application of excitation ratiometry to map V_m in cardiac muscle. We used pulsed LEDs for excitation light in combination with the voltage sensitive dye di-4-ANEPPS (Di-4), which is widely used in whole-heart and cardiac tissue preparations. We show that viable ratio signals can be achieved with ANEP dyes if the appropriate LED and emission filter wavelength bands are employed. We demonstrate the method in isolated perfused whole swine hearts.

II. Materials and Methods

A. Experimental Preparation

The use of experimental animals in this study was approved by the Institutional Animal Care and Use Committee at the University of Alabama at Birmingham. We studied Langendorff perfused hearts isolated from 4 domestic farm pigs of either sex weighing 34±3 kg. Details of anesthesia and heart excision are in [14]. The aortic root was cannulated and the coronary arteries were flushed with approximately 1 L of room temperature Tyrode’s solution containing (in mmol/L) 123 NaCl, 11 glucose, 0.98 MgCl2, 4.50 KCl, 1.01 NaH2 PO4, 1.80 CaCl2, and 20.00 NaH2CO3 plus bovine albumin (0.04 g/l) to reduce edema. The heart was then suspended by the aorta and connected to a constant flow perfusion system (200 ml/min) that recirculated 2 L of 37° C Tyrode’s solution bubbled with 95%O₂/5%CO₂. Electrodes for bipolar pacing and monitoring of a local unipolar electrogram were attached to the posterior right ventricle. The heart was defibrillated and after waiting approximately 15 minutes for the preparation to warm, 2,3-butanedione monoxime (BDM) was added to the perfusate (20 mM final concentration) to suppress contractions while allowing electrical activity to continue. The preparation was stained by injecting three 10 ml boluses of Di-4 dissolved in Tyrode’s solution (15 µmol/L) into the aortic cannula. Perfusion was stopped for 30 s after each injection and injections were separated by 2–4 minutes.

B. Model of Excitation/Emission Spectra for Di-4

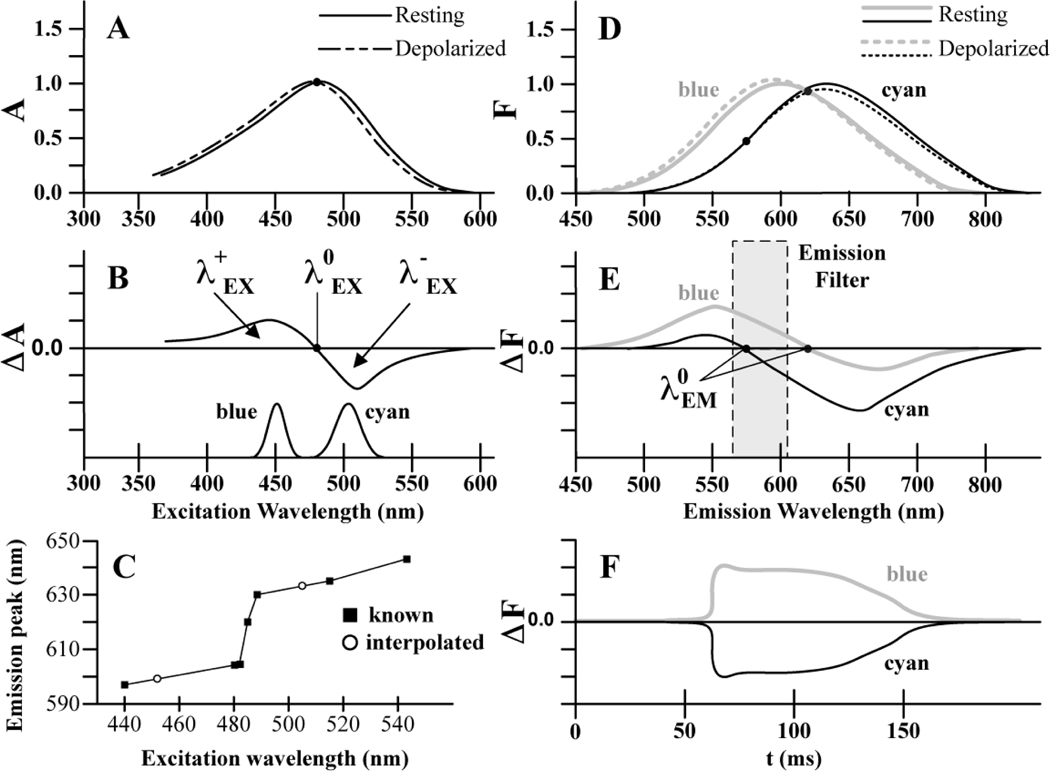
To aid selection of excitation bands and emission filters, we constructed a graphical model of the voltage sensitivity of Di-4 fluorescence using data from the literature. Our model incorporates the V_m-dependent shifts of the excitation and emission spectra that are the basis for voltage sensitivity. We represented individual spectra as skewed Gaussian functions. The Di-4 excitation spectrum for resting V_m (−90 mV) was modeled with a peak at 484 nm and inflection points (the wavelengths of steepest slope [15]) at 440 and 505 nm. This spectrum follows Fromherz and Lambacher [16] and is shown with the solid line in Figure 1A. A depolarizing change in V_m of ~+100 mV causes the Di-4 excitation spectrum to shift ~2–5 nm toward shorter wavelengths [17–19]. This spectrum is shown with the dashed line in Figure 1A. Subtracting the resting spectrum from the depolarized spectrum gives the difference spectrum, or change in absorption (ΔA), shown at the top of Figure 1B. The difference spectrum of Figure 1B has regions of positive ΔA (λ⁺_EX) and negative ΔA (λ⁻_EX) on either side of an isosbestic point (λ⁰_EX ~ 481 nm), which is where photon absorption is the same during depolarization and rest. Neglecting for the moment the voltage-sensitivity of the emission spectrum, excitation at wavelengths below λ⁰_EX should elicit positive ΔF because the dye absorbs more light during depolarization. The maximal signal is obtained from excitation in the λ⁺_EX band at ~440 nm [7, 16]. Conversely, excitation at wavelengths above λ⁰_EX should elicit negative ΔF during depolarization, with maximal signal obtained from excitation in the λ⁻_EX band at ~505 nm [7, 16]. Based on this, and the available wavelengths of high-power LEDs, we selected 450±10 nm for λ⁺_EX excitation (Luxeon rebel royal blue LEDs, Philips-Lumileds). This band (which we will refer to as “blue”) has somewhat longer wavelength than optimal, but is still within the λ⁺_EX range. For λ⁻_EX excitation, we chose 505±15 nm (Luxeon rebel cyan LEDs, Philips-Lumileds). We refer to this band as “cyan.” The power density spectra of both LEDs are shown at the bottom of Figure 1B.

Figure 1.

Model of di-4-ANEPPS voltage sensitivity (A) Vm-dependent spectral shift of excitation spectrum from Vm = rest (solid) to ΔVm = +100 mV (dashed). The black circle shows the isosbestic wavelength at which excitation is the same during depolarization and rest. (B) Difference spectrum taken by subtracting the resting excitation spectrum from the shifted excitation spectrum (top). Normalized power density spectrum for blue and cyan LEDs (bottom). (C) Emission spectrum peak as a function of excitation wavelength. Published peaks (squares) as well as peaks estimated for 450 nm and 505 nm excitation (circles) are shown. (D) Blue and cyan excitation result in two resting emission spectra (solid gray and black lines, respectively). The emission spectra undergo a Vm-dependent shift and amplitude modulation resulting from the Vm-dependent excitation shift (dashed lines). The black circles show the emission isosbestic points. (E) Difference spectra taken by subtracting the resting emission spectra from their respective shifted and amplitude modulated emission spectra. The gray box is the emission passband used in this study. (F) When emitted fluorescence is filtered with the passband shown in (E), upright OAPs result from blue excitation and inverted OAPs result from cyan excitation.

The emission spectrum of Di-4 is also voltage sensitive with a shift of the peak toward lower wavelengths occurring during depolarization. With λ⁺_EX excitation, the depolarized emission spectrum has greater amplitude than the resting spectrum because the voltage-induced shift of the excitation spectrum causes more light to be absorbed. Conversely, with λ⁻_EX excitation, the depolarized emission spectrum has lower amplitude than the respective resting spectrum. In addition, a review of published resting emission spectra shows that the peak of the resting emission spectrum increases with increasing excitation wavelength as shown in Figure 1C [7, 16–23]. Therefore, dual excitation with blue and cyan results in two resting emission spectra (solid curves in Figure 1D). From interpolation of the linear segments of the curve in Figure 1C, we modeled the resting emission spectra for blue and cyan excitation with peaks at 600 and 634 nm, respectively. Following Fromherz and Lambacher [16] and Kao et al. [18], we used a spectral half-width of 120 nm for both resting emission spectra. Depolarized emission spectra resulting from blue and cyan excitation are shown with grey and black dashed lines, respectively. Both of these spectra were constructed using a 2 nm blue shift from rest following Johnson et al. [17] and Knisley et al. [19]. We scaled the amplitudes of the two depolarized spectra relative to each resting spectrum so that each intersected at published emission isosbestic points (λ⁰_EM). These isosbestics were 620 nm for 462 nm excitation [24] and 575 nm for 505 nm excitation [21]. Difference emission spectra (depolarized minus resting) for excitation with blue and cyan are shown in Figure 1E. A fluorescence signal with positive deflections (ΔF>0) during depolarization is predicted for emission wavelengths in the 450 – 620 nm range with blue excitation. A fluorescence signal with negative deflections (ΔF<0) is predicted for emission wavelengths in the 575 – 800 nm range with cyan excitation. Recording from a single emission band in the range between 575 and 620 nm should therefore result in upright optical action potentials (OAP) for blue excitation and inverted OAPs for cyan excitation, as shown in Figure 1F.

C. Ratiometric Mapping System

The LEDs and emission passband identified above were integrated into an existing single wavelength optical mapping system. Excitation light was directed to the preparation through two bifurcated fiber optic bundles. The bundles were custom made using 0.75 mm diameter acrylic fibers (Nexxus Lighting). Each bundle had two input branches (15 mm diameter) and a single common output. Fibers from the input branches were randomized in the output branch so that light injected into either input would illuminate the preparation with approximately the same spatial pattern. The output ends of the two bundles were mounted approximately 10 cm from the preparation to produce overlapping illumination fields on the anterior left ventricle.

Blue or cyan LEDs were mounted in groups of 7 on metal core printed circuit boards (part MR16-2W-7-LUX-REB-LDLC112-S, Meodex, France). The LED boards were mounted on heat sinks and the light was shortpass filtered (525 nm) to remove residual red light. The light from each LED board was projected into one input of a fiber optic bundle using a 7-cell concentrator optic (part 140, Polymer Optics, UK). Each of the two bundles had one blue board and one cyan board. The LEDs were driven by custom made hardware that regulated drive current (up to 1 A) and enabled rapid switching between colors with digital control.

Fluorescence emission was recorded with a CCD video camera (iXon DV860, Andor Technologies) fitted with a 3 mm, F/1.0, 1/4” format lens (Pentax) and a 585±20 nm bandpass filter. This filter choice is slightly shorter than the band indicated by the model and was dictated by filter availability. The camera ran at 750 frames/s with 128 × 64 frame size. It was positioned between the output ends of the fiber bundles. At typical working distances, each pixel was ~0.5 mm square.

A 750 Hz pulse train generated by the camera was fed into a pulse generator (Pulsemaster A300, World Precision Instruments), which generated two 375 Hz pulse trains with 45% duty cycle and alternating phase. These signals were used to switch LED color with each camera frame.

D. Data Acquisition

Hearts were paced with a basic cycle length (BCL) of 500 or 600 ms. Mapping runs were 4.8 s (3600 frames) long. Excitation light was turned on for 5 s before each run to allow LEDs to warm and output to stabilize. After verifying adequate staining by recording runs with constant blue and cyan light, we recorded 2–5 ratiometric runs. In three of the four hearts, we next replaced the perfusate with fresh Tyrode’s solution that did not contain BDM. This allowed contractions to resume so that we could test the method’s ability to reduce motion artifact. The hearts were supported near the apex to minimize overall rigid-body motion (swinging and twisting) without restricting local contraction of the mapped region. We recorded an additional 3–5 ratiometric runs in this state.

The image data for each ratiometric mapping run was de-multiplexed into odd and even frames producing blue (b(t)) and cyan (c(t)) signals at each pixel. The ratio was computed according to r(t) = (b(t) - D) / (c(t) - D), where D is the signal present when the photodetector is not exposed to light.

E. Signal Characterization during Electromechanical Uncoupling

We characterized blue, cyan, and ratio recordings in the runs without heart motion (BDM present). Because only a subset of camera pixels imaged strongly illuminated myocardium, we implemented an algorithm to identify pixels containing OAPs to use in further analysis. This validation was performed on b(t) and c(t) signals that were first temporally smoothed with a 5^th order Savitzky-Golay polynomial filter with a 21 sample filtering window. This filter does not affect phase and also computes derivatives of the signal [25].

To determine if a signal contained OAPs, we first examined a window the length of the pacing BCL centered on the signal’s central frame. If the maximum change of fluorescence within the window relative to the background ((F_max-F_min)/F_min) was not at least 0.7% for both b(t) and c(t), the pixel was rejected. Phase-0 depolarization times for b(t) were then identified for the OAP in the window as the latest time before the maximum value where the fluorescence was less than half of the maximum relative to F_min. The same method, with reversed polarity, was used to identify the central depolarization time for c(t). The b(t) and c(t) depolarization times were then compared to the peaks of the first derivatives of each respective signal as well as to each other. If these times deviated by more than 10 samples, the window was changed to 75% of the cycle length about the center b(t) depolarization time with subsequent recalculation of the maximum, minimum, and depolarization times for c(t). This was done to avoid false negatives from inappropriate alignment of depolarizations in b(t) with depolarizations in c(t) from the preceding or succeeding pacing cycle. Pixels that failed this test were rejected. Each signal was then analyzed to determine whether every pacing stimulus gave rise to an OAP. This was achieved by first calculating the expected times of all other depolarizations using integer multiples of the BCL distanced from the average of the b(t) and c(t) center depolarization times. All remaining depolarization times were then compared to the peaks of the first derivative of each signal. If all first derivative maximum peaks were within a ±20 sample window of the expected depolarization times, the pixel was tagged as valid. For valid pixels, the depolarization times were recorded as the average of the b(t), c(t), and r(t) depolarization times.

Valid pixels were then characterized by the fractional fluorescence (ΔF/F) and signal to noise ratio (SNR) for b(t), c(t), and r(t). The two times where the first derivative was closest to zero within a 20-sample window about each depolarization were used to locate the baseline fluorescence (F₀) and peak fluorescence (F_p) for each OAP in each unsmoothed signal. The ΔF/F was then computed for each OAP in each of the three signals using

$$\frac{\mathrm{\Delta }F}{F}=\frac{F_p-F_0}{F_0}$$ (1)

A mean ΔF/F was then calculated for each signal by averaging over OAPs.

The SNRs for each of the three signals were also calculated for each OAP as ΔF divided by the root-mean-square (RMS) noise. RMS noise was calculated using the difference between samples and the signal’s mean over a temporal window set to 75% of the diastolic interval immediately preceding depolarization.

F. Analysis of Motion Artifact Correction

We characterized the extent of motion artifact removal in the mapping runs in which the heart was contracting (after BDM washout). We developed an algorithm similar to the one described in Section E to identify pixels with analyzable signals. We first applied an intensity threshold (1,300 analog-to-digital counts) to select well-illuminated pixels. To further validate a pixel, we smoothed and differentiated r(t) as described above and required positive peaks in the differentiated signal to occur with the same periodicity as the pacing stimulus. We further required that each such peak be within 5 ms of a positive peak in the derivative of b(t) and a negative peak in c(t). Because motion artifacts have the same polarity in both b(t) and c(t), such an alignment of first derivative peaks is likely to represent a depolarization. Pixels that did not meet these criteria were not further analyzed.

For each mapping run, a model signal, e(t), nominally free of motion artifact, was constructed by averaging 50 randomly selected pixels that showed normal cardiac action potential morphology in r(t) upon visual inspection. The 50 signals were aligned at the first depolarization before averaging. Any linear trend was removed from the e(t), b(t), c(t), and r(t) signals. To quantify the similarity between the model signal and each b(t), c(t), and r(t), the signals were initially aligned at the time of the first depolarization and the maximum cross-correlation coefficient (XC) was computed. In this calculation, the range of lags of the cross correlation function was limited to one pacing interval (±BCL/2). The model signal was inverted when cross-correlating with c(t).

III. Results

A. Signal Characteristics during Electromechanical Uncoupling

We analyzed 5 mapping runs from each of 2 animals, 4 runs from the third animal, and 2 runs from the fourth. There were a total of 8,092 valid pixels containing a total of 70,481 OAPs. Data are presented as mean ± std.

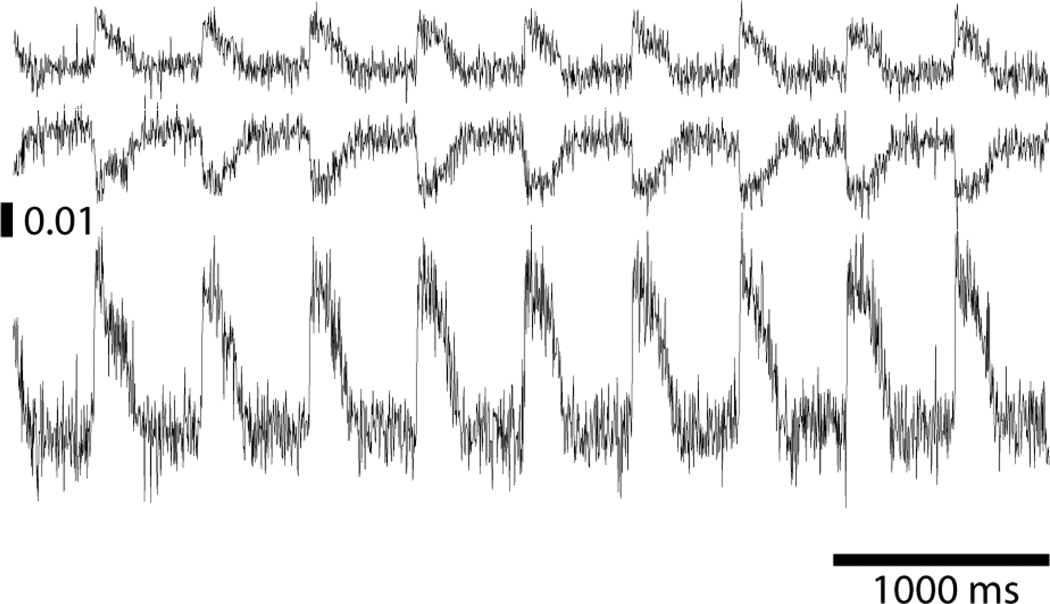
Example blue- and cyan-elicited signals (b(t) and c(t)) de-multiplexed from a pixel in the center of the mapped region are shown in the top two panels of Figure 2. OAPs are upright in b(t) and inverted in c(t). The corresponding ratio signal, r(t), is shown in the bottom panel. ΔF/F for OAPs in the signals shown in Figure 2 were 1.2% for b(t), 1.5% for c(t), and 3.1% for r(t). The SNRs for these signals were 3.2, 4.6 and 5.5, respectively.

Figure 2.

Example signals. Top: Blue-elicited fluorescence. Middle: Cyan-elicited fluorescence. Bottom: Ratio signal. The vertical scale bar indicates ΔF/F.

The ΔF/F averaged over all motion-arrested OAPs we recorded was 1.2 ± 0.3% for blue signals, 1.2 ± 0.3% for cyan signals, and 2.4 ± 0.6% for the ratios. The maximum and minimum recorded ΔF/F for the r(t) over all pixels were 4.4 and 0.7%, respectively. SNR averaged over all motion-arrested OAPs we recorded was 4.3 ± 1.4 for blue signals, 4.0 ± 1.2 for cyan signals, and 5.8 ± 1.9 for the ratios, with maximum and minimum r(t) SNRs of 13.9 and 1.6, respectively.

We used ANOVA to compare mean ΔF/F for all OAPs from b(t), c(t), and r(t) signals. As expected, there was a highly significant difference between the groups (p<0.0001). Post-hoc analysis showed that ΔF/F from blue and cyan signals both differed significantly from the ratio signals. A similar analysis with the mean SNR data returned the same results. Ratiometric signals are expected to display improved parameter sensitivity and noise because each temporal sample contains more information than either component signal alone.

B. Ratiometric Correction of Motion Artifacts

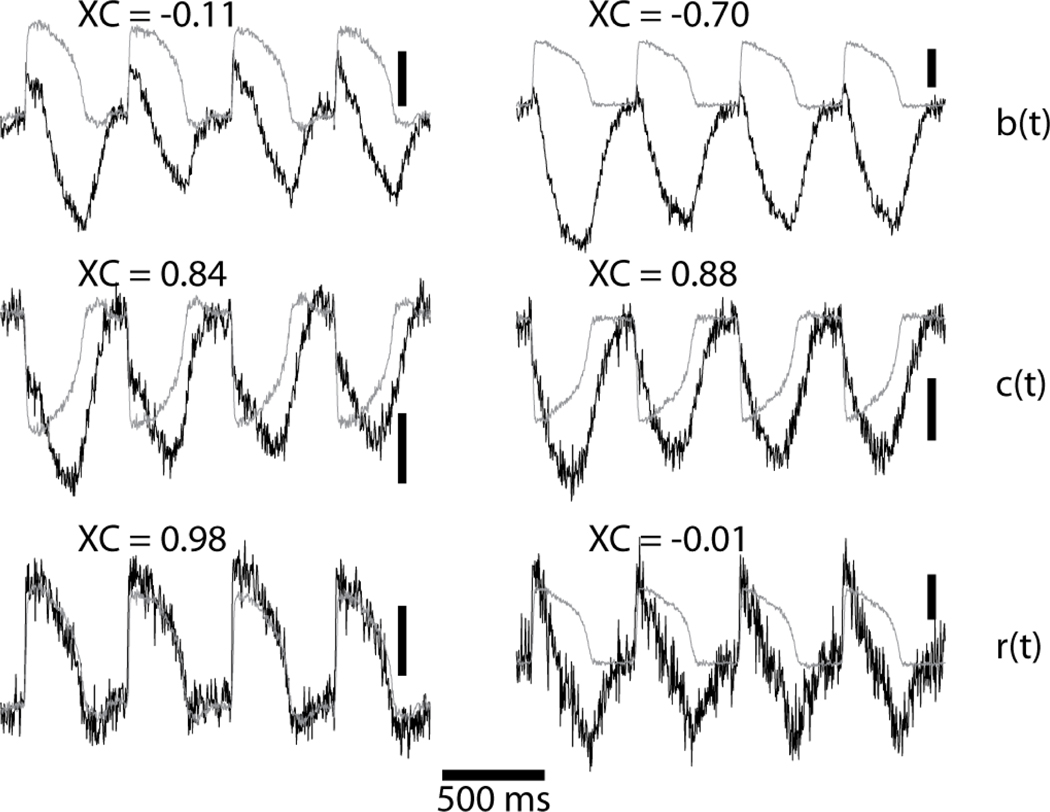
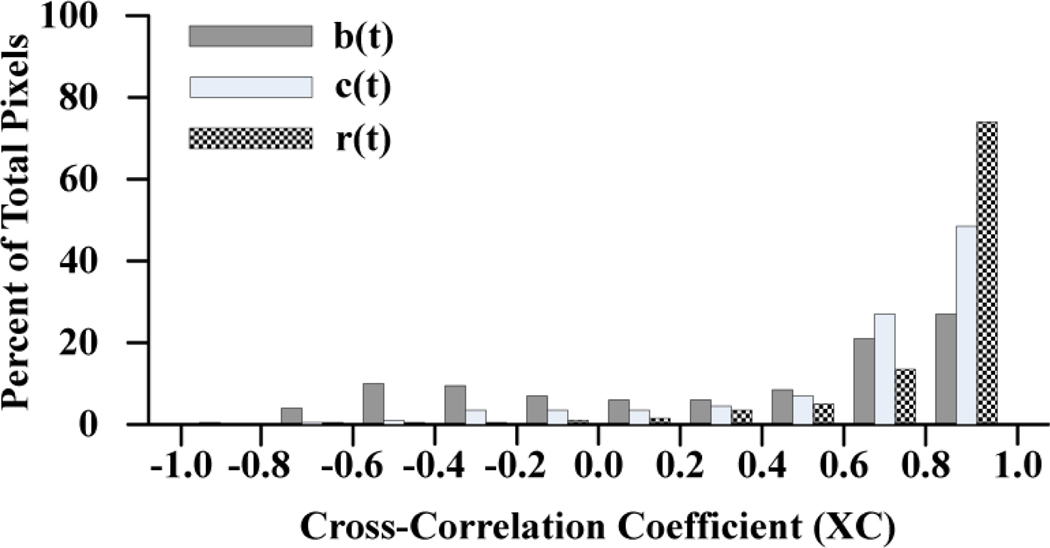
We computed XC for b(t), c(t), and r(t) for each valid pixel from 3 hearts after contractions resumed following BDM washout (3, 4, and 5 runs per heart, respectively). There were a total of 11,259 valid pixels. For comparison, we used the same algorithm to validate pixels and compute XC for the r(t) signals recorded from the same 3 hearts before BDM washout (11,994 valid pixels). Signals from 2 pixels together with their respective model signal, e(t), are shown in Figure 3. Motion correction was largely successful for the pixel on the left side of the figure with a final XC in the ratio signal of 0.98. However, this success was not achieved in all pixels. The ratio signal on the right has markedly abnormal morphology and XC of −0.01. The distributions of XC values for b(t), c(t), and r(t) in the beating hearts are shown in Figure 4. We used ANOVA to compare XC among the 4 groups (b(t), c(t) and r(t) beating; r(t) not beating). There was a highly significant difference (p<0.0001). Post-hoc analysis showed: (1) Mean XC for the ratio signals in the beating state (0.81±0.25) was significantly less than XC for the ratio signals while the hearts were not beating (0.84±0.14). (2) In beating-heart recordings, mean XC for the cyan- and blue-elicited signals were both significantly less than XC for the ratio signals (0.65±0.37, 0.34±0.53, and 0.81±0.25, respectively). Together, these data indicate that while ratiometry reduces motion artifact in many cases, it is not universally effective.

Figure 3.

Successful (left column) and unsuccessful (right column) correction of motion artifact. The model signal, e(t) is gray. XC is the cross-correlation coefficient between the respective gray and black signals. The vertical scale bars are 2% of background fluorescence.

Figure 4.

Histogram of cross-correlation coefficients of model signal e(t) with blue-elicited b(t) (dark), cyan-elicited c(t) (light), and ratio r(t) (hatched) signals from beating hearts.

IV. Discussion

An important limitation of conventional optical mapping of V_m is that fluorescence is dependent not only on V_m, but also on local effective dye concentration and excitation light intensity. This makes it difficult to calibrate V_m recordings or to detect changes that occur over time scales longer than an action potential. It is well known that this limitation can be greatly lessened by simultaneously acquiring fluorescent signals with differing voltage sensitivity, but similar artifact. This allows the common artifact to be arithmetically cancelled, usually by taking a ratio of the component signals [3, 19, 26]. To date, ratiometric V_m mapping studies in myocardium have excited the dye with a single wavelength and recorded two emission wavelengths (emission ratiometry) [3, 19, 26]. This method requires two photodetector pixels for each recording site.

In this report, we describe an excitation ratiometry method using the voltage-sensitive dye di-4-ANEPPS. To our knowledge, this is the first application of excitation ratiometry to V_m mapping in cardiac muscle. We demonstrate that when fluorescence emission is bandpass-filtered between 565 and 605 nm, blue (450 ± 20 nm) LED excitation produces upright OAPs and cyan (505 ± 30 nm) LED excitation produces inverted OAPs. As in conventional emission ratiometry, the ratio of the upright and inverted signals features improved ΔF/F and SNR relative to the component signals.

Excitation ratiometry has the advantage that it requires only one photodetector and is therefore significantly less expensive to implement than emission ratiometry. It is also simpler to implement because there is no need to align the photodetectors so that corresponding pixels image the same tissue. Both of these factors become especially important if ratiometry is desired in a system that images the heart from multiple viewpoints (e.g., panoramic optical mapping [9]). An important disadvantage of our excitation ratiometry implementation is that temporal resolution is half of the camera frame rate because two fluorescence signals are multiplexed into each recording channel. We anticipate that this method will be useful in the same applications that have previously employed emission ratiometry. It also expands the design options for future cardiac optical mapping studies that could involve the simultaneous use of fluorescent indicators for multiple physiological parameters.

A. Spectral Scheme for Excitation Ratiometry

The design of our system was guided by the model of Di-4 voltage sensitivity shown in Figure 1. The model was pieced together from studies in lipid vesicles and various types of excitable tissue using both Di-4 and di-8-ANNEPS, a structurally and functionally similar fluorophore [6]. The key wavelengths in Figure 1 are the isosbestic point for excitation (λ⁰_EX) and the emission isosbestic points (λ⁰_EM) for our chosen excitation wavelengths of 450 nm and 505 nm. The former was taken from difference spectra published by Montana et al. [7], and the later two from ΔF/F spectra (zero crossing of ΔF/F = emission isosbestic point) published by Fluhler et al. [24] and Hayashi et al. [21], respectively. The excitation and emission spectra that give rise to the difference spectra in Figure 1B, E are often inconsistent in the literature. The peak of the excitation spectrum is variously reported as 466 nm [7, 20, 21] or 484 nm [16]. We chose to model our excitation spectrum using a peak of 484 nm because 466 nm is less than the isosbestic point (481 nm). For an excitation peak to be consistent with an isosbestic point with a longer wavelength, depolarization must cause an increase in the amplitude of the excitation spectrum as well as a shift to shorter wavelengths. The peak of the emission spectrum has also been variously reported to lie between 595 nm and 640 nm [7, 16–23]. Interestingly, these published emission spectra peaks have an approximately sigmoid relationship with the excitation wavelength used to acquire them (Figure 1C). We used this relationship to estimate the emission peaks for the excitation wavelengths we employed.

The fact that we were able to obtain upright and inverted OAPs using the excitation and emission bands shown in Figure 1 indicates that the difference spectra in panels B and E are approximately correct. Detailed knowledge of difference spectra that are specific to myocardium and the dye being used would allow excitation and emission bands to be more finely optimized. For example, the 40 nm-wide emission band we used admits much less of the total fluorescence than 610 nm longpass or 585 nm shortpass filters, which are often used for emission ratiometry. This partly explains why maximum SNR in emission ratiometry studies (e.g., ~50 in Knisley et al. [19]) are larger that those we report (~14). Widening our emission band without causing upright and inverted OAPs to cancel would likely improve signal quality.

Entcheva et al. suggested that V_m excitation ratiometry with ANEP dyes was possible in principle; however, they were unable to observe upright OAPs when exciting with several wavelengths between 365 nm and 535 nm [11]. This may have been because they used longpass rather than bandpass emission filters, which would allow light above the emission isosbestic points associated with their excitation bands to reach the photodetector. Such light would contain inverted OAPs that could cancel the upright OAPs contained in shorter emission wavelengths.

B. Ratiometry and Motion Artifacts

Ratiometry (and conceptually similar subtraction schemes) are often put forth as a means to remove motion artifact (e.g., [3, 19, 26]). Motion artifact occurs when the correspondence between mapped tissue and photodetector pixel changes with time. The main sources of V_m distortion in this situation are (1) heterogeneous effective dye concentration and (2) heterogeneous/out-of-phase action potentials along the trajectory of tissue imaged by a particular pixel. The first source of error is common in both component signals and can be cancelled by ratiometry. However, the second is not, and a ratiometric signal from a moving heart will contain a mixture of action potentials encountered along the imaged trajectory. If activation is locally synchronous, then no motion artifact will be evident. It is likely that this is the reason our method was able to remove motion artifact in some, but not all signals. We believe that ratiometry by itself should be viewed as a way to attenuate motion artifact when the activation pattern is simple and motion is modest, but not as a comprehensive solution.

On the other hand, ratiometry may have more potential for motion correction if used in combination with other techniques. For example, suppose a motion-tracking scheme were used to collect fluorescence from a fixed patch of tissue as it moved with respect to the photodetector. In this scenario, the above two sources of error would largely be removed. Unfortunately, in the absence of complete spatial uniformity of excitation light, the excitation light incident on the moving recording site would vary with time, introducing a new source of signal distortion. However, this artifact would be common to both component signals and therefore subject to ratiometric correction.

Biographies

Andrew D. Bachtel received B.S. degrees in Electrical Engineering and Biology from the University of Alabama in Huntsville, Huntsville, AL, in 1996 and 2008, respectively. He received the M.S. in Biomedical Engineering from the University of Alabama in Birmingham in 2010. He is currently working as an engineer in the medical device industry.

Richard A. Gray received the B.S. degree in chemical engineering from Bucknell University in 1986. He received the M.S. and Ph.D. degrees from the University of Virginia, Charlottesville, in 1990 and 1993, respectively. He is a Biomedical Engineer at the Food and Drug Administration in Silver Spring, MD. His research is focused the mechanisms of cardiac fibrillation and its termination in relation to cardiac pacemakers and defibrillators using experimental, numerical, and theoretical approaches.

Jayna M. Stohlman received her BS degree in 2003 and her MSE degree in 2004, both in Biomedical Engineering from Tulane University. She is a Biomedical Engineer at the Food and Drug Administration in Silver Spring, MD in the Office of Science and Engineering Laboratories. Her research is currently focused on the topics of heart failure and mechanisms of arrhythmia induction and defibrillation.

Elliot B. Bourgeois received the B.S, M.S., and Ph.D. degrees in Biomedical Engineering from the University of Alabama at Birmingham in 2004, 2006, and 2010, respectively. He is currently a postdoctoral fellow at the Children's Hospital of Philadelphia. His current research interests include the use of optical mapping to investigate abnormalities in neural network inhibition in a developmental model of epilepsy.

Andrew E. Pollard received the B.S., M.S., and Ph.D.degrees in Biomedical Engineering from Duke University, Durham, NC in 1983, 1985 and 1988, respectively. He is a Professor of Biomedical Engineering at the University of Alabama at Birmingham. Dr. Pollard's primary research interests are in the study of cardiac arrhythmias, with particular emphasis on numerical modeling and experimental mapping

Jack M. Rogers received the B.S., M.S., and Ph.D. degrees in Bioengineering from the University of California, San Diego, in 1986, 1990, and 1993, respectively. He is an Associate Professor of Biomedical Engineering at the University of Alabama at Birmingham. His current research interests include the development of new cardiac mapping techniques and their application in studying the mechanisms of cardiac arrhythmias.