Mesoscale Simulations of Two Nucleosome-Repeat Length Oligonucleosomes

Abstract

The compaction of chromatin, accessed through coarse-grained modeling and simulation, reveals different folding patterns as a function of the nucleosome repeat length (NRL), the presence of the linker histone, and the ionic strength. Our results indicate that the linker histone has negligible influence on short NRL fibers, whereas for longer NRL fibers it works like, and in tandem with, concentrated positive counterions to condense the chromatin fiber. Longer NRL fibers also exhibit structural heterogeneity, with solenoid-like conformations viable in addition to irregular zigzags. These features of chromatin and associated internucleosomal patterns presented here help interpret structural dependencies of the chromatin fiber on internal and external factors. In particular, we suggest that longer-NRL are more advantageous for packing and achieving various levels of fiber compaction throughout the cell cycle.

Introduction

Chromatin structure

The 30×10⁹ nucleotide base pairs in each human cell are densely packed within the nucleoprotein complex that forms the chromatin fiber. The detailed architecture of the chromatin fiber, not to speak of its dynamics and energetics, have occupied experimental and theoretical scientists for decades. With recent discoveries of a nucleosome positioning code,¹ the need to understand chromatin organization has intensified, because the structural puzzle that explains nucleosome, and hence chromatin organization, underlies the most basic cellular functions, including transcription activation, gene silencing, and epigenetic control.^2,3

Nucleic acid simulations

While all-atom simulations of nucleic acids have steadily increased in accuracy, scope, and length (e.g., microsecond simulations of solvated B-DNA dodecamer⁴), coarse grained models are required to simulate macromolecular systems that are very large and highly dynamic, requiring sampling of millions of configurations to represent behavior over millisecond time frames. Creation of such general multiscale or coarse grained models requires as much art as science, to resolve key functional components of the molecular system while approximating others. Examples of such tailored models include various models of macromolecular assemblies of membrane systems^5–7 and simplified models of the chromatin fiber.^8–11

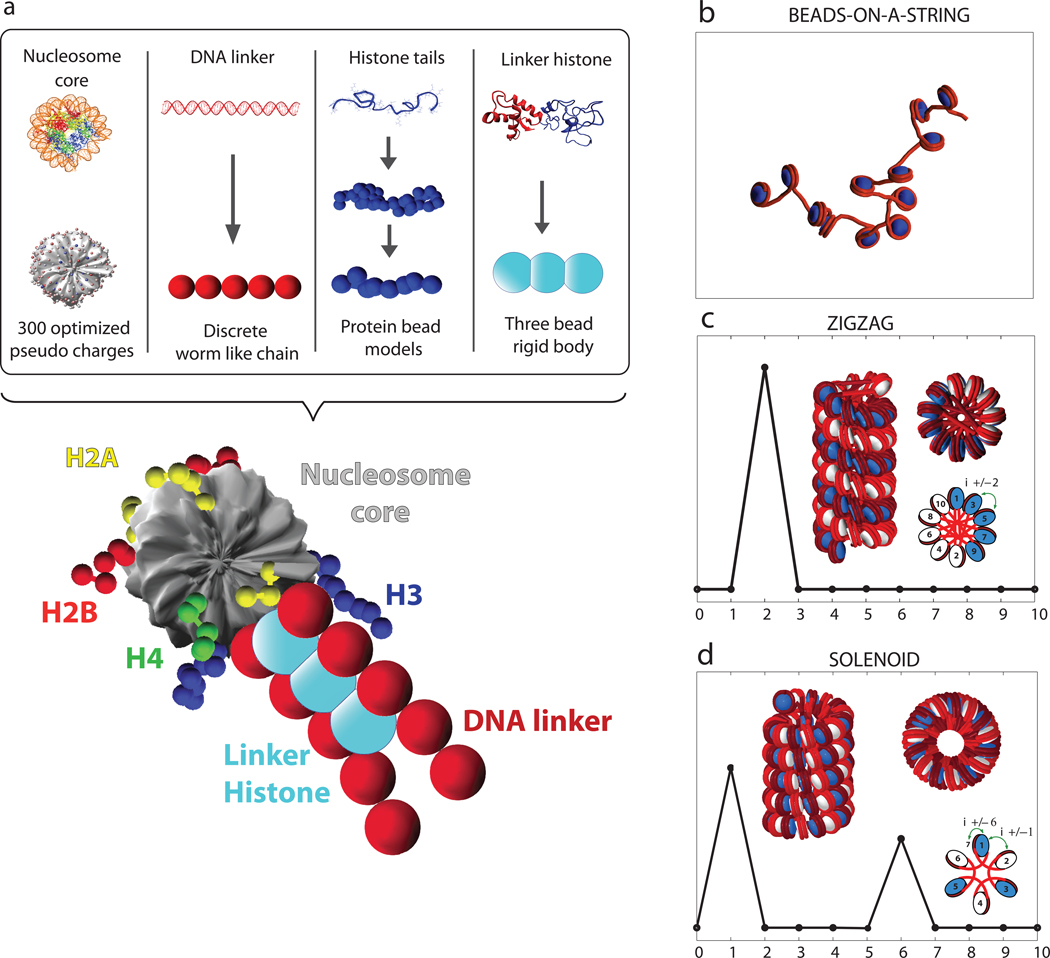
The chromatin fiber is made up of the nucleosome core particle building block which organizes 147 bp of DNA in a left-handed supercoil around an octamer of four core histone proteins (H2A, H2B, H3, and H4).^12,13 Nucleosomes are connected by linker DNA, and various linker histones can bind as well as dissociate with the polymer (Fig. 1).

Figure 1. The mesoscale model and basic chromatin fiber structures.

a) The mesoscale model of the basic chromatin building block. b) Beads-on-a-string fiber structure at low monovalent salt (0.01 M). c) An ideal zigzag configuration of the chromatin fiber with the nucleosome contact pattern. d) An ideal solenoid configuration of the chromatin fiber with the nucleosome contact pattern.

The chromatin structure puzzle

One of the current problemns that chromatin researchers address is elucidation of the 30 nm chromatin fiber architecture. As described in recent reviews (e.g.,^14,15), the detailed structure of the chromatin fiber has remained controversial for over three decades, with evidence supporting both zigzag (“two-start”) and solenoid (“one-start”) models (see Fig. 1) coming from various sources, including X-ray crystallography and electron microscopy. Only recently, have researchers begun to dissect the influence of key internal and external factors such as length of the connecting DNA segments between nucleosomes (which can vary from 10 to 70 bp), the binding of linker histones, and the presence of various concentrations of monovalent and divalent ions on chromatin structure.

For example, a crystallographic structure of the tetranucleosome¹⁶ with short linker DNAs between nucleosome and without linker histones produced irrefutable evidence for the zigzag model, in which DNA linkers are straight, and alternate nucleosomes (i±2) are in closest spatial proximity (Fig. 1). However, electron microscopy of reconstituted fibers with long linker DNAs and with linker histone and divalent ions produced strong evidence for the opposite, solenoid, model in which linker DNAs are strongly bent and nucleosomes crisscross one another, bringing neighboring nucleosomes and neighbors 5 or 6 nucleosomes away in close proximity (i±5, i±6)¹⁷ (see Fig. 1). More recently, Rhodes and colleagues continued to show that, depending on the linker DNA length and presence of linker histone, different fiber dimensions are produced; in particular, short linker DNAs cannot produce compact fibers.¹⁷ Modeling by Wong et al¹⁸ also showed the dependence of fiber width on the nucleosome repeat length (NRL) and the orientation of linker histones. Modeling of simplified coarse-grained nucleosome models by the Rippe group reinforced the large effect of the NRL and nucleosome twist angles on the extent of fiber compaction.¹⁰ More recently, single-molecule force microscope studies¹⁹ subjecting 25-nucleosome arrays with two NRL (167 and 197 bp) to forces up to 4 pN suggested a fundamental solenoid organization, stiffer fibers with short NRL, and only a stabilizing but not structure-determining effect of the linker histone.

Our mesoscale modeling of chromatin

Over the past several years, our group has developed a mesoscale model of chromatin (Fig. 1) in which the nucleosome, excluding the histone tails, with wrapped DNA is treated as an electrostatically charged object with Debye-Hückel charges approximating the atomistic electric field computed by the Poisson-Boltzmann equation using the DiSCO (Discrete Surface Charge Optimization) algorithm.^20,21 Linker DNA is treated as beads in the wormlike chain model used for supercoiled DNA, and linker histones and histone tails are coarse grained by beads from united-atom protein model. All the components are flexibly attached using parameters derived from experimental measurements. Full model and Monte Carlo simulation details, including model validation and various applications, were recently summarized in Arya and Schlick,¹¹ where the role of histone tails in compacting fiber structure was analyzed. A Methods section here summarizes key features for easy reference. A recent collaborative study with experimentalists probed nucleosome interaction patterns with and without linker histone, and with and without divalent ions, to dissect how each factor affects chromatin structure.²² These studies showed that linker histones tighten and strengthen an ordered zigzag fiber structure, and that divalent ions lead to bending of some linker DNAs to produce a zigzag fiber accented with solenoid-like features; the latter organization allows a more compact overall fiber. These studies thus give support for the both solenoid and zigzag models; moreover, they underscore the heterogeneous and polymorphic nature of the chromatin fiber.

A study of two NRL

In this communication, we report on structural features of the chromatin fiber at two different nucleosome repeat lengths: 173 and 209 bp; the former has NRL close to the value used in the tetranucleosome (167 bp),¹⁶ while the latter is a typical value of chromatin fibers occurring in Nature. Besides varying the NRL, we also consider the presence and absence of the linker histones and the presence and absence of divalent ions. Divalent ions are modeled as depicted in Ref.²² by a first-order approximation by reducing the DNA persistence length from 50 to 30 nm and by setting the Debye length of the linker DNA beads to the DNA diameter (2.5 nm), to allow beads to touch one another (see also Methods). We sample 12-oligonucleosome fibers at the two NRL values at two salt conditions: typical monovalent salt (0.15 M), and monovalent salt (0.15 M) as well as low concentrated divalent ions. The two NRL values at both salt conditions are sampled with and without linker histone. Configurations are sampled with local and global Monte Carlo moves as described recently.¹¹ The only change in the model required to account for the different NRL is the different twist between nucleosomes. For our standard model of 6 DNA linker beads (7 segments) or NRL of 209 bp, 6 full turns of DNA occur, but for the short, 173 bp NRL of 2 beads (3 segments, 9 nm, or 26.47 bp), 2.57 DNA turns occur. The difference from an integral number of turns (0.43) is accounted for as twisting energy penalty of 0.43 × 360°/26.47 = 6°per base pair or a total twist of 155° over the entire 26-bp segment of linker DNA.

For each system (NRL, salt condition, with and without linker histone), we conducted 24 simulations on 12 core arrays with 10 million Monte Carlo steps per trajectory; 12 simulations were started from the zigzag starting structure and 12 from the solenoid. Of these 12 simulations, three different intrinsic DNA twist values were sampled (0, ±12° about the mean), to account for small variations of the DNA twist from one nucleosome to the next, with four different random seeds each. The last 2 million steps per trajectory were included in the statistical analysis. For visualization of compact fibers, simulations of 24-core arrays started from the final configurations of the 12-core systems were also performed. Analysis techniques follow those previously developed;^11,22 see also Methods section here for additional details on computing the nucleosome/nucleosome interaction patterns of core/core interactions, sedimentation coefficients, fiber widths and packing ratios.

Results

Fiber packing

Table 1 shows the various sedimentation coefficients, packing ratios (# nucleosomes per 11 nm), and fiber widths for the short and regular NRL values. The packing ratio is calculated as the number of nucleosomes divided by the fiber length and multiplied by 11. A linear regression in all three coordinate axes was used to calculate the fiber length for each analyzed simulation frame (see Fig. S4).

Table 1.

Fiber properties at the two NRL (nucleosome repeat length) values (in base pairs).

	NRL	Sed. coeff. (S)	Nucl./11nm	Fiber width (nm)
− LH	173	51.13 ± 1.46	3.48 ± 0.37	20.48 ± 5.29
monovalent salt	209	42.15 ± 2.04	3.25 ± 0.76	25.26 ± 10.25
+LH	173	54.95 ± 1.35	3.99 ± 0.35	19.57 ± 5.02
monovalent salt	209	49.14 ± 2.97	5.74 ± 1.18	26.10 ± 9.16
− LH	173	50.10 ± 2.27	3.31 ± 0.42	20.15 ± 5.55
monovalent salt & Mg	209	48.56 ± 3.34	6.82 ± 1.54	25.26 ± 10.26
+LH	173	50.61 ± 2.10	3.56 ± 0.65	20.97 ± 5.96
monovalent salt & Mg	209	48.57 ± 4.21	5.65 ± 2.00	24.88 ± 11.09

We note a large difference in sedimentation coefficients for the longer NRL. The linker histone has a limited effect on short NRL fibers (173 bp), as seen in the nominal increase of the sedimentation coefficient, packing ratio, and fiber width.

The effect of Mg²⁺ on the packing ratio in short NRL fibers is not large. In contrast, the ion concentration and the presence of the linker histone have a strong compaction effect on the longer NRL (209 bp), as evident by the increase of the average sedimentation coefficient and of the packing ratio. The fiber width for the longer NRL is smaller than the experimentally measured values,^17,23 which reflected highly concentrated divalent ions.

Fiber architecture

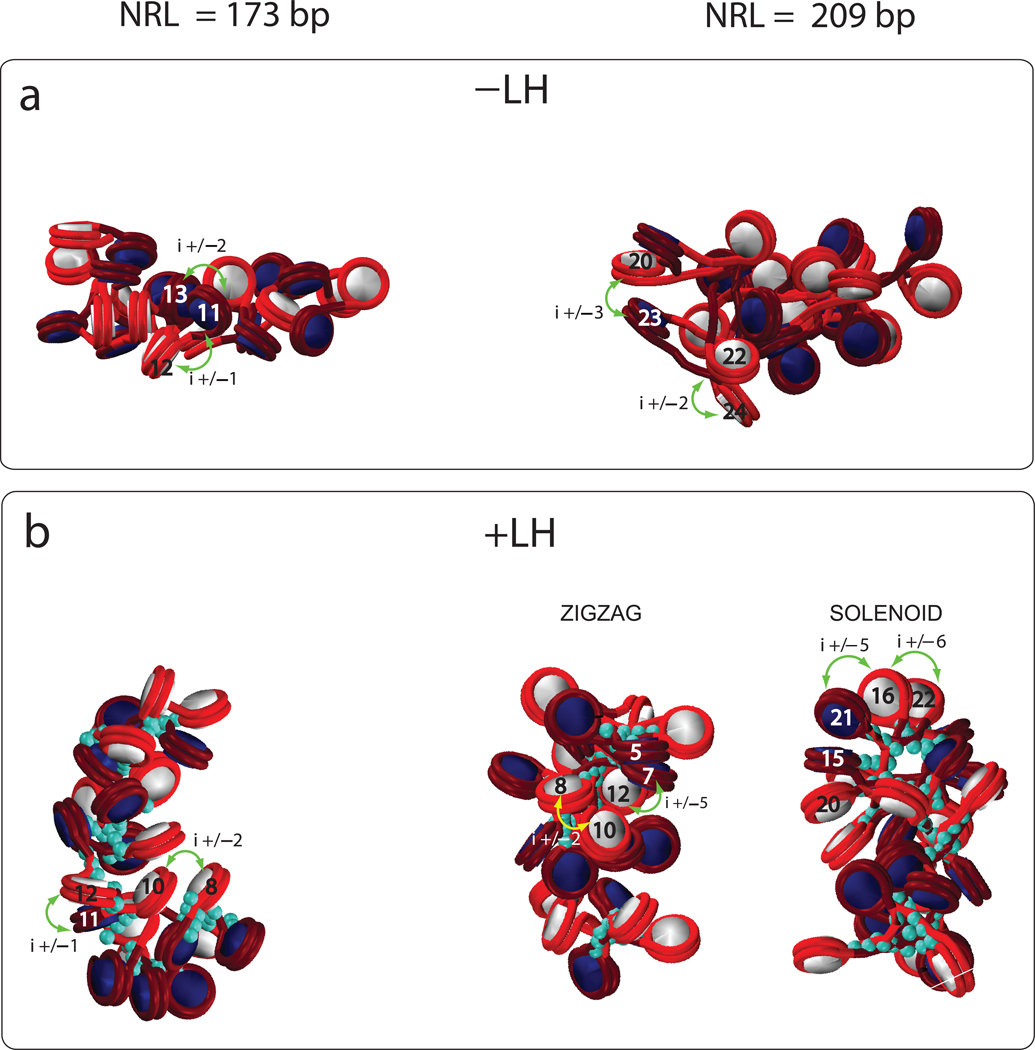
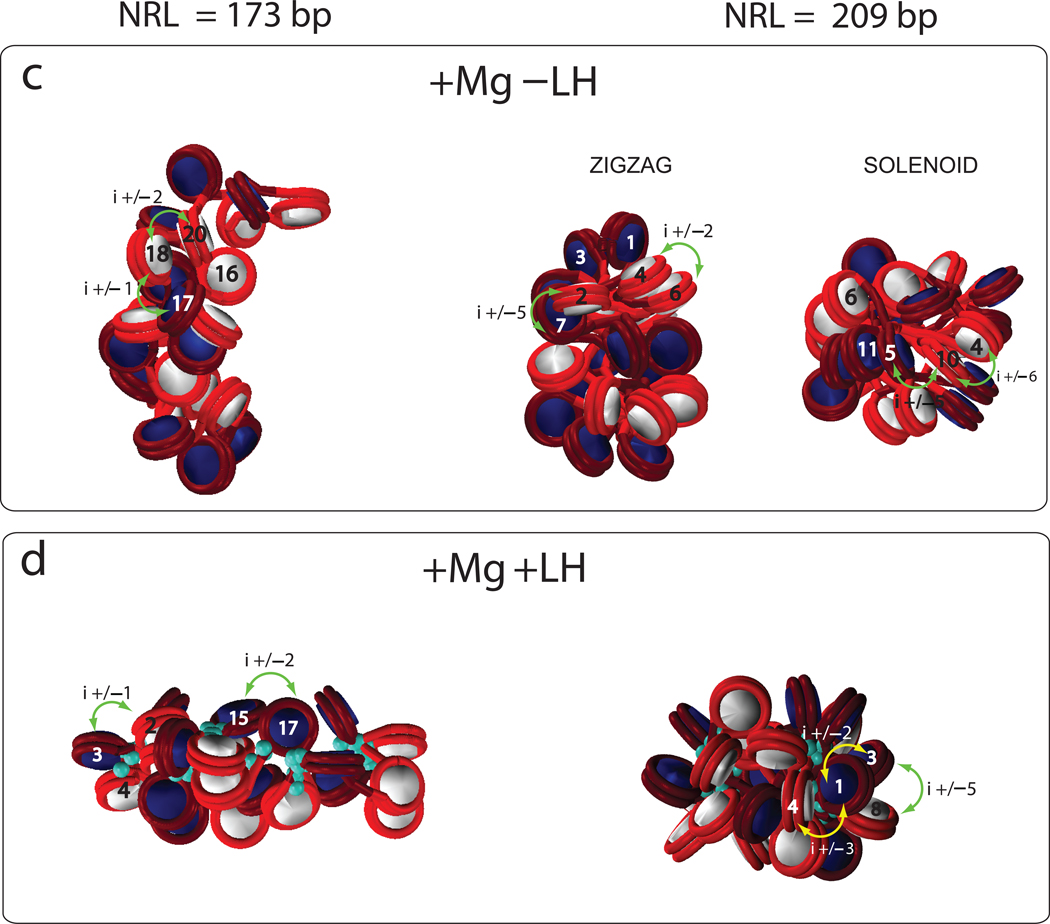
Figure 2 shows the fiber configurations at various conditions for 24 core arrays. In 6 of the 8 cases, only zigzag configurations are viable, whereas for 2 cases with NRL = 209 bp (−LH+Mg, +LH−Mg), distinct zigzag and solenoid configurations are possible. Those two structures are shown in Fig. 2. Without divalent ions, the short NRL arrays maintain the ladder–like zigzag organization at all conditions, while longer NRL compact into irregular structures. Both arrays exhibit a dependence on the linker histone: sedimentation coefficients and packing ratios increase with the addition of linker histone. For the longer NRL, a tighter zigzag structure is also evident, with long-distance i±5 interactions (Fig. 3), indicating increased compaction and order (analyzed below). The addition of divalent ions produces very compact structures for both NRL systems.

Figure 2. Fiber structures for two NRLs under different conditions for 24-core arrays.

For each case, the dominant zigzag conformation is shown and, for two cases where a solenoid conformation also exist, both the zigzag and solenoid models are shown. The turquoise beads indicate linker histones.

Various nucleosome contacts are illustrated to help interpret the profiles in Figure 3.

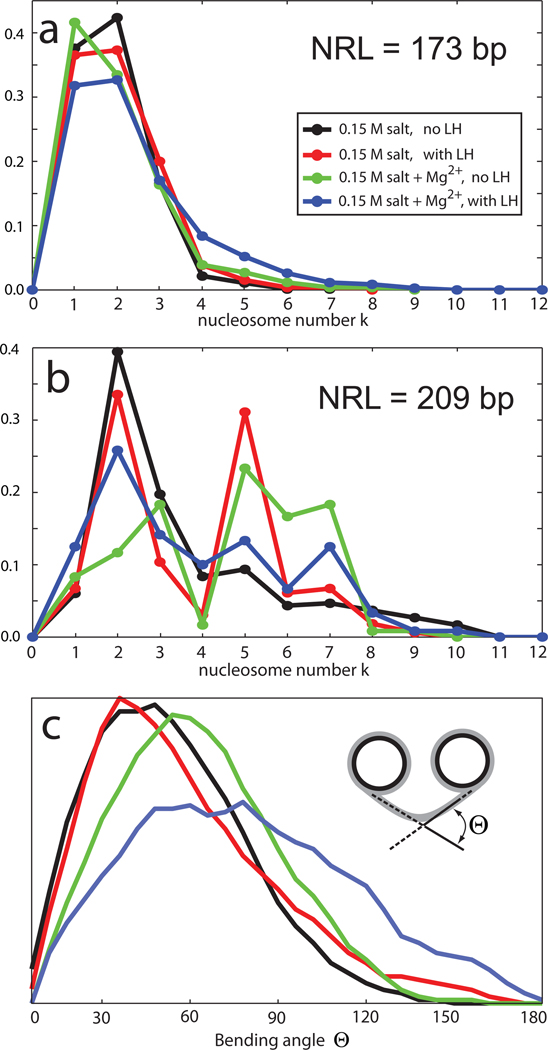
Figure 3. Contact patterns and bending angles under different experimental conditions.

a, b) The contact patterns for the 173 (Fig. 3a) and 209 bp (Fig. 3b) NRL fibers at 4 conditions as shown in the inset. c) The bending angle distribution for the 209 bp NRL fibers at 4 conditions as shown in the inset. See Fig. 2 for nucleosome contact illustrations.

The dominant internucleosomal patterns in Fig 3a help interpret these trends further. Fig. 3 shows that the short NRL fibers at typical monovalent salt (0.15 M) have strong i±1 interactions simply by construction (and not an indicator of solenoid–like forms), regardless of the presence of the linker histone. However, the addition of linker histone produces more compact fibers with zigzag-type i±2 dominant contacts. The short NRL fibers have negligible i±5 contacts, an indication of their ladder-like structure.

The contact patterns in Fig. 3 reflect averages from both zigzag and solenoid starting configurations (see supplemental Fig. S1). As discussed above, the separate analyses show that in 6 out of 8 cases considered both starting conformations (zigzag and solenoid) produce only zigzag forms, while two cases preserve both zigzag and solenoid organizations of nucleosomes. Note from Fig. S3 that both ensembles converge fairly quickly, though fluctuations for the solenoid configurations are larger. Figure S3 shows the total potential energy and the triplet angles measuring the orientation of each three successive nucleosomes. These two quantities are representative: the energy behavior mirrors global configurational properties (like sedimentation coefficients and packing ratios) while the triplet angle is more sensitive to the specific state (zigzag or solenoid). Thus, the level of overall convergence can be assessed from the behavior of these two quantities. In general computational time limitations rule out attributing relative percentages to each ensemble. This may be possible for much smaller arrays of nucleosomes or much faster computational platforms.

Fig. S2 shows that the zigzag architecture is dominant (from the prominent i±2 contacts) at all conditions for NRL = 173 bp, whereas the solenoid configuration is viable when either LH or divalent ions are present for NRL = 209 bp. Note that i±1 contact for short linkers originate from proximal distances and not from solenoid like architecture. The longer NRL fibers also have prominent higher order interactions, namely i±3, i±5, and i±7.

The DNA bending angle (Figure 3c), which measures the orientation between the DNA linker exiting one nucleosome and entering another (see Figure 3c inset), shows that the addition of linker histone to long NRL fibers at typical salt concentrations straightens the DNA linkers (the peak of the bending angle distribution moves from 40° to 30°) and favors the zigzag structure (Fig. S2). Divalent ions widen the bending of DNA between nucleosomes because of some bending of linker DNAs, to effectively minimize linker clashes along the fiber axis.²²

The DNA bending angle distributions in Figure S2 confirm the above finding and show that linker histones and divalent ions strongly affect DNA linker orientation. For NRL = 209 bp with both divalent ions and linker histones, the bending angle distributions from both starting configurations converge to the same orientation (Fig. S2d), as found in²², indicating a mostly zigzag conformation accented by some linker DNA bending. With LH without divalent ions, or without LH with divalent ions, the configurational ensemble of chromatin for NRL = 209 bp is more heterogeneous, with both zigzag and solenoid architecture feasible. These are the two cases out of 8 considered here where the zigzag is not the only viable form (Fig. 2).

Tail interactions

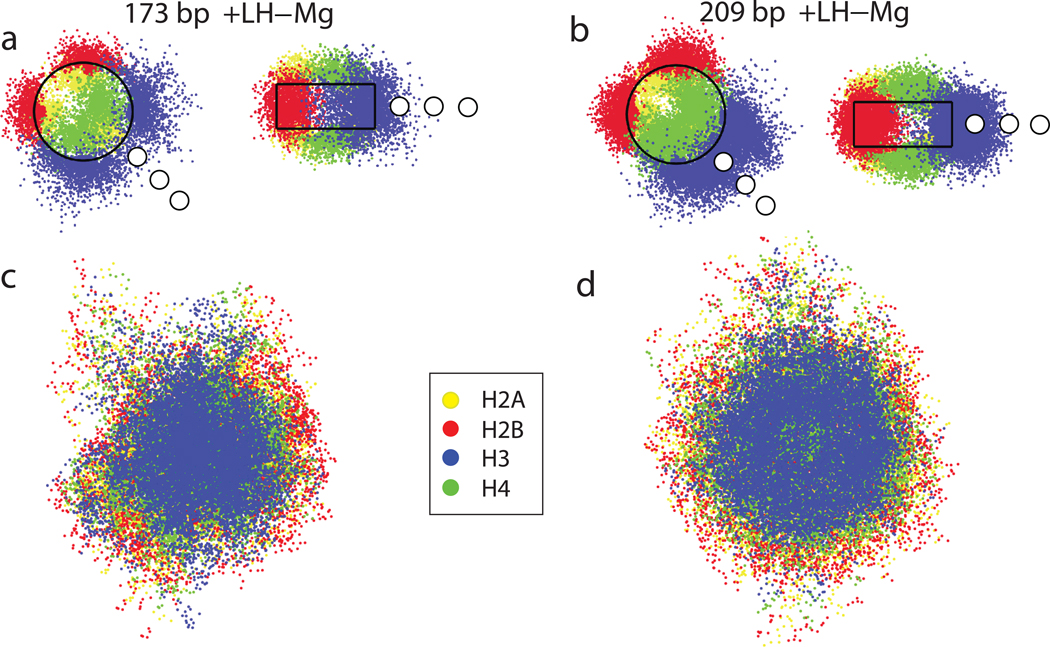
Figure 4 depicts the positional distributions of the histone tails at 0.15 M salt for the two NRLs, with linker histone, along the nucleosome and dyad planes of the nucleosome and within the whole chromatin fiber, projected on the planes perpendicular to fiber axis. The tail distributions for divalent ions are very similar (not shown). The H3 tails (blue) in longer NRL fibers are positioned in the interior of the fiber along the fiber axis close to the entry/exit positions of the parental DNA linkers with whom they mostly interact. These interactions help maintain linker DNA near the linker histone due to effective screening. Therefore, the DNA linkers in longer NRL fibers, together with the H3 tails and linker histones, reinforce the basic zigzag structural element, the DNA stem formed by the negatively charged linker DNA screened effectively by the H3 tails and the linker histone.

Figure 4. Tail distributions for a typical fiber configuration within a nucleosome and within the fiber with linker histone at 0.15 M salt.

The dots represent tail bead positions according to the color code shown. The positions of the three linker histone beads are shown as white circles.

In the short NRL fibers, the interaction of the H3 tails with the parental DNA linkers is reduced by the presence of adjacent positively charged parental and non parental linker histones and the presence of adjacent nucleosomes. These factors move the H3 tails away from the dyad axis and thus reduce their effectiveness.

The distribution of H4 tails (green) does not depend on the DNA linker length. Their short length and location on the flat surface of the nucleosome move them from the fiber axis. They interact with non-parent nucleosomes²⁴ to increase fiber compaction.

The H2A and H2B tails are mostly positioned on the periphery of the nucleosome and on the periphery of the fiber. They are involved in the histone core aggregation,²⁵ transcription control, and probably mediate inter-fiber interactions due to their position on the periphery of the nucleosome.²⁴

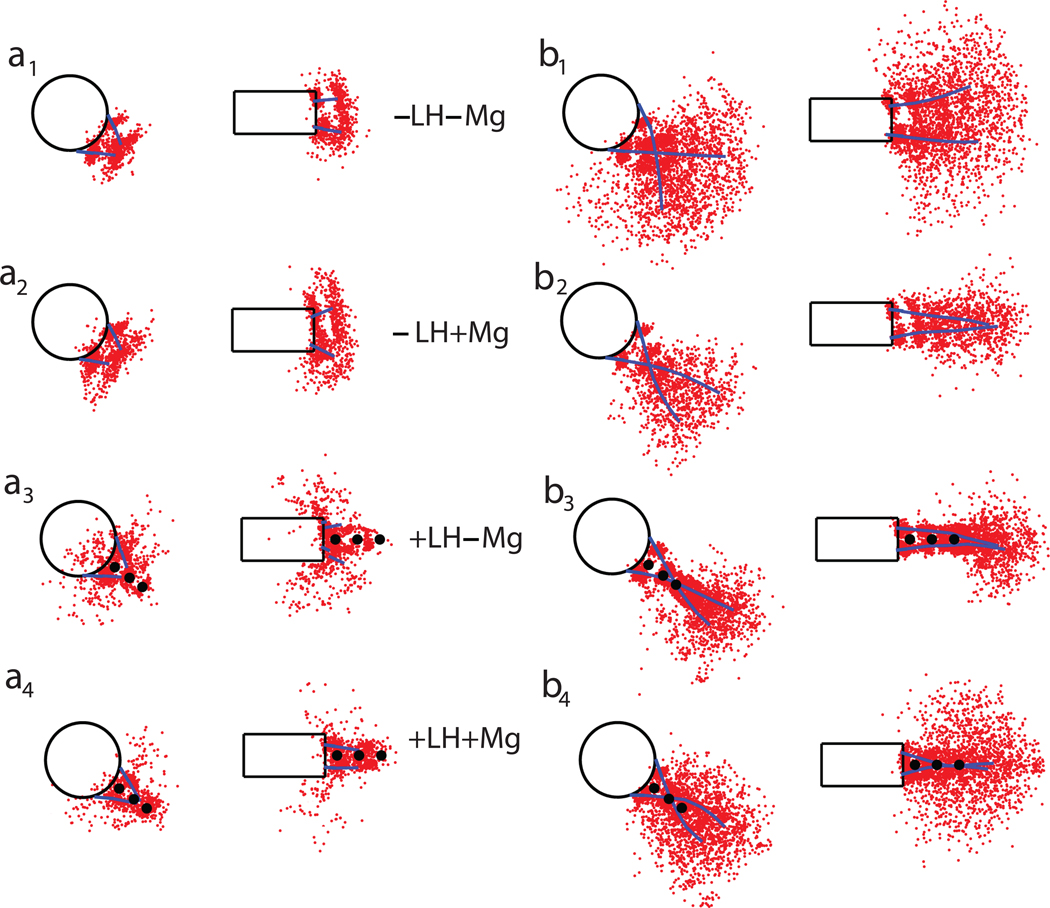
As shown in Fig. 5, where linker DNA distributions are projected on the nucleosome and dyad planes, the linker histone restricts the trajectory of the linker DNA by forming a rigid stem with the longer NRL but affects the shorter NRL much less significantly. Divalent ions have a similar tighthening effect but they also introduce heterogeneity in fiber orientation due to some bending, and this is reflected by wider distributions. The wider distributions are also caused by the increased DNA linker length.

Figure 5. Linker DNA positional distribution for a typical fiber configuration for various conditions projected on the nucleosome and dyad plane.

The red dots represent linker DNA bead positions. The mean trajectories of the DNA linkers are shown as blue lines. The positions of the three linker histone beads are shown as black circles.

Conclusion

Our studies which examined the configurations of chromatin fiber at NRL = 173 bp and NRL = 209 bp using a mesoscopic model help dissect the effects of NRL, LH, and the ionic strength on chromatin fiber packing and geometry. Our results show the negligible effect of LH on fibers with short NRL, which fold into zigzag structures. For longer NRL, both solenoid and zigzag configurations are viable and represent distinct feasible arrangements when either LH or divalent ions are present. However, when both LH and divalent ions exist, the longer-NRL fibers favor one type of hybrid conformation that resembles a zigzag accented by linker DNA bending. The important effect of linker histones and various salt conditions on chromatin organization, especially on long NRL systems, underscore the essential regulatory roles of these factors. The greater configurational heterogeneity in longer NRL systems may favor them over short DNA linker systems for performing fundamental biological processes that require various level of compaction to promote or hamper access to the genetic material.

Recent computational studies using a coarse-grained model described by several tunable parameters such as the linker DNA opening angle and twisting angle between successive nucleosomes¹⁰ found periodic patterns in fiber dimensions for NRL from 202 to 222 bp, a strong effect of NRL on the viable chromatin conformations (two-start and three-start were found), and increased structural irregularity for NRL>214 bp. While such patterns agree with X-ray scattering studies,²⁶ Robinson et al.¹⁷ recently reported two discrete classes of reconstituted fiber dimensions (radii of 33nm and 44nm, respectively) and densities (11 and 15~17 nucleosomes per 11 nm) for NRL < 207 bp and NRL > 217 bp, with a transition between those values. Modeling based on EM measurements of reconstituted fibers, however, show a range of possible conformations as NRL changes;¹⁸ the authors emphasize “the multiplicity of fiber structures!” tuned by the NRL.

Our results here show precisely how NRL, along with LH and positive couterions, shift the ensemble conformations of chromatin fibers at various conditions, making zigzag conformations always viable and also dominant for short NRL. The increased heterogeneity and increased polymorphic nature of the fiber as NRL increases agrees with the above studies^10,18 and adds further details on the associated internucleosome patterns and internal geometry. As argued previously,^10,22 the increased heterogeneity and irregularity may be energetically favorable and biologically important, for example, for transitioning to higher-order forms in chromatin that involve fiber/fiber interactions and higher orders of packing during the cell cycle.

While our studies consider two type of models, other topologies, such as ribbon-like conformations,²⁷ 3-start helix,²⁸ and 5-start helix,²⁹ are also possible. Such a multiplicity of conformations and a large number of tunable internal and external factors (LH, NRL, ionic conditions, variations in NRL from one core to the next) make the chromatin fiber not only infinitely interesting and suitable for performing a rich array of functions in the cell but also an attractive and continiously challenging subject for experimentalists and theoreticians alike.

Model and Methods

Appendix: Chromatin Model and Analysis Techniques

The chromatin model as developed over several years and updated recently to model histone tails, divalent ions and linker histones was just described thoroughly in Arya & Schlick (2009).¹¹ Included in that description were the different treatments of the multiscale chromatin model components (core, tails, linker DNA and linker histone), the mechanical and energetic interactions among them, monovalent and divalent salt modeling, interactions neglected or approximated in the mesoscale model, model validation studies, and Monte Carlo sampling methodology. A recent review paper also summarized the history of the developed model, from a macroscopic to mesoscale approach.³⁰ Essentially, our first-generation model^20,21 captured the fundamental monovalent-salt dependent mechanics of chromatin and the thermal fluctuations of the nucleosome and linker; the next-generation mesoscale model^24,31–33 accounts for the irregular surface of the nucleosome, the flexibility of the histone tails, the presence of linker histone, and divalent ion effects (to a first-order approximation). Because all these details are described comprehensive in Ref.¹¹, only bare-bone aspects are described here for a quick reference.

Multiscale Chromatin Model

The nucleosome core — histone octamer and wound DNA minus the N-termini of all four histones and short C-termini of H2A — is treated as a charged, rigid body (Fig. 1) as an irregular charged surface parameterized using the discrete surface charge optimization (DiSCO) algorithm.^21,33 This approach uses optimization^34,35 of a Debye-Hückel approximation to the salt dependent electric field of the atomistic nucleosome core to parameterize 300 pseudo-charges uniformly distributed across the nucleosome surface. An error of less than 10% over a large range of salt concentrations is considered acceptable. In addition to a point charge, each core point is assigned an effective excluded volume modeled using a Lennard-Jones (LJ) potential.

The linker DNA connecting adjacent nucleosome cores is treated using the discrete elastic wormlike chain model of Allison et al.³⁶ with electrostatic potential developed by Stigter.³⁷ Each monovalent-ion dependent charged bead segment represents 3-nm (~10 bp) of relaxed DNA (Fig. 1) and is also assigned an excluded volume using the LJ potential to prevent overlap with other components of chromatin. Moreover, the DNA beads have stretching, bending, and twisting potential energy components following macroscopic supercoiled DNA models.

The ten histone tails — eight N-termini of H2A, H2B, H3, and H4 and two C-termini of H2A — are treated using a coarse-grained protein bead model. Each tail bead represents five protein residues and has a corresponding charge modified by a scale factor close to unity, an excluded volume (LJ) potential, and intramolecular bond stretching and bond-angle bending energy components.³²

The linker histone (LH) is modeled after the rat H1d linker histone modeled by Bharath et al.^38,39 using three charged beads to represent the globular domain (one charged bead) and the C-terminal domain (two charged beads). These beads are placed in a straight line separated by a distance of 2.6 nm (see Fig. 1), and assigned Debye-Hückel charges to reproduce the electric field of the atomistic model as well as excluded volume parameters to account for the interaction of linker histones with parental cores, all linker DNA, and all other linker histones.

The components above are integrated to yield the repeating oligonucleosome motif shown in Fig. 1. The histone tails are attached to the nucleosome core via stiff harmonic springs; the rigidly-attached linker histone beads are placed on the dyad axis of each nucleosome at distances r = 6.2, 8.8, and 11.4 nm from the nucleosome center as suggested experimentally;^38–40 and each core is linked to an entering and exiting linker DNA segments where the linker DNA entering/exiting orientation has a corresponding value of θ₀ = 108° and wrapping of 1.7 turns of wound DNA according to the recent high-resolution nucleosome crystal with tails resolved.⁴¹

Each linker DNA bead and nucleosome is allowed to twist about the DNA axis with a twisting energy penalty implemented through local Euler coordinates for each bead. In addition, to measure DNA bending and twisting at core attachment points, two other coordinate systems describe the trajectory of the wrapped DNA on the nucleosome cores at the point where it diverges from the core to connect the two linker DNA. Additional coordinate frames are defined to transform each linker DNA bead to the next and each nucleosome core to/from preceding/succeeding DNA beads.

Governing Energetics

The total potential energy is expressed as the sum of stretching, bending and torsional components of linker DNA, stretching of histone tails, intramolecular bending to the histone tails, total electrostatic energy (accounting for all interactions among nucleosomes, linkers, tails, and cores with all other units), and excluded volume terms.

Ion modeling

Physiological salt conditions of monovalent and divalent cations are important for compacting chromatin by electrostatic repulsion between the linker DNAs. The solvent surrounding oligonucleosomes is treated as a continuum with a dielectric constant of 80. The effect of monovalent ions is treated using effective Debye-Hückel charges that are monovalent-salt dependent. Divalent ions are treated to a first-order approximation following studies on DNA bending,^42,43 which suggest a reduction of the DNA persistence length to promote linker bending. Specifically, we reduce the repulsion among linker DNA in linker/linker interactions by setting an inverse Debye length of κ = 2.5 nm⁻¹ to allow DNA to almost touch one another, and reduce the persistence length of the linker DNAs from 50 to 30 nm according to experimental findings.^42,43

Model Validation and Approximations

When properly developed and parameterized, a mesoscale model allows sampling of oligonucleosome systems for investigating key features systematically that depend on basic electrostatics and conformational flexibility. By construction and out of necessity, all-atom detail (e.g., sequence dependence) is not considered, and ion correlation effects are omitted. Behavior thus represents an average over sequence, protein binding, atomistic fluctuations, higher-order ionic correlations, explicit solvation interactions, etc.

Our mesoscale chromatin model has been validated for many experimentally-measured properties (see^11,24,31,32). These properties include salt-induced compaction of oligonucleosomes to reproduce experimental sedimentation coefficients⁴⁴ and nucleosome packing ratios;^45–47 diffusion and salt-dependent behavior of mononucleosomes, dinucleosomes, and trinucleosomes;^48–50 salt-dependent extension of histone tails measured via the tail-to-tail diameter of the core and radius of gyration for mononucleosomes over a broad range of monovalent salt concentrations;⁵¹ the irregular zigzag topology of chromatin fibers consistent with experimental models^16,27,47,50 and its enhanced regulatority upon LH binding;¹⁶ linker crossing orientations in agreement with various experiments;^47,52–54 and internucleosome interaction patterns consistent with cross-linking and EM experiments.²²

Monte Carlo Simulations

We use four tailored MC moves — pivot, translation, rotation, and tail re-growth- – with relative frequencies of 0.2:0.1:0.1:0.6, respectively.^24,32 The tail re-growth method which we use for the histone tail beads involves configurational bias MC^55–57 to re-grow a randomly selected histone tail bead by bead by using the Rosenbluth scheme⁵⁸ starting with the core-attached bead.

We employ two starting oligonucleosome configurations (zigzag and solenoid models) and employ both 12 and 24-core nucleosome simulations, the latter only for suggesting compact configurations of fibers as obtained from the extensive 12-array studies.

Calculation of Internucleosome Patterns

Nucleosome/nucleosome interaction patterns are calculated by an interaction intensity matrix that measures the fraction of time (or fraction of MC configurations) each nucleosome’s histone tail interacts with the other nucleosome, that is approach each other within 80% of their van der Waals radii. Such matrices^22,24 can be further decomposed to one-dimensional plots that depict the magnitude of each i, i+k interaction, as shown in Figure 3.

Calculation of Sedimentation Coefficients

We applied the method developed by Bloomfield et al.^59,60 to calculate the sedimentation coefficient of a given oligonucleosome array conformation, from the intercore distances.^44,61 The sedimentation coefficient S_20,w is approximated from S_N, where

$$\frac{S_N}{S_1}=1+\frac{R_1}{N}{\displaystyle \sum _i}{\displaystyle \sum _j}\frac{1}{R_{\mathit{\text{ij}}}}.$$ (1)

Here, S_N represents S_20,w for a rigid structure consisting of N nucleosomes of radius R₁, R_ij is the distance between the centers of two nucleosomes, and S₁ is S_20,w for a mononucleosome. This approach assumes spherical nucleosomes, a reasonable approximation. We use R₁ = 5.5 nm and S₁ = 11.1 Svedberg (1 S = 10⁻¹³ sec) as done previously.⁶¹ Similar results can be obtained by a more complex procedure implemented in the program HYDRO⁶² which calculates S_20,w using the radii of both the nucleosome core particle (5.0 nm) and the DNA bead (1.5 nm).

Calculation of Fiber Packing Ratio

To calculate the fiber packing ratio (number of nucleosomes per 11 nm of fiber length) for each simulation frame, we first compute the length of the fiber axis passing through a chromatin fiber core (see Fig. S4). The fiber axis is a parametric curve defined by three functions f(i), g(i) and h(i) (where i is a nucleosome core index) which are calculated by a method of least squares, using the nucleosome core center vectors as input parameters for each simulation frame. The least squares method produces n + 1 polynomial coefficients for a polynomial of an order n. We use n = 2, as it gives the best estimate of the fiber axis. The described procedure produces 12 points per spatial dimension for a 12-oligonucleosome fiber and 24 points per spatial dimension for a 24-oligonucleosome fiber and a 3D curve for the fiber axis. We sum the Cartesian distances between every consecutive odd point (f(i),g(i), h(i) and f(i+2), g(i+2), h(i+2), i = 1, 3, 5….) to obtain the fiber axis length L. We use odd points only to avoid overestimating the fiber length. The packing ratio (# of cores per 11 nm) is calculated as the number of cores multiplied by 11/L.

Calculation of Fiber Width

From the fiber axis computed above we define the fiber radius, for a given nucleosome core, to be the perpendicular distance between a nucleosome core center and its closest linear fiber axis segment plus the nucleosome radius (5.5 nm). We repeat this procedure for each configuration and average the value to obtain a mean fiber radius. The diameter is twice that value.