Directional persistence of chemotactic bacteria in a traveling concentration wave

Abstract

Chemotactic bacteria are known to collectively migrate towards sources of attractants. In confined convectionless geometries, concentration “waves” of swimming Escherichia coli can form and propagate through a self-organized process involving hundreds of thousands of these microorganisms. These waves are observed in particular in microcapillaries or microchannels; they result from the interaction between individual chemotactic bacteria and the macroscopic chemical gradients dynamically generated by the migrating population. By studying individual trajectories within the propagating wave, we show that, not only the mean run length is longer in the direction of propagation, but also that the directional persistence is larger compared to the opposite direction. This modulation of the reorientations significantly improves the efficiency of the collective migration. Moreover, these two quantities are spatially modulated along the concentration profile. We recover quantitatively these microscopic and macroscopic observations with a dedicated kinetic model.

Suspended Escherichia coli bacteria that swim in convection-free geometries such as capillaries or microchannels, collectively migrate towards nutrient-rich regions, in the form of propagating concentration waves (1–4). In homogeneous environments, the individual trajectories of these bacteria can be described by a random walk consisting in a succession of “runs” during which they swim in straight lines, and “tumbles” characterized by random [although not complete (5)] reorientations (6). The modulation of run lengths in response to temporal variations of chemoattractant concentrations (7) biases this random walk, driving the bacteria up spatial gradients (5). The collective wave-like behaviors emerge for high enough concentrations (8) and have been so far qualitatively described by several semiempirical models based on the production of chemoattractants by the bacteria themselves (3, 8–12). Nevertheless, a direct validation of these ideas still requires experimental data describing individual bacteria within these populations.

In the present work, we use a microfluidics-based approach that allows to simultaneously track the trajectories of hundreds of individual bacteria while measuring the global characteristics of the wave. We then derive a kinetic model that quantitatively describes the observations at both scales.

The experiments were conducted with the motile and chemotactic strain RP437 (5) and its mutants, in linear silicone polydimethylsiloxane (PDMS) microchannels (500 μm × 100 μm × 1.8 cm). The channels were first filled with homogeneous suspensions of cells grown to midlog phase (∼5·10⁸ cells/mL) in M9 minimal medium supplemented with D-Glucose and Casamino Acids (13), and immediately sealed.

As a reference, we measured the mean run [respectively (resp.) tumble] duration τ_run (resp. τ_tumble) and the run velocity (V_run) before centrifugation, in the absence of gradient, for each experiment. The distributions of run and tumble durations were exponential, with mean values in M9 medium being respectively 0.41 ± 0.39 s [standard deviation, (SD)] and 0.18 ± 0.18 s SD. The mean velocity of a run was 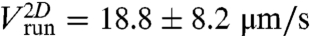corresponding to a mean three-dimensional (3D) velocity: 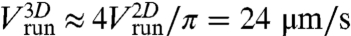(14). The mean value of the change in direction between successive runs was 69 ± 1° (absolute value of the projected angle). These values are in good agreement with previously reported values (5, 11, 15). In particular, the two-dimensional (2D) projected angle is directly comparable to the 3D value of 68° reported in ref. 5, as demonstrated in ref. 16 and confirmed by our own simulations.

The migration was initiated by the accumulation of the bacteria at one extremity of the microchannel by centrifugation (Fig. S1). The initial condition consisted therefore in a diffuse concentration profile that contained 99% of the bacteria initially present in the channel within a characteristic length of ca. 200 μm (17).

We then monitored the macroscopic evolution of this initial accumulation by videomicroscopy using transmitted scattered light (18). The statistics of the motion of the individual bacteria in space and time were obtained by tracking a small number of individual fluorescent bacteria (strain RP437-pZE1R-gfp) mixed in a nonfluorescent population (11). The distribution of run times and tumble times were thereafter extracted from these individual projected trajectories (11, 19).

Results and Discussion

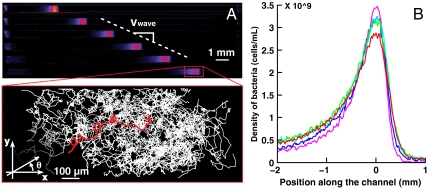
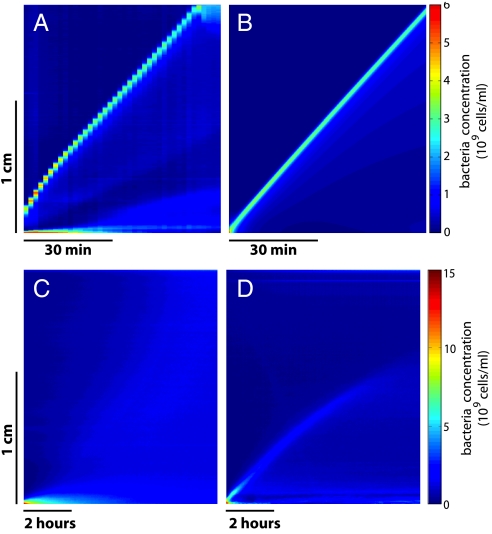
Within less than 10 min after the centrifugation was stopped, the initial accumulation of bacteria congregated into a dense band propagating at constant speed (V_wave = 3.8 ± 0.5 μm/s) along the main axis of the channel (Fig. 1A). After the initial transient regime, the concentration profile broadened only very slowly as a function of time (Fig. 1B, Fig. 2A). The total number of bacteria in the band remained constant within 15% during the time course of an experiment. This wave is the consequence of the chemotaxis of the bacteria as motile but nonchemotactic strains failed to migrate collectively (Fig. 2C), as did chemotactic bacteria in nutrient-deprived motility buffer (Fig. 2D). Hydrodynamic interactions between bacteria are also known to impact their behavior at high concentration. Although, in the present experiments, the highest measured densities (∼5·10⁹ cells/mL at the maximum of the concentration peak) were expected to remain too low to give rise to a significant effect (20), we have nevertheless checked its influence by mixing fluorescent beads of 1 μm diameter with the bacterial suspension. These passive tracers showed an enhanced diffusion as expected (21) (Fig. S2), but no significant global drift (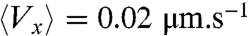 for the beads, to compare to V_wave ∼ 4 μm·s^-1 for the population of swimming bacteria) leading us to neglect hydrodynamic interactions to interpret the formation and propagation of the waves.

Fig. 1.

Collective migration of Escherichia coli in a PDMS microchannel. (A) Propagation of a concentration “wave” of E. coli chemotactic bacteria. Successive snapshots of the same channel are represented on Fig. 1A, demonstrating the uniform motion of the wave (500 s between successive images, the color code reflects the local concentration). The population migrates at a constant velocity (V_wave ∼ 4.1 μm/s for this particular experiment). Inset: projected trajectories of the fluorescent cells mixed with a nonfluorescent population during collective migration [superimposition of 100 trajectories extracted from seven different movies (1 min long, 10 fps)]. These trajectories are plotted in the moving frame of the wave whose position is measured independently. θ is the projected angle in the x-y plane (B) Superimposition of five concentration profiles measured at different times spanning 40 min in the quasi permanent regime of the wave migration. (purple: t = 1,000 s; blue: t = 1,500 s; cyan: t = 2,000 s; green: t = 2,500 s; red: t = 3,000 s).

Fig. 2.

Kymographs in several experimental and theoretical conditions. (A) Experimental kymograph corresponding to Fig. 1. The velocity of 4.1 μm/s is reached after 20 min. The staircase shape is due to a too large time lapse between successive images. (B) Simulated kymograph obtained with the conditions listed in the text (see Table 1) [same scales as box (A)]. (C) Experiment performed with the nonchemotactic RP2867 strain. No wave generation is observed. (D) Experiment performed with the chemotactic strain in Motility Buffer. The very slow initial wave is attributed to the remaining nutrients present in solution after resuspension. However, this wave decays rapidly and vanishes completely at mid length of the channel. Note the different scales for (C) and (D) compared to (A) and (B).

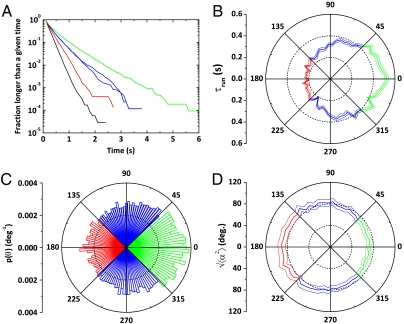
Average individual behaviors within the wave were characterized by τ_tumble = 0.15 ± 0.02 s, τ_run = 0.35 ± 0.03 s, and 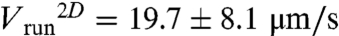yielding a 3D value of 25 μm/s (14). The average projected angle between successive runs was 64 ± 1° (absolute value of the projected angle). As the wave motion is sustained by chemical gradients created by the moving bacteria, we have analyzed the runs according to their directions. Although their velocity was largely independent on their direction (less than 7% variations for 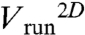), runs in the direction of global motion were in average longer than the ones perpendicular to it, themselves longer than the ones in the opposite direction (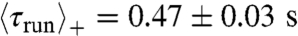, , 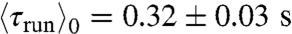and 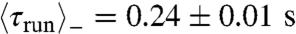) (Fig. 3 A and B). The same ordering was observed in an externally imposed glucose gradient (Figs. S3 and S4). We note that, here, 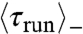is smaller than 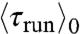, in contrast to previous observations (5). We speculate that the gradients experienced in the present experiments are steeper, corresponding to a fast decrease in chemoattractants concentrations and therefore smaller run lengths for bacteria swimming down the gradients (7). Quantitatively, however, the average drift velocity of the bacteria that can be estimated from these values is 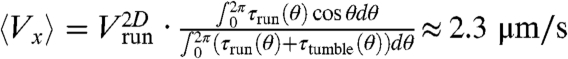, much smaller than V_wave, meaning that another physical mechanism has to be taken into account in the analysis.

Fig. 3.

Microscopic descriptions of the bacteria trajectories: (A) Cumulative distributions of run and tumble durations. (Mean run or tumble times result from a fit of these distributions by an exponential). Due to chemotaxis, runs in the direction of migration (green) are longer than runs in perpendicular directions (blue), themselves longer than runs in the opposite direction (red). The black curve is representative of the tumbles. (B) Dependence of mean run time with direction. (C) The angular distribution of the runs is biased in the direction of migration meaning that the reorientation is nonisotropic. (D) SD of the reorientation angle (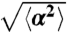) as a function of the direction of the preceding run. Runs in the same direction as the global motion reorient less than the ones directed backwards. In all these polar plots, the angle is θ as defined in Fig. 1A in the x-y plane (θ = 0 corresponds to the direction of migration). On boxes B and D, the thin lines are the error bars SEMs.

Indeed, the probability distribution of the angles θ between the projections of the runs in the observation plane and the main axis of the channel (Fig. 1) was also biased in the direction of migration (Fig. 3C). Taking this angular distribution, p(θ), into account in the estimation of the average velocity of the bacteria yields 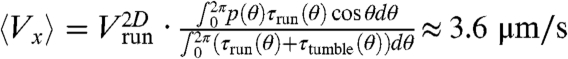, indeed much closer to the actual value of 3.8 μm/s than our previous estimate based only on the modulation of run length. This effect of modulation of the reorientation that accounts for ∼30% of the drift velocity was also observed in an externally imposed glucose gradient (Fig. S4).

To quantify the amount of reorientation after a run, we introduce the angle α between the projected directions of successive runs. For symmetry reasons, its mean value is 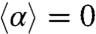. The persistence of the trajectories is accounted for by the SD of the distribution of this reorientation angle 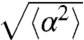. We observed that tumbles following positively oriented runs caused less reorientation than the ones following negatively oriented runs (Fig. 3D). As gradients affect the run length via the switching frequency of the flagellar motors, it has recently been proposed that this mechanism may also affect the amplitude of the reorientation of the cell after a run (22). If a cell swims up a gradient, the switching probability of its motors is reduced and therefore, it reorients less compared to the down-gradient direction (corresponding to a larger persistence of the trajectories). In the present situation, we measured a reorientation of 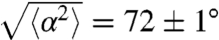in the forward direction (-45° < θ < 45°), compared to 88 ± 1° in the backward direction (135° < θ < 225°) (Fig. 3D). This difference of 16° between these two values has been shown in numerical simulations to be sufficient to contribute significantly to the chemotactically driven process (22).

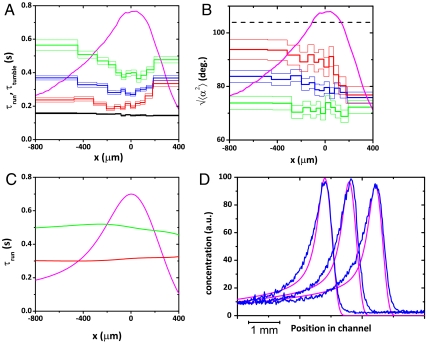
Because of the various gradients generated and experienced by the bacteria, their microscopic behaviors were expected to be modulated along the wave profile (2, 11, 23). This modulation is indeed evidenced on Fig. 4 A and B: runs in the positive (resp. negative) direction are significantly longer (resp. shorter) at the back of the peak compared to its front (Fig. 4A). The reorientation angles follow the opposite trend (Fig. 4B), suggesting a joint and antagonistic modulation of run lengths and tumbles reorientations. As a consequence, an individual at the back of the population “catches up” rapidly with the high concentration peak (with long positive runs followed by reduced reorientations and short negative runs associated with high reorientations). Ahead of the peak, the biases vanish; negative and positive runs are of similar length and the effective diffusion of the swimmers predominates over their drift causing the bacteria at the front of the peak to effectively “wait for the late ones.”

Fig. 4.

Modulation of the swimming parameters along the channel: (A) Spatially modulated directional variations of the runs mean durations reveal the changes in chemical signal sensed along the channel. The black curve represents the tumbles times. (B) The reorientation angle after a run is modulated along the peak in a parallel and opposite way as the runs durations (same color code as in Fig. 3A). The concentration profile is added for reference. A completely random reorientation would correspond to a reorientation of 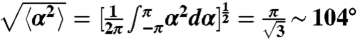(dashed line). In boxes (A) and (B), the thin lines represent the error bars SEM (C) Simulated run times using the kinetic model. The modulations of run times are well accounted for with runs in the positive direction decreasing in duration between the back and the front of the wave and runs in the negative direction following the opposite trend. In front of the wave the bias disappears. (D) Superimposition of the calculated concentration profiles (pink) and the experimental ones (blue) at three different times. The wave velocity obtained with this simulation was the same as the experimental one. The parameters of the simulation are listed in Table 1.

Model

These experiments can be modeled on the basis of the idea originally introduced by Keller and Segel (24): we assume that the bacteria respond to two main signals. They consume nutrients which drives the migration and they excrete chemoattractants that prevent the dispersion of the population. To go beyond an empirical estimation of the various fluxes, we have used a strategy proposed by Alt (25) to design a kinetic model inspired by the Boltzmann equation (26) where the tumbles appear as scattering events and all the fluxes are explicitly introduced (27).

By analogy with the kinetic theory of gases, the population of bacteria is described by the density f(t,x,v) of cells located at the position x and having a velocity v at a given time t. In the absence of tumbles, the local evolution of cell density is only caused by runs and cell division:

where r is the division rate of the bacteria (r = ln 2/τ₂ where τ₂ is the mean doubling time).

The contribution of the tumbles is introduced with a transition (scattering) kernel T(v,v^′) which stands for the change of velocity from v^′ to v and leads to :

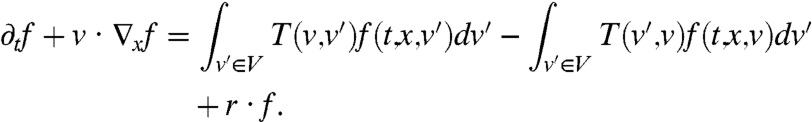This equation is indeed a variant of the Boltzmann equation for gases, where collisions are delocalized via the secretion or consumption of chemical cues.

This model is based on the following assumptions:

• Tumble events are poissonian

• Runs are strictly linear

• There are no memory effects (the response of the bacteria to changes in their environment is considered to be instantaneous).

We describe here a one-dimensional (1D) projection of the axially symmetric 3D phenomenon, our computations were performed with v∈[-V_run,V_run].

The transition kernel depends on the local concentration of chemoattractant S(t,x) and nutrient N(t,x). To estimate the respective contributions on V_wave of the bias of the run lengths and of preferential reorientation, it is possible to split this transition kernel T(v,v^′) in two contributions, one being the tumbling rate λ(v^′), and the other one the reorientation effect during tumbles, K(v,v^′):

with the condition ∫_v∈VK(v,v^′)dv = 1.

We now detail the two functions λ(v^′) and K(v,v^′):

For the tumbling rate λ(v^′), we assume that bacteria are sensitive to the temporal variations of attractant molecules via a logarithmic sensing mechanism (7, 28). Therefore, the tumble frequency only depends on the local gradients of nutrient and attractant, both gradients having independent and additive contributions. This gives

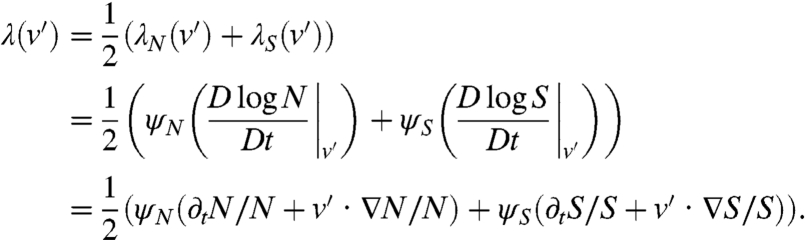The nutrient and chemoattractant response functions ψ (ψ_N and ψ_S) are both positive and decreasing, expressing that cells are less likely to tumble (thus perform longer runs) when the external chemical signal increases. These functions are smooth and characterized by their characteristic times δ^-1 (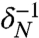 and 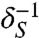) and their amplitudes in tumble frequency modulation χ (χ_N and χ_S). We have chosen the following analytical form that encompasses these characteristics:

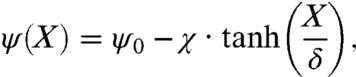where ψ₀ is the basal mean tumbling frequency.

The equations describing the behaviors of N and S are the same as in (27):

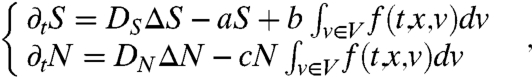where a, b, and c are respectively the degradation rate of the chemoattractant, its production rate and the consumption rate of the nutrient by the bacteria. D_S and D_N are the molecular diffusion coefficients.

In the present case, the parameters χ are of the same order as ψ₀ (typically, χ/ψ₀ ∼ 60%). Therefore, the diffusion approximation used in ref. 27 is not valid and the full kinetic description has to be carried out.

The second function involved in T(v,v^′) is K(v,v^′). K accounts for the persistence of the trajectories. In the absence of such an angular persistence, the turning kernel T(v,v^′) is proportional to the tumbling rate λ(v^′) (i.e., K = constant). A constant persistence corresponds to a fixed value of the reorientation 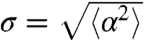(where α = θ-θ^′ is the reorientation angle). We have then used the generic form 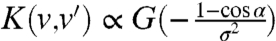and we have checked that the exact expression of the (increasing) function G did not affect our results. The simulations were performed with the simple function 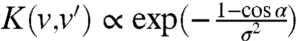. Finally, to account for the experimentally observed modulation of the orientational persistence, we performed the simulations where the reorientation σ was set as an increasing function of the tumbling rate λ(v^′) as observed in Fig. 3 B and D. Indeed, high tumble frequencies are correlated with more flagella leaving the bundle (29), and therefore a larger reorientation. Here, we assumed a linear correlation between σ and λ: σ(v^′) = σ₁ + σ₂·λ(v^′).

In the present work, we have focused on the influence of the reorientation on the shape and the velocity of the wave. The simulations were compared to a particular experiment characterized by a wave velocity of 4.1 μm/s Fig. 2A and the concentration profile depicted in Fig. 1B. The same procedure was reproduced for many different sets of parameters with consistent results, demonstrating the robustness of the model. The numerical parameters used in the simulations are listed in Table 1. Most of them are deduced from the literature (7) or directly inferred from the experiment (Figs. 1–4).

Table 1.

Summary of the values used in the simulation

Parameter	Value
1) run speed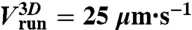
2) mean tumble freq.	ψ0 = 3 s-1
3) Modulation of tumble freq.	χN/ψ0 = 60%
4) Modulation of tumble freq.	χS/ψ0 = 20%
5) stiffness of the response functions	1/δN = 1/δS ≈ 20 s
6) space scale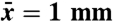
7) time scale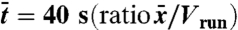
8) doubling time	τ2 = ln 2/r ≈ 1.15 h
9) degradation rate of the chemoattractant	a =5·10-3 mol/ sec
10) production rate of the chemoattractant	b =4·105 cell-1 s-1
11) consumption rate of the nutrient by the bacteria	c =2·10-7 cell-1 s-1
12) diffusion coefficient of the nutrient molecules	DN =8·10-6 cm2/s
13) diffusion coefficient of the chemoattractant molecules	DS =8·10-6 cm2/s

The parameters 1 to 4 are deduced from the experimental results of the present paper [they are consistent with previous studies (5), (27) and (14)]. The experimental geometry also sets the space scale and time scale (parameters 5 and 6). The stiffness δ of the response functions is inferred from Fig. 6 in ref. 7. Variations around this value resulted in less satisfactory results. The doubling time τ₂ (parameter 8), is measured experimentally from the growth in the channels. The values of a and b were taken from ref. 13. The parameter c (parameter 11) was chosen to be close to unity in the adimensional equations. We took a typical value for the molecular diffusion coefficients D_N and D_S (parameters 12 and 13).

Running the model with a constant persistence (σ₂ = 0) gave identical results independently of σ₁, including the limiting case where only a modulation of the tumble rate was considered (no persistence, K = constant). The simulations then resulted in robust and conserved travelling waves propagating at a constant velocity V_sim = 3.2 μm/s, much smaller than the experimentally measured value of 4.1 μm/s (Fig. S5).

We then introduced a modulation of the persistence by using the experimentally measured extreme values of σ (Fig. 3D) to set the parameters σ₁ and σ₂. The speed of the wave then significantly increased to reach the experimental value (V_sim = 4.1 μm/s) (Fig. 2B, 4D). Moreover, the concentration profiles obtained from the same simulations fit remarkably well the experimental data (Fig. 4D).

The simulated run durations (Fig. 4C) show the same trend as the experimental ones (Fig. 4A) with a larger bias at the back of the wave compared to its front and very close numerical values. In the details of the evolution of these times along the concentration profile however, the experimentally observed slight minimum near the concentration peak is not accounted for by the simulations. We think that this effect has a different origin likely linked to the enhanced diffusion at high concentration (Fig. S2).

To evaluate the influence of cell growth in the simulations, we have switched off this term by setting r = 0. Our simulations show that this contribution is of very limited influence. Namely, dispersion effects are slightly more visible and the wave velocity decreases slightly with time. Interestingly, this result contrasts with traditional reaction-diffusion models where growth is crucial for wave propagation (30).

Finally, we observed that the simulations were quite sensitive to the times δ^-1. We found that the experimental value of 20 s (7) gave very good fits between numerical simulations and experiments. Smaller values of δ decrease dispersion and increase V_sim; the resulting concentration profile narrows and changes its symmetry (by getting broader at its front side). We then recover the results described in ref. 27.

Therefore, the proposed model exhibits traveling bands solutions that closely match the experimental observations both at the scale of the population and at the one of the individual swimmers. Interestingly, these propagating wave-like solutions are observed numerically for a wide range of parameters, suggesting that collective migration is a robust feature of the model. We therefore confirm that this kinetic framework is well adapted for the description of traveling bands of chemotactic bacteria (31, 32). Furthermore, the model is also well suited to the description of bacteria in gradients. We provide an example of these simulations on Fig. S6, where we demonstrate the importance of the modulation of the reorientations in these situations as well.

Conclusion

In conclusion, traveling bands of chemotactic bacteria result from the local gradient experienced by each individual and generated by the whole population. Not only the bacteria increase their run length in average to progress in the favorable direction but we have demonstrated here that this run length is spatially modulated along the profile, which is predicted by the developed kinetic model. Moreover, bacteria also exhibit a persistence in their trajectories that depends on their direction of swimming, therefore increasing the efficiency of this collective motion. This last conclusion can be traced to the number of flagellar motors undergoing a counterclockwise-to-clockwise transition during the tumbles (30) and/or by a variation of the time spent tumbling, the two being probably correlated (7). This effect is particularly important in the present case because of the steep gradients suggested by the large biases in run lengths and predicted by the simulations around the concentration peak.

Materials and Methods

Bacterial Strains.

We used the strain RP437 (kindly provided by J. S. Parkinson, University of Utah), considered wild type for motility and chemotaxis (33), and the nonchemotactic strain RP2867 ΔcheRΔcheBΔtap (kindly provided by H. C. Berg, Harvard University) (34). Both strains were transformed with a PZE1R-GFP plasmid (kindly provided by C. Beloin and J.-M. Ghigo, Institut Pasteur, France) (35), by preparing chemically competent cells using TSS buffer, and transforming them with the plasmid by heat shock (36).

Bacterial Culture.

The medium used for the experiments was M9 Minimal Salts, 5× supplemented with 1 g·L^-1 Bacto™ Casamino Acids (both from Difco Laboratories, Sparks), 4 g·L^-1 D-Glucose, and 1 mM MgSO₄ (13). Cells were cultured in 3 mL medium with ampicilin at 30 °C, with shaking, up to an OD₆₀₀ of 0.5 (∼5.10⁸ bact/cm³).

For the tracking of individual fluorescent bacteria in a wave of nonfluorescent ones, the two strains were cultured independently before being mixed at a ratio of 1∶500 and then cultured for two more hours until reaching an OD₆₀₀ of 0.5.

“Motility buffer” (5) used for experiments in externally imposed gradients, was composed of 10 mM potassium phosphate buffer (pH = 7.0) supplemented with 0.1 mM EDTA, 1 μM L-Methionine, and 10 mM sodium lactate.

LB medium (Sigma) was also occasionally used for bacteria culture when specified.

Microfabrication.

Microchannels were fabricated by standard “soft lithography” technique (37). Briefly, a negative imprint (a “mold”) of the channels was microfabricated in a negative photoresist (SU8 2100, Microchem) by conventional photolithography resulting in ten parallel rectangular prisms (length 18 mm, width 500 μm, and thickness 100 μm). A negative replica of this master was then molded with PDMS a heat curable silicone elastomer (Sylgard 184, Dow Corning) at 65 °C for 24 h (the thickness of the elastomer block was of the order of 1 mm). Using PDMS ensured oxygen permeation thus maintaining the motility of the bacteria during the experiments (38).

After cross-linking, the elastomer replica was peeled off its mold, the extremities of the channels were cut and it was sealed with a glass slide after an air plasma treatment. This oxidizing treatment promoted a strong adhesion between the two surfaces and notably reduced the adsorption of bacteria on the channel walls. Immediately after their fabrication, 10 parallel microchannels were filled with the bacteria suspension by capillarity. The channels were then carefully sealed with a fast curing epoxy resin (Araldite 90s, Bostik).

Centrifugation.

To concentrate the bacteria at one extremity of the channels, they were gently horizontally centrifuged along their main axis (Fig. S1) at 65 g, for 35 min, on a modified spin-coater. At the end of this process, the bacteria were still motile and accumulated at the extremity of the channel.

Stereomicroscopy and Data Acquisition.

After centrifugation the channels were placed under a variable zoom fluorescence stereomicroscope (MZ16FA, Leica—magnification range 0.8X–10X) equipped with a CCD camera (CoolSnap_HQ, Roper Scientific) and a homemade shutter. The whole set-up was maintained at 30 °C, high humidity during the experiments (1 to 2 h). Fluorescence mode was used to track the individual fluorescent bacteria. In our set-up, the depth of field was ∼100 μm making possible to follow single bacteria over 20 s or more and measure the projections of their actual trajectories. Low intensity transmission illumination (dark field mode) was superimposed to simultaneously follow the motion of the (mostly nonfluorescent) wave (11). Several one-minute long movies of the collective migration were acquired at 10 fps (WinView/32 software, Princeton Instruments). The presented results were reproduced in at least 10 different independent experiments.

Data Analysis.

Movies were analyzed with ImageJ (39) in the following sequence:

Detection of the position of the population during migration.

For each image, the intensity was averaged along the direction perpendicular (y) to the channel main axis (Fig. 1). The successive positions of the population were then fitted using a linear regression, the resulting speed and initial position being used for the superimposition of all the trajectories in the frame of the wave.

Small defects in the channel geometry can cause the wave to slow down or to accelerate. Therefore, movies corresponding to excessively high or low speed of migration were discarded at that point. In the experimental results presented here, the measured wave velocity was 3.8 ± 0.5 μm·s^-1.

Tracking of the fluorescent bacteria.

Fluorescent bacteria were tracked with the plugin “ParticleTracker” for ImageJ (40) with a subpixel precision of 0.1 μm (SD obtained by tracking ∼200 immobile bacteria adsorbed on a glass slide for 1 min at 10 fps).

Analysis of the trajectories.

Subsequent analysis was performed using the Matlab software (Mathworks). In the present study, 970 trajectories longer than 2 s were extracted from seven different movies. Local speeds and accelerations were then calculated along each trajectory.

The run and tumble times were obtained from the analysis of the projected trajectories using an algorithm inspired by ref. 19. We used two thresholds to detect the tumbles: (i) for a given trajectory, if the change in angle between two successive time steps was more than 27° or (ii) if |γ| > 1.8·|γ₀|, where γ is the local acceleration and γ₀ is the average acceleration as it can be dynamically measured between the beginning of the last run and the current position. This second criterion allowed the detection of the tumbles that caused only a change in the z component of the velocity and that were shorter than the frame rate. These events represented ∼10% of the total number of tumbles. These criteria resulted from manual adjustments. We have verified that the main conclusions reached in the present study were robust if the thresholds were modified up to a factor 2.

For these exponential distributions, the short times are heavily weighted. Therefore the precision on the mean is controlled by the precision of the distribution on these short time scales (including times smaller than 0.2 s, not accessible experimentally). To avoid this effect, times smaller than 0.2 s (0.1 s for the tumbles) were removed from the distribution, the rest of the distribution was fitted by an exponential.

Unless otherwise noted, the errors regarding the run times or the tumble times are the standard error of the mean (SEM). Standard deviations are denoted by SD.

Local analysis.

In order to extract the spatial variations of the mean run and tumble durations we have defined boxes in the moving frame of the wave. Their widths were defined so that each box contained an equal number of run/tumble events (∼1,000), the width of the smallest box being still larger than the average run length.

Numerical Simulations.

Numerical simulations of the kinetic model were performed in 3-dimensions with axial symmetry using the software MATLAB 7.6. The numerical scheme was based on a splitting method: we first apply the free transport operator (upwind scheme), then the tumbling operator (in its explicit form).

We have opted for the following discretization (respectively for time, space, and velocity): dt = 0.4 s, dx = 20 μm and d(cos θ) = 0.1, dϕ = 0.1 where (ϕ,θ) is the solid angle (cos θ, sin θ· cos ϕ, sin θ· sin ϕ). The length of the space interval coincides with the length of the experimental microchannel.