Liquid water can slip on a hydrophilic surface

Abstract

Understanding and predicting the behavior of water, especially in contact with various surfaces, is a scientific challenge. Molecular-level understanding of hydrophobic effects and their macroscopic consequences, in particular, is critical to many applications. Macroscopically, a surface is classified as hydrophilic or hydrophobic depending on the contact angle formed by a water droplet. Because hydrophobic surfaces tend to cause water slip whereas hydrophilic ones do not, the former surfaces can yield self-cleaning garments and ice-repellent materials whereas the latter cannot. The results presented herein suggest that this dichotomy might be purely coincidental. Our simulation results demonstrate that hydrophilic surfaces can show features typically associated with hydrophobicity, namely liquid water slip. Further analysis provides details on the molecular mechanism responsible for this surprising result.

Protein folding (1), micelle and cellular membrane formation (2), and frictionless flow of water through carbon nanotube membranes (3–5) are only some manifestations of hydrophobic effects. Flat surfaces are arbitrarily classified as hydrophobic when a water droplet yields a contact angle larger than 90°, hydrophilic otherwise. A now famous 2008 commentary by Granick and Bae (6) initiated a scientific discussion to identify the molecular signature of hydrophobic vs. hydrophilic surfaces. The question is whether or not molecular properties exist for interfacial water molecules that change with the surface “degree of hydrophobicity.” Identifying such properties could advance practical applications (e.g., designing self-cleaning surfaces) as well as fundamental scientific endeavors including understanding self-assembly (7).

Molecular simulations should allow the discovery of such molecular signatures because they allow a systematic variation of the properties of a surface, as well as of surface-water interactions (8). Although the resultant substrates may not be realistic, the results are useful to interpret nature and to design innovative materials. It has so far been possible to relate some macroscopic observables to the degree of hydrophobicity [i.e., contact angle to adsorption free energy (9)]. Garde and coworkers employed equilibrium molecular dynamics (MD) to determine a number of quantities, including local density, contact angle, and adsorption of small solutes for water near surfaces of varying degrees of hydrophobicity (10). Whereas the local water density provided unsatisfactory characterization, the probability of cavity formation was found to be large near hydrophobic and small near hydrophilic surfaces.

The present work focuses on the relation between one important macroscopic signature of hydrophobic surfaces, the hydrodynamic liquid slip, to molecular interfacial water properties. Large liquid slip on hydrophobic surfaces could reduce the drag in vessels navigating the seas, the pressure drop encountered by fluids flowing inside pipes, and even repel ice formation. Liquid slip seems to appear when a fluid does not wet a surface (11–15). Because the extent of slip varies systematically with the contact angle (16–18), in the case of water, slip should occur on hydrophobic surfaces (19). In the present study the extent of water slip is quantified at various solid interfaces. Equilibrium and nonequilibrium MD are employed to search for molecular-level hydrophobic signatures.

Results and Discussion

The most important result presented herein is the demonstration that contact angles larger than 90° are not necessary to attain hydrodynamic slip. Instead, slip is determined by the distribution of water molecules at contact with the solid and by the strength of water–solid interactions. When favorable adsorption sites exist, but are separated from each other by well-defined subnanometer distances, no slip is observed. When favorable adsorption sites are present that are close to each other, liquid slip can occur, provided water–solid attractions are not too strong. Because hydrophobic surfaces, such as graphite, are typically characterized by uniform distributions of interfacial water molecules, whereas hydrophilic ones, such as crystalline silica, present isolated highly attractive adsorption sites that water molecules readily occupy and seldom leave (20), experiments typically show hydrodynamic slip on hydrophobic surfaces and no slip on hydrophilic ones. Our results suggest that such observations are just a coincidence: Should hydrophilic surfaces be manufactured with high density of adsorption sites close enough to each other to allow water molecules to easily migrate from one to the next, such hydrophilic surfaces could show liquid slip. Our interpretation is consistent with a recent simulation study for the thermal diffusion of carbon nanotube membranes (21), with the molecular mechanism proposed for liquid slip (22), and with experimental observations reported for alkanes (23). Our interpretation could also explain the experimental results by McCarthy and coworkers (24), according to which the contact angle hysteresis, and not the static contact angle, should be used, macroscopically, to determine the hydrophobic vs. hydrophilic character of a surface.

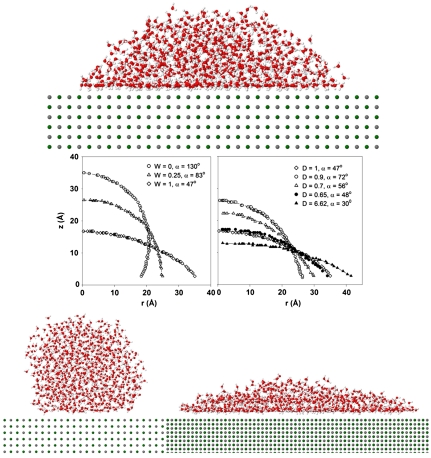
In Fig. 1 we show representative equilibrium simulation snapshots for water droplets of 1,000 water molecules on three surfaces. In all cases, water molecules are described using the single point charge/extended (SPC/E) model (25). The surface on the top is MgO, simulated by the CLAYFF force field (26), on which water dissociation is not permitted. The contact angle is approximately 47° indicating a hydrophilic surface. We arbitrarily modify the MgO surface following two protocols. In the first, we reduce the electrostatic interactions between water and the MgO atoms by a factor W, comprised between 0 and 1. When W = 1 we recover MgO. When W = 0 the surface interacts with water molecules only via weak dispersive interactions, and the contact angle becomes approximately 130° (Fig. 1, Bottom Left), characteristic of a hydrophobic surface. In the second modification protocol we maintain both dispersive and electrostatic surface-water interactions consistent with those of MgO, but we reduce the lattice parameter that separates Mg and O atoms by a factor D. When D = 1 we recover MgO. As D decreases the surface atomic density increases. When D = 0.62 (Fig. 1, Bottom Right) the contact angle is approximately 30°, consistent with a very hydrophilic surface. It is worth mentioning that the distance between Mg and O atoms in MgO is 0.21 nm, less than the diameter of one SPC/E water molecule. Thus all surfaces considered here are atomically smooth.

Fig. 1.

(Top) Simulation snapshot for one droplet of 1,000 SPC/E water molecules on MgO, showing that water wets the solid surface (water dissociation is not allowed). (Middle) Drop profiles obtained from simulation of water droplets on the various surfaces considered. As W decreases (Left) the contact angle systematically increases leading to hydrophobic substrates. As D decreases (Right) the contact angle changes, but not monotonically. In general the substrates remain hydrophilic, but when D = 0.62 very hydrophilic surfaces are obtained. (Bottom) Simulation snapshots for the most hydrophobic (Left, W = 0, contact angle approximately 130°) and the most hydrophilic (Right, D = 0.62, contact angle approximately 30°) substrates considered herein.

In Fig. 1, Middle, we show the drop profiles used to calculate the contact angles from our simulations as W and D vary. Macroscopically, the MgO surface, originally hydrophilic, becomes hydrophobic when W decreases. The contact angle changes non monotonically as D decreases, although remaining in all cases lower than 90° (consistent with hydrophilic surfaces), and reaches approximately 30° when D = 0.62. The nonmonotonic dependence of the contact angle with changes in D is found to depend on the structure of interfacial water, as detailed in SI Text, section 1, consistently with MD results reported by Giovambattista et al. (27) and by Lee and Rossky (28) for water on various model surfaces.

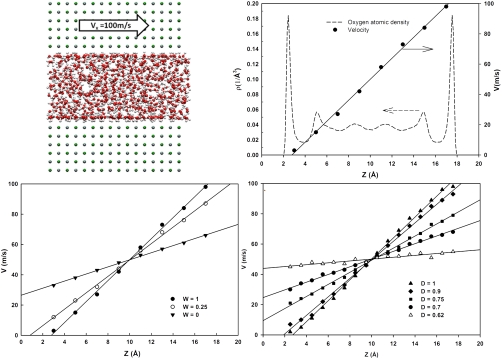
In Fig. 2, Upper Left, we report one simulation snapshot to illustrate the protocol implemented for determining the presence/absence of liquid slip (details in Appendix). To investigate the presence/absence of liquid slip one could implement either the Couette or the pressure-driven Poiseuille flow. Hydrodynamic slip is independent of the flow type (29). Following Thompson and Troian (14), we simulate a Couette flow. Two parallel mirror-image solid surfaces are displaced along the Z axis. The bottom surface is maintained at a fixed location. The top surface is displaced along the X direction with a constant velocity, v_X = 100 m/s. Admittedly, the resultant shear rate, which is limited by the current state-of-the-art computational resources, is much higher than shear rates typically explored experimentally (30), yet comparable to those found in high performance lubrication applications such as rocket engines and computer disk drives (31). Nevertheless, important insights can be attained from simulations, as shown, for example, by Martini et al. (22). In most simulations reported here the atoms within the solid are maintained rigid. To ensure that this simplification does not introduce spurious effects (32), we conducted representative simulations in which the surface atoms vibrate, while maintaining the entire system at the desired temperature. No statistically significant differences were observed between the results obtained for MgO. It should also be pointed out that the Couette-type simulations are initiated after the thin film of water confined within the slit-shaped pores has been equilibrated at ambient conditions. Consequently, liquid water wets all surfaces considered in the nonequilibrium simulations discussed herein.

Fig. 2.

(Upper) Simulation snapshot illustrating the protocol implemented to study the transport properties for confined water in a Couette flow (Left). The bottom surface is maintained in its fixed position, whereas the top one is moved with constant velocity of 100 m/s (0.001 A/fs) along the X direction. When the Couette flow is fully established we can study the density profile of the oxygen atoms of the confined water, as well as the velocity of the confined water molecules along the X direction as a function of their position within the narrow slit-shaped channel (Right; example for MgO substrate). When the velocity of the water molecules in contact with the solid substrates equals that of the solid (as in the case of MgO) the simulations suggest no slip. On the contrary, when the water velocity in contact with the solid surface differs from that of the solid, hydrodynamic liquid slip is observed. (Lower) Velocity profiles for confined water molecules as a function of the position within the narrow slit-shaped channel when reducing W from 1 to 0 (Left) or D from 1 to 0.62 (Right). In all cases T = 300 K. The results show that when W = 0.25 slip begins to be observed (it becomes very evident at W = 0). More interestingly, slip is also detected for hydrophilic surfaces, when D is 0.75 or less. Lines are guides to the eye. Estimations for slip lengths, useful for hydrodynamic calculations, can be attained by extrapolating the velocity profiles shown above to the distance at which the fluid velocity equals the surface velocity (34). For example, when D = 0.62 the slip length is approximately 6.7 nm.

At steady states the water molecules confined in the gap between the two surfaces manifest a characteristic velocity profile [v_w,X(z)]. In Fig. 2, Upper Right, we show the oxygen atomic density profile and the velocity profile for water molecules as a function of their Z position. The reference z = 0 is the center atomic position of the top layer of the bottom surface. The temperature is maintained at 300 K, as in all other cases. The surfaces considered are MgO. The results show that the contact water layer at z = 2.5 Å has the same velocity as the immobile surface. This observation confirms that MgO shows no liquid slip, in qualitative agreement with the contact angle of approximately 47°, denoting hydrophilic properties. In Fig. 2, Lower, we compare the velocity profiles for confined water molecules as a function of their position within the slit-shaped pore when W (Left) and D (Right) decrease. Liquid slip appears when the velocity of those water molecules in contact with the solid show different velocity than the solid. No slip is found otherwise. As W decreases the surface becomes more hydrophobic, whereas as D decreases the surface remains hydrophilic and the contact angle can be as low as approximately 30° (see Fig. 1). The results in Fig. 2, Bottom Left show that whereas the MgO surface is characterized by no slip, as the surface becomes more hydrophobic liquid slip appears, as expected (18). More interestingly, when the surface becomes very hydrophilic (D = 0.62) (Fig. 2, Bottom Right) slip is also possible, which contradicts conventional wisdom. It should be reiterated that for all cases considered the surfaces are atomically smooth and water wets all surfaces. The extent of hydrodynamic slip is expected to depend on the shear rate. Representative results at a shear rate half of that considered in Fig. 2 are reported in SI Text, section 2. In qualitative agreement with Thompson and Troian (14), our results show that the extent of slip decreases as the shear rate decreases. To estimate the extent of slip at much smaller shear rates, in alternative to nonequilibrium MD simulations one could employ the Green–Kubo formalism as applied to results from equilibrium simulations, following for example Barrat and Bocquet (11). These Authors found that slip lengths estimated conducting nonequilibrium MD simulations were comparable to those obtained employing the Green–Kubo formalism for Lennard–Jones fluids simulated at equilibrium between two solid surfaces.

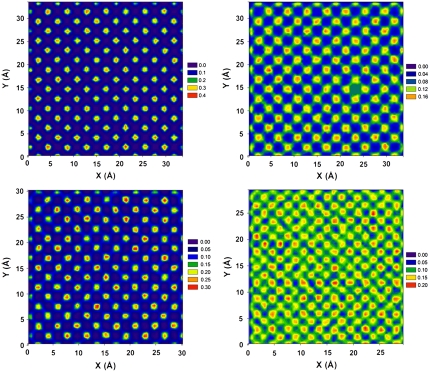
In Fig. 3 we report the in-plane density profiles obtained from equilibrium simulations for water molecules within the first layer near four surfaces: the MgO surface (Upper Left); the W = 0 surface (Upper Right); the D = 0.9 surface (Lower Left); and the D = 0.70 surface (Lower Right). These results are obtained for water confined within the slit-shaped pores used for the Couette-flow calculations, but at equilibrium (v_X = 0 m/s). On the two surfaces on the left no hydrodynamic slip is observed. The transition from no-slip to slip is observed when D decreases to 0.75 and below. Slip is observed on both surfaces on the right (see Fig. 2). The density profiles of Fig. 3 suggest that for slip to occur it is necessary for the water molecules adsorbed on the contact layer to be able to migrate from one adsorption site to the next without leaving the contact layer, irrespectively of the contact angle.

Fig. 3.

Surface density distribution of water molecules in the first layer on MgO surface (Upper Left), W = 0 surface (Upper Right), D = 0.9 surface (Lower Left), and D = 0.70 surface (Lower Right). Densities are expressed in number of atoms per ų. The red areas indicate the positions preferably occupied by water molecules in the contact layers. On the MgO surface (Upper Left) and on the D = 0.9 surface (Lower Left) water molecules adsorb in well defined adsorption spots. No connection between these high-density regions implies that water molecules seldom migrate from one to another. As a consequence, no hydrodynamic slip can be observed. On the W = 0 (Upper Right) and on the D = 0.70 (Lower Right) surfaces the preferable adsorption sites are connected to each other (see green lines connecting the yellow/red spots). On these surfaces water molecules can easily migrate from one preferable adsorption site to a neighboring one, leading to liquid slip.

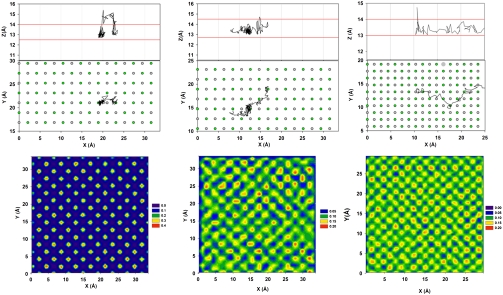
In Fig. 4 we report the trajectory of representative contact water molecules near three substrates as obtained after the Couette flow is fully established. Lateral and top views of the trajectories are reported in Fig. 4, Top and Middle, respectively. The lateral views identify, via two red lines, the position of the contact water layer. The top views also report the atomic positions on the solid substrates. The Left panels in Fig. 4 are for contact water on MgO (which shows no slip). The center panels are for contact water on the W = 0 surface (which shows slip). The right panels are for contact water on the D = 0.70 surface (which shows slip). The trajectories have been obtained from 35, 20, and 30 ps—long simulation fragments, respectively. On MgO (Left), to migrate from one adsorption site (on top of a surface Mg atom) to a neighboring one, the water molecule has to first desorb from the contact water layer, manifesting a hopping diffusion mechanism. On the contrary, the water molecules on either the W = 0 and D = 0.70 surfaces easily migrate from one adsorption site to a number of neighboring others without necessarily leaving the contact layer. This slide mechanism is possible because the preferable adsorption sites are connected to each other on the W = 0 and D = 0.70 surfaces. As a quantification of the interpretation just provided, in Fig. 4, Lower, we report the density distributions of water molecules at contact with the three surfaces just described. These results differ from those presented in Fig. 3 because they are obtained after the Couette flow has reached steady states. On MgO the density distribution obtained when shear is applied (Fig. 4, Lower Left) is practically indistinguishable from that obtained at equilibrium (Fig. 3, Upper Left), because water molecules move from one preferential adsorption site to another following the hopping trajectories described above. On the contrary, the density distributions obtained under shear on the W = 0 and on the D = 0.70 surfaces (Fig. 4, Lower Center and Lower Right) clearly show the formation of “density bridges” that connect the preferential adsorption sites observed at equilibrium (see Fig. 3, Left). These density bridges are due to water molecules sliding from one preferential adsorption site to another upon the application of shear, following the trajectories described in Fig. 4, Top and Middle.

Fig. 4.

(Upper) Trajectory of three representative water molecules as they migrate from one adsorption site to neighboring ones on MgO (Left; no slip), W = 0 surface (Center; slip), and D = 0.70 surface (Right; slip). The two red lines on the top panels identify the position of the contact water layer. Surface solid atoms are identified by green and gray circles (Mg and O, respectively). The black line describes the trajectory of one water molecule. On the MgO substrate the trajectory is 35 ps long. On the W = 0 surface the trajectory is 20 ps long. On the D = 0.70 substrate the trajectory is 30 ps long. (Lower) Planar density distributions are reported on the bottom panels for water molecules at contact with the three surfaces after the Couette flow is fully established.

To verify whether the distribution of water molecules on the contact layer is sufficient to support hydrodynamic slip vs. no-slip conditions we conducted additional simulations for the D = 0.7 surface (on which hydrodynamic slip was observed), in which we doubled the electrostatic interactions between water and surface (W = 2 in the nomenclature adopted herein). As shown in SI Text, section 3, our results show that the new surface does not support hydrodynamic slip, as expected because the water molecules adsorbed at contact with the surface are tightly bound to their respective preferential adsorption sites and therefore cannot slide following trajectories such as those shown in Fig. 4, Center and Right.

Conclusions

In conclusion, in this contribution we demonstrated, using molecular dynamics simulations, that slip and no-slip boundary conditions can both be observed for liquid water flowing on solid surfaces on which the static water contact angle is less than 90°. The responsible molecular signature appears to be the distribution of water molecules within the contact layer at equilibrium, coupled with the strength of water–surface interactions. When preferential adsorption sites exist that are sufficiently close to each other that water migration from one to the next can occur without requiring hopping events, hydrodynamic liquid slip occurs. Because of computing-power limitations, the shear rates considered herein are high, but comparable to those found in high performance lubrication applications [e.g., rocket engines (31)]. When verified experimentally our results could lead to the advancement of a variety of applications, including the design of hydrophilic nanoporous membranes with high permeation and self-cleaning hydrophilic surfaces. The desired surfaces should permit atomic-scale sliding of contact water molecules, which could be attained by providing a sufficient amount of preferential adsorption sites, by, for example, atomic-scale etching, molecular grafting, or by integrating nanoparticles on a surface.

Appendix: Simulation Methods and Algorithms

All simulations were conducted using LAMMPS (33), and performed at ambient conditions. Water was simulated implementing the SPC/E model (25), MgO via the CLAYFF force field (26). The algorithms implemented to study equilibrium properties of contact water molecules, including their limitations, are described at length elsewhere (20). Following ref. 27, the contact angle was assessed by equilibrating a droplet of 1,000 water molecules on the desired surfaces. A plane perpendicular to the surface and passing through the droplet center of mass was identified. Along this plane the drop was sectioned in 0.5 Å-wide bins used to calculate the atomic densities. The vacuum–water interface was defined when the water density decreased to 0.2 g/cm³.

Nonequilibrium molecular dynamics simulations were implemented to study water transport in the Couette flow, similarly to refs. 14 and 34. A slit-shaped channel of width 2.0 nm was obtained by separating two mirror images of the solid substrate across the Z direction of the pore. Initial configurations were obtained from equilibrium simulations. The bottom surface was maintained stationary, the top one was maintained at a constant velocity of 100 m/s along the X direction. The time step was of 1 fs. The temperature was maintained constant throughout the system implementing the Berendsen thermostat. As shown in SI Text, section 4, no significant differences in the velocity profiles were observed when the Nose–Hoover thermostat was implemented. The simulations were continued until a linear profile for the velocity of confined water was obtained across the pore width. The pore width was divided in bins of width 1 Å to calculate density and velocity profiles. The results reported are averages over the last 2 ns of simulations.

For completeness, it should be pointed out that nonequilibrium MD simulations conducted to estimate the hydrodynamic slip can be performed implementing the algorithm described in the previous paragraph, or by thermostatting only the sliding surfaces while allowing the confined fluid to heat during the course of the simulation. Different experimental conditions are consistent with the two protocols (high thermal dissipation in the algorithm implemented herein, no thermal dissipation in the alternative). Because, as demonstrated by Khare et al. (31), the differences in the temperature profiles expected at the shear rate considered in the present work are minimal and only present at the center of the channel, the structure of interfacial water will not depend on the thermostat, and the conclusions from the present work will hold independently on the situation considered.

Supplemental Information

Detailed information regarding the changes in the contact angle for water on the MgO surface as a function of the parameter D (SI Text, section 1), velocity profiles for confined water after the Couette flow is established at half the shear rate considered in the manuscript (SI Text, section 2), velocity profiles for water confined between two surfaces characterized by W = 2 and D = 0.7 (SI Text, section 3), and velocity profiles obtained when the Berendsen or the Nose–Hoover thermostat are implemented (SI Text, section 4) are provided as SI Text.