Laboratory simulations show diabatic heating drives cumulus-cloud evolution and entrainment

Abstract

Clouds are the largest source of uncertainty in climate science, and remain a weak link in modeling tropical circulation. A major challenge is to establish connections between particulate microphysics and macroscale turbulent dynamics in cumulus clouds. Here we address the issue from the latter standpoint. First we show how to create bench-scale flows that reproduce a variety of cumulus-cloud forms (including two genera and three species), and track complete cloud life cycles—e.g., from a “cauliflower” congestus to a dissipating fractus. The flow model used is a transient plume with volumetric diabatic heating scaled dynamically to simulate latent-heat release from phase changes in clouds. Laser-based diagnostics of steady plumes reveal Riehl–Malkus type protected cores. They also show that, unlike the constancy implied by early self-similar plume models, the diabatic heating raises the Taylor entrainment coefficient just above cloud base, depressing it at higher levels. This behavior is consistent with cloud-dilution rates found in recent numerical simulations of steady deep convection, and with aircraft-based observations of homogeneous mixing in clouds. In-cloud diabatic heating thus emerges as the key driver in cloud development, and could well provide a major link between microphysics and cloud-scale dynamics.

Clouds have been termed the “big bad player in global warming” (1) and are listed among the most urgent scientific problems requiring attention by the Intergovernmental Panel on Climate Change (2); more effective cumulus parameterization schemes can significantly improve predictions of the Indian monsoons. In particular, convective clouds (3) represent a set of complex interactions among microphysics, flow turbulence, and radiation (4). They involve multiple phases, some of which change into each other releasing or absorbing considerable quantities of heat, whereas many (including aerosols) affect radiative transfer. Much attention has recently been devoted to investigating the interaction between fine-scale cloud turbulence and water-droplet distribution and growth, and between cloud and radiation (2, 4–6). However, cloud-scale dynamical processes, in particular the entrainment and mixing that affect microphysics (2), rain formation (7), and cloud lifespan, remain puzzles despite numerous studies over the last five decades. To this day there are no satisfactory fluid-dynamical models for cloud flows, and entrainment continues to remain a matter of deep concern (8). In fact, the connections between cloud fluid dynamics and microphysics pose a major scientific challenge (9).

Here we show how a variety of observed cumulus-cloud types (sometimes even shapes), and their associated life cycles, can be successfully simulated in the laboratory. This capability enables direct measurement of entrainment rates using laser-Doppler and particle-image velocimetry. The data so obtained exhibit the so-called anomalous entrainment characteristics (10) that have remained serious problems in cumulus-cloud modeling. Analysis of the data suggests that in-cloud diabatic heating, including its variations in time and altitude, can play a central role in determining the evolution and entrainment dynamics of cumulus clouds.

Background

The ability to simulate cloud processes under controlled and repeatable conditions in the laboratory has long been recognized as a potentially valuable aid in studying cloud physics and dynamics. Many laboratory studies have been directed toward understanding the effect of small-scale turbulence on droplet microphysics (5, 9), among other issues. Recent experiments on a jet of moist air in a cloud chamber (11) have shown that the small-scale turbulence at the cloud-clear air interface is anisotropic. In another laboratory study (12) cloud-top entrainment induced by radiative effects in stratiform clouds was simulated. None of the experiments devised to date, however, has been able to shed light (9) on the interaction of microphysics with such cloud-scale turbulent processes as entrainment in cumulus clouds. In the present work we describe an apparatus capable of simulating such processes in the laboratory. This apparatus differs from others in use in two essential ways. First, it generates externally controlled amounts of volumetric heat within the flow, thereby decoupling heat release from phase change; secondly, it permits working with a single-phase “cloud fluid” (water in the present instance), enabling us to focus on the essential macroscale physics of cloud flows.

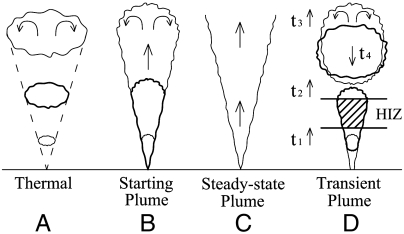
Laterally entraining turbulent plumes and thermals (Fig. 1 A–C) have been proposed in the past as physical models for cumulus-cloud flows, often employing self-similarity ideas (13–16). Such models are severely limited (17) and stand discredited by observations (especially in shallow cumuli), as they overpredict entrainment rates and underpredict cloud-top height (18–20). These discrepancies, which have been collectively referred to as entrainment “anomalies” (10), have so far remained without a satisfactory dynamical explanation. This failure was in part due to the assumption of a self-similarity that is not applicable to cloud flows (16). Furthermore, these models could not account for the Riehl–Malkus protected cores (21) observed in midtropospheric clouds. Alternative proposals, such as episodic vertical mixing (22, 23) and shedding thermal (16) models, have been found to be applicable primarily close to the cloud top (16, 24, 25). Some recent studies (25–27) show that lateral entrainment rates in cumulus clouds are large near cloud base and drop significantly at higher altitudes. Again no available cloud model adequately explains these observations.

Fig. 1.

(A–D) Schematic of different physical models for cumulus-cloud evolution with time. Arrows inside plumes indicate the direction of mean motion relative to plume head.

Herein we propose [extending earlier work on steady flows (10, 28, 29)] the transient plume subjected to off-source diabatic heating as an appropriate low-order physical model for nonprecipitating cumulus-cloud flows. The transience of the plume reflects the fact of generally short cumulus life times [O (10³–10⁴ s) in nature and O (10² s) in the laboratory]. [Another instance where a nonstationary entrainment model has been proposed is magmatic systems (30).] Volumetric heat generated in an appropriate region of the plume simulates the release of latent heat above condensation level in clouds, including other contributions such as from radiation. The present model (Fig. 1D) thus emphasizes the inherently nonself-similar and evolutionary character of turbulent cloud-flow dynamics, and provides a unified framework to explore entrainment/detrainment across the whole cloud boundary.

Simulated Cloud Forms and Evolution

The canonical cloud flow studied here is basically a round turbulent plume or jet. The flow apparatus (Fig. 2) built for the purpose represents a considerable enhancement in capability over the original version (10) which was intended chiefly for investigating steady flows. The off-source diabatic heating is achieved through ohmic losses generated in the plume fluid, which is water rendered electrically conducting (“active”) by addition of acid (see Materials and Methods and SI Text, section 1). The appropriate nondimensional parameter for fluid-dynamical simulation of the diabatic heating experienced by the cumulus clouds is the heat-release number (10),

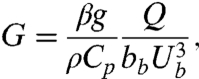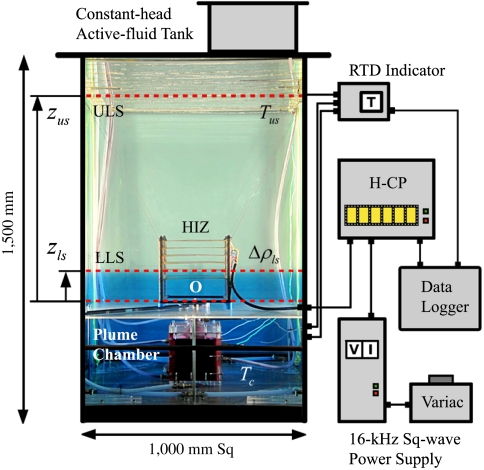
where β is coefficient of thermal expansion of the cloud fluid, g is acceleration due to gravity, C_p and ρ are respectively specific heat at constant pressure and density of the ambient fluid, Q is off-source volumetric heating rate, and b_b and U_b are length and velocity scales; e.g., at condensation level in the cloud or beginning of heat generation in the apparatus. In the atmosphere Q is O (1 Wm^-3) (31) and G = 0.1–2 (28). The same range of values of G can be obtained in water subjected to a heating rate of O (4 MWm^-3), which over a volume of order 250 cm³ is a manageable 1–2 kW. The heat “injection” zone (HIZ) extends over a selected height range in the plume (Fig. 2 and Fig. S1), over which flow is accelerated by the enhanced buoyancy due to heating. Both heating “history” (i.e., temporal variation of Q) and its “profile” (distribution in the vertical) can be varied in the apparatus, enabling generation of any model flow in Fig. 1, and management of flow evolution by manual active control. The apparatus can also simulate the boundary-layer-topped inversion that subjects the cloud to stratification at lower levels (LLS), and/or the trade-wind inversion which does the same at higher levels (ULS); in between, the ambient fluid (nonconducting deionized water) is neutrally stable.

Fig. 2.

Photo schematic of the present apparatus. Active fluid issues vertically upward into tank of deionized water from an orifice (O) at the base. Flow is ohmically heated in the HIZ which consists of a set of six netted electrodes placed across the flow. Heating rate and profile are controlled by varying supply voltage over appropriately selected electrodes through the heating-control panel (H-CP). A lower-level stratification (LLS) can be created at z_ls by introducing urea solution into the bottom of the tank. The upper-level stratification (ULS) can be created at z_us by activating a wire heater just below the free surface of the water in the tank. Temperature is measured at three points: in the plume chamber (T_c), in the ambient fluid (T_a), and at the ULS (T_us), using resistance temperature detectors (RTD). Δρ_ls is the density jump at the LLS.

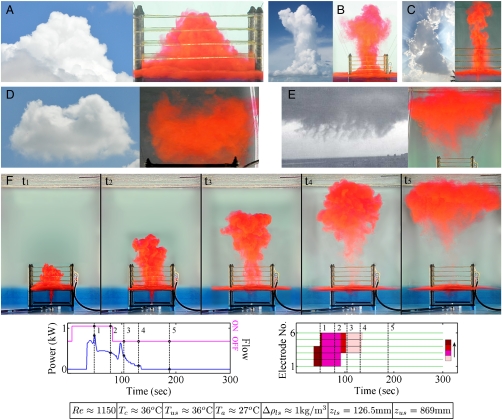
To demonstrate the versatility and power of the present experimental technique and flow model, we first illustrate pictorially a few of the many varieties of cumulus flows that can be created in the apparatus merely by varying flow, heating and stratification parameters (other examples can be found in ref. 32). Fig. 3 presents a set of five paired images comparing laboratory-simulated cloud flows with observed natural clouds (henceforth “simulations” and “clouds” respectively; corresponding heating histories and profiles are given in Fig. S2). Fig. 3A depicts a typical cumulus congestus formed when convection is vigorous and heat generation occurs over an appreciable volume. (Cloud types are designated as in ref. 33.) In the simulation, plume growth is constrained by stratification at LLS, first spreading active fluid around this level. With injection of sufficient heat active fluid penetrates the inversion (compare Fig. 3F) and forms a “cauliflower” shaped congestus. The cumulus “tower” in Fig. 3B is a commonly seen deep convective cloud; it has a core that seems glaciated. In such clouds considerable positive buoyancy is added near cloud base (where water-vapor concentration is high due to presence of warmer air), and then again at middle levels following glaciation, with accompanying microphysical processes and precipitation that remove condensed water from the cloud (31). In the simulation, these effects are achieved by corresponding variations in heating rate and profile over time (Fig. S2). In another example of a cumulus tower (Fig. 3C), the top is about to break away from the rest of the cloud (as discussed in refs. 34 and 35), as also seen in the corresponding simulation.

Fig. 3.

(A–F) (Rows 1 and 2) Comparison of clouds (Left) with simulations (Right). [In some pictures backgrounds of the images, especially (E) and (F), have been digitally denoised]. (Row 3) Sequence of snapshots in cumulus-cloud evolution following a Namias scenario (34). (Lower) (Left) Heating and flow history, (Right) heating profile during cumulus evolution; color code at extreme right shows increased rate of heating in the direction of the arrow. Reynolds number is defined as Re = Ud/ν, where U is orifice-exit velocity, d is orifice diameter and ν is kinematic viscosity. For other symbols see Fig. 2 caption. Note that the temperatures are averaged over the duration of the experiment. Classification: (A), (B), (C), (F): t₁–t₄)—cumulus congestus; (D)—cumulus mediocris (in dissipating stage); (E)—cumulus fractus (popularly known as “scud”); (F): t₅)—altocumulus cumulogenitus. The natural cloud in (E) is from ref. 36 and in (B) image from NOAA Research, courtesy of Jim W. Lee, National Weather Service.

The relatively shallow cloud and the accompanying simulation in Fig. 3D indicate weak convective motions as in cumulus mediocris. The diffuse base and edges indicate a dissipating cloud. In the simulation, heating is injected for a short duration to make the active fluid rise, and then both power and flow are switched off (Fig. S2). This produces, in combination with the ULS, a slowly sinking transient plume whose shape (including the saddle-like depression on the top surface) is strikingly similar to that of the counterpart cloud. Both cloud and simulation appear to be tending toward a cumulus fractus characterized by frayed edges.

Fig. 3E shows an example of a cloud with shreds dangling below the nominal cloud base, perhaps dragged down by precipitation loading and/or evaporative cooling. In the simulation the heating history and profile are the same as in Fig. 3F: heat is added for 100 s and then switched off along with the flow. At the time of the picture (t = 265 s) the top of the simulation plume is held nearly stationary by the warm ULS, and the heavier fluid near the base starts descending. The rather irregular descent is probably due to inhomogeneities caused by convective turbulent motion, in nature (36) as in the laboratory, resulting in the frayed edges of a cumulus fractus.

We now illustrate simulation of an evolving cumulus-cloud flow. Fig. 3F (with lower panels showing heating history and profile) is a sequence of snapshots depicting major stages in the evolution of a cumulus congestus into an altocumulus (culminating in the image in Fig. 3E). At t₁ we see the classical cauliflower type congestus which turns into a tower at t₂. Here the LLS, mimicking a boundary-layer-capping inversion, forms the cloud base, and the convective flow is a diabatically heated starting plume. After the flow to the plume chamber is turned off and a burst of heating applied just before t₃, the transient plume thins down close to the LLS and detaches from it soon afterward. At t₄ there is neither active fluid nor heat generation in the HIZ, and the flow collects into an isolated congestus. It then ascends further and encounters the ULS between t₄ and t₅. Finally the flow spreads around z_us (at t₅), and ends up simulating an altocumulus cumulogenitus (illustrated in ref. 33, 36). The transformation seen in Fig. 3F largely follows the scenario mentioned by Namias (34) for vigorously growing clouds. Other simulated evolution histories can be found in ref. 32.

Dynamics of Anomalous Cumulus Entrainment

Fig. 3 demonstrates that the present flow model and apparatus can capture remarkably well many observed features of several cumulus-cloud types (two genera and three species) and cloud evolution through three different types. We now show that laboratory studies of diabatic plumes offer unique insights into the long-debated entrainment anomalies of cumulus clouds, and help unravel the dynamics underlying certain distinguishing features of cumulus-cloud flows. For this purpose we present a critical analysis of long-time averaged data on diabatically heated steady-state jets and plumes acquired using laser Doppler (10, 37) and particle imaging (29, 38) velocimetry. The steady flow is a limiting case of the transient-plume model, and allows us to focus exclusively on the effect of heating on lateral entrainment as a first step in understanding the more complicated dynamics of evolving clouds that involve cloud-top entrainment as well. Furthermore, it makes possible cross-validation of laboratory results with recent computations (26) of a steady-state deep convection model.

Many different definitions of entrainment rate have been reported in the cloud-physics literature (8, 15, 39). The most appropriate formulation for the present cloud-flow model is the entrainment coefficient (15) first introduced by Taylor (40),

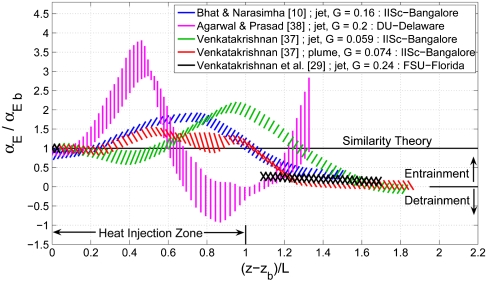
where m is the total vertical mass-flow rate at z, b the velocity width of the flow, and U_c the centerline velocity, all the quantities being long-time averages. Fig. 4 shows the vertical variation of α_E measured in three different laboratories (10, 29, 38) in apparatus similar to that originally developed in ref. 10. Four (10, 29, 37) of the five datasets shown are in broad agreement on the effect of heating. Over the lower HIZ α_E exhibits a mild increasing trend above the cloud-base level (z_b), reaches a maximum, and then falls relatively rapidly, often virtually to zero, in the upper HIZ and/or beyond. This variation is broadly consistent with observations in natural clouds (25, 41, 42). The fifth dataset (38) shows α_E rising first to a very high value in the lower HIZ, later falling to zero or even negative values in the middle, and rising once again toward the end. Although the precise reasons are not known, the excessive turbulence levels found at the base of HIZ in the experiments may be responsible, among other factors (43), for this behavior (SI Text, section 3 and Table S1). Otherwise the overall results of Fig. 4 clearly show that, with off-source heating, values of α_E depart significantly from the constancy suggested by similarity theory. A plausible explanation for such behavior stems from current understanding of the fluid dynamics of mixing in turbulent shear flows. In this picture molecule-level mixing (44) in such flows is preceded by two other stages (45, 46), namely engulfment of ambient fluid by coherent structures in the flow, and drawing the engulfed fluid into stretched and squashed shapes that vastly increase their interface area through a stirring action (also called “mingling”). Visualization by laser-induced fluorescence has shown (10, 28, 37) that off-source heating disrupts coherent structures in the upper region of HIZ and beyond, and can therefore disable the entrainment process at the engulfment stage itself (see also refs. 47 and 48). Furthermore, experiments (28) in steady diabatic plumes have also revealed the presence of the protected cores of ref. 21 (see SI Text, sections 4 and 5 and Figs. S3 and S4). Taken together with the demonstration of nonsimilarity, the present diabatic-plume model helps resolve major puzzles in cumulus entrainment dynamics (16).

Fig. 4.

Vertical variation of measured entrainment coefficient, with uncertainty band (see SI Text, section 3), in diabatically heated steady jets and plumes. L denotes vertical extent of HIZ, α_Eb is entrainment coefficient in unheated flow at z_b.

These results from steady-flow laboratory simulations are directly applicable to tropical deep convection, for which steady-state numerical solutions of a fully compressible cloud-resolving model (CRM) have recently been presented (26). The computations are carried out for a cloud system in radiative-convective equilibrium with a model for microphysics (49). A major output of this work is a dilution-related variable termed “purity” (p), obtained by releasing passive “purity tracers” at cloud base z_b and computing their concentration in “cloudy parcels” (taken as those with liquid-water mixing ratio > 10^-5 kg/kg and updraft velocity > 1 m/s) at any height z. A time-averaged flux-weighted purity (p_c) is then computed, with p_c(z_b) = 1. To make connections with the experiments reported here, we need a surrogate for liquid-water content in the natural cloud. This may be formulated, to a first approximation, by realizing that the latent-heat release accompanying condensation into liquid water results in temperature differences, which are present in the laboratory simulation by heat generation in dye-colored active fluid. The dye particles used for flow visualization in the laboratory can, therefore, act as the purity tracers of ref. 26. We now introduce the concept of a “diabatic purity” (p_d) for laboratory flows based on dye concentration. To facilitate comparison with the results in ref. 26 we further define a flux-weighted average diabatic purity, which can be written as

(see Materials and Methods for the derivation), with p_d(z_b) = 1.

Fig. 5 compares laboratory estimates of purity with the CRM values (26). From unity at z_b the diabatic purity drops rapidly in the HIZ, displays a “knee” at (z - z_b)/L ≅ 1, and decreases much more slowly further above. The extreme limits in variation of p_c obtained in the CRM solutions (26) for different grid resolutions, shown in Fig. 5, also display a similar knee around z - z_b = 1.8 km. This length is therefore used as a surrogate for L to normalize z - z_b in these computations (see SI Text, section 5). The close agreement of the index of entrainment-driven dilution from laboratory experiments with the CRM results, seen in Fig. 5, lends support to the present diabatic-plume model of cumulus-cloud flows.

Fig. 5.

Comparison of flux-weighted average purity in the laboratory experiments with that in the CRM computations (26). The error bar shows typical uncertainty in the measurements of Venkatakrishnan (37).

A further point must be noted. Whereas the laboratory data on α_E do not extend very much beyond z - z_b = L, the CRM solutions go all the way to the tropopause. The behavior of purity in the height range 3–9 km (above z_b) seen in Fig. 5 indicates another cycle of higher and lower entrainment in the CRM results, due to glaciation now rather than condensation as in the first cycle. Glaciation appears to start soon after condensation (see figure 8 in ref. 26), and it is for this reason that the plateau near 1.8 km in the CRM solutions is not as marked as in the laboratory.

Implications of Laboratory Cloud Simulations

As an illustrative example of the far-reaching implications of the present findings, we present here the case of “homogeneous” vs. “inhomogeneous” mixing [as it has been called (7)] in clouds. This is of great significance in current microphysical studies (7, 9). Mixing of environmental with cloudy air is called homogeneous (inhomogeneous) if the ratio of the turbulent mixing time scale (τ_mix) to a thermodynamic time scale associated with droplet evaporation (7) is small (large). In recent airborne measurements of trade-wind cumuli (50), the mixing was found to become more homogeneous with increasing height from cloud base (with τ_mix decreasing approximately from 12 s to 7 s over a height of about 650 m; see SI Text, section 6). In another study (7) the mixing was reported to be predominantly homogeneous near cloud tops in two growing clouds out of the four on which measurements were made. Qualitatively similar behavior is observed in the present experiments on steady diabatic flows, in which rough estimates of the turbulent mixing time scale indicate that it decreases approximately by a factor of two (from 1.5 s to 0.7 s) with height over the extent of the HIZ (for details on the estimates of τ_mix see SI Text, section 6 and Table S2). This is consistent with lower dilution due to the distortion [owing to axial acceleration (47, 51)] and disruption of coherent structures (10, 48), accompanied by faster mixing due to intensification of small-scale vorticity caused by the baroclinic torque (48), both resulting from off-source diabatic heating. These physical effects make conditions favorable for more homogeneous mixing as we move up beyond cloud base.

Another area where the present results can prove of value is the representation of convective clouds in weather and climate models. In certain parameterization schemes using plume models (52, 53), the mass-flux profiles generated are particularly sensitive to the precise variation of the environmental-inflow rate with height (52), and its specification so far has been more or less ad hoc. Data like those in Figs. 4 and 5 can provide a rational basis for more realistic specification of cloud-dilution rates. This can potentially enhance the effectiveness of cumulus parameterization schemes, thereby improving skill in weather/climate predictions.

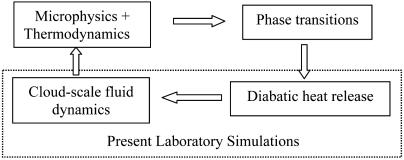
The success of the present laboratory simulations suggests that diabatic off-source heating, with its temporal and spatial variations, may be the missing link between cumulus microphysics and macroscale dynamics. The block diagram in Fig. 6 summarizes the emerging picture. We believe simulations of the type presented here offer a powerful tool that can complement the current emphasis on the effect of small-scale turbulence on cloud physics.

Fig. 6.

Block diagram showing the proposed first-order connections between certain major aspects of the physics and dynamics of cumulus clouds.

Materials and Methods

Experimental Procedure.

In the beginning, the test tank is filled with deionized water. The active fluid supplied to the plume chamber is prepared by adding about 6 mL of hydrochloric acid per liter of deionized water, along with a small quantity of anodizing dye (Aludin Red PVC) for coloring the flow, and acetone for density balance. Lower-level stratification is introduced into the tank by adding urea to deionized water in a separate tank and slowly pumping the solution through each of four diffuser sectors on the floor of the tank (Fig. S1). The flow rate is kept low to avoid disturbances and is carefully adjusted to be the same through all the sectors. Once there is enough water in the tank, the upper-level free-surface heater is turned on for about 10–30 min to obtain the required temperature rise (2–9 °C in present experiments) to effect upper-level stratification. To perform whole-field flow visualization, the region of interest is illuminated using LED (light emitting diode) panels and halogen lamps. Videos and photographs are captured using a Nikon D-90 DSLR camera. The values of temperature, voltage, and current are recorded over the entire duration of the experiment (typically 5 min for one run). Using real-time data displayed by the data-logger as sensor inputs, and the flow-control valve, applied voltage and control-panel switches as actuators, active control can be exerted manually to manage the flow.

Estimation of Diabatic Purity (p_d).

In the CRM computations (26), the flux-weighted average purity of cloudy updrafts at a given altitude z is 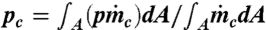, where the integral is taken across the cloud area A(z) and 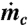is cloudy updraft mass flux (i.e., mass-flow rate per unit area); note that both p(z_b) and p_c(z_b) = 1 by definition. On lines similar to Romps and Kuang (26), the flux-weighted average concentration of dye particles (which serve as purity tracers in the laboratory) is . To calculate “cloudy” mass flux in the laboratory flows we write 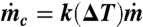, where k is an analogue of the “activity operator” of ref. 8, ΔT (a surrogate for the liquid-water content in ref. 26) is the excess temperature of the diabatically heated flow over the corresponding unheated flow, and 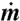is the measured mass flux. (Note that k = 1 for cloudy parcels and 0 otherwise). Because ΔT was not measured in the experiments of refs. 10 and 37, it is not possible to determine the activity operator k directly. In another study (54), temperature measurements in the HIZ in a heated jet show that the time-averaged ΔT (and hence also the probability of finding a parcel with higher ΔT) is higher near the core of the flow than at the edges, as the laboratory flows in question (10, 37, 54) are statistically stationary. This implies that the action of k is to reduce the effective width of the flow. It is thus reasonable to assume that the effect of this reduction on the terms 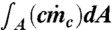and 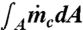is of the same order, and therefore 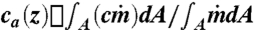. The average diabatic purity for the laboratory flows can now be defined as p_d(z) = c_a(z)/c_a(z_b) (choosing the value at the base of HIZ for normalization). Noting that 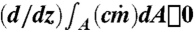because dye mean flux must be conserved, we have c_a(z)/c_a(z_b) = m(z_b)/m(z), where 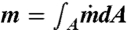. Thus the diabatic purity may be estimated as p_d(z) = m(z_b)/m(z). Note that the diabatic purity, derived here, is best seen as a laboratory counterpart of (and not necessarily identical to) the purity computed in ref. 26. However, both are dilution-related in the same way as detailed above and this makes the comparison in Fig. 5 in the main text meaningful. (See SI Text, section 5 for further details.)