Global biodiversity and the ancient carbon cycle

Abstract

Paleontological data for the diversity of marine animals and land plants are shown to correlate significantly with a concurrent measure of stable carbon isotope fractionation for approximately the last 400 million years. The correlations can be deduced from the assumption that increasing plant diversity led to increasing chemical weathering of rocks and therefore an increasing flux of carbon from the atmosphere to rocks, and nutrients from the continents to the oceans. The CO₂ concentration dependence of photosynthetic carbon isotope fractionation then indicates that the diversification of land plants led to decreasing CO₂ levels, while the diversification of marine animals derived from increasing nutrient availability. Under the explicit assumption that global biodiversity grows with global biomass, the conservation of carbon shows that the long-term fluctuations of CO₂ levels were dominated by complementary changes in the biological and fluid reservoirs of carbon, while the much larger geological reservoir remained relatively constant in size. As a consequence, the paleontological record of biodiversity provides an indirect estimate of the fluctuations of ancient CO₂ levels.

Partly as a result of the episodic nature of sedimentary processes, studies of the Earth's biologic, geologic, and climatic history have typically focused on isolated extreme events (1) such as mass extinctions (2–4) or anomalous excursions of stable chemical isotope records (5). Whereas the importance of unusual events may be nearly self-evident (6), a different, potentially powerful approach is to seek not what makes some events different from others, but that which is common to them all (7–10). In this way, one should expect to learn how fundamental invariants—for example, the conserved mass of certain chemical species—manifest themselves over geologic time.

Here we focus on biological aspects of the carbon cycle during Phanerozoic time [0–543 million years ago (Ma)]. Two types of records are studied: paleontological data for the diversity of marine animal (11) and terrestrial plant (12) life, and the sedimentary record of carbon isotope fractionation between carbon buried in organic form and carbon buried as carbonates (13). We find an unexpected significant correlation between the paleontological and geochemical records for the last 400 million years and provide evidence that it reflects the fluctuations of CO₂ levels in the atmosphere and oceans. Our analysis shows not only that the diversification of life appears to have depressed CO₂ levels (14), but also how deep this depression appears to have been.

The paper proceeds as follows. We first show the correlations of interest and subject them to several tests of statistical significance. We then discuss why CO₂ levels, and specific mechanisms that control them, appear to provide the link between the various records. Simple mathematical models are then formulated to clarify and quantify our arguments. Among the results is an estimate of trends in the long-term evolution of CO₂ levels, which we proceed to compare with previous efforts (15–19). Finally, we conclude with brief remarks on the relationship of our quantitative conclusions to their mechanistic interpretation.

Paleontological-Geochemical Correlations

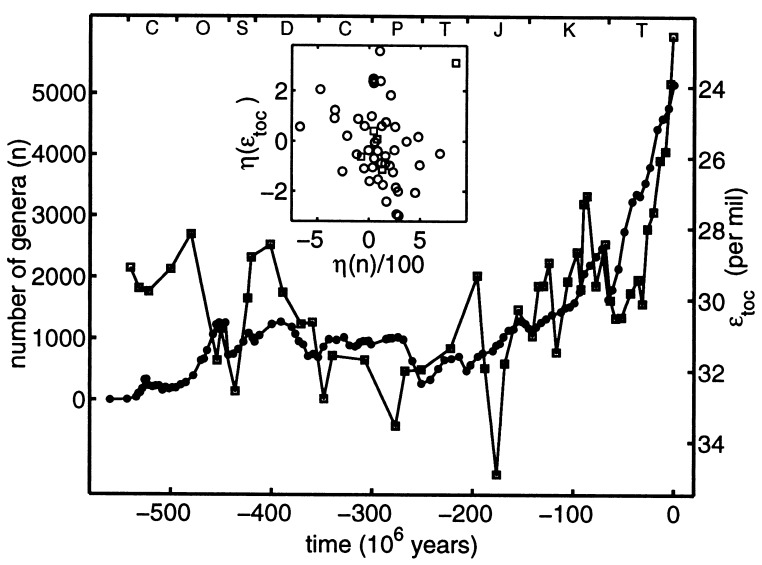
The first of two correlations is shown in Fig. 1. The data for diversity were compiled by Sepkoski† and edited by Bambach‡; they are based on the first and last geologic occurrence of 35,967 marine animal genera, including invertebrates, vertebrates, and animal-like protists (foramaniferans and radiolarians). For each of 108 geologic stages and substages that range over Phanerozoic time, the number of genera that originate or become extinct during that stage is tabulated. If a genus passes from one (sub)stage to the next (a condition satisfied by approximately 63% of the genera), it is labeled “continuing.” The time series n(t) in Fig. 1 represents the number of continuing genera at each stage or substage boundary.

Figure 1.

Phanerozoic fluctuations of diversity n(t), the number of marine animal genera (filled circles) (11), and ɛ_toc(t), the isotopic fractionation between inorganic and organic carbon [open squares, in per mil (‰)] (13). The vertical axis for ɛ_toc increases downward. The data track each other reasonably well after 455 Ma. Sample standard deviations for the geochemical data range from 0.3 to 2.9‰, averaging 1.5‰ before the Cretaceous (144 Ma) and 0.9‰ afterwards (13). Rough error bars for diversity may be inferred from ref. 11. The time scale for ɛ_toc has been revised (slightly) from the original to match the updated scheme used for diversity. The capital letters (except for K) correspond to the following geologic periods: Cambrian, Ordovician, Silurian, Devonian, Carboniferous, Permian, Triassic, Jurassic, Cretaceous, and Tertiary. (Inset) The whitened sequence η_j(ɛ_toc) vs. η_j(n) obtained by prediction-error filtering. Squares and circles represent data before and after 455 Ma, respectively.

The carbon isotope record in Fig. 1 was compiled by Hayes et al. (13). The time series shown is obtained from measurements of the isotopic composition of organic and carbonate carbon found in sedimentary rocks formed at geologic time t. From globally averaged measurements of isotopic abundance ratios R_x = (¹³C/¹²C)_x for carbon in sample x, the isotopic fractionation between sample x and a standard sample, δ_x = 1,000[(R_x − R_STD)/R_STD], is obtained for carbonate (δ_a) and organic (δ_o) carbon. The isotopic fractionation ɛ_toc between total organic carbon and sedimentary carbonates is then given approximately by ɛ_toc = δ_a − δ_o (13). Fig. 1 compares ɛ_toc(t) to n(t); the values of ɛ_toc, which were obtained from global averages of thousands of independent measurements (13), are specified at 50 discrete points in time.

The two records displayed in Fig. 1 are strikingly similar after 455 Ma. Not only do both records change sharply (increasing n, decreasing ɛ_toc) at the end of the Cretaceous (65 Ma), but visually one can see that many smaller transient fluctuations are exhibited jointly. To quantify this correlation, the more finely sampled paleontological data are resampled by linear interpolation so that they are specified at the same times t_j as the geochemical data. The Spearman rank correlation coefficient R_s (25, 26) is then computed from the resulting N pairs of n and ɛ_toc. We find R_s = −0.74 after 455 Ma. Similar results, here and elsewhere in this paper, are obtained if “standing” diversity, the number of genera extant during a given interval, is substituted for continuing diversity.

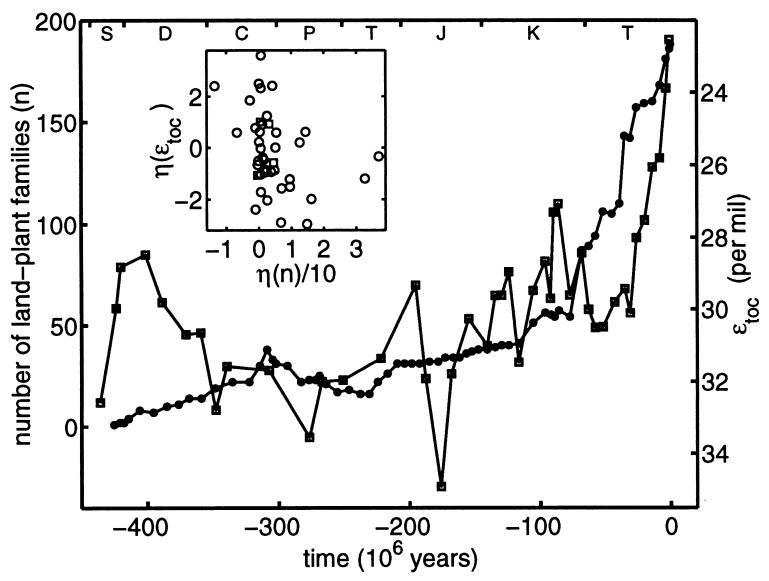
The second correlation, shown in Fig. 2, is between the diversity of land plant families (12) and the same geochemical data. The plant data§ represent standing diversity at the family level in 67 geologic stages since the rise of land plants in the Silurian (425 Ma). From the late Devonian (370 Ma) onwards, the correlation between the two records is essentially the same as that found in Fig. 1: R_s = −0.77.

Figure 2.

The diversity n of terrestrial plant families (filled circles) (12) plotted with the same geochemical data (open squares) of Fig. 1, beginning with the rise of land plants in the Silurian (425 Ma). The vertical axis for ɛ_toc again increases downward. The data track each other reasonably well after 370 Ma. The geologic time scale is the same as in Fig. 1. The diversity curve shown is the “minimal” curve of the plant family database; rough error bars may be inferred by comparison with the corresponding “maximal” curve. (Inset) The whitened sequence η_j(ɛ_toc) vs. η_j(n) obtained by prediction-error filtering. Squares and circles represent data before and after 370 Ma, respectively.

We use three different methods to assess the statistical significance P of these correlations. The results are summarized in Table 1. For completeness, we report results for the entire available interval in addition to the slightly shorter periods cited above. We argue later that only the latter periods are relevant to our conclusions.

Table 1.

Spearman rank correlation coefficients R_s from correlations of ɛ_toc with the diversity of marine animal genera and land plant families

Data	Rs	P	N	Rs	P	N
Marine animals		After 540 Ma			After 455 Ma
Raw	−0.52	0.084	50	−0.74	<10−3	45
PEF	−0.32	0.013	49	−0.40	0.003	44
Differences	−0.20	0.087	49	−0.28	0.035	44
Land plants		After 425 Ma			After 370 Ma
Raw	−0.58	0.026	42	−0.77	<10−4	38
PEF	−0.37	0.010	41	−0.40	0.007	37
Differences	−0.26	0.052	41	−0.29	0.041	37

In each case, correlations are computed three ways: by using the raw data, by correlating the output of a prediction-error filter (PEF) computed for each time series, and by correlating serial differences. Results are shown for the entire available intervals and also subsets formed by deleting the first few data points. The one-sided statistical significance P is computed by a Monte Carlo technique for the raw data and from Student's t-distribution in the other cases. 

In the first method, a Monte Carlo technique, we construct random realizations of each time series that satisfy the autocorrelations of the original data. Denoting either the diversity or ɛ_toc data as x_j = x(t_j), the method proceeds by Fourier transforming x [after multiplying by a Hanning window (26) and removing the mean] to obtain N complex Fourier coefficients x̂_k. Random time series x′_j are then generated by computing the inverse Fourier transform such that x′_j = ∑_k|x̂_k|e^{i(φ_k+2πjk/N)}, where φ_k is uniformly distributed between −π and π while satisfying the symmetries required for x′_j to be real. P values are then estimated by computing the fraction of 10⁶ simulated time-series pairs that yield rank correlation coefficients R_s less than those obtained for the actual data.¶

The second method applies a first-order prediction-error filter (27) to each time series. In principle, this converts the time series to white noise, thereby eliminating the additional variance of the estimated correlation coefficient caused by significant autocorrelation of x_j at nonzero lags (28). Denoting the white-noise sequence by η_j = x_j + ax_j−1, we choose a by minimizing the sum of the squared forward and backward prediction error, ∑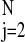(x̃_j + ax̃_j−1)² + (x̃_j−1 + ax̃_j)², where x̃_j = x_j − N⁻¹∑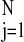x_j. We obtain a = −0.98 for both diversity series and a = −0.73 for ɛ_toc. The rank correlation coefficient between η_j(n) and η_j(ɛ_toc) is then computed, along with the associated one-sided statistical significance P obtained from Student's t-distribution with N − 3 degrees of freedom. The Insets in Figs. 1 and 2 show plots of η_j(n) vs. η_j(ɛ_toc).

The third method, included as a reference, constructs η_j by computing serial differences, i.e., by setting a = −1 above. This is equivalent to assuming that all three time series are realizations of a random walk.

Table 1 shows that all three methods find that the negative correlations quoted above are statistically significant, usually with P < 0.01. The Monte Carlo method typically yields the lowest P values, whereas serial differencing yields the highest. Because the former method requires the fewest assumptions and the latter the most, it seems reasonable to associate the greatest credence with the Monte Carlo results.

Decomposition of the Geochemical Signal

To understand why the paleontological and geochemical data correlate negatively, consider the following decomposition of ɛ_toc (13):

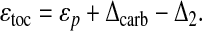1

Here ɛ_p represents the isotopic effects of primary production (i.e., photosynthesis), Δ_carb is the isotopic depletion of dissolved CO₂ in surface waters relative to sedimentary carbonate, and Δ₂ represents isotopic shifts caused by the reworking of organic carbon before burial. The quantity Δ_carb depends mainly on surface water temperature and ranges from about 7 per mil (‰) at 30°C to 10‰ at 3°C (13); this 3‰ range is much less than the 12‰ range of ɛ_toc. The secondary processes symbolized by Δ₂ are defined such that Δ₂ is positive when the process enriches the ¹³C content of organic matter. One of the principal components of Δ₂ derives from the structure of food webs: the ¹³C content of many animals is enriched by approximately 1‰ relative to its food (29–31). Thus as diversity grows, one might naively expect the size of food webs and therefore the length of food chains to grow, and thus also Δ₂, thereby explaining the negative correlation of ɛ_toc with n. However, contemporary food chains nearly always contain about four trophic levels, and this length depends so weakly on the size of the food webs within which the chains are embedded (32) that it appears unlikely that food chains are responsible for the correlation. Moreover, the net effect of all secondary biological processes is such that even the sign of Δ₂ is debated (31), and recent estimates put Δ₂ at the relatively small and constant value of 1.5‰ throughout the Phanerozoic (13). In summary, the combined fluctuations of Δ_carb and Δ₂ should amount to no more than about 3‰, which is less than one-fourth of the variation of ɛ_toc during the Phanerozoic.

The photosynthetic processes represented by ɛ_p (13, 31, 33, 34) thus encode the only plausible explanations for the bulk of the ɛ_toc's variations. Recent research indicates that plankton photosynthesis produces an isotopic shift in ¹³C content that may be approximated by the empirical relation (34)

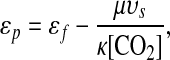2

where ɛ_f ≃ 25–30‰ (35) is the isotopic shift associated with carbon fixation, κ is proportional to the permeability of the algal cell wall, υ_s is the volume-to-surface-area ratio of the cell, μ is the specific growth rate, and [CO₂] is the concentration of dissolved carbon dioxide. The isotopic enrichment ɛ_f derives primarily from the kinetic discrimination against ¹³C by the enzyme Rubisco in the Calvin-Benson or photosynthetic carbon reduction cycle. It may be expected to have remained approximately constant in marine environments since the first appearance of eukaryotes at least two billion years ago (35). However, the physiological parameters κ, υ_s, and μ can vary significantly across phytoplankton species (33, 34). Along with [CO₂], they control the relative rate at which CO₂ diffuses into the algal cell compared to the rate at which CO₂ is consumed by photosynthetic reactions within the cell. Whereas the long-term evolution of [CO₂] should be independent of these parameters, they may have evolved in response to changes in [CO₂]. For example, decreases in [CO₂] could have led to increases in cell permeabilities κ such that the diffusive flux of CO₂ into the algal cell was relatively unchanged. Provided that such evolutionary innovations are not fully compensating—i.e., so long as κ[CO₂] increases with [CO₂]—then the correlations between diversity and ɛ_toc should reflect correlations between diversity and [CO₂]. More generally, this conclusion remains valid for any dependence of the physiological parameters on [CO₂], provided that μυ_s/(κ[CO₂]) decreases with increasing [CO₂] and no direct relationship between the physiological parameters and diversity exists.

Mechanisms and Dynamics

Unlike the short-term carbon cycle, which is dominated by exchanges of carbon between the biosphere, atmosphere, oceans, and soils on time scales ranging from about 10⁰–10⁴ years, the long-term carbon cycle is dominated by exchanges between rocks and the atmosphere and oceans on time scales of roughly 10⁵–10⁹ years (14–16, 36, 37). Three slow processes dominate the long-term evolution of CO₂ levels: chemical weathering of silicate minerals, degassing caused by metamorphic and volcanic processes, and the burial and weathering of organic carbon. Because the latter acts as an independent subcycle (14), the former—weathering and degassing—are considered the major controls on atmospheric and oceanic CO₂ levels. They are thought to be in rough balance via reactions such as (14, 36, 38)

3

A similar reaction may be written by substituting Mg for Ca. Left to right, such reactions schematically represent the uptake of CO₂ from the atmosphere, its transformation to dissolved HCO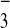 during weathering of silicate rocks, and its eventual precipitation and burial in the oceans as carbonate minerals. Right to left, the reaction represents metamorphism and magmatism and the subsequent transfer of CO₂ back to the atmosphere and oceans by volcanism and related processes.

The mechanistic basis of our observed correlations is simple: increased plant diversity should result in increased chemical weathering of silicate minerals. We assume, following others (14–18, 39), that the increased chemical and physical alterations of soils—e.g., the mechanical breakdown of rocks and the production of organic acids—induced by the advent of vascular land plants should have led to substantial increases in weathering rates. This notion is augmented with two assumptions: (i) increased plant diversity increases the area occupied by plants (by, for example, migration of plants to higher altitudes), therefore enhancing weathering rates and lowering CO₂ levels via Eq. 3; and (ii) increased weathering increases the seaward flux of limiting nutrients such as phosphorus, which in turn leads to increased marine animal diversity. The former assumption is sufficient to explain the correlation between land plant diversity and ɛ_toc, whereas the latter is also required to explain the correlation with the marine ecosystem. Both of these assumptions may be subsumed in part by the simpler supposition that global diversity increases with global productivity or biomass, a point we return to below.

To complete our argument, we must show not only that increased plant diversity can lead to lower CO₂ levels, but also that the lower CO₂ levels are dynamically stable. The rate of uptake of CO₂ by the weathering reactions should increase with the partial pressure of atmospheric CO₂, which at long time scales should be an increasing function of the total mass m_f of carbon in the Earth's fluid envelope (i.e., atmospheric and oceanic carbon) (14). We represent the bare uptake rate, in the absence of plants, by the positive monotonically increasing function k(m_f) while representing the return flux of CO₂, from volcanic and other sources, by υ [which should not depend on m_f (14)]. All other processes aside, the rate of change of the mass of atmospheric and oceanic carbon is then

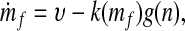4

where g(n) ≥ 1 is a monotonically increasing function that represents the ratio of the CO₂ uptake rate when plant diversity equals n to the bare uptake rate k.

The steady state m^*_f of this system occurs when ṁ_f = 0; thus

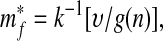5

where k⁻¹ is the inverse of k such that k⁻¹[k(x)] = x. Because k⁻¹ must also be a monotonically increasing function, Eq. 5 shows that increasing plant diversity n causes the steady-state mass of atmospheric and oceanic carbon, m^*_f, to decrease. The steady state is stable if dṁ_f/dm_f < 0 when m_f = m^*_f. From Eq. 4, one finds that m^*_f is indeed stable, because

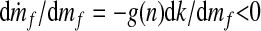6

for any m_f. This result follows immediately by noting that dk/dm_f > 0 and g(n) ≥ 1.

A complete representation of the long-term carbon cycle is of course vastly more complex (14–16, 36). The model expressed by Eq. 4 does, however, serve to formalize our main point: if increasing plant diversity increases weathering rates, then CO₂ levels fall. We proceed to quantify by how much.

Relative Fluctuations of Carbon Reservoirs

We consider the mass of three reservoirs of carbon: the fluid reservoir, already denoted by m_f, the biological reservoir m_b (i.e., biomass plus biological debris), and the geological reservoir m_g (i.e., rocks). Present-day estimates give m_b ≃ 10⁻¹m_f ≃ 10⁻⁵m_g (35, 37).

In globally averaged steady-state conditions, [CO₂] increases with m_f (40). The inverse relationship is likewise increasing, i.e.,

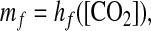7

where h_f is a monotonically increasing function.

A monotonic relationship probably also exists between diversity and m_b. Waide et al. (41) have recently compiled a comprehensive review of over 200 published relationships between present-day diversity and primary productivity, where primary productivity is broadly defined to include various surrogates, such as biomass, that vary positively with it. One of the few unambiguous patterns to emerge from their survey is the dependence of the diversity–productivity relationship on scale. Whereas at local scales (<20 km) simple relationships (positive, negative, or unimodal) are usually not found [or when they are, they are often unimodal (42)], at continental to global scales (>4,000 km), a positive correlation dominates the literature, particularly for plants. Additional evidence of such scale dependence is given in ref. 43, and examples of unambiguously positive large-scale relationships may be found in ref. 44. The positive large-scale relation may derive from the tendency of ecosystems to diversify when more energy is available for consumption (45). Similar relationships appear to hold for the past: Bambach (46) cites a wealth of evidence indicating that the biomass of marine animals has trended upward during the Phanerozoic. Thus it appears reasonable to assume that the mass m_b of the biological reservoir of carbon increases with diversity n, i.e.,

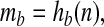8

where h_b is monotonically increasing. The assumption that increased diversity is associated with increased weathering rates may be viewed as a natural consequence of this relationship.

We may now relate the correlations between n and ɛ_toc to m_b and m_f. First, rewrite Eq. 2 as

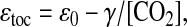9

where γ = μυ_s/κ represents the physiological parameters appropriately averaged over all phytoplankton species, and

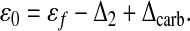10

Now assume that ɛ₀ is constant and γ/[CO₂] decreases with increasing [CO₂]. In the former case, the only time dependence should come from Δ_carb, and as we have already remarked, its mean-square fluctuations must be much smaller than those of γ/[CO₂]. Thus this assumption appears reasonable. The latter assumption is satisfied automatically if γ is constant. The less stringent condition used here derives from the aforementioned evolutionary considerations, i.e., γ can change, but never so much that it fully compensates (or overcompensates) changes in [CO₂].

Let R_l(x, y) and R_s(x, y) be the functions that compute the linear [product-moment (25)] and rank correlation coefficients, respectively, between discretely sampled time series x(t) and y(t). Because R_s is a correlation of ranks, it is invariant with respect to any monotonically increasing transformation of its arguments (25). From Table 1 and Eqs. 7, 8, and 9, we have

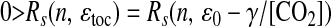11

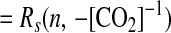12

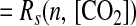13

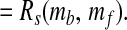14

These results derive from the invariance property of R_s, the condition that [CO₂] > 0, and the assumptions that ɛ₀ is constant, γ/[CO₂] decreases with increasing [CO₂], and γ is uncorrelated with n. The final equality shows that the mass fluctuations of the biological and fluid reservoirs of carbon are negatively correlated, with the same magnitude as found for diversity and ɛ_toc.

This conclusion may be sharpened. In the following, we assume that any measurable coupling between m_b and m_f requires m_b to be sufficiently large, as a consequence of sufficient diversification on land. We therefore explicitly consider only the period after 370 Ma, when both marine animals and land plants exhibit their strongest correlations to ɛ_toc.

Because the Earth's total carbon is conserved,

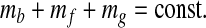15

The fluctuations m̃_i = m_i − 〈m_i〉, where 〈⋅〉 signifies the mean over the entire interval, satisfy

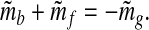16

Squaring both sides, rearranging terms, and averaging over time, one obtains

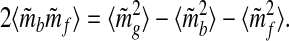17

We seek the sign of 〈m̃_bm̃_f〉. Mathematically, it must have the same sign as the linear correlation coefficient R_l(m_b, m_f). R_l and its variance may be estimated from R_s under the assumption that m̃_b and m̃_f are Gaussian. We use the relations R_l = 2sin(πR_s/6) and var R_l = (π²/9)(1 − R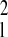/4) var R_s (25). Substituting R_s = −0.40 from Table 1 (i.e., the estimate obtained by prediction–error filtering) and an estimate of var R_s obtained by the bootstrap method (47) (averaged for both marine animals and land plants), we find R_l = −0.42 ± 0.13 (one standard deviation). Consequently, 〈m̃_bm̃_f〉 < 0 with high probability, and therefore, on substitution into Eq. 17,

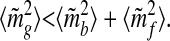18

This inequality, which we have obtained here for the long-term million-year time scale, is an important counterintuitive result. It shows that the mean-square fluctuations of the geologic reservoir are less than those of the biological and fluid reservoirs combined—despite the fact that rocks contain nearly all the Earth's carbon! The long-term depletion of m_f is therefore not only due to the growth of m_b, but most of m_f's fluctuations are complementary (i.e., of opposite sign) to m_b's. Consequently, an estimate of the changes of either quantity provides an estimate of the changes of the other.

Estimate of Past CO₂ Levels

We define the dimensionless CO₂ concentration φ = [CO₂]ɛ₀/γ and substitute into Eq. 9 to obtain

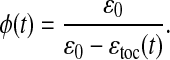19

In this formulation, the physiological parameters subsumed into γ no longer appear. We are obliged, however, to choose a value for ɛ₀. In the following, ɛ₀ ranges from 36‰ to 38‰, which is consistent with the known variations of its constituents.

Rather than obtaining φ directly from Eq. 19, we estimate it indirectly from a combination of the geochemical and diversity data of Fig. 1. We fit the estimate of φ obtained from Eq. 19 to a linear model for φ(n):

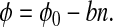20

In this model, φ₀ is the dimensionless CO₂ concentration before the diversification of animals and land plants, whereas the second term represents the first-order effect of increasing diversity. For ɛ₀ = 38‰, we find φ₀ = 6.6 ± 0.4 and b = (8.0 ± 1.7) × 10⁻⁴ by linear regression.

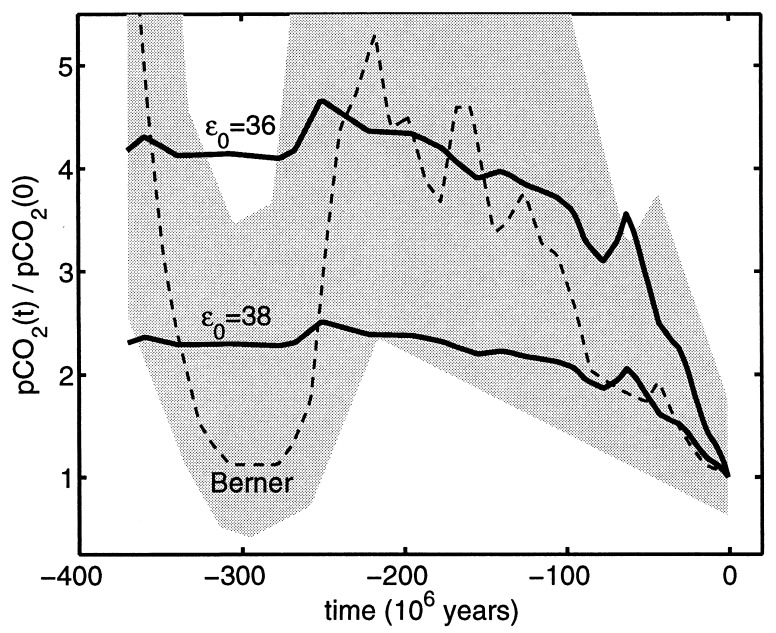
Given estimates of φ₀ and b, we then estimate φ(t) itself by setting n = n(t) in Eq. 20. The result, normalized by φ(0), is shown in Fig. 3 for the cases ɛ₀ = 36‰ and ɛ₀ = 38‰. Fig. 3 also shows a comparison with analogous predictions from the numerical model of Berner (15–18). Berner's model is a detailed integration of estimated carbon fluxes caused by chemical weathering, volcanic degassing, and carbon burial; the uncertainty of his estimates is qualitatively reflected by the gray area in Fig. 3.

Figure 3.

Smooth curves: estimates of the normalized partial pressure of atmospheric CO₂ [pCO₂, which is proportional to [CO₂] (40)] for the last 370 million years, obtained from the model Eq. 20 and the least-squares estimates of the parameters φ₀ and b, for the cases ɛ₀ = 36‰ and ɛ₀ = 38‰. Because Eq. 20 is linear in n, these curves are simply the diversity curve of Fig. 1 upside down and rescaled. Dashed curve and gray area: prediction from the model of Berner (15, 16) and its region of qualitative uncertainty, respectively, from ref. 17.

Comparison of the results from our model with Berner's shows that the pattern of decreasing CO₂ levels since ∼225 Ma is roughly equivalent in both. This trend is also qualitatively consistent with estimates based on the carbon isotopic composition of paleosols (48–51), plant stomatal ratios (52), carbon isotopic measurements from marine sediments (53), and an alternative reconstruction based on estimates of the Earth's inventory of buried carbon (19). However, the period before 225 Ma shows distinct differences from Berner's predictions. Although our estimate falls within Berner's region of uncertainty, it shows relatively no change compared to Berner's steep decrease at ∼300 Ma. Moreover, recent estimates from paleosols (54, 55) and plant stomatal ratios (52) are in accord with this dip. If the dip is indeed real, the mismatch with our model would presumably be caused by missing ingredients, such as changes in the burial rate of organic carbon accompanied by compensatory changes in algal cell permeabilities.

Conclusion

Surprising correlations exist between paleontological records of biodiversity and the carbon isotope fractionation evident in the sedimentary record for the last 370 million years. Proceeding from the assumptions that (i) chemical weathering rates grow with plant diversity; (ii) diversity grows with biomass at the global scale; and (iii) changes in phytoplankton physiology neither correlate with diversity nor fully compensate changes in CO₂ levels, we find that the correlations express complementary fluctuations in the size of the organic and inorganic carbon reservoirs within the biosphere, atmosphere, and hydrosphere. Consequently, CO₂ levels decreased as biodiversity increased. These conclusions imply that fluctuations of CO₂ levels have been driven primarily by changes within the biosphere and only secondarily by purely geologic and geophysical processes. However, such a causal relationship is not required for our principal quantitative conclusions—the Inequality 18 and the downward trend in Fig. 3—to hold. Indeed, our analysis leaves open the possibility, for example, that tectonically induced reductions of CO₂ levels led to increased diversity in both continental and marine ecosystems. A definitive statement of causation will require further work that includes not only the study of other geochemical signals (10) but also improved paleontological records.

Abbreviation

Ma

million years ago