Behavior of several two-dimensional fluid equations in singular scenarios

Abstract

We give conditions that rule out formation of sharp fronts for certain two-dimensional incompressible flows. We show that a necessary condition of having a sharp front is that the flow has to have uncontrolled velocity growth. In the case of the quasi-geostrophic equation and two-dimensional Euler equation, we obtain estimates on the formation of semi-uniform fronts.

We announce results on several equations for the motion of an incompressible fluid in two space dimensions. Under certain assumptions, our results rule out the formation of a sharp front in finite time.

The equations we study are as follows:

The Quasi-Geostrophic (QG) Equation

Here the unknowns are a scalar θ(x, t) and a velocity field u(x, t) = [u₁(x, t), u₂(x, t)] ∈ R², defined for x ∈ R² or R²/Z², and for t ∈ (0,T) with T ≤ ∞. The equations for θ, u are as follows

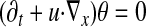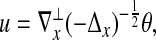where ∇ 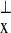f = (− ∂f/∂x₂, ∂f/∂x₁) for scalar functions f. The initial condition is θ(x,0) = θ₀(x) for a smooth initial datum θ₀.

The Ideal Two-Dimensional (2D) Magneto-Hydrodynamics (MHD) Equation

Here again the unknowns are a scalar θ(x, t) and an incompressible velocity field u(x, t) = [u₁(x, t), u₂(x, t)] ∈ R², with x = (x₁,x₂) ∈ R² or R²/Z², and t ∈ (0,T) with T ≤ ∞. We denote by w(x, t) the vorticity of u, given by w = ∂u₁/∂x₂ − ∂u₂/∂x₁. The MHD equations are as follows

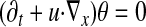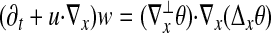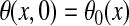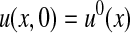with θ₀(x), u⁰(x) smooth initial data.

The 2D Euler Equation

The unknown is an incompressible velocity field u(x, t) as above with vorticity again denoted by w. The 2D Euler equation may be written in the form

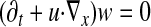with u(x,0) equal to a given smooth divergence free u⁰(x).

The Boussinesq Equation

The unknowns are a scalar θ(x, t) and an incompressible velocity field u(x, t). As before x = (x₁,x₂) ∈ R² or R²/Z², and t ∈ (0,T). Again, we let w denote the vorticity of u. The Boussinesq equations are as follows

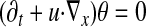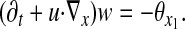Again, θ and u are specified at time t = 0.

We are concerned here with the possible formation in finite time of singularities of solutions to these equations, as well as large time behavior of solutions without singularities.

A classic criterion for formation of singularities in fluid flows is the theorem of Beale-Kato-Majda (BKM); see ref. 1. Analogues of the BKM theorem for the above 2D equations include the following results.

For QG, a singularity cannot develop at a finite time T, unless we have

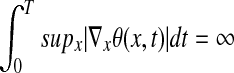(see ref. 2).

For 2D Euler, a singularity cannot develop at a finite time. From the BKM viewpoint this follows from the fact that w is advected by the fluid, and therefore sup_x|w(x, t)| is independent of t (see ref. 1).

For MHD, a singularity cannot develop at a finite time T, unless we have

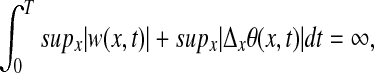where w denotes the vorticity (see ref. 3).

For Boussinesq, if a singularity develops at a finite time T then

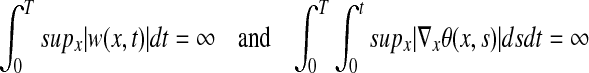(see ref. 4).

See also refs. 2 and 5 for other conditions involving direction fields that rule out formation of singularities in fluids.

Numerical studies have led to well-known scenarios that serve as natural candidates for the possible formation of singularities in solutions of the above equations.

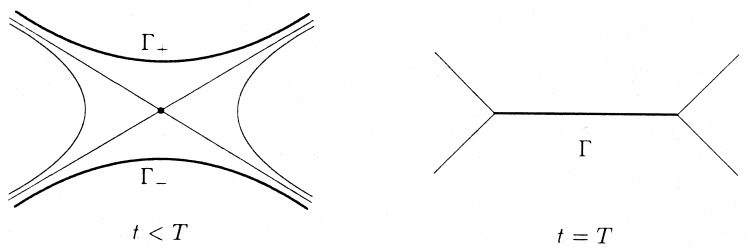
For MHD, the standard candidate is the closing of an X-point into two Y-points, joined by a current sheet, as in Fig. 1 (see refs. 7–9).

Figure 1.

Level curves of θ.

For the QG equation, the standard candidate is a closing hyperbolic saddle, which is an analogue of the closing of an X-point, but the literature in QG does not discuss any Y-points (see refs. 2 and 10–12).

For Boussinesq, in early numerical simulations by Pumir-Siggia (6) there has been observed evidence for a formation of a front in finite time, across which θ varies dramatically, on a cap of a symmetric rising bubble. E and Shu (4) performed numerical simulations with the same initial data as in ref. 6, which suggest that the thickness of the bubble decreases only exponentially.

These scenarios have in common that two distinct time-dependent arcs Γ₊(t), Γ₋(t) move with the fluid and collapse at finite time into a single arc Γ. More precisely, suppose the arcs are given by

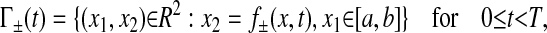1

with

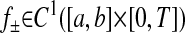and

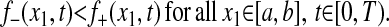2

We call the length b-a of the interval [a,b] the length of the front. The assumption that Γ_±(t) move with the fluid means that

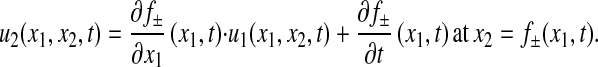3

This holds in particular for level curves of scalar functions g(x, t) that satisfy (∂_t + u⋅∇_x) g = 0. The collapse of Γ_±(t) into a single curve Γ at time T means here simply that

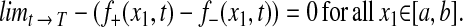4

and f₊(x₁,t) − f₋(x₁,t) is bounded for all x₁ ∈ [a,b], t ∈ [0,T).

When Eqs. 1–4 hold, then we say that the fluid forms a sharp front at time T. For 0 ≤ t < T, we define the thickness of the front to be

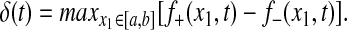We investigate the possible formation of a sharp front, and the rate of decrease of the thickness δ(t), for solutions of QG, MHD, 2D Euler, and Boussinesq.

Either of the following two assumptions will allow us to rule out formation of sharp fronts. One assumption is that

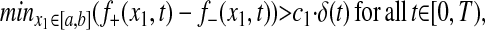5

with c₁ independent of t. If Eq. 5 holds, then we say that Γ_±(t) form a semi-uniform front, and we call c₁ the semi-uniformity constant.

In place of Eq. 5, we may assume that the fluid velocity does not grow too quickly. We say that the fluid has controlled velocity growth if we have

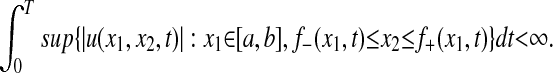6

If Eq. 6 fails, then we say that the fluid has uncontrolled velocity growth.

Our results for 2D fluids are as follows

Theorem 1. Let u(x, t) be a divergence-free velocity field, with controlled velocity growth. Then a sharp front cannot develop at time T.

In particular, solutions of QG, MHD, or Boussinesq with controlled velocity growth cannot form a sharp front in finite time.

Theorem 2. For a QG solution with a semiuniform front, the thickness δ(t) satisfies

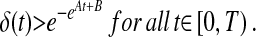Here, the constants A and B may be taken to depend only on the length of the front, the semiuniformity constant, the initial thickness δ(0), and the norm of the initial datum θ₀(x) in L¹ ∩ L^∞.

Theorem 3. For a 2D Euler solution with a semiuniform front, the thickness δ(t) satisfies

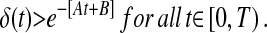Here, the constants A and B may be taken to depend only on the length of the front, the semiuniformity constant, the initial thickness δ(0), and the norm of the initial vorticity in L¹ ∩ L^∞.

Theorem 2 greatly weakens the geometrical assumptions made in Cordoba (11), which ruled out the collapse of a simple hyperbolic saddle in finite time. Our interest in Theorem 3 arises from the important problem of deciding whether the vorticity gradient for a 2D Euler solution can grow super-exponentially.

The proofs of our results are simple. The point is that they have interesting consequences for important fluid scenarios.

Theorem 1 provides a test for numerical simulations that appear to develop sharp fronts. Many numerical simulations exhibit rapid vorticity growth. There is far less numerical evidence to support rapid velocity growth.

Abbreviations

QG

quasi-geostrophic

2D

two-dimensional

MHD

magneto-hydrodynamics