Efficiency perspectives on adaptive designs in stroke clinical trials

Abstract

An adaptive design allows the modifications of various features such as sample size and treatment assignments in a clinical study based on the analysis of interim data. The goal is to enhance statistical efficiency by maximizing relevant information obtained from the clinical data. The promise of efficiency, however, comes with a “cost” that is seldom made explicit in the literature. This article reviews some commonly used adaptive strategies in early phase stroke trials and discusses their associated costs. Specifically, we illustrate the tradeoffs in several clinical contexts, including dose finding in the Neuroprotection with Statin Therapy for Acute Recovery Trial, futility analyses and internal pilot in phase 2 proof-of-concept trials, and sample size considerations in an imaging-based dose selection trial. Through these illustrations, we demonstrate the potential tension between the perspectives of an individual investigator and the broader community of stakeholders. This understanding is critical to appreciate the limitations, as well as full promise, of adaptive designs, so that investigators can deploy an appropriate statistical design—be it adaptive or not—in a clinical study.

Introduction

Clinical development of new therapies for acute ischemic stroke has seen limited success since the approval of tissue plasminogen activator¹ by the Food and Drug Administration (FDA). Many factors contribute to the difficulty in developing and testing new therapies, including challenges in consenting patients, variability in the standard of care, inadequate patient recruitment rates, and delays between trial phases as drugs move from early dose finding to efficacy trials. An adaptive design is a statistical tool that is hoped to accelerate drug development. Recent FDA draft guidance defines an adaptive design as a “prospectively planned opportunity for modification of one or more specified aspects of the study design” based on interim analysis of a study.² The term “prospective” means that the modification is planned before data are examined in an unblinded manner. Behind this overarching definition, the literature of adaptive designs has a long and multifarious history. The concept of adaptive randomization³ was introduced in the 1930s, sample size recalculation⁴ in the 1940s, sequential dose finding⁵ in the 1950s, and play-the-winner strategies⁶ and group-sequential methods⁷ in the 1960s. These concepts have since been studied and refined to suit practical purposes,^8–15 and were recently reviewed by the FDA¹⁶ and the PhRMA group.¹⁷ In early phase stroke trials, appropriate use of adaptive designs, possibly in conjunction with advanced biomarkers, has been shown effective at reducing the required number of subjects while maintaining comparable accuracy.¹⁸ However, there are “costs” associated with the use of adaptive designs, and such compromise is seldom made explicit in the literature. It is the purpose of this article to review some commonly used adaptive designs and their implied trade-offs, so as to aid in the decision of adopting (or not adopting) an adaptive design in a clinical study. While it is futile to attempt to exhaust all possible adaptive designs, we aim to cover the most common early phase trial settings, namely, phase 1 dose finding, phase 2 proof-of-concept and dose selection trials.

Continual reassessment method in dose finding studies

Phase 1 trials are dose-escalation studies that assess toxicity of a drug. A specific aim is to estimate the maximum tolerated dose (MTD), a dose associated with a target rate of dose limiting toxicity (DLT). The Neuroprotection with Statin Therapy for Acute Recovery Trial (NeuSTART) drug development program was initiated to test the role of high-dose statins as early therapy in stroke patients. (KC was the study statistician, and PK served on the Safety Monitoring Board.) In a phase 1B trial under NeuSTART, high-dose lovastatin was given to patients for three days. The DLT was defined as clinical or laboratory evidence of hepatic or muscle toxicity, and the objective was to identified the dose associated with a 10% DLT rate.¹⁹ The trial was conducted in 33 subjects in a dose escalation fashion among 5 possible dose tiers, and the MTD estimate was 8 mg/kg per day.²⁰ Dose assignments for the subjects enrolled to the trial were determined by the time-to-event continual reassessment method (CRM).²¹ The time-to-event CRM was used as an alternative to the 3+3 dose escalation scheme; the latter, originally motivated by applications in oncology, was previously shown inappropriate for stroke trials because it would choose doses at a much higher toxicity level.¹⁸

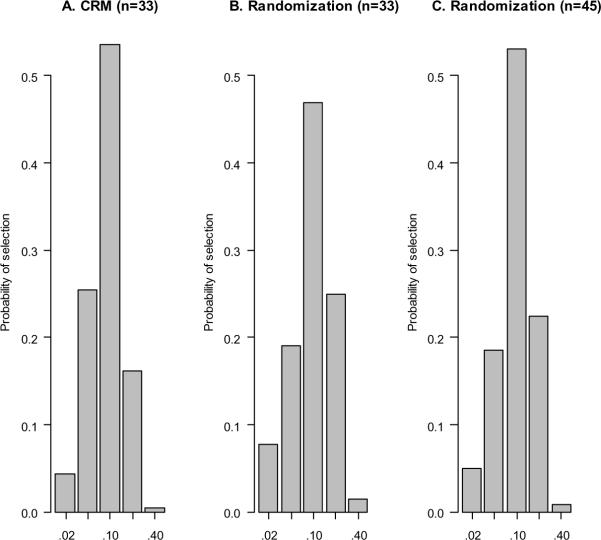
The CRM is efficient at estimating the MTD. Figure 1A displays the distribution of MTD selection by the NeuSTART design under a scenario where the third dose tier is the MTD and the toxicity odds ratio of each subsequent dose tier is 2.5: the MTD was correctly identified with a probability of 0.54. If we use a non-adaptive design by randomizing 33 subjects to the five dose tiers with equal likelihood, the MTD will be selected with a probability of 0.47 (Figure 1B). Also, the CRM selects an overdose (i.e., dose tiers 4 or 5) less often than the randomization design. If we increase the sample size and randomize 45 subjects evenly to the doses, we will have comparable accuracy to the CRM with 33 subjects in terms of selecting the MTD; however, the tendency to select an overdose remains (Figure 1C).

Figure 1.

Distribution of MTD selection by the CRM and even randomization. The true MTD is dose tier 3 (which has 10% DLT). Logistic regression is used to make dose selection at the end of each simulated trial.

The CRM does not only improve accuracy, but also prescribes doses that reduce risks to the study subjects. Under the scenario in Figure 1, the CRM on average enrolls 13 of the 33 subjects at the MTD and 6 at an overdose, whereas randomization will place an average of 13 subjects at an overdose and 7 at the MTD (Table 1). This reflects that the CRM adapts to the interim observations in an ethically appropriate manner: No escalation will take place for the next enrolled subject if the current subject experiences a DLT.²² However, as the design tends to treat majority of the patients at the MTD, it is unable to accrue sufficient information at the other doses to allow accurate estimation of dose-response across the test doses. Table 1 row (e) shows that the estimated odds ratio (having a median of 5.2) using the CRM overestimates the true odds ratio (2.5), whereas randomization allows for an unbiased estimate of the odds ratio. The inability to estimate dose-response may not be concerning in phase 1 trials, as long as the MTD can be accurately identified: this makes the CRM a versatile dose finding tool. However, in situations where dose-response information is crucial to the understanding of the drug mechanism, the odds ratio may be a key quantity that renders the CRM as inappropriate.

Table 1.

Comparison of the NeuSTART CRM and even randomization with 33 subjects, under a dose-toxicity curve where dose tier 3 is the MTD and the toxicity rate increases with an odds ratio of 2.5 at each increment.

Design characteristics	CRM	Randomization
(a) Probability of selecting the MTDa	0.54	0.47
(b) Probability of selecting an overdosea	0.17	0.26
(c) Average number of subjects at MTD	13	7
(d) Average number of subjects at an overdose	6	13
(e) Median of toxicity odds ratio estimatea	5.2	2.6

^aThe MTD and the odds ratio are estimated using logistic regression at the end of each simulated trial for the CRM and the randomization design.

Futility interim analysis in proof-of-concept studies

Phase 2 studies serve as a proof-of-concept by examining pilot efficacy of a new drug. A main consideration is the choice of a biomarker that correlates with stroke outcome. A promising biomarker is the magnetic resonance imaging (MRI) response.¹⁸ The simplest phase 2 trial design is a single-arm study in which patients are given the experimental drug, and the experimental response rate is compared to a historical control rate. Based on the results by MR Stroke Collaborative Group (MRSCG),²³ we may assume 25% MRI response among untreated stroke patients. In order to have 80% power to detect a 45% response rate at a 5% significance level, we will need to observe at least 14 responses in a fixed sample size of 36 subjects.

For the same power, significance level, and treatment rate, we may alternatively use a two-stage design with a futility interim analysis:²⁴ In stage 1, enroll 17 subjects and conclude futility if there are 5 or fewer responses; if there are at least 6 responses in stage 1, treat an additional 24 subjects in stage 2 and declare the drug efficacious if there are at least 15 responses in the 41 subjects. Because of the provision of early stopping, this two-stage design will enroll an average sample size of 23 subjects if the experimental response rate is in truth the same as the control rate of 25%. To interpret an average sample size, imagine that 100 single-arm trials of different drugs use this two-stage design; assuming most of the drugs are no better than control, we will expect to enroll about a total of 23 × 100 = 2,300 subjects to these trials, although some of the trials will stop after 17 subjects and some will continue to stage 2 and enroll 41. In contrast, if we use the fixed design with 36 subjects, we will need 3,600 subjects for the same 100 trials. Looking at a portfolio of several trials, the two-stage design is the obvious choice, assuming that most drugs do not work. On the other hand, for investigators who hope to show their drug is efficacious, the fixed sample size design is more appealing than the two-stage design, because the former will take them 5 fewer subjects (36 versus 41) than the latter. This numerical comparison demonstrates a potential tension between the individual investigator's perspective and the broader community's. A statistical theory²⁵ stipulates that, in order to achieve the same power at the same significance level, the maximum sample size required by any adaptive designs will always be at least as large as a fixed sample size design; that is, the advantage of an adaptive design lies in the reduction of the average sample size. This theory thus implies that an adaptive design cannot resolve the fundamental difference in perspectives. The individual investigator's interest resides in keeping the sample size of a single trial small. Given limited resources and finite numbers of stroke patients, the community's interest resides in keeping the average sample size small so that more trials can be performed.

Internal pilot in randomized studies

For randomized studies comparing event rates of a new treatment to a concurrent placebo, sample size calculation requires an assumption on the placebo rate as well as the effect size. The assumed placebo rate should reflect the aggregate experience about the natural history of stroke patients, formed through literature search or the investigators' clinical experience. However, it is very possible that the assumed placebo rate misses the truth—this is exactly why a randomized study is needed instead of a single-arm study.

Consider an MRI trial where patients are randomized between an experimental treatment and a placebo. With an assumed 10% placebo rate and a target effect size of 20 percentage points, a one-sided test with 5% type I error and 80% power requires 49 subjects per arm. If the true placebo rate is 25% and the treatment rate is 45%, the power due to this sample size will reduce to 64%, despite the fact that the effect size remains to be 20 percentage points. If we assume a 25% placebo rate and a 45% treatment rate, the required sample size for 80% power is 70, which may prove unnecessary if the placebo rate is in truth 10%.

Conducting an internal pilot provides a means to circumvent the dilemma due to uncertainty in the placebo rate.^11,13 The idea is to calculate the sample size using the blinded estimates of the response rates in an internal pilot. Table 2 shows the properties of a two-stage design with an internal pilot of n₁ = 30 subjects, and that of fixed sample size designs with N=49 and N=70. (Details of two-stage design are given in online supplement.) When the true placebo rate is 10%, the fixed design with N=70 is overpowered, whereas the two-stage design gives adequate power with an average sample size much lower than 70. On the other hand, when the true placebo rate is 25%, the fixed design with N=49 is underpowered, whereas the two-stage design achieves 80% power. The adaptable sample size of internal pilot thus offers great flexibility in trial planning.

Table 2.

Comparison of a two-stage design with internal pilot and fixed sample size designs in a randomized study assuming a 20-percentage-point effect size and 80% power at 5% significance.

Scenario	Properties	Fixed design (N=49)	Fixed design (N=70)	Internal pilot (n1=30)
Placebo: 10% Treatment: 30%	Power	80%	91%	84%
	Ave Na IQRb	49 (49–49)	70 (70–70)	54 (50–56)
Placebo: 25% Treatment: 45%	Power	64%	80%	80%
	Ave Na IQRb	49 (49–49)	70 (70–70)	70 (68–74)

^aPer arm;

^bInterquartile range.

However, since we use the internal pilot data twice—in the sample size estimation and in the final analysis—adjustments are needed for the final statistical test in order to preserve the type I error rate (see online supplement). The sample size calculations in Table 3 indicate that the adjusted statistical test (with n₁ = 30) suffers only a slight loss in efficiency when compared to the Z-test in a fixed design. Generally, the efficiency loss depends critically on the ratio of the internal pilot sample size (n₁) to the final sample size (N). Suppose the investigators decide to perform a sample size calculation at n₁ = 15 without advance planning, Table 3 (last row) shows that the sample size inflation from the fixed design can be substantial; however, since a fixed design with a misspecified placebo rate can be underpowered, an unplanned re-estimation is arguably superior by providing greater flexibility. However, in view of efficiency, planned sample size re-estimation is preferred to unplanned interim calculation.

Table 3.

Sample size comparison between Z-test in a fixed design and the adjusted test in a two-stage design with internal pilot (with n₁ = 30, 15 respectively). The total sample size (per arm) is calculated to achieve 80% power under a 20-percentage-point effect size at 5% significance (one-sided).

Placebo rate	10%	15%	20%	25%	30%	35%	40%
Z-test	49	57	64	70	74	76	77
Adjusted test (n1 = 30)	50	58	66	71	75	78	79
Adjusted test (n1 = 15)	51	63	72	79	85	88	89

Dropping-the-loser in dose selection trials

If we believe a dose below the MTD may be efficacious, it is appropriate to conduct a phase 2B dose selection study, where the primary objectives are to make a “go-or-no-go” decision and to decide which dose to move forward. Fisher et al.¹⁸ describe a drop-the-loser strategy for a three-arm, placebo-controlled, dose selection trial using MRI response. The design eliminates at least one of the two doses if the early response rates in the treatment arms are not promising. By assuming a 10% placebo MRI response and a 20-percentage-point effect size, the two-stage design requires a maximum of 126 subjects to achieve 80% power and 5% type I error; see Table 2 in [18]. In contrast, a fixed sample size randomization design requires 216 subjects to achieve the same power and significance level. This comparison stands in contrast with that in single-arm studies, where an adaptive design will always need larger maximum sample size than a fixed design. In this regard, an adaptive strategy has a universal advantage over the non-adaptive design in multiple-arm dose selection trials. The intuition is by eliminating inferior doses at an interim time point, resources can be directed toward the promising dose for precise comparison against the placebo.

However, by forcing us to drop at least some doses, we will not be able to estimate the odds ratio of MRI response between two doses, which may provide evidence to evaluate the risk-benefit ratio. Therefore, if one holds a “local” perspective to fully evaluate the dose-response and other clinical parameters of a drug in a study, dropping-the-loser may not provide us with the answer. However, with a “global” drug development perspective to identify efficiently a good dose to go to a phase 3 trial, adaptive designs have much to offer.

To make the matters more complicated, the power of a dose selection trial depends on the placebo rate. The abovementioned drop-the-loser strategy was designed before the MRSCG analysis became available, and would have had only about 72% power with a 25% placebo response rate. Further adaptation can be made to accommodate unknown placebo rate.²⁶ However, the greater the uncertainty at the design stage, the larger the sample size one will need. Therefore, meta-analysis of the natural history of stroke patients will prove to be extremely valuable in terms of reducing the necessary resources.

Discussion

The importance of prospective planning in an adaptive design is, first of all, the elimination of (the perception of) bias due to unplanned looks at the data. From an efficiency viewpoint, any ad hoc adaptation potentially leads to inefficiency as illustrated in the discussion of internal pilot. More importantly, the flexibility offered by an adaptive design should not replace careful planning and preliminary investigation. For example, while sample size re-estimation techniques can in theory be used to adapt to the uncertainty in effect size, it raises a variety of issues including the necessity of unblinding, a potentially prohibitive final sample size, and inefficiency.²⁷ Thus, it is crucial for the investigators to carefully consider what constitutes a minimally relevant effect size in the planning stage. In the abovementioned dose selection trial, a relatively large improvement (i.e., a 20-percentage-point effect size) in the MRI response was believed necessary for translation into meaningful clinical benefits. For another example, thorough investigation of the natural history of stroke outcomes in prior clinical data can reduce our uncertainty in placebo rate; thus, meta-analysis is particularly useful to build reliable historical controls as was done by MRSCG. Finally, understanding of the dose-response and drug mechanism in preclinical data can help zero in the appropriate doses and endpoints in the clinical phase. These conventional good practices may result in more substantial efficiency gain than what adaptive designs can achieve.

Adaptive designs can be associated with logistical challenges such as forecasting budgets, planning for drug supply, and the potential needs for real time DSMB decisions. However, these challenges can be addressed, and adaptive designs have much to offer in view of statistical efficiency: from the reduction of average sample size in a futility interim analysis to the adaptive dose assignments in the CRM. These advantages are not new in the literature. In this article, we have emphasized that whether we gain efficiency by using an adaptive design depends on one's perspective. And, the tension between perspectives is irreconcilable by any statistical design, be it adaptive or not. Rather, the debate about the appropriate perspective for a study should precede and dictate the choice of statistical methods. Indeed, adaptive design is no panacea and should not be mistaken as one.