EFFECTS OF MUSCLE FATIGUE ON MULTI-MUSCLE SYNERGIES

Abstract

We studied the effects of fatigue of ankle dorsiflexors on multi-muscle synergies defined as co-varied adjustments of elemental variables (M-modes) that stabilize a task related performance variable (trajectory of the center of pressure, COP). M-modes were defined as muscle groups with parallel changes in activation levels. Healthy participants performed voluntary body sway in the anterior-posterior direction while trying to minimize sway in the medio-lateral direction at 0.25, 0.5 and 0.75 Hz. The trials were repeated before and during fatigue induced with a timed voluntary contraction against a constant load. Factor extraction using the principal component method was used to identify four M-modes within the space of integrated indices of muscle activity. Variance in the M-mode space at different phases across sway cycles was partitioned into two components, one that did not affect the average value of COP shift and the other that did. There were no significant effects of fatigue on variability of performance of the explicit task and on the amplitude of the COP shift. Variance of muscle activation indices and M-mode magnitudes increased during fatigue for muscles (and M-modes) both involved and not involved in the fatiguing exercise. Most of the M-mode variance increase was within the sub-space compatible with the unchanged COP trajectory resulting in an increase of the index of the multi-M-mode synergy. We conclude that one of the adaptive mechanisms to fatigue within a redundant multi-muscle system involves an increase in the variance of activation of non-fatigued muscles with a simultaneous increase in co-variation among muscle activations. The findings can be interpreted within the referent configuration hypothesis on the control of whole-body actions.

Introduction

Muscle fatigue leads not only to a drop in peak muscle force and in time to task failure, but also to an increase in motor variability (reviewed in Enoka and Duchateau 2008; Enoka et al. 2011) and changes in motor coordination (Huffenus et al. 2006). Some of these changes attenuate the detrimental effects of fatigue on motor performance. Several studies have shown that, if a motor task involves a redundant set of elements, goal-relevant features of performance are relatively preserved during fatigue of one (a few) of the elements (Forestier and Nougier 1998; Côté et al. 2002, 2008; Huffenus et al. 2006; Gates and Dingwell 2008; Fuller et al. 2009; Singh et al. 2010a, 2010b). In those tasks, mechanical performance variables produced by individual elements and by the whole system were studied. The main purpose of this study has been to study adaptive adjustments to fatigue in redundant multi-muscle systems.

We selected, as the object of study, the control of vertical posture, which is one of the most common multi-muscle actions in everyday life. The notion of muscle synergies has been used to address the neural control of posture since the classical studies of Babinski (1899) and Bernstein (1947, 1967). Bernstein defined muscle synergies as large muscle groups that “work together”. This definition has been developed recently with computational methods (typically, matrix factorization methods) applied to indices of muscle activation to discover groups of muscles with parallel scaling of activation levels over time and/or across repetitive attempts at a task (d'Avella et al. 2003; Ivanenko et al. 2005, 2006; Ting and Macpherson 2005; Torres-Oviedo et al. 2006; Torres-Oviedo and Ting 2007). The organization of muscles into such groups (”synergies”) has been assumed to reduce the number of variables manipulated by the brain.

A somewhat different view on motor synergies has been developed using the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2007; Latash 2010). According to the UCM hypothesis, the neural controller acts in a space of elemental variables. It organizes in that space a sub-space (UCM) corresponding to a desired value of a performance variable to which all the elemental variables contribute. Further, the control is organized to keep variance of the elements across trials within the UCM.

The described method of control allows attenuating potentially harmful effects on performance when one of the elements shows increased variance of its output under fatigue. In recent studies, we have shown that fatigue of a finger leads to counter-intuitive consequences in multi-finger accurate force production tasks (Singh et al. 2010a, 2010b). Both fatigued and non-fatigued fingers showed comparable increases in their force variability, while co-variation of finger forces increased. As a result, most of the increased force variance was channeled into the UCM sub-space, that is, it had little effect on variance of the total force.

Within this study, we used the notion of muscle modes (M-modes) as elemental variables manipulated by the neural controller (Krishnamoorthy et al. 2003a, 2003b; Danna-dos-Santos et al. 2007). M-modes have been defined as muscle groups with parallel scaling of activation; typical sets of M-modes are low-dimensional as compared to the individual muscle activation space but they are still redundant with respect to typical sets of performance variables (Robert et al. 2008; Klous et al. 2010). The neural controller has been assumed to manipulate gains at the M-modes in a way compatible with the UCM hypothesis, that is, to ensure that most M-mode variance lies within the UCM for the important performance variable(s).

Since this is the first study of the effects of fatigue on multi-muscle synergies within the described theoretical framework, we explored several possibilities. First, fatigue of a muscle group could lead to a change in the composition of the M-modes. In particular, muscles could be expected to show more or less co-contraction within the agonist-antagonist pairs acting at leg joints (cf. Weir et al. 1998; Danna-dos-Santos et al. 2008; Missenard et al. 2008a). Second, the relations between small changes in the M-mode magnitudes and changes in the performance variable (the Jacobian of the system) could change under fatigue. Third, we did expect fatigue to lead to an increase in variability of the activation level of the fatigued muscle (Zijdewind et al. 1995; Missenard et al. 2008b) and, consequently, in the M-mode to which the fatigued muscle contributes significantly. Based on earlier studies (Singh et al. 2010a, 2010b), we also expected other muscles and other M-modes to show an increase in variability of their activation levels. Fourth, we expected to see an increase in the co-variation in the M-mode space computed across repetitive trials. This co-variation was expected to be organized to stabilize the important performance variable, which in this case was the trajectory of the center of pressure in the anterior-posterior direction. Overall, the main hypothesis has been that the neural controller uses non-trivial adaptive strategies, such as an increase in variance of activation of non-fatigued muscles and corresponding M-modes, to protect important performance variables (center of pressure trajectory in our study) from detrimental effects of fatigue, such as increased variability.

Methods

Participants

Eleven participants (seven males) with the mean age 22.2 ± 3.4 years (mean ± standard deviation), mean mass 67.9 ±10.1 kg and mean height 1.75 ± 0.09 m participated in the experiment. All the participants were free of known neurological or muscular disorders. All participants were right-leg dominant based on their preferred leg to kick a soccer ball. They gave informed consent based on the procedures approved by the Office for Research Protection of The Pennsylvania State University.

Apparatus

A force platform (AMTI, OR-6) was used to record the moments of force around the frontal and sagittal axes (M_Y and M_X, respectively) and the vertical component of the reaction force (F_Z). Disposable self-adhesive electrodes (3M™ Red Dot™ Pediatric Monitoring Electrodes, #2248-50) were used to record the surface muscle activity (EMG) of twelve muscles: tibialis anterior (TA), soleus (SOL), gastrocnemius lateralis (GL), gastrocnemius medialis (GM), biceps femoris (BF), semitendinosus (ST), rectus femoris (RF), vastus lateralis (VL), vastus medialis (VM), tensor fasciae latae (TFL), lumbar erector spinae (ES), and rectus abdominis (RA). The electrodes were placed on the right side of the body over the muscle bellies. The distance between the two electrodes of each pair was 2.5 cm. A goniometer (Biometric Inc, UK) was used to give feedback on the ankle joint flexion angle in the sagittal plane during the fatigue exercise (explained in Procedures). The signals from the electrodes were amplified (×5000). All the signals were sampled at 1000 Hz with a 12-bit resolution. A personal computer (Dell 2.40 GHz) was used to collect the data using a customized LabVIEW software (Labview-8.2—National Instruments, Austin, TX, USA).

Procedures

Before-Fatigue Trials

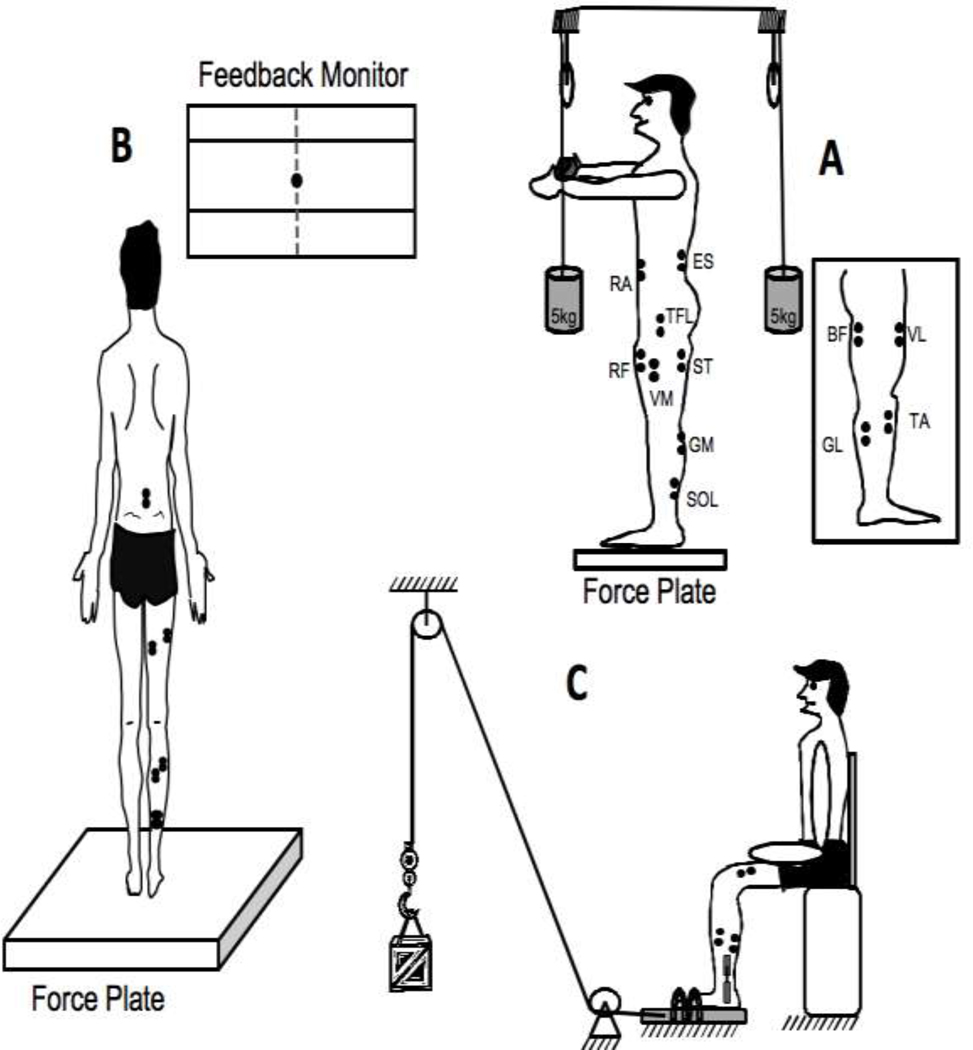
The experiment started with three control trials that were later used for normalization of the EMG signals (see the next section). EMG normalization was performed to facilitate across-subjects comparisons. In the first two control trials, the participants were instructed to stand quietly and hold a standard load (5 kg) for 10 s keeping the arms fully extended (see Figure 1A). The participants held the load by pressing on two circular panels attached to the ends of a bar. The load was either suspended from the middle of the bar or it was attached through a pulley system such that it produced an upward acting force on the bar (Danna-dos-Santos et al., 2007). Two trials were performed with the load acting downward and upward. The time interval between the two trials was 30 s. This was followed by a 10-s quiet stance trial. For this trial, the participant was instructed to stand quietly, arms by the sides and look at a fixed point on the wall in front of him/her.

Figure 1.

A: The experimental setup for the sway trials with the force plate and the computer monitor for feedback. B: The setup for the control trials and the EMG electrode placement. TA – tibialis anterior; SOL – soleus; GM – medial gastrocnemius; GL – lateral gastrocnemius; VM – vastus medialis; VL – vastus lateralis; RF – rectus femoris; TFL – tensor fascia latae; ST – semitendinosus; BF – biceps femoris; RA – rectus abdominis; ES – erector spinae. C: The fatigue setup and the right leg of the participant with the EMG electrodes and goniometer.

The main task was to sway in the anterior-posterior direction at three different frequencies (0.25, 0.5 and 0.75 Hz) paced by a metronome. Different frequencies were used because an earlier study documented significant effects of frequency on synergy indices (Friedman et al. 2009). Before the sway, the participants were instructed to stand quietly on the force plate with their feet in parallel and shoulder-width apart. This foot position was marked on the top of the platform and participants were asked to reproduce this stance in each trial. The arms were always kept by the sides. Participants were instructed to perform full body sways about the ankle joints. They were watched by the experimenter and, if excessive hip involvement was observed, the trials was stopped and repeated. First, they were asked to lean as far as they could without a danger of losing balance. Then, two targets were placed corresponding to the maximal backward and forward COP locations. The instruction was to produce a continuous sway in the anterior-posterior direction (COP_AP) while keeping full contact of both feet with the platform during the movement, and to keep medio-lateral COP deviations (COP_ML) as close to zero as possible. The latter part of the instruction was used to ensure that the subjects do not place more weight on the non-fatigued leg and reduce the involvement of the fatigued leg. Feedback on both COP_AP and COP_ML was given on a computer screen located approximately one meter in front of the participant at the eye level (Figure 1B).

A period of familiarization with the task was given to each participant prior to actual data collection. Participants performed sways at each frequency for about 2 minutes; the order of frequencies was randomized across participants. Each trial started with the participant standing quietly. Then, the metronome was turned on, and the participant was asked to begin swaying. Data recording started after the participant had completed at least five complete sway cycles and it lasted for 30 s. Four trials were collected at each frequency. A 10-s rest was given after each trial with a frequency condition, and a 30-s rest was given between two frequencies.

During-Fatigue Trials

To induce unilateral fatigue of the right foot dorsiflexor muscle group a foot-contraption system was custom built. Participants were comfortably seated on a chair, with their backs rested, the knee flexed at 90° and inserted their right foot into the contraption (Figure 1C). A nylon rope attached to the contraption and pulled over a pulley system supported a load that the participants were supposed to lift by dorsiflexing their ankle. This method of inducing fatigue is similar to the method of holding a position against an external load used in earlier studies (Enoka and Duchateau 2008; Enoka et al. 2011). The weight of the load was between 7–10% (on average, 8%±1.8%) of the body-weight of the participant. Participants were asked to lift the load by dorsiflexing the ankle to approximately 10–15° (0° being the neutral position). A goniometer was attached to the medial part of the foot to provide feedback on the ankle angle. The load was lifted for two minutes. The median power frequency (Cifrek et al., 2009) of the TA muscle was recorded at 0 and 115 s on-line and presented immediately after the exercise. If there was a drop of at least 25% of the median power frequency (f_M) by 115 s, the exercise was considered successful. If the drop was under 25%, the load was increased by 0.25 kg and the participant repeated the fatiguing exercise (this happened only in two subjects). The cutoff of 25% was chosen based on a pilot study performed with three participants from our laboratory group. A 25% drop in f_M was accompanied by an average 8.3 rate of perceived exertion (Borg scale 0–10).

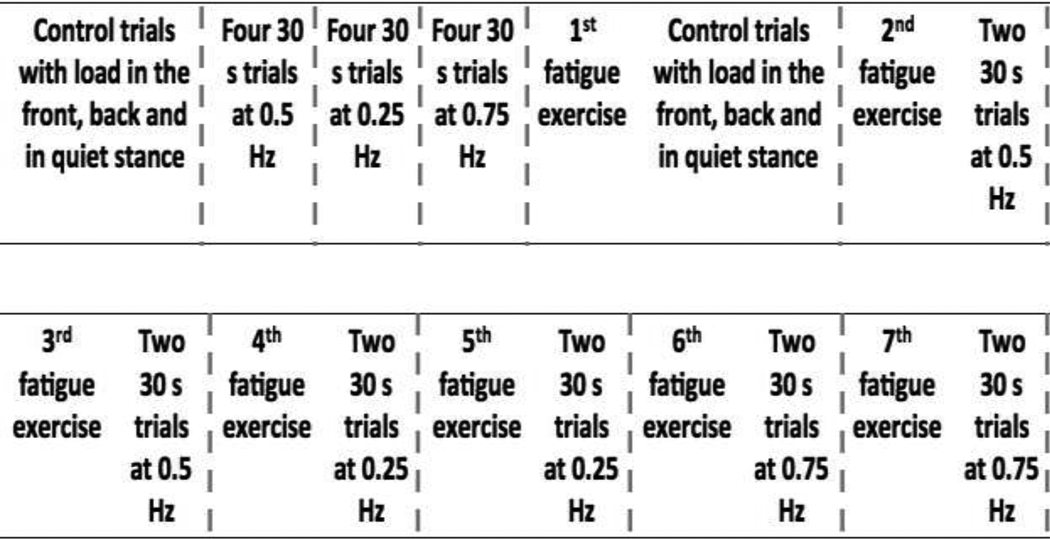
After the first fatiguing exercise, the participant completed three during-fatigue control trials. The order of the trials was the same as in the before-fatigue trials. After the control trials the participants were given a 2–3 minute rest after which they started the second fatiguing exercise, which was identical to the first one. After the successful completion of the second fatiguing exercise, the participants stepped back on the force-plate and performed two trials of full-body sway at the first frequency at which they swayed during the before-fatigue trials. After the two sway trials, participants performed another fatiguing exercise and then returned to the force-plate for two sway trials. This process was repeated for all three frequency conditions presented in the same order as during the before-fatigue trials (see Figure 2 for the time sequence of the experimental protocol).

Figure 2.

The time sequence of the experimental protocol. The blocks are separated by vertical dashed lines. After each block the participant had at least a 2–3 minute rest. The order of different sway frequencies was balanced across participants.

Data Processing

All signals were processed offline using MATLAB 7.10 software. Signals from the force plate were filtered with a 20 Hz low-pass, second-order, zero-lag Butterworth filter. COP_AP and COP_ML were computed from the filtered data (Nigg and Herzog, 1994). For each 30-s trial, only the data in the interval {3 s; 28 s} were accepted to avoid edge effects. Within each trial, a cycle was defined as the time between two successive anterior-most COP_AP displacements. The duration of each cycle was time normalized to 100%.

A notch-filter at 60 Hz was first applied to the EMG data to get rid of the noise due to the electrical supply. Then, a wavelet-based adaptive filter was applied to the EMG signals from the RA and ES muscles to remove the ECG artifacts (Zhan et al. 2010). Further, the EMG signals were rectified and a moving average filter of 100 ms duration was applied. The EMG signals were then integrated over 1% time windows of each sway cycle (IEMG), corrected for background activity and normalized:

$${\mathit{\text{IEMG}}}_{\mathit{\text{norm}}}=\frac{\mathit{\text{IEMG}}-{\mathit{\text{IEMG}}}_{\mathit{\text{qs}}}}{{\mathit{\text{IEMG}}}_{\mathit{\text{ref}}}},$$

where IEMG_qs is average rectified EMG during the quiet stance trial integrated over a time window of the same duration as IEMG; IEMG_ref is average rectified EMG in the middle of a control trial when holding a 5 kg load in front of or behind the body integrated over a time window of the same duration as for IEMG. For the dorsal muscles (SOL, GL, GM, BF, ST, ES) IEMG_ref were obtained from the trial when the load was held in front of the body and for the ventral muscles (TA, VM, VL, RF, RA, TFL), the load was suspended behind the body (Krishnamoorthy et al. 2003a; Klous et al. 2010).

Defining M-modes

The purpose of this step was to define groups of muscles (muscle modes or M-modes) that showed co-varied levels of muscle activation during the sway task. We used the same method as in earlier studies (Danna-dos Santos et al. 2007; Klous et al. 2010). For each subject and each frequency condition the IEMG_norm data formed a matrix with twelve columns representing the twelve muscles and the number of rows corresponding to 1% time windows of the cycles analyzed (i.e., 10 sway cycles produced 1000 rows). The correlation matrix of the IEMG_norm was subject to factor analysis using the principal component method. We selected the first four eigenvectors to reduce the 12-dimensional muscle space to a four-dimensional muscle-mode space. The selection of the four principal components (PCs) was based on the Kaiser criterion (Kaiser 1960). We also computed the muscle loading matrix by multiplying the matrix containing the eigenvectors in its columns by the diagonal matrix that had the square root of eigenvalues on its diagonal (Johnson and Wichern 1982). The first four PCs explained, on average, (86.1%±0.97%) of IEMG_norm variance in the before-fatigue trials and (83.9%±0.95%) of variance in the during-fatigue trials. M-modes were obtained by multiplying the IEMG_norm matrix with the PCs after Varimax rotation (Kaiser 1959).

In order to estimate similarity of PCs across the conditions and participants, we used a method that compares a group of vectors in the muscle activation space (for example, the PC₁ vectors for a given participant across all the sway frequencies for the during-fatigue condition) to a central vector representing the same or another group of vectors (for example, the PC₂ vectors for another participant across the same sway frequencies during-fatigue). The central vector is the mean vector within a group. The method uses the cosine magnitude of the angle between a central vector and a vector from either the same M-mode group or from a different M-mode group (for details see Krishnamoorthy et al. 2003a; Danna-dos-Santos et al. 2007). The cosine values were further transformed into z-scores using Fisher’s z-transformation.

Defining the Jacobian (J matrix)

Linear relations were assumed between a vector of small changes in the magnitude of the M-modes (ΔM) and the change (ΔCOP_AP) in the COP_AP coordinate. Multiple linear regressions over all cycles within a frequency condition were used to define the relations between ΔM and ΔCOP_AP for each participant and each condition separately:

$$\mathrm{\Delta }{\mathit{\text{COP}}}_{\mathit{\text{AP}}}=k_1\mathrm{\Delta }{M}_1+k_2\mathrm{\Delta }{M}_2+k_3\mathrm{\Delta }{M}_3+k_4\mathrm{\Delta }{M}_4$$

A priori, we assumed that, across conditions, both the M-mode composition and the Jacobian could change. For each participant, ΔM and ΔCOP_AP values were computed over all cycles for each 1% of the cycle duration. The coefficients of the regression equation were arranged into a Jacobian matrix (J) in this case reduced to a vector:

$$J={[k_1{k}_2{k}_3{k}_4]}^T$$

Analysis of M-mode synergies

The UCM hypothesis assumes that the controller manipulates a set of elemental variables (M-mode magnitudes in our study) and tries to limit their variance to a subspace corresponding to a desired value of a performance variable (COP_AP in our study). Within the UCM analysis, the trial-to-trial variance in the elemental variables is divided into two components, within a subspace (UCM) where the selected performance variable does not change (the null-space of J) and within the orthogonal complement to the UCM. Comparing the two components of the variance, normalized by the dimensionality of their respective subspaces, produces an index of variance that is compatible with stabilization of COP_AP coordinate.

In the current study, the M-mode space has dimensionality n = 4. The hypothesis that ΔCOP_AP is stabilized, accounts for one degree-of-freedom (d = 1). For each time window, the mean change in the magnitude of each of the M-modes was calculated ($\overline{\mathbf{\Delta }\mathit{M}}$, over cycles) and was subtracted from the vectors of the individual changes in the magnitudes of the M-mode (ΔM) for each cycle, for each time window. The residual mean-free vectors ΔM_demeaned were computed for each frequency condition as per:

$$\mathbf{\Delta }{\mathit{M}}_{\mathit{\text{demeaned}}}=\mathbf{\Delta }\mathit{M}-(\overline{\mathbf{\Delta }\mathit{M}})$$

The UCM subspace was approximated with the nullspace of the corresponding Jacobian matrix J. The null-space is spanned by basis vectors, ε_i. The vector ΔM_demeaned was resolved into its projection onto the UCM (f_UCM) and the orthogonal space (f_ORT):

$$\begin{array}{c}{f}_{\mathit{\text{UCM}}}={\displaystyle \sum _{i=1}^{n-d}}{({\mathit{\epsilon }}_{\mathit{i}}^{\mathit{T}}·\mathbf{\Delta }{\mathit{M}}_{\mathit{\text{demeaned}}})}^T{\mathit{\epsilon }}_{\mathit{i}}\hfill \\ f_{\mathit{\text{ORT}}}=\mathbf{\Delta }{\mathit{M}}_{\mathit{\text{demeaned}}}-{(f_{\mathit{\text{UCM}}})}^T\hfill \end{array}$$

The trial-to-trial variance in each of the two subspaces (V_UCM and V_ORT) as well as the total variance (V_TOT) normalized by the number of DOF of the respective spaces was calculated as:

$$\begin{array}{c}{V}_{\mathit{\text{UCM}}}={\sigma }_{\mathit{\text{UCM}}}^2=\frac{1}{(n-d)(N_{\mathit{\text{trials}}})}{\displaystyle \sum _{i=1}^N}|f_{\mathit{\text{UCM}}}{|}^2\hfill \\ V_{\mathit{\text{ORT}}}={\sigma }_{\mathit{\text{ORT}}}^2=\frac{1}{(d)(N_{\mathit{\text{trials}}})}{\displaystyle \sum _{i=1}^N}{|f_{\mathit{\text{ORT}}}|}^2\hfill \\ V_{\mathit{\text{TOT}}}={\sigma }_{\mathit{\text{TOT}}}^2=\frac{1}{(n)(N_{\mathit{\text{trials}}})}{\displaystyle \sum _{i=1}^N}{(\mathbf{\Delta }{\mathit{M}}_{\mathit{\text{demeaned}}})}^2\hfill \end{array}$$

To quantify the relative amount of variance that is compatible with stabilization of COP_AP trajectory, an index of synergy ΔV was calculated:

$$\mathrm{\Delta }V=\frac{V_{\mathit{\text{UCM}}}-V_{\mathit{\text{ORT}}}}{V_{\mathit{\text{TOT}}}}$$

The normalization of the index by the total amount of variance was carried out as described in earlier studies (Robert et al. 2008; Klous et al. 2010) to compare the index across subjects and conditions. All variances were computed per degree of freedom. For statistical analyses, ΔV was z-transformed adjusted for the limits of ΔV inherent to its computation, max(ΔV) = 1.33; min(ΔV) = −4.

Statistics

The data are presented in the manuscript and figures as means ± standard errors. The study had a 3-factor design with Fatigue (before-fatigue and during-fatigue as two levels) and Frequency (0.25, 0.5 and 0.75 Hz) as fixed factors and Participants as random factor. For some of the analyses, we used another factor, Phase (‘−5 to 5%’ (−5 to 5% represent the phase 95–100% of sway cycle n−1 and phase 0–5% of cycle n), ’20–30%’, ’45–55%’ and ’70–80%’ phase of the cycle) to explore the dependence of fatigue induced changes in the outcome variables on the phase of the sway cycle. Repeated-measures ANOVAs and MANOVAs were used to test hypotheses on the effects of Fatigue on such outcome variables as magnitudes and variances of muscle activation (IEMG) and M-mode magnitudes, M-mode vector direction (estimated with absolute magnitudes of cosines with the central vectors), variances in the M-mode space, and index of synergy (ΔV). We also explored whether the effects were consistent across the three levels of Frequency and across sway cycle Phase levels. A linear-mixed model for repeated measures was fit to the data. We chose the appropriate covariance structure for our analyses based on maximizing the Akaike's Information Criterion (AIC) (Vallejo et al. 2008). For multiple comparisons Bonferroni’s correction were used. The level of significance was chosen as α = 0.05.

Results

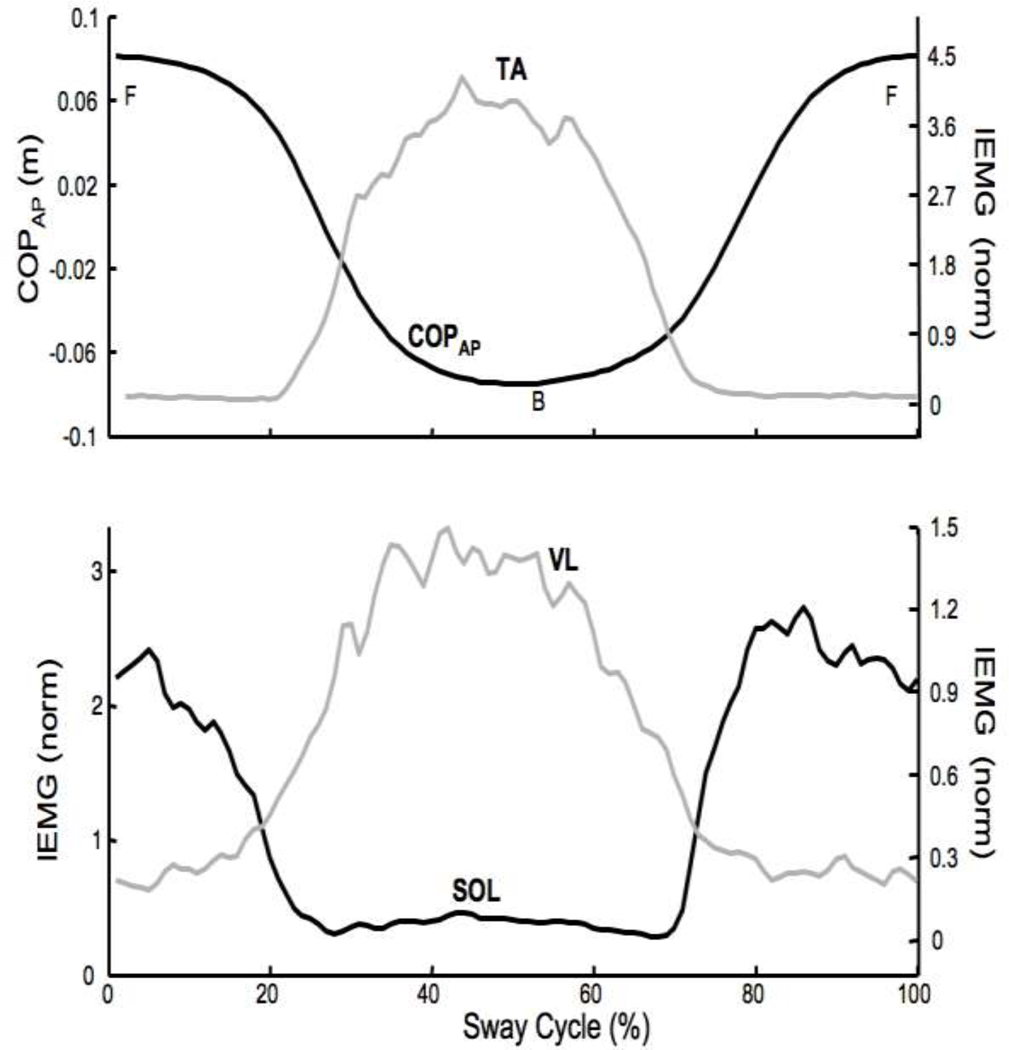
All eleven participants were able to perform the sway task with relative ease both before and during fatigue. Figure 3 shows the mean COP_AP and selected IEMG_norm averaged over 68 accepted sway cyles performed at 0.75 Hz by a typical participant. The left panel shows mean COP_AP (black) and IEMG_norm of TA, while the right panel shows IEMG_norm of SOL and VL. At 0% and 100% of the time cycle, the participant was in the most forward position (F). At approximately 50% of the sway cycle the participant was in the most backward position (B).

Figure 3.

Typical IEMG_norm and COP_AP time profiles for a representative participant. The data were averaged at each 1/100^th time-point over all the accepted cycles. Top: COP_AP displacement (m) and IEMG_norm for tibialis anterior (TA) muscle. Bottom: IEMG_norm for soleus (SOL) and vastus lateralis (VL). F – forward; B – backward.

The average drop in the median power frequency (f_M) for the eleven participants was 37.3%±2.7%. Since co-activation of the triceps surae group was expected, the activity of the GL was also monitored during the fatiguing exercise. The average drop in f_M of GL was 30.0%±2.1%. A two-way repeated-measures ANOVA Muscle (TA and GL) × Frequency (0.25, 0.5 and 0.75 Hz) showed that TA showed a larger drop in the median frequency than GL (main effect of muscle F_(1,37.81) = 9.47; p < 0.01). No other effects were significant.

To quantify effects of fatigue on the performance of the sway task, a 95% confidence ellipse was fit to the COP_AP vs COP_ML trajectories of all the accepted cycles for each subject and condition. The area of the ellipse, length of the major and minor axes and the orientation of the major axis with respect to the x-axis (anterior-posterior) were calculated. During-fatigue no significant changes were seen in any of those variables (no effects in a two-way MANOVA, Fatigue × Frequency).

Effect of Fatigue on Muscle Activation Indices

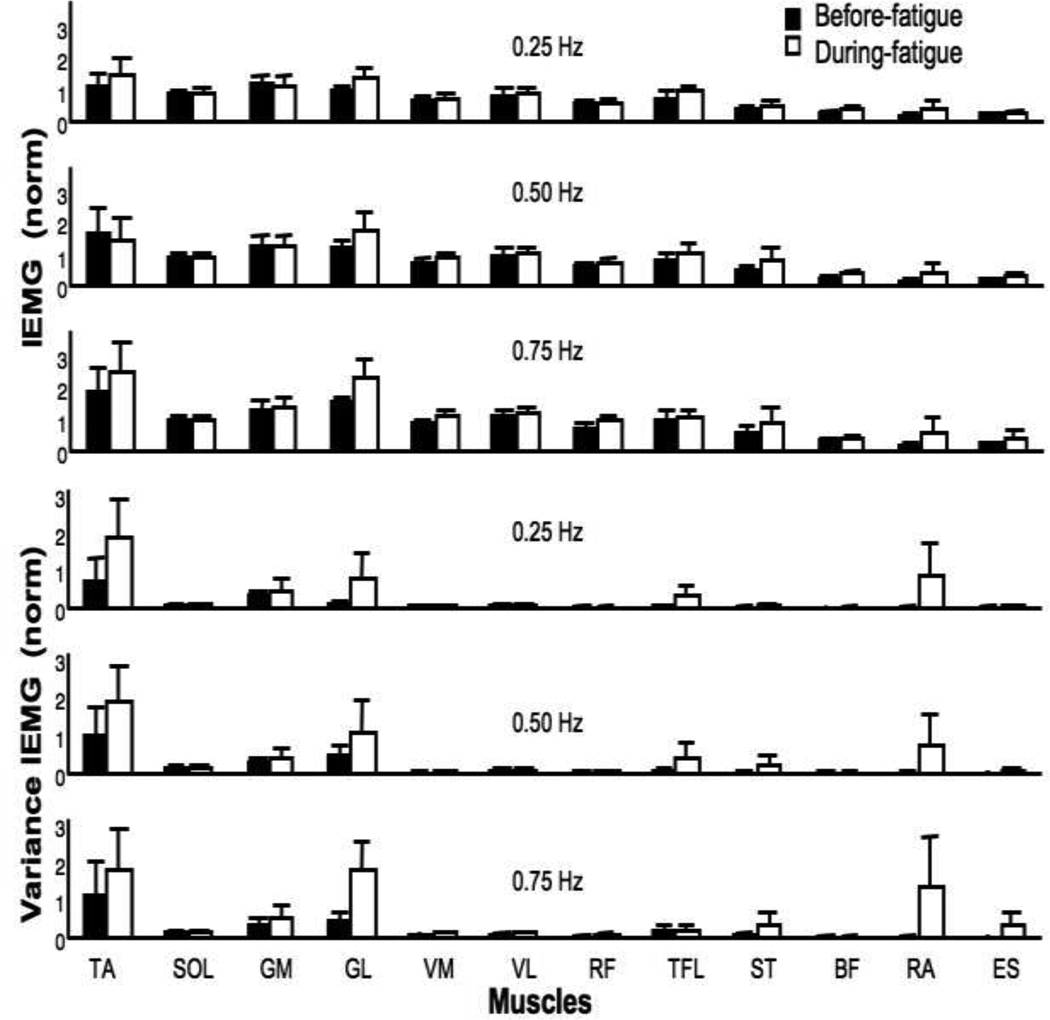
There was a trend towards an increase in the activation indices for several muscles during fatigue (Figure 4 upper panel). For example, the mean IEMG_norm of RA increased by about 135% during fatigue. IEMG_norm for TA, VM and TFL muscles increased by about 20%. This trend, however, was not significant according to a two-way MANOVA, Fatigue × Frequency. This was due, in part, to the large variability of the activation indices during fatigue. Figure 3 (lower panel) also shows the IEMG_norm variance in the before-fatigue and during-fatigue trials for the three Frequency conditions. There was a significant increase in the IEMG_norm variance during-fatigue for both ventral and dorsal muscles. On average, the variance of IEMG_norm increased by about 70% for the ventral muscles and by 120% for the dorsal muscles.

Figure 4.

Mean amplitude of IEMG_norm averaged over the sway cycle (top panels) and mean variance (bottom panels) for the 12 muscles and three sway frequencies. Before fatigue (black bars) and during fatigue data (open bars) are shown with standard error bars. See Figure 1 for the abbreviations.

A two-way MANOVA, Fatigue × Frequency on variance of the IEMG_norm revealed significant effect of Fatigue on the variance index for both dorsal (F_(6,55) = 2.53; p < 0.05) and ventral (F_(6,55) = 3.24; p < 0.01) muscles. There were no other effects. The univariate tests with Fatigue as a factor revealed a significant increase in variance for the VM, RF, GM, BF, and ES IEMG_norm (p < 0.05). The average increase in IEMG_norm variance for these muscles was 150%.

Effect of Fatigue on M-Modes and the Jacobian

IEMG_norm was subjected to factor extraction with the principal component method to identify muscle modes (M-modes, see Methods). This reduced the 12-dimensional muscle activation space to a four-dimensional M-mode space. The first four PCs accounted for 85% (±0.98%) of the total variance. The amount of variance explained by the first 4 PCs dropped by about 2% during fatigue from 86.1%±0.97% to 83.9%±0.95% (effect of Fatigue, F_(1,51.99) = 6.62; p < 0.05).

Table 1 shows the PC loadings for the before- and during-fatigue conditions for the 0.5 Hz sway for a typical participant. The significant loadings (with magnitudes over 0.5) are in bold. The number of co-contraction patterns was quantified across all the subjects and sway frequencies prior to fatigue and during fatigue. We found consistent co-contraction patterns only between RA and ES. An example of co-contraction for the during-fatigue case is presented in Table 1. Across subjects and conditions, there were a total of 11 PCs with co-contraction prior to fatigue and 14 during fatigue (out of 132; no significant effect of Fatigue).

Table 1.

Muscle Loadings in the Factor Analysis

	Before-Fatigue				During-Fatigue
	PC1	PC2	PC3	PC4	PC1	PC2	PC3	PC4
TA	0.44	−0.76	0.19	0.00	0.38	−0.10	0.42	0.62
SOL	−0.88	0.32	−0.12	0.17	−0.91	−0.02	−0.24	−0.24
GM	−0.89	0.32	−0.12	0.16	−0.90	−0.01	−0.25	−0.26
GL	−0.89	0.19	−0.10	0.20	−0.89	−0.04	−0.19	−0.12
VM	0.16	−0.27	0.06	−0.91	0.13	−0.02	0.82	−0.10
VL	0.28	−0.72	0.08	−0.44	0.24	0.09	0.75	0.24
RF	0.35	−0.72	0.08	−0.38	0.22	−0.01	0.75	0.27
TFL	0.32	−0.79	0.18	−0.19	0.21	−0.01	0.08	0.90
ST	−0.88	0.31	−0.14	0.09	−0.82	−0.01	−0.17	−0.19
BF	−0.79	0.44	−0.15	0.07	−0.57	0.04	−0.46	−0.24
RA	0.16	−0.28	0.91	−0.09	0.04	−0.97	0.01	0.03
ES	−0.75	0.32	0.43	0.07	−0.68	−0.61	−0.08	0.07

The principal component (PC) loadings are shown for the before- and during-fatigue conditions for the 0.5 Hz sway performed by a typical participant. PC₁, PC₂, PC₃ and PC₄ are the four PCs (arranged in columns). The muscle loadings for the 12 muscles are in the rows. The significant loadings (with magnitudes over 0.5) are in bold. The presence of a co-contraction pattern between RA and ES muscles is underlined for the during-fatigue case. TA – tibialis anterior; SOL – soleus; GM – medial gastrocnemius; GL – lateral gastrocnemius; VM – vastus medialis; VL – vastus lateralis; RF – rectus femoris; TFL – tensor fascia latae; ST – semitendinosus; BF – biceps femoris; RA – rectus abdominis; ES – erector spinae.

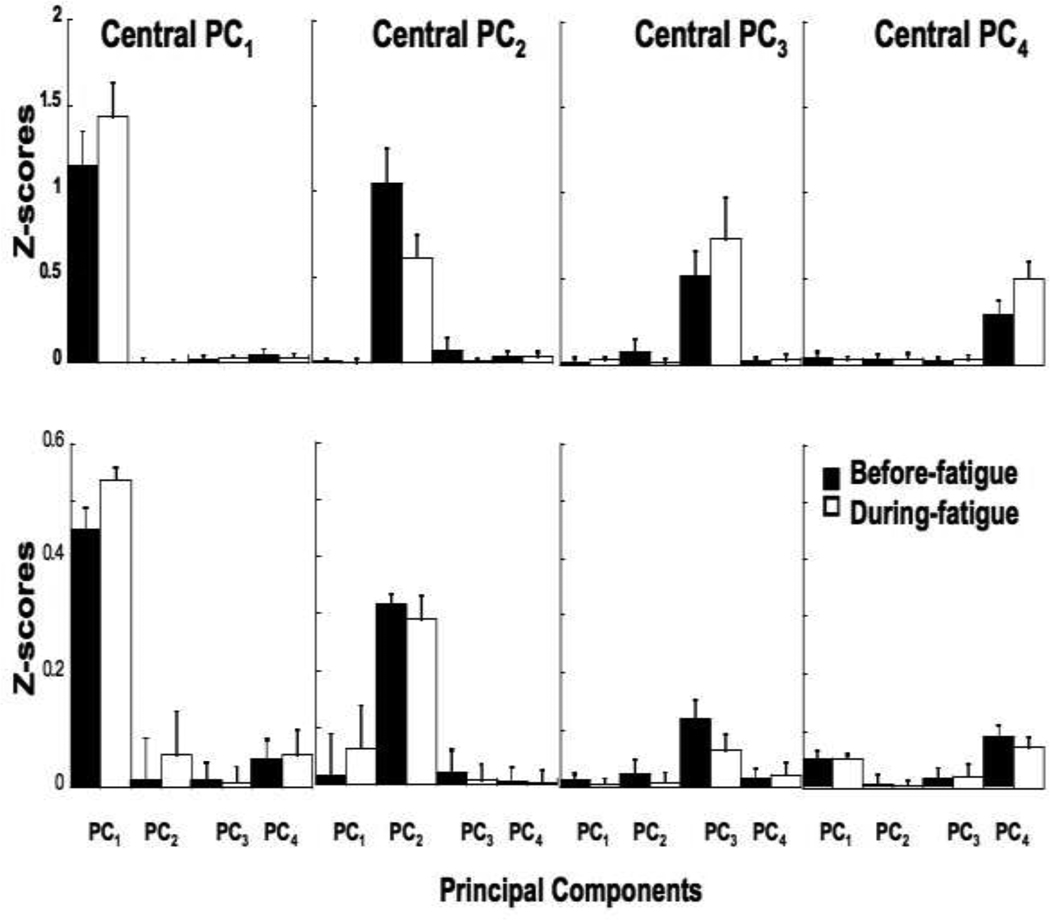
To quantify similarity of M-modes, cosines between central vectors, p_i, and each individual eigenvector (PC) were computed and compared across the participants and conditions (see Methods). This analysis showed that the composition of the M-modes was more similar across conditions for the same participant than across participants within the same condition. Fatigue and Frequency did not have a significant effect on the composition of the M-modes. We also found that PC₁ was more reproducible across both participants and conditions than PC₂, PC₂ was more reproducible than PC₃, and PC₃ was more reproducible than PC₄.

Mean z-scores of the absolute values of the cosines are shown in Figure 5 (top panel: across conditions; bottom panel: across participants). The higher z-scores in the top panel compared to the bottom panel indicate that the composition of the M-modes (PCs) were more similar across conditions than across participants. Note the substantially higher z-scores between a central vector and individual vectors of the same M-mode and low z-scores otherwise. This shows that, a vector PC_i is close to being collinear to a central vector p_j if i = j (where i, j = 1, 2, 3, 4) and almost orthogonal to it if i ≠ j. A repeated-measures ANOVA confirmed main effect of PC (F_(3,56.1) = 113.78; p < 0.001) without an effect of Fatigue.

Figure 5.

Z-scores of the absolute values of the cosine between the central vector and each of the PCs when the central vectors were computed for each participant p_i(p) (top panels) and for each sway frequency p_i(f) (bottom panels). The values are averaged across frequencies. Before fatigue data are shown with black bars, and the during fatigue data are shown with open bars.

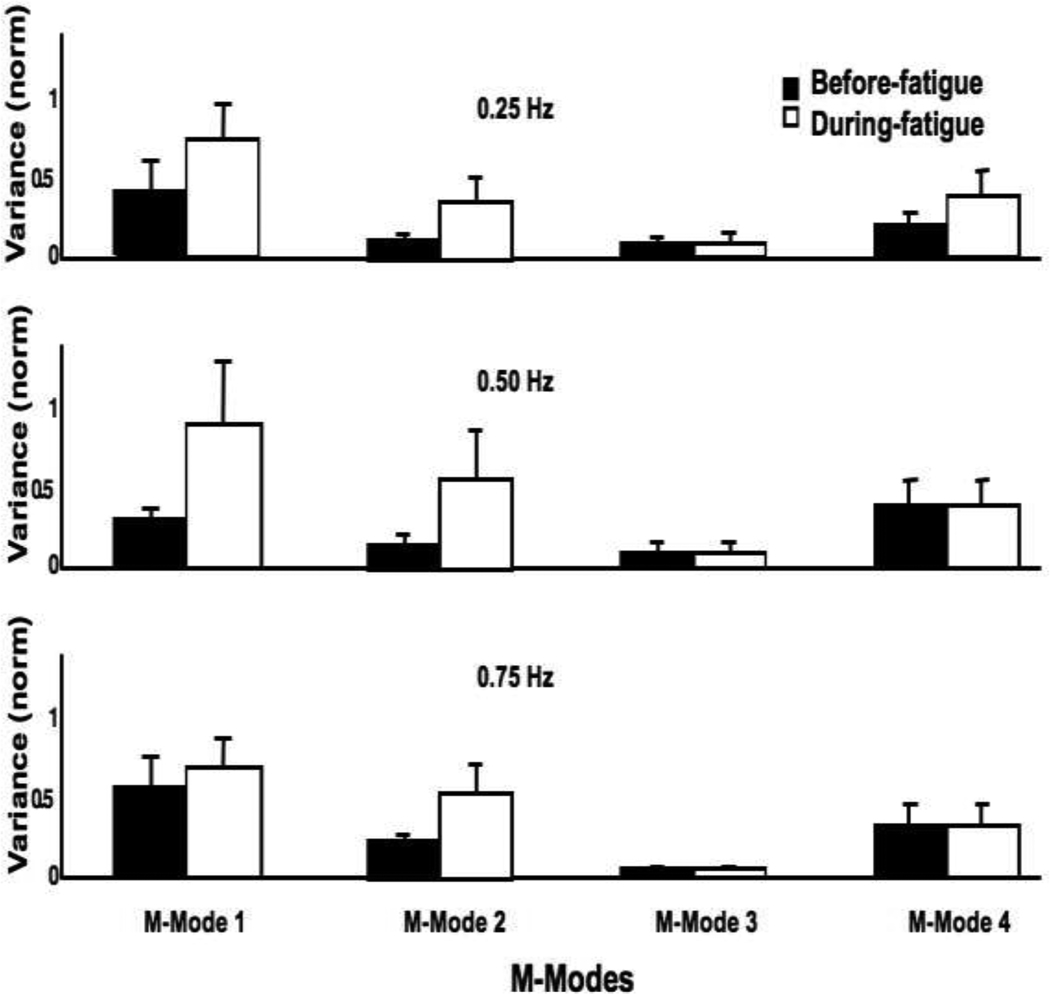
The means magnitudes of the M-modes showed no significant changes during fatigue. In contrast, variance of M-mode magnitudes increased during fatigue (Figure 6) by about 80% for M₁-mode, by about 200% for M₂-mode and M₄-mode, and by about 400% for M₃-mode. A two-way repeated-measures ANOVA, Fatigue × Frequency showed a significant effect of Fatigue for M₁-mode (F_(1,22.41) = 7.2; p < 0.05), M₂-mode (F_(1,12.12) = 9.15; p < 0.05) and M₃-mode (F_(1,24.99) = 7.74; p < 0.05) with no other effects; no significant effects for M₄-mode.

Figure 6.

Mean variance (±SE) of M-modes (M₁, M₂, M₃ and M₄) over all the accepted sway cycles for the three sway frequencies. Before fatigue data are shown with black bars, and the during fatigue data are shown with open bars.

Effects of small changes in M-mode magnitudes on COP_AP displacement (the Jacobian) were computed using multiple linear regressions for each participant and for each condition. For each regression analysis, the data were pooled over the 1% time intervals within a cycle across all the accepted cycles. On average 50% of the variance was explained by the regression models. All M-mode magnitudes were significant predictors of COP_AP shifts. There were no significant effects of fatigue on the regression coefficients (checked by a two-way MANOVA).

Effects of Fatigue on Multi-Muscle Synergies

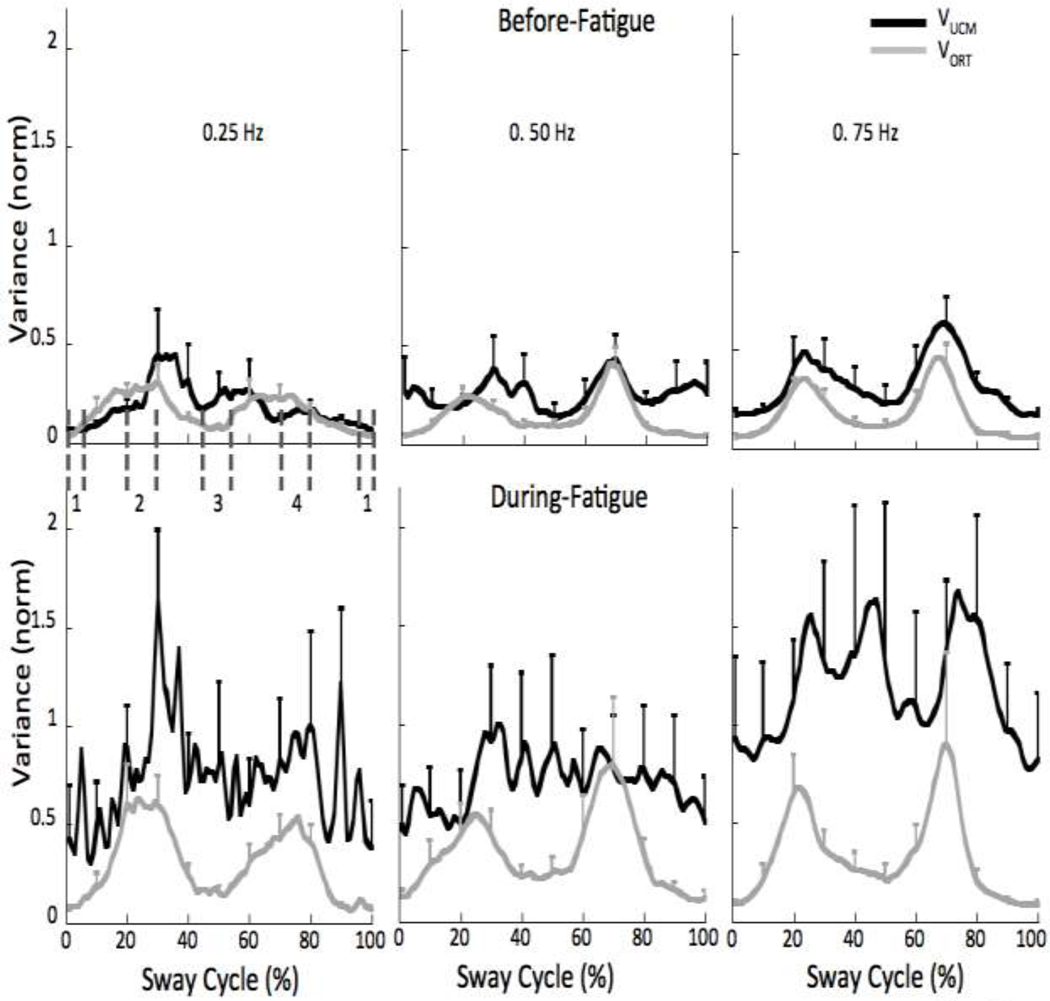
To quantify multi-M-mode synergies stabilizing the COP_AP trajectory, two components of variance in the M-mode space were quantified, one that did not affect the averaged across cycles value of COP_AP (V_UCM) and the other that did (V_ORT). The averaged values of V_UCM and V_ORT over the sway cycle, quantified per degree-of-freedom, are shown in Figure 7 for each condition. The M-mode space has dimensionality n = 4. ΔCOP_AP accounts for one degree-of-freedom (d = 1) and the orthogonal space has 3 (n−d=3) degrees of freedom (see Methods). Note an increase in both indices, which is particularly pronounced for V_UCM. On average, V_UCM increased by about 240% during-fatigue, while V_ORT increased by about 98%.

Figure 7.

Average V_UCM (black lines) and V_ORT (grey lines) before-fatigue (top panel) and during-fatigue (bottom panel). Note the greater changes in V_UCM for the 0.25 and 0.75 Hz frequencies. Four phases were defined as 10% of the sway cycle (−5 to 5%, 20–30%, 45–55%, and 70–80% referred to as phase-1, -2, -3, and -4, respectively). Phase 1 corresponds to the most anterior displacement of the COP and Phase 3 corresponds to the most posterior displacement of the COP. Phases 2 and 4 correspond to intermediate phases. These phases are shown as vertical dashed dark grey lines for the 0.25 Hz condition.

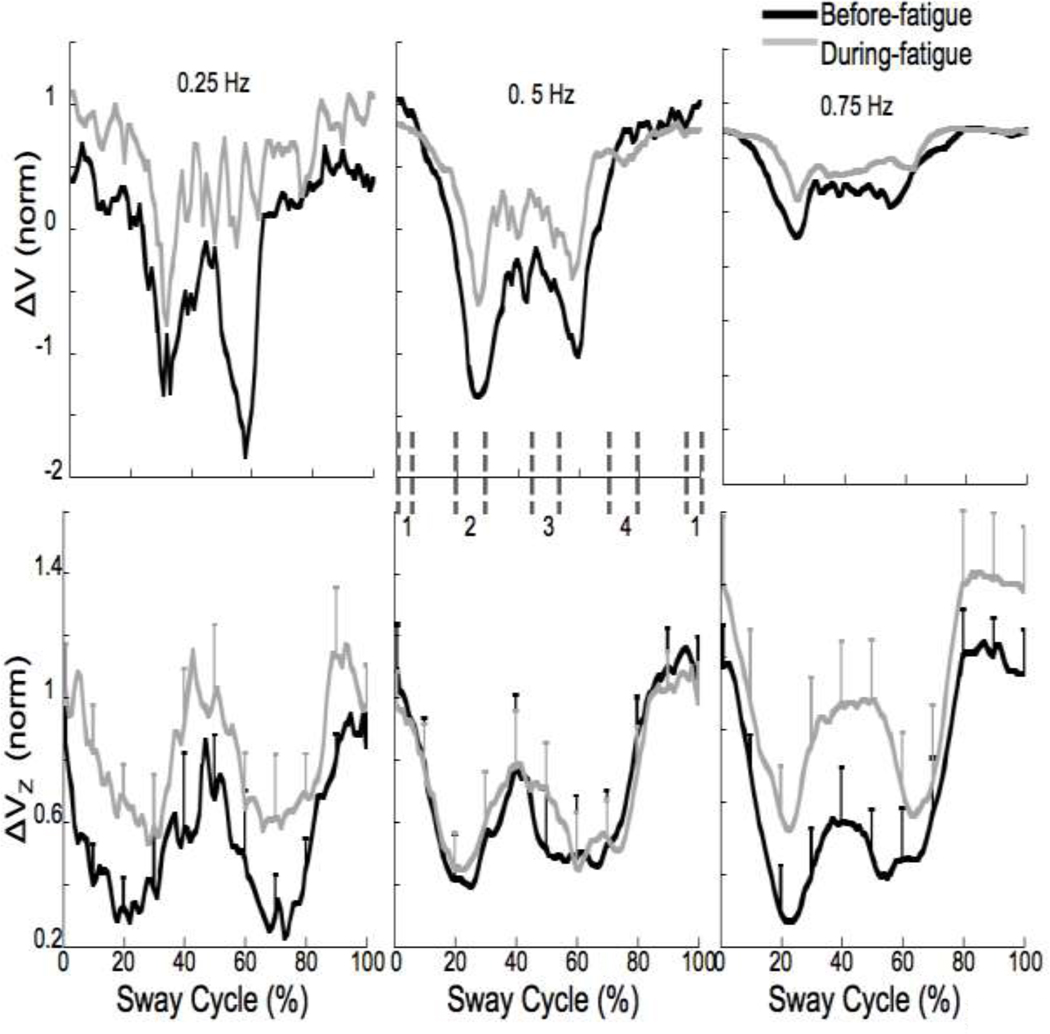
A synergy index (ΔV) was computed, reflecting the difference between V_UCM and V_ORT (see Methods). ΔV over the sway cycle for each condition for a typical participant is shown in Figure 8 (upper panel). Positive values of ΔV are interpreted as reflecting a multi-M-mode synergy stabilizing the COP_AP trajectory. Note that ΔV values increased during fatigue for the 0.25 and 0.75 Hz conditions but did not change much for the 0.5 Hz condition. On average, ΔV values increased by 27% during-fatigue. ΔV values were z-transformed (ΔV_Z) and are shown in the bottom panel of Figure 8 with error bars.

Figure 8.

The synergy index, ΔV before (upper panel) and after z-transformation (ΔV_Z, lower panel). Note the greater changes in ΔV during-fatigue (grey lines) for the 0.25 and 0.75 Hz frequencies. Four phases were defined as 10% of the sway cycle (−5 to 5%, 20–30%, 45–55%, and 70–80% referred to as phase-1, -2, -3, and -4, respectively). Phase 1 corresponds to the most anterior displacement of the COP and Phase 3 corresponds to the most posterior displacement of the COP. Phase 2 and 4 correspond to intermediate phases. These phases are shown as vertical dashed dark grey lines for the 0.5 Hz condition. Mean across subjects data are shown with standard error bars.

All the variance indices showed visible modulation over the sway cycle (Figures 7 and 8). To test whether there was a differential effect of fatigue on V_UCM and V_ORT across different phases of the sway cycle, four phases were defined as 10% intervals of the sway cycle, −5 to 5%, 20–30%, 45–55%, and 70–80% referred to as phase-1, -2, -3, and -4, respectively (illustrated for the 0.5 Hz condition in Figure 8), and the indices were averaged over each phase. Overall: a) the difference between phase-1 and -3 was significant for V_ORT but not for V_UCM; b) there were no differences between phase-2 and -4 for either V_UCM or V_ORT; and c) all other pairwise differences were significant for both V_UCM and V_ORT. These conclusions were supported by a three-way repeated-measures ANOVA, Fatigue × Frequency × Phase, on V_UCM, V_ORT and ΔV_Z. For V_UCM, we found main effects of Fatigue (F_(1,43.26) = 11.71; p < 0.01), Frequency (F_(2,126.96) = 3.65; p < 0.05) and Phase (F_(3,195.31) = 18.1; p < 0.001). For V_ORT, we found main effects of Fatigue (F_(1,41.36) = 9.28; p < 0.01) and Phase (F_(3,194.79) = 148.16; p < 0.001). For ΔV_Z, we found main effects of Fatigue (F_(1,50.39) = 9.28; p < 0.05), Frequency (F_(2,103.71) = 5.87; p < 0.01) and Phase (F_(3,177.64) = 25.88; p < 0.001). There were no significant interaction effects.

Discussion

The main hypothesis of the study has been confirmed. In particular, we observed significant changes in variance of muscle activation indices and of M-mode magnitudes. These changes were widespread, not limited to the muscles (and M-modes) that were directly involved in the fatiguing exercise. Note that the significant increase in variance of muscle activation indices and M-mode magnitudes during fatigue was not associated with significant changes in the magnitude of the variables; so, it is unlikely to represent a direct consequence of signal-dependent noise (Harris and Wolpert 1998; Jones et al. 2002). Most of the increased variance at the level of muscle activations was channeled into “good variance” (V_UCM), that is, variance component that did not affect displacement of the center of pressure in the anterior-posterior direction (COP_AP). This observation supports the general view on motor variability as a potentially positive factor in repetitive actions (Madeleine et al. 2008; Madeleine and Madson 2009). As a result, characteristics of the task variable, COP trajectory, showed no significant changes during fatigue. In particular, no significant changes in the medio-lateral COP deviations were seen, compatible with studies demonstrating no effects of unilateral fatiguing exercise on the medio-lateral sway (Nardone et al. 1997; Caron 2003). So, we can conclude that multi-muscle synergies reorganized during fatigue at the level of co-variation of the elemental variables (magnitudes of M-modes) without a comparable reorganization at the level of composition of the M-modes. Further, we discuss implications of the study for the notion of multi-muscle synergies and possible mechanisms of fatigue induced synergy adaptations within the referent configuration hypothesis (Feldman and Levin 1995).

Effects of fatigue on muscle synergies in whole-body tasks

The notion of multi-muscle synergies is rather old (Babinski 1899; Bernstein 1947, 1967) The classical view that synergies are large muscle groups that work together has been developed recently using a variety of matrix factorization methods applied to indices of muscle activation (for recent reviews see Ting and McKay 2007; Tresch and Jarc 2009). Such methods identify muscle groups with a close to proportional scaling of activation across trials and/or time samples. Note that identification of such groups is only the first step in our analysis of synergies.

We view muscle synergies as a hierarchical neural organization characterized by two features. At the lower level of the hierarchy, muscles are united into groups with proportional scaling of activation (M-modes); M-modes play the role of elemental variables that are recruited at different magnitudes by the higher level of the hierarchy. The first feature of a multi-muscle synergy is M-mode composition. Several earlier studies have shown that M-mode composition changes in challenging conditions and with practice (Krishnamoorthy et al. 2004; Asaka et al. 2008; Danna-dos-Santos et al. 2008), while other studies emphasized similarity of M-mode (“synergy”) composition across tasks (Torres-Oviedo et al. 2006; Ivanenko et al. 2006; Torres-Oviedo and Ting 2007; Danna-dos-Santos et al. 2007). The second feature is co-variation among magnitudes of the M-modes that may or may not be organized to reduce variance of (stabilize) an important performance variable. Earlier studies have shown that such variables as COP coordinate and magnitude of shear force may be stabilized by co-varied adjustments of M-mode magnitudes (Robert et al. 2009; Klous et al. 2010).

Fatigue of the ankle dorsiflexors in our study did not lead to significant changes in the M-mode composition. In particular, we did not observe a significant increase in the number of so-called co-contraction M-modes (those involving parallel changes in the activation levels of agonist-antagonist muscles acting at leg/trunk joints). This result is in contrast to earlier reports of an increase in the number of co-contraction M-modes in challenging conditions, for example during standing on a board with the reduced support area, standing on one foot, and standing with vibration of the Achilles tendons (Asaka et al. 2008; Danna-dos-Santos et al. 2008). Our current result matches the generally unchanged performance of the subjects during fatigue and suggests that performing the task during fatigue was not challenging. There was a significant 2.2% drop in the amount of variance accounted for by the set of M-modes during fatigue. The relatively small magnitude of this effect, however, suggested to us that it did not warrant increasing the number of accepted M-modes. So, we conclude that the first feature of synergies, M-mode composition, was not affected significantly by fatigue.

Another important issue is that the analysis does not involve “silent” M-modes, that is, M-modes that have no significant effect on performance. If such elemental variables exist, they can lead to an inflation of the number of degrees-of-freedom and spurious results. In our experiment, all M-modes were significant predictors of COP_AP shifts. Hence, we conclude that no “silent” M-modes were included into the analysis both before and during fatigue.

As expected from earlier studies (Zijdewind et al. 1995; Missenard et al. 2008a), fatigue led to a significant increase in the variability of muscle activation indices. This increase was not limited to the muscle that was directly involved in the exercise (TA). It involved other muscles including a TA antagonist (GM) and also muscles crossing other joints (VM, RF, BF, and ES) (cf. Danna-dos-Santos et al. 2010). Several earlier studies documented fatigue-induced adaptations in non-fatigued muscles (Morris and Allison 2006; Kanekar et al. 2008; Strang et al. 2009). In particular, Strang et al. (2009) concluded that fatigue-induced changes are centrally mediated through adjustments of motor commands, in line with our observations.

Fatigue also led to an increase in variance of the M-mode magnitudes. This result is similar to earlier reports of an increase in variance of commands to fingers of the hand after fatigue of only the index finger (Singh et al. 2010a, 2010b) and to a recent study of the changes in the muscle activation pattern vector after a fatiguing gripping exercise (Danna-dos-Santos et al. 2010). As in the mentioned earlier studies, we suggest that this increase in variance of all the elemental variables (M-mode magnitudes) is adaptive: It allows, in combination with increased co-variation among the variables, to protect from detrimental effects of fatigue a functionally important performance variable, to which all the elemental variables contribute.

Indeed, our analysis of the two components of M-mode variance (V_UCM and V_ORT) has shown that V_UCM increased significantly more during fatigue resulting in higher values of the index of synergy ΔV. We can conclude, therefore, that fatigue led to changes at the higher level of the assumed hierarchy leading to significant changes in the second feature of synergy, co-variation among elemental variables. These changes attenuated effects of fatigue on the task variable, COP_AP trajectory. A recent paper (Bisson et al. 2011) reported significant effects of ankle muscle fatigue on kinematic characteristics of postural sway; in that study, effects of fatigue were seen during quiet standing, not during voluntary sway. It is possible that the relatively small COP deviations during spontaneous postural sway are not stabilized by multi-muscle synergies and thus show no adaptive effects after fatigue of a subgroup of muscles.

The increase in ΔV during fatigue was robust across all the phases of the sway cycle but it was less pronounced during the sway at 0.5 Hz as compared to faster (0.75 Hz) and slower (0.25 Hz) tasks. In a post-hoc pilot study, we asked our subjects to sway at a self-selected frequency; on average, the subjects swayed at 0.43 Hz (±0.08 Hz). Self-selected frequencies of cyclic actions have been shown to be close to the natural frequency of the system (Treffner and Turvey 1993). Note that minimal control is required to maintain cyclic action at close to the natural frequency; for example, minimal changes of control signals were reported during elbow movements at frequencies close to the estimated natural frequency of the system (Latash 1992). It is not obvious that the notion of natural frequency can be easily applied to a complex system such as the human body, for example, because the modulation of activation of the muscles acting at the ankle joint leads to modulation of the apparent joint stiffness (Latash and Zatsiorsky 1993). Nevertheless, the special behavior of the effects of fatigue at 0.5 Hz and the closeness of this value to the self-selected sway frequency suggest that adaptive adjustments of neural strategies may be smaller for actions performed at a frequency close to the natural one.

Based on recent studies (Belaid et al. 2007; Vuillerme et al. 2009; Carpenter et al. 2010), one could have also expected fatigue to lead to higher variability in the COP (in particular, COP_ML) displacements to optimize sensory feedback to better deal with the challenge of performing the task during fatigue. Ths idea, however, is not supported by the lack of effects of fatigue on characteristics of COP trajectory. On the other hand, it is possible that the increased variability of muscle activations served in part to improve feedback during fatigue.

Synergies within the referent configuration hypothesis

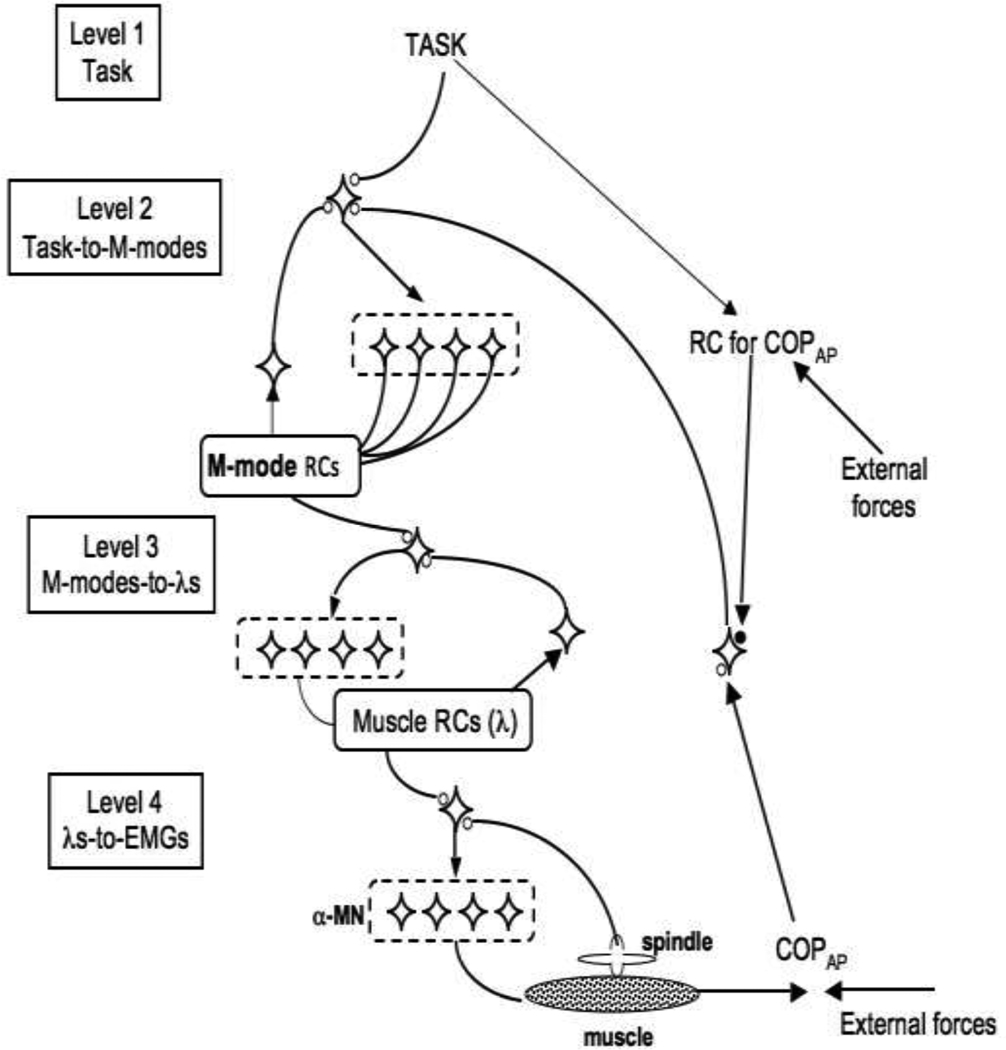
In earlier studies, we tried to link the idea of multi-muscle synergies to the referent configuration (RC) hypothesis (Klous et al. 2011; Krishnan et al. 2011). The RC-hypothesis is a development of the equilibrium-point (EP) hypothesis (Feldman 1966, 1986) for multi-effector, whole-body actions. Both hypotheses assume that the CNS uses, as control signals, subthreshold depolarization of neuronal pools (Figure 9, top insert). The EP-hypothesis assumes that subthreshold depolarization of alpha-motoneuronal pools defines threshold of the tonic stretch reflex. Given an external load, this signal defines as equilibrium state of the system “muscle with its reflex loops plus load” – an equilibrium point.

Figure 9.

A hypothetical control hierarchy within the referent configuration hypothesis. At level 1, the task-specific input is one-dimensional (corresponding to COP_AP trajectory). This input is shared among a higher-dimensional set of signals (Level 2) that translate into M-mode magnitudes. At level 3, each M-mode magnitude signal maps on inputs (λs, thresholds of the tonic stretch reflex) into motoneuronal pools that contribute to that particular M-mode. At Level 4, the inputs into the motoneuronal loops translate into muscle activations (as well as forces and displacements) as a result of interactions with the external load.

The RC-hypothesis may be viewed as reflecting a hierarchical system (Figure 9; Latash 2010), where at the upper level of the hierarchy, subthreshold depolarization of a neuronal pool defines a referent configuration of the body (given external force field), that is a configuration at which all muscles are at thresholds of their activation. RC may not be attainable due to external forces and anatomical constraints; as a result, an equilibrium state may emerge with non-zero levels of muscle activation reflecting the difference between the actual configuration and RC. RC is related to task specific variables such as, for example, COP_AP coordinate.

Imagine that producing a desired COP_AP trajectory is the only component of the task (which it is obviously not, for example because of the necessity to keep balance in the medio-lateral direction). Then, at the upper level, the task-specific input is one-dimensional (Level 1 in Figure 9). We assume that this input is shared among a higher-dimensional set of signals (Level 2 in Figure 9) that translate into M-mode magnitudes. In Figure 9, we illustrate such a mechanism with back-coupling loops (as in Latash et al. 2005; see also Martin et al. 2009), which is also compatible with ideas of optimal feedback control (Todorov and Jordan 2002).

At the next level, each M-mode magnitude signal maps on many motoneuronal pools that contribute to that M-mode (Level 3 in Figure 9). This mapping from M-modes to inputs into motoneuronal pools (λs, thresholds of the tonic stretch reflex, Feldman 1986) is organized in a synergic way with similar back-coupling loops. Finally, at Level 4, the inputs into the motoneuronal loops that translate into muscle activations (as well as forces and displacements) as a result of interactions with the external load.

Actual changes in COP_AP are assumed to be sensed by a higher-order sensory neuron (possibly using the visual system since the study involved visual feedback on COP_AP coordinate) that projects back onto the upper level of the hierarchy and ensures that the system reaches an equilibrium only when COP_AP actual coordinate matches its referent coordinate. The scheme is Figure 9 is compatible with the recent developments of the RC-hypothesis (Feldman 2011).

Effects of fatigue within the referent configuration hypothesis

At each level of the scheme illustrated in Figure 9 the combined activity of the output elements is driven by a referent value defined by the input. The presence of a global feedback loop from performance to the upper level ensures that muscle activation continues until the system reaches a state in which values of important performance variables are equal to their referent values. Variability of performance within this scheme is defined primarily by variability of the input into the upper level, while changes in variance of the outputs of elements are not expected to have a major effect on the performance (e.g., Shapkova et al. 2008). Within such a system, redundancy turns into a blessing, not a curse.

In particular, the redundant design combined with the feedback loops ensures stable performance in conditions when one (or a few) of the elements at any lower level of the hierarchy shows increased variance due to fatigue or other problems. This is done by channeling any increased variance at the level of elements into V_UCM. A recent study has suggested that fatigue may lead to increased contribution of peripheral afferents to coupling across the muscle with fatigue (Kattla and Lowery 2010). This suggestion fits well the scheme in Figure 9.

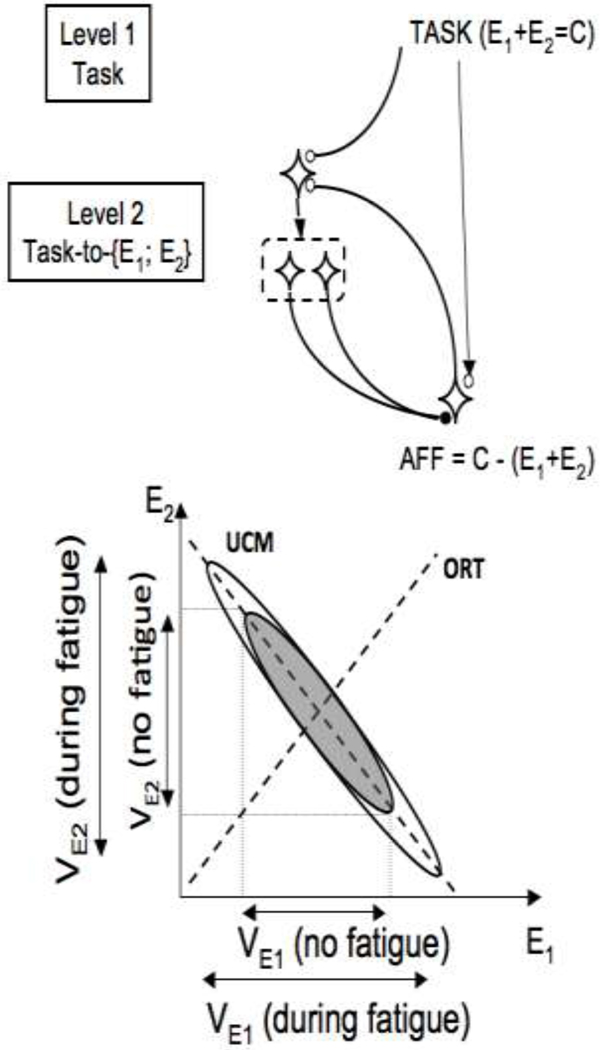
To illustrate effects of fatigue of an element in a redundant system, consider a much more simple system with only one level and only two elements (Figure 10). Prior to the fatiguing exercise, there was a synergy between the elements that stabilized their summed output. This means that, in the space of elemental variables (E₁ and E₂), most variance across trials lies along a line E₁ + E₂ = C, where C is the required output magnitude (thick dashed line in Figure 10). This variance component is V_UCM. Variance along the orthogonal direction (V_ORT) reflects primarily variance of the input into the system. After fatiguing exercise by one of the elements, for example E₁, its variance is increased. The feedback loop in the scheme in Figure 10 will change both E₁ and E₂ until the output matches the one specified by the input. Two results are expected. First, variance of both E₁ and E₂ will change. Second, this increase will be within V_UCM.

Figure 10.

Top: A simplified version of the scheme in Figure 8 for a hypothetical task of producing a constant sum of two elemental variables (E₁ + E₂ = C). Bottom: Two hypothetical data point distributions are shown, before fatigue of one of the elements (grey) and after fatigue (white). Prior to fatigue, most variance is along the line E₁ + E₂ = C (the UCM for the task). After fatiguing exercise by element E₁, its variance (V_E1) is increased. The feedback loop (shown in the upper panel) will adjust both E₁ and E₂ leading to increased variance of both.

This analysis is certainly very much simplified. We have not considered possible effects of fatigue on the input into the upper level of the scheme, which is likely to be present given the reported effects of fatigue on combined cognitive and motor tasks (Freeman 1933; Lorist et al. 2000, 2002). Fatigue can also lead to changes in feedback loops from proprioceptors (Vuillerme and Boisgontier 2008; Pinsault and Vuillerme 2010) and hence affect efficacy of the feedbacks assumed in the scheme in Figure 9 (compatible with the significant increase in V_ORT in our study). Finally, even if the task is formulated with respect to one performance variable only (COP_AP in our study), in reality, many other variables have to be constrained. During voluntary postural sway, these may relate, for example, to coordinates of the center of mass and stability of gaze (cf. Vuillerme et al. 2001).

Despite all these simplifications, the main message remains: Motor redundancy is not a source of computational problems (cf. Feldman and Latash 2005;), but an important feature of the design of the human neuromotor system that simplifies neural control and helps performance stability across conditions and states of the body. Using this mode of control naturally protects important performance variables from effects of higher variance at the levels of elements. Our study shows that this happens during fatigue of a muscle group, which led to higher variability at the level of muscle activations and elemental variables (M-modes) but not at the level at which the task as explicitly formulated (COP trajectory).