Three Force Fields' Views of the 3₁₀ Helix

Abstract

Slowly but steadily bibliographic evidence is accumulating that the apparent convergence of the various biomolecular force fields as evidenced from simulations of proteins in the folded state does not hold true for folding simulations. Here we add one more example to the growing list of peptides and proteins for which different force fields show irreconcilable differences in their folding predictions, even at such a fundamental level as that of a peptide's secondary structure. We show that for an undecamer peptide that is known from two independent NMR structure determinations to have a mainly 3₁₀-helical structure in solution, three mainstream biomolecular force fields give completely disparate predictions: The CHARMM force field (with the CMAP correction) predicts an outstandingly stable α-helical structure, in disagreement not only with the experimental structures, but also with experimental evidence obtained from circular dichroism. OPLS-AA shows an almost totally disordered peptide with the most frequently observed folded conformation corresponding to a β-hairpin-like structure, again in disagreement with all available experimental evidence. Only the AMBER99SB force field appears to qualitatively agree with not only the general structural characteristics of the peptide (on the account of both NMR- and CD-based experiments), but to also correctly predict some of the experimentally observed interactions at the level of side chains. Possible interpretations of these findings are discussed.

Introduction

Physics-based simulations of protein folding hold the promise of offering a deeply satisfying ab initio solution to the protein-folding problem at a level of atomistic detail not accessible by experimental methods. The increased availability of computing power led to a concomitant increase of the length of the simulations that can be performed, with the simulations finally reaching the timescales required for folding of short polypeptides. As the number of reported folding simulations increases, the initial optimism (1) is being replaced with the realization that the various empirical biomolecular force fields differ very significantly not only with respect to their predictions concerning the kinetics of folding, but most importantly, they differ even in their ability to identify (or even visit) the experimentally known native folded state (2–7). Here we add one more piece of evidence in support of this growing skepticism by showing that for a peptide of experimentally known NMR structure, three popular biomolecular force fields give totally different views of not only the peptide's folding kinetics and stability, but even of its secondary structure and native folded state.

The peptide whose folding we simulated is a variant of residues 101–111 of human α-lactalbumin (αLa). Two independent NMR structure determinations are available for this peptide—the first for the native αLa sequence (IDYWLAHKALA) (8) and the second (and more recent) for a designed variant with sequence INYWLAHAKAG (9). Both determinations (and despite the sequence differences) showed that the peptide folds in a helical 3₁₀-like structure for its N-terminal part, with a highly disordered C-terminus. Starting from a fully extended structure, we performed, using three different force fields, extensive all-atom simulations with explicit solvent and full electrostatics amounting to a grand total of 7.6 μs of simulation time. In what follows, we describe the simulation protocol and analyses performed, and compare the results obtained from the three force fields with the experimental findings. We conclude by discussing possible interpretations of these results.

Methods

Force fields, system preparation, and simulation protocol

The three force fields used in our simulations are the CHARMM force field (version c36a2) with the CMAP correction (10,11), the OPLS-AA force field (12), and the AMBER99SB force field (13,14). These will be hereafter referred to as the CHARMM, OPLS, and AMBER force fields. From the two sequence variants available for this peptide, we have chosen to simulate the one studied by Araki and Tamura (9) due to the availability of additional (to NMR) experimental data in the form of circular dichroism spectroscopy and self-association studies that verified the peptide's monomeric state in solution. The system preparation procedure and simulation protocol are identical with those we have previously reported (15). In summary, the starting structure (corresponding to the sequence INYWLAHAKAG) was in the fully extended state as obtained from the program Ribosome (http://www.roselab.jhu.edu/∼raj/Manuals/ribosome.html). For both the CHARMM and OPLS force fields, missing hydrogen atoms were built with the program PSFGEN from the NAMD distribution (16) and solvation-ionization were performed with VMD (17). In the case of AMBER, system preparation was performed with the program XLEAP from the AMBER tools distribution (18).

The peptides were prepared assuming an acidic pH (with the histidine residues fully protonated) in agreement with the conditions used for both experimental structure determinations (8,9). The peptide termini were unprotected also in agreement with the experimental conditions used for the 2DX2 structure (9). The final systems for the three force fields comprised 5798 atoms for AMBER (177 peptide atoms, two ions, and 5619 TIP3 water atoms), 6343 atoms for OPLS (177 peptide, four ions, and 6162 TIP3 water atoms), and 6352 atoms for CHARMM (177 peptide, four ions, and 6171 TIP3 water atoms). The number of waters and ions that were added to the systems was adjusted in such a way as to 1), maintain a minimum separation between PBC-related images of 16 Å (15), and 2), minimize the difference between the systems' equivalent ionic strength with the target value of 100 mM NaCl.

We followed the dynamics of the three folding simulations using the program NAMD (16) for a grand total of 7.6 μs (1.3 μs for CHARMM, 2.9 μs for AMBER, and 3.4 μs for OPLS) as follows (15): The systems were first energy-minimized for 1000 conjugate gradient steps followed by a slow heating-up phase to a final temperature of 320 K (with a temperature step of 20 K) over a period of 32 ps. Subsequently the systems were equilibrated for 10 ps under NpT conditions without any restraints, until the volume equilibrated. This was followed by the production NpT run with the temperature and pressure controlled using the Nosé-Hoover Langevin dynamics and Langevin piston barostat control methods as implemented by the NAMD program (and maintained at 320 K and 1 atm). The Langevin damping coefficient was set to 1 ps⁻¹, and the piston's oscillation period to 200 fs, with a decay time of 100 fs. The production run was performed with the impulse Verlet-I multiple timestep integration algorithm as implemented by NAMD. The inner timestep was 2 fs, short-range nonbonded interactions were calculated every one step, and long-range electrostatics interactions every two timesteps using the particle-mesh Ewald method with a grid spacing of ∼1 Å and a tolerance of 10⁻⁶. A cutoff for the van der Waals interactions was applied at 8 Å through a switching function, and SHAKE (with a tolerance of 10⁻⁸) was used to restrain all bonds involving hydrogen atoms. Trajectories were obtained by saving the atomic coordinates of the whole system every 0.8 ps.

Trajectory analysis

The program CARMA (19) was used for most of the analyses, including removal of overall rotations/translations, calculation of RMSDs from a chosen reference structure, calculation of the radius of gyration, calculation of the average structure (and of the atomic root mean squared fluctuations), production of PDB files from the trajectory, Cartesian space principal component analysis (20,21) and corresponding cluster analysis, dihedral space principal component analysis (22,23) and cluster analysis, calculation of the frame-to-frame RMSD matrices, etc. Secondary structure assignments were calculated with the programs STRIDE (24) and DSSP (25). All molecular graphics work and figure preparation was performed with the programs VMD, RASMOL (26), and CARMA. Sequence logos were prepared with the program WebLogo (27).

Sufficient sampling and convergence

To demonstrate sufficient sampling, we divided the trajectories into two nonoverlapping halves and performed both Cartesian and dihedral angle principal component analysis on each half. This was followed by calculation of the eigenvector overlap (as a function of the number of eigenvectors) for the two halves obtained from each force field. For the CHARMM simulation, the overlap in Cartesian space is 0.97 using only the top two eigenvectors, and 0.95 in dihedral space with three eigenvectors, thus indicating that full convergence has been achieved. Similarly, for the OPLS simulation, the overlap in Cartesian space is 0.98 with two eigenvectors, and 0.89 in dihedral space with three eigenvectors. Finally, the AMBER force field converged slightly more slowly with the top six eigenvectors giving an overlap of 0.98 in Cartesian space and 0.85 in dihedral space, becoming 0.94 and 0.70 if the overlap of only the top four eigenvectors is calculated.

Results

Structural stability

The top row of Fig. 1 shows a color representation of three matrices containing the root mean-squared deviation (RMSD) between all possible structure pairs recorded from each trajectory. To allow a direct comparison with the experimental data, the upper-half of the matrices was calculated using all Cα atoms, whereas the lower-half was calculated using the Cα values of residues 1–7 (known from the experiment to be the stably folded part). The blue areas of the diagrams correspond to low RMSDs between the corresponding structures, and hence indicate the presence of a stable and persistent structure for the peptide. Conversely, the yellow-red areas correspond to high RMSDs and indicate significant structural differences, and thus absence of a stable conformation.

Figure 1.

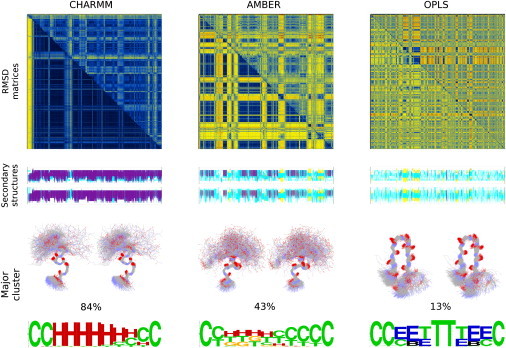
Stability, secondary structures, and major clusters. Direct comparison among the RMSD matrices (top row), the secondary structure assignments (middle row), and the prominent structures obtained from each of the three force fields. For both the RMSD matrices and the secondary structure assignments, the horizontal axes correspond to simulation time and range from zero to 1.3 μs for CHARMM, 2.9 μs for AMBER, and 3.4 μs for OPLS. The RMSD matrices (top row) have been calculated using either all Cα atoms (upper half of the matrices), or only those of residues 1–7 (lower half). For all three matrices, the origin is at the top left-hand corner and the linear color scale ranges from dark blue (corresponding to an RMSD of zero), through yellow (for intermediate RMSDs), to dark red (large RMSDs). For the lower halves of the matrices the RMSDs range from 0.0 to 6.2 Å, becoming 0.0 to 10.9 Å when using all Cα atoms (upper halves). For the secondary structure assignments, both the DSSP (upper graph) and STRIDE-derived assignments (lower graph) are shown. (For both graphs, the color code is: α-helix → magenta, 3₁₀-helix → red, β-structure → yellow, turns → cyan, and coil → white.) The third row shows the structures (wall-eyed stereodiagrams), the frequencies, and the secondary structure assignments (in the form of a weblogo) for the major clusters obtained from each trajectory. For the structure diagrams only backbone atoms are shown to reduce clutter. For the weblogo, H is α-helix, G is 3₁₀-helix, C is coil, T is turn, E is extended structure, and B is bridge as reported by the program STRIDE. Calculation of RMSD matrices and cluster analysis was performed with the program CARMA.

Clearly, the three force fields lead to completely different predictions concerning the peptide's structural stability: The CHARMM-derived prediction is that the peptide is a very fast and extremely stable folder. Within <80 ns, the peptide acquires a stable conformation that persists essentially unchanged for the whole length of the simulation. The difference in the average RMSDs observed between the lower- and upper-halves of the matrix indicate that the stably folded part of the peptide lies in its N-terminus, in good agreement with the experimental data. The OPLS-derived prediction appears to be CHARMM's antipode. The peptide hardly takes-up any long-lived stable conformation, and appears to be completely disordered with the exception of two short-lived folding-unfolding events recorded at approximately one-third of the trajectory's length (corresponding to the two neighboring blue squares in the upper-left quadrant of the matrix in Fig. 1). Comparison of the upper- and lower-halves of the matrix for these folded structures shows that the RMSDs are lower when all Cα atoms are used, indicating that that the folded part is not just the peptide's N-terminal half. The AMBER force field appears to be intermediate between the extremes presented by the CHARMM and OPLS force fields. There are several folding and unfolding events of a recurring structure as indicated by the presence and extend of off-diagonal regions with low RMSD (corresponding to the off-diagonal blue rectangles in the matrix). Integration of these low RMSD regions shows that this persistent structure accounts for ∼50% of the trajectory. Comparison between the lower- and upper-halves of the matrix establishes that this structure is folded in its N-terminal part. Closer examination of the matrix reveals the presence of a second minor structure (accounting for ∼10% of the trajectory), most clearly seen in the lower-right quadrant of the matrix.

Comparison of these predictions with the experimental evidence clearly favors the AMBER force field, even at such a coarse level of analysis. Based on the [Θ]₂₁₅/[Θ]₁₉₈ and [Θ]₂₀₈/[Θ]₁₉₈ ellipticity ratios obtained from CD experiments, Araki and Tamura (9) assigned the peptide to two major folded structural states, the first corresponding to a helical structure with an estimated population of 44%, and the second to a β-hairpin structure with an estimated population of 18%. Although, and as will be discussed later, the experimental uncertainty for these measurements is possibly too high to validate AMBER, it is probably low enough to invalidate the CHARMM- and OPLS-derived predictions.

Secondary and tertiary structure

The second row of Fig. 1 is a color representation of the secondary structure assignments of all structures from all three trajectories as obtained from both DSSP (upper graph) and STRIDE (lower graph). The secondary structure assignments are vertically aligned (in a one-to-one correspondence) with the RMSD matrices shown in the top row of this figure. The DSSP- and STRIDE-derived assignments are in excellent agreement between them and when taken together with the RMSD matrices, demonstrate unequivocally the pronounced differences among the three force fields: according to CHARMM the peptide is an extremely stable α-helix for its N-terminal part (colored magenta in the assignments), with a disordered coil-like C-terminal tail (white). OPLS shows a highly disordered peptide interchanging between coil (white) and turns (cyan), with only a small interval during which β-structure is formed (colored yellow). This folded structure's assignments are β-turn-β and correspond to a β-hairpin structure. AMBER, on the other hand, shows a rather complex pattern. The most frequently observed structure is assigned as a mixture of α- and 3₁₀-helical conformations (magenta and red in the figure), interleaved with unfolding events during which the peptide is mostly assigned to coil (white) and turn (cyan) states. Four times during the trajectory the peptide visits a β-hairpin structure (yellow-cyan-yellow in the assignments). The frequencies of the two folded states, at 43% (helical) and 9% (β-hairpin), are in good agreement with the CD-derived frequencies (at 44% and 18%, respectively (9)).

To place these observations on a firm basis, the last row of Fig. 1 shows wall-eyed stereodiagrams of the structures corresponding to the major peptide conformation obtained from each force field. The frequencies of the corresponding structures are also shown, together with a weblogo representation of the per residue secondary structure assignments for the specific cluster. The CHARMM-derived structure is an α-helix extending roughly from residue 2 to residue 8. The OPLS-derived structure is a β-hairpin with disordered terminal residues. AMBER gives for its major cluster a helical 3₁₀-like structure for residues 3–6 (as observed in the NMR structure determinations), and for the minor cluster a β-hairpin (structurally similar to the one shown for OPLS). The expression “helical 3₁₀-like structure” we used above, together with the secondary structure assignments shown in AMBER's weblogo (where the same residues from a seemingly well-conserved structure are simultaneously assigned to three different states (α, 3₁₀, and turn), do deserve some explanation. The experimentally observed structure is not a pure 3₁₀ helix: both the presence of bifurcated hydrogen bonds involving residues (i) with (i+3) and (i+4), together with the presence of φ,ψ angles that are neither typical of α-helix nor of 3₁₀-helix, makes the secondary structure assignments very sensitive to otherwise small differences in atomic positions.

To demonstrate that this is indeed the case, we calculated the DSSP assignments for each of the models deposited with the 1CB3 entry. We find that depending on the NMR model examined, residues 3–7 are again assigned by DSSP to either α-helix or 3₁₀-helix or turn—a situation similar to what is seen in the AMBER weblogo of Fig. 1. The proportion of 3₁₀ assignments for the experimental structures is significantly higher than that of the α-helical assignments, but this difference is not due to the presence of large structural differences between experiment and simulation. To put this in numbers, we calculated the RMSD for all backbone atoms of residues 3–6 (inclusive) between the 40 deposited NMR models of 1CB3, and 7500 representative structures from AMBER's major cluster. The average RMSD over all (40 × 7500) combinations was 0.41 Å, with some NMR models having an average RMSD (from the 7500 AMBER structures) as low as 0.28 Å for all backbone atoms of residues 3–6.

To place these observations on a firm ground, we performed a direct comparison of the three trajectories with the raw experimental data as deposited with the PDB. For this peptide (9), only nuclear Overhauser effect (NOE) distance upper bounds are available. Using established procedures (28), we calculated, for each force field and for the 138 deposited NOE restraints, 1), the total number of upper bound violations, and 2), the value of the average violation. For the CHARMM force field we observed a total of 21 violations with an average violation of 0.137 Å. For OPLS we obtained 25 violations with an average of 0.192 Å. AMBER, on the other hand, gave only 11 violations with an average violation of 0.050 Å. For 22 NOEs that involved atoms belonging to amino acids separated by two or more residues, the violations and their averages were: 9–0.37 Å for CHARMM, 10–0.40 Å for OPLS, and 9–0.29 Å for AMBER. It is worth noting in passing that the deposited NMR-derived peptide models, gave (when compared with the raw data) a total of 23 violations over the 138 deposited restraints with an average violation of 0.066 Å, indicating that the AMBER-derived trajectory better accounts for the experimental data than the NMR structures derived from them.

To summarize the results up to now, the three force fields show significant differences on almost all aspects examined thus far, from stability and secondary structure, to tertiary structure and the frequencies of their major clusters. Their differences are so pronounced that the selection of the force field that best agrees with the experimental data appears to be trivial: the AMBER99SB force field outperforms CHARMM and OPLS on the predictions concerning the stability, the relative frequencies of major structural clusters, and the secondary and tertiary structures of these clusters. As will be discussed in the next section, even the detailed placement of side chains in the AMBER's helical structure bears a strong resemblance to the NMR structures.

So far the emphasis of our analysis was placed on identifying the major clusters that characterize structurally each force field, tacitly ignoring other minor peptide conformations that the simulations may have visited. Although this is fully understandable given that our intention is to compare the simulations with the experimental results, it does leave the analysis of the trajectories, per se, somewhat incomplete. Although we will not attempt to characterize structurally the numerous minor conformations observed in the trajectories, it is instructive to show a reduced-space representation of the three force fields' folding landscapes to further demonstrate their differences. Fig. 2 shows wall-eyed stereodiagrams of three-dimensional folding landscapes that were calculated by projecting the trajectories on the space defined by the top three eigenvectors obtained from dihedral principal component analysis. Some of the observed minima have been marked with their corresponding structures, as described in the figure's legend.

Figure 2.

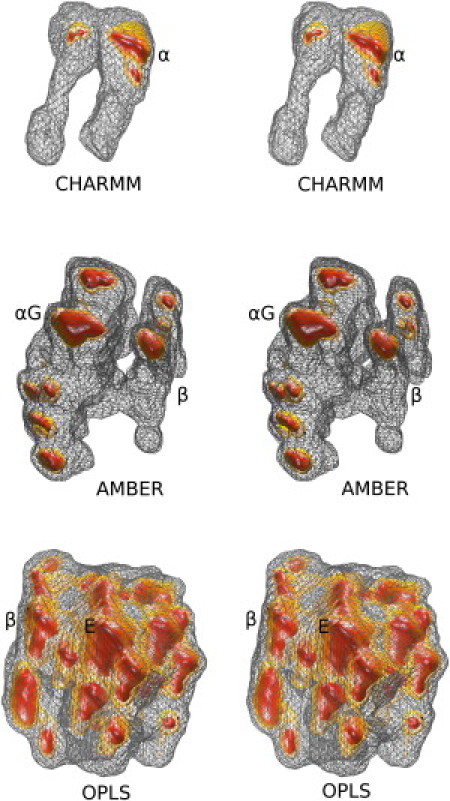
Three-dimensional folding landscapes. Wall-eyed stereodiagrams of the projection of the three trajectories on the space defined by the top three eigenvectors as obtained from dihedral principal component analysis with the program CARMA. For each diagram, three isosurfaces are shown, drawn at mean density (wireframe), 2σ above mean (light surface), and 4σ above mean (dark surface) of the corresponding distributions. (The structural assignments of the most prominent peaks are also shown with α for α-helix, αG for a mixture of α-helix and 3₁₀-helix, β for β-hairpin structure, and E for extended structure.)

The three landscapes—and in agreement with the analyses presented above—are fundamentally different. The CHARMM landscape is essentially a single-minimum distribution, with this minimum corresponding to the α-helical structure analyzed above. The OPLS-derived distribution is CHARMM's diametrical opposite: well over 20 relatively shallow minima can be identified in this map, with almost all of them corresponding to extended and turnlike conformations. It is worth noting that minima corresponding to helical structures are so rare, that they cannot be identified in this map. AMBER is again intermediate between the two other force fields. It has two well-formed and deep minima corresponding to the helical and β-hairpin structures (marked as αG and β in Fig. 2) plus a significant number of other peaks corresponding to extended and turnlike conformations of the peptide. We also note in passing that the minima corresponding to the two major structures are separated by a high ridge—a finding that suggests that the passage from the helical to the β-hairpin structure (and vice versa) probably proceeds through other persistent and unrelated peptide conformations.

The hydrophobic cluster

Both NMR structure determinations (8,9) showed the presence in the peptide structure of a hydrophobic cluster comprising the side chains of Tyr³, Trp⁴, and His⁷. The possible stabilizing effect of that interaction for the 3₁₀-like structure was also extensively discussed. Fig. 3 shows a direct comparison between the experimental, AMBER, and CHARMM structures (OPLS, having failed to converge to any type of helical structure, is rightly excluded from this figure).

Figure 3.

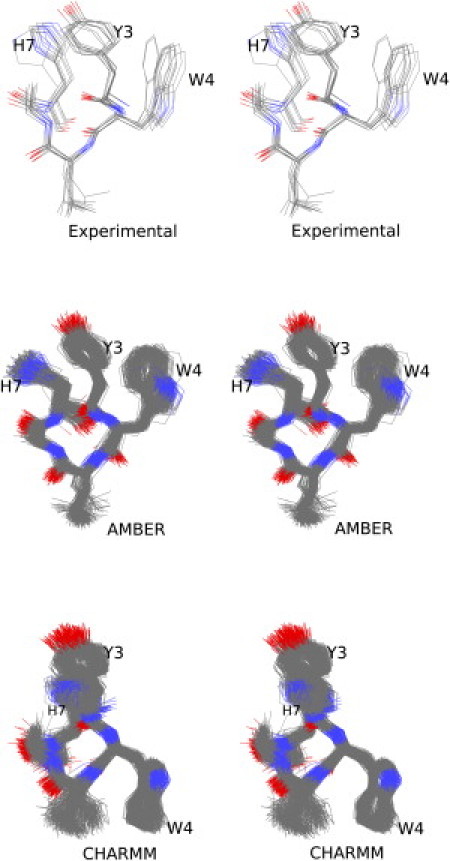
The hydrophobic cluster. The three wall-eyed stereodiagrams compare the experimental, AMBER- and CHARMM-derived structures of the hydrophobic cluster comprising residues Tyr³, Trp⁴, and His⁷. The experimental structure is entry 2DX2 and all deposited NMR models are shown. For the two force fields, ∼500 structures from each of the corresponding major clusters (see text for details) are shown superimposed. The three side chains of the cluster are marked with their one-letter code. To reduce clutter, only the nonhydrogen atoms of residues 2–7 are shown.

The similarity of the AMBER-derived structure to the experimentally determined one is reassuringly obvious with all three side chains having the correct χ₁ conformations (trans for Tyr, gauche⁺ for Trp and His). On the other hand, CHARMM—by converging to gauche⁺ for Tyr and trans for Trp—is clearly inconsistent with the experimentally determined side-chain conformations. The most important difference between the AMBER and experimental structures is the rotation of Trp₄ about its χ₂ dihedral angle by ∼120°. This rotation leads to an edge-to-face stacking with Tyr₃ in the AMBER structure, significantly different from the edge-to-edge interaction seen in the NMR structure. It should be noted, however, that the mode of interaction between these three side chains shows significant differences even between the two independent NMR determinations, with the entry 1CB3 giving a gauche⁻ for Tyr and a gauche⁺ for both Trp and His, leading to an offset stacking between tyrosine and tryptophan. These changes in side-chain orientation may well be the result of the sequence differences between the peptides used for the NMR experiments (see the Introduction).

Discussion

There are two aspects of the calculations presented above. The first is the divergence of the three force fields studied: the same system, with otherwise identical simulation parameters, shows a completely different behavior depending on the force field used. Even without any reference to the actual experimental data, the fact that for the same system we observed anything from extreme stability to almost total disorder, and from an α-helical structure to a β-hairpin, does show that, at least for folding simulations, current empirical (nonpolarizable) force fields are divergent with irreconcilable differences in their predictions.

The second aspect is the comparison with the experimental data. CHARMM with the CMAP correction, and in agreement with previous studies (2,4,6,15), shows a very strong α-helical bias, to the point of becoming inconsistent with the experimentally determined peptide stability. On the other hand, it correctly predicts the order-disorder pattern of the peptide's N- and C-terminal parts, and by converging to a helical structure, its major cluster is structurally not very different from the deposited NMR models.

OPLS's failure to even stably visit helical structures was rather unexpected. The amount of simulation time devoted to OPLS (3.4 μs), together with the calculations described in Sufficient Sampling and Convergence, make it rather unlikely that the problem is lack of sufficient sampling (noting, however, that this force field is known to demonstrate slower conformational sampling (29)). The fact that the only marginally stable structure obtained from the OPLS simulation was a β-hairpin, may be indicative of a β-bias in this force field.

AMBER did so well, that it is tempting to enthuse about it: It correctly predicted the number of structurally major clusters, their relative and absolute stabilities, the peptide's unusual backbone conformation and secondary structure, and even the presence and detailed structure of a hydrophobic cluster formed by three surface-exposed side chains. Although the inherent flexibility present in such short peptides makes it a dangerous proposition to present these results as an unconditional validation of the AMBER99SB force field for the given system, the comparison with the other two force fields does give a clear take-home message about this force field's ability to reproduce the experimentally accessible physical reality.