Tank Treading of Optically Trapped Red Blood Cells in Shear Flow

Abstract

Tank-treading (TT) motion is established in optically trapped, live red blood cells (RBCs) held in shear flow and is systematically investigated under varying shear rates, temperature (affecting membrane viscosity), osmolarity (resulting in changes in RBC shape and cytoplasmic viscosity), and viscosity of the suspending medium. TT frequency is measured as a function of membrane and cytoplasmic viscosity, the former being four times more effective in altering TT frequency. TT frequency increases as membrane viscosity decreases, by as much as 10% over temperature changes of only 4°C at a shear rate of ∼43 s⁻¹. A threshold shear rate (1.5 ± 0.3 s⁻¹) is observed below which the TT frequency drops to zero. TT motion is also observed in shape-engineered (spherical) RBCs and those with cholesterol-depleted membranes. The TT threshold is less evident in both cases but the TT frequency increases in the latter cells. Our findings indicate that TT motion is pervasive even in folded and deformed erythrocytes, conditions that occur when such erythrocytes flow through narrow capillaries.

Introduction

The physics that governs the interaction of deformable particles with viscous fluids remains largely intractable at a quantitative level, despite its importance in the dynamics of the human circulatory system, specifically the motion of red blood cells (RBCs) in shear flow. The flow of blood, a complex fluid nearly 50% of whose volume is taken up by RBCs, is mostly determined by the intricate coupling of various RBC morphologies with the ambient plasma (1). Gaining insights into the dynamics and morphologies of RBCs remains a challenging task; theoretical work continues to drive progress in this area (see (2–5) and references therein), with a continuing scarcity of experiments (see (6,7) and references therein). Physicists have long regarded RBCs as viscoelastic capsules (made of a lipid membrane) filled with an incompressible Newtonian liquid. In equilibrium, such capsules are biconcave, due to which RBCs have a 40% greater surface area than is required to enclose their volume (8); they can, consequently, bend and fold without increasing surface area. Biophysical properties of RBCs, like shape, size, and bending modulus, have been extensively investigated (9–11). In nonequilibrium situations, as experienced under shear flow conditions, RBCs can tumble and roll (12), and can assume different shapes, such as elongation into an ellipsoid while undergoing tank-treading motion (13–17).

In an RBC, the cytoskeleton and the plasma membrane form a tightly coupled layer around the cell with the help of cytoskeleton proteins (18) embedded within the membrane. However, the absence of cytoskeletal elements in the cytoplasm allows the membrane and cytoskeleton to differentially revolve around the cytoplasm: this constitutes tank treading (TT). Such motion also occurs in the case of lipid vesicles under shear flow (19–21). Such vesicles are somewhat akin to RBCs in that they may be regarded as closed fluid membranes that are inextensible and composed of a phospholipid bilayer that separates inner and outer aqueous solutions. In shear flow, such vesicles undergo deformation and they tend to incline relative to the direction of the flow as they tank-tread and move away from surfaces. Tank treading also influences the flow dynamics of suspensions through tubes and, in a broader context, highlights the possibility of shear to induce particle transport in a direction that is perpendicular to fluid flow velocity (20). This appears to be in contradiction to the expectations of a Stokes equation that governs the dynamics of a purely viscous fluid wherein the presence of lift perpendicular to the fluid flow is not permitted for spherical particles suspended in a plane shear flow. However, tank treading allows lift forces due to inertia, enabling flowing particles to be pushed away from walls. In the case of lipid vesicles and RBCs, such lift forces have been quantified (21,22).

Physiologically, TT motion in flowing RBCs produces a lift force that brings them to the center of the blood vessel (trajectory T1, Fig. 1) and inhibits trajectories that lead to migration toward the periphery of blood vessels (trajectory T2). TT motion, therefore, increases flow efficiency and oxygen transfer. Another implication is that TT motion creates an RBC-free layer adjacent to the capillary walls, causing RBCs to travel faster than the average velocity of the plasma. Because blood viscosity depends on RBC concentration, there is a reduction in the localized viscosity as RBCs flow faster than the plasma (the Fahraeus-Lindqvist effect (23)). In the in vivo Poiseuille flow conditions, RBCs assume a slipperlike shape and tank tread when they are near the edges, where the shear acting on the RBCs is high; toward the center, where little or no shear exists, RBCs take up a parachute-like shape (1,24).

Figure 1.

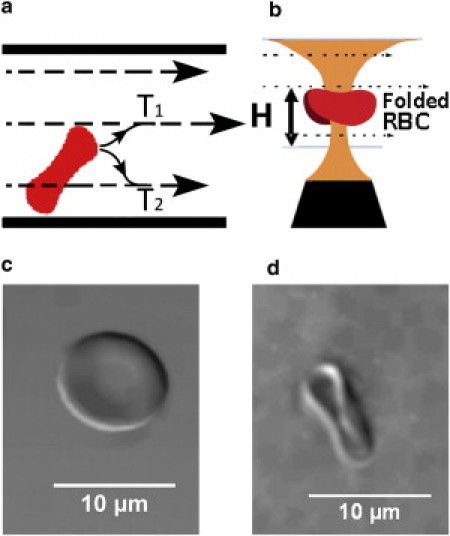
(a) Tank-treading motion gives rise to a lift force on flowing RBCs that tends to propel them to the center of the blood vessel (trajectory T1); this lift force also inhibits RBCs from migrating toward the periphery of blood vessels (trajectory T2). (b) Schematic representation of the optical trap and flow cell. A trapped RBC folds and is subjected to a shear flow. (Horizontal arrows) Direction of flow. (c) DIC image of a biconcave RBC. (d) DIC image of a trapped, folded RBC.

Theory predicts TT motion to depend on the ratio of the minor to major axes of the ellipsoidal RBC, the sphericity index, and the ratio of internal to external viscosities (8). Tank treading has also been predicted to depend on RBC membrane viscosity (25) and shape memory (14). A threshold shear is required to initiate TT motion, but experimental measurements remain limited (26). In TT motion, the motion of the membrane drives the cytoplasm into eddylike flow such that an RBC resembles a triaxial ellipsoid whose longest axis lies parallel to the flow with the intermediate axis parallel to flow vorticity (13). Work done on the RBC by the fluid dissipates in the cytoplasm and membrane. Dissipation also occurs in the cytoskeleton due to its periodic deformation. Tank treading is believed to be strongly dependent on RBC orientation in shear flow and on the projected cell dimensions (27). Probing TT motion in optically trapped cells is important for erythrocytes affected in shape and membrane fluidity, as in patients of certain hematological disorders.

We report here TT motion in optically trapped single, live RBCs flowing in biologically relevant media; incorporation of 100-nm diameter fluorescent beads on the surface of such RBCs enables us to directly visualize TT motion and permits us to establish a shear threshold (1.5 ± 0.3 s⁻¹) beyond which TT motion occurs and below which it ceases. We also engineer shape changes in RBCs by altering osmolarity or cholesterol content in the cell membrane. Under hypotonic conditions, or conditions of depleted cholesterol, the threshold shear for TT motion becomes less pronounced. In hypertonic conditions, the RBCs act like rigid particles and, thus, TT motion does not occur. We have also discovered that temperature (and, thereby, membrane viscosity) has a greater influence on TT motion than viscosity of the suspending fluid. We show that a change in TT frequency of as much as 10% can be obtained by changing temperature by 4°C (such temperature changes can occur within human bodies). The change in temperature induces changes in membrane viscosity. However, when cytoplasmic viscosity is changed (by incubating RBCs in hypotonic solutions and inducing uptake of water), the change in TT frequency is approximately four-times less compared to when equivalent changes occur in membrane viscosity. Hence, the RBC membrane is the dominant energy sink.

Materials and Methods

Preparation of red blood cells

For human RBCs, 100 μL of blood was drawn from a finger prick into a vial containing 0.9 mg of an anticoagulant, acid citrate dextrose. The blood serum proteins were discarded by washing the blood in isotonic phosphate-buffered saline (PBS) at least five times. The final hematocrit was made to be 50%. A quantity of 100-nm silica beads were attached onto the membrane of these RBCs (28) and the suspension was diluted 1000-fold to allow access to single RBCs in the optical trap. The suspending medium was generally isotonic PBS except in the case of viscosity experiments where bovine serum albumin (BSA) was mixed with PBS.

For mouse RBCs, 100 μL of blood was drawn from a retro-orbital puncture into a vial with 0.9 mg of anticoagulant powder. The blood processing and bead attachment were carried out using the same process as for human RBCs. Male Swiss albino mice (6–8 weeks old) were used.

All our experiments were conducted in accordance with rules and procedures adopted by the Tata Institute of Fundamental Research Human and Animal Ethics Committee.

Chemicals used

PBS tablets and BSA powder were obtained from Sigma Aldrich (St. Louis, MO). Silica beads (500 nm diameter), polystyrene beads (2 μm), and fluorescent beads (100 nm) were obtained from Polysciences (Warrington, PA).

Optical trap and flow cell

Our experimental setup comprised optical tweezers coupled to a liquid flow cell (see (29–32) for details of the apparatus). A schematic diagram is shown in Fig. 1. Optical trapping was achieved by focusing 1064-nm wavelength, linearly-polarized light from an Nd:YVO₄ laser through a 100× objective (numerical aperture 1.3) onto our flow cell. The trapped cells were imaged through the same objective by a charge-coupled device camera coupled to a computer for real-time recording; individual movie frames were analyzed with ImageJ software (National Institutes of Health, Bethesda, MD). Our flow cell (100-μm height, 8-mm width, and 48-mm length) was connected to a syringe pump used to pump fluids at controllable rates. The laser power at the trap was directly measured by an integrating sphere attached to a calibrated photodiode to be 5–50 mW.

Experimental procedure

The diluted blood suspension was pumped through the flow cell at a constant rate (0 μL/h to 750 μL/h). Flow speeds at different heights from the flow cell base were measured in a separate experiment by imaging flowing 2-μm polystyrene beads. The velocity of the flowing beads at a particular height provided a measure of the fluid velocity at that height. Data obtained at different heights (see Fig. S1 in the Supporting Material) were fitted to a parabola and differentiated to yield the shear rate at a particular height (see Fig. 2, where each data point is the average of measurements made on 25 beads). Typical shear rates ranged from 0.2 s⁻¹ to ∼48 s⁻¹ within a height of 50 μm. Although the shear rate is not constant across the entire RBC diameter, the difference is negligible (<1 s⁻¹, contributing an uncertainty in measured tank-treading frequency of <0.1 radian s⁻¹).

Figure 2.

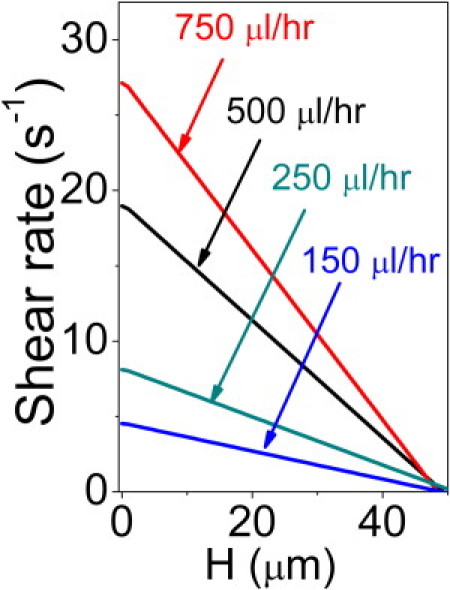
Shear rate was determined by measuring flow velocities up to a height of 50 μm from the bottom of a 100-μm diameter flow cell (H is the height from the bottom of the flow cell). Typical errors in shear rate are ±2.5%.

Earlier work has shown that a live, biconcave RBC folds into a rodlike shape when placed in an optical trap (Fig. 1 d); the folded RBC orients along the laser polarization direction (31–33). In our experiments, such a folded RBC tank-treads when held in a liquid such as isotonic PBS flowing in appropriate shear flow (Fig. 1). Real-time videos of the trapped RBCs undergoing tank treading were recorded for off-line quantification of tank treading at different values of temperature, viscosity, and osmolarity of the suspending fluid using RBCs (8-μm diameter) from healthy humans and with mouse RBCs, which exhibit a wide size variation (2–10 μm).

To probe viscous dissipation within the cytoplasm we also made measurements with Heinz bodies within RBCs. Heinz bodies are spherical hemoglobin precipitates within RBCs that can be imaged; these were induced using an established protocol (13).

For temperature-dependent measurements, the source and sink of the flowing liquid were temperature-controlled, using insulated tubing to minimize dissipation. Temperature differences never exceeded ±0.5°C. We also measured tank-treading frequencies at different fluid viscosities obtained by dissolving BSA in PBS. BSA concentrations of 5% (w/v), 10% (w/v), and 15% (w/v) with viscosities of 1.01 cP, 1.25 cP, 1.51 cP, respectively, at 25°C were used. These solutions of BSA were made in isotonic PBS, with the pH value always adjusted to 7.2, ensuring 300 mOsm osmolarity and avoiding cell shrinkage. Isotonic PBS at 25°C yielded a viscosity of 0.92 cP (1 cP = 1 mPa s).

We also performed experiments at different osmolarities: with 30-min cell incubation in isotonic (300 mOsm) and hypotonic (150 mOsm) PBS. For experiments involving depletion of cholesterol from the RBC membrane, the cells were treated with varying concentrations of methyl β-cyclodextrin (MBCD); cholesterol sequestered from the membrane was quantified by staining cells with a lypophilic dye—Nile red (34)—and using flow cytometry.

Results and Discussion

We imaged TT motion in real-time by attaching a 100-nm fluorescent bead to an RBC membrane and trapping the cell at different heights in the flow cell, thereby exposing it to different shear rates (see Fig. 1). Typical results and cartoon depictions are shown in Fig. 3 (see the real-time Movie S1 in the Supporting Material). TT motion was probed as a function of temperature, cell size, viscosity, and osmolarity. In all results that we present in the following, each data point represents an average of measurements made on ≥25 RBCs; error bars in the individual plots designate 1 SD.

Figure 3.

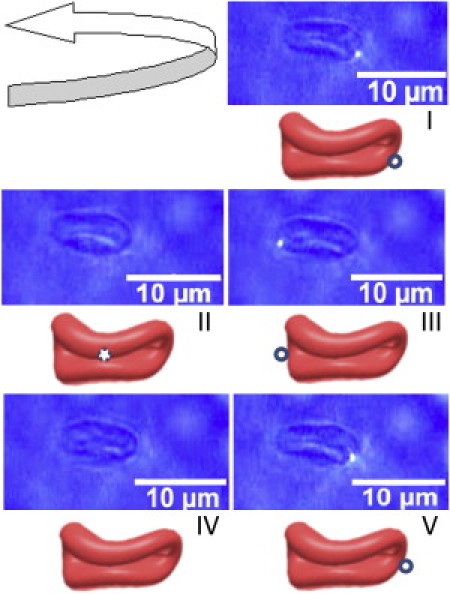
Images (in numbered order) depicting tank-treading motion of an RBC with a 100-nm fluorescent bead attached on the surface (see the cartoon drawings of the folded RBC). (Arrow) Direction of rotation of the bead as tank treading occurs. (Left to right) Fluid flow. The cell is trapped 30 μm from the flow-cell base.

We note from the images shown in Fig. 3 that upon trapping, optical forces distort the shape of a normally biconcave RBC such that it folds into a rodlike shape. The dynamics pertaining to such optically induced shape distortion have been studied previously and a model has been developed in which the shape change is rationalized in terms of Euler buckling (33). Here, an RBC is modeled as a flat elastic disk with an energy cost for bending and deformation. The elastic energy for such a disk comprises the energy costs related to 1), extrinsic (mean) curvature of the membrane, and 2), strain internal to the membrane (shear and compression). In an untrapped RBC, both intrinsic and extrinsic curvatures (and the associated energies) are zero. The RBC membrane only assumes shapes with zero intrinsic curvature because it takes far greater energy to change the intrinsic geometry. When the trap is switched on, the gradient force overcomes the membrane's extrinsic energy and the cell folds. The constraint of preserving the intrinsic geometry forces the membrane to fold into a cylinderlike shape rather than any other shape that has nonzero intrinsic curvature. The allowed configurations are similar to those of a paper disk that can be bent into a cylinder but not into a sphere, as this deforms its internal geometry (33). A nonchanging intrinsic curvature ensures that whereas a trapped RBC experiences a shape change, properties like membrane viscosity and surface tension remain unaltered.

As discussed later, tank-treading dynamics are related to these properties and, consequently, we anticipate that optical forces in our trap will not, per se, affect the essential facets that govern TT motion. At values of laser power used in our experiments, we measure the optical force acting on a trapped RBC to be ∼6 pN using the escape velocity method in a flow cell setup (31,32). This force is negligible compared to that required for stretching an object like an RBC (>400 pN (35)). At our laser powers (which are only 5–50 mW), there will thus be negligible stretching induced by our trap. However, we note that details of the TT dynamics may well be somewhat different in a folded RBC. For instance, we expect the rate of dissipation per unit surface area to remain constant whereas the total dissipation across the entire surface area may differ between a folded and a normal RBC. It is clearly of interest to explore such differences. Furthermore, we show below that variation of laser power incident on a trapped RBC does not affect TT frequency, thereby offering further indication that optical forces generated in our trap have, at best, minimal influence on TT dynamics.

The images in Fig. 3 show that the fluorescent bead revolves about the folded RBC's cross section. In image I, the bead is initially located at the rightmost part of the folded cell. In II, it enters the folded central portion of the RBC to emerge, in III, at the leftmost corner of the cell. Thereafter, in IV, the bead goes behind the cell, to emerge back at the rightmost location in V. Movie S1 illustrates this motion in real-time. In the following, we interpret the observed motion in the light of existing theoretical understanding of TT motion.

Previous attempts at describing TT motion have utilized the Keller-Skalak (KS) model (8,25,36), which uses parameters like ellipsoidal axes and angle in the shear plane. In our trap, such parameters are distorted due to RBC folding. In addition, we observe TT motion in low viscosity fluids, like PBS (viscosity = 0.92 cP), whereas previous measurements utilized suspending fluid viscosities of 10 cP or more (6,27). The KS model predicts that, at our viscosities, RBCs would tumble at all shears, and no TT motion would be expected. In light of these inconsistencies, the question arises: are we observing tank treading at all?

We have adopted various approaches to answer this question. We observe that the orientation and shape of the optically trapped RBC remains unchanged as the bead moves about the cell's cross-section (Fig. 3), indicating motion of the membrane. We have measured the frequency of such motion (denoted the tank-treading frequency, f_tt) for human and mouse RBCs (Fig. 4); our f_tt values for human RBCs are in accord with earlier measurements (13,14), which showed that in highly viscous media (10–100 cP) the viscosity of the suspending media plays a significant role near threshold but not at higher shear rates (27). Therefore, tank-treading frequencies obtained by us at high shear rates should be comparable to those obtained in more viscous media; however, at low shear rates the behavior may well be expected to be different. This is, indeed, the case. Far beyond threshold, at a shear rate of 20 s⁻¹, Fischer (27) measured f_tt to be ∼6.3 radians s⁻¹ whereas we obtain a value of 7.8 ± 0.5 radians s⁻¹. At 30 s⁻¹ shear, the accord improves; the measurement of Fischer (∼9.4 radians s⁻¹) is close to our value (10.3 ± 1.0 radians s⁻¹). It is of interest to note this agreement in the light of different cell shapes in the two sets of experiments. We find the functional dependence of f_tt on shear rate for human RBCs to be essentially independent of the polarization angle of the trapping laser. Taken together with our observation that laser power does not affect TT frequency (Fig. 4 a), it appears confirmed that the optical trap, per se, does not alter TT motion.

Figure 4.

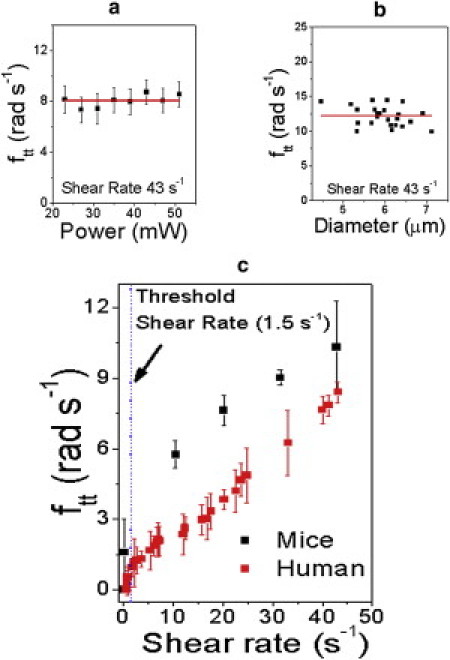
Dependence of TT frequency on (a) incident laser power, (b) size (using mouse RBCs), and (c) shear rate (for human and mouse RBCs). (c, Dashed line) Tumbling and tank-treading regimes for human RBCs (see text). (a and b, Horizontal lines) Guide to the eye.

Our technique allows another important observation, namely, the existence of a threshold shear below which TT motion ceases. We measure this threshold to be 1.5 ± 0.3 s⁻¹ when the suspending fluid has a viscosity of 0.92 cP. In the case of mouse RBCs, the threshold shifts to significantly lower values.

The existence of a distinct threshold for RBCs indicates the active role played by the cytoskeleton and its periodic deformation during our experiments. These periodic deformations are reflected in potential energy oscillations (36) that are a result of each point on the RBC membrane being unique, a property also known as “shape memory” (14). The cytoskeleton is intrinsically attached to the membrane and these oscillations are due to the alternate contraction and stress relaxation of the cytoskeleton. Due to such oscillations, a threshold shear appears beyond which the RBC gets enough energy for tank treading whereas below which it behaves like a solid body and tumbles as it flows (26). A clip of flowing RBCs showing such tumbling at shear rates below 1.5 s⁻¹ is shown in Movie S2. In this shear regime, we also attached a bead to the RBC and confirmed absence of TT. Another real-time movie clip (see Movie S3) shows the situation obtained with a trapped RBC at the tumbling regime of shear rate of 0.5 s⁻¹. No TT motion is seen; as the trap is switched off, the RBC tumbles away.

We also measured TT frequencies of mouse RBCs, which display a wider range of sizes: no size correlation was observed (Fig. 4 b). Interestingly, inherently higher TT frequencies were measured even though there is little evidence to suggest that these RBCs are biophysically dissimilar to human RBCs, other than in size. To our knowledge, this is the first report of TT motion in mouse RBCs.

Because a salient feature of the KS model is viscous dissipation in the cytoplasm and the membrane, we explored the presence of viscous lag between consecutive layers of the cytoplasm during TT motion. Heinz bodies (13) were produced within the RBCs (Fig. 5), and then the RBCs were made spherical in shape in a hypotonic medium. These Heinz bodies are visible as small, beadlike structures within the membrane. A few of them attach to the cell membrane while others remain suspended in the cytosol. When such cells were allowed to tank-tread, we observed relative motion between Heinz bodies attached to the membrane and those in the cytosol, thus providing strong evidence for the existence of viscous dissipation.

Figure 5.

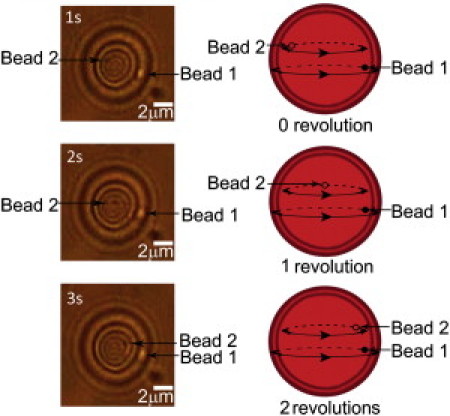
Real-time movie frames showing an RBC undergoing tank treading (frequency 1 s⁻¹). Each frame is separated from the previous one by 1 s. (Arrows) Two Heinz bodies within the RBC, one very close to the membrane (Bead 2) and one away from it (Bead 1, located deeper within the cytoplasm). At each rotation cycle, the outer bead (Bead 2) is at the same place as during the start of the cycle whereas the inner bead (Bead 1) develops a distinct lag. Cartoon depictions are given alongside the movie frames.

Our results show that although the orientation and shape of trapped RBCs is different from the viscous ellipsoid considered by the KS model, TT motion is faithfully performed, with measured frequencies in consonance with those for viscous ellipsoids in shear flow. This raises an interesting question: is an ellipsoidal shape a consequence of tank treading, or is an ellipsoidal shape a prerequisite for tank treading?

Our work indicates that shape-distorted RBCs do perform TT motion. We note that the KS model predicts that work done on unfolded RBCs by the shear flow depends on major and minor axes of the ellipsoid whereas dissipation depends on the total surface area that is exposed to the shear flow. In our case, TT motion is observed in a flow regime in which the KS model would predict only tumbling. This apparent violation of theoretical prediction may be attributed to the fact that the altered (folded) morphology of trapped cells causes both the work done and the dissipation to be different. Proper modeling of these differences remains to be carried out. This is important in the human circulatory system where RBCs shapes distort as capillaries are traversed. Our results confirm findings of earlier models, namely that 1), energy supplied to the tank-treading RBC by the suspending fluid is dissipated in the viscous action of the membrane and cytoplasm (25), and 2), potential energy oscillations in the membrane cytoskeleton (6,36) control the TT dynamics, albeit in somewhat modified form due to trap-induced shape changes.

We now address the parameters on which TT motion depends. Theory predicts that parameters such as membrane viscosity, cytoplasmic viscosity, and cytoskeletal rigidity affect TT motion. We have varied these parameters by suspending RBCs in solutions at varying temperature (changing membrane viscosity), osmolarity (changing shape and cytoplasmic viscosity), and viscosity.

It is known that temperature rise causes exponential decrease in RBC membrane viscosity (37). We have measured how f_tt varies over the temperature range 20–40°C (Fig. 6). At 25°C, the surface viscosity is 7.4 × 10⁻² cP cm; at 37°C the corresponding value is 3.6 × 10⁻² cP cm (38). We have measured that such change in membrane viscosity brings about an increase of ∼3 rad s⁻¹ in f_tt at a shear rate of 43 s⁻¹. This is expected because a decrease in membrane viscosity would lead to decrease in viscous dissipation over each TT cycle, with concomitant increase in the total number of cycles. That a 4°C change in temperature results in as much as 10% change in f_tt at high shear rate (∼43 s⁻¹) is attributed to the RBC membrane being the dominant energy sink during TT motion.

Figure 6.

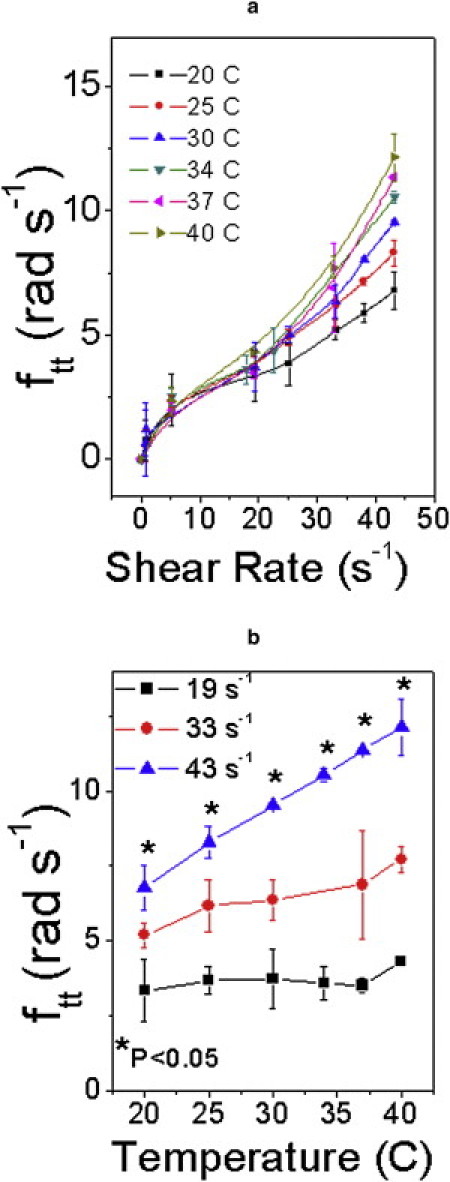
(a) Dependence of tank treading frequency, f_tt, on shear rate at different temperatures. (b) Variation of f_tt with temperature at different shear rates.

We imaged TT motion at various physiologically relevant viscosities by suspending RBCs in different BSA concentrations; results (see Fig. S2) indicate only marginal dependence on viscosity, in accord with earlier measurements (27). The human circulatory system exhibits high variation in blood viscosity (23). Our results confirm that such variation has, at best, marginal bearing on TT motion and, thus, on the efficiency of RBC transport.

Recent theoretical work has postulated that the asymmetry of the cytoskeleton and its periodic deformation might play a major role in TT dynamics (39). We shape-engineered RBCs by suspending them in hypotonic and hypertonic media. Under hypotonic conditions, RBCs swell up, causing two changes: 1), the cytoplasmic viscosity decreases as water mixes with cytoplasm, and 2), the biconcave shape is lost. For TT motion to occur, RBCs have to overcome a minimum potential energy that maintains their normal biconcave shape. For spherical RBCs, theory expects such a threshold to be either absent or reduced. Our measurements indicate that this is, indeed, the case (Fig. 7). We thus establish that the shape asymmetry of the RBCs determines the sharpness of the threshold: spherical RBCs have nonzero values of f_tt even at 0.6 s⁻¹ shear rate, although it must be noted that for purely spherical cells, it is difficult to distinguish between tank treading and tumbling as symmetry ensures degeneracy of these two motions (see Movie S4). Nevertheless, our experiments with Heinz bodies clearly established viscous dissipation in the cytoplasm, thereby validating our notion that tank treading persists even for spherical cells. Furthermore, we note that the three-dimensional structures of the spectrin network and the cell membrane may be different at the depressions and sides of biconcave RBCs; however, they are likely to remain unaltered when the RBCs become spherical and, consequently, the TT threshold reduces but never disappears because of this persistent asymmetry, as is clearly highlighted in Fig. 7.

Figure 7.

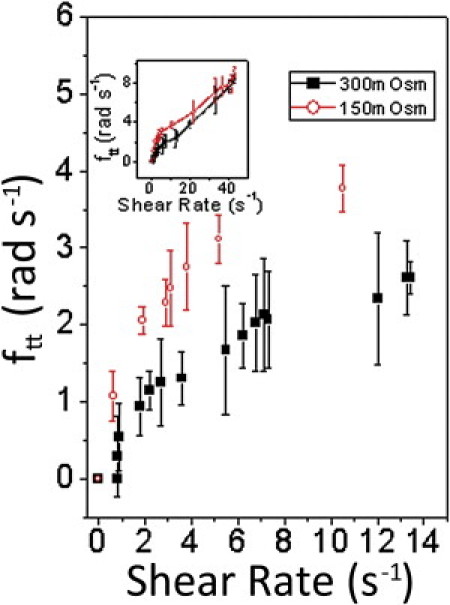
Variation of TT frequency with shear rate for spherical RBCs (red open circles) and biconcave ones (black squares) near threshold. For spherical RBCs, symmetry ensures that distinction between TT and tumbling is difficult to establish. (Inset) Functional dependence over a larger range of shear rates.

We also induced cytoplasmic viscosity change (from 5.4 cP to 3.1 cP) in spherical RBCs by incubating human RBCs in PBS (osmolarity 150 mOsm) for 30 min. Measuring the cytoplasmic viscosity involved lysing packed RBCs (both spherical and biconcave) by sonication and then removing the membrane by pelleting them by high speed centrifugation, whereas the supernatant was used for the viscosity measurements. Due to reduction in viscosity one would expect f_tt to increase. However, we find that the increase in f_tt is only marginal because the membrane, rather than the cytoplasm, is the dominant energy sink, as also indicated in earlier work (25,40). Our experimental data enable us to quantify this, as discussed in the following.

By making use of earlier measurements (38), we deduce the change in RBC surface viscosity as temperature changes from 25°C to 34°C (Fig. 8). Temperature affects membrane viscosity and we probed its effects on f_tt: 44.5% change in surface viscosity results in ∼46% change in f_tt. On the other hand, for almost similar change in cytoplasmic viscosity (42%), achieved by making the cells spherical, the corresponding change in f_tt was only 13% (Fig. 8 b). It is pertinent to note that earlier theoretical and experimental work on biconcave RBCs showed energy dissipation in the membrane to be 2–4 times more than in the cytoplasm (25,36,40). On the other hand, as of this writing, our work is on folded RBCs and yet we obtain a ratio of 4:1 for relative change in f_tt and, hence, in energy dissipation, for similar changes in membrane and cytoplasmic viscosity values. Our experiments clearly indicate that the theories of viscous dissipation may not necessarily be restricted to an ellipsoidal body; they may have wider applicability as far as cell morphology is concerned.

Figure 8.

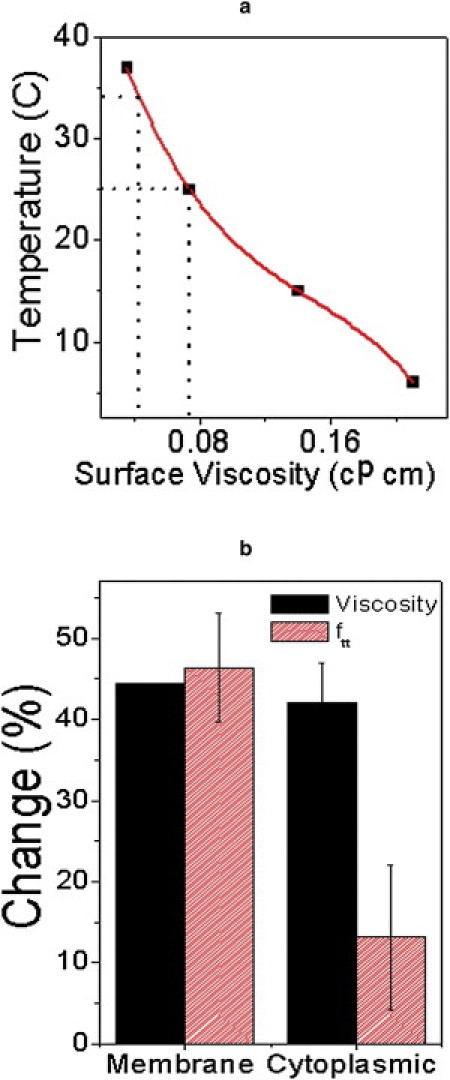
(a) Variation of RBC surface viscosity with temperature. (Solid points) Measured data (38). (Solid line) Third-order polynomial fit. (Dashed lines) Surface viscosity at 25°C and 34°C (see text).) (b) Histogram showing similar changes in membrane viscosity (due to temperature change) and cytoplasmic viscosity (due to change in osmolarity) with corresponding changes in f_tt in both cases. (Error bars) 1 SD from five measurements.

Cholesterol and its esters are found in RBC membranes and have significant effect on biophysical properties, like increasing viscosity (41), ordered states, and links with the cytoskeleton (42) so as to regulate cytoskeleton deformability. Because almost four-times more energy is dissipated in the membrane than in the cytoplasm, and energy is also dissipated in the periodic deformation of the cytoskeleton during TT motion, the energy dissipated is expected to depend on cytoskeleton deformability and membrane viscosity. Hence, reduction in membrane cholesterol is expected to reduce this dissipation because it causes an increase in membrane fluidity and decrease in cytoskeleton deformability. Consequently, the rate of TT motion would have to increase for the same amount of energy to be dissipated.

RBCs were stained with varying concentrations of Nile red dye and the cholesterol content was quantified by flow cytometry (see Fig. S3). MBCD was used to solubilize and remove cholesterol and its esters from the RBC membrane (43). Fluorescence and differential interference contrast (DIC) images enabled study of cell shape changes. Even at high MBCD concentrations the RBCs appeared essentially normal (slight stomatocyticity was seen in some cells, as shown in Fig. S4). Cholesterol-depleted cells showed a marked increase in f_tt (Fig. 9); this may be due to 1), decrease in viscosity, 2), orderedness of the membrane, and 3), increased cytoskeleton deformability. However, with decreasing cholesterol, the threshold was less apparent; TT motion did not cease even at very low shear values (0.5 s⁻¹). Rationalization of our observations lies in the fact that, along with regulating biophysical properties of the membrane, cholesterol and its esters occur asymmetrically in the two leaflets of the RBC membrane and regulate its shape and inherent asymmetry and it is known that compounds distributed differentially among the two lipid leaflets influence the RBC shape (44). On removing cholesterol and its esters preferentially from the outer leaflet, there is a stomatocytic effect on the RBCs (45). As with our experiments in hypotonic media, when an RBC becomes spherical or stomatocytic, it starts to lose its asymmetry due to its biconcavity. Reduction in asymmetry either decreases the threshold or its sharpness.

Figure 9.

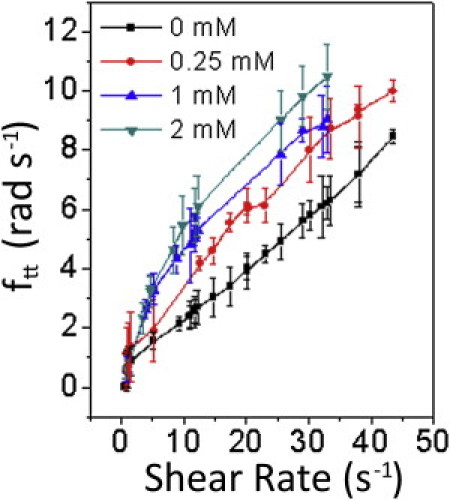
Variation of f_tt with shear rates of RBCs after treatment with various concentrations of MBCD. (Solid points) Measured data. (Lines) Guide to the eye.

In hypertonic conditions, the RBCs shrink and act like rigid particles with spicules on their surface. In such cases, TT motion did not occur. Furthermore, our experiments indicate that the tumbling motion might be influenced by the number of spicules on the surface of the RBC (see Movie S5).

Summary

We have made systematic measurements of tank treading in RBCs optically trapped in flowing media, enabling us to image TT motion in detail and allowing reliable measurements of TT frequency as a function of viscosity, temperature, and RBC size and shape. Our measurements indicate that even when the orientation and shape of RBCs are highly distorted from the viscous ellipsoid considered in existing theories (8,25), TT motion continues to occur at frequencies that are in consonance with values for viscous ellipsoids in shear flow.

Our experiments establish a threshold shear rate (1.5 ± 0.3 s⁻¹) above which TT motion occurs and below which cells tumble. We have shown that this threshold value can be altered by inducing changes in cell shape (by immersing cells in hypotonic solutions or by depleting membrane cholesterol). The TT frequency changes by as much as 10% as temperature changes by ∼4°C (such temperature changes can occur within human bodies). Temperature change induces alterations in membrane viscosity. However, when we effect changes in cytoplasmic viscosity, by incubating RBCs in hypotonic solutions and inducing uptake of water, we find that the change in TT frequency is four-times less. This offers another perspective to what is already established, namely that the RBC membrane is the dominant energy sink.

Specifically, our work has shown that theories of viscous dissipation and potential energy oscillations may not necessarily be confined to ellipsoidal bodies but may have wider applicability as far as cell shape is concerned. Our work on mouse RBCs indicates that cell size does not matter. Our results have physiological implications in that TT motion is more pervasive in the human circulatory system, where shape changes are common, than originally anticipated. In various disease conditions, such as hereditary spherocytosis, elliptocytosis, and sickle cell disease, the RBC shapes are known to be distorted. Limited information exists regarding the rheological properties of such RBCs (46,47). Extrapolations of the results of our experiments with misshaped RBCs and the possibility of using optical traps for direct TT measurements of such cells should help in better understanding of the disease manifestations.