Measurements of the Acidification Kinetics of Single SynaptopHluorin Vesicles

Abstract

Uptake of neurotransmitters into synaptic vesicles is driven by the proton gradient established across the vesicle membrane. The acidification of synaptic vesicles, therefore, is a crucial component of vesicle function. Here we present measurements of acidification rate constants from isolated, single synaptic vesicles. Vesicles were purified from mice expressing a fusion protein termed SynaptopHluorin created by the fusion of VAMP/synaptobrevin to the pH-sensitive super-ecliptic green fluorescent protein. We calibrated SynaptopHluorin fluorescence to determine the relationship between fluorescence intensity and internal vesicle pH, and used these values to measure the rate constant of vesicle acidification. We also measured the effects of ATP, glutamate, and chloride on acidification. We report acidification time constants of 500 ms to 1 s. The rate of acidification increased with increasing extravesicular concentrations of ATP and glutamate. These data provide an upper and a lower bound for vesicle acidification and indicate that vesicle readiness can be regulated by changes in energy and transmitter availability.

Introduction

The acidification of the synaptic vesicle lumen is a crucial component of neurotransmitter uptake (1), a feature that allows vesicles to undergo multiple rounds of fusion. The main components of the uptake system are the H⁺-ATPase, glutamate transporter (VGLUT), which may contain a chloride activation site, and a putative chloride transporter that remains to be identified, as shown by the cartoon presented in Fig. 1 A. Synaptic vesicles contain a V-type H⁺-ATPase, which generates an electrochemical gradient across the vesicle membrane by shuttling protons into the vesicle interior. This gradient provides the driving force utilized by the VGLUT transporter to move glutamate up its concentration gradient (2). In addition to the proton gradient, VGLUT also requires cytosolic chloride in a concentration range of 2–8 mM to pump at its maximal rate (3).

Figure 1.

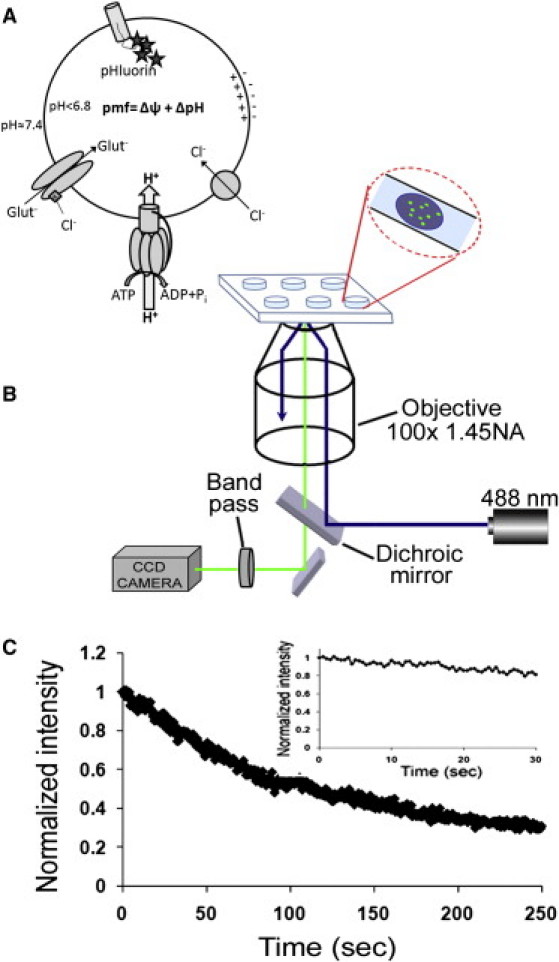
Measurement of the acidification kinetics of synaptic vesicles using isolated SynaptopHluorin (SpH) vesicles and total-internal-reflection fluorescence (TIRF) microscopy. (A) Schematic representation of the glutamate uptake components. The proton motive force generated by the V-ATPase is utilized by VGLUT to transport glutamate into the vesicle lumen. Chloride (2–8 mM) is required for optimal glutamate loading. In SpH vesicles, pH-sensitive GFP molecules (stars) are bound to the luminal domain of VAMP-2. (B) Home-built TIRF setup using 488-nm laser light as excitation source. SpH vesicles were placed in PDMS well for imaging. Fluorescence was collected with a charge-coupled device camera. (C) SpH vesicle bleaching curve, indicating that photobleaching is insignificant over our experimental timescale (<30 s). (Inset) Bleaching of SpH vesicles over 250 s in load buffer (no ATP or glutamate present); 70% decrease in fluorescence intensity.

The rate of synaptic vesicle acidification has been measured using synaptosomes (axon terminals) (4) and cultured neurons. In synaptosome preparations, vesicle acidification is typically measured using acridine orange, a membrane-permeant dye that accumulates in acidic compartments with concomitant quenching due to aggregation (5). A more recent method utilized SynaptopHluorin (SpH), a pH-sensitive green fluorescent protein (GFP) fused to the lumenal domain of a transmembrane synaptic vesicle protein, synaptobrevin/VAMP-2 (6), to estimate time constants of vesicle acidification after recycling in cultured neurons (7). Using single action potential stimulation, Gandhi and Stevens (8) derived an acidification time constant of 430 ms from endocytic/refilling events in SpH vesicles. In contrast, Atluri and Ryan (7) reported an acidification time constant of 4–5 s for vesicles in a single bouton using trains of action potential stimulation. In both cases, the acidification step had to be deconvolved from the endocytosis step because the poststimulus decay of SpH fluorescence reflects both the endocytosis of the vesicle and its reacidification. As a result, the interpretation of the data to obtain the acidification rate could be affected by the presence of different pools of synaptic vesicles at the nerve terminal as well as by the variation in response depending on the type and duration of the stimulus used to initiate release. These studies were also complicated by the presence of SpH in the plasma membrane as well as in synaptic vesicles. Diffusion of this pool of SpH may be mistaken for fast endocytosis/acidification of vesicles (9).

The purpose of this study was to measure acidification rates in isolated synaptic vesicles. By using individual vesicles purified from mice brain expressing a synaptopHluorin transgene (10), we are able to separate effectively acidification kinetics from endocytosis kinetics. The use of isolated SpH vesicles also allows the passive proton leakage, proton permeability, and buffering capacity to be quantified. Understanding the vesicle's permeability to protons will provide further clues as to how synaptic vesicles regulate the proton motive force; respond to rapidly changing conditions at the synapse; and store neurotransmitters. We measured acidification rates under different loading conditions to determine the effect of glutamate and chloride on the acidification rate. Quantifying the rate at which synaptic vesicles acidify provides information about synaptic vesicles' ability to undergo rapid fire recycling. Our approach also provides a measure of intervesicle variance and thus sets the upper and lower bounds for acidification rates.

Materials and Methods

Details regarding synaptic vesicle isolation, microwell fabrication, and total internal reflection fluorescence (TIRF) microscopy and data analysis are described in the Supporting Material.

Results

Measuring fluorescence intensity of individual SpH vesicles

Acidification of isolated SpH vesicles was monitored using a home-built TIRF microscopy setup (Fig. 1 B). The pH-sensitive green fluorescent protein (GFP) fluoresces when excited by 488 nm light at neutral pH (∼7.4). As the pH decreases, the excitation peak at 475 nm is eclipsed until it disappears completely in pH < 6.0 environments; this spectral shift is reversible within 20 ms (6). Thus, we can monitor individual vesicle acidification by the reduction in the fluorescence intensity. Monitoring individual vesicles removes the need to synchronize each vesicle's exposure to the external buffer containing ATP and glutamate.

To facilitate SpH imaging, PDMS microwells of ∼100 μL volume were fabricated and bonded to a glass coverslip that formed the floor of the well. Microwells allowed for easy solution exchange, control of vesicle adsorption, and single-vesicle TIRF microscopy measurements. Vesicle density on the coverslip surface was optimized such that fluorescence could be recorded from 100 to 200 SpH vesicles simultaneously. To keep vesicles from popping off the surface of the coverslip during imaging, which could have been construed as rapid quenching, coverslips were treated with 3-aminopropyltriethoxysilane (APTES). APTES is widely used to immobilize biomolecules on glass surfaces. It contains silane groups that bind covalently to glass and amine groups that adhere strongly to the negatively charged synaptic vesicle (11,12). This step stabilized vesicle attachment for the duration of the experiment.

To measure effects of photobleaching, which could contribute to apparent acidification rates, SpH vesicles were immobilized on an APTES-coated coverslip and imaged at a frame rate of 0.5 s and an excitation intensity of 0.5 mW. The frame rate and excitation intensity chosen reflect the conditions utilized for acidification measurements. Although there was significant photobleaching at longer exposure times (70% decay in 250 s), within the 30 s timeframe of our measurements, photobleaching was <20% (Fig. 1 C). Thus, photobleaching contributed only a small portion of the fluorescence decrease resulting from vesicle acidification.

A pH calibration curve was generated (Fig. 2 A) to correlate the change in vesicular pH with the decrease in fluorescence signal. SpH vesicles were exchanged into 20 mM 1,4-piperazinediethanesulfonic acid, 4 mM MgSO₄, 4 mM KCl, 130 mM potassium acetate (PIPES) buffer at pH 7.4 with 10 μg/mL nigericin. Nigericin is a K⁺/H⁺ ionophore that exchanges internal potassium ions for external protons, which allowed for rapid proton equilibration and prevented the buildup of a potassium gradient. For each pH measurement, vesicles were equilibrated for 1 min in PIPES buffer at the desired pH in a microwell, after which the fluorescence was measured. The data are presented as the ratio of the final intensity to the initial intensity (measured at pH 7.4). The calibration curve was fit in the software KaleidaGraph (Synergy Software, Reading, PA) with a single site titration model, Eq. 1, where pKa and n_H (Hill coefficient) are fitted parameters (13):

$$\frac{F}{F_0}=A+B\left[1+{10}^{\left(\mathrm{pKa}-\mathrm{pH}\right)\mathrm{nH})}\right]-1.$$ (1)

The calibration data were well fit by this equation with a pKa of 7.13 and a Hill coefficient of 1.64. Error bars shown in Fig. 2 A represent the standard deviation for each intensity ratio after normalization, revealing the variation in GFP fluorescence intensity at each pH value. The GFP in SpH vesicles is fused to synaptobrevin/VAMP-2, a protein with very high copy numbers (14) that may be polydisperse among vesicle populations (15). Thus, the number of GFP molecules may vary widely from vesicle to vesicle.

Figure 2.

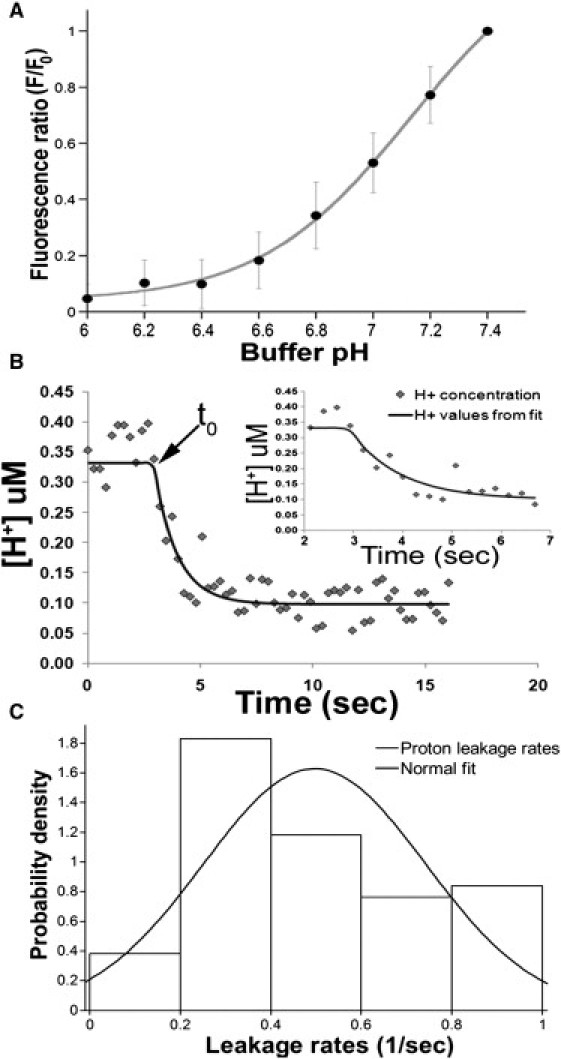
Characterization of isolated SpH vesicles. (A) SpH vesicle calibration curve. Vesicles were exchanged into PIPES buffer with 10 μg/mL nigericin at pH 7.4 for the initial intensity measurement, F₀. Buffer was then exchanged for each subsequent pH measurement to obtain the corresponding fluorescence intensity, F. Data fit with a single site titration model, which was used to determine the proton concentration at various ratios of fluorescence intensities. (B) Leakage of protons from SpH vesicles. (Open diamonds) Raw data fit to Eq. 2 (solid line). Start of leakage is denoted by t₀. (Inset) Expanded view of the fluorescence decay as well as the resulting fit that provided the leakage rate. (C) Histogram of leakage rate constants from individual SpH vesicles. SpH vesicles were equilibrated to pH 6.0 in PIPES buffer then exchanged into PIPES buffer at pH 7.4 with continuous fluorescence monitoring. The rates of proton leakage were binned into a histogram (n = 226) and fit with a normal distribution. The average leakage rate constant determined by the fit was 0.50 ± 0.02 s⁻¹ (mean ± SD).

Quantification of passive proton leakage from SpH vesicles

To determine proton leakage, SpH vesicles were equilibrated in PIPES buffer (pH 6.0), after which the external buffer was exchanged with pH 7.4 PIPES buffer (no nigericin present) with constant fluorescence monitoring. Within 10 frames, the vesicles had reached maximum fluorescence intensity. The fluorescence intensity ratio (F/F₀) was calculated for each vesicle at each time point where F₀ was the maximum fluorescence intensity achieved (∼pH 7.4) and F was the intensity at pH 6.0. The fluorescence intensity ratio was then converted to pH using Eq. 1 with fitted parameters determined from the calibration curve. The calculated pH value was converted to proton concentration using the standard definition of pH. The change in internal proton concentration with respect to time was plotted as shown in Fig. 2 B. The rate of proton leakage from the vesicle interior to the exterior buffer was determined by fitting each SpH leakage curve in MATLAB (The MathWorks, Natick, MA) using Eq. 2,

$$F\left(t\right)\propto \left[H^{+}\right]\left(t\right)={\left[H^{+}\right]}_{out}+\left({\left[H^{+}\right]}_{in}-{\left[H^{+}\right]}_{out}\right)\left(e^{-k_{leak}\left(t-t_0\right)}\right),$$ (2)

where F(t) is the fluorescence ratio (as determined above), which is proportional to the H⁺ concentration; [H⁺]_out and [H⁺]_in are the proton concentration (M) outside the vesicle and inside the vesicle, respectively; k_leak is the rate of proton leakage; and t₀ is the start of proton leakage as determined by the initial time of fluorescence intensity increase (see Fig. 2 B). The rate constants for 226 vesicles were calculated and binned into a histogram (Fig. 2 C). A normal fit was applied to the histogram, which produced an average alkalinization rate constant of 0.50 ± 0.02 s⁻¹ (mean ± SD). The variance in alkalinization rates is ∼20%, which has been noted for other trafficking vesicles (16), namely early endosomes. Early endosomes range in size from 100 to 160 nm whereas synaptic vesicles have a size range of 30–80 nm. It may be that the distribution of vesicular size contributes to the distribution of proton leakage rates measured for both types of vesicles. In addition to size, the physical state of the membrane, i.e., fluidity, thickness, etc., can influence the leakage rate of protons (17,18). However, bulk studies have shown that the average rate of proton efflux can be correlated to the average value of the vesicle radius (19). The rate of proton efflux is the product of the vesicle buffering capacity and the alkalinization rate.

The buffering capacity of SpH vesicles was measured using a modified ammonium pulse technique (20). Briefly, SpH vesicles were acidified in the presence of ATP, the proton pump was quenched by the addition of bafilomycin, and 5 mM aliquots of NH₄Cl were added sequentially to achieve a final concentration of 20 mM. Buffering capacity was calculated from the change in the internal vesicle pH induced by the addition of NH₄Cl as shown by Eq. 3:

$$\beta =\frac{\Delta {\left[N{H}_4^{+}\right]}_i}{\Delta \rho H_i}.$$ (3)

The internal ammonium concentration is equivalent to the amount of removed protons that can be calculated using Eq. 4, where [NH₃]_tot is the total ammonium chloride concentration, K_a is the dissociation constant of NH₃, and [H⁺]_int and [H⁺]_ext are the internal and external proton concentrations, respectively (21):

$${\left[N{H}_4^{+}\right]}_{\mathrm{int}}=\frac{\left({\left[N{H}_3\right]}_{tot}\ast {\left[H^{+}\right]}_{\mathrm{int}}\right)}{\left(K_a+{\left[H^{+}\right]}_{ext}\right)}.$$ (4)

The buffering capacity for SpH vesicles was linear over the pH range measured (data not shown); therefore, we compiled all values to calculate an average buffering capacity of 139 ± 29 ΔmM/ΔpH.

The rate of proton efflux was then normalized for the vesicle surface area and volume, assuming vesicles are spherical with an average diameter of 42 nm (22):

$$J_H+\left(\frac{pmol}{c{m}^2\ast s}\right)=J_H+\left(\frac{mM}{s}\right)\ast \left(\frac{V}{SA}\right).$$ (5)

Equation 5 converts the measured rate of alkalinization, $J_{H^{+}}\left(mM/s\right)$, to the flux of protons, $J_{H^{+}}\left(pmol/c{m}^2\ast s\right)$, per vesicle area, where V is vesicle volume and SA is vesicle surface area. The vesicle proton permeability can be calculated for conditions of minimal membrane potential (130 mM potassium acetate) using the proton flux calculated in Eq. 5,

$$P_{H^{+}}=\frac{J_{H^{+}}}{\left({\left[H^{+}\right]}_i-{\left[H^{+}\right]}_o\right)},$$ (6)

where [H⁺]_in and [H⁺]_out are the same as Eq. 2 (22). The permeability coefficient for H⁺ was determined to be 2.1 × 10⁻² cm/s at a ΔpH of 1.4. Proton permeability coefficients have been measured for other trafficking organelles, such as liver endosomes, Golgi complex, and lysosomes with permeabilities ranging 4.8–0.67 × 10⁻³ cm/s (endosomes) (22), 8.1 × 10⁻⁶ cm/s (Golgi) (23), and 0.97–5.9 × 10⁻⁸ cm/s (lysosomes) (17). The measured proton permeability for synaptic vesicles is within the range measured for similar trafficking vesicles.

Measuring vesicle acidification

Analysis of acidification rates of individual SpH vesicles was performed as follows. SpH vesicles were added to APTES-coated microwells, allowed to settle, and then ATP and/or glutamate were added with continuous fluorescence monitoring. Data were collected for 80 s during which all vesicles (100–200) in the field of view acidified as determined by fluorescence quenching. Each experiment was performed in duplicate. The normalized fluorescence ratio (F/F₀) was calculated for each vesicle as was done for the calibration curve. The decay curves were analyzed via a MATLAB program that identified the initial time of decay (t₀) for each vesicle then fit each curve with an exponential decay function. The use of single vesicle experiments allowed the initial time to be determined for each vesicle, thus removing the need to decouple the mixing time from the acidification kinetics. An example vesicle acidification curve and the fit obtained from the MATLAB script are shown in Fig. S1 in the Supporting Material. Each exponential decay curve was analyzed using the sum of squared error to determine the goodness of fit to the fluorescence decay data. Vesicles with low sum-of-squared-error values were aggregated to form a single data set for each set of experimental conditions. These fluorescence decay rate constants were then binned into a histogram that was fit to obtain the average acidification rate constant for each set of conditions. The first-order time constant, τ, for each acidification reaction was calculated as the reciprocal of the average rate constant. The first-order time constant reveals the amount of time necessary for the fluorescence to decrease to 1/e of the initial value. Vesicle acidification was saturable in relation to ATP concentration; therefore, rate curves were fit with the Michaelis-Menten function. To ensure that the fluorescence quenching was due to H⁺-ATPase-mediated acidification, SpH vesicles were treated with 1 μM bafilomycin, an H⁺-ATPase inhibitor, for 2 min before addition of ATP. Fig. 3 A (dashed line) shows that vesicles did not acidify in the presence of bafilomycin even at high concentrations of ATP.

Figure 3.

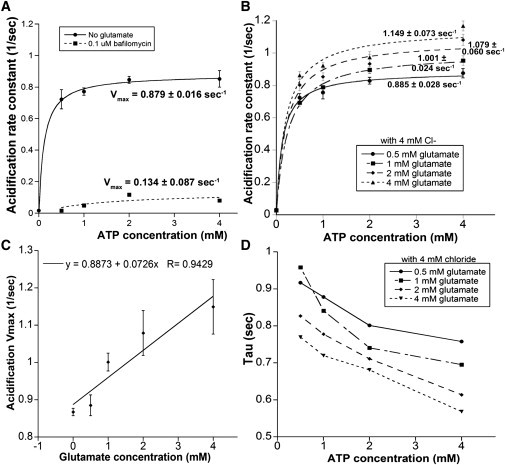
Effect of glutamate on acidification rates. (A) Acidification due to ATP only. Plot of average acidification rate against ATP concentration (solid line) displays Michaelis-Menten kinetics with a maximum acidification rate of 0.879 ± 0.016 s⁻¹. SpH vesicles treated with 1 μM bafilomycin for 2 min (dotted line) before ATP addition did not acidify (SD of rate measurements is ∼10%). V_max values are shown with the corresponding curves. (B) Average rates of SpH acidification at varying glutamate concentrations. (Curves) Fit with Michaelis-Menten function; V_max shown for each curve. (C) Effect of increasing glutamate concentrations on acidification V_max. Data fit with a linear trend line displaying an R² value of 0.94. (D) Time constants (τ) of SpH acidification versus ATP concentration. (Lines drawn to guide the eye.)

The baseline acidification rate constant for SpH vesicles was established by measuring the acidification rate constant in the presence of ATP only; no glutamate was present in these reactions, load buffer contained 4 mM Cl⁻. The acidification rate constants were binned into histograms that were best fit with a normal distribution (see Fig. S2 A). From the normal distributions, average acidification rate constants were obtained and plotted as a function of ATP concentration (Fig. 3 A). The maximum acidification velocity (V_max) was 0.879 ± 0.016 s⁻¹ and the Michaelis constant (K_m) for ATP was calculated to be 114 ± 20 μM. Table 1 summarizes the baseline acidification kinetic values.

Table 1.

Kinetic parameters determined for SpH vesicles at different chloride and glutamate concentrations

0 mM chloride
	No glut	1 mM glut	2 mM glut	4 mM glut
Vmax (1/s)	0.681 ± 0.027	0.833 ± 0.094	0.874 ± 0.053	0.857 ± 0.049
Km (mM ATP)	0.377 ± 0.065	0.619 ± 0.241	0.408 ± 0.104	0.276 ± 0.083
τ (ms)	1050	860	850	820
N	83	99	101	168
P		∗	∗	∗

4 mM chloride
	No glut	0.5 mM glut	1 mM glut	2 mM glut	4 mM glut
Vmax (1/s)	0.879 ± 0.016	0.885 ± 0.028	1.001 ± 0.024	1.079 ± 0.060	1.149 ± 0.073
Km (mM ATP)	0.114 ± 0.021	0.126 ± 0.037	0.236 ± 0.033	0.203 ± 0.073	0.197 ± 0.082
τ (ms)	779	758	696	614	568
N	131	86	57	172	109
P			∗	∗	∗

10 mM chloride
	No glut	1 mM glut	2 mM glut	4 mM glut
Vmax (1/s)	0.983 ± 0.020	1.121 ± 0.076	1.009 ± 0.099	1.147 ± 0.108
Km (mM ATP)	0.038 ± 0.020	0.256 ± 0.096	0.135 ± 0.114	0.151 ± 0.112
τ (ms)	685	592	671	578
N	87	85	58	80
P		∗	†	∗

V_max and K_m values were determined by fitting plots of the average acidification rates against the ATP concentration with the Michaelis-Menten function (mean ± SD). First-order time constants (τ) were calculated from the fluorescence quenching rate constants at 4 mM ATP for each glutamate concentration. The ΔpH was determined for each glutamate/chloride concentration at 4 mM ATP. Sample sizes are given by N; P is determined by unpaired t-test comparing V_max at each glutamate concentrations to the V_max obtained in the absence of glutamate.

^∗P < 0.0001.

^†P < 0.005.

Effect of glutamate concentration on the rate of SpH acidification

As acidification is an important component of glutamate loading, we next tested whether the addition of glutamate would affect the kinetics of vesicle acidification. Glutamate was added to the PDMS well simultaneously with ATP at varying concentrations with continuous fluorescence monitoring. The distribution of SpH acidification rate constants in the presence of glutamate was normally distributed as shown in Fig. S2 B (shown for 1 mM glutamate). Fig. 3 B shows the Michaelis-Menten fits. The maximum acidification velocity increased linearly with respect to glutamate concentration (Fig. 3 C). Low glutamate concentrations produced only a slight increase in the acidification rate from 0.879 ± 0.017 s⁻¹ (0 mM glutamate) to 0.885 ± 0.028 s⁻¹ (0.5 mM glutamate). At physiologically relevant concentrations, glutamate caused a significant increase in acidification velocity at each concentration tested. The addition of 1 mM glutamate increased the maximal acidification rate to 1.001 ± 0.024 s⁻¹ (13% increase) whereas 2 mM glutamate increased acidification velocity to 1.079 ± 0.060 s⁻¹ (22% increase), and with 4 mM glutamate the acidification velocity increased to 1.149 ± 0.073 s⁻¹ (30% increase).

Plotting the time constants of the acidification reactions against ATP concentration revealed that SpH acidification occurs at a faster rate when ATP and glutamate are in abundant supply. For example, at 2 mM glutamate, which is above VGLUT's K_m for glutamate, the acidification time constant decreased from 826 ms to 614 ms as the ATP concentration was increased from 0.5 mM to 4 mM. Fig. 3 D shows the relationship between the acidification time constant and increasing glutamate and ATP concentration. These measurements provide an upper and lower bound for synaptic vesicle acidification depending on the extravesicular concentration of glutamate and ATP. In the presence of glutamate, acidification time constants are on the order of ∼1 s (0.5 mM ATP) to ∼500 ms (4 mM ATP). When ATP is removed, glutamate alone still induces acidification much more slowly with a time constant of ∼20 s. Table 1 summarizes the kinetic parameters obtained for increasing glutamate concentrations.

Consistent with the idea of functional coupling between the transporter and ATPase, SpH acidification was affected by the addition of a VGLUT inhibitor, Trypan blue (24). The inhibition by Trypan blue is not fully understood but the minimum requirements for inhibition include a naphthalene template, and an azo linkage that is juxtaposed to an electron-releasing group or a hydrogen donor group. These requirements suggest that the dye molecule may inhibit VGLUT by spanning the entire transporter tunnel and binding both inner and outer domains or by blocking both the active site and an allosteric activator site (24). When SpH vesicles were treated with 0.5 μM Trypan blue for 2 min before the addition of 2 mM ATP and 2 mM glutamate in load buffer (contains 4 mM Cl⁻), the acidification rate decreased by ∼30% of the control rate (Fig. 4). Here, the control rate is determined with SpH vesicles acidified in the presence of 2 mM ATP and 2 mM glutamate in load buffer. Comparatively, the removal of extravesicular glutamate only decreased the acidification rate by ∼10%, and chloride removal decreased the acidification rate by ∼23%. These results are consistent with the conclusion that VGLUT is responsible for chloride conductance in synaptic vesicles (25).

Figure 4.

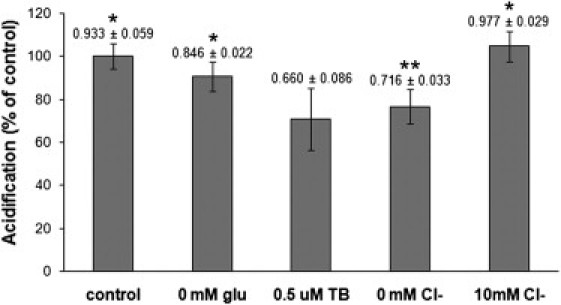
Effect of inhibiting glutamate transporter on SpH acidification. Comparison of the acidification rates of SpH vesicles at 2 mM ATP when glutamate is present (4 mM; control), when glutamate is absent (0 mM Glu), when VGLUT is blocked by Trypan blue (0.5 μM TB), and in the presence of low (0 mM Cl⁻) or high (10 mM Cl⁻) concentrations of chloride. Acidification rate reduced to ∼90% of control when glutamate was removed but ATP (2 mM) and Cl⁻ (4 mM) were present. When VGLUT was blocked, acidification rate was reduced to ∼70% of control similar to the reduction seen (∼76%) when ATP and glutamate were present but chloride was removed (0 mM Cl⁻). High concentrations of chloride (10 mM Cl⁻) did not reduce the acidification rate. Acidification rate (s⁻¹) for each condition shown above bar. Data analyzed with two-tailed unpaired t-tests against the addition of Trypan blue (0.5 μM TB). ^∗P < 0.0001; ^∗∗P 0.001.

Effect of chloride concentration on the rate of SpH acidification

Optimal glutamate uptake in synaptic vesicles requires the presence of low concentrations of chloride ions (26). Thus, we sought to investigate the effect of chloride ions on the acidification kinetics of isolated SpH vesicles in the presence of glutamate. Acidification rate constants were initially determined for SpH vesicles in the absence of chloride. To achieve this condition, SpH vesicles were exchanged into potassium gluconate buffer before immobilization on the glass surface. All stock solutions were made in potassium gluconate buffer as well. Interestingly, acidification rate constants obtained in the absence of chloride revealed a skewed distribution best fit with a log-normal distribution as seen in Fig. S2 C (1 mM glutamate results shown). In the absence of chloride, the membrane potential is increased leading to an inhibition of acidification, which skews the distribution toward smaller acidification rate constants.

Fig. 5 A presents the acidification rate curves for varying glutamate concentrations in Cl⁻ free buffer. Without any counterion (absence of glutamate and Cl⁻), SpH acidification achieved a maximum velocity of 0.681 ± 0.027 s⁻¹. The addition of glutamate increased the acidification velocity; however, increasing the glutamate concentration did not cause a significant further increase. The addition of glutamate resulted in a maximum acidification velocity of 0.855 ± 0.021 s⁻¹, an increase of 26% over the rate in the absence of glutamate. Even with the addition of glutamate, SpH vesicles acidified slower than in the presence of chloride. These results suggest that glutamate cannot serve as the counterion despite its negative charge at physiological pH. The presence of chloride is required to achieve the maximal acidification rate, possibly because of direct interaction with or activation of the V-ATPase. Table 1 presents the kinetic values obtained in the absence of chloride.

Figure 5.

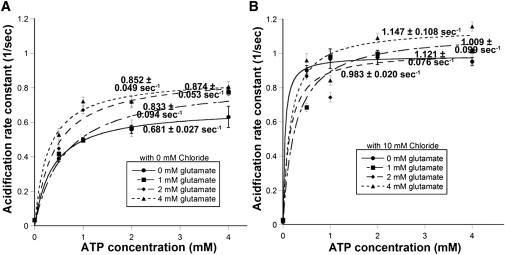
Effect of Cl⁻ concentration on the kinetics of SpH vesicle acidification. (A) Rates of SpH acidification measured without Cl⁻ at different ATP concentrations with 1 mM glutamate. Removal of chloride resulted in skewed distributions best fit by log-normal distributions (see Fig. S2C). Average acidification rates plotted against ATP concentration and fit with Michaelis-Menten function. The addition of glutamate increased the maximal acidification rate in a statistically significant manner (P < 0.0001 for each glutamate concentration). (B) SpH acidification rates measured in the presence of 10 mM Cl⁻ (20 mM HEPES, 104 mM potassium acetate,10 mM KCl, 4 mM MgSO₄, pH 7.4) at different ATP/glutamate concentrations. Presence of chloride produced normally distributed acidification rates (see Fig. S2D) from which average acidification rates were determined then plotted against ATP concentration and fit with Michaelis-Menten function. Addition of glutamate increased the acidification rate in a statistically significant manner (P < 0.005).

We also measured acidification rate constants in the presence of high chloride concentration, because glutamate uptake displays a biphasic dependence on chloride; chloride concentrations >20 mM have been shown to reduce glutamate transport (27). Therefore, we chose to look at acidification in the presence of 10 mM chloride, which is just above the optimal concentration range. Experiments were conducted in load buffer with the KCl concentration increased to 10 mM and a concomitant decrease in potassium acetate concentration to keep the osmolarity constant. Stock solutions were made in the high KCl buffer as well. Fig. S2 D reveals that the acidification rate constants were again normally distributed (1 mM glutamate results shown). Fig. 5 B presents the acidification rate curves for varying glutamate concentrations in high Cl⁻ buffer. In the absence of glutamate at high concentrations of Cl⁻, acidification reached a V_max of 0.983 ± 0.020 s⁻¹, a 12% increase over the acidification velocity measured at 4 mM Cl⁻. The addition of glutamate (1 mM) increased the acidification velocity by ∼15% to 1.121 ± 0.076 s⁻¹. Overall, acidification in the presence of 10 mM Cl⁻ leveled off at the same rate achieved at 4 mM Cl⁻. These results suggest that the magnitude of the membrane potential may be the controlling parameter for acidification. Kinetic parameters are summarized in Table 1.

Without chloride or glutamate, vesicles exhibit a steady state ΔpH of 0.57 ± 0.01 units with an acidification lifetime of ∼1 s, consistent with previous results showing that synaptic vesicles exhibit an endogenous ΔpH (27). Adding chloride increased the ΔpH achieved to 1.41 units (4 mM Cl⁻) and 2.05 units (10 mM Cl⁻). In the presence of glutamate, the average ΔpH (at 4 mM ATP) was similar for all concentrations of extravesicular chloride. The vesicles acidified to an average ΔpH (mean ± SD) of 1.68 ± 0.21 units (0 mM Cl⁻), 1.78 ± 0.15 units (4 mM Cl⁻), and 1.85 ± 0.07 units (10 mM Cl⁻). The transmembrane pH gradient can be approximated by the relationship (16)

$$\frac{d\left(\Delta pH\right)}{dt}=-P_H\left(\Delta pH\right)+I_{ATP},$$ (7)

where P_H is the passive proton leakage and I_ATP is the proton pump activity. At steady state, (d(ΔpH))/dt = 0, therefore, ΔpH = I_ATP/pH. Thus, an increase in ΔpH is due to a shift in the ratio of proton pump activity to passive proton leakage. The introduction of chloride reduces the membrane potential against which the proton pump operates, which may lead to an increase in proton pump activity. The bulk of glutamate transport is driven by Δψ, however, suggesting that passive proton leakage is an important regulator between vesicle acidification and glutamate loading.

Discussion

Here we studied the acidification kinetics of synaptic vesicles without interference from endocytosis. We systematically measured the rate of acidification for isolated synaptic vesicles in response to changes in ATP, glutamate, and Cl⁻ concentrations. The acidification time constant depends on the extravesicular glutamate concentration and occurs on the order of ∼700 ms.

Our study represents, to our knowledge, the first time that the proton leakage rate of synaptic vesicles has been quantified. Proton leakage rates exhibited a variance of ∼20%, probably due to the variation in synaptic vesicle makeup. Transient pH dynamics are sensitive to volume, surface area, and buffering capacity (23), thus variation in vesicle size, membrane thickness, and protein expression may contribute to the variation seen in proton leakage rates. Synaptic vesicles were found to exhibit a proton permeability of 2.1 × 10⁻² cm/s, which suggests that the steady-state pH is governed by the ratio of the proton pump activity to the proton leakage rate (16,23). The V-ATPase present on synaptic vesicles functions exclusively as an ATP-dependent proton pump and cannot efficiently catalyze ATP synthesis. This inability has been attributed to the presence of a built-in proton-slip (28). Furthermore, it has been suggested that the presence of a proton-slip is a general feature of V-ATPases that provides control over organelle acidification by holding the proton motive force to a certain range (29).

The introduction of glutamate increases the rate of acidification at all chloride concentrations. Glutamate-induced acidification was first noted by Maycox et al. (30) when they qualitatively measured synaptic vesicles acidification using acridine orange. From their data, they obtained a K_m for glutamate-induced acidification of 0.32 mM glutamate. Using isolated SpH vesicles, we obtained a K_m of 0.2 mM glutamate (data not shown), which is comparable given the differences in experimental design and the amount of ATP used (4 mM vs. 50 mM). Time constants for SpH acidification were found to decrease with increasing ATP and glutamate concentration showing that synaptic vesicles acidify faster when ATP and glutamate are in abundant supply.

Acidification velocity was linearly proportional to the concentration of external glutamate (Fig. 4 C), which suggests a functional coupling between VGLUT and V-ATPase, i.e., that transport activates the V-ATPase. From the acidification experiments in the absence of chloride, we found that glutamate alone could not fully activate acidification suggesting that it does not function as the counterion to proton uptake. To further clarify the role of VGLUT in acidification, we looked at how inhibition of VGLUT affects acidification rates. The role of VGLUT in glutamate-induced acidification was analyzed using Trypan blue, a competitive inhibitor of VGLUT. Blocking VGLUT with Trypan blue reduced the SpH acidification rate by 30% compared with normal loading conditions, which was significantly larger than the rate reduction caused by removing glutamate from the buffer (∼10% decrease). Therefore, the coupling between acidification and glutamate transport does not depend on glutamate, per se, but on a functioning transporter.

Our experiment produced a larger inhibition of vesicle acidification than that measured by Schenck et al. (25) when they used Evan's blue (31) to block VGLUT. However, their vesicles were preloaded with 100 mM Cl⁻, which may have activated the V-ATPase (32) allowing the vesicles to acidify on the same timescale as their control. In our experiment, the vesicles were only provided with extravesicular chloride whose entry into the vesicle was seemingly blocked by Trypan blue. It has been shown that inhibition by Trypan blue (or the structurally similar inhibitor Evan's blue) strictly requires the entire molecule (24), suggesting that Trypan blue may block both the VGLUT active site and an allosteric binding site for chloride (33) or alter the conformational state of VGLUT. In the absence of glutamate, VGLUT could still translocate Cl⁻, thereby dissipating Δψ and allowing ΔpH to build, which explains why the acidification rate decreases by only 10%. Full blockage of the glutamate binding site prevents both glutamate loading and Cl⁻ translocation, generating a large, positive Δψ that inhibits the generation of ΔpH. This supports previous work showing that VGLUT contains a distinct binding site for chloride (33), which activates acidification either by influencing glutamate transport into the vesicle or through a conformational change that has not been identified.

To further understand the role of chloride in vesicle acidification, we analyzed acidification in response to complete chloride removal and to high chloride concentrations (10 mM). Interestingly, we found that the removal of chloride shifted the distribution of acidification rate constants from normal distributions to log-normal distributions. Skewed distributions were only found for vesicles loaded in the absence of chloride, revealing the direct effect of chloride on acidification. Although the vesicles did acidify in the absence of chloride, they did so more slowly even with maximal amounts of ATP and glutamate (4 mM each). Here the addition of glutamate produced a ∼20% increase in the acidification rate, although increasing the glutamate concentration did not further increase the acidification rate. Acidification enhancement in the presence of glutamate supports observations that VGLUT may operate as an H⁺/glutamate exchanger in the absence of a counterion (25). As the V-ATPase requires the presence of Cl⁻ for maximal activity, the acidification rate is not fully recovered even if VGLUT can function as an exchanger. However, this would provide a backup method for loading glutamate under conditions of low extravesicular chloride.

Acidification in the presence of high chloride concentrations produced normally distributed acidification rate constants that had similar maximum acidification velocities attained in the presence of 4 mM Cl⁻. In the presence of high chloride, the effect of extravesicular glutamate was lessened as no significant increase in acidification rate constant was seen beyond the addition of 1 mM glutamate. The ΔpH was slightly increased at 10 mM Cl⁻ compared with 4 mM Cl⁻ due to dissipation of Δψ by the additional chloride. On average, the SpH vesicles exhibited a ΔpH of ∼2 units under glutamate loading conditions regardless of external chloride concentration, even though the acidification rate varied widely. The establishment of ΔpH regardless of Cl⁻ concentration supports the hypothesis that chloride concentration specifically affects the rate of vesicle filling, not the final gradient achieved (34,35).

Acidification is an important step in membrane trafficking and may be responsible for regulation of trafficking events such as budding, target recognition, docking, or fusion. In other trafficking vesicles, such as endosomes, acidification has been shown to be important for receptor-ligand dissociation (36), and, in lysosomes, the activation of hydrolytic enzymes (37). The acidic interiors of endosomes are also due to an electrogenic proton gradient created by a V-ATPase that functions in parallel with a chloride conductance (22). The many roles of vesicle acidification has led to the proposal that the V-ATPase itself may be a multifunctional complex that is capable of not only generating a pH gradient across the vesicular membrane but also sensing the intravesicular pH and transmitting this information from the luminal side to the cytosolic side of the membrane (38).

Previously, we have shown that isolated synaptic vesicles undergo a large size change (∼25% in diameter) upon loading glutamate (39). The size change requires the presence of both glutamate and ATP and is reversible upon removal of ATP (39) as the ΔpH is required for retention of glutamate within synaptic vesicles (3). This result, combined with the fact that the maximum ΔpH attained in the presence of ATP and glutamate is the same regardless of Cl⁻, suggests a sensing role for the V-ATPase. Synaptic vesicles acidify to a setpoint monitored by the V-ATPase, which then transmits this information to the luminal side through a concerted conformational change. Overall, this points to synaptic vesicle proteins acting in a highly concerted manner during acidification and neurotransmitter loading.

Conclusions

Using isolated synaptopHluorin vesicles, we were able to quantify acidification rates under various extravesicular concentrations of glutamate, chloride, and ATP. These data provide both an upper/lower bound for the timescale required by vesicles to acidify and a better understanding of how the rate of vesicle filling may be regulated by changes in energy and transmitter availability. Having such information will make it easier to interpret in vivo data relating to endocytosis. Additionally, we also present what we believe to be the first measurement of the proton leakage rate of synaptic vesicles, which is an important factor in controlling the proton motive force established during acidification. As synaptic vesicles are model trafficking organelles, quantitative information regarding acidification and proton leakage will contribute to the development of more accurate molecular models of trafficking and vesicle function.