Variation of selfing rate and inbreeding depression among individuals and across generations within an admixed Cedrus population

Abstract

We investigated the variation and short-term evolution of the selfing rate and inbreeding depression (ID) across three generations within a cedar forest that was established from admixture ca 1860. The mean selfing rate was 9.5%, ranging from 0 to 48% among 20 seed trees (estimated from paternally inherited chloroplast DNA). We computed the probability of selfing for each seed and we investigated ID by comparing selfed and outcrossed seeds within progenies, thus avoiding maternal effects. In all progenies, the germination rate was high (88–100%) and seedling mortality was low (0–12%). The germination dynamics differed significantly between selfed and outcrossed seeds within progenies in the founder gene pool but not in the following generations. This transient effect of selfing could be attributed to epistatic interactions in the original admixture. Regarding the seedling growth traits, the ID was low but significant: 8 and 6% for height and diameter growth, respectively. These rates did not vary among generations, suggesting minor gene effects. At this early stage, outcrossed seedlings outcompeted their selfed relatives, but not necessarily other selfed seedlings from other progenies. Thus, purging these slightly deleterious genes may only occur through within-family selection. Processes that maintain a high level of genetic diversity for fitness-related traits among progenies also reduce the efficiency of purging this part of the genetic load.

Introduction

Forest trees, generally outcrossing species, are characterized by a huge genetic diversity within populations (Hamrick and Godt, 1989), including for adaptive traits (Kremer, 1994; Notivol et al., 2007). This diversity is maintained at the expense of a high mutation load (Ledig, 1986; Petit and Hampe, 2006; Scofield and Schultz, 2006), which can only be purged whenever inbreeding occurs. Investigating the processes that dynamically maintain the genetic load and the adaptive genetic variation within populations cannot rely only on a theory that assumes a demographic and genetic equilibrium. This is particularly true in forestry where transient situations frequently occur: recently established forests (in terms of the number of generations), marginal areas of expansion or retraction in the distribution range, maturation phase of the silvigenesis, or simply pioneer species in disturbed areas (riparian forests, forest fires, and so on). The demo-genetic approach provides a general framework to study short-term evolution in non-equilibrium populations (Lande, 1988; Benton et al., 2006; Coulson et al., 2006; Pichot et al., 2006). In these models, the genetic variation of individual capacities such as survival, growth potential, fecundity, and dispersal ability determines the demographic structure of the population. As a feedback, the demographic structure regulates competition and the mating system, thus driving the evolution of the genetic diversity by affecting the intensities of drift and selection.

Inbreeding results from particular types of mating systems, such as selfing or mating among relatives, and it has a higher probability when population size is limited and mating is at random. Most studies generally consider the selfing rate through a mean value for a population but it has been shown that it can be highly variable among individuals (O'Connell et al., 2004). Under the mass action model (Gregorius et al., 1987; Holsinger, 1991), in hermaphroditic or monoecious species with no incompatibility system, the selfing rate is determined by the ratio of autopollen vs allopollen that is locally available for each female flower. Therefore, individual variation of the selfing rate is partly explained by the local demographic density as observed in several conifer species (Farris and Mitton, 1984; Knowles et al., 1987; Robledo-Arnuncio et al., 2004; Restoux et al., 2008). However, other mechanisms, such as dichogamy, also determine the individual selfing rate. One feature of the monoecious Atlas cedar, Cedrus atlantica Manetti, is a continuous variation of male/female allocation to reproduction among individuals, which ranges from quasi-male trees to quasi-female trees and everything in between (Krouchi et al., 2004). In such situations, both demographic and biological features may affect the mating system.

Effective purging of inbreeding depression (ID) depends not only on the mating system that generates inbred individuals but also on the genetic make-up of ID (Byers and Waller, 1999). ID that is caused by a small number of recessive genes that have major deleterious effects on fitness is expected to vary among individuals depending on their genotype at these few major genes and, therefore, to respond rapidly to selection. Purging is less efficient when selfed offspring do not contribute to the next generation (Scofield and Schultz, 2006), or when dominance and epistatic interactions among major genes occur (Williams et al., 2003). By contrast, ID because of many genes with small individual effects is not expected to vary drastically among individuals and is less easily purged in the population.

Seed abortion is often because of embryonic lethal equivalents, a number of deleterious alleles whose cumulative effects are the equivalent of one lethal allele (Lee et al., 1996; Keller and Waller, 2002). The number of embryonic lethal equivalents could be as high as 11 in conifers (Savolainen et al., 1992) and experimental results generally support the assumption of an additive effect of recessive alleles (Remington and O'Malley, 2000a). However, in Pinaceae, a stage-specific death peak occurring during early embryogenesis could be caused by partial dominance or overdominance of deleterious genes (Williams, 2007, 2008). In Pinus taeda L., Remington and O'Malley (2000b) showed that embryonic lethals do not contribute to ID later in the life cycle. Beyond seed abortion, ID delays seed germination (Sorensen, 2001), increases juvenile mortality (Koelewijn et al., 1999), depresses growth (Sorensen and Miles, 1982; Bower and Aitken, 2007), causes morphological abnormalities later in the life cycle (Wilcox, 1983), and decreases seed production and fertility in young trees (Kärkkäinen and Savolainen, 1993; Durel et al., 1996). At this later stage mildly deleterious mutations or polygenic mutations, which difficult to purge, are likely the main actors (Husband and Schemske, 1996).

ID has been experimentally assessed in controlled pedigrees of trees (Eriksson, 2006; White et al., 2007). Within forest tree populations, the common trend of increased heterozygosity in older age classes is considered as an indicator of previous selection against inbred individuals in younger age classes (Shaw and Allard, 1982; Farris and Mitton, 1984; Yazdani et al., 1985; Marquardt and Epperson, 2004; Jones et al., 2006). Some studies have shown increasing heterozygosity with age, suggesting that a rapid purging of inbred individuals occurs in these classes (Pichot et al., 2006). In this study, we assessed ID at the individual level within progenies (this term is used throughout the text to designate the set of seeds or seedlings issued from the same seed tree), comparing the performance of naturally produced selfed and outcrossed genotypes that we identified using chloroplast DNA markers. Molecular markers such as allozymes (Ritland and El-Kassaby, 1985) or microsatellite markers (Collevatti et al., 2001) have long been used for estimating the selfing rate in nature. In Cedrus, as in most Pinaceae species, the chloroplast genome is uni-parentally inherited from the male parent and does not recombine (Fady et al., 2003). Consequently, this provides an efficient tool to assess the probability of a selfing event by comparing the chloroplast genotypes of progenies and their seed trees.

We studied the C. atlantica forest of Luberon (South Eastern France) as a model situation of a transient population of trees experiencing rapid demographic evolution. The species was introduced locally from North Africa for afforestation of degraded lands in the 1860s (Cointat, 1996). From the founder trees that survived until sexual maturity (most of them are still alive), two generations have developed through natural regeneration, expanding from the initial plantation areas to a broader continuous forest, which currently shows a spatially heterogeneous pattern of density. A previous study based on isozymes revealed an initial population admixture through a transient genotypic disequilibrium in the founder generation that disappeared in the subsequent generations (Lefèvre et al., 2004). The three objectives of this work were (i) to assess the variation of the selfing rate at the individual level and test the predominance of demographic or sexual parameters on this variation, (ii) to quantify early stage ID during seed germination and the first year of seedling growth by comparing selfed and outcrossed seeds within progenies, thus avoiding maternal effects, and (iii) to test the existence of purging during the first three generations after the establishment of the Luberon cedar forest.

Materials and methods

Seed trees and seed collection

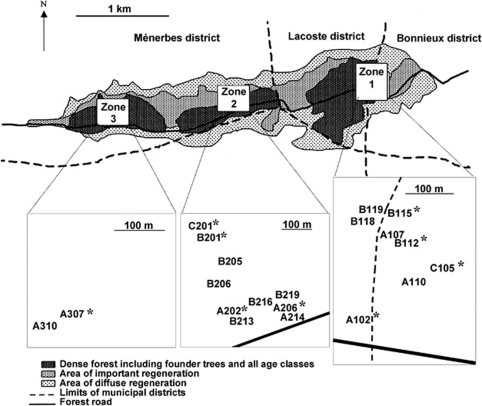
Twenty reproductive trees belonging to three different generations were sampled in different zones of the forest (Figure 1). The assignment of each tree to its corresponding generation was based on the estimate of the age of each tree from wood cores at a height of 60 cm (Lefèvre et al., 2004). The stem circumference at breast height was measured on each tree. The fecundity of Cedrus trees varies greatly across years and the trees show different allocations to male and female reproduction that remain relatively stable (Krouchi et al., 2004). For this reason, the male flowering intensity was scored following a 0–3 scale as an indication of the potential male fecundity of the reproductive trees, as the seeds used for the germination test resulted from pollination that occurred 2 years before. Spatial location of individual trees was obtained with a laser telemeter and a compass. Local stand density around each tree was approached as the mean distance to its five nearest mature trees (Table 1).

Figure 1.

Location of the 20 seed trees within the Luberon forest. The nine trees with effective selfing are indicated by ^*.

Table 1. Characterization of sampled seed trees: zone of origin, generation, circumference at breast height (in cm), male flowering intensity (using a 0–3 scale), and local density.

Tree	Zone	Generation	Circumference	Male flowering intensity	Local density
A102	Z1	G0	291	2	5.8
A107	Z1	G1	198	3	6.6
A110	Z1	G0	285	1	7.3
B112	Z1	G1	144	1	5.6
B115	Z1	G1	134	3	3.5
B118	Z1	G2	117	0	4.0
B119	Z1	G1	144	2	5.2
C105	Z1	G2	63	0	2.5
A202	Z2	G0	203	2	4.9
A206	Z2	G0	243	2	6.4
A214	Z2	G0	263	0	7.1
B201	Z2	G1	149	0	13.5
B205	Z2	G1	159	0	6.9
B206	Z2	G1	100	0	6.1
B213	Z2	G1	96	0	5.8
B216	Z2	G1	149	3	7.0
B219	Z2	G1	92	0	6.1
C201	Z2	G2	58	0	5.5
A307	Z3	G0	219	3	12.9
A310	Z3	G0	245	1	7.1
Mean (s.d.)			167.5 (72.0)	1.2 (1.2)	6.5 (2.6)

In relation to the age class, G0 included the founder trees planted in 1863, G1 was the first generation issued from G0, and G2 was the next generation that issued from G0 and G1 (Lefèvre et al., 2004). Local density was measured as the mean distance from the seed tree to the five nearest neighbour trees (in metre).

Three cones were collected from each tree just before disarticulation, in October 2003. For each tree, 120 well-conformed seeds were sampled for the germination test, that is, 2400 seeds for the totality of the selected trees. Non-developed seeds were assumed to correspond to non-pollinated ovules (Mosseler et al., 2000) and were discarded.

Germination test

To avoid fungal contamination, the seeds were imbibed in cryptonol (2%) for 1 h and chilled. To remove dormancy, the seeds were maintained in darkness at 2–4 °C for 40 days. For the germination test, a randomized block design with four blocks was used. Each progeny was divided into four sub-samples of 30 seeds that were sown into each block. Each block consisted of four Petri dishes (25 cm × 25 cm). Seeds were grouped as single plot units per seed family and were randomly distributed within each Petri dish, which were also randomly distributed within each block. Petri dishes were kept in a climatic chamber at 15 °C, with a cycle of 15 h of light per day, and 40% relative humidity. During the stratification period and the germination test, seeds were laid on a thick layer of filter paper that was re-hydrated three times a week. Petri dishes from the same block were located on the same shelf in the climatic chamber.

Three times a week, germinated seeds were identified when the radicle exceeded 2 mm in length. When this occurred, the individual germination date was recorded. The germinated seeds were then transplanted into mini-containers (40 ml). The germination of seeds lasted for 72 days after sowing. Non-germinated seeds were dissected under binoculars to check for the presence of embryos. Empty seeds or infected seeds, because of the presence of Megastigmus sp. larvae, were observed. As this insect is suspected, in some cases, to induce the development of full seeds from non-pollinated ovules (Rouault et al., 2004), these full sized but infected seeds could not be assigned to either the pollinated or un-pollinated ovule groups. Therefore, we computed the germination rate as the ratio between germinated seeds and the total number of ‘healthy' seeds, removing all empty and infected seeds.

Nursery test for selfing effects

Immediately after the germination test, a maximum of 50 seedlings were selected within each progeny to represent the whole range of germination dates. These seedlings were transplanted from mini-containers to 400 ml WM containers that were filled with peat and bark substrate, and grown in a glasshouse for 1 year. For an accurate comparison between selfed and outcrossed individuals within each progeny, seedlings from the same progeny were located within a single plot. As a consequence, progeny effect and micro-local environment were confounded. The whole experiment covered less than 2 m × 5 m in the glasshouse. The individual height (mm from cotyledons to apical bud) and diameter (mm at the base of the stem) were recorded at the end of the first year. Any developmental abnormalities or deaths that occurred during the growing season were also recorded.

Genetic markers

To elucidate the selfed or outcrossed origin of each seedling, we used three chloroplast microsatellites: Pt71936, Pt96916, and Pt36713 (Vendramin et al., 1996). The few seeds that developed abnormally were also included in the study. DNA was extracted from 50 mg of fresh plant tissue using the Qiagen Extraction kit (Qiagen, Courtaboeuf, France). The PCRs were performed following the protocol by Fady et al. (2003). Electrophoresis was conducted in an Li-Cor sequencer. As allelic variation occurs as a single base polymorphism for these markers, we paid particular attention to avoid genotyping errors. In all gels, five repeats of the same set of three control genotypes and three ladders were regularly distributed and systematically included. Furthermore, each progeny was distributed in the gels as groups of 10 individuals, surrounded by two samples of the corresponding mother tree, one on each side, which were also used as an extra-control among gels. Finally, 553 seedlings (18–39 per progeny) and all the seed trees were successfully genotyped.

Detection of selfing events

Chloroplast haplotypes were defined as the combination of the three microsatellite alleles. Outcrossed seedlings were unambiguously identified by the difference in haplotype between the seedling and mother. A seedling that shared the same haplotype with its seed tree may result either from selfing or from outcrossing, with a probability that depends on the frequency of this particular haplotype in the pollen pool. Therefore, an estimation of the haplotype frequency in the pollen pool is required to estimate the selfing rate. Thus, we developed a maximum likelihood estimate that combined both parameters (selfing rates and haplotype frequencies) as follows.

Considering P_i^m,j the probability for mother m with haplotype (chlorotype) j to produce a seedling with haplotype i, we can write

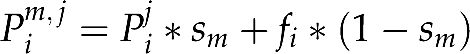where P_i^j is the probability for a mother with haplotype j to produce a seedling with haplotype i after selfing (P_i^j=0 for i≠j and P_j^j=1); s_m is the selfing rate of mother m; f_i is the frequency of haplotype i in the pollen pool and, assuming panmixia, f_i ^* (1−s_m) is the probability of producing a seedling with haplotype i after outcrossing.

To estimate the frequency f_i of haplotype i in the pollen pool, we have to consider that for a mother tree of haplotype j≠i, each seedling with haplotype i is issued from outcrossing and represents one haplotype i of the pollen pool. However, when the mother tree has haplotype i, its seedlings with haplotype i partly result from outcrossing and partly from selfing. In this case, it is necessary to remove the selfed seedlings from the count of i haplotypes in the pollen cloud. Finally, we have

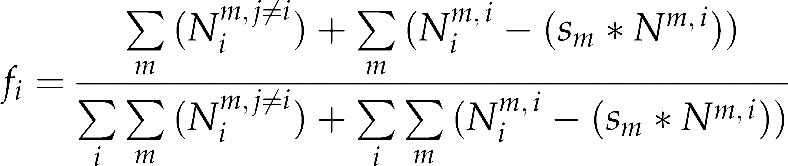where the N_i^m,i is the number of seedlings with haplotype i produced by mother m of haplotype i; N_.^m,i is the total number of seedlings produced by mother m of haplotype i and (s_m*N_.^m,i) is the number of selfed seedlings; and N_i^m,i−(s_m*N_.^m,i) is the number of purely outcrossed seedlings with haplotype i produced by mother m of haplotype i.

Finally, assuming that all mating events were independent, the overall probability of the observed haplotypes is

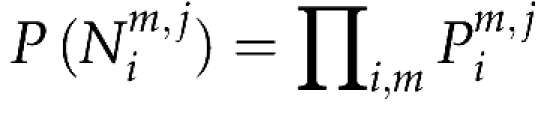Selfing rates (s_m) and haplotype frequencies (f_i) were jointly estimated by the maximization of the log likelihood (∑log (P_i^m,j)) using the ‘optim' function from the R Stats package (R version 2.6.2. in http://www.r-project.org/). Confidence intervals were estimated from 1000 bootstrap redraws of individuals within progenies from the observed data. Each seedling k from a mother m was assigned a probability p.self_m,k of resulting from a selfing event as follows:

p.self_m,k=0 if the seedling and seed tree have different haplotypes; otherwise, the conditional probability of being selfed given the seedling and its mother tree share the same haplotype i, is given by

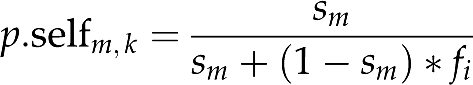Haplotype diversity was estimated as H=(1−∑f_i²) where f_i is the frequency of haplotype i. We used the rarefaction method to compare the number of different haplotypes between different sub-samples (seed trees, zones, and so on.).

The effects of male flowering intensity, local density, and tree size on the individual selfing rate were tested using the following fixed linear model and type III tests:

where f(s_m) is the arc.sine(sqrt) transformation of the selfing rate of mother tree m; male_m is the male flowering score (0–3) of the mother tree m that we treated either as a two-level factor (0 vs 1–2–3) or as a four-level factor (note that a score 0 only means no observed male strobili); dens_m is the local density of trees around mother tree m; poly(circ_m, 2) is a quadratic function of the individual circumference of the mother tree m.

We constrained the model to pass through the origin. We obtained the same results using a generalized linear model with the number of selfed and outcrossed seeds estimated from s_m as the dependant variable (matrix) and a quasibinomial distribution (data not shown).

Assessment of maternal and ID effects

From the subset of genotyped seedlings, the effect of selfing on the seed germination time was tested using the following mixed effect ANCOVA model:

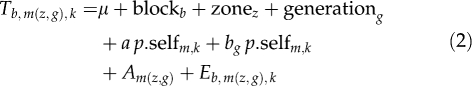where T_{b,m(z, g),k} is the germination time (number of days after sowing, log transformed) of seed k from mother tree m, from zone z and generation g, grown in block b; block_b is the fixed effect of block b in the germination experiment; zone_z is the fixed effect of the zone z of the forest where mother tree m is located; generation_g is the fixed effect of the generation g to which mother tree m belongs; p.self_m,k is the probability of seed k from mother tree m being selfed, used as a covariate; an interaction with generation is also introduced into the model; A_m(z,g) is a random term, variance var(A_m(z,g)) is the variance among seed trees within zone and generation; var(E_b,m(z,g),k) is the residual variance.

Similarly, the maternal and inbreeding effects on seedling growth beyond their effects on germination time were analysed as follows:

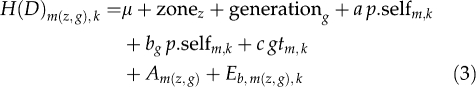where H(D)_{m(z, g),k} is the height (resp. basal diameter) of seedling k from seed tree m; gt_{m, k} is the germination time of seedling k from seed tree m, used as a covariate to account for the effect of different growing periods; other terms are similar to that in model (2).

Considering that p.self_m,k is also the expected proportion of true selfed individuals within the progeny, its effect represents the absolute difference between selfed and non-selfed individuals, which is a measure of ID, assumed to be constant among seed trees in this model. Alternatively, ID can also be expressed relatively to the intercept term of the model that represents the predicted mean of outcrossed progenies (that is, for value p.self_m,k=0 of the covariate).

Considering the mean value of a progeny, it is made of two components: an expected value without selfing (combining the additive value of the genes inherited from the parent, or parental breeding value, and maternal effects) and a correction because of the impact of selfing (selfing rate × ID). Therefore, we graphically represented ID through the relationship between the selfing rate and the difference between the actual and the expected progeny values. The actual progeny values were estimated from a sub-model without the p.self_m,k covariate, whereas the potential progeny values were estimated from the global model at the value p.self_m,k=0 of the covariate.

We used type III tests for the fixed effects and covariates. We used REML estimates of the variance components. All statistical tests were computed on R, and scripts are available on request.

Results

Seed germination

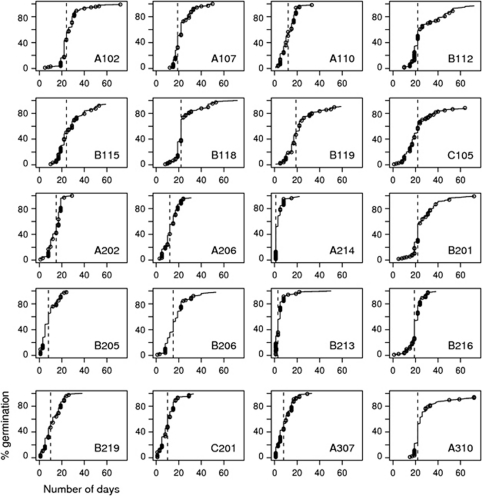
The percentage of full seeds varied from 58 to 99% depending on the progeny. The germination rate was high and varied from 88 to 100%. Some progenies started germination immediately after the stratification period but others were delayed for up to 15 days (Figure 2), suggesting important maternal effects on the progenies for this trait. Furthermore, the variation of germination time within progeny varied among seed trees, from just 1 day to 24 days before the level of germinated seeds reached 50% (Table 2). In particular, there was a significant difference between zones 1 and 2 (Wilcoxon test, P=0.034 for the date of first germination; P=0.006 for the date of 50% germination).

Figure 2.

Seed germination kinetics for the 20 Cedrus atlantica progenies. Dashed lines indicate the time to reach 50% germination; dots represent the sub-sample of genotyped seedlings.

Table 2. Germination parameters for each progeny: percentage of healthy embryos (not empty, not infested), germination rate, number of days from sowing to the first germination, number of days until 50% of the seeds within the progeny germinated.

Tree	Zone	% Healthy embryos	Germination rate (%)	Days to germination	Days 50% germination
A102	Z1	90	99	5	24
A107	Z1	89	100	12	19
A110	Z1	96	98	1	12
B112	Z1	82	97	10	22
B115	Z1	72	94	10	24
B118	Z1	88	100	8	22
B119	Z1	80	91	1	19
C105	Z1	87	88	1	22
A202	Z2	84	100	1	15
A206	Z2	74	97	3	12
A214	Z2	63	99	1	1
B201	Z2	93	99	5	22
B205	Z2	90	99	1	8
B206	Z2	87	98	1	15
B213	Z2	58	100	1	3
B216	Z2	77	99	1	19
B219	Z2	99	100	1	10
C201	Z2	87	99	1	10
A307	Z3	90	100	1	8
A310	Z3	72	94	15	22
Mean (s.d.)		83 (11)	98 (3)	4.0 (4.5)	15.5 (7.1)

Polymorphism of the markers

The three microsatellites used showed four, five, and six variants for Pt36713, Pt96916, and Pt71936, respectively. A total of 35 haplotypes was identified over the whole set of genotyped individuals: seedlings and seed trees. In our sample, the highest frequencies of these haplotypes were 0.21 and 0.17, and the lowest was 0.002. The haplotype diversity was high (H=0.90).

Selfing rate

Selfing rate estimates varied considerably among the reproductive trees, ranging from 0 to 0.479 (Table 3). Of the 20 reproductive trees, 9 showed significantly positive selfing rates. These trees were dispersed in the population (Figure 1). Considering the forest as a single panmictic unit, selfing rates and haplotype frequencies from the whole set of seed trees could be estimated regardless of their location in the forest. Then the mean selfing rate was 0.095±0.140. The selfing rates were also independently estimated within zone 1 and zone 2 (the sample in zone 3 was too small for this analysis): the within-zone estimates of selfing rates were very similar to the global estimations (data not shown).

Table 3. Selfing rate estimates (s_m) for each seed tree considering the whole forest as a panmictic unit.

Seed tree	Nb of genotyped seeds	Selfing rate	Nb of haplotypes
A102	28	0.092	8.01±0.79
A107	28	0	8.62±1.06
A110	28	0	8.77±1.09
B112	38	0.273	6.69±0.88
B115	34	0.479	10
B118	26	0	6.88±0.89
B119	26	0	8.63±0.83
C105	39	0.331	5.97±0.8
A202	25	0.158	7.27±0.7
A206	27	0.109	7.07±0.77
A214	20	0	9.48±0.6
B201	26	0.107	10.18±0.95
B205	19	0	7.95±0.22
B206	19	0	8.68±0.46
B213	26	0	6.19±0.73
B216	29	0	10.25±1.11
B219	29	0	7.41±0.93
C201	29	0.054	9.62±1.06
A307	39	0.288	—
A310	18	0	—
Mean (s.d.)		0.095 (0.141)

The number of different haplotypes in the outcrossed progeny of each seed tree was computed after rarefaction using the smallest sample size of 18, observed for B115, as a reference.

The variation in selfing rate among trees was not determined by local density (Table 4). The effect of male flowering intensity was marginally significant (P=0.032), only when considered as a two-level factor (Table 4).

Table 4. Effects of male flowering intensity (treated as a two-level factor in (a), or as a four-level factor in (b)), local density, and tree circumference (quadratic effect) on the individual selfing rate (arc.sine(sqrt) transformed).

	Num d.f.	Den d.f.	F	P-value
(a)
Male flowering (0/+)	1	16	5.53	0.0318	*
Local density	1	16	0.61	0.4480	NS
Circumference (quadratic)	2	16	1.68	0.2175	NS
(b)
Male flowering (0–3)	4	13	1.26	0.3326	NS
Local density	1	13	0.29	0.5995	NS
Circumference (quadratic)	2	13	0.91	0.4263	NS

^*P<0.05.

The number of different haplotypes in the pollen cloud, estimated after performing the rarefaction method, varied from 5.97 to 10.25 among seed trees (Table 3). There was no correlation between individual selfing rate and the diversity of haplotypes in the outcrossed progeny.

Effects of selfing on germination

As mentioned above, the final germination rate was very homogenous among progenies, but germination dynamics did vary among progenies. Considering the subset of individually genotyped seedlings, which represented the whole germination period within each progeny (Figure 2), the number of days needed for germination after stratification varied significantly among progenies (Table 5). At the individual seed level, we detected a significant effect of the probability of being selfed on the germination time and a significant interaction effect between the probability of being selfed and the generation: this selfing effect was only significant within G0 but not in the subsequent generations (Table 5). At progeny level, in generation G0, the selfing rate was not a predictor of the actual progeny values but only a predictor of the difference between actual and potential progeny values (Figure 3).

Table 5. Inbreeding effect on the germination time of each seed (mixed effect ANCOVA model).

	Num d.f.	Den d.f.	F	P-value
Fixed effects and covariates
Block	3	527	0.89	0.4462	NS
Zone	2	15	4.15	0.0368	*
Generation	2	15	0.18	0.8407	NS
Probability of selfing (p.self)	1	527	7.28	0.0072	**
Generation × p.self	2	527	6.31	0.0020	**
Selfing effect within each generation	Estimate		95% Confidence interval
p.self within G0	−1.010		[−1.440; −0.581]
p.self within G1	0.053		[−0.392; +0.497]		NS
p.self within G2	−0.151		[−0.672; +0.370]		NS
Variance components	s.d. estimate		95% Confidence interval
Among progenies (at p.self=0)	0.583		[0.397; 0.856]
Residual	0.769		[0.724; 0.817]

The covariate p.self is the probability of each seed being selfed, which provides an estimate of inbreeding depression. The random variation among progenies includes variation of genetic values of the mother trees and maternal effects.

^*P<0.05; ^**P<0.01.

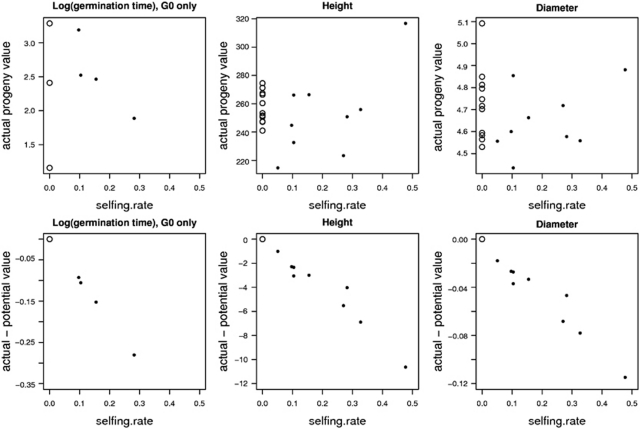
Figure 3.

Inbreeding effect at progeny level. The actual progeny means are not related to the individual selfing rate (top line graphs), but selfing rate indicates the difference between actual and potential progeny means because of inbreeding depression (bottom line graphs). The actual and potential progeny values of non-selfed progenies are equal (represented in the open circle). For partially selfed progenies, the actual values were computed as the best linear unbiased predictions (BLUP) in a sub-model without the covariate ‘probability of selfing', whereas the potential values were the BLUP estimates for a null value of this covariate in the global model. For germination time, the selfing effect was only significant in the G0 generation, which is represented here.

Surprisingly, within progenies, the selfed seeds germinated earlier than the outcrossed seeds. Early germination seems to be positively correlated with fitness in our environmental conditions as earlier growth confers a competitive advantage by increasing the period of vegetation.

Effects of selfing on growth in nursery

Seedling survival did not appear to be affected by selfing as there was no correlation between the mortality rate (low, 0–12%) and the selfing rate at the progeny level. Morphological abnormalities and mortality appeared at a very low frequency in both self and cross-fertilized seedlings and no significant differences were observed (data not shown).

The selfing effect was significant at the individual level for both height and diameter after 1year of growth, and it did not vary across generations (Table 6). The effect of the germination date on height and diameter growth was also significant but much less important than ID (Table 6). Within progenies, ID accounted for an 8 and 6% reduction in height and diameter growth, respectively. At the progeny level, the selfing rate was not a predictor of the actual progeny values (Figure 3), as previously observed for the germination time.

Table 6. Inbreeding effect on seedling growth in height and diameter (mixed effect ANCOVA model).

	Num d.f.	Den d.f.	F	P-value
(a) Height growth
Fixed effects and covariates
Zone	2	15	0.30	0.7500	NS
Generation	2	15	1.30	0.3005	NS
Probability of selfing (p.self)	1	500	6.41	0.0116	*
Germination time (gt)	1	500	78.6	<0.0001	***
Generation × p.self	2	500	2.28	0.1032	NS
Selfing and germination time effects	Estimate		95% Confidence interval
Probability of selfing (p.self)	−20.675		[−37.364; −3.986]
Germination time (gt)	−1.687		[−2.067; −1.307]
Variance components	s.d. estimate		95% Confidence interval
Among progenies (at p.self=0)	24.588		[16.444; 36.767]
Residual	45.646		[42.910; 48.557]
(b) Diameter growth
Fixed effects and covariates	Num d.f.	Den d.f.	F	P-value
Zone	2	15	1.98	0.1725	NS
Generation	2	15	1.33	0.2953	NS
Probability of selfing (p.self)	1	500	7.22	0.0075	**
Germination time (gt)	1	500	52.24	<.0001	***
Generation × p.self	2	500	0.48	0.6206
Selfing and germination time effects	Estimate		95% Confidence interval
Probability of selfing (p.self)	−0.288		[−0.493; −0.082]
Germination time (gt)	−0.017		[−0.022; −0.013]
Variance components	s.d. estimate		95% Confidence interval
Among progenies (at p.self=0)	0.162		[0.095; 0.276]
Residual	0.579		[0.544; 0.616]

The covariate p.self is the probability of each seedling being selfed, which provides an estimate of inbreeding depression. The covariate gt is the time before germination of the original seed, accounting (negatively) for the length of the growing period. The random variation among progenies includes variation of genetic values of the mother trees and maternal effects.

^*P<0.05; ^**P<0.01; ^***P<0.001.

Discussion

Variation in selfing rate among seed trees

Traditionally, studies on ID have been carried out by performing controlled crosses. There are only a few studies that have estimated the individual selfing rates and ID under natural mating systems, by calculating the proportion of empty seeds and with biparentally inherited molecular markers such as isozymes, which need more complicated statistical estimators (Kärkkäinen and Savolainen, 1993; Ritland and Travis, 2004; Bower and Aitken, 2007). In this study, we took benefit of the high diversity and paternal inheritance of cpSSRs markers in Pinaceae species (Parducci et al., 2001; Ribeiro et al., 2002; Naydenov et al., 2005) and particular Cedrus (Fady et al., 2003; Terrab et al., 2006). In Cedrus, we measured a mean selfing rate circa 0.1, which is in agreement with the absence of incompatibility mechanisms and the values reported in other conifers (Franklin, 1969; Cottrell and White, 1995; Sorensen, 1999; Restoux et al., 2008). A considerable variability among seed trees was observed, reminding us that selfing rate is not a fixed trait of the species, but that it can vary both between and within populations (Barret and Eckert, 1990).

To explain this variability, under the mass action model, a reduced number of male strobili surrounding a seed tree may restrict the relative amount of non-self pollen and, hence, increase the proportion of self-pollen proportion in the seed tree's crown. On the one hand, we found no relationship between local density of adult trees and selfing rate. Concerning the effect of local density on selfing rate, various results were obtained in similar studies on conifers (Farris and Mitton, 1984; Neale and Adams, 1985; Morgante et al., 1991; Sorensen and Adams, 1993; Parraguirre-Lezama et al., 2004; Restoux et al., 2008). Furthermore, we did not find any correlation between the selfing rate and the diversity of the allopollen cloud captured by the seed tree, as would be expected for isolated trees under the hypotheses of pollen limitation and gene mixing effects because of long distance pollen dispersal (Klein et al., 2006). On the other hand, we detected a weak but significant effect of the production of male strobili of each seed tree on its selfing rate. Therefore, individual variation of selfing rate was determined by the amount of self-pollen and not by the local amount of non-self-pollen. In this case, this means that the mating system is controlled by the biology of the species and not only by the demography. In C. atlantica, sex allocation to male and female functions is highly variable and Krouchi et al. (2004) have found that this variation is stable at least across several years. From an evolutionary perspective, such a tendency to dioecy in trees can be interpreted in the light of ID avoidance (Scofield and Schultz, 2006).

Our selfing rate estimates might be down biased because they were computed from the number of mature seeds and not directly from the number of fertilized ovules. In most conifers, during early embryogenesis, ID acts more or less severely depending on the number of embryonic lethal alleles in the parental genome (see Introduction). Kärkkäinen and Savolainen (1993) suggest that polyembryony, which occurs frequently in Pinaceae, can diminish the cost of embryonic lethals and make embryo competition possible, leading to an underestimation of the primary selfing rate. In this regard, the genus Cedrus shows simple polyembryony, derived from the fertilization of about half of three to six archegonia in each female gametophyte, and cleavage polyembryony, which leads to genetically identical embryos (Wilson, 1923; Favre-Duchartre, 1970). Although cleavage embryos offer no selective advantage, simple polyembryony is also a weak or even non-existent barrier against selfing because, during early embryogeny, an advantage is conferred to the embryo based on its position in the female gametophyte. The embryo closest to the corrosion cavity, which is genotype independent, is conferred the advantage (Williams, 2007).

Effects of selfing on germination and first year growth in nursery

The rate of empty seeds among well-conformed seeds, which generally indicates the presence of embryonic lethals (Savolainen et al., 1992), was low (17%) and its variation was not related to selfing rate. Furthermore, juvenile mortality was also very low in this study. These results suggest that major recessive lethal alleles with additive effects had efficiently been purged in this Cedrus population. This could either reflect a general feature of the species or a particular situation in this population that suffered very high mortality after their initial plantation. Similarly, juvenile mortality was not observed in studies on P. pinaster Ait. and Pseudotsuga menziesii (Mirb.) Franco (Durel et al., 1996; Sorensen, 1997).

Germination dynamics differed significantly among progenies collected in two zones of the forest. Germination time is determined both by the genotype of the embryo and by maternal effects, either genetically or environmentally determined, that affect seed physiology. As we suspect no genetic differentiation among these zones (Lefèvre et al., 2004 and marker data from this study), the difference in germination dynamics would rather be explained by the difference of environmental conditions among zones.

Within progenies (skipping maternal effects at this level), we detected a selfing effect on the germination time in the founder generation G0 but not in the following generations G1 and G2. In our controlled and artificial conditions, selfed seeds germinated earlier than outcrossed seeds, a finding that is in contradiction with results reported for other conifers, such as P. contorta var. murrayana (Sorensen, 2001) and Picea abies (L.) Karst (Skrøppa, 1996). In P. menziesii and P. ponderosa Dougl. ex Laws., germination was hardly affected by selfing (Sorensen and Miles, 1974). Therefore, we hypothesize that transient outbreeding depression (OD) might occur in this admixed Cedrus population because of diverse origins of the plant material. OD occurs in particular when hybridization disjuncts co-adapted gene complexes (Ledig, 1986). In the founder generation G0, seedlings from selfing are obviously a result of within-gene pool crosses, whereas part of the seedlings issued from outcrossing result from between-gene pool crosses and could suffer from OD. This hypothesis is further supported by the evolution across generations: as observed in this study, OD would not be expected to correlate to the selfed or outcrossed origin of the seeds that are produced by the next generations because of recombination among gene-pools.

Studies of the effects of ID on growth parameters in trees have often been performed on juvenile trees of at least 4-years-old. This is because first-year growth can be influenced by the time of emergence, a possible effect of maternal influences, as shown here. Moreover, many studies are conducted at the family level comparing selfed and outbred controlled crosses (which, by the way, also imply artificial conditions during pollination and seed development). In 1-year-old P. contorta var. murrayana seedlings, Sorensen (2001) found an ID of 17.7% in height; in 1-year-old P. menziesii and P. ponderosa, Sorensen and Miles (1974) observed an ID for height of 18 and 21%, respectively; in 2-year-old P. menziesii, Sorensen (1997) found an ID of 30% in height and 40% in diameter. In this work, we used a different approach that consisted of a model that included maternal effects and germination time in the analysis. This approach was used to estimate ID beyond these effects at the individual seed level. In doing so, we detected a small but significant ID effect, 8 and 6% on height and diameter growth, respectively. In contrast with OD, ID did not change across the three generations, suggesting that ID mainly relates to the additive effects of many slightly deleterious genes that are not easily purged in the population. Indeed, we detected no purge of ID at this short time scale. The effectiveness of purging is not frequently observed in plant populations, even when inbreeding occurs (Byers and Waller, 1999). Comparing selfed and crossed progenies obtained in a natural population of P. sylvestris, Koelewijn et al. (1999) observed an effect of ID on survival and seed set up to an age of 23 years, but no significant differences in height and flowering, indicating that high levels of ID both for early stage (seed production) and later stages of the life cycle were maintained in the population in the long run. As explained below, our results reveal a possible mechanism that might explain low purging of slightly deleterious genes in trees.

In this study, no effect of selfing rate on family means was observed, suggesting a previous efficient purge of the most deleterious alleles in this species. Although significant, the ID effect was weaker than that of the global seed tree effect, that is, selfed seeds only differ from their outcrossed relatives but not from all outcrossed seeds. Owing to between-family variation, selfed seedlings can still outcompete outcrossed seedlings from other progenies. The design we used in the nursery to determine growth traits was oriented towards within-family comparisons, where seed tree effects (parental breeding value and maternal effects) were slightly up-biased and partly confounded with micro-environmental conditions in the nursery. The micro-environmental conditions in the nursery were still much less variable than small-scale environmental conditions in the forest. Therefore, we expect that ID is even weaker relatively to progeny effect in natural conditions, which means that purging such type of ID in nature is only possible through within-family selection. Under this scenario, seed dispersal, which affects the spatial distribution of various progenies, would also affect purging. More generally, during the regeneration phase of the forest, when the most intense demographic reduction and selection for competing ability occur, seed dispersal is widespread enough so that competition occurs between seedlings from different progenies and, therefore, we would expect no early purging of inbred genotypes. After the regeneration phase, demography decreases more slowly and inbred trees could remain present in the forest and contribute to the next generation, even though they have a reduced fitness. By contrast, in some particular situations such as a very low density in a colonization front, we could expect within-family competition at the seedling stage and more efficient purging. Of course, the most deleterious mutations are more rapidly purged from the embryonic to later stages of the life cycle.

Thus, ID that has a lower effect than the variation of breeding values is maintained in the population for the long term. Part of these slightly deleterious genes might become a source for adaptational changes when environmental conditions change.

The authors declare no conflict of interest.