Evolutionary study of a potential selection target region in the pig

Abstract

Domestication, modern breeding and artificial selection have shaped dramatically the genomic variability of domestic animals. In livestock, the so-called FAT1 quantitative trait locus (QTL) in porcine chromosome 4 was the first QTL uncovered although, to date, its precise molecular nature has remained elusive. Here, we characterize the nucleotide variability of 13 fragments of ∼500 bp equally spaced in a 2 Mb region in the vicinity of the FAT1 region in a wide-diversity panel of 32 pigs. Asian and European animals, including local Mediterranean and international pig breeds, were sequenced. Patterns of genetic variability were very complex and varied largely across loci and populations; they did not reveal overall a clear signal of a selective sweep in any breed, although FABP4 fragment showed a significantly higher diversity. We used an approximate Bayesian computation approach to infer the evolutionary history of this SSC4 region. Notably, we found that European pig populations have a much lower effective size than their Asian counterparts: in the order of hundreds vs hundreds of thousands. We show also an important part of extant European variability is actually due to introgression of Asian germplasm into Europe. This study shows how a potential loss in diversity caused by bottlenecks and possible selective sweeps associated with domestication and artificial selection can be counterbalanced by migration, making it much more difficult the identification of selection footprints based on naive demographic assumptions. Given the small fragment analyzed here, it remains to be studied how these conclusions apply to the rest of the genome.

Introduction

Livestock, and domestic species in general, provide excellent models to study and understand adaptation at an accelerated pace. Domestication, the creation of modern livestock breeds contemporary with industrial revolution and, more recently, the emergence of very efficient artificial selection methods must have exerted a dramatic influence on nucleotide diversity. Bottleneck processes, but selective sweeps also, have been important in domestication. It is, however, relevant to mention that humans, by breeding fancy phenotypes that would otherwise have been removed in the wild by natural selection, has also maintained deleterious alleles at high frequencies (Fang et al., 2009; Ludwig et al., 2009; Schmutz and Berryere, 2007). Overall, however, little is known so far on the precise molecular history and of the effects of artificial selection in livestock, including the species studied here, the pig.

Of all extant livestock species, the pig has a particularly interesting demographic history. Its wild ancestor still has a widespread natural habitat, from Eastern Asia to Western Europe and North Africa, and there are well-documented multiple independent domestication events in Asia and in Europe (Larson et al., 2005), followed by introgression of Chinese germplasm into European breeds. In addition, porcine populations are heavily structured and arranged in breeds; some breeds are specialized and strongly selected for traits of economic interest and raised in strictly controlled environments, whereas other have not undergone modern artificial selection but are adapted to local outdoor conditions. Nevertheless, demography and selective history of the majority of domestic animals at the molecular level are, to a large extent, still uncertain. Many questions remain unanswered like the presence and extent of bottleneck(s), the likely migration rate between Asia and Europe or the amount of variability in Asia vs Europe as well as the extent of breed differentiation at the DNA level.

Among genome regions, those that potentially harbor genes that have been selection targets are of particular interest. In the pig, the first identified quantitative trait locus (QTL) was shown to affect fat deposition and growth; it was identified in chromosome 4 (SSC4) (Andersson et al., 1994). Here we considered a region that surrounds two interesting positional candidate genes for FAT1, FABP4 and FABP5. In previous studies (Ojeda et al., 2008a, 2006), the nucleotide variability and haplotype structure of these two genes were analyzed and compared. Given their close physical location and metabolic roles, it has been found that one of the most surprising results was a dramatic difference in nucleotide variability and haplotype structure between these two genes. The FABP4 nucleotide variability was sixfold higher than FABP5 (π=1.17 vs 0.19%, respectively). Nucleotide diversity in FABP4 was astonishingly high, and we hypothesized that balancing selection might have been involved in maintaining such a high diversity. The Hudson, Kreitman and Aguade (HKA) test showed an imbalance between FABP4 and FABP5 intra- and interspecific nucleotide variation (χ²=6.84, P=0.009). Therefore, the differences between these two loci could not be explained by a stationary neutral model.

Given these surprising differences between both genes, its importance for FAT1 QTL and to gain insight into the evolutionary history of the species in this particular region, we have here characterized the porcine nucleotide variability along a 2 Mb region in chromosome 4 (SSC4). We sequenced 13 fragments of 500 bp each in 32 pigs sampled with a worldwide distribution, including local Mediterranean and Asian breeds together with international breeds. To make computations feasible for parameter inference, we resorted to approximate Bayesian computation (ABC) based on summary statistics (Beaumont et al., 2002).

Materials and methods

Pigs resequenced

We resequenced a panel of 32 pigs pertaining to Asian populations, Vietnamese pot belly (from Madrid's Zoo; n=1), Meishan (China; n=1), Fengjing (China; n=1), Minzhu (China; n=1), Licha Black (China; n=1) and Luchuan (China; n=1), and European populations, Iberian from Retinto and Guadyerbas strains (IB, Spain, n=5), Duroc (DU, Spain, UK and USA, n=6), Nero Siciliano (SI, Italy, n=5), Landrace (LR, hyperprolific line of French origin, n=4), Tamworth (UK, endangered breed, n=1), British Lop (UK, endangered breed, n=1), Berkshire (UK, n=1), Hampshire (UK, n=1), Large White (Spain, n=1) and synthetic breed (Spain, n=1). One babirusa (Babyrusa babiroussa) from Madrid's zoo (Spain) was used as outgroup.

This panel should contain a large fraction of extant variability in the porcine domestic species. Landrace, Large White and Duroc are representatives of the three most widespread breeds, and are used in selection schemes worldwide. Tamworth and British Lop are British local breeds that have undergone strong bottlenecks in the past. In contrast, Iberian and Sicilian are local representatives of the Mediterranean pig that have remained relatively isolated from the process of creation of modern breeds in Northern Europe starting in the nineteenth century. Both have been traditionally reared in semiextensive conditions. Sicilian pigs make up an ancient black pig population that has traditionally been reared in the island, prevalently in the mountainous areas of Nebrodi and Madonie. As for Asian breeds, the pigs sequenced here come from North-Eastern China and adapted to cold climate (Minzhu), some are highly prolific like the breeds around Taihu lake in central East, adapted to subtropical climate (Meishan and Fengjing), whereas Licha Black (Shandong province) is among the leanest breeds in China; Luchuan and Vietnamese potbelly are miniature pigs living in tropical environment.

Sequence and polymorphism detection procedures

Using the BAC sequence of chromosome 4 available at http://www.sanger.ac.uk/Projects/S_scrofa/, we determined the positions of FABP4 and FABP5 genes. We focused on a 2 Mb region around these two genes, according to assembly v. 9. Three more genes were located in that region: Zinc finger and BTB domain (ZBTB), inositol-monophosphatase 1 (IMPA1) and a Zinc finger protein (ZNF) gene. We resequenced 13 fragments of ∼500 bp within the 2 Mb that comprised intron 1 fragments of the five annotated genes along with eight additional fragments without annotations (see scheme in Figure 1). Sequences are available at GenBank with accession numbers HM012040-HM012073 (fragment 1), HM012074-12107 (2), HM012108-HM012141 (3), HM012142-HM012175 (4), HM012176-HM012209 (5), HM012210-HM012242 (6), HM012243-HM012276 (7), HM012277-HM012308 (8), HM012309-HM012342 (9), HM012343-HM012376 (10), HM012377-HM012410 (11), HM012411-HM012443 (12), HM012444-HM012477 (13).

Figure 1.

Scheme of the 2 Mb region showing the approximate position of the thirteen fragments sequenced; arrows indicate noncoding fragments and annotated genes are represented by gray boxes, approximately at scale; fragments within genes were positioned in the first intron. Gene names: IMPA, inositol-monophosphatase 1; FABP4, fatty acid binding protein 4; FABP5, fatty acid binding protein 5; ZNF, zinc finger protein gene and ZBTB, zinc finger and BTB domain. The starting position of fragment 1 on S. scrofa assembly 9 is 55815727, fragment 13 ends in 57794510 bp.

PCRs were performed in a 25 μl final volume containing 1.5 m MgCl₂, 200 μ dNTPs, 500 n of each primer, 50 ng DNA and 0.6 U AmpliTaq Gold (Applied Biosystems). Thermocycling was 95 °C for 10 min, 35 cycles of 94 °C for 0.5 min, 63 °C for 1 min and 72 °C for 1.5 min, and a final extension of 72 °C for 15 min. The amplified products were sequenced using the BigDye Terminator version 3.1 Ready Reaction Cycle Sequencing Kit in an ABI PRISM 3730 (Applied Biosystems). The diploid sequences obtained were analyzed using the SeqScape version 2.5 software (Applied Biosystems) with standard filter settings and manually edited and verified. Double peaks, that is, presence of two nucleotides in the same position for an individual, were individually checked and assigned as polymorphisms if confirmed.

Data analysis

Nucleotide diversities (π), computed as pairwise average number of differences, and Tajima's D statistics were obtained per breed and per fragment as well as globally using DnaSP (Rozas et al., 2003) and MANVa (Ramos-Onsins, Windsor and Mitchell-Olds, available from authors). Haplotypes per fragment were inferred with PHASE (Li and Stephens, 2003). Patterns of polymorphism and divergence were contrasted against the neutral model with the multilocus HKA test (Hudson et al., 1987). Nucleotide divergence relative to the outgroup (babirusa) was calculated and corrected for multiple hits with the Jukes and Cantor method. These analyses were calculated with MANVa. We used Structure 2.2 (Pritchard et al., 2000) to infer population structure using single nucleotide polymorphisms from all fragments. We inferred the number of clusters through its posterior distribution, as suggested by the authors.

Demographic history inference

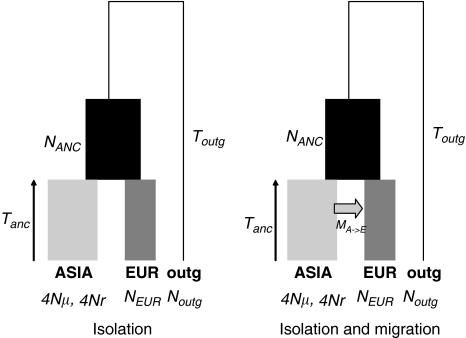
To analyze the evolutionary history for this region, we first considered a demographic framework as the simplest approach to explain the data for this region. We used two nested models (Figure 2); the first model, the ‘isolation model' states that an ancestral porcine population of effective size N_ANC was split into two populations, Europe (population size N_EUR) and Asia (N) T_ANC generations ago, where generations is in N units; these populations remained isolated after divergence. The divergence with respect to the outgroup occurred T_OUTG generations ago. The second model is an ‘isolation plus migration model', which additionally allows from migration from Asia to Europe at a scaled rate M_{A → E}, also expressed in N units. We assumed that the mutation and the recombination rates were the same for all the 13 fragments (loci) studied, and that the loci were unlinked. This assumption follows from our previous estimate of scaled recombination rate in the region, ρ=0.001 (Ojeda et al., 2006). Given the spacing between fragments and the models analyzed, we believe that the assumption of no linkage should not affect the results strongly. Furthermore, linkage disequilibrium among loci for the analyzed data set was tested using LIAN software (Haubold and Hudson, 2000) to confirm the lack of linkage disequilibrium among fragments. Thus, both models allow for bottlenecks that may have been of different intensity in Europe and Asia. The key difference lies in the rate of unidirectional migration from Asia into Europe. Although Asia → Europe migration is well documented, its impact on European breeds in terms of nucleotide diversity has not been quantified yet at the autosomal level. Therefore, if that impact is small, the isolation model would be favored compared with the isolation and migration model because the former is more parsimonious. Given that population structure was evident within Europe (see below), and to facilitate the interpretation of the data and to avoid the effect of local population structure, we obtained the European sample chosen for the demographic inference from selecting a single line for each of the different breeds in Europe (named EUR1).

Figure 2.

Demographic models considered for demographic inference. The left image depicts the isolation model, with parameters ancestral effective size (N_ANC), outgroup size (N_OUTG), European (N_EUR) and Asian (4Nμ) effective sizes, speciation time (T_OUTG) and split time between Asian and European populations (T_ANC). In addition, the isolation plus migration model (on the right) allows for unidirectional migration from Asia to Europe at a scaled rate M_{A → E}.

For the inference by ABC analysis, we used the sum across all 13 loci of the following 15 statistics: Sx1, Sx2, Sxo (exclusive variants for ASIA, EUR1 and the outgroup Babirusa, respectively), Sf1, Sf2, Sfo (fixed variants for ASIA, EUR1 and the outgroup, respectively), Sx1f2, Sx2f1 and Ss (putatively ancestral variants between ASIA and EUR1 (Ramos-Onsins et al., 2004). We also considered Fay and Wu's H, Tajima's D and Wall's Q for each population ASIA or EUR1, but not normalized to avoid nonavailable numbers, that is, without dividing the value by its standard variance or the total positions. The complete set of observed statistics is listed in Supplementary Table S1. The complete algorithm is detailed in the Appendix. In brief, it involved running 10⁵ coalescence simulations for each locus according to the prespecified model with parameters sampled from previous distributions, using mlcoalsim version 1.92 (Ramos-Onsins and Mitchell-Olds, 2007), calculating the correlation between observed and simulated statistics following Hamilton et al. (2005) with modifications, saving the best 1% of the iterations following the criterion indicated in Beaumont et al. (2002). Finally, a composite probability Cst, which defines the probability for each evolutionary model given the observed data, was computed as 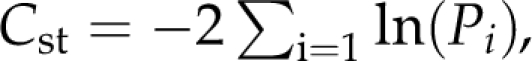where the sum is overall 15 statistics specified above, and where P_i is the P-value considering both tails (Ramos-Onsins et al., 2008). The composite probability was used to compare both models, with and without migration. We calculated the statistic CL=Cst_H0−Cst_H1 and contrasted the result using Monte Carlo simulations with the empirical distribution of CL, obtained from 1000 iterations of the null model (H₀=no migration). Once the best model was inferred, the statistics and neutrality tests calculated for each locus were contrasted against this model (using as the null distribution the 1000 chosen iterations of the this model), to detect specific-locus differences, which may indicate the effect of selection over a specific fragment. For HKA test, the mean and the variance for the number of segregating sites and for the divergence at each locus were obtained from the 1000 chosen iterations. Thus, the value of the HKA test was obtained empirically given the isolation and migration model. The P-value was obtained empirically by Jacknife, that is, calculating for each of the iterations the mean and the variance for the remaining 999 iterations and obtaining an empirical distribution of the HKA values.

To study the statistical power of the CL statistic in this scenario, we performed computer simulations. Using the observed values for, for example, sample size, base pair length, we simulated 1000 replicates of each model using the same previous distributions as in the ABC analysis. The CL statistic was calculated for each of the 1000 replicates to estimate the statistical power of this procedure. The probability of choosing the isolation and migration model over the isolation model when migration was true was 0.955, that is, a statistical power of 95%.

Results

Nucleotide variability and structure

We classified the samples in six groups: the four breeds with more than one animal sequenced (Duroc, Iberian Landrace, Sicilian), Asian samples (ASIA), and a last group (EUR1) that was made up of one individual of each population Duroc, Iberian Landrace, Sicilian, along with each individual from Tamworth, British Lop, Berkshire, Hampshire, Large White and the synthetic breed (a terminal sire line). In EUR1, only one haplotype of each individual was used. For the sake of demography inference, only ASIA and EUR1 were used because of structuring the evidence of subdivision within Europe (see below) and the relatively low number of individuals within each of the breeds (Wakeley and Aliacar, 2001).

Figure 1 shows approximately the position of each gene and of the fragments sequenced. Tables 1 and 2 show nucleotide variability and statistics Tajima's D and Fay and Wu's H per fragment per population. A total of 56 segregating sites were detected in all 13 fragments sequenced (7.4 kb in total), 46 single nucleotide polymorphisms in Asia and 33 in European populations. Asian populations were more variable overall θ=2.1 × 10⁻³ vs 1.6 × 10⁻³ in Europe, whereas within breed variability was in the order of 10⁻³, that is, very similar to what has been reported in the human species. Interestingly, there were no differences in variability between European breeds: nucleotide diversities in local ‘unimproved' breeds, Iberian or Sicilian, were very similar to those in international and highly selected breeds, like Duroc and Large White breeds θ=∼1 × 10⁻³. Similarly, The nucleotide differences of these breeds and ASIA were also very similar (π_(EUR1,ASIA)=0.0033, π_(IB,ASIA)=0.0034, π_(SI,ASIA)=0.0033, π_(DU,ASIA)=0.0032, π_(LR,ASIA)=0.0034), suggesting a common origin of European and International breeds, divergent from ASIA. There were large differences between fragments, though FABP4 intron 1 (fragment 6) was by far the most variable fragment, θ=1%, corroborating our previous results (Ojeda et al., 2006) where we found θ=1.17%. Note that, for Iberian breed, a local relatively isolated breed, θ at that fragment was higher (6.5 × 10⁻³) than in Asia (4.8 × 10⁻³) and comparable to that found when pooling all European breeds analyzed (EUR1). In contrast, it was 0 in Landrace and 0.8 × 10⁻³ in Sicilian Black, also a Mediterranean local breed. Again in accordance with our former results (Ojeda et al., 2008a), FABP5 was much less variable; it was actually the second least variable fragment analyzed after fragment 2, where no single nucleotide polymorphism was found. According to Tajima's D and a variety of other statistics, such as Fu-Li's and Fay and Wu's H (normalized), there were few departures from the stationary neutral model when each locus was analyzed per breed (Table 2). The most significant values were Fay and Wu's H test at fragment 1, which indicates an excess of new variants at high frequency. This might be interpreted as a result of natural selection or, alternatively, migration or introgression events affecting this region. Departures from the stationary neutral model were also compared by the multilocus HKA test, which compares within breed polymorphism and divergence with babirusa. Significant values were found only in Iberian breed (HKA=23.81, P=0.022) and in Landrace (HKA=24.52, P=0.017). Both showed the largest departure at the IMPA locus (as indicated by the partial χ² value; 10.20 at Iberian and 8.82 at Landrace). At this locus, we found an unbalanced divergence value in comparison to the polymorphism. It should be noted that departures from HKA test can be explained not only by selective process acting on one or several loci, but also by demographic processes such as population structure.

Table 1. Nucleotide diversity per fragment per population.

Fragment	n sites	KJC ( × 10−3)b	Nucleotide diversity ( × 10−3)a
			ASIA (12)c	EUR1 (10)	IB (10)	SI (10)	DU (12)	LR (8)	All (64)
1	653	22.4	4.1	2.7	1.6	2.7	3.0	2.9	2.6
2	691	11.7	0.0	0.0	0.0	0.0	0.0	0.0	0.0
3	665	10.7	1.0	0.0	0.0	0.0	0.0	0.0	0.6
4 (IMPA)	435	10.5	3.8	3.3	4.1	0.8	3.0	3.5	3.4
5	358	25.8	3.7	3.0	1.8	3.9	0.0	3.2	3.0
6 (FABP4)	487	58.9	4.8	6.8	6.5	0.8	5.4	0.0	9.8
7	559	18.4	1.2	1.3	0.0	1.3	1.2	1.4	0.8
8 (FABP5)	760	16.0	0.0	0.5	0.0	0.5	0.0	0.0	0.3
9	703	19.4	4.9	0.5	0.0	0.0	0.0	0.0	3.1
10	732	30.1	1.8	1.9	1.4	1.4	1.8	1.6	1.7
11 (ZNF)	512	10.0	1.3	0.0	0.0	0.0	0.6	0.0	0.8
12	559	12.9	1.9	1.9	1.9	1.3	1.2	2.1	1.5
13 (ZBTB)	724	24.6	0.9	1.0	0.0	1.0	0.9	0.0	0.6
All	7838	18.8	2.1	1.6	1.1	0.9	1.2	1.0	1.7

^aNucleotide diversity (θ, Watterson's estimate).

^bDivergence between pig and babirusa corrected by Jukes and Cantor method using all data.

^cThe sample sizes for each sample group is within parentheses, except: ASIA for fragment 12 (n=10), EUR1 except for fragment 6 (n=9), SI n=10 except for fragments 6, 8 and 11 (n=8), ALL n=64 except for fragments 8, 10 and 11 (n=62).

Table 2. Tajima's D and Fay and Wu's H statistics per fragment per population.

Fragment	Tajima's Da							Fay and Wu′s Hb
	ASIA	EUR1	IB	SI	DU	LR	All	ASIA	EUR1	IB	SI	DU	LR	All
1	1.53	−1.14	−1.03	1.33	1.25	1.51	1.38	0.24	−4.13**	−4.78***	−0.84	−0.64	0.44	−2.77*
2	—c	—	—	—	—	—	—	—	—	—	—	—	—	—
3	−0.85	—	—	—	—	—	−1.32	0.58	—	—	—	—	—	0.16
4 (IMPA)	0.67	1.11	−1.04	−1.11	0.95	1.70	0.46	0.66	−0.33	−0.56	0.39	−0.77	0.26	0.31
5	0.22	−1.56	0.02	−1.67	—	0.46	−0.25	0.43	−1.39	−1.16	−0.98	—	−0.31	−0.21
6.(FABP4)	1.20	−0.43	1.89*	0.33	0.57	—	1.37	0.15	−1.37	0.45	0.61	−1.72	—	−0.48
7.	0.22	1.03	—	1.03	0.55	1.45	2.2*	0.76	−1.80	—	−1.80	−2.52	−1.01	−0.83
8 (FABP5)	—	−1.11	—	0.33	—	—	−0.89	—	0.39	—	0.61	—	—	0.16
9	1.9*	−1.11	—	—	—	—	−0.92	−0.06	0.39	—	—	—	—	−4.39**
10	−0.90	0.93	1.60	1.23	1.55	0.46	0.98	−0.03	0.16	−0.80	−1.29	0.51	−0.31	0.29
11 (ZNF)	−0.85	—	—	—	0.54	—	−0.97	0.58	—	—	—	0.61	—	0.30
12	0.85	0.70	1.76	1.84*	0.82	−0.81	1.37	0.20	0.60	0.30	0.00	−1.80	−2.34	0.60
13 (ZBTB)	1.82*	0.02	—	0.02	1.76	—	1.41	−0.31	−1.16	—	−1.16	−0.09	—	−0.92
All	0.67	0.22	0.87	0.52	1.29	1.06	0.83	0.23	−1.22	−1.13	−1.20	−1.32	−0.65	−1.39

^aTajima's D.

^bFay and Wu's H normalized (Zeng et al., 2006).

^cNot able to calculate because of lack of segregating sites. Nominal significance values are indicated by asterisks: ^*P<0.05; ^**P<0.01; ^***P<0.001.

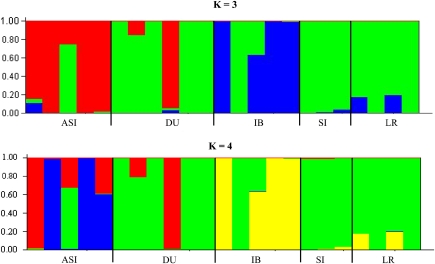
Population structure was analyzed only for those breeds with more than one animal (Duroc, Iberian Landrace, Sicilian); F_st estimation and permutation tests showed clear differentiation between breeds except between Duroc and Landrace (data not shown). In agreement, Structure shows clear evidence of population differentiation with either K=3 or 4 clusters (either number of clusters was equally likely), but not always in strict correspondence to breed (Figure 3). With exceptions, most individuals were ascribed nearly to a single cluster. Grossly, European breeds were made up of two clusters whereas Asian animals clustered apart and were a composite of two (K=3) or three clusters (K=4). Nevertheless, all populations showed some degree of admixing, mainly Asian, Duroc and also Iberian pigs. Therefore, the unsupervised method Structure illustrates that breeds are neither completely distinct between them nor genetically uniform. The method also suggests that Asian pigs are the most distinct although some commercial animals, for example, a Spanish Duroc, can be ascribed to the cluster predominant in Asia; symmetrically, some Asian animals can belong to the major European cluster. All these suggest already a strong influence of Asian germplam into Europe, as confirmed by the ABC demographic inference (see below).

Figure 3.

Population structure for K=3 and K=4 clusters by Structure software for the five populations. Each breed or population is separated by a black vertical line; DU, Duroc; IB, Iberian; SI, Sicilian and LR, Landrace. Each color represents a different cluster. Each column represents a different animal. Within Asia, the order of animals is Licha Black, Fengjing, Meishan, Minzhu and Vietnamese potbelly. In Duroc, the first four animals are from Spain, and the latter two from UK and USA. A full color version of this figure is available at the Heredity Journal online.

Bayesian demographic inference

We first considered a demographic framework as the simplest approach to explain the data for this region. To infer demographic parameters for this region, we considered all 13 fragments as independent (not linked) because we did not observe significant linkage disequilibrium among these fragments (using LIAN software (Haubold and Hudson, 2000), P>0.05), which also agreed with the estimated genetic distance among them (see Materials and methods). The prior bounds used were flat, either in the normal or log scale (Table 3). The statistics Cst, based on the composite probability of each model using the closest 1000 iterations to the observed data, were Cst_IM=46.97 and Cst_IMM=24.71 for each of the competing models isolation and isolation with migration, respectively. The contrast between evolutionary models was performed with the statistic CL=Cst_IM−Cst_IMM=22.26 (P=0.002). Therefore, the alternative migration model significantly better explains the observed data than the isolation only model. This is in agreement with previous molecular data and historical records (Giuffra et al., 2000), and evidences that a relevant genetic flux between Asia and Europe can be detected not only with mtDNA but at the autosomal level as well.

Table 3. Main parameters for the isolation and migration model, together with posterior distribution statistics.

Parameter	Symbola	Prior boundsb	Posterior mean	Posterior median	Posterior s.d.	Posterior 95% HPD
Nucleotide diversity (Asia)	q=4Nμ	0.000001–0.01	7.8 × 10−4	7.2 × 10−4	3.7 × 10−4	2.4 × 10−4–1.4 × 10−3
Effective size (Europe), relative to Asia	NEUR	0.001–10	0.006	0.002	0.49	0.001–0.111
Migration rate (Asia → Europe)	MA → E =4 Nm	0.0001–1000	434.5	407.4	275	47.1–911.3
Ancestral effective size, relative to Asia	NANC	0.001–100	10.2	5.2	13.9	0.03–34.9
Time to Asia–Europe split in N generation units	TANC	0.03–1.00	0.35	0.28	0.25	0.05–0.89
Time to outgroup divergence in N generation units	TOUT	1+T ANC –50+T ANC	16.5	14.2	9.8	5.33–38.9

Abbreviation: HPD, highest posterior density.

^aN is Asiatic effective size.

^bPrior bounds were flat between specified bounds. Prior bounds for effective sizes N_EUR and N_ANC were on the log scale.

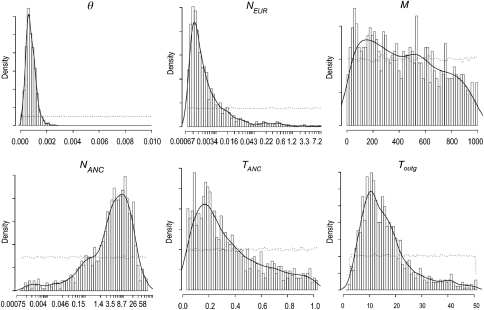
The posterior distributions for main parameter are shown in Figure 4. Except for nucleotide diversity (θ), the distributions were far from normal, with heavier tails than in a normal distribution. Therefore, we show the median in addition to the mean of posterior distributions in Table 3 because the former is more informative in the absence of normality. There are several noteworthy results, some particularly noticeable. First, the analysis supports a bottleneck process, specially for European populations relative to a putative common ancestral population, resulting in a reduction in the order of 10⁻⁴ (N_ANC × N_EUR) relative to the ancestral population. Second, a strong European bottleneck is accompanied by large amounts of genetic flow from Asia into Europe (M∼410, in relation to N_EUR, it is approximately 0.8, see Table 3). Although this parameter is inferred with a large error, the 95% posterior density suggests in any case that migration was very important.

Figure 4.

Posterior distributions for main parameters in the isolation and migration model. The discontinuous line represents the previous distribution. The continuous line represents the estimated density for the posterior distribution.

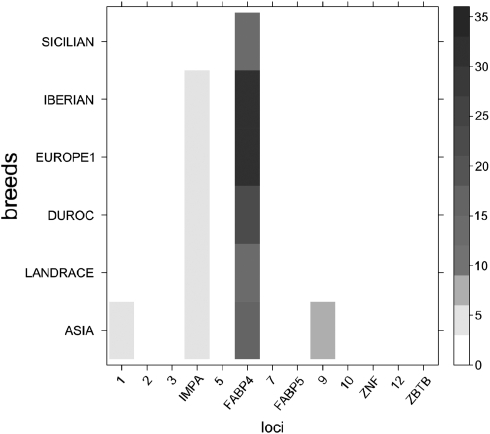
Further, we explored whether any of the 13 loci departed significantly from predictions under the isolation and migration model. To do that, we computed the P-values of several observed statistics for the ASIA and EUR1 populations under simulations with the migration scenario. There were no overall departures in any population, except for a few exceptions (Fay and Wu's H normalized in fragment 1, P=0.018; Tajima's D in fragment 5, P=0.032 and θ in fragment 6, FABP4, P=0.012). These values are not significant, nonetheless, when a multiple test correction is applied. This result suggests that most variability in this region can be explained by demographic processes alone, without need to resort to selection. We also performed the HKA test using the isolation and migration model as the null model not only in EUR1-ASIA but also in the other included breeds (that is, IB, SI, DU and LR). In agreement with other neutrality tests, the HKA test under the migration model was not significant. Nevertheless, the locus FABP4 showed consistently high values of the χ²-statistics for all breeds (Figure 5) as a result of an excess of polymorphism. Locus IMPA also showed higher values in the partial χ²-test for all breeds except Sicilian, suggesting again some departure from the migration model.

Figure 5.

Values of the HKA tests (partial χ²-values of the HKA test for each locus in a breed) for ASIA, EUR1, Landrace, Duroc, Iberian and Sicilian breeds. Each square represents the value of (S−E(S))²/var(S)+(K−E(K))²/var(K), where S is the number of segregating sites for the analyzed locus and breed and K the divergence for the analyzed locus between the breed and the outgroup (babirusa). The scale for the HKA statistics is in gray, as represented by the bar on the right of the figure. Values calculated using the isolation and migration model as a null model. Means and variances have been obtained from empirical distributions.

Discussion

We have analyzed the nucleotide diversity in a region near the first QTL described in porcine (FAT1), which comprised two candidate genes, FABP4 and FABP5. To detect a putative selection footprint in this region, we resequenced 13 noncoding fragments spanning about 2 Mb. In the presence of a strong selective sweep, we would expect a spatial pattern of nucleotide diversity (drop of nucleotide variation and a distorted distribution in the frequency spectrum of segregating sites) along the fragments studied. We have not observed any spatial patterns across all these fragments, the autocorrelation coefficient for θ between successive fragments was in fact negative in most breeds, ranging from 0.10 (Iberian) to −0.31 (Duroc). No clear selection signal using classical selection tests like Tajima's D or Fay and Wu's H was found either, suggesting that there was not a strong selective sweep in the region studied or that we were not able to detect it. Reasons for missing a true selective sweep include an old selective sweep smoothed out by recombination, or a recombination hotspot. A strategy to improve detection of selective sweeps in this case is to detect outlier patterns against a demographic model for the region, as discussed below.

Nevertheless, some unusual results are worth noticing like the high level of variation observed at the FABP4 locus, which contrasts notably with the remaining studied fragments in the region (Figure 5). This elevated level of polymorphism confirms our previous results (Ojeda et al., 2008a, 2006). This is remarkable especially in the Iberian pig, where the nucleotide diversity for FABP4 was the largest across all fragments and breeds, and showed a significant positive Tajima's D (Table 2). In contrast, the Landrace—a breed strongly selected for leanness—had a much lower variability at this gene. Given that FABP4 was significantly associated with the FAT1 QTL in an Iberian × Landrace intercross (Mercade et al., 2006), it is noticeable that the fragment with largest F_st between Iberian and Landrace was fragment 6, that is within the FABP4 gene (F_st=0.49, P<0.004). Gene IMPA1 also showed an apparent discrepancy between expected and observed polymorphism that was consistent across all Asian and European populations, except Sicilian, suggesting a relaxed selection intensity in the Sus lineage about the outgroup.

The data presented here represent an important step toward refining the demographic history of the FAT1 region. The evolutionary models posited here, the isolation model and the isolation plus migration model, represent probably the simplest possible demographic scenarios (Figure 2). As new resequencing data will accrue dramatically in the coming years, we shall be able to fit more sophisticated models; the amount of data here precludes increasing too much the complexity of the models. In fact, we also tried a model with a European expansion but did not improve upon the models studied. Yet our analyses do provide very valuable information. Perhaps, the most remarkable finding was an Asia → Europe migration rate that seems to be far higher than suspected, a migration that compensates the strong bottleneck that European populations have undergone (Table 3; Figure 4).

The Sus clade originated in Asia; consistent with that, our data clearly indicate that Asian populations harbor much larger variability than European breeds. Overall, θ in Asia was 30% larger than in Europe (2.1 × 10⁻³ vs 1.6 × 10⁻³; Table 1). This fact also results in an inferred much larger bottleneck in Europe than in Asia (Table 3; Figure 4). The ABC inference suggests than European effective size is in the order of at some orders of magnitude smaller than in Asia. Although the associated variances of the posterior distributions are large, there is little doubt of a true dramatic difference in effective sizes. This is agreement with numerous mtDNA studies, which have consistently shown signals of a bottleneck followed by a population expansion in European pigs and wild boar; this signal is absent in Asian populations (Fang and Andersson, 2006). Besides, other studies have shown that Chinese breeds harbor less extensive linkage disequilibrium than their European counterparts (Amaral et al., 2008; Du et al., 2007; Megens et al., 2008) and is also in agreement with our own studies in FABP5 (Ojeda et al., 2008a) and in SERPINA6 (Esteve et al., unpublished data). It is relevant to note that within breed variability was comparable across all European breeds studied (∼1 × 10⁻³; Table 1), irrespective of whether they were local or internationally distributed breeds. A comparison with Asian's variability (approximate 2 × 10⁻³), where only one animal per breed was analyzed, prompts us to hypothesize that a large part of genetic diversity can be between rather than within breeds. Although more data are needed to corroborate this, it would be supported at least by microsatellite data in Megens et al. (2008).

Importantly, the ABC approach can also be used to get educated guesses about additional parameters of interest. For instance, assuming an approximate speciation time of 19 Myr ago between S. scrofa and B. babiroussa (Thompsen et al., 1996) and a generation interval of 2 years, Asian effective population size can therefore be estimated from the posterior distribution of T_OUT (Table 3; Figure 2) because T_OUT is indicated in 4N (Asian N) generations. Then, N=19 × 10⁶ years × (1 gen/2 years)/(4 × 14.13)=1.7 × 10⁵, where T_OUT is replaced by the median taken from Table 3. This is a rather large effective size; for comparison, the estimated effective size in humans is approximately 30 000, or even smaller according some recent estimates (Tenesa et al., 2007). This large effective size is, nevertheless, coherent with other results, for example, divergence, as measured in 4N generations is 0.28 (Table 3) and then T_ANC=0.28 × 4 × 1.7 × 10⁵=1.9 × 10⁵ generations or ∼400 000 years, an estimate that is within the range estimated from mtDNA for the divergence between Asian and European pigs that ranges from 58 000 (Kim et al., 2002) to 900 000 years ago (Fang and Andersson, 2006; (Giuffra et al., 2000). Finally, the scaled migration rate, when measured in European effective population size units, is M_EUR=407 × N_EUR∼0.8 (median=0.64), a non-negligible value. Now, if we consider that European effective size is in the order of 2 × 10⁻³ N Asian effective size units, this means that N_EUR is in the order of hundreds, that is, very small and incompatible with observed nucleotide variability in these breeds. Therefore, current nucleotide diversity in Europe has been heavily influenced by migration from Asia (Ramirez et al., 2009). It remains to be studied how general are these results when genome-wide data are available, but they represent a reasonable starting point.

Our study results also bear interesting data on population structuring. As expected, pigs as the rest of livestock populations are structured, a structure that is not in complete concordance with breed (Figure 3). In a previous work, we analyzed the haplotype structure around a causative mutation of IGF2 in a worldwide pig panel, and proposed a model whereby breeds were mosaics of the same haplotypes; breed differences were caused primarily by differences in haplotype frequencies rather than in specific haplotypes unique to a particular breed (Ojeda et al., 2008b). The results reported here are in agreement with this model and the demographic inference suggests that the widespread haplotype sharing between breeds may be caused by extensive migration between populations and incomplete lineage sorting. However, this hypothesis needs to be confirmed with more ample data both from more breeds and individuals and from additional genome regions. Also compatible with strong migration is the fact that nucleotide variabilities were relatively similar across breeds.

To conclude, we have consistently reported higher than expected polymorphism at the FABP4 locus but no clear signal of a nearby selective sweep. Besides, our study reveals in the region studied: (1) a dramatic bottleneck in Europe regarding the ancestral population and (2) a significant and strongly influential migration rate from Asia into Europe; a migration that results in elevated polymorphism levels despite very low initial effective population sizes. Given the small fragment analyzed here, it remains to be studied how these conclusions apply to the rest of the genome; in either case they are relevant to understand the population dynamics of domestic species.

Appendix

ABC algorithm

The algorithm used was as follows:

(1) Draw random parameters following the previous distributions (Table 3).

(2) Run 10⁵ coalescent simulations (using mlcoalsim 1.92, Ramos-Onsins and Mitchell-Olds, 2007, available from authors) for each locus using the given prior (same conditions for all loci in each iteration).

(3) Calculate the correlation between the statistics and parameters as in Hamilton et al. (2005), with modifications:

3.1 Calculate the correlation coefficient matrix C={c_ij} between all parameters and statistics using all iterations.

3.2 The weight value between parameter i and statistic j is calculated from w_ij=−ln(1−c_ij²), scaling to sum one, as suggested in Hamilton et al. (2005), except that we used all iterations.

3.3 Compute the average of each statistic across parameters w̄._j and scale to sum one.

3.4 Use this weighted calculation to calculate the Euclidean distance between each value of the empirical distribution and the observed value.

(4) Choose the best 1000 iterations (tolerance 1/100) and calculate the local linear regression, as in Beaumont et al. (2002).

(5) Use the selected iterations from the empirical distribution to calculate a composite probability, which defines the probability for each evolutionary model given the observed data. The composite probability Cst was calculated as the sum of −2 × ln(P_i) for all 15 used statistics, being P_i the P-value considering both tails and calculated as P_i=(0.5−abs(0.5−P_{i_inf}))+(0.5−abs(0.5−P_{i_sup}))+P_{i_eq}, were P_{i_inf} =P(observed < simulated), were P_{i_sup} =P(observed > simulated) and were P_{i_eq} =P(observed=simulated) (Ramos et al., 2008).

(6) The composite probability was used to compare both models (IM and IMM). We calculated the statistic CL=Cst_H0−Cst_H1 and contrasted the result using Monte Carlo simulations with the empirical distribution of CL, calculated using 1000 iterations of the null model.

The authors declare no conflict of interest.