Density-regulated population dynamics and conditional dispersal alter the fate of mutations occurring at the front of an expanding population

Abstract

There is an increasing recognition that the interplay between ecological and evolutionary processes shapes the genetic footprint of populations during and after range expansions. However, more complex ecological processes regularly considered within spatial ecology remain unexplored in models describing the population genetics of range expansion. In this study we integrate flexible descriptions of population growth and competition as well as conditional dispersal into a model that simulates the fate of mutations occurring at the wave front of an expanding population. Our results show that the survival and distribution of a mutation is not only affected by its bias (that is, whether it is deleterious, neutral or beneficial) but also by the mode of local density regulation and conditional dispersal of the simulated populations. It is in particular the chance of a mutation to establish at the front of advance and ‘surf' to high frequencies that critically depends on the investigated ecological processes. This is because of the influence of these processes on demographic stochasticity in the system and the differential responses of deleterious, neutral and beneficial mutations to this stochasticity. Generally, deleterious mutations rely more on chance and thus profit the most from ecological processes that enhance demographic stochasticity during the period of establishment. Our study emphasizes the importance of incorporating more ecological realism into evolutionary models to better understand the consequences of shifting geographic ranges for the genetic structure of populations and to find efficient adaptation strategies to mitigate these effects.

Introduction

Recently, considerable progress has been made in integrating evolutionary and ecological aspects into the study of geographically structured populations (Hänfling and Kollmann, 2002; Excoffier and Ray, 2008; Filin et al., 2008). The results of this work stress the importance of considering the co-action of key ecological processes such as dispersal and population growth, and evolutionary dynamics such as mutation and genetic drift for understanding observed genetic patterns. To date, most research in this field is based on stationary models with population dynamics at equilibrium (Iizuka, 2001; Kaitala et al., 2006; Ranta et al., 2008). Although this approach holds for populations with fixed geographic distributions, it is clearly not applicable for describing dynamics during range shift or range expansion (for example, during invasion events, Lee, 2002; Sharma et al., 2005, or during periods of shifting climate, Parmesan and Yohe, 2003).

In expanding populations, spatial population dynamics can significantly affect evolutionary trajectories (Hänfling and Kollmann, 2002; Lambrinos, 2004; Hastings et al., 2005; Travis et al., 2007; Thuiller et al., 2008; McInerny et al., 2009) and thus the spread of beneficial, neutral and deleterious mutations (Travis et al., 2007; Excoffier and Ray, 2008). Resulting spatial patterns, such as geographic segregation of distinct phylogenetic lineages and high frequencies of non-beneficial mutations, could easily be misinterpreted as being the result of well-known processes such as allopatry or convergence in distinct refuge areas (Excoffier and Ray, 2008). However, recent work has shown that spatial patterns in neutral mutations can occur even in homogeneous landscapes, without barriers and selection pressure, and that this is because of a phenomenon called mutation surfing (first described by Eswaran, 2002, and named by Edmonds et al., 2004; Klopfstein et al., 2006). Mutation surfing is the propagation of low-frequency alleles on the wave front of a population's range expansion (Edmonds et al., 2004; Klopfstein et al., 2006). Two factors facilitate this process: first, small population sizes at the front of the expansion result in reduced competition pressure, and second, because dispersal is limited, the progeny of colonizers of the last range expansion step mainly contribute to the next step, resulting in the acceleration of genetic drift. This mutation surfing effect has been demonstrated in microbial microcosms (Hallatschek et al., 2007). It has also been proposed that the evolution of modern humans may have occurred because of the surfing of alleles during population expansion out of Africa (Eswaran, 2002; Eswaran et al., 2005; Hofer et al., 2009). Travis and co-workers (2007) extended the theoretical work on neutral mutations to non-neutral mutations and found that even substantially deleterious mutations can reach high densities during range expansions when surfing at the wave of advance. Besides the bias of a mutation (that is, whether it is neutral, beneficial or deleterious), its origin is also of considerable importance for its likelihood of spreading; mutations arising near the expanding edge of an invasion have a higher chance of surfing (Travis et al., 2007) because of the above-mentioned reasons. On the other hand, the probability of a mutation occurring is higher just behind the front than on the front itself because of a larger population density in that area of the range (Hallatschek and Nelson, 2008; Burton and Travis, 2008a). Hallatschek and Nelson (2008) show that this tradeoff leads to a bell-like distribution of successful lineages inside the wave front. Furthermore, the type of habitat edge influences the surfing process: in models with reflective habitat boundaries, surfing is much more probable for mutations arising at a habitat edge, whereas with absorbing boundaries it is more likely when the mutation occurs well away from the edge (Burton and Travis, 2008b).

These initial steps towards integrating evolutionary and ecological processes in models of range expansion dynamics have led to new insights into the relations of colonization pathways and genetic footprints. However, these models have typically assumed extremely simplified ecological rules, neglecting processes that are regularly incorporated within theoretical spatial ecology and that may have significant impacts on the resulting genetic structure. Two of these features are considered in the following.

Local population dynamics

Models of population dynamics in spatially structured populations have demonstrated that the form of density regulation in population growth has strong effects on species abundances, spatial synchrony of ecological dynamics and ultimately survival (Allen et al., 1993; Murrell et al., 2002; Münkemüller and Johst, 2007). In many models used to study the population genetics of range expansion, population sizes are assumed to remain constant from one generation to the next. However, in reality, most species will have more complex dynamics—often driven by the form of density regulation (Godfray et al., 1990; Hastings et al., 1993). In ecological models exploring range expansion, it has been demonstrated that species with over-compensating density regulation potentially invade much faster and are able to track a rapidly shifting climate (Best et al., 2007; Filin et al., 2008). Allee effects may considerably decrease the rate of spread (Lewis and Kareiva, 1993; Kot et al., 1996; Davis et al., 2004), thereby increasing the effective population size of the wave and decreasing genetic drift (Hallatschek and Nelson, 2008). Considering the type of density regulation is also important when investigating the development of habitat specialization during invasion and range expansion (Filin et al., 2008).

Dispersal

It has been shown that dispersal characteristics such as dispersal rates and distances can strongly influence population dynamics in static landscapes (Ylikarjula et al., 2000; Johst et al., 2002; Murrell et al., 2002; Münkemüller and Johst, 2006). This is especially true for conditional dispersal for which emigration or immigration rates depend on the conditions of origin or final sites, for example, they depend on population density or patch area (Johst and Brandl, 1997; Ruxton and Rohani, 1998; Travis and French, 2000; Poethke and Hovestadt, 2002; Münkemüller and Johst, 2008; Smith et al., 2008). Dispersal characteristics can also have considerable effects on spatial genetic patterns. For example, for plant populations that have undergone recent range expansion, long-distance dispersal events may be among the most important factors inducing spatial clustering of genotypes, which may persist for hundreds of generations (Ibrahim et al., 1996; LeCorre et al., 1997; Lewis and Pacala, 2000; Białozyt et al., 2006). However, although the literature is replete with studies showing that the strength of unconditional dispersal matters for both the spatial population dynamics (Kot et al., 1996; Hastings et al., 2005) and genetics (Ibrahim et al., 1996; Austerlitz and Garnier-Gere, 2003; Białozyt et al., 2006; Burton and Travis, 2008b) of range expansion, relatively few studies consider the effects of conditional dispersal. There has been some progress in understanding the role of density dependence of dispersal on the rate of spread of populations (Best et al., 2007; Travis et al., 2009). However, to the best of our knowledge, there has been a complete lack of work considering the role of conditional dispersal on the genetic dynamics of range expansion.

So far, surfing mutations have been analysed by simple logistic growth models with condition-independent nearest-neighbour dispersal. Competition between mutants and wild types has been described by binomial (for neutral mutations, see, for example, Klopfstein et al., 2006) or Wallenius' noncentral hypergeometric distributions (for beneficial or deleterious mutations, see, for example, Travis et al., 2007; Burton and Travis, 2008a, 2008b). More complex descriptions of density regulation in the local population growth and dispersal processes remain unexplored. The question is how these elements, well established in ecological modelling, influence range expansion dynamics and the resulting genetic spatial patterns.

In this study we extend an existing model of range expansion that integrates evolutionary and ecological approaches (Travis et al., 2007) by incorporating more realism in the ecological processes. Population dynamics follow a well-established growth and competition model that includes both more complex forms of local population dynamics and competition between different species or, in our case, mutants. Dispersal is described by flexible functions allowing for a range of possible dispersal strategies: density-independent emigration and immigration, as well as linear, convex or concave density-dependent emigration and/or immigration. Using this model, we ask the following questions: (1) Do local demographic processes (growth rate, type of density regulation, carrying capacity, environmental disturbances) affect survival and surfing of neutral, beneficial and deleterious mutations? (2) Does the form and strength of dispersal (emigration rates, density dependence of emigration and/or immigration) influence survival and surfing of the three different mutation types?

Materials and methods

The model

We build a direct extension of the models used in earlier studies on surfing mutations (for example, for neutral mutations by Edmonds et al., 2004 and Klopfstein et al., 2006, and for beneficial and deleterious mutations by Travis et al., 2007 and Burton and Travis, 2008b). Our model simulates population dynamics of haploid individuals expanding their range from the far left side of a rectangular two-dimensional lattice with 25 by 600 patches. Initially, the lattice is empty. To initiate the range expansion, four identical individuals are introduced in the central cell at the left border of the lattice (position <0,12>). In each generation, individuals reproduce, disperse and face density-independent mortality because of disturbances. During each simulation, the population spreads towards the right side of the grid. In generation T after colonization of patch <10,12>, a single individual in this patch is selected at random to carry a new allele, the mutation. The value of T determines the position of the first mutation relative to the range front and is varied across simulation runs. Individuals carrying the mutant allele then experience the same series of events as wild-type individuals but may have fitness advantages (beneficial mutation) or disadvantages (deleterious mutations), manifesting as increased and decreased competitive ability, respectively. Simulations run for 500 generations unless all mutants die before this point in time.

Growth processes

In earlier models of range expansion, reproduction in a patch was logistically regulated by the carrying capacity K and the growth rate R. Competition between mutants and wild types and ultimately selection and genetic drift were modelled using a binomial distribution for neutral mutations (Edmonds et al., 2004; Klopfstein et al., 2006) or a Wallenius' noncentral hypergeometric distribution (Wallenius, 1963) for beneficial or deleterious mutations (Travis et al., 2007; Burton and Travis, 2008b). In this study, we extend these previous models by describing reproduction and competition in a more flexible way with an extended version of the well-established Maynard Smith and Slatkin (1973) reproduction and competition model (see also Hassell and Comins, 1976). This model allows for competitive differences between species and is able to produce not only logistic but also more complex population growth, and thus it is able to capture a variety of competitive interactions prevailing in nature.

The population sizes of the wild type and the mutant in each patch are given by N_wild and N_mut. Both have the same maximum growth rate, R, and local carrying capacity K. The fitness difference is described by the competition coefficients a and 1/a, respectively. A value of a=1.0 means that the competitive abilities of wild type and mutant are equal and the model simulates the dynamics of a neutral mutation (which can also be simulated using a binomial distribution or a bias of 1.0 in the hypergeometric distribution, cf. Klopfstein et al., 2006 and Travis et al., 2007). A value of a>1.0 means that the mutant's competitive ability is higher and the model simulates the dynamics of beneficial mutations, whereas at a<1.0 the model simulates the dynamics of deleterious mutations.

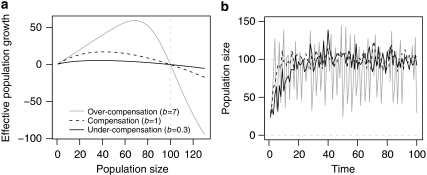
The parameter b describes the type of density regulation ranging from under-compensatory (b<1) via compensatory (b=1) to over-compensatory (b>1) regulation (cf. Figure 1). Over-compensatory regulation (or scramble competition) occurs where resources are spread equally across a number of individuals. At low population sizes, this results in high growth rates, but is soon followed by population crashes as the population grows and resources become too thinly spread across the population. Population densities exhibit cyclic or chaotic dynamics over time that can significantly increase local extinction risk (see, for example, Allen et al., 1993; Costantino et al., 1997; Ripa and Lundberg, 2000). Compensatory regulation (or contest competition) is exhibited where resources are allocated in a one-off contest between competing individuals, and the overuse of resources is avoided. Population densities over time develop towards equilibrium dynamics and fluctuations are only due to stochastic events (Münkemüller and Johst, 2006). Under-compensatory regulation occurs where dynamics are delayed and the adjustment of population sizes to carrying capacities is slow (Münkemüller and Johst, 2007). For instance, storage capacities or complex mating behaviour may lead to a delayed response.

Figure 1.

Population growth dynamics for different types of density regulation. (a) The effective population growth for different population sizes under deterministic conditions (as a result of the Maynard Smith and Slatkin formula) is shown. (b) The development of population sizes over time including demographic stochasticity (adding a normally distributed random term with μ=0 and σ=20) is shown. Grey dashed lines mark the extinction threshold (population sizes <=0) and the carrying capacity (carrying capacity, K=100; growth rate, R=2).

Comparable to earlier models, offspring in our model inherit their genotype from their parent. In contrast to earlier models (see, for example, Travis et al., 2007), competition influences reproduction already when the sum of N_wild and N_mut is smaller than the carrying capacity. This influence depends on the growth rate and the type of density regulation (Figure 1). To introduce stochasticity, the number of offspring is drawn at random from a Poisson distribution with mean expected number of offspring as given by the reproduction model (N_wild or N_mut).

Dispersal

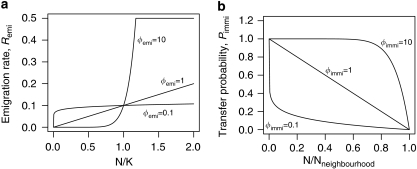
We follow the four-neighbourhood description of dispersal used in previous models of range expansion, that is, dispersal can occur with individuals moving from their natal patch to one of the nearest four neighbouring patches. However, we allow for both unconditional and conditional dispersal strategies. Dispersal may depend on the density in the natal patch (density-dependent emigration, cf. Figure 2a) and/or on the density in the four neighbouring patches (density-dependent immigration, cf. Figure 2b). Emigration rate, R_emi, is calculated by 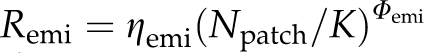but never exceeds 0.5. N_patch is the number of all individuals in a patch. Emigration is density independent when Φ_emi=0 resulting in R_emi=η_emi, and linearly density dependent when Φ_emi=1. The transfer probability between the natal patch, i, and a neighbouring patch, j, is calculated by 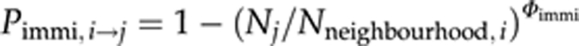, with Φ_immi between 0 and 10 in our simulations. Final values are standardized by N_{neighbourhood,i}, the number of all individuals in the neighbourhood of the natal patch, such that they sum to one for all neighbours. Immigration is density independent when Φ_immi=0 and linear density dependent when Φ_immi=1. To account for stochasticity, the number of emigrants is drawn from a binomial distribution with parameters N_patch and R_emi and the number of immigrants from a natal patch to one of the neighbouring patches is drawn from a multinomial distribution with parameters number of emigrants and P_{immi,i → j}. We apply absorbing boundary conditions such that individuals dispersing off the edge of the lattice are assumed to die.

Figure 2.

Conditional dispersal strategies. (a) For density-dependent emigration, the emigration rate depends on the relation of population size and carrying capacity. This dependency can be linear (Φ_emi=1), concave (Φ_emi<1) or convex (Φ_emi>1). Emigration rates never exceed 0.5. (b) For density-dependent immigration, the transfer probability to any one possible destination patch depends upon its population density relative to the three other potential patch destinations (four-neighbourhood dispersal). This dependency can be linear (Φ_immi=1), concave (Φ_immi>1) or convex (Φ_immi<1).

Disturbances

Environmental disturbances may occur after reproduction and dispersal. Disturbance frequency per patch, F_dist, is spatially and temporally uncorrelated. Disturbance events follow Bernoulli trials with probability F_dist and cause mortality of half of the local population.

Simulation experiments

We started our analysis from a baseline model with reference parameter values and kept those parameter values for all simulation runs if not stated otherwise (cf. Table 1).

Table 1. Baseline model with reference parameters.

Parameters	Values
Disturbance frequency, Fdist	0
Carrying capacity, K	10
Growth rate, R	1.8
Density-dependent immigration, Φimmi	0
Density-dependent emigration, Φemi	0
Emigration factor, ηemi	0.1
Density regulation type, b	1
Competition coefficient, a	1
Time since colonization, T	0

Before approaching our research questions, we repeated simulations conducted in Travis et al. (2007) and confirmed that the results for the Wallenius' noncentral hypergeometric distribution and the Maynard Smith and Slatkin growth model are qualitatively identical under the assumption of compensatory density regulation (b=1, results not shown).

In previous models exploring mutation surfing, it has been shown that some mutants will survive even though they have not surfed, whereas others may survive because they have surfed (Travis et al., 2007). To separate these possibilities, in the analyses of growth processes and dispersal strategies, we compared survival probabilities after 500 generations of mutations without surfing (all simulations with surviving mutations that did not occur at the rightmost front of the grid, for simplicity called ‘non-surfing survival' in the following) and with surfing at the rightmost front (all simulations with surviving mutations that did occur at the rightmost front of the grid, called ‘surfing survival' in the following) for strongly deleterious, strongly beneficial and neutral mutants (a=0.667, a=1.5 and a=1). We varied the type of density regulation (b=[0.5; 6]), the growth rate (R=[1.3; 10]) and the local carrying capacity (K=[5; 30]). When analysing density-dependent dispersal, we varied the shape of density dependence from concave via linear to convex (Φ_emi=[0.1; 10]). We repeated each simulation scenario 1000 times.

To aid our interpretation of the results, we trialled the use of boosted regression trees to identify the importance of the different model parameters and the ecological processes they influence on variation in both the non-surfing survival and the surfing survival of mutations. Note that in the analyses of parameter importance, the resulting importance measures can depend on the explored parameter ranges. The numerical comparison of importance is valid only for the analysed system with the analysed ranges. Further increasing the range and therefore analysing more extreme values of a parameter can result in more extreme responses and thus higher relative importance. On the contrary, in a system where the range of parameter values is reduced, the importance of a parameter tends to decrease. It is therefore very important to carefully choose and justify explored parameter ranges (see Table 2 for parameter ranges, see Appendix for details of this methodology).

Table 2. Parameters varied in the simulation scenarios presented in the Results section (Rs) and in the sensitivity analysis presented in the Appendix (A).

Parameters	Values (Rs)	Values (A)
Disturbance frequency, Fdist	0	0, 0.1, 0.2, 0.5
Carrying capacity, K	5, 10, 30, 90	5, 10, 30, 90
Growth rate, R	[1.3; 10]	1.8
Density-dependent immigration, Φimmi	0	0, 1
Density-dependent emigration, Φemi	[0.1; 10]	0, 1
Emigration factor, ηemi	0.1	0.05, 0.1, 0.2, 0.4
Density regulation type, b	0.5, 1, 2, 6	0.5, 1, 2, 6
Competition coefficient, a	0.667, 1, 1.5	0.667, 1, 1.5
Time since colonization, T	0, 1, 2, 3, 4, 5	0, 1, 2, 3, 4, 5

Results

Simulation experiments

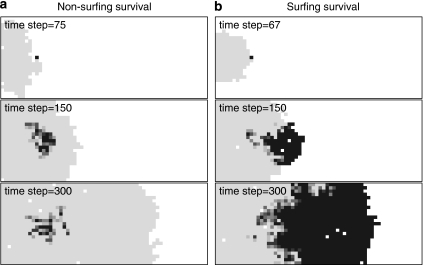
There are two potential ways for a mutation to persist throughout the simulation: either relatively high densities close to the location of introduction enable the mutation to locally outcompete the wild type (Figure 3a), or it surfs at the wave front of advance and increases its density by populating empty patches (Figure 3b). Generally, surviving mutants that have not surfed obtain relatively low abundances and small spatial distributions, whereas survival through surfing leads to high abundances and large spatial distributions.

Figure 3.

Fate of a neutral mutation during range expansion: (a) non-surfing survival and (b) surfing survival. The grey scale corresponds to the relative abundance of the mutant, black indicates pure mutant populations and the lightest grey scale indicates pure wild-type populations. White patches are not occupied. Simulations are based on the reference parameters (Table 1).

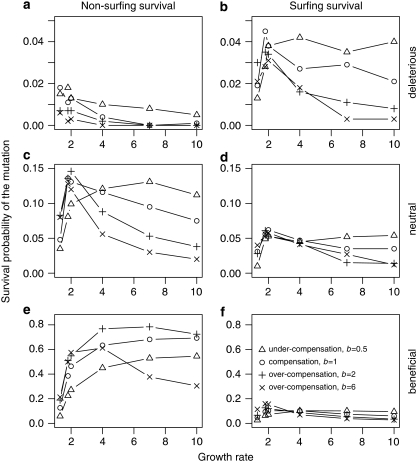
The growth rate and the type of density regulation strongly influence the probability of non-surfing survival as well as surfing survival, but affect deleterious, neutral and beneficial mutations differently (Figure 4). For deleterious mutations, the probability of surfing survival is greatest at an intermediate growth rate (about R=2.0). Growth rates above and below this optimum result in lower probabilities of surfing survival, and the decline in surfing survival probability as R increases are greatest with stronger over-compensatory density regulation. This relationship is similar for non-surfing survival, but survival without surfing is almost impossible for deleterious mutations (Figure 4a).

Figure 4.

Non-surfing survival (panels a, c, e) and surfing survival (panels b, d, f) of the mutant depend on population growth dynamics. We varied growth rate (R=[1.3; 10]) and the type of density regulation (from under-compensation (b>1) via compensation (b=1) to over-compensation (b>1)) and conducted the analyses independent for deleterious (a=0.667, panels a, b), neutral (a=1, panels c, d) and beneficial mutations (a=1.5, panels e, f).

Non-surfing survival and surfing survival probabilities are much higher for neutral mutations, and survival frequently occurs without surfing (Figures 4c and d, consider the different range of the y axis). The general trend of increasing non-surfing survival and surfing survival of neutral mutations up to moderate growth rates and then decreasing non-surfing survival and surfing survival for further increasing growth rates is similar to deleterious mutations. Again, surfing survival and non-surfing survival probabilities for under-compensators are much higher than for over-compensators at higher growth rates, and for under-compensators a decrease in non-surfing survival occurs only at very high growth rates (R>7).

For beneficial mutations, non-surfing survival probabilities are very high (Figure 4e). Surfing survival probabilities are higher than for neutral mutations but only have a minor role when compared with non-surfing survival (Figure 4f). For beneficial mutations there is almost no decrease in non-surfing survival and surfing survival for increasing growth rates except for very strong over-compensators. Interestingly, beneficial mutations survive much more frequently without surfing when the competition is either compensatory or over-compensatory. For neutral mutations, we only observe this effect at very small growth rates. Surfing survival of over-compensators is still reduced for high growth rates.

In sum, the growth rate and the type of density regulation have strong collinear effects on the mutation's survival. Under-compensation and low growth rates result in low effective increase of population sizes from low densities, which is especially dangerous for the rare mutant at the time of origin. Over-compensation and high growth rates result in high effective increases in population sizes and complex dynamics, which leads to a quick filling of low-density patches with the most abundant competitor, that is, the wild type. The rare mutant has highest chances when it can reproduce efficiently (moderate joint effects of growth rate and type of density regulation) but when it also has some time to fill its home patches before the more abundant wild type overflows them.

Increasing carrying capacities tend to increase non-surfing survival and surfing survival probabilities, regardless of whether mutations are deleterious, neutral or beneficial (Table 3). However, if growth rates are high (R=4), this relation reverses for surfing survival. Surfing survival of species with high growth rates is more probable if carrying capacities are rather small (K=5 vs 30). The latter result is because of the fact that high growth rates in combination with high carrying capacities result in quick filling of newly occupied habitat patches and ultimately in high numbers of immigrants for patches at the invasive front. Therefore, the chances to win new patches at the front of the more abundant wild type relative to the rare mutant are increased and surfing is less probable.

Table 3. Non-surfing survival and surfing survival of the mutant are influenced by carrying capacity (K) and growth rate (R).

	Non-surfing survival		Surfing survival
Growth rate	R=1.3	R=4	R=1.3	R=4
Deleterious	10 vs 15	9 vs 2	10 vs 29	32 vs 30
Neutral	8 vs 90	111 vs 133	6 vs 40	60 vs 41
Beneficial	21 vs 219	489 vs 791	12 vs 56	106 vs 58

Numbers in the table compare survival and surfing events for K=5 vs K=30 and for 1000 repetitions.

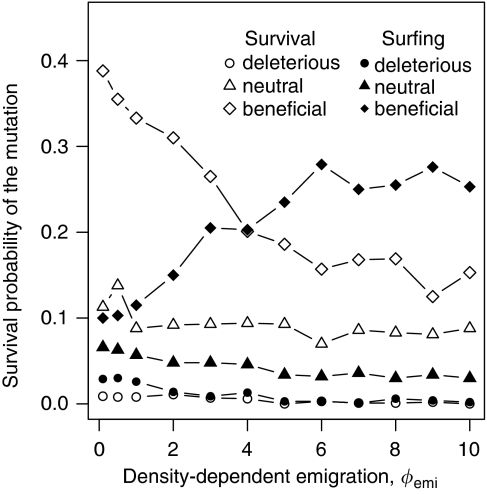
The non-surfing survival and surfing survival of mutations is influenced not only by growth processes but also dispersal mechanisms. Beneficial mutations in particular are strongly affected by density-dependent emigration (Figure 5). The more concave the density dependence is (high emigration rates only for patches with high densities), the higher the surfing survival probability. For non-surfing survival, model output shows a reverse pattern: more concave relations lead to a decrease in survival. The different shapes of density-dependent emigration do not have an important role in the fate of deleterious and neutral mutations (Figure 5), and the shape of density-dependent immigration (as we described it here) is not very influential for mutations at all (see Appendix Figure 7). With strong density-dependent emigration (concave density dependence), range expansion is slowed down considerably because individuals at the thinly occupied front disperse much less than individuals in the fully occupied centre of the distribution. The chances to reach the wave front are higher if the front advances less quickly. However, this is only true for the beneficial mutations as they are the better competitors and can outcompete the less strong wild type in already occupied patches on their way to the front.

Figure 5.

Non-surfing survival and surfing survival of the mutant depend on conditional dispersal strategies. We varied the dependence of the emigration rate on the density in the natal patch from concave (Φ_emi<1) via linear (Φ_emi=1) to convex (Φ_emi>1) and conducted the analyses independent for deleterious (a=0.667), neutral (a=1) and beneficial mutations (a=1.5).

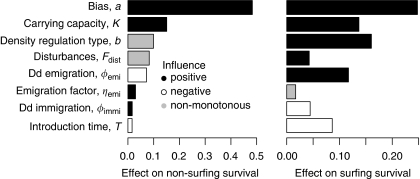
Figure 7.

Comparative analysis showing the importance of six variables on the variation in non-surfing survival and surfing survival of the mutant. Estimates of importance are the result of analyses using boosted regression trees. The colour coding refers to the response curves, that is, how changing values of the variable influence values of the response. Response curves are classified to be either monotonous positive, monotonous negative or non-monotonous. Dd, density dependent.

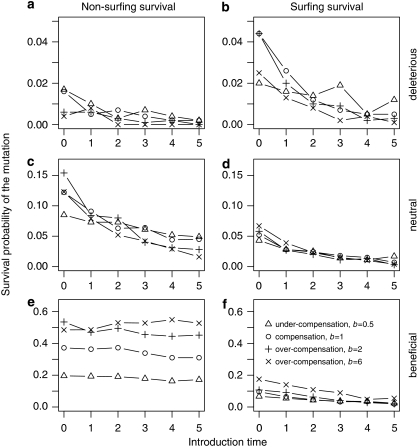
In almost all cases, a later introduction time of the mutation influences both non-surfing survival and surfing survival negatively. Especially, deleterious mutations have almost no chance to survive if introduced too far behind the wave front (Figure 6). For beneficial mutations, only surfing survival is negatively influenced by later introduction time, whereas non-surfing survival is not affected at all (Figures 6e and f). The type of density regulation does not show any interaction with introduction time. For deleterious and neutral mutations, there are no big differences between the different types of density regulation for later introduction times (Figure 6; for introduction time equal zero and interactions with higher growth rates, see Figure 4). However, non-surfing survival (also, to a lesser extent, surfing survival) of beneficial mutations increases with stronger over-compensation.

Figure 6.

Non-surfing survival (panels a, c, e) and surfing survival (panels b, d, f) of the mutant depend on introduction time. We varied introduction time (T=[0; 5]) and the type of density regulation (from under-compensation (b>1) via compensation (b=1) to over-compensation (b>1)) and conducted the analyses independent for deleterious (a=0.667, panels a, b), neutral (a=1, panels c, d) and beneficial mutations (a=1.5, panels e, f).

The general negative effect of later introduction on surfing is because of the fact that mutants are not able to reach the wave front when introduced too far behind it. The observation that, especially for neutral mutations, there also exists a negative effect on non-surfing survival can be explained by temporary surfing; that is, in some simulations, mutants are able to surf just for a certain time period before they are finally overtaken by the wild type. This period is sufficient to increase overall density enough to survive later on behind the wave front. As beneficial mutations are anyway good competitors, they do not profit from temporary surfing.

Discussion

Previous work describing the mutation surfing phenomena and its consequences for the spread of neutral, beneficial and deleterious mutations (Edmonds et al., 2004; Klopfstein et al., 2006; Travis et al., 2007) had used only very simple descriptions of demography. We extended these previous models by incorporating more realistic and flexible functions for both population growth and dispersal. Our results clearly demonstrate the importance of demographic processes in determining the fate of mutations during and after range expansions: The probabilities that a mutant arising towards the front of an expanding population will both survive and surf can be substantially modified by the nature of density dependence in both within- and between-patch dynamics. Additionally, our results emphasize that the roles of local density regulation and conditional dispersal strategies differ depending upon whether the mutant is deleterious, neutral or beneficial (Figures 4, 5, 6).

Demographic stochasticity is important for mutant survival

Changing the demographic parameters (for example, growth rate, type of density regulation or the density dependence of dispersal) in either pure wild-type or pure mutant populations would have identical effects on the ecological range expansion dynamics. However, survival and surfing of a mutant arising in a wild-type population can be considerably modified by the nature of both the within- and between-patch dynamics (Figures 4, 5, 6).

When the mutant arises, the wild type already occupies a number of patches and therefore has much higher population sizes and spatial distribution. Despite this disadvantage, the mutation may still survive, if it is lucky in the game of demographic stochasticity. Demographic stochasticity may lead to randomly low numbers of wild-type immigrants, or to randomly low (high) reproductive success of the wild type (mutant) in the patch of origin of the mutant. Additionally, the mutant may be even luckier and be the first to reach a high number of unoccupied patches at the wave front of expansion. This is more probable the shorter introduction time and therefore the closer to the wave front the origin of the mutation is (Travis et al., 2007). As competition is reduced at the wave front, the mutant can reproduce quickly, establish dominance via high numbers and finally surf at the front of advance. Having succeeded in establishing local dominance, lower competitive ability is balanced against high local abundance and the mutant can outpace the wild type even though it would be inferior in one-to-one encounters. Once the mutant is surfing on the wave front, it has a substantial probability of surviving even when behind the front it is rapidly displaced by a more competitive wild type. Beneficial mutations are far less reliant on luck, and subsequently on demographic stochasticity, to survive the period of low density. Both the probabilities of survival and surfing are much higher and, in particular, survival without surfing is much more frequent for beneficial mutations than for neutral or deleterious mutations (Travis et al., 2007). Changes in demographic parameters modify surfing and survival probabilities, even though they affect individuals of wild type and mutant equally, because they alter the strength and influence of demographic stochasticity. Because demographic stochasticity is more influential when abundances are low, it has a greater impact on the fate of the rare mutant than on the well established and abundant wild type.

The impact of population growth dynamics

The growth rate and the type of density regulation determine the effective growth rate (the observed increase or decrease) at low population densities (Figure 1). Higher R and b result in larger effective growth and more complex population dynamics (Figure 4). For static landscapes it has been shown that both low effective growth (slow increase and high extinction risk because of demographic stochasticity) and too fast an effective growth (rapid increase and high extinction risk because of chaotic fluctuations) are detrimental for population survival (Murrell et al., 2002; Münkemüller and Johst, 2007). Our results demonstrate that a similar optimum curve exists for the surfing and survival of mutations in expanding populations (Figure 4). Too slow a recovery from small densities is detrimental because of high extinction risks, but too quick a recovery is also detrimental as it reduces the influence of demographic stochasticity. Either local population growth is rapid and the more abundant wild-type drives the rare mutation to extinction or many wild-type emigrants from the quickly growing neighbouring subpopulations exclude the mutant from the landscape. The optimal effective growth for survival and surfing depends on the bias of the mutation (Figure 4). Deleterious and neutral mutations surf and survive better under slower growth, whereas beneficial mutations do better under faster growth. This is because deleterious mutations depend more on demographic stochasticity. As discussed above, deleterious mutations at the time of origin are not only in low numbers but also have a competitive disadvantage. The first step to survival is to increase density. Owing to the competitive disadvantage, this cannot be done by outcompeting the wild type, but only by being lucky in the game of demographic stochasticity. Reduced influence of demographic stochasticity is also the reason why higher carrying capacities decrease the surfing probability when growth rates are already high (Table 3, cf. Kaitala et al., 2006 for similar results in stationary subdivided populations).

The impact of conditional dispersal

Given the investigated parameter ranges, the influence of conditional dispersal strategies on survival and surfing of mutants in our simulation experiments was weaker than that of population growth dynamics (Figures 5 and 7). For us, this was initially surprising as, intuitively, dispersal would seem to be the more important determinant for populations under geographic range shift. The most substantial effect of conditional dispersal in our simulation experiments was a relative increase in surfing survival of beneficial mutations under density-dependent emigration (Figure 5). Increasing the dependency of dispersal on high local densities (Φ_emi>1) decreases dispersal at the low-density wave front and hence slows down the overall speed of spread. Therefore, the time frame that allows the mutant catching the wave front is then larger for a very quickly advancing population and the chance of a beneficial mutation catching the wave front is enhanced.

Outlook

Our results serve to highlight the importance of incorporating ecological realism if we are to gain a full appreciation of the genetic dynamics of range expansions. In this paper we considered more realistic population growth dynamics and conditional dispersal, but learned from the results some more general relationships. The most important finding of this study is the importance of demographic stochasticity for mutation survival and mutation surfing. As differences in ecological parameters influence both the wild type and the mutant in the same way, it is intuitive to expect a marginal influence on mutant performance. Only when considering that different ecological parameters influence demographic stochasticity differently and that this may have an effect on the mutant, it becomes obvious that ecological realism is important for studies on surfing mutations. We have shown this with the examples of reproduction and dispersal parameters, but expect consistent results if ecological realism is included for further processes. Besides population growth dynamics and conditional dispersal, there are many other potential directions in which models of this type can fruitfully be extended. We suggest that one particularly important development will be the formation of models that can incorporate population genetics together with both the ecological processes we have highlighted here and more realistic representation of spatial and temporal environmental variability.

Over the last decade, the role of environmental variability, especially its temporal correlation structure, has been studied within population ecology (Halley, 1996; Ripa and Lundberg, 1996; Johst and Wissel, 1997; Heino et al., 2000). It has become clear that understanding the interaction between the underlying ecological dynamics, particularly the form of density regulation and the structure of the temporal variability, is essential for predicting extinction risk (Schwager et al., 2006; Münkemüller et al., 2009). In a recent paper, Ranta et al. (2008) investigated the role of temporal environmental variability on the rate of genetic drift and the degree of spatial genetic structuring, incorporating ecological dynamics similar to those described here. Their results suggested that the genetic structuring among the population subunits may be more pronounced when there is positive temporal correlation in environmental conditions.

Some initial results have shown how important landscape structure can be for the fate of mutants during range expansion (Burton and Travis, 2008b). By adopting methods widely applied in spatial ecology, there is scope for the rapid development of models investigating the landscape genetics of shifting or expanding populations. For example, a frequently applied approach to explore the limits and shapes of species' ranges is to simulate populations across an environmental gradient (given by gradients in one or more vital rates, see, for example, Case et al., 2005; Roy et al., 2008). This general method has been extended to consider species assemblages along environmental gradients (Travis et al., 2006) or under environmental change (Mustin et al., 2009). Recently, a similar method has been used in a population genetic model (McInerny et al., 2009), and the results indicated that lineages derived from the leading edge of an expanding population are increased, whereas those at a trailing edge are reduced. However, the model of McInerny et al. (2009) incorporated neither within-patch ecological dynamics nor conditional dispersal strategies. We suggest that models similar to that we described in this paper should be applied in the context of spatial environmental gradients as well to facilitate our understanding of how genetic diversity within species may be maintained (or eroded). This is indispensable to make predictions about genetic impoverishment during climate change, and to develop adaptation strategies to counteract this risk.

Appendix

The earlier presented results show one-way, two-way and three-way interactions between different parameters of the simulation model. To complement these analyses, focussing only on effects of a small number of parameters at one time, we run a global sensitivity analysis to compare the importance of the different model parameters. We utilized boosted regression trees (BRTs) to support the interpretation. The great advantages of this analysis are: (1) it helps establishing the influences of different parameters in simulation models as those models become increasingly complex in nature and (2) it automatically copes with interactions of predictor variables and nonlinearities. Furthermore, BRTs have shown to provide strong predictive performance and reliable identification of relevant predictors and interactions (see Elith et al., 2008). However, the results of such a sensitivity analysis (comparable to all studies trying to identify parameter and variable importance) always depend on the chosen parameter ranges and therefore we start by justifying our choices. Afterwards, we describe BRT and its application to ecological data in a sketch (see Elith et al., 2008 for full detail). Finally, we present the results.

Parameter choice

As we were not simulating a specific system but tried to cover a range of different systems, we aimed at choosing broad but still realistic ranges for all parameters (Table 2). We cannot prove that the chosen ranges are the most realistic ones but think that we have some strong arguments for our choices: (1) Introduction time: the negative influence of increasing introduction time is mainly because of the disconnection of the origin of the mutation from the wave front, and therefore changes in introduction time have strongest impacts for small values (cf. Figure 6). Increasing the parameter range further should not have strong additional effects. (2) Density regulation type, disturbance frequency, emigration factor and carrying capacity: these factors depend strongly on specific species and landscapes. More extreme values than the chosen ones may occur in natural systems but using these would only strengthen the point that ecological parameters are important. (3) Density-dependent dispersal and competition coefficient: here, we chose values that are commonly analysed in literature. More extreme forms of density-dependent dispersal (for example, non-linear forms) are of course possible and we analysed a small subset in independent simulation runs (Figure 5). For the competition coefficient we took values utilized in former studies on the surfing mutation phenomenon (see, for example, Travis et al., 2007) to make results comparable.

Overall, the aim of our sensitivity analysis is to test whether the importance of ecological parameters is comparable to the importance of evolutionary parameters (the aim is not to quantify absolute importance).

BRT modelling approach in a sketch

BRTs belong to the family of machine learning algorithms. They combine the strength of regression trees (models that use recursive binary splits to relate a response to its predictors) and boosting (an adaptive method that allows combing many simple models—like regression trees) with the aim of improved predictions. Technically, BRTs are additive regression models in which the individual terms consist of regression trees. A single tree is grown by recursive binary splits of predictor variables. The resulting hierarchical structure of a regression tree means that the response to one predictor depends on values of other predictors (earlier splits). This way, interactions between predictors are automatically modelled. BRTs are assembled in a forward, stagewise procedure: the first regression tree is the one that maximally reduces the predictive deviance. In each further model building step, a new tree is built that best reduces the predictive deviance of the residuals of the former steps. To avoid overfitting of the data, BRTs are regularized by jointly optimizing (1) the number of trees, (2) tree complexity and (3) the learning rate that downweights the single trees with cross-validation algorithms.

Even so, the final BRTs are quite complex (typically consist of >1000 single trees), and they do not have to be treated as black boxes as there exist algorithms to summarize, evaluate and interpret them. Here, we use a measure developed by Friedman (2001). It is based on the number of times a variable is used in the regression trees for splitting, weighted by the improvement to the model because of these splits and averaged over all trees. The values are scaled such that the relative contributions of all predictor variables add to 100, with higher values indicating stronger influence. The importance values that we finally report are the identified relative contributions of the parameters multiplied by the coefficient of variation for the output variable. We multiplied by the coefficient of variation (ratio of the s.d. to the mean) to correct for different variability in the different BRT outputs and to make importance estimates comparable between different models.

The simulation experiments for our sensitivity analysis (Table 2) resulted in almost 20 000 data points for each of the two response variables: ‘non-surfing survival' and ‘surfing survival'. This data set was randomly divided into six groups. The first group was used for fitting two BRT models, one for the non-surfing survival of mutations and the other for surfing survival. The remaining five groups were used for model cross-validation. In the model fitting of our data, we followed the instructions given in Elith et al. (2008) and used the code for the software R provided by the authors. This resulted in an optimal BRT predicting non-surfing survival with a tree complexity of 15, a learning rate of 0.01 and 3200 trees. Optimal tree complexity and learning rate were the same for the model predicting surfing survival. The resulting value for the number of trees was 3300.

BRT results

The BRT models on which we based our analysis of parameter importance performed well: validation showed a very good fit between simulation results (observed data) and BRT predictions (explained deviance >96% for models considering interactions between processes). Interestingly, those BRT models that were only allowed to fit main effects (tree complexity of one) do considerably less well. More than 30% of the deviance in the simulation results cannot be explained by simple main effects. This result highlights the importance of performing global sensitivity analysis when aiming at the identification of parameter importance because global sensitivity analyses allow considering the higher-order interactions between model parameters.

Comparing the importance of the different processes in the model on the basis of the investigated parameter ranges, we found that the bias of the mutation (that is, whether it is deleterious, neutral or beneficial) has by far the strongest influence on non-surfing survival (Figure 7). Its importance is followed by those of carrying capacity (positive relation with survival), over-compensatory density regulation dynamics (non-monotonous relation), disturbance frequency (non-monotonous relation) and density dependence of emigration (negative relation). We have discussed the influence of mutation bias, carrying capacity, over-compensatory density regulation and density dependence of emigration above. Increasing disturbance frequency first increases non-surfing survival but decreases it again for higher values. The reason for the increase at low disturbances is reduced competitive pressure and increased stochasticity from which the rare mutant profits most. However, too high disturbance pressure is deleterious for the mutant because of its low density.

For surfing survival, the mutation bias is still most important but ecological processes become much more influential. The most important effects on surfing survival are over-compensatory density regulation (positive relation; please note that the reference value for the growth rate is small, R=1.8, when comparing it with Figure 4; we used this relatively small value to keep results similar to earlier studies, for example, Travis et al., 2007), carrying capacity (positive relation) and density dependence of emigration (positive relation). Interestingly, the importance estimates of the ecological parameters and the mutation bias are relatively high in comparison to introduction time. One reason is the above-described influence of the ecological parameters on stochasticity and therefore on the survival and surfing fate of the mutation. However, it is also important to note that surfing requires survival. Of course, it is important for the mutant not to be too far behind the wave front to be able to reach it for surfing, but if the mutation is maladapted it has a high probability to die in the first place.

Overall, the direction of the parameter effects on non-surfing and surfing survival is in concordance with the results presented before. However, with the overall sensitivity analysis we are able to directly compare the importance of the evolutionary and ecological processes in the model considering at the same time their interactions. The results highlight that both evolutionary and ecological processes significantly influence the fate of surfing mutations.

The authors declare no conflict of interest.