Power and false-positive rate in QTL detection with near-isogenic line libraries

Abstract

Libraries of near-isogenic lines (NILs) were used for quantitative trait locus (QTL) detection in model species and economically important crops. The experimental design and genetic architecture of the considered traits determine the statistical properties of QTL detection. The objectives of our simulation study were to (i) investigate the population sizes required to develop NIL libraries in barley and maize, (ii) compare NIL libraries with nonoverlapping and overlapping donor segments and (iii) study the number of QTLs and the size of their effects with respect to the power and the false-positive rate of QTL detection. In barley, the development of NIL libraries with target segment lengths of 10 c and marker distances of 5 c was possible using a BC₃S₂ backcrossing scheme and population sizes of 140. In maize, population sizes larger than 200 were required. Selection for the recipient parent genome at markers flanking the target segments with distances between 5 and 10 c was required for an efficient control of the false-positive rate. NIL libraries with nonoverlapping donor chromosome segments had a greater power of QTL detection and a smaller false-positive rate than libraries with overlapping segments. Major genes explaining 30% of the genotypic difference between the donor and recipient were successfully detected even with low heritabilities of 0.5, whereas for minor genes explaining 5 !or 10%, high heritabilities of 0.8 or 0.9 were required. The presented results can assist geneticists and breeders in the efficient development of NIL libraries for QTL detection.

Introduction

A near-isogenic line (NIL) library is a set of homozygous lines that carry marker-defined chromosome segments in a common genetic background (Eshed and Zamir, 1994). These segments cover the entire genome of a donor line, and were introgressed into the genetic background of a recipient line by marker-assisted backcrossing. NIL libraries were suggested to detect quantitative trait loci (QTLs) in tomato (Lycopersicum esculentum, Eshed and Zamir, 1995) and were subsequently developed in Arabidopsis (Keurentjes et al., 2007; Törjek et al., 2008) and in a wide range of crops such as rice (Oryza sativa L., Lin et al., 1998), barley (Hordeum vulgare L., Matus et al., 2003; Schmalenbach et al., 2008), wheat (Triticum aestivum L., Liu et al., 2006), maize (Zea mays L., Ribaut and Ragot, 2007; Szalma et al., 2007) and rye (Secale cereale L., Falke et al., 2009b).

The experimental designs that were used in these studies for the development of NIL libraries were based on ad hoc approaches. A first investigation on the experimental design for developing NIL libraries in rye was carried out by Falke et al. (2009a), who analyzed the effect of various selection strategies on the recovery of the recipient genome and the number of marker data points required for the marker-assisted backcrossing programs. However, no studies are available that investigate the effects of the experimental design used for the development of NIL libraries or the genetic architecture of the trait under consideration on the power and rate of false positives in QTL detection.

A comparison of the phenotypes of NILs with overlapping donor chromosome segments was suggested for fine mapping of QTLs (Kearsey, 2002). However, the statistical properties of QTL detection in NIL libraries with overlapping segments were not yet studied and compared with those of QTL detection with nonoverlapping segments.

The objectives of our simulation study were to (i) investigate the population size required in backcrossing programs to develop NIL libraries in barley and maize, depending on the desired length of donor segments and the density of the marker map, (ii) compare the power and false-positive rate of QTL detection in NIL libraries with those of nonoverlapping and overlapping donor chromosome segments and (iii) study the power and false-positive rate depending on the number of QTLs and the size of QTL effects.

Materials and methods

Genetic map

We investigated models of barley and maize genomes. For barley, we considered seven chromosomes of 140 c length (n_c=7, l_c=1.4) and for maize 10 chromosomes of 160 cM length (n_c=10, l_c=1.6). Barley and maize were chosen because of their economical importance and their character as a model species for crops. Barley has a rather short genome and maize has a longer one. This allows investigating the effect of genome length on the development of NIL libraries.

The genome was covered with equally spaced markers. Map distances ranging from 2.5 to 20 c (d=0.025, 0.05, 0.1 and 0.2) were investigated. All markers were polymorphic between the donor and recipient. Linkage maps with evenly distributed markers were assumed, because they greatly enhance the efficiency of marker-assisted backcrossing (Prigge et al., 2009) and can be constructed for model species and for most crops of economical importance.

To model recombination along the chromosomes, no interference in crossover formation (Stam, 1979) was assumed and recombination frequencies were related to the corresponding map distances with Haldane's (1919) mapping function. Haldane's mapping function is based on a simplified model of meiosis and assumes no interference in crossover formation. Nevertheless, the model resulted in simulations that are close to reality (Prigge et al., 2008).

Genomic composition of the NIL libraries

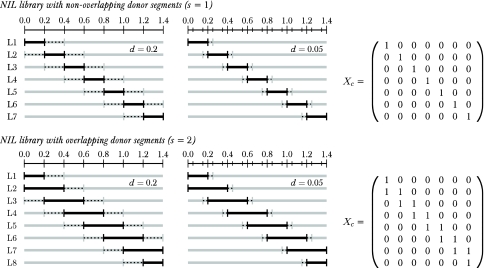
The target regions to which the QTL effects should be mapped were of 10 or 20 c length (l=0.1, 0.2). For NIL libraries with nonoverlapping segments (s=1), each NIL carried one target region. For overlapping segments, 2n_c NILs carried one target region and (l_c/l−1) n_c NILs carried two adjacent target regions. The genomic composition of the NIL libraries is illustrated for d=0.2, 0.05 and s=1, 2 using the example of one barley chromosome in Figure 1. The number of NILs per library ranged from n=49 for l=0.2 and s=1 in barley to n=170 for l=0.1 and s=2 in maize.

Figure 1.

Genomic composition of the NIL libraries. NILs (L1–L7, L1–L8) carrying the donor segments for one chromosome in barley and the corresponding design matrices X_c. Top: NIL library with nonoverlapping donor segments (s=1). Bottom: NIL library with overlapping donor segments (s=2). The marker distances were d=0.2 and d=0.05. The scales above NILs denote the map distances on the chromosome. Black lines: Donor segments. Gray lines: genetic background of the recipient. Dashed lines: segments of unknown genomic origin, located between markers at the end of the donor segments and flanking markers.

Backcrossing scheme

The development of an NIL library started with crossing a homozygous donor line with a homozygous recipient line. The resulting F₁ plants were backcrossed to the recipient to create the BC₁ population. For each NIL to be generated, one BC₁ plant was selected with a two-stage selection strategy. In the first selection stage, plants carrying donor alleles at all markers on the target region(s) were preselected (foreground selection). In the second stage, selection was based on an index, counting the number of recipient alleles at the entire set of markers outside the target region(s).

The selected BC₁ plants were backcrossed to the recipient to produce BC₂ populations. In each BC₂ population, one plant was selected using a three-stage selection strategy. In the first selection stage, foreground selection was carried out. In the second selection stage, a selection index was determined on the basis of recombination events between target region(s) and the flanking markers. The index was two for recombination between target region(s) and both flanking markers, one for recombination on one side of the target region(s) and zero for no recombination. All plants with the greatest value of index were preselected. In the third stage, selection was based on the entire set of markers outside the target region(s). The selected BC₂ plants were backcrossed to generate BC₃ populations, which were followed by two selfing generations. Three-stage selection was used in BC₃ and the selfing generations.

Success criteria

To quantify and compare the effect of population size and marker distance on the genomic composition of NIL libraries, we used the following success criteria: (i) RPM, which is the proportion of recipient parent alleles at markers outside the target region(s); and (ii) LDM, which is the number of NILs carrying donor alleles at markers outside the target region(s).

The aim of developing an NIL library is to obtain NILs with a defined genomic composition at the chosen set of markers. Markers in the target region(s) of an NIL should originate from the donor. If all NILs of a library carry donor alleles at all markers in the respective target region(s), the donor genome coverage of the library would be 100%. Markers outside the target region(s) should originate from the recipient. A complete recovery of the recipient genome is achieved if (i) the recipient genome proportion at markers outside the target region(s) (RPM) is 100% and (ii) the number of lines with donor alleles at markers outside the target region(s) (LDM) is 0. An LDM value smaller than 1 indicates that, on expectation, less than one NIL of the final library carries donor genomes at markers outside the target region(s). This value was used as a threshold for the successful construction of an NIL library.

Quantitative genetic models

We considered a polygenic trait and assumed that the genotypic value of the donor is 100 units superior to that of the recipient. The trait was controlled by major genes, minor genes and genes with small effects. In all scenarios, 10 genes with small effects of size 1 were assumed. The remaining 90% of the difference between donor and recipient was assigned to major and minor genes in eight scenarios. These differed in the number of (n_a of major and n_i of minor) genes and their corresponding effect sizes (s_a of major and s_i of minor) (Table 1). The genes with small effects were included as background noise, as it seems unrealistic that all genetic effects underlying a trait can be modeled and detected. The sizes of major and minor effects intend to model oligogenic resistance or quality traits. For each simulation run, genes were assigned to a different set of random locations in the genome.

Table 1. Overview of quantitative genetic scenarios.

Scenario	Major genes		Minor genes
	na	sa	ni	si
I	3	30	—	—
II	5	18	—	—
III	—	—	9	10
IV	—	—	18	5
V	2	30	3	10
VI	2	30	6	5
VII	1	30	6	10
VIII	1	30	12	5

n_a, number of major genes; s_a, effect size of major genes; n_i, number of minor genes; s_i, effect size of minor genes.

For barley, the difference between NILs and the recipient is considered per se; hence, the effects represent additive gene action. For maize, the difference between NILs and the recipient is for testcross performance (assuming a broad tester and neglecting tester effects); hence, the effects represent additive and dominant gene action. Epistasis was neglected for both models.

QTL detection

To detect QTL on the donor segments of an NIL library, we assumed phenotypic evaluation in a balanced factorial design with fixed effects and homogeneous residual variances comprising o=3 locations, q=2 years and r=2 replications. The recipient was included in the experiment either as one entry p=1 or 10-fold p=10.

The genetic variance of an NIL library was defined as

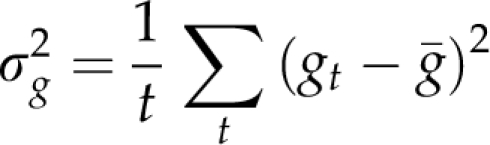where g_t is the genotypic value of a line and the summation index refers to all NILs of the library and the recipient. We assumed heritabilities of h²=0.5, 0.7, 0.9 and 1.0 using 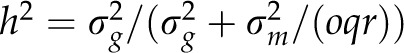and random realizations of the masking variance σ_m².

The effects of target regions were estimated with a linear model (Searle, 1971, pp 110) as β̂=(X′X)⁻¹X′y. The parameter vector β consisted of the genotypic value of the recipient β₀ and an effect β_u (u=1…n_u, n_u=n_cl_c/l) for each target region. The vector of observations y and the design matrix X consisted of n_u+1 rows for each replication. The design matrix of the first replication was

where X_i values are the design matrices of the individual chromosomes as illustrated in Figure 1. The hypothesis H₀: k′β=0 was tested for each target region. For the u-th region, k_u+1=1 and k_v=0 for all v≠u+1. The corresponding F-statistic is

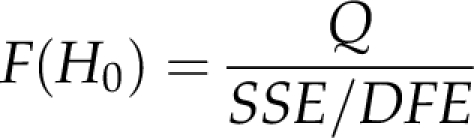where

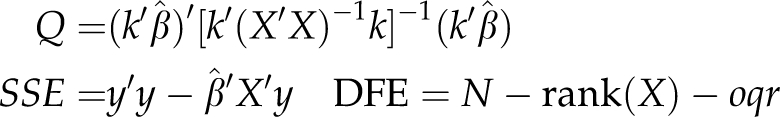Under the null hypothesis, F(H₀)∼F_1,DFE. The resulting P-values were adjusted with the Bonferroni–Holm procedure (Holm, 1979) for an experimentwise type I error rate of 0.05.

Simulations

Using the methods described above, we conducted three series of simulations. In the first series, we considered maize and barley genomes, nonoverlapping donor segments (s=1), marker distances of d=0.2, 0.1, 0.05 and 0.025 and segment lengths of l=0.1, 0.2. The recipient was included as a single entry in the phenotyping (p=1). For all combinations of these parameters, we varied the population size b, used in each generation of each of the n backcrossing programs, from b=20 to 200 in steps of 20 and assessed the RPM and LDM values.

In the second series, we considered the barley genome and a segment length of l=0.2. We investigated scenario III (Table 1) consisting of nine minor genes (n_i=9) with an effect of 10 (s_i=10) and heritabilities of h²=0.5–1.0 in steps of 0.1. We varied marker densities d and population size b according to the following scheme: (d=0.2/b=60), (d=0.1/b=100), (d=0.05/b=160), (d=0.025/b=200). Population size b was chosen such that, for a given marker distance d, values of LDM <1 were reached for s=1 and s=2. The results of these preliminary simulations are not presented. We compared NIL libraries with (i) nonoverlapping donor segments, including the recipient once in the phenotyping (s=1, p=1); (ii) nonoverlapping segments, including the recipient 10-fold (s=1, p=10); and (iii) overlapping segments, including the recipient 10-fold (s=2, p=10). We used two measures assessing the accuracy of QTL detection. Power was quantified by the sum of correctly detected effects, which was determined by summation of the true QTL effects for all segments in cases in which the null hypothesis of no QTL effect was discarded. Compared with the summation of the estimated effects, this procedure avoids introduction of bias caused by overestimation of QTL effects. The false-positive rate was determined by summation of all estimated effects located on segments, for which the null hypothesis was incorrectly discarded.

In the third series, we investigated the maize genome, a segment length of l=0.1, a marker distance of d=0.05, a population size of b=200 and nonoverlapping donor segments s=1. For this parameter set, we investigated the quantitative genetic scenarios I–VIII (Table 1) and determined the sum of correctly detected effects and the sum of false positives.

Software Plabsoft (Maurer et al., 2008) was used for the simulations. Simulations were repeated 5000 times to reduce sampling effects and obtain results with a high numerical accuracy.

Results

In the first series of simulations, a population size of at least b=40 was required to reach LDM values ⩽1 for a marker distance of d=0.2 and a length of the target region of l=0.2 in barley (Table 2). With decreasing marker distances, the required population sizes increased, and for d=0.025, an LDM value ⩽1 was not reached even with b=200. The LDM values reached with b=200 were 1.46 for l=0.2 and 2.73 for l=0.1. In maize, LDM values ⩽1 were reached only for marker distances d=0.2 and 0.1. For the smaller marker distances, this threshold was not reached with the greatest investigated population size of b=200. The LDM values for b=200 were much greater than in barley and amounted to 10.51 for l=0.2 and 19.57 for l=0.1.

Table 2. Recipient genome recovery in NIL libraries in barley and maize depending on the marker distance d and population size b.

Marker distance d		Population size b
		20	40	60	80	100	120	140	160	180	200
Barley, length of the target regions l=0.2 (n=49)
0.2	RPM	99.63	99.98	100.00	100.00	100.00	100.00	100.00	100.00	100.00	100.00
	LDM	8.49	0.58	0.09	0.00	0.00	0.00	0.00	0.00	0.00	0.00
0.1	RPM	99.17	99.87	99.96	99.99	100.00	100.00	100.00	100.00	100.00	100.00
	LDM	21.56	5.13	1.70	0.56	0.15	0.18	0.02	0.02	0.01	0.00
0.05	RPM	98.77	99.63	99.85	99.94	99.97	99.98	99.99	99.99	100.00	100.00
	LDM	33.18	16.03	7.66	3.79	2.20	1.23	0.74	0.55	0.32	0.22
0.025	RPM	98.48	99.36	99.69	99.82	99.89	99.93	99.96	99.97	99.98	99.99
	LDM	41.33	28.68	18.68	12.34	8.08	5.44	4.18	2.82	2.05	1.46
Barley, length of the target regions l=0.1 (n=98)
0.1	RPM	99.28	99.89	99.98	99.99	100.00	100.00	100.00	100.00	100.00	100.00
	LDM	40.50	8.78	2.20	0.86	0.18	0.10	0.03	0.01	0.00	0.02
0.05	RPM	98.86	99.69	99.88	99.95	99.98	99.99	99.99	100.00	100.00	100.00
	LDM	66.55	29.87	13.53	6.42	3.62	2.22	1.13	0.64	0.50	0.31
0.025	RPM	98.54	99.43	99.70	99.84	99.91	99.94	99.96	99.97	99.98	99.99
	LDM	83.91	56.95	37.51	23.68	15.01	9.76	7.22	5.39	3.74	2.73
Maize, length of the target regions l=0.2 (n=80)
0.2	RPM	99.26	99.89	99.97	99.99	100.00	100.00	100.00	100.00	100.00	100.00
	LDM	35.56	7.81	1.90	0.46	0.15	0.04	0.02	0.00	0.00	0.00
0.1	RPM	98.81	99.67	99.88	99.95	99.97	99.98	99.99	99.99	100.00	100.00
	LDM	57.76	27.74	13.07	6.19	3.36	2.03	1.05	0.64	0.37	0.29
0.05	RPM	98.48	99.42	99.71	99.84	99.90	99.94	99.96	99.97	99.98	99.99
	LDM	69.78	47.46	31.69	20.87	13.98	9.65	7.19	5.46	3.90	2.97
0.025	RPM	98.32	99.21	99.52	99.70	99.79	99.85	99.90	99.92	99.94	99.95
	LDM	75.40	62.49	49.53	37.92	29.54	24.09	18.65	15.89	12.49	10.51
Maize, length of the target regions l=0.1 (n=160)
0.1	RPM	98.93	99.73	99.90	99.96	99.98	99.99	99.99	100.00	100.00	100.00
	LDM	111.38	49.48	21.57	10.24	4.88	2.74	1.71	0.85	0.73	0.36
0.05	RPM	98.61	99.47	99.74	99.87	99.92	99.95	99.97	99.98	99.98	99.99
	LDM	137.69	92.09	59.62	38.21	26.26	17.59	12.26	9.35	6.57	5.08
0.025	RPM	98.44	99.25	99.55	99.72	99.81	99.87	99.90	99.93	99.94	99.96
	LDM	151.69	125.65	97.75	74.23	56.80	44.39	36.01	28.65	23.32	19.57

RPM, proportion of recipient alleles at markers outside the target regions; LDM, number of NILs carrying donor alleles at markers outside the target regions.

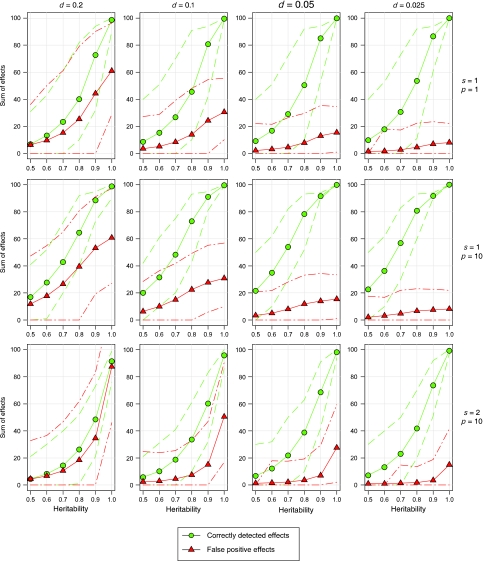
In the second series of simulations, decreasing the marker distances resulted in a moderate increase in the sum of correctly detected QTL effects, and also in a considerable reduction in false-positive effects (Figure 2). This trend was observed for both nonoverlapping (s=1) and overlapping (s=2) donor segments, irrespective of the number of replications of the recipient p and heritability h². Increasing the number of replications of the recipient from p=1 to 10 resulted in a strong increase in the sum of correctly detected effects. The sum of correctly detected effects was considerably greater and the false-positive rate was considerably smaller for nonoverlapping (s=1) than for overlapping (s=2) donor segments.

Figure 2.

Sum of correctly detected and false-positive effects in NIL libraries of barley with a length of target regions of l=0.2 and varying marker distances d, heritabilities h² and replications of the recipient in the phenotyping P for NIL libraries with nonoverlapping (s=1) and overlapping (s=2) donor segments. Values were averaged over the 5000 simulation runs. The dashed lines are the 5th and 95th percentiles of the 5000 simulation runs.

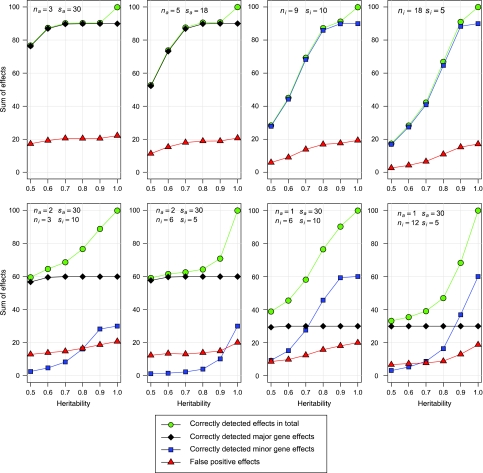
In the third series of simulations, QTL with major effects of size s_a=30 were successfully detected, even with low heritabilities of h²=0.5 and 0.6 (Figure 3). With decreasing effect sizes, the heritabilities required for successful QTL detection increased. The detection of minor genes with effect sizes n_i=5 or 10 in the presence of a major gene (n_a=30) was only successful for very large heritabilities of h²⩾0.9.

Figure 3.

Sum of correctly detected and false-positive effects in NIL libraries of maize with a length of target regions of l=0.2, marker distance d=0.05, varying heritabilities h² and different numbers of major genes n_a and minor genes n_i with different effect sizes of the major genes s_a and minor genes s_i.

Discussion

Comparison with earlier studies

Syed et al. (2004) optimized the construction of a substitution library in Arabidopsis with computer simulations. Their aim was to determine a crossing scheme to construct a substitution library from a set of recombinant inbred lines with known RFLP genotypes. For the scenario investigated, between 10 and 73 individuals needed to be marker assayed. In our study, populations of at least 40 individuals were required to construct introgression libraries with LDM <1 (Table 2). These differences are due to the shorter genome length of Arabidopsis compared with barley and maize, and because of the fact that our simulations start with crossing homozygous inbred lines instead of using recombinant inbred lines.

Kaeppler (1997) reported that populations of recombinant inbred lines generally provided a better power of QTL mapping than sets of NILs. He used a single-marker analysis of variance (ANOVA) technique for QTL detection in the set of NILs. The main difference when compared with our model is that, in our analysis, all lines of an NIL library are investigated jointly, whereas the model of Kaeppler separately compares pairs of NILs. From a theoretical point of view, our model including multiple NILs should provide a more exact estimation of the residual variance and, hence, a greater detection power than a model investigating a single pair of NILs.

Falke et al. (2009a) optimized the construction of introgression libraries in rye (n_c=7, l_c=1). They found that with the BC₃S₂ backcrossing scheme used in this study, population sizes of n=40, 80, 120, 160, 200 in generations BC₁ to BC₃S₂, and marker distances of d=0.05, the construction of an introgression library consisting of n=35 NILs with segment lengths of l=0.2 required 80 000 marker data points. The number of marker analyses required for a marker-assisted backcrossing program is approximately proportional to the genome length (Prigge et al., 2009). Hence, for the construction of introgression libraries in barley and maize investigated in this study, more than 200 000 marker data points are required. This can be considered as a limiting factor for marker systems, such as simple sequence repeats. However, with high-throughput marker technology, we no longer regard the number of required marker data points as a limiting factor.

Properties of the linear model used for QTL detection

The multiple linear regression approach used for QTL detection in our study is characterized by the joint analysis of all markers and all NILs in one single model. Therefore, all QTL effects are accounted for in the parameter vector and do not inflate the residual variance, as is the case for single-marker ANOVA models that include all genotypes of a mapping population. Compared with single-marker ANOVA models investigating only one pair of NILs (or one NIL and the recurrent parent), the more precise estimation of the residual variance in our model is expected to result in improved statistical properties.

The Bonferroni–Holm procedure for adjustment of P-values in multiple testing is known to be conservative. It controls the familywise type I error rate at the cost of a rather large type II error. Benjamini and Hochberg (1995) suggested a less-conservative procedure controlling the false discovery rate (FDR). This procedure assumes that the false-positive rate is the result of cumulated type I errors due to multiple testing. In our analysis, false positives are not only a consequence of multiple testing but also occur because of QTLs located on chromosome segments adjacent to the target region. Therefore, an actual control of the false-positive rate is not expected, and the advantage of using the Benjamini–Hochberg procedure instead of the Bonferroni–Holm adjustment reduces to less-conservative testing. In addition to the results presented in Figure 2, we carried out the same analyses using an adjustment of P-values for an FDR of 5%. Both, the rate of correctly detected effects and the rate of false-positive effects, were greater than for the Bonferroni–Holm adjustment (results not shown), but no difference in the reported trends with respect to the marker distance d, the replications of the recurrent parent in the field trial r or the use of overlapping segments s was observed. We conclude that our results are robust with respect to the adjustment procedure for multiple testing.

A further refinement of the multiple linear regression analysis could be achieved by techniques for selection of regression variables, such as stepwise selection, and by comparison of the goodness-of-fit of alternative models. The use of multiple testing procedures for comparison of one standard (the recurrent parent) with a set of treatments (the NILs) could also result in an improvement in the statistical properties. We plan further investigations in this interesting area of research.

Donor genome coverage and recipient genome recovery

The two- and three-stage selection strategies used included a preselection for the donor alleles in the target region(s). This resulted in NIL libraries with a donor genome coverage of 100% for all investigated scenarios. We conclude that complete donor genome coverage can be reached solely by using an appropriate selection strategy, irrespective of further design factors of the NIL library.

The successful development of NIL libraries with target regions of length l=0.2 and marker distances of d=0.2 required the development of n=49 NILs and a population size of b=40 in barley (Table 2). In maize, almost twice the number of NILs (n=80) and twice the population size (b=80) were required. Hence, the increase in genome length of 1.6 from barley to maize resulted in an increase in the effort of almost factor 4. This overproportional increase indicates that the genome length is a crucial factor in determining the effort required for the construction of NIL libraries.

In barley, it was possible to reach LDM ⩽1 for marker distances d=0.05 and a length of the target regions of l=0.1 with population size b=140. In maize, however, d=0.1 was the smallest marker distance for which LDM⩽1 was reached using population size b⩽200 (Table 2). We conclude that, in barley, NIL libraries with short segments and marker distances can be developed with reasonable effort, whereas in maize, developing NIL libraries with short segments and marker distances requires large resources, which may only be available for a few applications.

Overlapping donor segments

NILs with overlapping donor segments were suggested for fine mapping of QTLs (Kearsey, 2002). The appeal of NIL libraries with overlapping segments (s=2) is a more precise detection of QTL effects than with nonoverlapping segments (s=1). This improvement is expected, as each target region is present in two NILs and hence its effect is assessed with twice the replications in the phenotyping process.

Our simulations showed, however, that the power of QTL detection was considerably smaller for NIL libraries with s=2 than for s=1 (Figure 2). This can be explained by the fact that, with overlapping segments, the QTL effects of two adjacent target regions are confounded. Therefore, it is not possible to unequivocally assign a phenotypic effect to one single target region. This confounding outweighs the increase in power expected from the repeated phenotypic assessment of the effect of a target region.

From a practical point of view, a further complication arises for NIL libraries with overlapping segments. If a target region with a favorable QTL allele is detected, then it needs to be separated from the second target region by further crossing and selection steps. Only after performing these steps is the resulting line applicable in the breeding process, without risking the introduction of linkage drag with potentially negative effects on the breeding pool.

Our results suggest that a loss of power complicates the fine mapping of QTL by comparison of NILs with overlapping donor segments. Therefore, we conclude that our study was unable to reveal advantages of NIL libraries with overlapping donor segments.

Replicated phenotyping of the recipient

The power of QTL detection with NIL libraries depends on the standard error of linear contrasts for the differences between NILs and the recipient. In experiments with treatment–control comparisons, the standard error of a comparison can be efficiently reduced by including the control as a replicated entry. We adopted this principle for QTL detection with NIL libraries by including the recipient as a 10-fold entry (p=10) in the phenotyping process. This resulted in a considerable increase in the power of QTL detection compared with that using the recipient as single entry (p=1, Figure 2).

Although the replicated phenotyping of the recipient increases the required effort, it provides a relatively simple means of substantially enhancing the power of QTL detection. In contrast, duplicated evaluation of the target regions by NILs with overlapping donor segments did not increase the power.

Marker distances

NIL libraries with short marker distances required large population sizes to reach small LDM values (Table 2). However, they allow assigning a phenotypic difference between an NIL and the recipient to the correct target region with a high probability. In contrast, with greater marker distances, smaller populations were sufficient. However, here the risk of incorrectly assigning the effect of a QTL, located between a target region and its flanking marker, to that target region is higher. Consequently, finding a suitable marker distance, with a balanced trade-off between the required effort and the accuracy in QTL detection, is a crucial decision in the development of NIL libraries.

The sum of correctly detected effects increased as the marker distance decreased from d=0.2 to 0.1. However, with smaller marker distances, further improvements were only marginal (Figure 2). We conclude that, with respect to the power of QTL detection, marker distances smaller than d=0.1 are not necessary.

The sum of false-positive effects was extremely high for d=0.2 and declined consistently down to the smallest investigated marker distance of d=0.025 (Figure 2). Values below 20% (of the difference between recipient and donor) were only observed for marker distances of d=0.05 and 0.025. The large sums of false positives observed for large d are due to the incorrect assignment of QTLs, which are located on the chromosome segments between a target region and its flanking markers (the dashed regions in Figure 1), to that target region. Furthermore, an overestimation of the QTL effects assigned to these segments contributes to the large values of the sum of false positives. The reduction in false positives with decreasing flanking marker distance results from a decrease of such incorrectly assigned QTLs. This shows that a control of the donor genome attached to the target regions with tightly linked flanking markers is mandatory in situations in which false positives need to be minimized.

Summarizing, a marker distance between d=0.1 and 0.05 seems optimal for many practical applications, because it can be reached with reasonable population sizes and simultaneously provides a sufficient power of QTL detection and a moderate rate of false positives.

Effect size and heritability

Major genes controlling 30% of the trait under consideration (s_a=30) were successfully detected in all quantitative genetic scenarios, even for the rather low heritabilities of h²=0.5 and 0.6. Their successful detection was not affected by the number and size of further minor genes (Figure 2). With decreasing effect sizes, higher heritabilities were required for successful QTL detection. For an effect size of s_a=18, a heritability h²=0.7 was necessary, and for minor effects of size s_i=5, even the very high heritability of h²=0.9. A considerable decrease in the rate of correctly detected minor genes was observed in the presence of major genes. Consequently, the detection of major genes is a strength of NIL libraries and has a high potential for practical applications, but the successful detection of minor genes is only possible for highly heritable traits or with high efforts in phenotyping.

Additional quantitative genetic scenarios

Genetic resources promise to contribute favorable alleles to breeding programs, even if their performance with respect to the trait under consideration is worse than that of elite breeding material (Tanksley et al., 1996; Xiao et al., 1998; McCouch 2004; Falke et al., 2009b). NIL libraries provide the possibility of detecting such favorable QTL alleles as experimentally shown for plant height in rye (Falke et al., 2009b).

To investigate scenarios in which the performance of the donor is inferior to that of the recipient, we conducted additional simulations with a donor carrying positive and, at the same time, negative alleles for the trait under consideration (results not shown). For the rates of correctly detected and false-positive effects, the same trends were observed as reported above for a superior donor. We conclude that the detection of positive QTL alleles is not hindered by the presence of negative alleles for the trait under consideration, unless these do occur at closely linked loci.

Promising application areas

Our results suggest promising application areas for QTL detection with NIL libraries. For longer genomes, the large effort required may limit their use; however, NIL libraries provide an efficient tool for QTL detection in species with short genomes. To justify the considerable effort required even for short genomes, ideally the donor parent should carry favorable QTL alleles for several traits. The traits under consideration should be controlled by QTLs with major effects, or, in case of smaller effects, the traits should be highly heritable.

The authors declare no conflict of interest.