Modeling developmental patterns of spontaneous activity

Abstract

Spontaneous activity is found in many regions of the developing nervous system; such activity is thought to be instructive for guiding developmental processes. In particular, the developing retina generates correlated patterns of activity known as retinal waves. We review the main theoretical models that have been developed to study the mechanisms for generation and propagation of retinal waves. Much of the progress in this field has been due to the close interaction between experimentalists and theorists in analyzing and modeling spontaneous activity. We conclude by describing spontaneous activity models in other systems and suggestions for future modeling work.

Introduction

Neurons in the developing retina generate spontaneous activity in the absence of sensory input. This activity is highly structured, often generating waves of activity that travel across the retinal ganglion cell layer, followed by long periods of silence. These retinal waves generate distance-dependent correlations among retinal ganglion cells (RGCs). The initial in vivo recordings of correlated activity in embryonic rat [1] have subsequently led to a large number of studies in which the pharmacological mechanisms underlying wave generation and propagation have been studied [2]. Retinal waves have been observed in a wide range of species including mouse, rat, ferret, turtle and rabbit [3], with the one exception in Xenopus tadpoles [4]. We review the general mechanisms responsible for wave generation and propagation, which have been the key assumptions for building theoretical models of retinal waves. Furthermore, spontaneous neural activity is present not only in developing retina, but in many other parts of the nervous system, including hippocampus, spinal cord and cochlea [5, 6]. Some of the known principles for retinal waves may also be appropriate for modeling spontaneous activity in these other systems.

Theoretical models of retinal waves

Over the years, several studies have proposed theoretical models to account for the detailed spatio-temporal properties of retinal waves. In two of the four models [7, 8], there has been a very close relationship between modeling and experiments, with models published together with new experimental data. We believe such close interactions between theory and experiments are invaluable in furthering our understanding of the neural circuits underlying wave propagation.

The first model of retinal wave activity was published in 1994 [9, 10], at a time when relatively little was known about wave generation. As more experimental data has appeared, the theoretical models have become more tightly constrained [7, 11, 8]. In particular, two essential findings were the key role of cholinergic neurotransmission [12, 13] and the refractory mechanism [14] in starburst amacrine cells.

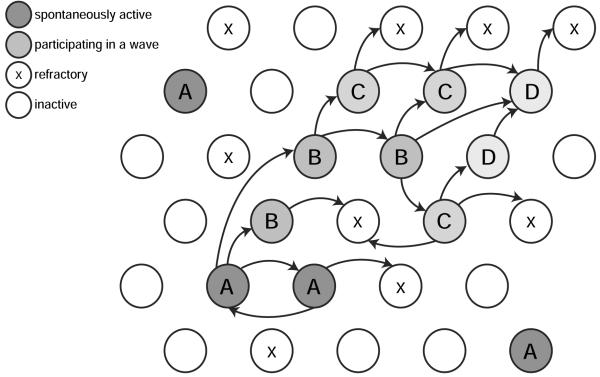
There are three main mechanisms to consider when modeling spontaneous activity (Figure 1):

1. How do waves start? Given that there is no external input (e.g. from visual stimulation), there must be some intrinsic mechanism by which neurons become active.

2. How do waves propagate? Once some neurons become spontaneously active, how do they excite neighboring neurons?

3. How do waves stop? Once a wave becomes initiated, does it continue traveling until it spreads over the entire retina, or is the activity spatially-restricted?

Figure 1.

Schematic of wave generation. Each circle represents an individual neuron. At any time a neuron is quiet, firing or refractory. Individual neurons may fire spontaneously independent of each other (neurons marked A); co-activation of e.g. two neighboring neurons, as at the bottom, may be sufficient to cause a wave to propagate to neighboring regions (A → B → C → D). The wave stops when it can no longer recruit neurons that are still in their refractory period (marked with x).

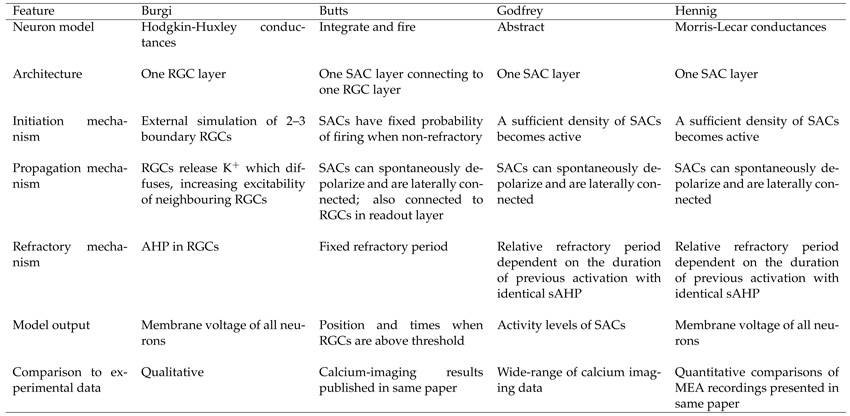
Before addressing these mechanisms, we first summarize the modeling frameworks used. We refer to each model by the name of the primary researcher that developed the model: Burgi [9], Butts [7], Godfrey [11] and Hennig [8]. Table 1 compares the main features of these models. A longer review of some of these models, describing underlying mechanisms in detail, has been undertaken elsewhere [15].

Table 1.

Summary of the models of retinal wave generation.

Modeling framework and connectivity

Individual neurons have been modeled as either relatively abstract activation units, integrate and fire neurons, or detailed conductance models. Before the primary role of cholinergic neurotransmission upon retinal wave generation was discovered, the Burgi model used a single layer of retinal ganglion cells (RGCs). After starburst amacrine cells (SACs) were highlighted as the source of cholinergic-mediated activity, subsequent models included populations of SACs connected to RGCs [7, 16]. Within the Butts model, the RGC layer was needed to ‘read out’ the underlying activity in the SACs. After that, the Godfrey model showed that only an individual layer of neurons (SACs) was required, which has since been adopted by later models.

RGCs have been modeled either as receiving synaptic input from SACs (Butts) or without synaptic inputs but with diffusion of ions mediating wave propagation (Burgi). By contrast, in the models which implement only a SAC layer, SACs have large overlapping dendritic arbors that form an extensive network of synaptic connections (Godfrey and Hennig).

Initiation

Most models assume that waves initiate by the coincident activation of sufficient numbers of SACs. One exception is the earliest model by Burgi, which requires external input to RGCs. In the other models (Butts, Godfrey and Hennig) two processes contribute to the initiation of a wave: (1) SACs spontaneously depolarize, and (2) SACs receive excitatory input from other neighboring SACs. In the Butts model, each SAC spontaneously depolarises with a fixed probability. In contrast, in the Godfrey model SACs spontaneously depolarise deterministically, either when the cell’s threshold for activation decays to zero or when the level of excitation of the cell exceeds the current threshold. Hennig modeled wave initiation by injecting cell-driven noise into each amacrine cells, whose source has not been determined. The amount of noise was determined to match recent experimental measurements of the probability of spontaneous depolarization of SACs in rabbit [14].

Propagation

In the absence of synaptic connections, the Burgi model assumed potassium released by one RGC could diffuse locally to excite neighboring RGCs. In the remaining models, activity propagated among SACs via the lateral synaptic connectivity of SACs. This connectivity was fixed in the Butts model, decayed with distance between pairs of SACs (Hennig model) or depended on the area of dendritic overlap (Godfrey model).

In the Butts model, activity also propagated from SACs to RGCs via synaptic connections. RGCs fired only if sufficient neighboring SACs were coincident, and thus provided a filter to prevent small numbers of active SACs generating waves in the ganglion cell layer.

Refractoriness

To prevent the continued activation of neurons, after firing for a certain period neurons enter a refractory period. Butts used a distribution of refractory periods with a mean set to the peak of the interwave interval distribution. The refractory periods of each SAC had to be significantly variable to prevent synchronization of activity across the network. Godfrey and Hennig followed subsequent experimental evidence that longer and more intense SAC depolarizations increased the duration of the slow afterhyperpolarizing potential (sAHP) of the SACs [14]. Both models assumed that the refractory period of an amacrine cell was inversely related to the duration of its previous depolarisation. However, the two models implemented different assumptions to desynchronize the network. Godfrey’s model implemented additional nonlinearities to boost differences in refractory times between the center and the boundaries of a wave; thus the decay from refractory state was nonlinear. Hennig’s model assumed activation of the sAHP via a fast and a slow timescale, initiated by autonomous bursts and bursts which occur as parts of waves, respectively. Thus, despite the linear decay from refractoriness, the nonlinearity of the activation led to desynchronization of the network.

These models therefore propose two different mechanisms for wave variability. (1) In the Godfrey and Hennig models, frequent spontaneous SAC depolarizations generate wave variability, with subsequent refractoriness (sAHP with a constant timescale) limiting wave propagation. Thus, SACs that are spontaneously active between waves become less excitable, limiting their ability to depolarize in the near future and participate in a wave. (2) In the Butts model, variability in the sAHP timescale limits wave propagation. If only relatively infrequent spontaneous SAC depolarizations were implemented in the model, SACs would rarely be refractory and waves would propagate across the entire retina. By making the sAHP timescale highly variable, SACs stop being refractory at different times, thus generating variable wave trajectories.

Evaluation

The current retinal wave models also differ in their ability to capture experimentally-observed distributions of event sizes, for instance, wave size and interburst intervals. Indeed, the output from several of these models has been carefully compared to different experimental data. Both the Butts and Godfrey models were based on calcium imaging data. The Godfrey model can account for retinal waves from a range of species and developmental ages under different parameters. The Butts model was based on calcium imaging data in ferret, and likewise identified parameter regimes for generating different types of waves (“small” vs “large” vs “hyperactive”) [16]. The Hennig model perhaps provides the most detailed quantitative comparison of simulated and observed waves from MEA recordings in turtle and mouse retina. In particular, the model can recreate the power-law like nature of retinal wave properties including wave duration and wave size. (See below for alternative models that generate power-law distributions of activity size and duration.) The Hennig model has not yet been compared to calcium imaging recordings, but it is likely to also reproduce this type of data.

Spontaneous activity in other systems

Spontaneous activity occurs in many areas during development and adulthood. Like retinal SACs, other neurons known as pacemakers form networks which can initiate spontaneous activity [17, 18, 19]. While the amacrine cells which can initiate and propagate spontaneous activity in the retina serve as an example of an intrinsic pacemaker to the network, the initiation zones driving activity also can be extrinsic to the network which propagates this activity, as seen in the midbrain [20].

Retinal wave propagation has been modeled as a chaotic process on a two-dimensional lattice, where the spatial locations of initiation and propagation of the waves are mostly random. Other tissue where spontaneous activity occurs has much more stereotyped patterns of initiation and propagation. In the developing cortex, for instance, spontaneous waves are always initiated in two specific parts of an in-vitro slice and are localized to specific parts of the slice [18, 19]. The waves can vary in the spatial extent of the propagation and the timing between events, but not in the direction of propagation. These events have yet to be modeled and analyzed for the information content they may carry for the developing cortex.

Spontaneous activity is also observed in motor networks, of which the developing spinal cord has received most modeling attention. The earliest models used a similar mechanism as for the generation of retinal waves, activity-dependent depression [21], and could capture the basic periodic patterns of activity. Newer models can explain more complex patterns regarding the duration of the active and quiet periods of the network [22]. Even though this system is quite simple, it provides another good example of linking theory and experiment. It also demonstrates that different systems use a range of mechanisms to generate activity, though synaptic depression is not thought to be involved in generating retinal waves [14].

Other studies have focused on building more abstract networks and understanding the propagation of activity in these networks as a function of connectivity, synaptic strength and intrinsic dynamics of the network neurons. Spontaneous activity propagation in adult cortical cultures can be described with equations that govern avalanches [23]. In these avalanches, events emerge as the activation of one unit initiates the successive activation of other units causing a cascade which propagates through the entire system. The spatial and temporal distributions of these avalanches show no characteristic scale, and have been fit to a power law with an exponent of −3/2. Hennig et al. [8] found such scale-free distributions in retinal waves, such that waves occur in all sizes, including frequent waves mediated by a few SACs and rare events spreading over the entire retina. However, unlike previous models, the Hennig model provided a biophysical mechanism for the generation of scale-free distributions through sAHP-mediated desynchronization.

The studies by Beggs and Plenz [23] proposed that the power-law distributed event sizes could be explained with a theory for a critical branching process with a branching parameter close to the critical value of 1 (at which activity does not die out nor explode in the network, but it propagates in exactly a one-to-one manner). Such approaches are useful because they may answer the question “what is spontaneous activity good for?” since they suggest that these networks optimize information transmission. For instance, in the simulated cortical networks which could propagate avalanches, Beggs and Plenz [23] computed the information between the input stimulus and the output response as the difference of entropies (the entropy of the entire response set minus the entropy of a response given a stimulus). Thus, for networks with a branching parameter close to 1, the information was maximized, meaning that the response of the network carried the most information about the presented stimulus, compared to networks with branching parameters smaller or larger than 1. A different approach is taken by studies which examine the conditions for activity propagation or for the emergence of synchrony in a network (reviewed in [24]), but these are often criticized for having little experimental application.

We have aimed to understand the generation of retinal waves because of their utility in synaptic refinements and retinotopic organization in higher visual areas. However, the theoretical work on activity propagation, information transmission and neural coding has developed new tools which can be used to understand not only the mechanisms but also the computations performed by propagating activity in networks.

Future directions

Modeling of retinal waves has so far been quite successful, partly because of the close interaction between theorists and experimentalists. However, there is still much modeling work to be done to further our understanding of the development of neuronal circuitry. We close by mentioning some theoretical issues likely to be of interest in the coming years:

1. With the exception of [11], most modeling work has focused on waves driven by cholinergic circuitry. Waves are thought to be generated by different mechanisms across development, from gap-junctions (stage 1), cholinergic neurotransmission (stage 2), and glutamatergic neurotransmission (stage 3) [25, 26]. How can mechanistic models account for stage 3 waves, given that there is currently no evidence for a mechanism to generate a refractory period?

2. Stage 2 wave properties can vary considerably, e.g. from P1 to P5 in mouse [8]. Recent results from rabbit retina [27] suggest the effective cholinergic network grows rapidly over the first two postnatal weeks. How do simulated wave patterns change as more SACs are added throughout the cholinergic network?

3. Most experimental observations of retinal waves have been limited to recording from a small fraction of the retinal area. In such small recordings, boundary effects may dominate. Higher-density MEAs now allow us to see finer structure within retinal waves across larger areas. For example, recent recordings from a 512-electrode array suggest that waves may preferentially travel roughly along one retinal axis [28]. Likewise, a new 4096-electrode array [29] opens the possibility for recording across the entire neonatal mouse retina [30]. When the models are scaled up to simulate larger portions of the retina, hence reducing border effects, will they replicate the observed patterns?

4. When the cholinergic network is genetically perturbed, waves disappear but resume a few days later [31]. Such homeostatic recovery of activity is widely seen in developmental contexts [6, 5]. Abnormal activity patterns are also seen in mutant mice [32, 28]. What extra mechanisms are required within the models to generate these perturbed patterns?

These theoretical models can help evaluate hypotheses for the generation of retinal waves. Their simulated wave patterns can also be used in other models [33, 34, 35] to explore how spontaneous neural activity refines neural connectivity [25, 36, 37]. (Note that sometimes, rather than simulate spontaneous activity, experimentally-observed spike trains could be input directly into models to assess their instructional properties [38, 39].) However, spontaneous activity is essential for many other developmental processes such as motor axon guidance, expression of guidance molecules and neurotransmitter specification [5]. We hope that in the future theoretical modeling can contribute to elucidating the key features of spontaneous activity in these processes.

Abbreviations

(s)AHP

(slow) afterhyperpolarization

LGN

lateral geniculate nucleus

MEA

multi-electrode array

RGC

retinal ganglion cell

SAC

starburst amacrine cell