Reconstruction of fully 3-D high spatial and temporal resolution MR temperature maps for retrospective applications

Abstract

Many areas of MR-guided thermal therapy research would benefit from temperature maps with high spatial and temporal resolution that cover a large 3-D volume. This paper describes an approach to achieve these goals that is suitable for research applications where retrospective reconstruction of the temperature maps is acceptable. The method acquires undersampled data from a modified 3-D segmented EPI sequence and creates images using a temporally constrained reconstruction algorithm. The 3-D images can be zero-filled to arbitrarily small voxel spacing in all directions and then converted into temperature maps using the standard proton resonance frequency (PRF) shift technique. During HIFU heating experiments, the proposed method was used to obtain temperature maps with 1.5×1.5×3.0 mm resolution, 288×162×78 mm field of view, and 1.7 second temporal resolution. The approach is validated to demonstrate that it can accurately capture the spatial characteristics and time dynamics of rapidly changing HIFU-induced temperature distributions. Example applications from MR-guided high intensity focused ultrasound research are shown to demonstrate the benefits of the large coverage fully 3-D temperature maps, including characterization of volumetric heating trajectories and near-and far-field heating.

Introduction

Treatments using magnetic resonance-guided high intensity focused ultrasound (MRgHIFU) for non-invasive thermal therapies are currently attracting a lot of attention and research. Investigators are using this technology to develop methods for ultrasound mediated drug delivery (1), thrombolysis for stroke treatment (2), and tumor ablation (3–10). There is a great deal of ongoing research to investigate important questions about how to improve MRgHIFU procedures. For example, researchers are investigating how tissue thermal and acoustic properties change with HIFU heating (11–13), optimal heating trajectories for treatment time minimization (14–15), transducer design for different focal zone shapes and sizes (16–19), the effects of pre-focal heating (20–22), the potential of inadvertent heating outside of the focus at tissue/bone or tissue/air interfaces (6,23), and how thermal dose correlates with tissue damage (24–26). For many of these pre-clinical studies, high spatial resolution and large volume coverage are required to accurately measure the HIFU temperature distribution over the entire heated region, but real time availability of MR temperature maps is not essential, as long as the temperature data can be obtained retrospectively for analyzing the results of an experiment. For such applications where retrospective temperatures are acceptable, we have developed an MR temperature measurement technique that is capable of obtaining fully 3-D temperature maps with high spatial resolution, large volume coverage, and high temporal resolution. The only drawback to the technique is that the image reconstruction algorithm, as currently designed and implemented, cannot create the temperature maps to be available in real time.

The method is based on the standard proton resonance frequency (PRF) shift approach to MR thermometry (27) and utilizes a modified 3-D segmented EPI gradient echo sequence (GRE) in conjunction with undersampled data acquisition and a temporally constrained reconstruction (TCR) algorithm. The segmented EPI readout and data undersampling allow for large 3-D k-space coverage in an acceptable amount of time. Artifacts that would be present using standard reconstruction methods on undersampled data are removed by using the constrained reconstruction approach. The 3-D imaging allows for zero-filled interpolation in all three directions to create arbitrarily small voxel spacing. The result is temperature maps that have high enough spatial resolution to accurately measure the HIFU-induced temperature distribution, large enough volume coverage to visualize the entire focal zone and most of the ultrasound propagation path, and high enough temporal resolution to accurately track the dynamically changing temperatures. In this paper we present the implementation and validation of the method along with three example applications that demonstrate the utility of the technique.

Methods

3-D Segmented EPI Sequence

The phase encode ordering of a 3-D segmented EPI gradient echo sequence was modified to accommodate k-space undersampling. The sampling is done such that for each time frame used in the TCR algorithm, k_y is evenly undersampled with one echo train of read-out lines and k_z is fully sampled. The undersampled data sets are acquired such that the entire 3-D k-space will eventually be fully sampled. If the undersampling factor is found to be too large, the data can rearranged to give each k_z plane a set of two echo trains of read-out lines, thereby halving the reduction factor and doubling the time per undersampled data set.

TCR Algorithm

The TCR algorithm reconstructs a sequence of artifact-free images, m, from undersampled k-space data, d, by iteratively minimizing a cost function that consists of a data fidelity term and a constraint term (28–29):

$$m=\underset{m\text{'}}{\text{arg min}}\left({\Vert WFm\text{'}-d\Vert }_2^2+\alpha {\Vert {\nabla }_{t}m{\text{'}}_i\Vert }_2^2\right)$$ [1]

Here F is the Fourier Transform, W is a binary matrix that represents which phase encoding lines have been acquired, m’ is the image estimate, α is a spatially varying matrix of weights for the constraint term, and ‖*‖₂ represents the L₂ norm. In this implementation, the constraint term penalizes abrupt changes in time in the image, weighted by the free parameter α. Using the entire 4-D data set and 200 iterations, the algorithm takes many minutes to converge to an alias-free image. For example, a data set with a 192×108×30 imaging matrix and 79 time frames took 61 minutes to reconstruct using a MATLAB (MathWorks, Natick, Massachusetts) implementation on a compute box with dual 2.8 Ghz Intel Xeon Quad core processors and 32 GBs of RAM.

Implementation

To begin the retrospective reconstruction process, low temporal resolution temperature maps are created from the fully sampled k-space data sets using the standard PRF reconstruction and used to create the 3-D spatially varying weighting, α. The α value is set to 0.5 for all voxels that experience less than 1.0°C of heating. For all heated regions, α values are scaled linearly from 0.5 to 0.005 for voxels with temperatures ranging from 1.0°C to the maximum temperature. This is done so that the temporal constraint will be relaxed in regions where it is known that the image phase will be changing in time due to heating. The k-space data is scaled to give magnitude image intensities is in the range of 10 to 100, split into undersampled data sets, and recombined at the higher frame rate in a sliding window fashion to be used as the initial estimate in the TCR algorithm. The entire 4-D set of k-space time frames is used in the TCR algorithm to create a 4-D set of images with high temporal resolution. If multiple acquisition channels are used, an image sequence is reconstructed separately for each channel by the TCR algorithm and combined afterward. These images undergo zero-filled interpolation to obtain the desired voxel spacing (typically 1 mm isotropic), and are converted into temperature maps using the standard PRF phase subtraction method. If non-temperature induced phase changes are suspected (for example due to field drift or out-of-FOV motion) then a reference-less temperature reconstruction method can be applied (30–32).

Validation

The first goal of this study is to validate the proposed approach for obtaining temperature measurements against the standard PRF approach, which has been well validated in previous studies (33–34). Experiments were performed to determine how large of a 3-D data set can be acquired and still have the TCR algorithm reconstruct images that accurately capture the spatial features and temporal dynamics of a HIFU-induced temperature distribution. Multiple HIFU heating runs were performed using an agar phantom and the identical ultrasound parameters of a single point sonication at 33 acoustic Watts for 30 seconds. The 3-D sequence was used with the following parameters for all runs: 1.5×1.5×3.0 mm spatial resolution; 288×162 mm in-plane FOV; TR/TE = 28/10 ms; EPI factor = 9; bandwidth = 744 Hz/pixel; flip angle = 29°. Runs were performed with increasingly larger data sets and correspondingly longer times to fully sample the data: 16 slices (5.4 seconds per fully sampled data set), 24 slices, (8.1 seconds), 30 slices (10.2 seconds), 40 slices (13.5 seconds), 48 slices (16.2 seconds), and 56 slices (18.9 seconds). These runs were broken into undersampled data sets at data reduction factors of 12X and 6X and temperature maps were created using the proposed approach. To obtain a measurement of the temperature distribution that could be used as “truth”, the sequence was run 3 times with only 8 slices (2.75 seconds), once each at the beginning, middle, and end of the experiment. These 8-slice data sets were reconstructed using a sliding window approach (data reduction factor of 6X for a frame rate of 0.5 seconds) and the standard PRF technique. For each reconstructed data set, the following metrics were calculated to determine how accurately they were able to capture the temporal and spatial characteristics of the true temperature evolution: the maximum measured temperature from the time frame corresponding to the end of sonication; the initial slope of the temperature-time curve for the hottest voxel calculated from the first 6 seconds of heating; the full width at half maximum (FWHM) of the temperature distribution at the time frame corresponding to the end of sonication; the volume of the sample that received a thermal dose of 240 CEM or greater (35); and the root mean square error (RMSE) over a 5×5×15 voxel region and all time frames. Note that for the RMSE calculation: 1) the unequal time steps of the different data sets meant that only the subset of time frames that fell within 0.2 seconds of one another were compared, 2) the time for each sliding window frame was taken to be the middle of the full data acquisition window for the frame.

Applications

To demonstrate the utility of this approach, we present the following example applications. For all experiments, the HIFU heating was performed using a 256-element phased-array ultrasound transducer (f = 1MHz, radius of curvature = 13 cm) MRgHIFU system (IGT, Inc., Bordeaux, France) and imaging was performed in a Siemens 3T TIM Trio MRI scanner (Siemens Medical Solution, Erlangen, Germany).

Characterization of Volumetric Heating Trajectories

The example presented shows temperature mapping for a heating trajectory consisting of a 12-point, 16 mm diameter circle, 200 ms sonication per point, 60 W of acoustic power, repeated 25 times for 60 seconds of total heating. The proposed method was used with 30 k_z phase encodes (26 slices plus 15% oversampling to avoid aliasing in the slice direction) and a data reduction factor of 6X. The reconstruction gave temperature maps with 1.5×1.5×3.0 mm spatial resolution (zero-filled to 0.5 mm isotropic spacing), 288×162×78 mm FOV, and 1.7 seconds per time frame.

Temperature mapping for Transcranial MRgHIFU

In vivo brain imaging was performed without heating using the proposed method with 36 k_z phase encodes (30 slices plus 20% oversampling) and a data reduction factor of 6X. Temperature maps were reconstructed with 1.5×2.0×3.0 mm resolution (zero-filled to 1.0 mm isotropic spacing), 288×216×108 mm FOV, and 1.8 seconds per time frame, and demonstrate the stability, precision, and large coverage of the proposed approach.

Visualization of near- and far-field heating during in vivo MRgHIFU

In this example, the proposed method was used during in vivo MRgHIFU heating of rabbit muscle at 42 W of acoustic power with 30 k_z phase encodes (24 slices plus 25% oversampling) and a data reduction factor of 6X. The resulting temperature maps with 2.0×2.0×3.0 mm resolution (zero-filled to 1.0 mm isotropic spacing), 256×216×72 mm FOV, and 2.0 seconds per time frame show hotspots outside of the ultrasound focal zone that may not have been visualized with 2-D imaging.

Results

Validation

The results from the validation study are summarized in Table 1. The signal-to-noise ratio (SNR) of the 8-slice images was calculated to be 80. Results for the 8-slice imaging runs are given as a mean and standard deviation over the three runs. For comparison, results from a sliding window reconstruction of the data sets at 12X undersampling are also shown. A few trends can be seen. First, as the amount of acquired data increases, the measured values of all metrics show a trend towards greater error for each of the reconstructions shown. For each metric, this error is worst for the sliding window reconstruction, followed by the TCR method at a 12X data reduction factor, and least pronounced for the TCR method at a 6X data reduction factor. The largest errors occur in the measurement of the initial slope of the heating curve, a metric that indicates how well rapid changes in the time dynamics of the temperature evolution can be measured. The remaining four metrics are measured with sufficient accuracy by the 6X TCR method for even the largest data sets.

Table 1.

Results from the validation study. Metrics measuring the maximum temperature, slope of the heating curve at the onset of ultrasound sonication, FWHM of the hotspot, volume dosed to 240 CEM or greater, and RMSE were calculated for all data sets using a sliding window reconstruction at 12X undersampling, TCR reconstruction at 6X undersampling, and TCR reconstruction at 12X undersampling.

	8 Slices	16 Slices	24 Slices	30 Slices	40 Slices	48 Slices	56 Slices
	2.8 sec	5.4 sec	8.1 sec	10.1 sec	13.5 sec	16.2 sec	18.9 sec
Max Temp (°C)
Sliding Window	26.5 (+/− 0.7)	26.9	26.6	25.9	25.8	25	24.6
TCR, 6× reduction		27.1	27	26.1	26.5	26	25.9
TCR, 12× reduction		26.8	26.8	25.9	26.2	25.7	25.5
Slope (°C/sec)
Sliding Window	2.33 (+/− 0.09)	1.86	1.1	0.8	0.71	0.54	0.49
TCR, 6× reduction		2.48	2.18	1.91	1.86	1.73	1.53
TCR, 12× reduction		2.29	1.85	1.75	1.62	1.54	1.37
FWHM (mm)
Sliding Window	4.2 (+/− 0.1) × 14.0 (+/−0.2)	4.1 × 14.2	3.9 × 13.9	3.9 × 13.9	3.9 × 13.9	3.9 × 13.9	3.9 × 13.7
TCR, 6× reduction		4.1 × 14.4	4.0 × 14.1	4.1 × 14.3	4.1 × 14.4	4.1 × 14.4	4.1 × 14.2
TCR, 12× reduction		4.1 × 14.1	4.1 × 14.1	4.1 × 14.1	4.1 × 14.3	4.1 × 14.3	4.1 × 14.2
Vol. Dosed (mm3)
Sliding Window	71 (+/− 3)	69	65	65	64	62	59
TCR, 6× reduction		72	70	68	71	68	68
TCR, 12× reduction		71	70	67	67	68	66
RMSE (°C)
Sliding Window	0.24 +/− 0.01	0.36	0.38	0.47	0.47	0.51	0.63
TCR, 6× reduction		0.38	0.38	0.45	0.36	0.39	0.44
TCR, 1× reduction		0.38	0.38	0.46	0.42	0.46	0.51

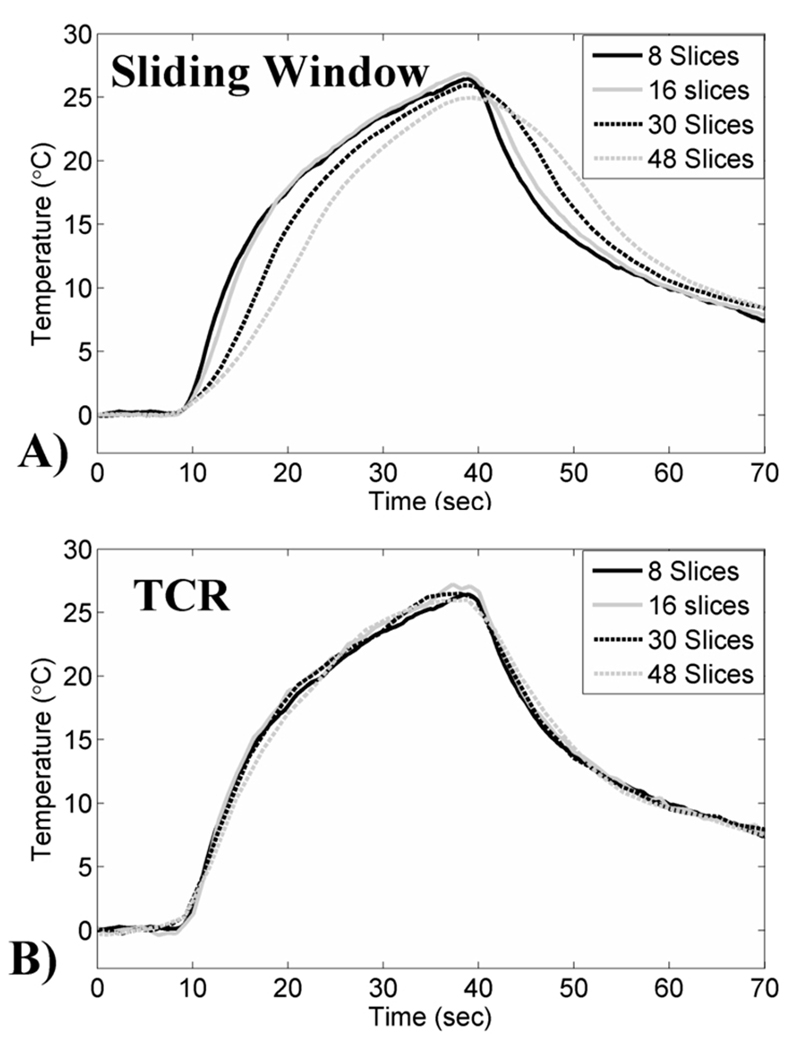
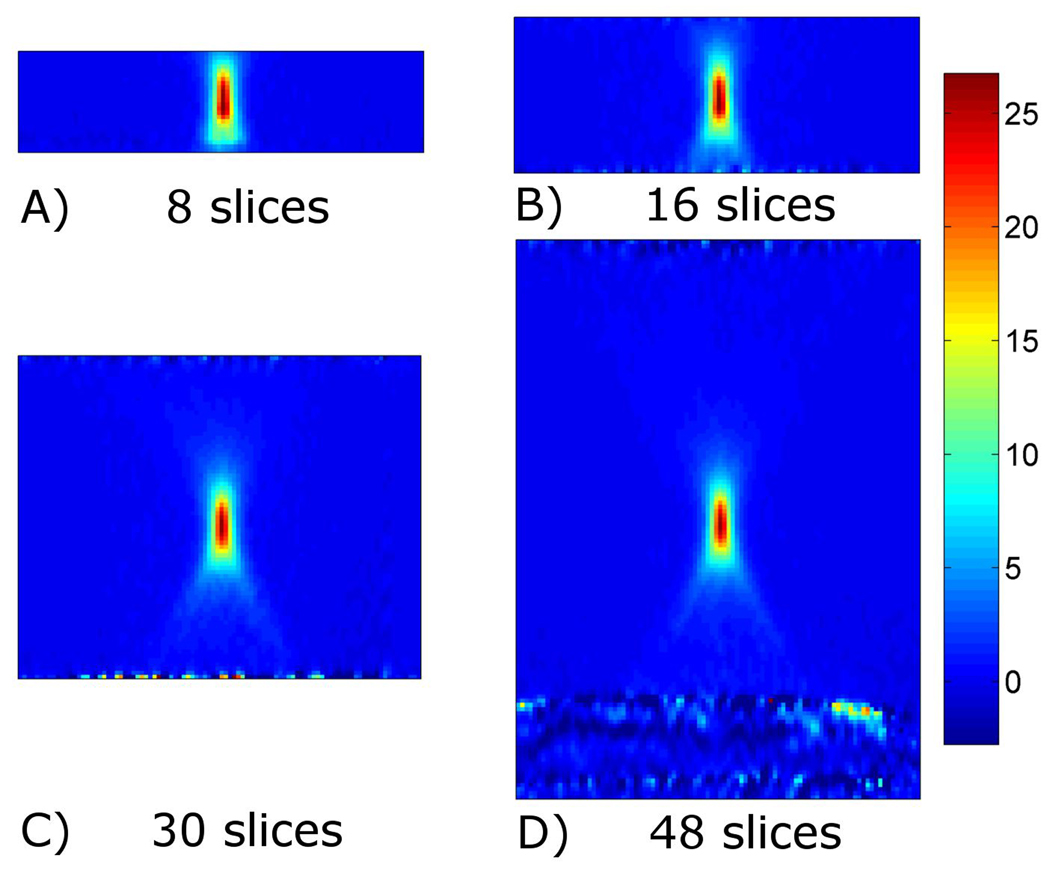
Four representative temperature plots from different heating runs are shown in Figure 1. Figure 1A shows the plots for the sliding window reconstruction, where the time averaging effects are seen to get worse as the amount of acquired data increases. Figure 1B shows the corresponding plots for the data reconstructed using the 6X TCR method, where it can be seen that the time averaging effects are significantly reduced. Figure 2 shows temperature maps at the end of sonication reconstructed using the 6X TCR method for each of these four runs.

Figure 1.

Temperature-time plots from the validation study. A) Data reconstructed using a sliding window approach with 12X undersampling. Time averaging effects can be seen in the temperature curves for the larger data sets. B) The same data reconstructed using the proposed TCR approach with 6X undersampling.

Figure 2.

Temperature maps using the proposed TCR approach with 6X undersampling. Transverse slice through the 3-D temperature volume at the time of greatest temperature increase shown for data acquired with 8, 16, 30, and 48 slices.

Applications

Characterization of Volumetric Heating Trajectories

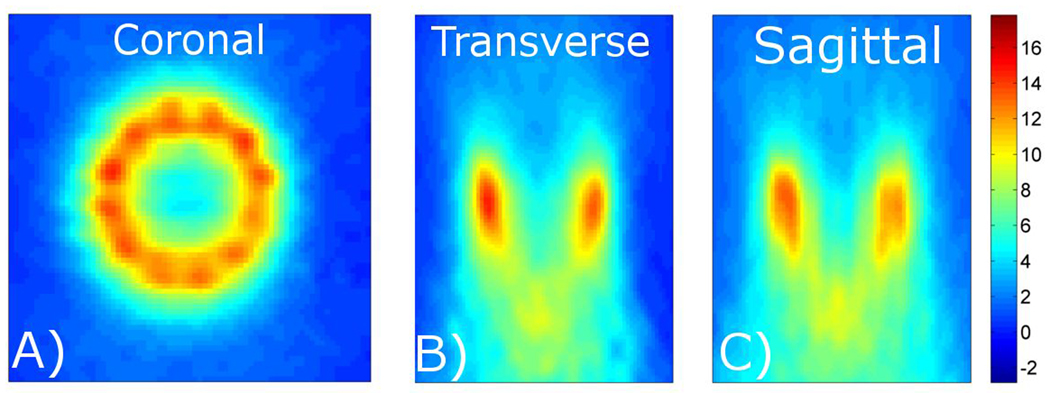
Figure 3 shows three orthogonal slices through the 3-D temperature volume reconstructed using the proposed method. The SNR of these images was calculated to be 43. The temperature map covers the entire volume over which the circular heating trajectory induced significant temperature rises. The coronal slice through the center of the focal zone clearly shows the 12 separate foci. The transverse and sagittal slices show the temperature distribution in the near and far fields of the ultrasound beam path.

Figure 3.

Characterization of a volumetric heating trajectory. The proposed approach is used to acquire 3-D temperature maps with 1.5×1.5×3.0 mm spatial resolution (zero-filled to 0.5 mm isotropic spacing), 288×162×78 mm FOV, and 1.7 seconds per time frame. Coronal, transverse, and sagittal slices through the 3-D volume are shown.

Temperature mapping for Transcranial MRgHIFU

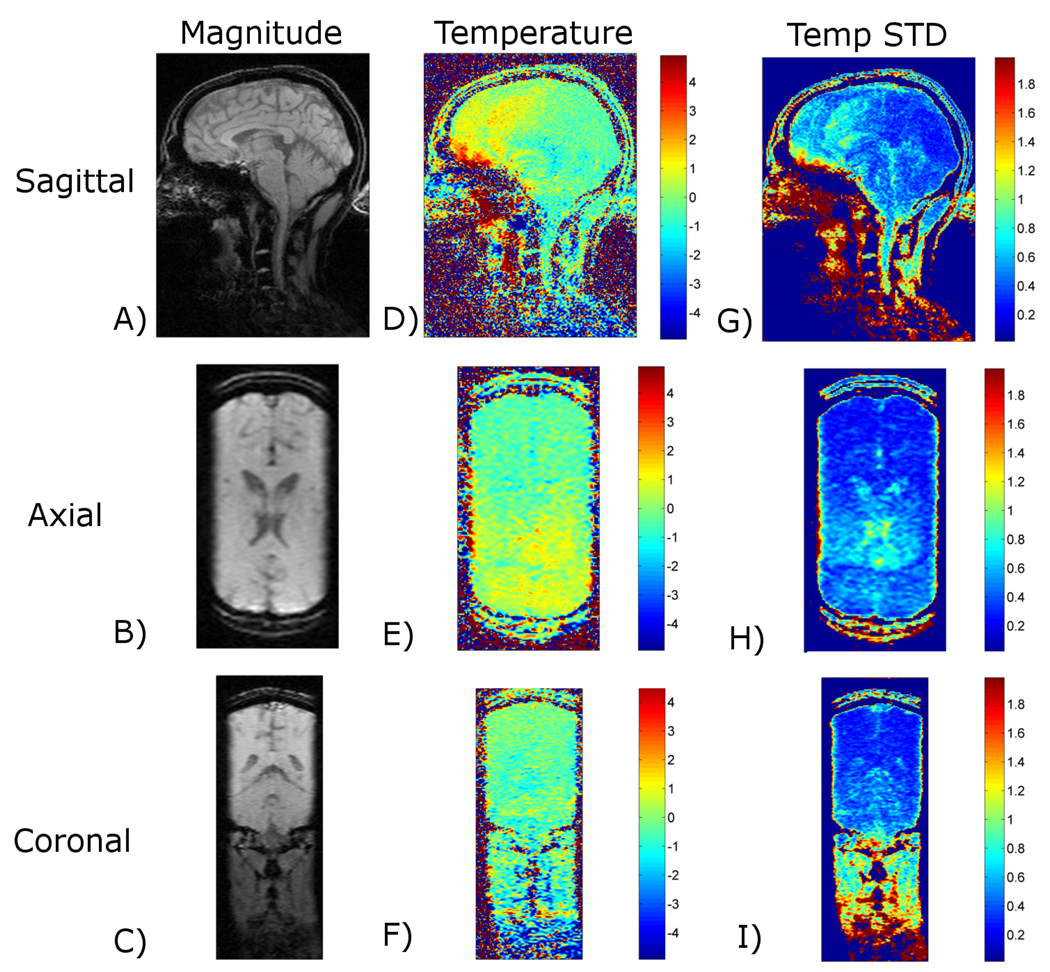
Figure 4 shows data reconstructed using the proposed method from in vivo human brain imaging without heating. The SNR of these images was calculated to be 33. The first column displays the magnitude images, the second column displays temperature maps, and the third column displays the pixel-by-pixel temperature standard deviation over time. The three rows show sagittal, axial, and coronal slices through the 3-D volume. For most regions of the brain, the temperature uncertainty (standard deviation) is less than +/− 1°C, with a few small areas rising just above +/− 1°C.

Figure 4.

Temperature mapping for transcranial MRgHIFU. The proposed approach is used to acquire 3-D temperature maps during in vivo brain imaging with 1.5×2.0×3.0 mm resolution (zero-filled to 1.0 mm isotropic spacing), 288×216×108 mm FOV, and 1.8 seconds per time frame. The rows shown sagittal, axial, and coronal slices through the 3-D imaging volume and the columns show magnitude images, temperature maps, and temperature standard deviation maps.

Visualization of near- and far-field heating during in vivo MRgHIFU

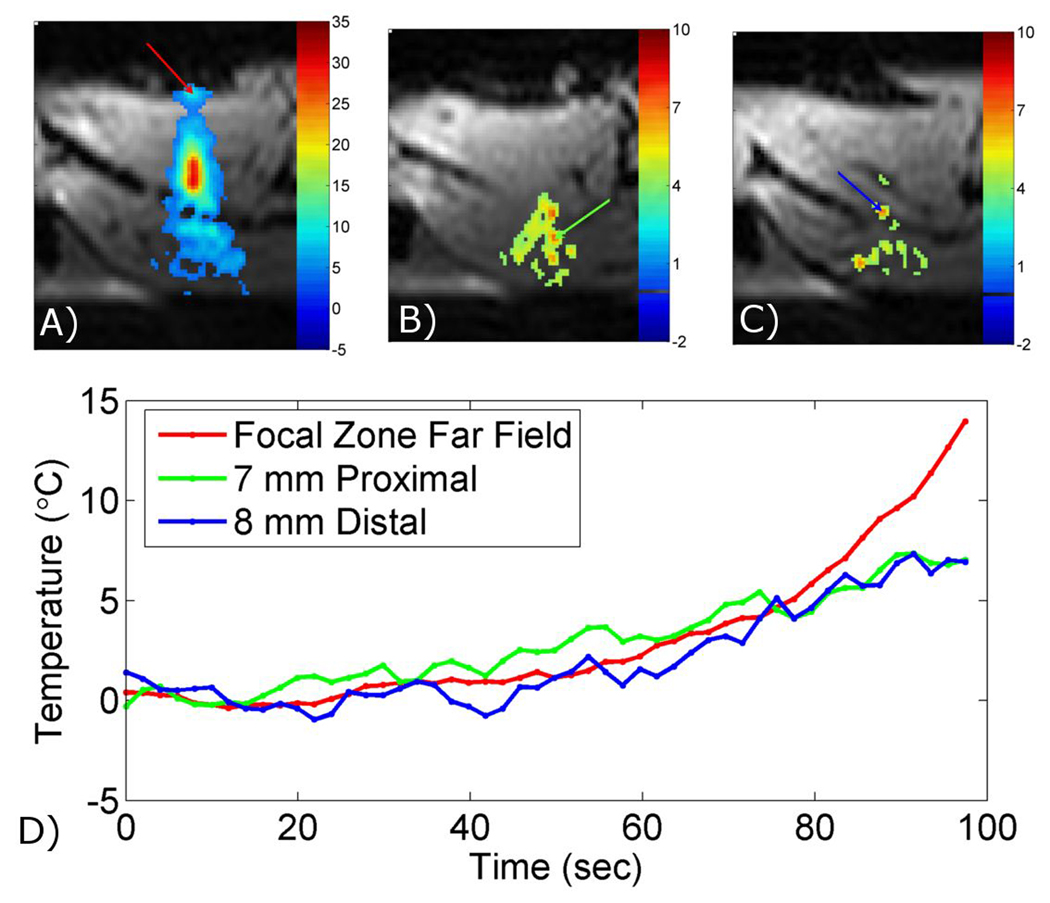
Figure 5 shows an example of inadvertent heating that can occur outside of the ultrasound focus. The SNR of these images was calculated to be 34. The three images are transverse temperature maps overlaid on magnitude images from in vivo HIFU heating of a rabbit thigh. Figure 5A shows a plane through the focal zone, where the temperature increase was approximately 30°C above body temperature at the focal spot, and also a hotspot in the far field that occurred at a tissue/air interface (red arrow). Figures 5B and 5C show two images with hotspots outside of the focal zone that reached more than 6°C above body temperature (green and blue arrows). These hotspots occurred 7 mm proximal and 8 mm distal, respectively, from the focal zone. Temperature-time plots are shown for the three hotspots in Figure 5D.

Figure 5.

Visualization of near- and far-field heating during in vivo MRgHIFU. The proposed approach is used to acquire 3-D temperature mapping during in vivo HIFU heating of a rabbit thigh muscle with 2.0×2.0×3.0 mm resolution (zero-filled to 1.0 mm isotropic spacing), 256×216×72 mm FOV, and 2.0 seconds per time frame. Images show temperature change overlaid on magnitude images. A) Transverse slice through the focal zone showing heating at a tissue/air interface in the ultrasound far field (red arrow). B) & C) Transverse slices 7 mm proximal and 8 mm distal, respectively, from the focal zone showing heating at a tissue/tissue interfaces in the ultrasound near (green and blue arrows). D) Temperature curves from the three locations shown in A), B), and C).

Discussion

We have presented a method for obtaining MR temperature maps with good spatial resolution, high temporal resolution, and large volume coverage. Despite the limitation of needing retrospective reconstruction, the approach still has significant utility as a tool for pre-clinical research being carried out on minimally invasive MR-guided thermal therapies. As shown in the example applications, the 3-D TCR temperature maps have a number of advantages over the multi-slice 2-D temperature maps that are currently used by most investigators. The 3-D temperature maps cover a much larger field-of-view without sacrificing significant spatial or temporal resolution. For MRgHIFU treatments, this allows visualization of a much greater portion of the ultrasound propagation volume, and therefore important potential heating effects that may occur in the near- and far-field regions of the ultrasound beam can be analyzed. The contiguous nature of the 3-D volume also means that there are no gaps in the temperature maps. And finally, because the data is acquired using a 3-D MR sequence, zero-filled interpolation can be applied in all three directions for arbitrarily small voxel spacing that will help to reduce partial volume effects.

The validation results indicate that the amount of 3-D data to be acquired should be application dependent. The proposed approach is quite good at accurately representing spatial characteristics of a heating distribution. The largest errors occur at times when the temperature is changing sharply in time (i.e. large second temporal derivatives). For applications that will induce large, abrupt changes in the temperature, (e.g. single point heating at high power), a smaller 3-D data set may have to be acquired in order to accurately measure the temporal dynamics. However, if those changes are not important for the study, or if the study is using a heating trajectory that will raise the temperature more gradually (e.g. scanning through multiple points and/or low power), then a much larger 3-D data set can be obtained. For regions where the temperature changes are the slowest, a simple sliding window reconstruction would suffice.

As currently implemented, the proposed 3-D temperature mapping technique has two notable limitations. First, it is not designed for use in the presence of motion occurring inside the field of view (although is able to handle motion occurring outside the field of view). The TCR algorithm assumes that the image volume is stationary, and therefore artifacts will appear in the reconstructed images if motion occurs inside the field of view during imaging. Second, as previously noted the algorithm cannot currently be used for real-time applications. The first hurdle that needs to be overcome for real-time use is implementing the algorithm such that it uses only data up the current time frame (instead of the entire 4-D set). This has been investigated previously for a 2-D implementation of the method (28) and future work will be done to implement and validate this approach for the current 3-D version. The second hurdle requires reducing the computation burden so that the images are reconstructed with acceptable latency (e.g. less than 1 second). To achieve these time gains, the data matrix size could be cut in both the time dimension and the read-out dimension such that only the focal zone is reconstructed using the TCR algorithm while the more slowly changing regions are reconstructed using the much more efficient sliding window approach. The remaining time savings would have to come from faster computer processing speed or an improvement over the currently used gradient descent algorithm for convergence.

Conclusion

This work has demonstrated that the 3-D TCR algorithm has the ability to measure MR temperature maps with good spatial resolution, high temporal resolution, and large volume coverage. The technique is currently limited to situations where motion is not present, and where the temperatures can be used retrospectively. While trade-offs between coverage, resolution, and speed still exist and must be appropriately chosen for the particular application, the method allows for a much greater amount of data to be acquired without sacrificing temporal resolution. The additional coverage and/or spatial resolution provided by this data would be greatly beneficial for a variety of MRgHIFU research applications.