Abstract
Micro-RNAs (miRNAs) play a crucial role in post-transcriptional gene regulation by pairing with target mRNAs to repress protein production. It has been shown that over one-third of human genes are targeted by miRNA. Although hundreds of miRNAs have been identified in mammalian genomes, the function of miRNA-based repression in the context of gene regulation networks still remains unclear. In this study, we explore the functional roles of feedback regulation by miRNAs. In a model where repression of translation occurs by sequestration of mRNA by miRNA, we find that miRNA and mRNA levels are anti-correlated, resulting in larger fluctuation in protein levels than theoretically expected assuming no correlation between miRNA and mRNA levels. If miRNA repression is due to a catalytic suppression of translation rates, we analytically show that the protein fluctuations can be strongly repressed with miRNA regulation. We also discuss how either of these modes may be relevant for cell function.
Keywords: microRNA, negative feedback regulation, sequestration model, mean field theory, kinetic suppression model, linear noise approximation
1 Introduction
miRNAs are short (on average of 22 nucleotides long), non-coding RNA molecules that act as post-transcriptional regulators [1]. miRNAs regulate gene expression by base-pairing to target mRNA molecules at conserved sites in the 3′untranslated regions of mRNAs, ultimately leading to a reduction in the levels of protein encoded by the target mRNA [2]. Extensive evidence suggests that this suppression can occur by either the repression of translation or induction of mRNA degradation. In the former, miRNAs act as catalytic factors, preventing the initiation of translation, suppressing the production of proteins. In the latter, miRNAs act in a non-catalytic fashion, leading to the degradation of the target mRNA and the miRNA itself. Through either mechanism, miRNAs can keep gene products at extremely low copy numbers. Although thousands of mammalian genes are potentially targeted by miRNAs [2] and miRNAs have been identified as the primary negative regulators of gene expression, the functions of miRNAs in the context of gene networks are still not well understood [3, 4, 5, 6].
Of particular relevance is the accumulating evidence that small non-coding RNAs combine with trancsriptional activators and repressors to regulate key developmental events [4, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]. Bioinformatic analysis have identified an abundance of negative feedback motifs involving miRNAs and transcriptional activators and repressors that control differentiation [3, 4, 6, 17]. These observations imply the existence of considerable crosstalk between the miRNA-mediated posttranscription layer, and the transcriptional regulation layer, whose dominant players, the transcription factors (TFs), regulate the production of protein-coding mRNAs. Analysis of transcription factor mediated feedback loops suggests that they serve to maintain protein expression at a fixed level. In this way, negative feedback loops buffer against fluctuations arising from environmental variations as well as intrinsic stochasticity of biochemical reactions, imparting precision and robustness to regulation of gene expression. However, it is not clear whether miRNA-mediated negative feedback regulation similarly acts to suppress fluctuations in TF numbers. Moreover, it is not known how the feedback regulation of TF levels by miRNAs impact the activation of other genes regulated by the same TFs.
To address these questions, we study the dynamics of a negative feedback circuit consisting of a TF that activates the production of a miRNA, which in turn acts as a translational repressor of the transcription factor. This model circuit is motivated by a recent study suggesting that transcription factor, pitx3 and the microRNA, miR-133b, form a negative feedback circuit in midbrain dopamine neurons [4]. Pitx3 is a transcription factor for genes that mark the differentiation of precursor cells into dopaminergic neurons in the mammalian midbrain. These neurons release dopamine, an important neuromodulator involved in motivated behavior, learning and memory, and the loss of these neurons results in Parkinson’s disease. miR-133 suppresses the translation of pitx3 mRNA while pitx3 induces transcription of miR-133b. Thus, the control of pitx3 levels by this feedback circuit may play a vital role in the maintenance and survival of dopaminergic neurons.
We propose two simplified models which implement the non-catalytic and catalytic mode of translational repression by miRNA: which we term the sequestration model and the kinetic suppression model respectively. We show that these arise as limiting cases of a more complete model of miRNA based repression. We characterize and compare the steady-state behavior and noise properties of the two different modes of action of miRNA in this circuit. Specifically, we ask 1) how is the intrinsic noise of a gene network influenced by miRNA regulation and 2) whether miRNA: mRNA degradation and degradation-independent translational repression have a similar effect on the noise properties of the network. Finally, we show that these two modes of translational repression have distinct effects on genes controlled by the common transcription factor.
2 Results
miRNAs are transcribed from independent miRNA genes or are portions of introns of protein-coding RNA polymerase II transcripts as precursor RNAs that are processed by the enzymes, Dicer and Drosha. The processed miRNA is assembled into a characteristic stem loop structure, cleaved into single strands and loaded onto specialized proteins of the Argonaute (Ago) family, forming an RNA-induced silencing complex (RISC). The RISC complex can then bind to its target mRNA at complementary sequences (7–8 nucleotides long) in the untranslated 3′ region of the target. This binding leads to suppression of translation in a number of different ways [18, 19]. Perfect or almost perfect complementary leads to the cleavage of miRNA-mRNA duplex [1, 20]. However, this mechanism is relatively rare in animals [1, 21]. Instead, miRNAs tend to destabilize mRNAs by deadenlylation, leading to marked reduction in their abundance, and a consequent decrease in protein levels. The most prevalent mechanism of miRNA action is to repress translation by blocking steps in translation initiation or elongation [1, 19]. The repressed mRNAs accumulate into specialized protein aggregates called P-bodies, where they are either degraded or stored. Importantly, accumulation of miRNA/mRNA complexes into these P-bodies is correlated with fewer translating ribosomes, leading to lowered translational output for that mRNA. In all cases, mRNA and miRNA can pair with each other in a stoichiometric fashion and move to a translationally incompetent pool.
Extensive work has shown that the complex machinery of gene expression can be described by a coarse-grained model that treats transcription of mRNA and translation of the mRNA message into proteins as discrete events, lumping together many of the component steps into single processes. We assume that the gene encoding the transcription factor (TF) is transcribed at a rate αm, possibly specified by upstream environmental factors and translated from the mRNA at a constant rate kp. The TF is degraded at a constant rate γp. The transcription factor in turn activates miRNA synthesis. Thus, the rate of miRNA synthesis, αμ is a function of the number of transcription factors modeled as a Hill function: , where σ is the constant transcriptional rate with sufficient TFs, kd is the dissociation constant of transcription factor complex from the promoter region of miRNA gene, and n is the Hill coefficient. A coefficient of one indicates TFs bind to the gene regulatory region independently of each other and coefficients greater than one indicate positive cooperativity between TFs. As many TFs dimerize and activate the transcription of the miRNA (i.e., fos/fos, fos/jun, creb, etc.), we choose a Hill exponent of 2. Thus, the transcriptional rate of miRNA can be written as . This implicitly assumes that the dimerization of the transcription factors and their binding to the miRNA gene promoter is rapid relative to other timescales in the system. However, we note that relaxing the dimerization assumption does not qualitatively alter our results below. Note that here we have assumed that the promoters of the TF and miRNA genes are always active with no “bursting” due to remodeling of the chromatin environment [22, 23, 24]. Both mRNA and miRNA are degraded at constant rates γm and γμ respectively. Figure 1 shows a schematic diagram of the generic miRNA based feedback network. The component processes of translational regulation by miRNA have been described by Levine et al. and can be generalized to include the negative feedback (Supplementary Information). A key parameter in this model the probability with which miRNA is co-degraded with the mRNA in the processed state. Considering the limit where miRNA and mRNA interact as an irreversible second-order process that forms a RISC complex at a constant rate κ, yields the “sequestration model ”. Importantly, we note that the suppression of translation following miRNA/mRNA interaction is relatively rapid [18], justifying our assumption that the mRNA/RISC complex is effectively incapable of translation. On the other hand, assuming that the miRNA is released and available for reuse leads to a model where miRNAs act catalytically to suppress translation leads to a second model, which we term the “kinetic suppression model”. Below, we analyze the steady-state and noise properties of the miRNA-based feedback network in the two limiting cases and postpone the discussion of the more complete model to a later publication.
Figure 1.
Schematic illustration of the miRNA-mediated negative feedback loop.
2.1 Sequestration model
A large body of evidence suggests that gene expression is inherently stochastic in nature [22, 23, 25, 26, 27, 28, 29, 30, 31], with both intrinsic fluctuations generated by the noisy timing of individual chemical reactions and extrinsic fluctuations due to environmental and other cell-extrinsic factors. Assuming that the intermediate states of the miRNA-mRNA complex are at steady-state, the phase space of the network is characterized by the following three variables, the mRNA number, m, the miRNA number, μ and the protein number, p. The probability of having m mRNA, μ miRNA and p protein molecules at time t thus satisfies the following master equation:
| (1) |
where P (m, μ, p) is the joint probability for mRNA, miRNA and protein numbers to be m,μ and p respectively. The steady state joint distribution, P (m, μ, p) cannot be solved analytically. However, experimentally accessible variables are often not the entire distribution, but the mean molecule numbers and their variance. A generating function approach can be generally used to derive these moments, but the presence of the nonlinear term, κmμ, means that the moment equations do not close. However, some progress can be made by multiplying this master equation in turn by m, μ and p, and summing over all possible m, μ and p, to obtain the familiar mass action equations:
| (2) |
The angle brackets represent the average values of a large ensemble of different realization of these stochastic processes. At steady-state, the average value over large population equals the mean value over the time, showing correspondence between the mass-action and the mean-field models.
2.1.1 miRNA-based feedback introduces an expression threshold
These mass action equations cannot be solved analytically. In the following, we will explore the general steady-state properties and the nature of intrinsic fluctuations within this negative feedback circuit. For concreteness, we fixed some of the parameters based on experimental observations [32, 33, 34, 35]. Specifically γm, γp have been measured in eukaryotic cells. Across the population, typically , i.e., protein life times are significantly longer than their mRNA. Since the rates of degradation of miRNA have not been extensively measured, we assumed γm = γμ. In order to make analytic progress, we derive a mean-field model by assuming that the miRNA and mRNA numbers are uncorrelated. Then, the nonlinear term in Eq. 13 factorizes to yield 〈mμ〉 = 〈m〉〈μ〉. This allows us to simplify the equations and obtain steady state solutions for the mean-field equations. Under this approximation, mRNA production can be treated as a birth-death process, with a birth rate α and an effective degradation rate . Since miRNA-mediated suppression involves an intermediary species, another natural control parameter is the rate of mRNA synthesis itself. As such, this serves as a proxy for upstream control factors, such as environmental signals, developmental events etc., that engage transcriptional machinery to initiate synthesis of the TF. As shown in Figure 2, the mean mRNA number and the mean TF number exhibit a threshold-linear behavior as a function of the mRNA transcription rate αm in this negative feedback loop. This has been previously shown for the case when miRNA serves to repress translation in feed-forward fashion [36] and also appears to be qualitatively operant in a similar fashion even when the miRNA acts in a feedback mode. Thus, in either case, miRNAs serve to impose an expression threshold allowing cells to buffer against environmental fluctuations.
Figure 2. miRNA-based feedback introduces an expression threshold in sequestration model.
The mean value of mRNA (A), miRNA (B) and protein (C) are shown as a function of αm for four different values of the peak miRNA transcriptional rate (σ). When σ is extremely small, m and p are proportional to αm because there is almost no miRNA synthesis. For larger σ, the miRNA-based feedback introduces a threshold at αm ≈ σ. All the asymptotic lines are parallel to each other. γm = γμ = 0.01, γp = 0.002, κ = 1.0, kp = 0.1 and kd = 200.0.
A second natural control parameter is the peak transcriptional rate of miRNA, σ. When it is very small relative to mRNA production (α), (as in Figure 2 for σ=0.01), the miRNA production is very small, almost negligible. Thus, the system can be treated as the simplest case with the property of linear relationship between gene product and αm: 〈m〉 = αm/γm, 〈p〉 = αm * kp/(γmγp).. For larger σ, depending on the value of transcription rate of αm compared to the peak transcriptional rate of miRNA, σ, the system can be classified into three regimes: the repressed regime (αm ≪ σ), the crossover regime (αm ≈ σ) and the expressing regime (αm ≫ σ). While in the repressed regime, mRNA synthesis is strongly repressed by miRNA, keeping overall TF levels very low. This threshold ensures that only strong enough signals, which can drive the αm value to the expressing regime can trigger the synthesis of gene products.
Increasing the strength of the negative feedback, κ, leads to a sharper crossover between the repressed regime and the expressing regime until it reaches a saturating value as shown in Figure 3. Beyond the threshold (α ≈ σ), i.e., in the expressing regime, there is a linear relationship between the number of mRNA (m), TFs (p) and αm and the slope of the 〈m〉-αm curve represents the sensitivity of the system in response to external signals. Both m and p are proportional to . The linearized relationship between < p > and αm is plotted as black line in Figure 3, denoted by . While the mRNA and protein abundance show a threshold-linear behavior, the miRNA levels within this feedback circuit exhibit a non-monotonic behavior (Figure 2B): at low mRNA synthesis rate, there is very little synthesis of the TF and consequently, the synthesis of the miRNA is low. At high synthesis rates, most of the miRNAs stoichiometrically combine with mRNAs and accumulate in the translationally inactive pool. Since the mRNA is in excess, all the miRNAs are consumed, leaving a large number of translationally competent mRNAs that can engage in synthesis of the TF protein. Moreover, since this pool does not feel the effect of miRNA based repression, the effective degradation rate of this excess pool of mRNAs is the native degradation rate of the mRNA, γm. We note that the non-monotonicity of mean miRNA number and the threshold linear behavior of the mean protein levels are observed for a wide variety of parameter combinations.
Figure 3. Increasing miRNA-mediated feedback strength sharpens the expression threshold.
Mean protein numbers as a function of upstream transcription rate. The different curves show how threshold expression depends on the strength of miRNA/mRNA association rate. Mean protein expression shows a crossover regime from low expression to linear expression with increasing transcription rate. As the strength of miRNA/mRNA association, κ, increases, the threshold becomes sharper. The solid curve is a perfect threshold-linear behavior. The parameters are set as γm = γμ = 0.01, γp = 0.002, σ = 0.5, kp = 0.1, kd = 200.0.
2.1.2 miRNA based negative feedback amplifies noise in the sequestration model
A conventional interpretation of negative feedback motifs in genetic circuits is that they generally serve to decrease expression noise, suppressing fluctuations while maintaining near constant mean levels of the components. However, depending on the timescales of the various component process (RNA polymerase binding, repressor multimerization and binding etc.), noise levels can moderately increase relative to unregulated systems with increasing negative feedback strength [37, 38, 39, 40, 41]. These insights have been derived from examining the behavior of genetic circuits that involve genes that code for repressor proteins that block their own transcription by binding to promoter (or promoter-proximal) regions of their own genes. In order to assess the impact of miRNA based negative feedback, we next examined the intrinsic noise properties of our network using the Fano factor as a measure of the fluctuations. The Fano factor [42] is typically independent of system volume and measures how much the size of internal fluctuations deviates from what is expected from Poisson statistics, for which the Fano factor equals one.
We first consider how noise properties depend on environmental control signals that are encoded in the parameter αm, the synthesis rate of the target mRNA. The mean field model states that steady state mRNA number should reach a Poisson distribution with Fano factor, (the ratio of the mRNA number variance and mean) . The Fano factor of the TF can be readily calculated to be
| (3) |
As expected, the Fano factor for protein numbers is larger than 1, because each mRNA leads to the synthesis of a burst of proteins before degradation, with a ”burst” size of [38]. In the mean-field model, the effect of the miRNA is to increase the degradation rate of mRNA, leading to a smaller burst size and lower variability. In order to validate our assumptions, we used the Gillespie algorithm to perform stochastic simulations of the full model. We find that the mRNA and miRNA levels are strongly anti-correlated (Figure 4), with periods of high mRNA levels corresponding to low miRNA levels and vice versa, as has been widely noted in experiment [43]. This can be understood as follows: increases in mRNA levels lead to the synthesis of the TF, which then leads to the transcription of the miRNA. These miRNA molecules can now bind to the mRNA, and move them to the translationally inactive pool, resulting in a net loss of both mRNA and miRNA. However, if the mRNA levels are high to begin with, most of the miRNA molecules are saturated, with only an excess of mRNA levels remaining. On the other hand, a large fluctuation in miRNA levels reduces mRNA numbers stoichiometrically, leaving excess miRNA free. These observations imply that our assumption that the nonlinear term can be factorized is invalid and that the effective degradation rate must include the effects of this correlation between mRNA and miRNA levels. Moreover, since the correlation is negative, we would expect that the effective degradation rate be smaller than when there is no miRNA-based translational repression. Consequently, we should see an increase in the effective burst size, and hence a larger Fano factor for protein fluctuations than without miRNA-mediated repression.
Figure 4. miRNA and mRNA levels are anti-correlated.
Temporal evolution of mRNA (black) and miRNA (gray) in a Monte-Carlo simulation of the sequestration model using the Gillespie algorithm. The parameters are set as αm = 1, γm = γμ = 0.01, γp = 0.001, κ = 1.0, σ = 1.0, kd = 200.0, kp = 0.1. The anti-correlation suggests that assuming 〈mμ〉 = 〈m〉〈μ〉 is not valid.
To verify our intuitive observations, we conducted large scale simulations to study the noise properties of the network as a function of key control parameters. Surprisingly, the Fano factors of all three components showed non-monotonic behavior as αm was increased, with peak Fano factors well in excess of what is predicted by the mean field model as well as the case of the unregulated gene (Figure 5). Furthermore, the non-monotonicity is obtained over a wide range of values for the negative feedback strength κ, peak miRNA transcription rate, σ and protein synthesis rates kp (data not shown). Moreover, we find that the mean field model is only applicable in certain limiting regimes. If the mRNA synthesis rate, αm is much smaller or much larger than σ, the mean field model can capture the noise properties of the system. In the case where αm is low and m ≪ μ, the mRNA is strongly repressed by miRNA. Because of the excess miRNA, 〈μ〉, the denominator is large in Eq. 3 is large and thus the Fano factors of mRNA and TF are small. On the other hand, when m ≫ μ, the miRNA number is strongly repressed due to the binding of mRNA and miRNA, leaving the excess mRNA translationally active. Thus, the effect of miRNA regulation diminishes and can be neglected. In this case, the Fano factor of both mRNA and protein number asymptotically tends to the value where there is effectively no miRNA-mediated repression, i.e., , which is plotted as the asymptotic line in Figure 5. This is also in accordance with Eq. 3 while κμ → 0. Interestingly, when am ≃ σ, i.e., the synthesis rates of mRNA and miRNA are comparable, the Fano factors of mRNA and TF numbers are much larger than the mean field prediction as can be seen in Figure 5. This amplification is due to the anti-correlation between the mRNA and miRNA. Noise in stoichiometrically coupled systems such as miRNA-based gene regulation has been studied earlier [44, 45, 46, 47]. These studies suggest the existence of a crossover regime characterized by enhanced stochastic fluctuations. This near-critical behavior is reminiscent of the critical fluctuations near phase transitions [48]. Accordingly, we find that the TF number distribution shows a long tail (Figure 5D), which suggests that while negative feedback by miRNA keeps the mean TF number low, there can be large temporal or population variation. This variation naturally arises because the effect of miRNA is to reduce the overall number of mRNA. Thus any surviving mRNA has to rapidly engage in a burst of translation before it is consumed either by mRNA decay or binding to a miRNA-loaded RISC complex. We will examine the effect of this variation in a gene cascade in a later section. Moreover, we note that such large fluctuations in the protein levels can be obtained even without transcriptional bursting, i.e. for promoters that are continuously active.
Figure 5. Negative feedback amplifies expression noise in the sequestration model.
(A)–(C). Fano factor of mRNA, miRNA and protein are plotted versus αm. Solid lines represent the simulation results and dashed lines represent the analytical calculation from the mean field model. The mean field model cannot be used to describe the system around the threshold, where the mRNA and miRNA levels are comparable. The solid straight line in (C) represents the asymptote for protein Fano factor value for large αm. (D). Histogram protein numbers at steady state for αm = 1.0: the mean values are 〈p〉 = 600, . The protein distribution shows a long tail, which suggests that while mean values may be kept low, protein numbers can exhibit large values across the population allowing the transcription factor to act at promoters with widely different sensitivities.
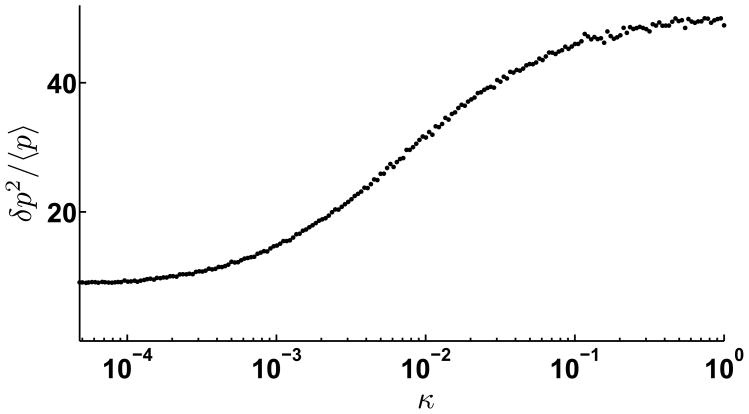
We next examined the noise properties as a function of the strength of negative feedback, in this case represented by the bimolecular association rate, κ. We focused on the region where the noise properties of the network are amplified relative to no miRNA based feedback. Thus, we fixed α = 1.2, a value around which the Fano factor of TF levels peaks (Figure 5C), to see how the Fano factor varies with the strength of negative feedback. While κ = 0, there is no negative feedback, the noise in the system is at a minimum as shown in Figure 6, which is close to that of an unregulated system. As κ increases, the interaction between mRNA and miRNA is strengthened and the noise in TF numbers become larger. Then finally, when κ is very large, the Fano factor saturates to an asymptotic value, much larger than that for an unregulated gene. The limiting values of the Fano factor with increasing feedback strength are distinct from the case of negative feedback mediated by a protein repressor, where increasing the strength of negative feedback (i.e. the affinity of the repressor to the gene promoter) for a fixed transcription rate increases the Fano factor over what would be expected for an unrepressed gene while tending to a lower value for weak and intermediate feedback strengths [37, 39, 40, 41]
Figure 6. Expression variability increases with negative feedback strength.
Fano factor of TF numbers is plotted versus the strength of bimolecular miRNA-mRNA association rate, κ for sequestration model. The transcription rate, αm = 1.2, at the cross-over point in Figure 3. Other parameters were set at γm = γμ = 0.01, γp = 0.001, σ = 1.0, kp = 0.1, kd = 100.0. For κ =0, there is no miRNA-mediated translational repression, and Fano factor is the lowest. The Fano factor increases with κ, until it reaches a saturating value.
However, we note that the origins of the increased fluctuations are similar. For protein-based repression with a given transcriptional rate, the high affinity of the repressor implies that most of the time, the gene is inactive with few mRNAs being transcribed. Upon brief dissociations of the repressor from the gene, transcription can commence and result in bursts of synthesis of both mRNA and the repressor protein. Thus, the effective timescale of these bursts is determined by the dissociation rate of the repressor. For repressors with weak affinity to the promoter, this additional noise source vanishes as the repressor-gene interaction approaches steady-state and the Fano factor tends to an asymptotic value , the burst size, b = kp/(γm+γp) is the average burst size and η = γp/γm. On the other hand, in miRNA mediated feedback repression, increasing the miRNA/mRNA association rate lowers the overall mRNA levels, leading to rare bursts of synthesis, while reducing it approximates a situation with no feedback regulation. In summary, in the sequestration model, miRNA-based negative feedback in physiologically relevant regimes actually amplifies the noise relative to what would be expected either in case of a protein-repressor mediated feedback [38] or the case where there is no feedback.
2.2 Kinetic suppression model
Given the abundance of miRNA and the diversity of targets for a single miRNA, under some conditions, translational regulation by miRNA can be considered to act catalytically, i.e., miRNAs bind to mRNA at the regulating sites and repress translation initiation or elongation with the number of miRNA itself being unchanged. This scenario is valid under conditions of relatively weak miRNA/mRNA binding and large miRNA concentrations. We represent this catalytic mode of action by assuming that the miRNAs act in a Michaelis-Menten fashion to repress translation (see Supplementary Information). The transcription of mRNA and miRNA as well as the degradation of mRNA, miRNA and TF protein have the same form as in the previous (sequestration) model. We model the translational repression by taking translation rates to be decreasing Hill functions of the number of miRNA regulatory molecules. i.e., . In the circuit analyzed here, we denote β as the strength of negative feedback representing the effect of the control of TF synthesis by the miRNA. Given the abundance of the components, we model the post-transcriptional regulation through miRNAs using mass action equations with three molecular species: the number of miRNA molecules μ, the number of target mRNA molecules m, and the number of regulated TF molecules, p [36, 46, 47, 49, 50, 51].
The effect of intrinsic noise is included by Langevin terms, ηm, ημ and ηp denoting the intrinsic fluctuations of the mRNA, miRNA and protein respectively, that describe the statistical fluctuations in the underlying biochemical reactions [52]. The dynamics of these processes can then be described by the following Langevin equations:
| (4) |
The Langevin terms ηi model intrinsic noise by treating the birth and death of the different species as independent Poisson processes, representing the stochastic creation and destruction of mRNA, miRNA and TF. We have dropped the cross-term ηm,μ since we assume that miRNAs act catalytically, where these two levels are uncorrelated.
The Langevin terms are characterized within the linear noise approximation [52] by two-point time correlation functions:
| (5) |
The linear-noise approximation is a good approximation even for nonlinear systems with small fluctuations. This is confirmed by the simulation results which use the exact Gillespie algorithm (see Figure 7 and Supplementary Figure 13). In order to obtain expressions for the noise properties of the different species, we find the steady state solution of the model and then linearize around this to compute the response of the variables m, μ and p to the Langevin forcing terms ηm, ημ and ηp. In the linear approximation, the steady state is also the mean value. So m =< m > +δm, μ =< μ > +δμ and p =< p > +δp. Linearizing the Langevin equations around their steady states, we obtain:
| (6) |
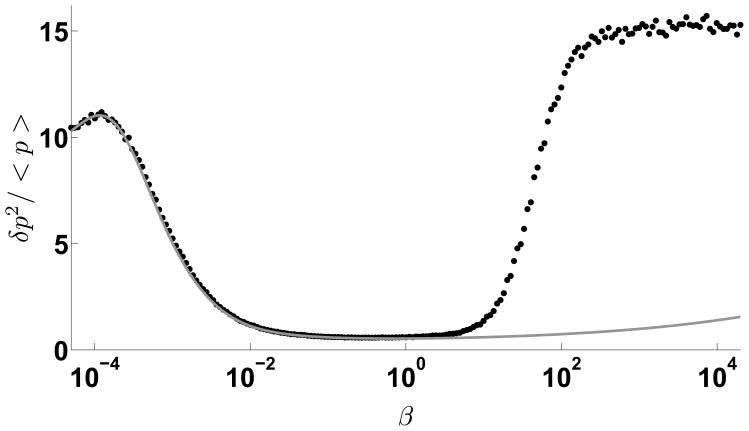
Figure 7. Negative feedback in the catalytic suppression model shows reduced expression variability over a large range of feedback strength.
The Fano factor of TF is plotted versus β for kinetic suppression model. The solid line is the analytical solution from the linear noise approximation method, dots represent results of Gillespie-algorithm simulation. Other parameters are set as: αm = 1.2, γm = γμ = 0.01, γp = 0.001, σ = 1.0, kp = 0.1, kd = 100.0. Although there is a temporary increase of the noise for low feedback strengths, it decreases very rapidly over a long range. For large values of β, linear noise approximation breaks down and single molecule effects dominate. Note that the variability is lower than in the sequestration model.
We now transform these linearized equations into Fourier space, with δ̂i(ω) and η̂i(ω) corresponding to the temporal variables δi(t) and ηi(t) where i equals to m,μ or p in the spectral domain. Thus,
| (7) |
where
| (8) |
Using the Wiener-Khinchin theorem, the spectral density , we can get:
| (9) |
Based on these expressions, we can obtain and using Eq. 7. Next, using the relation to inverse transform back to the time domain, we can get the exact solution of the variance 〈δm2〉, 〈δμ2〉 and 〈δp2〉. (see Supplementary Information) These expressions are somewhat lengthy and we have omitted them for brevity.
2.2.1 Negative feedback represses noise in kinetic suppression model
We now analyze the properties of the number fluctuations of different species in the network. Because in the kinetic suppression model, miRNAs act catalytically to repress the translation of TF, mRNAs are always Poisson distributed. We now focus on the fluctuations in the number of TFs which can be quite different depending on the negative feedback and promoter strengths (Figure 7). When the negative feedback strength β, equals zero, the Fano factor of TF numbers equals . With sufficient production of mRNA (αm not too small), the Fano factor slightly increases from the zero-feedback value for small values of β, i.e. weak feedback strengths. For increasing β, the Fano factor decreases very rapidly to a small value over a long range of β. Note the correspondence between the expressions derived from the linear noise approximation and the full model using stochastic simulations. For very large values of β, denoting large negative feedback, the analytic approximation breaks down since the mean TF levels are small and the relative fluctuations are high. In this case the Fano factor asymptotes to a value above what would be expected for the no repression case.
We next study the effect of varying the strength of negative feedback on the TF number fluctuations as a function of the promoter strength αm (Figure 8). We find that for weak promoters, the effect of negative feedback is to continuously decrease the variability. This is in part due to the fact that weak mRNA production implies an even weaker synthesis of the miRNA itself. However, as the promoter strength is increased, we find the emergence of a peak in the protein number fluctuations at very weak feedback strength, subsequent suppression and then increasing fluctuations for very strong feedback. This latter increase is due to the fact that the fluctuations are large and the small noise approximation breaks down. A substantial amount of experimental evidence suggests that miRNA based translational repression usually serves to reduce mean target protein levels in a modest fashion (2–4 fold reduction) [53]. Thus, we anticipate that the large negative feedback regime considered here is more for the sake of completeness and not meant to represent any physiological situation in general.
Figure 8. Negative feedback strength in the catalytic suppression model affects expression variability for different promoter strength.
The relationship between the Fano factor of TF and β with four different values of αm. γm = γμ = 0.01, γp = 0.002, σ = 0.5, kp = 0.1, kd = 200.0.
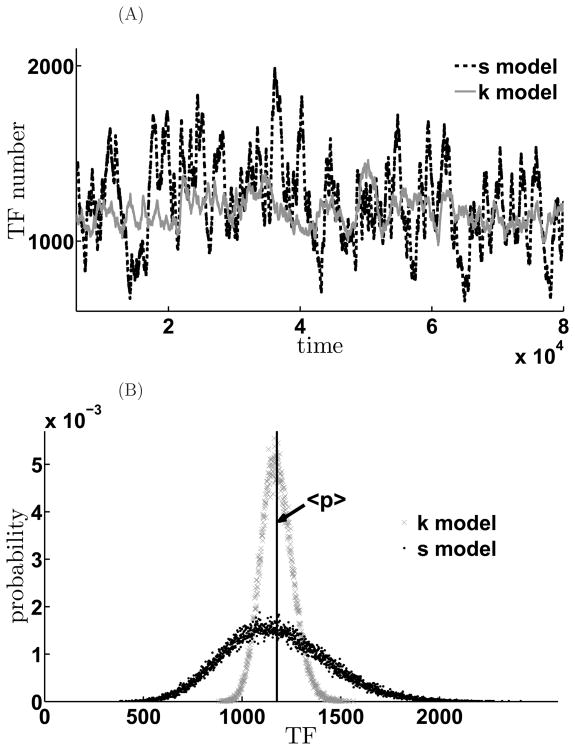
We next compare the noise properties of the feedback network depending on the mode of action of the miRNA. In sequestration model, where miRNA and mRNA pair stoichiometrically and are rendered translationally incompetent, the relevant parameter that determines the extent of negative feedback is the affinity of the bimolecular interaction, κ. On the other hand, in the kinetic suppression model, the strength of mRNA translation is modulated by the parameter, β. In order to compare the noise properties of these two cases, we set all the other parameters the same for these two models and then chose the feedback strength β and κ so that they result in similar mean value of TF but different noise terms (Figure 9A). As shown in Figure 9, the two genetic circuits produce almost the same mean value of the TF, but the population distributions of the TF in the two cases are quite different. In the kinetic model, TF numbers are tightly restricted near the mean value, but distribution of TF in the sequestration model is more broad and is characterized by long tail which indicates that there can be large bursts in the number of TF.
Figure 9. Expression variability depends on the mode of translational repression by miRNA.
Comparison of the different effects on the noise of the two negative feedback schemes. A. Time evolution of the mean TF values for sequestration (black curves) and kinetic suppression model (gray). B. Histogram of the steady state TF distribution for the sequestration model (black) and for the kinetic suppression model (gray). The parameters are αm = 1.1, γm = γμ = 0.01, γp = 0.001, σ = 1.0, kp = 0.1, kd = 100.0, κ = 1.0, β = 0.00087. κ and β are chosen so that their mean TF values are almost the same in both models. In the sequestration model, < p >= 1174.6, , However, in the kinetic suppression model, < p >= 1176.2, . Thus, in K model, both signal and noise are suppressed; while in S model, signal is suppressed, however, noise are amplified.
2.3 The impact of transcription factor fluctuations in gene networks
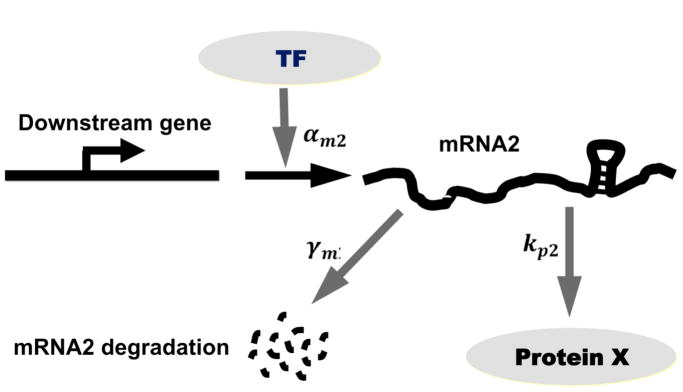
Considering that the miRNA-regulated protein is a TF, the qualitatively different distributions of TF obtained under different modes of feedback regulation by miRNA can affect the transcription of genes that are also regulated by the same TF. Concretely, we envision the genes downstream of the transcription factor pitx3, would exhibit different patterns of gene expression depending on population levels of pitx3. Here, we examine how qualitatively different modes of miRNA based negative feedback affect the transcription of such downstream genes using a simple regulatory cascade as shown in (Figure 10). We assume the transcription rate of downstream genes is a generic Hill function: as shown in Figure 11A. In this study, we choose n = 10 because with large Hill coefficient, the promoter essentially acts like a switch. qualitatively similar results obtain for smaller n. We assume that the downstream protein (p2) is synthesized at a rate kp2 and degraded at a rate γp2, its mRNA is degraded at a rate γm2. We assume that three representative target genes with different dissociation constants, that denote varying promoter strengths, to see how the variability of the TF levels affect the downstream protein distribution (Figure 11A).
Figure 10.
Scheme of transcriptional cascade involving the feedback-regulated TF and a downstream gene.
Figure 11. Scheme of information propagation in downstream gene.
(A). Three different model genes with similar promoter strength (Hill coefficient n = 10.) but with different sensitivities. (B). The TF number histograms are plotted to display their overlap with the expression regions.
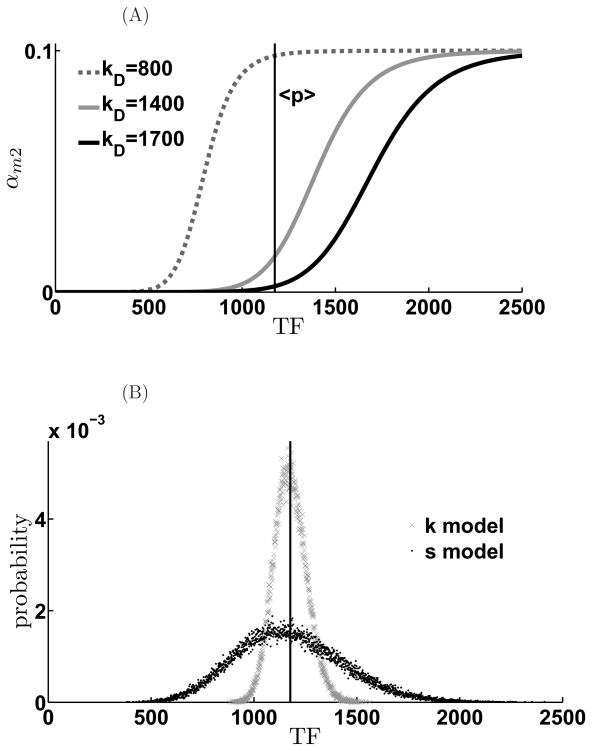
For a highly-sensitive downstream gene, (small disassociation constant), the mean TF number is in the saturation regime. Thus, TFs that are either stoichiometrically or catalytically suppressed are equally effective in driving the expression of the downstream gene (Figure 12A) with similar mean values. However, owing to the switch-like behavior of p2 promoter, the population distribution of p2 is broader when driven by the stoichiometrically suppressed TF as compared to the catalytically suppressed one. In particular, we note the presence of a long tail of low p2 expressors. On the other hand, for a downstream gene with a weaker promoter, i.e. dissociation constant such that the mean TF levels lies in the linear regime of αm2(T F) (the dashed curve in Figure 11A), expression of p2 is reduced. However, the p2 distribution is broad and skewed towards high expressors for the case when the TF is stoichiometrically regulated (Figure 12B). For the extreme case where the dissociation constant of the downstream gene promoter is much higher than the mean TF levels, TFs that are stoichiometrically regulated by miRNA are able to drive considerable expression (Figure 12C) while TFs that are catalytically regulated cannot.
Figure 12. Mode of miRNA-mediated negative feedback can affect noise transmission to downstream genes in transcriptional cascades.
Different noise level effect on downstream gene for different dissociation constants. When KD is small, the downstream gene of both models are triggered. The mean value of downstream proteins in the K model is larger than in the S model. However, while KD increases, although both mean values of downstream proteins decreases, The mean value of downstream proteins in the K model will be smaller than in the S model while KD is over some value because of the long tail noise of S model. (A) KD = 800, (B) KD = 1400, (C) KD = 1700. α = 1.1, γm = γμ = 0.01, γp = 0.001, kd = 100.0, kp = 0.1, κ = 1.0, β = 0.00087, σ = 1.0, ε = 0.1, γm2 = 0.01, kp2 = 0.1, γp2 = 0.001.
3 Discussion
The post-transcriptional control of protein expression in animal cells by micro-RNAs plays an important role in almost every cellular process and changes in their expression may underlie developmental disorders and diseases such as cancer. miRNAs base-pair with seed sequences in the 3′ UTRs of their target mRNA and block steps in the initiation of transcription, sequestering mRNAs into sites of repression or by accelerating mRNA decay [18]. As a result, miRNAs reduce mRNA and protein abundance, often modestly and sometimes sharply [53, 54]. Genome-wide studies have shown that miRNAs target many transcription factors, which in some cases regulate their own transcription. Given the importance of miRNAs in cellular function an analysis of the impact of miRNA-mediated regulation on the mean levels and fluctuations of genetic circuits is vital. Here, we have shown that depending on the mode of miRNA action, negative feedback by miRNA can have differential impact on the noise levels of protein expression. In particular, if miRNAs act in a stoichiometric fashion, whereby both the target mRNA and miRNA are removed from the population into an inactive pool (Figure 1), then negative feedback regulation by miRNA largely amplifies the intrinsic noise in the system, leading to long-tailed distributions of transcriptional factor numbers. Our simulations show that this enhancement of protein number fluctuations is sensitive to environmental factors as seen in Figures 5 and Figure 6. However, if miRNAs act catalytically to repress protein synthesis, the net effect is to reduce variability in protein levels, as would be conventionally expected for a negative feedback circuits.
A number of experimental observations justify the distinction of the modes of miRNA action made in our models. Early studies of miRNA effects seemed to reveal that mRNA degradation was minimal but protein expression was reduced consistent with a catalytic mode of regulation [54]. This could result from imperfect seed sequence complementarity between the miRNA and mRNA, the presence of multiple miRNA targets, weak and reversible association of the target mRNA with the RISC machinery, rapid accumulation of the RISC/mRNA complex into P-bodies or accumulation in stress granules accompanied by the release of the miRNA. More recent studies have shown that mRNA degradation is significant [54]. These could arise from a higher degree of complementarity of miRNA seed sequence in the mRNA 3′ UTR, multiple pairing locations, post-translational modifications of the RISC machinery that enhance binding of miRNA/mRNA and subsequent translational repression and P-body accumulation. These latter effects are best represented mathematically by a sequestration model where both miRNA and mRNA are stoichiometrically degraded. In order to keep the models relatively simple and to gain intuition, we have abstracted many of the intermediate steps, modeling component processes as first and second-order reactions. Such coarse-grained representations have been quite successful in elucidating many aspects of deterministic and stochastic gene networks [38, 55, 56, 57]. We have neglected additional aspects of miRNA biogenesis and function, such as multiple miRNA seed sequences on the same target mRNA, delays in processing mature miRNA from precursor transcripts etc. However, we expect that consideration of these steps would not qualitatively change our results.
Our studies expand the repertoire of miRNA action in gene circuits that govern cell fate specification and commitment during development, processes where miRNA function was first highlighted. The commitment of cells to specific lineages derives from the coordinated expression of different patterns of genes within a relatively uniform population of cells. These expression patterns are then crystallized by downstream gene networks to result in stable expression of lineage specific genes that is maintained throughout the individual’s life. Cell fate choices are often under the control of restricted subsets of upstream transcription factors. How population diversity is achieved from cells that possess identical genomes is a fundamental question of developmental biology. It is well known that genetic circuits with extensive feedback loops, both negative and positive, play an important role in cell fate choices. In particular, feedback imparts a network with multiple steady states, which can denote the multiple cell fates controlled by the network. Moreover, the steady states of feedback circuits are well separated, preventing spontaneous transitions, imparting robustness to the gene circuits controlling cell fates. The role of miRNAs in animal development has been examined in these contexts. Most studies to date have focused on the impact of miRNA-mediated control of the mean protein levels on developmental and cell fate specification circuits [11, 13, 14, 15, 16].
However, miRNAs translational repression also shapes the intrinsic variability within developmental gene networks. Noisy gene expression in developmental circuits has the potential to be harmful leading either to arrested development, aberrant positional expression of tissue specific genes or over-representation of specific cell types. miRNAs are thought to tune the fluctuations of protein expression within developmental networks, buffering them against environmental fluctuations. The imposition of an expression threshold by miRNAs renders the network insensitive to small sub-threshold variations, preventing stochastic transitions between steady states. This has been directly demonstrated in Drosophila, where the miRNA, miR-7, is required to maintain normal gene expression and sensory organ fate determination under fluctuating temperature conditions [15] by buffering the levels of its downstream target, the transcriptional repressor, yan.
Our modeling studies suggest a new role for miRNA-based feedback regulation, namely, by modulating the levels of TFs at the level of translational repression, miRNAs can drive large fluctuations in TF levels across the population. In turn, these fluctuations can drive the expression of different constellations of genes across the population, thereby allowing the expression of multiple cellular phenotypes in a uniform precursor population. Given the extensive complexity of the component processes, cells may be able to tune the manner of miRNA-based feedback, from stoichiometric repression to catalytic repression to tune the level of protein number fluctuations in gene circuits and consequently drive stochastic cell fate choices. A number of recent studies suggest that such tuning may be operant in cells. RISC protein phosphorylation can control the loading of miRNAs [58]. Alternately, the seed site for miRNA binding on the target mRNA may be made more accessible [59]. Thus, cells may control expression noise in miRNA-based negative feedback circuits to determine cell fates in different contexts. In general, cell fate decisions during developmental are robust, in order to generate reproducible body plans. However, in certain cases, cell fate decisions are made at random, generating cell fate diversity. Diversified cell fates in a homogeneous progenitor population increases the spectrum of responses to environmental stimuli. One example is the choice of Rhodopsin type during photoreceptor differentiation in the Drosophila eye [60]. Thus, miRNA based translational repression may serve as an important mechanism that controls fluctuations of protein number promoting cell fate diversity.
Supplementary Material
Acknowledgments
We thank Xiaohua Xu for a critical reading of the manuscript. The work was supported by grants NSF-064200, NIH-DA027807 and NIH-EY019303 to SR.
References
- 1.Bartel David P. Micrornas: genomics, biogenesis, mechanism, and function. Cell. 2004 Jan;116(2):281–297. doi: 10.1016/s0092-8674(04)00045-5. [DOI] [PubMed] [Google Scholar]
- 2.Lewis Benjamin P, Burge Christopher B, Bartel David P. Conserved seed pairing, often flanked by adenosines, indicates that thousands of human genes are microrna targets. Cell. 2005 Jan;120(1):15–20. doi: 10.1016/j.cell.2004.12.035. [DOI] [PubMed] [Google Scholar]
- 3.Tsang John, Zhu Jun, van Oudenaarden Alexander. Microrna-mediated feedback and feedforward loops are recurrent network motifs in mammals. Mol Cell. 2007 Jun;26(5):753–767. doi: 10.1016/j.molcel.2007.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kim Jongpil, Inoue Keiichi, Ishii Jennifer, Vanti William B, Voronov Sergey V, Murchison Elizabeth, Hannon Gregory, Abeliovich Asa. A microrna feedback circuit in midbrain dopamine neurons. Science. 2007 Aug;317(5842):1220–1224. doi: 10.1126/science.1140481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cohen Stephen M, Brennecke Julius, Stark Alexander. Denoising feedback loops by thresholding–a new role for micrornas. Genes Dev. 2006 Oct;20(20):2769–2772. doi: 10.1101/gad.1484606. [DOI] [PubMed] [Google Scholar]
- 6.Zhao Chunnian, Sun GuoQiang, Li Shengxiu, Shi Yanhong. A feedback regulatory loop involving microrna-9 and nuclear receptor tlx in neural stem cell fate determination. Nat Struct Mol Biol. 2009 Apr;16(4):365–371. doi: 10.1038/nsmb.1576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Carrington James C, Ambros Victor. Role of micrornas in plant and animal development. Science. 2003 Jul;301(5631):336–338. doi: 10.1126/science.1085242. [DOI] [PubMed] [Google Scholar]
- 8.Brennecke Julius, Hipfner David R, Stark Alexander, Russell Robert B, Cohen Stephen M. bantam encodes a developmentally regulated microrna that controls cell proliferation and regulates the proapoptotic gene hid in drosophila. Cell. 2003 Apr;113(1):25–36. doi: 10.1016/s0092-8674(03)00231-9. [DOI] [PubMed] [Google Scholar]
- 9.Xu Peizhang, Vernooy Stephanie Y, Guo Ming, Hay Bruce A. The drosophila microrna mir-14 suppresses cell death and is required for normal fat metabolism. Curr Biol. 2003 Apr;13(9):790–795. doi: 10.1016/s0960-9822(03)00250-1. [DOI] [PubMed] [Google Scholar]
- 10.Johnston Robert J, Chang Sarah, Etchberger John F, Ortiz Christopher O, Hobert Oliver. Micrornas acting in a double-negative feedback loop to control a neuronal cell fate decision. Proc Natl Acad Sci U S A. 2005 Aug;102(35):12449–12454. doi: 10.1073/pnas.0505530102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li Yan, Wang Fay, Jin-A Lee, and Fen-Biao Gao. Microrna-9a ensures the precise specification of sensory organ precursors in drosophila. Genes Dev. 2006 Oct;20(20):2793–2805. doi: 10.1101/gad.1466306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gao Fen-Biao. Posttranscriptional control of neuronal development by microrna networks. Trends Neurosci. 2008 Jan;31(1):20–26. doi: 10.1016/j.tins.2007.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lu Jun, Guo Shangqin, Ebert Benjamin L, Zhang Hao, Peng Xiao, Bosco Jocelyn, Pretz Jennifer, Schlanger Rita, Wang Judy Y, Mak Raymond H, Dombkowski David M, Preffer Frederic I, Scadden David T, Golub Todd R. Microrna-mediated control of cell fate in megakaryocyte-erythrocyte progenitors. Dev Cell. 2008 Jun;14(6):843–853. doi: 10.1016/j.devcel.2008.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li Ji, Greenwald Iva. Lin-14 inhibition of lin-12 contributes to precision and timing of c. elegans vulval fate patterning. Curr Biol. 2010 Oct;20(20):1875–1879. doi: 10.1016/j.cub.2010.09.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li Xin, Cassidy Justin J, Reinke Catherine A, Fischboeck Stephen, Carthew Richard W. A microrna imparts robustness against environmental fluctuation during development. Cell. 2009 Apr;137(2):273–282. doi: 10.1016/j.cell.2009.01.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Herranz Hctor, Cohen Stephen M. Micrornas and gene regulatory networks: managing the impact of noise in biological systems. Genes Dev. 2010 Jul;24(13):1339–1344. doi: 10.1101/gad.1937010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Srivastava Deepak. Making or breaking the heart: from lineage determination to morphogenesis. Cell. 2006 Sep;126(6):1037–1048. doi: 10.1016/j.cell.2006.09.003. [DOI] [PubMed] [Google Scholar]
- 18.Filipowicz Witold, Bhattacharyya Suvendra N, Sonenberg Nahum. Mechanisms of post-transcriptional regulation by micrornas: are the answers in sight? Nat Rev Genet. 2008 Feb;9(2):102–114. doi: 10.1038/nrg2290. [DOI] [PubMed] [Google Scholar]
- 19.Pillai Ramesh S. Microrna function: multiple mechanisms for a tiny rna? RNA. 2005 Dec;11(12):1753–1761. doi: 10.1261/rna.2248605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hutvgner Gyrgy, Zamore Phillip D. A microrna in a multiple-turnover rnai enzyme complex. Science. 2002 Sep;297(5589):2056–2060. doi: 10.1126/science.1073827. [DOI] [PubMed] [Google Scholar]
- 21.Tomari Yukihide, Zamore Phillip D. Perspective: machines for rnai. Genes Dev. 2005 Mar;19(5):517–529. doi: 10.1101/gad.1284105. [DOI] [PubMed] [Google Scholar]
- 22.Raser JM, O’Shea EK. Control of stochasticity in eukaryotic gene expression. Science. 2004;304(5678):1811–1814. doi: 10.1126/science.1098641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Raj Arjun, Peskin Charles S, Tranchina Daniel, Vargas Diana Y, Tyagi Sanjay. Stochastic mrna synthesis in mammalian cells. PLoS Biol. 2006 Oct;4(10):e309. doi: 10.1371/journal.pbio.0040309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Janicki SM, Tsukamoto T, Salghetti SE, Tansey WP, Sachidanandam R, Prasanth KV, Ried T, Shav-Tal Y, Bertrand E, Singer RH, Spec-tor DL. From silencing to gene expression: Real-time analysis in single cells. Cell. 2004;116(5):683–698. doi: 10.1016/s0092-8674(04)00171-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297(5584):1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 26.Ozbudak EM, Thattai M, Kurtser I, Grossman AD, van Oudenaarden A. Regulation of noise in the expression of a single gene. Nat Genet. 2002;31(1):69–73. doi: 10.1038/ng869. [DOI] [PubMed] [Google Scholar]
- 27.Blake WJ, Kaern M, Cantor CR, Collins JJ. Noise in eukaryotic gene expression. nature. 2003;422(6932):633–637. doi: 10.1038/nature01546. [DOI] [PubMed] [Google Scholar]
- 28.Rosenfeld Nitzan, Young Jonathan W, Alon Uri, Swain Peter S, Elowitz Michael B. Gene regulation at the single-cell level. Science. 2005 Mar;307(5717):1962–1965. doi: 10.1126/science.1106914. [DOI] [PubMed] [Google Scholar]
- 29.Golding Ido, Paulsson Johan, Zawilski Scott M, Cox Edward C. Real-time kinetics of gene activity in individual bacteria. Cell. 2005 Dec;123(6):1025–1036. doi: 10.1016/j.cell.2005.09.031. [DOI] [PubMed] [Google Scholar]
- 30.Chubb JR, Trcek T, Shenoy SM, Singer RH. Transcriptional pulsing of a developmental gene. Current Biology. 2006;16(10):1018–1025. doi: 10.1016/j.cub.2006.03.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gregor Thomas, Tank David W, Wieschaus Eric F, Bialek William. Probing the limits to positional information. Cell. 2007 Jul;130(1):153–164. doi: 10.1016/j.cell.2007.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Eden Eran, Geva-Zatorsky Naama, Issaeva Irina, Cohen Ariel, Dekel Erez, Danon Tamar, Cohen Lydia, Mayo Avi, Alon Uri. Proteome half-life dynamics in living human cells. Science. 2011 Feb;331(6018):764–768. doi: 10.1126/science.1199784. [DOI] [PubMed] [Google Scholar]
- 33.Grigull Jrg, Mnaimneh Sanie, Pootoolal Jeffrey, Robinson Mark D, Hughes Timothy R. Genome-wide analysis of mrna stability using transcription inhibitors and microarrays reveals posttranscriptional control of ribosome biogenesis factors. Mol Cell Biol. 2004 Jun;24(12):5534–5547. doi: 10.1128/MCB.24.12.5534-5547.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Siwiak Marlena, Zielenkiewicz Piotr. A comprehensive, quantitative, and genome-wide model of translation. PLoS Comput Biol. 2010;6(7):e1000865. doi: 10.1371/journal.pcbi.1000865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Miller Christian, Schwalb Bjrn, Maier Kerstin, Schulz Daniel, Dmcke Sebastian, Zacher Benedikt, Mayer Andreas, Sydow Jasmin, Marcinowski Lisa, Dlken Lars, Martin Dietmar E, Tresch Achim, Cramer Patrick. Dynamic transcriptome analysis measures rates of mrna synthesis and decay in yeast. Mol Syst Biol. 2011 Jan;7:458. doi: 10.1038/msb.2010.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Levine E, Zhang Z, Kuhlman T, Hwa T. Quantitative characteristics of gene regulation by small rna. Plos Biology. 2007;5(9):1998–2010. doi: 10.1371/journal.pbio.0050229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. nature. 2000;405(6786):590–593. doi: 10.1038/35014651. [DOI] [PubMed] [Google Scholar]
- 38.Thattai M, van Oudenaarden A. Intrinsic noise in gene regulatory networks. Proc Natl Acad Sci U S A. 2001 Jul;98(15):8614–8619. doi: 10.1073/pnas.151588598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hornung Gil, Barkai Naama. Noise propagation and signaling sensitivity in biological networks: a role for positive feedback. PLoS Comput Biol. 2008 Jan;4(1):e8. doi: 10.1371/journal.pcbi.0040008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dublanche Yann, Michalodimitrakis Konstantinos, Kmmerer Nico, Foglierini Mathilde, Serrano Luis. Noise in transcription negative feedback loops: simulation and experimental analysis. Mol Syst Biol. 2006;2:41. doi: 10.1038/msb4100081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Marquez-Lago Tatiana T, Stelling Jrg. Counter-intuitive stochastic behavior of simple gene circuits with negative feedback. Biophys J. 2010 May;98(9):1742–1750. doi: 10.1016/j.bpj.2010.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Fano U. Note on the theory of radiation-induced lethals in drosophila. Science. 1947 Jul;106(2743):87–88. doi: 10.1126/science.106.2743.87-a. [DOI] [PubMed] [Google Scholar]
- 43.Stark Alexander, Brennecke Julius, Bushati Natascha, Russell Robert B, Cohen Stephen M. Animal micrornas confer robustness to gene expression and have a significant impact on 3′utr evolution. Cell. 2005 Dec;123(6):1133–1146. doi: 10.1016/j.cell.2005.11.023. [DOI] [PubMed] [Google Scholar]
- 44.Paulsson J, Ehrenberg M. Noise in a minimal regulatory network: plasmid copy number control. Q Rev Biophys. 2001 Feb;34(1):1–59. doi: 10.1017/s0033583501003663. [DOI] [PubMed] [Google Scholar]
- 45.Elf J, Ehrenberg M. Fast evaluation of fluctuations in biochemical networks with the linear noise approximation. Genome Research. 2003;13(11):2475–2484. doi: 10.1101/gr.1196503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Elf Johan, Paulsson Johan, Berg Otto G, Ehrenberg Mns. Near-critical phenomena in intracellular metabolite pools. Biophys J. 2003 Jan;84(1):154–170. doi: 10.1016/S0006-3495(03)74839-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mehta Pankaj, Goyal Sidhartha, Wingreen Ned S. A quantitative comparison of srna-based and protein-based gene regulation. Mol Syst Biol. 2008;4:221. doi: 10.1038/msb.2008.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Goldenfeld N. Frontiers in physics. Addison-Wesley, Advanced Book Program; 1992. Lectures on phase transitions and the renormalization group. [Google Scholar]
- 49.Lenz Derrick H, Mok Kenny C, Lilley Brendan N, Kulkarni Rahul V, Wingreen Ned S, Bassler Bonnie L. The small rna chaperone hfq and multiple small rnas control quorum sensing in vibrio harveyi and vibrio cholerae. Cell. 2004 Jul;118(1):69–82. doi: 10.1016/j.cell.2004.06.009. [DOI] [PubMed] [Google Scholar]
- 50.Mitarai Namiko, Andersson Anna MC, Krishna Sandeep, Semsey Szabolcs, Sneppen Kim. Efficient degradation and expression prioritization with small rnas. Phys Biol. 2007 Sep;4(3):164–171. doi: 10.1088/1478-3975/4/3/003. [DOI] [PubMed] [Google Scholar]
- 51.Shimoni Yishai, Friedlander Gilgi, Hetzroni Guy, Niv Gali, Altuvia Shoshy, Biham Ofer, Margalit Hanah. Regulation of gene expression by small non-coding rnas: a quantitative view. Mol Syst Biol. 2007;3:138. doi: 10.1038/msb4100181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Van Kampen NG. Stochastic Processes in Physics and Chemistry. North-holland publishing company; 1981. [Google Scholar]
- 53.Baek Daehyun, Villn Judit, Shin Chanseok, Camargo Fernando D, Gygi Steven P, Bartel David P. The impact of micrornas on protein output. Nature. 2008 Sep;455(7209):64–71. doi: 10.1038/nature07242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Guo Huili, Ingolia Nicholas T, Weissman Jonathan S, Bartel David P. Mammalian micrornas predominantly act to decrease target mrna levels. Nature. 2010 Aug;466(7308):835–840. doi: 10.1038/nature09267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kepler TB, Elston TC. Stochasticity in transcriptional regulation: Origins, consequences, and mathematical representations. Biophysical Journal. 2001;81(6):3116–3136. doi: 10.1016/S0006-3495(01)75949-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Maheshri Narendra, O’Shea Erin K. Living with noisy genes: how cells function reliably with inherent variability in gene expression. Annu Rev Biophys Biomol Struct. 2007;36:413–434. doi: 10.1146/annurev.biophys.36.040306.132705. [DOI] [PubMed] [Google Scholar]
- 57.Raj Arjun, van Oudenaarden Alexander. Single-molecule approaches to stochastic gene expression. Annu Rev Biophys. 2009;38:255–270. doi: 10.1146/annurev.biophys.37.032807.125928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Rdel Sabine, Wang Yanli, Lenobel Ren, Krner Roman, Hsiao He-Hsuan, Urlaub Henning, Patel Dinshaw, Meister Gunter. Phosphorylation of human argonaute proteins affects small rna binding. Nucleic Acids Res. 2010 Nov; doi: 10.1093/nar/gkq1032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kedde Martijn, van Kouwenhove Marieke, Zwart Wilbert, Oude Vrielink Joachim AF, Elkon Ran, Agami Reuven. A pumilio-induced RNA structure switch in p27-3′ UTR controls mir-221 and mir-222 accessibility. Nat Cell Biol. 2010 Oct;12(10):1014–1020. doi: 10.1038/ncb2105. [DOI] [PubMed] [Google Scholar]
- 60.Losick R, Desplan C. Stochasticity and cell fate. Science. 2008;320(5872):65–68. doi: 10.1126/science.1147888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Levine Erel, Jacob Eshel Ben, Levine Herbert. Target-specific and global effectors in gene regulation by microrna. Biophys J. 2007 Dec;93(11):L52–L54. doi: 10.1529/biophysj.107.118448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Komorowski M, Miekisz J, Kierzek AM. Translational repression contributes greater noise to gene expression than transcriptional repression. Biophys J. 2009;96(2):372–84. doi: 10.1016/j.bpj.2008.09.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.