A fuzzy-based histogram analysis technique for skin lesion discrimination in dermatology clinical images

Abstract

A fuzzy logic-based color histogram analysis technique is presented for discriminating benign skin lesions from malignant melanomas in dermatology clinical images. The approach utilizes a fuzzy set for benign skin lesion color, and alpha-cut and support set cardinality for quantifying a fuzzy ratio skin lesion color feature. Skin lesion discrimination results are reported for the fuzzy ratio and fusion with a previously determined percent melanoma color feature over a data set of 258 clinical images. For the fusion technique, alpha-cuts for the fuzzy ratio can be chosen to recognize over 93.30% of melanomas with approximately 15.67% false positive lesions.

1. Introduction

A significant number of malignant melanomas, especially early melanomas curable by excision, are not diagnosed correctly in the clinical setting [1–4]. The diagnostic sensitivity reported for unaided dermatologist observers ranges from a low of about 66% to about 81% [1–3,5]. Diagnostic accuracy for non-dermatologists is believed to be lower. The relatively low diagnostic sensitivity of dermatologist and non-dermatologist detection of malignant melanoma demonstrates the uncertainty involved in skin lesion analysis. Paramount in the process of skin lesion analysis is the identification of features that can be consistently interpreted by dermatologists and non-dermatologists in the recognition of abnormal skin lesions. For 2002, there are 53,600 new cases and 7400 deaths estimated from malignant melanoma in the United States [6]. This is a 4% increase in invasive melanoma from 2001. Melanoma is easily cured if detected at an early stage.

Current melanoma detection techniques rely on simple rules based on the ABCD’s of melanoma (Asymmetry, Border irregularity, Color variegation, Diameter greater than 6 mm or growing) [4]. Most melanomas have a diameter of more than 6 mm, although public awareness has enabled more small melanomas to be found. The ABCD rule has not been specific enough for physicians. The lack of a quantifiable measurement makes it difficult to diagnose a skin lesion with certainty. It is not easy to judge the asymmetry or irregularity of a skin lesion by just looking at it. The diameter is easy to measure, but the high chance of cure of an early lesion is somewhat reduced by the time the skin lesion has grown to over six millimeters. In this paper, we do not refer to diagnostic aids such as dermoscopy, digital dermoscopy or hyperspectral images. We use clinical digital images without magnification and rely on digital image analysis to provide additional information using color alone.

Color is an important skin lesion feature for detecting malignant melanoma [7]. Melanocytic lesions are typically associated with certain colors, including shades of tan, brown or black and occasional patches of red, white or blue. The red, green and blue (RGB) color space is used to represent colors characteristic of melanoma. Many color descriptors that have been applied to melanoma detection, including variation of hues [8], analytical color techniques for detecting color variegation [9], RGB color channel statistical parameters [10–12], spherical color coordinates and (L,a^*,b^*) color coordinate features [13], percentage of the skin lesion containing absolute shades of reddish, bluish, grayish and blackish areas and the number of those color shades present within the skin lesion [14]. Color quantization for the different color shades examined in [14] was performed using the median cut color quantization algorithm [15]. Melanoma detection has also been performed based on probability analysis for three classes of colors (benign, melanoma and other colors) found from relative color histograms [16,17]. Relative color histogram region growing and neighborhood color clustering analysis have also been explored [16].

There are two primary difficulties associated with melanoma detection based on color. First, quantifying the colors considered characteristic of melanoma is difficult due to variations in lighting and slide processing whether using photography or digital imaging. The use of relative color [18], in which the average background skin color is subtracted from each lesion pixel, has been proposed as a technique to help compensate for color distortion in the imaging process. This technique equalizes color changes due to different skin types as well as to lighting and image processing techniques [18]. Second, the inconsistency of colors characteristic of melanomas across skin lesions makes it difficult to reliably detect melanoma, based on identifying those characteristic colors. An alternative approach to melanoma detection is to identify colors that are most characteristic of benign skin lesions and to evaluate the color difference in a skin lesion with those characteristic colors. In this study, a fuzzy logic-based approach for skin lesion color analysis is investigated for differentiating benign skin lesions from melanomas in clinical images. A fusion technique is also presented for enhancing melanoma discrimination that combines the color feature generated from the fuzzy logic approach with the percent melanoma color determined by previous research using the same color histogram analysis technique [16,17].

The relative color histogram techniques [9,16,17] supply the foundation for the fuzzy-based histogram analysis technique presented in this research. Specifically, benign skin lesion color histogram analysis provides the basis for expressing benign skin lesion color using a fuzzy set analysis for differentiating benign skin lesions from melanomas. The color analysis technique is based on the automated histogram mapping of colors representative of benign skin lesions within the training set of clinical images. The color maps are applied to skin lesions in corresponding clinical test images for melanoma detection. The remaining sections of the paper include: (1) an overview of the clinical image acquisition, (2) the application of fuzzy logic to benign skin lesion color and color histogram analysis, (3) the automated approach for melanoma detection, (4) experiments performed, (5) results and discussion and (6) conclusions.

2. Methodology

2.1. Clinical image data

Imaging of skin lesions provides an important diagnostic aid to dermatologists in the detection of malignant melanoma. In this research, clinical images were used for skin lesion analysis based on the RGB color space. For RGB space there are 8-bits per pixel, providing 256 possible values for each of the components. Thus, there are a total of 256³ or 16,777,216 possible colors in this color space. Clinical images are acquired using 35 mm camera shots of skin lesions. Image analysis of clinical images has been shown to improve diagnostic sensitivity and specificity of detecting malignant melanoma [13,19,20].

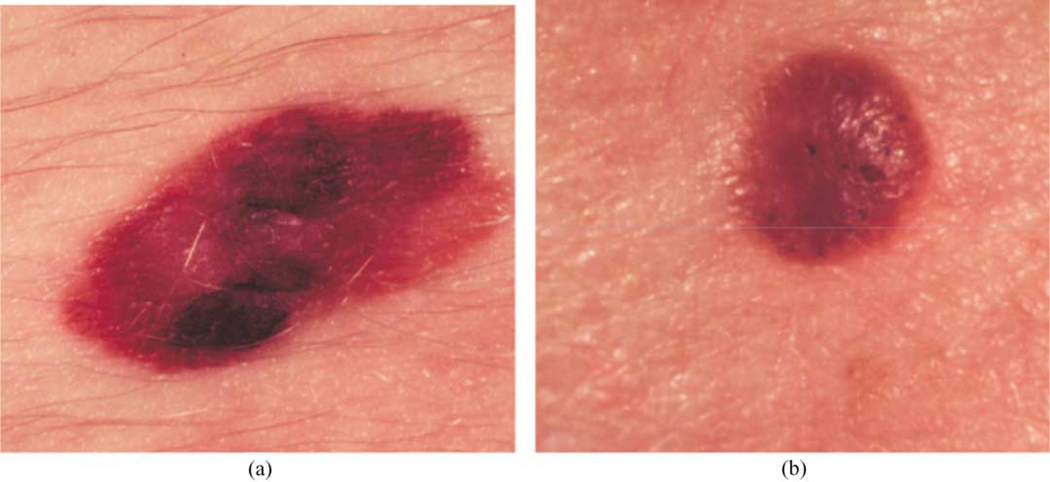
Fig. 1 shows clinical image examples from our image database consisting of a malignant melanoma (a) and a seborrheic keratosis benign lesion (b). The data set used for this research consists of 129 melanoma and 129 benign clinical images. These images are part of the data set acquired from New York University Department of Dermatology, Dr William V. Stoecker (Rolla, MO) and Dr Bruce Kornfeld (Ft Leonard Wood, MO). The diagnoses of these images include malignant melanoma that are predominately advanced lesions typically exhibiting ‘melanoma color’ to a greater degree than early lesions, 51 seborrheic keratoses and 79 nevocellular nevi. For comparative purposes, this is the same data set applied to melanoma detection using color histogram analysis [16] and other features including color descriptors [13].

Fig. 1.

Clinical image examples of benign and melanoma skin lesions: (a) melanoma image; (b) benign image (seborrheic keratosis).

2.2. Diagnostic assessment

Table 1 shows the diagnostic interpretations of skin lesions for evaluating the automated skin lesion classification results that were applied in this investigation. A true positive (tp) means diagnosing a melanoma as a melanoma. A false negative (fn) means diagnosing a melanoma as a benign skin lesion. A true negative (tn) means diagnosing a benign skin lesion as benign. A false positive (fp) means diagnosing a benign skin lesion as a melanoma. A fn purports delaying therapy for a melanoma, with worse consequences for the patient, while a fp, results in an unnecessary biopsy.

Table 1.

Skin lesion diagnosis categorization based on the type of skin lesion

Actual skin lesion diagnosis	Computer-assisted skin lesion diagnosis
	Benign	Melanoma
Benign	tn	fp
Melanoma	fn	tp

2.3. Skin lesion border determination

In this research, skin lesion borders are found using the following procedure. Points along the border are manually chosen using a program called xborder developed by McLean [22]. Once the points are chosen, they are joined in a closed curve that minimizes the second derivative of the associated function (spline curve) to create the closed skin lesion border. A dermatologist verified all borders drawn, and borders were modified as recommended by the dermatologist. For an M row by N column RGB image, I, each pixel I(x, y) = (r_(x,y), g_(x,y), b_(x,y)), where 1 ≤ x ≤ N and 1 ≤ y ≤ M.

2.4. Relative color

For classification of skin lesions, it is useful to have a system that will be relatively tolerant to different lighting conditions, different cameras, different film types and variations of skin color. This is particularly true for our data set because the image data was digitized from 35 mm slides acquired from three sources, where we had no control over cameras used to capture original photographed skin lesion data. In order to make this possible, a relative color method was used. The relative color of a skin lesion pixel is the difference between the actual pixel value and the value of some ‘surrounding skin’. Let O denote the skin lesion region within the color clinical image and be referenced as O = {(x, y)| (x, y) ∈ I and (x, y) is inside the closed skin lesion boundary}. Then, the relative color for all skin lesion pixels is given as O_rel(x, y) = (r_rel(x,y), g_rel(x,y), b_rel(x,y)) = (r_(x,y) − r_skin, g_(x,y) − g_skin, b_(x,y) − b_skin), where −255 ≤ r_rel(x,y), g_rel(x,y), b_rel(x,y) ≤ 255. r_skin, g_skin and b_skin are the average r, g and b values computed from the surrounding skin. The procedure for finding the surrounding skin is presented in Section 2.5.

There are several advantages for using relative color in skin lesion color analysis. First, relative color aids in alleviating the error in digitization due to differences in ambient lighting. Second, relative color in the case of digitized photographic images, can be used to minimize the error due to different film types and differences in processing. Third, relative color more closely approximates the operation of the mammalian visual system. Finally, relative color may minimize errors due to variation in normal skin color among persons.

2.5. Surrounding skin color determination

To eliminate pixels (red, green, blue) that are non-skin-colored, and those that are in deep shadow and those that represent direct reflection of the flash, several empirical relationships were determined. The skin pixel finder used in this research was derived from an existing dermatology image database under the guidance of a dermatologist and has been applied to skin lesion analysis in other research [21,22]. Surrounding skin color is approximated using an automated, empirically determined circular region calculation technique. The circular region neighbors the skin lesion with origin at the lesion centroid. The surrounding skin region size is determined as a function of the skin lesion size [17,22]. The average surrounding skin color (r_skin, g_skin, b_skin) is computed within the circular region that is outside of the lesion, excluding the non-skin-colored pixels.

2.6. Color histogram bin determination

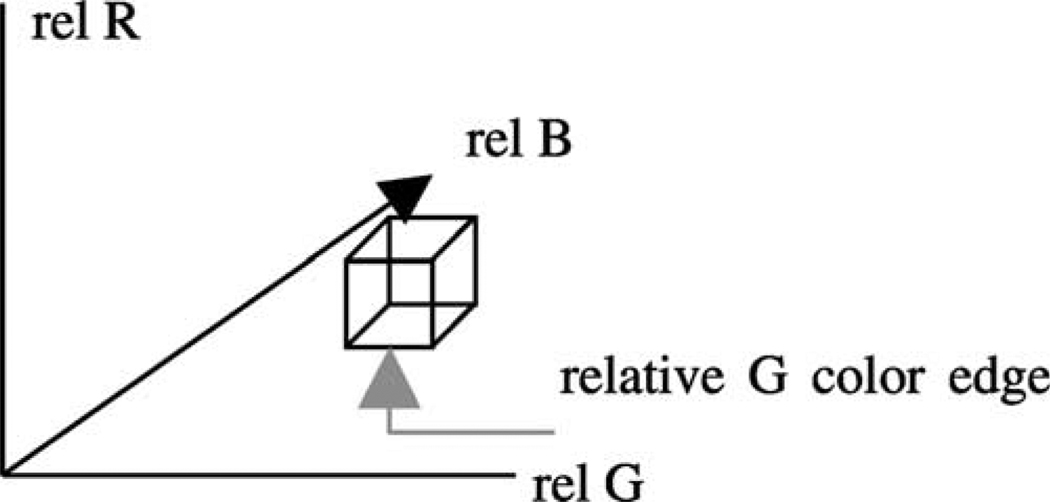
The fuzzy logic-based techniques developed in this research are based on relative color-based histogram analysis. The relative color skin lesion image region O_rel can take on the integer values in the range [−255,255] for R, G and B. Thus, the color histogram has 511³ total bins. Requantizing the relative RGB histogram bins is appropriate to represent discrete ranges of colors that are characteristic of melanoma and benign skin lesions. In this research, we are interested in applying benign skin colors to color feature determination. The 511 × 511 × 511 relative color histogram is requantized to include 64 distinct colors in each histogram bin. This is done by dividing each relative color range by 4, yielding a 128 × 128 × 128 relative color histogram that is used for analysis. Fig. 2 shows the relative color space with a labeled bin of dimension 4 × 4 × 4 and its three color bin edges. From Fig. 2, each relative color bin edge consists of four color levels.

Fig. 2.

Relative RGB space showing one bin of dimension 4 × 4 × 4 and its three color bin edges.

Let C denote the set of relative color bins, and let C_(x,y) denote the relative color bin into which the skin lesion pixel (x, y) maps. Because there are 511 relative colors for R, G and B, dividing by 4 will result in histogram bins containing 4 × 4 × 4 relative colors, except for some bins on the edges of the cube that are 4 × 4 × 3 and one bin in the corner of the cube that is 3 × 3 × 3. Based on examining the training relative color histograms for the data set used in this research, the bin containing −255 for R, G and B was chosen to have only three color levels in each dimension (3 × 3 × 3) because of the unlikelihood of its occurrence in clinical images.

2.7. Color histogram analysis technique

2.7.1. Fuzzy set description for trapezoidal membership function

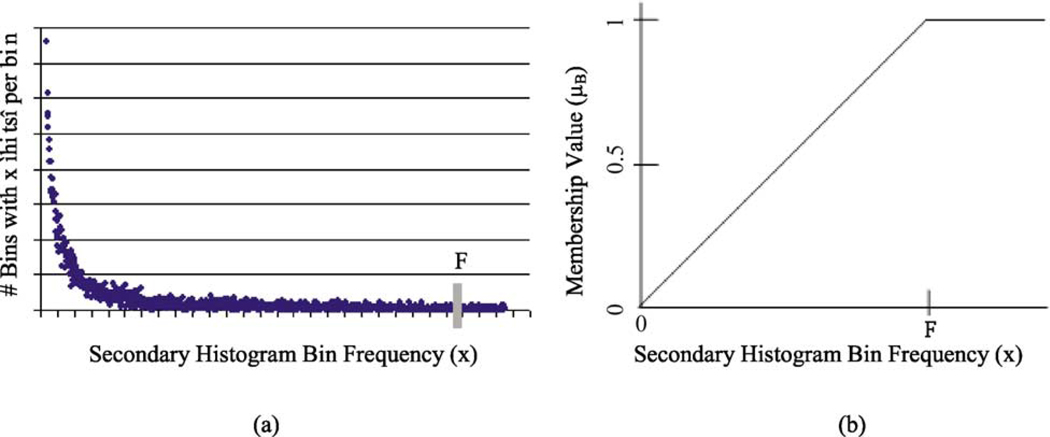
A fuzzy logic-based approach is used for representing relative skin lesion color. Specifically, let B denote the fuzzy set [23] with a trapezoidal membership function for relative skin lesion color, for the specified skin lesion class. The following procedure was used to assign membership values to the colors within the color histogram bins defined in Section 2.6. Using batch mode, the training set of images for the specified class is used to populate the three-dimensional relative color histogram bins, where each bin contains the sum of all skin lesion pixels over all training images with relative color mapping to that bin. A secondary histogram is defined as a histogram of the three-dimensional relative color histogram. The secondary histogram is a function of x which indicates the number of bins of the three-dimensional relative color histogram that are populated with x lesion pixels summed over all benign images in the training set.

The fuzzy set B is determined based on the benign skin lesion training data. Membership values are assigned continuously for each count in the secondary histogram for the relative colors, for the specified class. For secondary histogram bin frequency count x, the membership function µ_B(x) denoting the fuzzy set [23] is given as

$${\mu }_{\mathbf{B}}=\{\begin{array}{c}x/F\text{ for }0\le x<F\hfill \\ 1\text{ for }x\ge F\hfill \end{array}.$$

F is empirically determined as the frequency count such that 5% of the total bins comprising the secondary histogram have frequency F or greater, and x represents the number of hits in a bin over the training set of benign images. The membership values are reflective of increasing membership in the specified class of skin lesions with increasing frequency count. Fig. 3 shows a representative secondary histogram with the frequency count F labeled in (a) and the trapezoidal membership function generated in (b). The horizontal axis provides the frequency of occurrence (x) that a bin is populated over all benign images of the training set. The vertical axis gives the number of bins with x ‘hits’ per bin over the training set of benign images.

Fig. 3.

A relative secondary histogram (a) and its corresponding trapezoidal membership function for fuzzy set B (b). The frequency count F is labeled on the secondary histogram and membership function plot.

2.7.2. Color feature determination

In a given skin lesion, the pixels with relative colors that had at least a certain degree of membership in the relative color fuzzy B are used for feature calculation. Let |^αB| denote the cardinality of the α-cut, i.e. the number of lesion pixels where µ_B(C_(x,y)) ≥ α, for a specified α on B [19]. Let S(B) refer to the support of B, where S(B) = {(x, y) : µ_B(C_(x,y)) > 0 for (x, y) contained in the skin lesion}, and let |S(B)| denote the cardinality of S(B), that is, the number of pixels within the skin lesion with nonzero membership in B [23].

The metric used as a baseline for evaluating the relative color content in B is given as the ratio R(α) = |^αB|/|S(B)|. The ratio R(α) is the ratio of the number of pixels within the skin lesion that have at least α membership in B to the number of pixels within the skin lesion that have nonzero membership in B. Note that R(α) is computed based on the pixels within the skin lesion. The surrounding skin pixels are only used for computing the average surrounding skin color for determining the relative color of all pixels within the skin lesion. Thus, for α = 0, R = 1, provided that at least one pixel within the skin lesion has a non-zero membership value in B. R(α) gauges how strongly the color information within the skin lesion correlates with the colors perceived to be most commonly associated with the relative color fuzzy set B. If B represents the fuzzy set for benign skin lesion relative color as determined from the training set of images, then R(α) represents the degree to which the benign colors within the skin lesion are the colors perceived to be associated with benign skin lesions. As α is increased, ^αB contains pixels that are more strongly perceived as benign lesion pixels.

Benign image training data are used to determine relative color histogram bin membership in B. The next step is to compute R(α) for all benign and melanoma skin lesions from the training data for a specified value of α. A threshold T is automatically determined from the ratios R(α) calculated from the training data. The procedure for finding T is presented in Section 2.7.3. Skin lesions are categorized as either benign or melanomas for the data set used in this research. A given skin lesion is classified as benign if R(α) > T. Otherwise, the skin lesion is labeled as a melanoma.

2.7.3. Threshold determination procedure

The ratios R(α) computed from the training data were sorted to facilitate automated threshold (T) selection. The approach used for automatically selecting T for a particular a is based on computing the tp and tn rates for the training data. The procedure for choosing the optimal T involves iterating T through the sorted ratios R(α) from [0,1] in increments of 0.001. For each T; tp and tn are determined from the training images. T is chosen as the threshold where the tp = tn.

It is possible that the tp and tn rates do not become equal over the threshold iteration process due to the discrete training set and to differences in the training tp and tn rates. In this situation, T is determined as follows. If while iterating, threshold T_i results in tp < tn, and the next threshold T_i+1 (in the threshold iteration process) yields tp > tn, then T_i is selected as the threshold. The other possibility is if while iterating, threshold T_i generates tp > tn, and the next threshold T_i+1 (in the threshold iteration process) yields tp < tn, then T_i is chosen as the threshold. The final melanoma and benign lesion classification results are obtained for the training and the test data using the final threshold T. The procedure is repeated for specified α values.

3. Experiments performed

For this research, there were 129 melanoma and 129 benign clinical images for analysis. A training set of 70% of the images (90 melanomas and 90 benign) is used, and the remaining 30% of the images is used for the test set. The relative color fuzzy set B is chosen to represent benign skin lesion skin color. The trapezoidal fuzzy set is used to quantify the different degrees of association for colors within a skin lesion as benign colors. The benign training images are used to construct the secondary histogram for assigning trapezoidal membership values to histogram bins for benign skin lesion relative color. Based on the trapezoidal membership assignments, the ratio R(α) is computed for each training image. Automated threshold selection is performed using the computed ratios over the training set of images. The optimal threshold found from the training data is used to classify the skin lesions as melanoma or benign in the test set. Seven different values of α are used for computing R, including α = 0.05, 0.1, 0.2, 0.4, 0.6, 0.8 and 1.0. This procedure is repeated over 18 random selections of training and test sets. After the threshold is calculated on the training sets, the test classification rates are found for each of the 18 test sets.

3.1. Benchmark technique

The percent melanoma color feature [16,17] is used as a benchmark for comparing the fuzzy ratio-based feature. To compute this feature, training images are used to populate the relative color histogram one image at a time. The relative color histogram bins are quantized to include 128 × 128 × 128 bins, which is identical to the histogram bin quantization used for the fuzzy logic-based histogram analysis technique presented in this paper. A minimum percentage (0.125%) of the skin lesion area must be contained within a histogram bin for that bin to be considered populated. Histogram bin population is performed for each melanoma and each benign training image. Uncertain bins are neither melanoma nor benign bins. Unpopulated bins denote bins that lack enough pixels to label the bins as either melanoma or benign.

Melanoma and benign relative color bin probability densities are determined based on the number of melanoma and benign images that populate each histogram bin. Each bin is labeled as melanoma, benign, uncertain and unpopulated based on comparing the corresponding melanoma and benign probabilities at each bin. Uncertain bins are neither melanoma nor benign bins. Unpopulated bins denote bins that lack enough pixels to label the bins as either melanoma or benign. An iterative region growing technique for relabeling uncertain and unpopulated histogram bins is performed on the bin’s 26 connected neighbors in the three-dimensional relative color histogram (except for the histogram boundary cases) to provide the final histogram bin labeling. Using the labeled relative color histogram bins, the percentage of the skin lesion that is melanoma colored is determined for all training images, melanoma and benign. The percent melanoma color feature (P) is the ratio of the number of skin lesion pixels that are melanoma colored divided by the skin lesion area. Each skin lesion pixel that has a relative color that falls into one of the melanoma labeled bins is counted as a melanoma pixel.

For the percent melanoma color feature, a threshold D is determined from the training data for skin lesion discrimination. If the skin lesion percent melanoma color P ≥ D, the skin lesion is labeled as a melanoma. Otherwise, it is labeled as benign. The threshold D is determined based on iterating through thresholds in the range [0,100] in increments of 0.01 and computing the training tp and tn rates. D is chosen as the threshold where the training tp = tn. For the situation tp ≠ tn over the increments of D; the same approach to finding T in this situation are applied here to find the threshold D. Using the same training/test sets as for the fuzzy ratio feature analysis, classification results were generated.

3.2. Fusion approach

The percent melanoma color and fuzzy ratio features were combined for melanoma detection. Using the same training images, the thresholds T and D were automatically determined for the fuzzy ratio (for a specified α) and the percent melanoma color features, respectively. In the fusion algorithm, the thresholds are adjusted to enhance the combined feature training classification tn and tp classification rates. Specifically, constants t and d were added to T and D, respectively, to generate adjusted thresholds for rule-based classification. The procedure for selecting optimum values of t and d required iterating t from −T/2 to +T/2 in increments of 0.001, and iterating d from −D/2 to +D/2 in increments of 0.1. For the training set of images, tp and tn rates were determined using the rules for classifying each skin lesion:

1. If R(α) ≥ T + t and P ≤ D + d, the lesion is classified as benign.

2. If R(α) < T + t and P > D + d, the lesion is labeled as a melanoma.

3. If rules 1 and 2 were not satisfied and P ≥ D, the lesion is called a melanoma.

4. If rules 1 and 2 were not satisfied and P < D, the lesion is classified as benign.

Rules 3 and 4 are simply the percent melanoma color feature classification rules for the case that the fusion rules are not satisfied. The tp and tn rates are computed based on the fusion algorithm for all specified combinations of t and d. The fusion algorithm finds the values of t and d that maximize the sum of tp and tn. The approach to find t and d differs from the tp = tn approach used for determining the individual thresholds T and D and is done to enhance overall discrimination capability. The maximum sum of tp and tn is not used for choosing the thresholds T and D in order to maintain a balance between melanoma discrimination rate and fp benign discrimination rate.

4. Results and discussion

4.1. Fuzzy ratio results

The fuzzy logic-based color histogram analysis technique is evaluated on 18 randomly chosen training and test sets. For each randomly chosen training and test set, R(α) is computed using α = 0.05, 0.1, 0.2, 0.4, 0.6, 0.8 and 1. For each training and test set, the histogram is generated over the benign skin lesion image set to find the total frequency count for each relative color histogram bin. These frequency counts are used for generating a secondary histogram to determine the parameter F. The parameter F allows the trapezoidal membership function to be generated to assign membership values to each histogram bin for its degree of membership as a benign color. The ratio R(α) is computed for each melanoma and benign image in the training set. A threshold T is automatically found from the training data for each α-cut independently and is applied to the test set skin lesions for melanoma/benign discrimination.

Table 2 presents training and test results obtained over the 18 trials for α = 0.05. The results presented include the threshold value selected, tp rate (% of melanoma images correctly called melanomas), the tn rate (% of benign images labeled as benign) and the average and standard deviation tp and tn rates over the 18 trials. Table 3 presents the summary average and standard deviation training and test results over the 18 random training/test sets for all α-cuts examined, including α = 0.05, 0.1, 0.2, 0.4, 0.6, 0.8 and 1. Column 1 shows the α value. Columns 2 and 3 provide the training tp and tn rates. Columns 4 and 5 give the test tp and tn rates.

Table 2.

Training set and test set results over 18 trials for fuzzy ratio technique for α = 0.05. The threshold T used for discrimination is shown in column 2

Trial number	Threshold value	Training data		Test data
		tp Rate (%)	tn Rate (%)	tp Rate (%)	tn Rate (%)
1	0.863	86.67	90.00	87.18	74.36
2	0.891	87.78	91.11	92.31	82.05
3	0.890	88.89	92.22	89.74	66.67
4	0.889	87.78	91.11	97.44	84.62
5	0.892	86.67	90.00	92.31	84.62
6	0.864	90.00	90.00	89.74	87.18
7	0.876	92.22	92.22	82.05	74.36
8	0.872	90.00	93.33	82.05	69.23
9	0.923	86.67	88.89	94.87	71.79
10	0.896	86.67	90.00	97.44	76.92
11	0.926	83.33	86.67	97.44	66.67
12	0.898	90.00	88.89	92.31	69.23
13	0.883	87.78	90.00	89.74	76.92
14	0.909	87.78	86.67	92.31	82.05
15	0.895	88.89	91.11	92.31	87.18
16	0.903	87.78	88.89	92.31	84.62
17	0.857	88.89	91.11	92.31	82.05
18	0.915	86.67	90.00	97.44	74.36
Average		88.02	90.12	91.74	77.49
Standard deviation		1.95	1.80	4.62	7.01

Table 3.

Average and standard deviation training set and test set results over 18 trials for fuzzy ratio technique for α = 0.05, 0.1, 0.2, 0.4, 0.6, 0.8 and 1.0

α	Training data		Test data
	tp Rate (%)	tn Rate (%)	tp Rate (%)	tn Rate (%)
Average
0.05	88.02	90.12	91.74	77.49
0.1	87.53	89.81	90.17	79.20
0.2	86.30	88.58	88.32	81.62
0.4	84.01	85.80	87.46	82.34
0.6	83.15	85.06	86.89	81.34
0.8	81.98	83.89	86.18	81.77
1.0	81.36	83.21	86.04	81.48
Standard deviation
0.05	1.95	1.80	4.62	7.01
0.1	2.00	1.92	6.42	5.48
0.2	1.70	1.65	6.17	3.96
0.4	1.67	1.30	6.40	4.89
0.6	2.20	0.95	4.73	5.82
0.8	1.96	1.44	4.32	4.81
1.0	2.11	1.94	3.32	4.70

The experimental results shown in Table 2 highlight two observations. First, from Table 2 the training tn rate exceeds the tp rate for most random training/test sets as well as for the average results. This occurs because the threshold T is found based on computing tp and tn starting with the case T = 0. At T = 0 the tn = 100% because all benign lesions have R(α) ≥ 0. Because the case tp = tn seldom occurs, T is found based on the transition tn > tp for T_i and tn < tp for T_i+1, where T is chosen as T_i. Second, from Table 2 the test tp rate exceeds the tn rate for all 18 test sets. For the corresponding training results, the tn rate generally exceeds the tp rate. This could be attributed to the approach used for deriving the fuzzy set B, the membership function µ_B and the threshold selection for T. For fuzzy ratio R(α) calculations, the numerator |^αB| and the denominator |S(B)| are dependent on the training set of benign images. Every pixel within every benign training image has a nonzero membership in B. Accordingly, |S(B)| is equal to the lesion area for those training images, and each pixel within every training skin lesion is included in |^αB| for some range of α > 0. This is not necessarily true for the melanoma training images and the melanoma and benign test images. Because the training benign fuzzy ratios R(α) are slightly skewed from the test benign fuzzy ratios R(α), the threshold T determined from the training set of images may not be as reflective of the test fuzzy ratios for the benign images as for the melanoma images.

The test discrimination results from Tables 2 and 3 lead to several remarks. First, the results from Table 3 show a trend of declining training tp rate with increasing α-cuts, with a maximum tp rate of 91.74% for α = 0.05. The corresponding tn rates are similar for the different α-cuts, except for the lowest α-cuts of 0.05 and 0.1. Second, the average melanoma recognition rates range from 91.74% (α = 0.05) to 86.04% (α = 1.0) correct, showing the low variation in melanoma detection capability over the α-cuts examined. A similar range of average benign recognition rates is observed from 77.49% (α = 0.05) to 82.34% (α = 0.4). The low variation in the melanoma and benign skin lesion recognition rates shows that the degree of association for color pixels as benign does not have a significant impact on classification capability. The average test results over 18 trials from all the α-cuts cases yield tp rates of greater than 86.0% and tn rates of greater than 77.0%. These results are close to the diagnostic sensitivity reported for unaided dermatologist observers [1–3,5]. Third, the experimental results demonstrate that the fuzzy logic-based histogram analysis technique can be successfully applied to differentiating melanoma from benign skin lesions in clinical images. The results from the benchmark percent melanoma color feature over the same 18 training and test sets trials show an average tn rate of 83.0%, and average tp rate of 84.6% [17]. Overall, the fuzzy ratio yields higher tp test results, but slightly lower tn test results than the benchmark percent melanoma color technique. From a diagnostic perspective, minimizing the fp rate is more significant from a diagnostic perspective for the patient. The standard deviations shown for the classification results in Table 3 show that the test set results obtained are consistent over the 18 randomly generated training/test results.

4.2. Fusion algorithm results

The fusion technique integrates the fuzzy ratio R(α) with the percent melanoma color feature P to improve the discrimination results obtained for the individual features. The fuzzy ratio approach uses relative benign color as the basis for feature calculation, and the percent melanoma color utilizes relative melanoma color as the foundation for feature computation. Table 4 presents the average fusion training and test results and average T, t, D and d parameter values obtained over the 18 trials for α = 0.05, 0.1, 0.2, 0.4, 0.6, 0.8 and 1.0. Column 1 gives the α value used for computing R(α): Column − provides the average threshold T. Column 3 shows the parameter t to offset the threshold T. Column 4 presents the average threshold D for the percent melanoma color feature. Column 5 gives the parameter d to offset the threshold D. Columns 6 and 7 provide the average training tp and tn results. Columns 8 and 9 present the average training tp and tn results.

Table 4.

Average fusion results over 18 training/test sets with average parameter values T, t, D and d for α = 0.2, 0.4, 0.6, 0.8 and 1.0

α	T	t	D	d	Training set		Test set
					Average tp rate (%)	Average tn rate (%)	Average tp rate (%)	Average tn rate (%)
0.05	0.891	0.039	43.594	12.153	95.43	88.46	92.59	85.47
0.1	0.801	−0.132	43.594	15.720	96.79	87.59	93.30	84.33
0.2	0.685	−0.213	43.594	15.886	96.67	87.59	93.30	84.47
0.4	0.534	−0.185	43.594	15.842	95.74	87.59	92.74	84.76
0.6	0.435	−0.130	43.594	12.392	94.75	87.96	91.17	85.19
0.8	0.351	−0.015	43.594	3.564	92.59	89.20	89.17	86.04
1.0	0.288	0.859	43.594	−0.023	92.78	88.64	89.89	85.47

From Table 4, the fusion technique provides up to a 9.0% improvement in melanoma detection over the baseline percent melanoma color feature, with a maximal melanoma detection rate of 93.30% for α = 0.1 and α = 0.2. There are two factors that may contribute to this improvement. First, the fuzzy ratio feature is based on benign color, thereby, giving supplemental information to the percent melanoma color feature. The fuzzy ratio attempts to quantify colors that are perceived to be associated with benign skin lesions, where the perceived association is quantified using the relative color histogram analysis technique presented.

Second, the denominators for the percent melanoma color and fuzzy ratio features lead to different interpretations of the respective color features. The denominator of the percent melanoma color feature is the area of the skin lesion, an explicit measure of skin lesion size. The denominator of the fuzzy ratio for a skin lesion is the cardinality of the support of the fuzzy set for benign color, which equals the number of pixels within the skin lesion with at least some degree of membership as a benign color. Obviously, the denominator for the fuzzy ratio is dependent on the skin lesion size; however, it is not an explicit size measure. The percent melanoma color feature is the percentage of the skin lesion that contains colors characteristic of melanoma, where the melanoma colors are determined based on automated color histogram analysis over a training set of images. From the fuzzy logic perspective, the fuzzy ratio can be interpreted as the ratio of skin lesion pixels that have at least a specified degree of association or membership as benign color to all pixels within the skin lesion that have any (nonzero) degree of membership as benign color. Thus, the percent melanoma color and fuzzy ratio features are not complementary features in a strict sense, facilitating supplementary information to be obtained from the fuzzy ratio.

In order to compare the fuzzy ratio and fusion results, Ercal et al. have examined a neural network classification scheme for melanomas and benign lesion discrimination using the same data set [13]. Fourteen features were used in that study, including irregularity index (border irregularity measure), percent asymmetry (of the lesion), RGB color variances over the lesion, relative chromaticity, spherical color coordinates and L^*, a^*, b^* color coordinates. The average experimental test results ranged from 74.2 to 86.0% for melanomas and 83.2 to 86.3% for benign lesions. The fuzzy ratio and fusion results using one and two color features, respectively, are close to the 14 feature results from the Ercal et al. study.

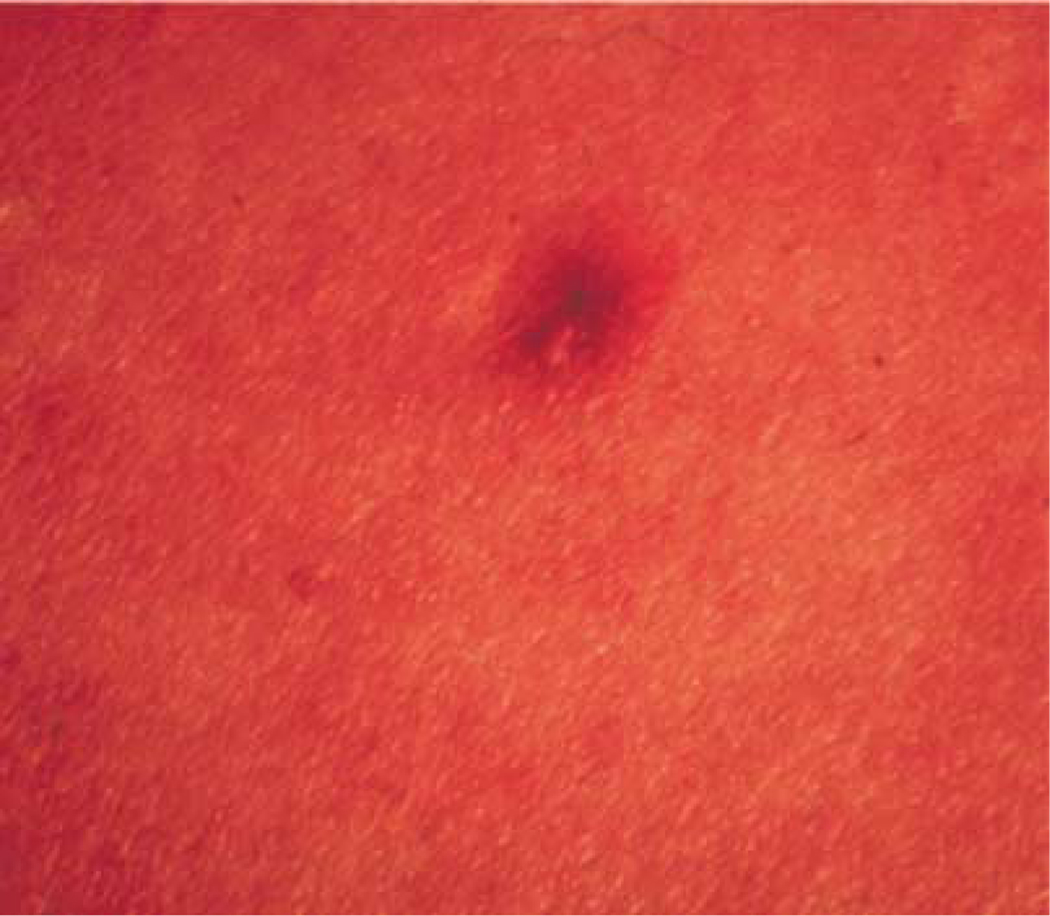
A dermatologist examined the skin lesions that are commonly missed in the 18 different test sets. The dermatologist pointed out that he would classify the missed skin lesions as difficult to very difficult to distinguish as melanoma or benign. Fig. 4 contains an example of a benign mimic to melanoma that is consistently missed when included in the test set. There are images within the data set that have highly red backgrounds. Re-digitization of the slides could assist with eliminating the overly red backgrounds. Whether approaching the analysis from the perspective of identifying melanoma relative colors or finding benign colors, color histogram analysis has demonstrated the capability to differentiate melanoma from benign skin lesions.

Fig. 4.

Example of a benign mimic consistently classified as a melanoma.

5. Summary

In this research, a fuzzy logic-based color analysis approach was investigated for differentiating benign skin lesions from melanomas in clinical images. A fuzzy set with a trapezoidal membership function was used to represent relative benign skin lesion color and the degree to which relative skin lesion colors are benign colors. Color histogram analysis on a training set of images provided the basis for benign skin lesion color membership assignment. A fuzzy ratio was computed to reflect the area of the skin lesion with a specified degree of association to benign color to the overall area of the lesion with any degree of benign color. An automated thresholding technique, using intersection between tn and positive rates, was developed to differentiate benign skin lesions from melanomas based on the computed ratios over a training set of images. The thresholding determined from the training data is applied to the test data. Experimental results (as summarized in Table 3) demonstrate that this technique can be used to successfully differentiate benign skin lesions from melanomas with tp rates between 86.04 and 91.74% and tn rates between 77.49 and 82.34%, respectively. These results are comparable to a baseline percent melanoma color feature. The benign histogram color analysis approach was fused with the percent melanoma color feature to optimize skin lesion classification. The fusion approach showed considerable improvements in the results, reflected in the tp rates between 89.17 and 93.30% and tn rates between 84.33 and 86.04%, respectively.

Biographies

R. Joe Stanley received the BSEE and MSEE degrees in electrical engineering and a PhD degree in Computer Engineering and Computer Science from the University of Missouri-Columbia. As a graduate student at the University of Missouri-Columbia, he worked under training grants from the National Library of Medicine and the National Cancer Institute. Upon completing his doctoral study, he served at Principal Investigator for the Image Recognition program at Systems and Electronics, Inc. in St Louis, MO. He is currently an Assistant Professor in the Department of Electrical and Computer Engineering at the University of Missouri-Rolla. His research interests include signal and image processing, pattern recognition and automation.

Randy H. Moss received the BSEE and MSEE degrees in electrical engineering from the University of Arkansas where he was a National Merit Scholar and the PhD degree from the University of Illinois, where he was an NSF Graduate Fellow. He is currently a Professor of Electrical Engineering at the University of Missouri-Rolla. His research interests are in the areas of image processing, pattern recognition and computer vision. He is especially interested in medical and industrial applications of machine vision techniques. He serves as an Associate Editor of Pattern Recognition and Computerized Medical Imaging and Graphics. Dr. Moss is a member of Sigma Xi, the Pattern Recognition Society, Eta Kappa Nu, Tau Beta Pi and Phi Kappa Phi.

William V. Stoecker received the BS in mathematics from Caltech in 1968, the MS in systems science from U.C.L.A. in 1970, and the MD from University of Missouri-Columbia in 1977. He is Clinical Assistant Professor of Internal Medicine-Dermatology at University of Missouri-Columbia and Adjunct Assistant Professor of Computer Science at University of Missouri-Rolla. He is past president of the International Society for Digital Imaging of the Skin (ISDIS), past vice-president of the Sulzberger Institute for Dermatologic Education, and has been Chairman of the American Academy of Dermatology Task Force on Computer Data Bases, which has developed diagnostic and therapeutic software for dermatologists. He is president of Stoecker and Associates, developers of dermatology application software. His interests include intelligent systems and computer vision in dermatology and diagnostic problems in dermatology.

Chetna Aggarwal graduated from Mithibai College in Bombay in 1995. She received the BS degree in electronics engineering from the Sardar Patel College of Engineering in Bombay, India in 1999. She received the MS degree in computer engineering from the University of Missouri-Rolla in 2002. She is a member of the Indian Students Association, the International Students Club, the Society of Women Engineers, and Sigma Xi.