Finding Differentially Expressed Genes in Two-Channel DNA Microarray Datasets: How to Increase Reliability of Data Preprocessing

Abstract

Due to the great variety of preprocessing tools in two-channel expression microarray data analysis it is difficult to choose the most appropriate one for a given experimental setup. In our study, two independent two-channel inhouse microarray experiments as well as a publicly available dataset were used to investigate the influence of the selection of preprocessing methods (background correction, normalization, and duplicate spots correlation calculation) on the discovery of differentially expressed genes. Here we are showing that both the list of differentially expressed genes and the expression values of selected genes depend significantly on the preprocessing approach applied. The choice of normalization method to be used had the highest impact on the results. We propose a simple but efficient approach to increase the reliability of obtained results, where two normalization methods which are theoretically distinct from one another are used on the same dataset. Then the intersection of results, that is, the lists of differentially expressed genes, is used in order to get a more accurate estimation of the genes that were de facto differentially expressed.

Introduction

Microarrays were introduced in the mid-1990s (Schena et al., 1995), and today are widely used for analyzing the expression of thousands of genes simultaneously. However, as the number of genes on a microarray is usually several orders of magnitude higher than the number of replicates or conditions analyzed, new statistical and data mining approaches are being proposed to overcome this drawback. Furthermore, there are many sources of variation influencing a microarray experiment, ranging from differences in biological samples, array quality, dye bias, etc. Data preprocessing of microarray datasets is necessary to make the accross-array comparison possible. In the presented work we focused on the impact of preprocessing on data obtained from commercially available and custom-designed two-channel microarrays.

Basically there are three microarray data analysis steps. The first one consists of data preprocessing, including background correction and normalization. It is user-dependent and can include, for example, filtering out spots with a signal-to-noise ratio below a predefined threshold value. The filtered out spots are usually given a weight of 0 and the rest are weighted with 1. Following this, a background correction is usually made. Background estimation serves as a measure of noise (e.g., nonspecific hybridization), and there are several methods for its determination. The choice of using a background correction or not is dependent on the presence of (high) local noise density. One can decide not to correct for background noise at all, because it imposes data transformations that can disturb the already fragile reproducibility of the signal between biological replicates. If a background correction is used, however, the most straightforward method to use is background subtraction (here named subtract)

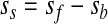(1)

where background noise s_b is subtracted from foreground intensity s_f. However, this can yield negative values of background subtracted intensities s_s. To deal with this problem one option is to reset all negative and very low values after background subtraction to a common value, for example, 0.5. This option (named half) is implemented in one of the Bio-conductor packages, limma (Smyth, 2005), as is also the option subtract. More computationally intensive background corrections such as normexp are available in the same package. In the latter method, a convolution of normal and exponential distributions is fitted using the maximum likelihood estimation to the signal intensities α and background intensities μ: normal(μ,σ²) + exp(α). Only positive background-corrected intensities are returned by this method.

There are various normalization methods available: quantile, cyclic loess, invariantset, and others are used with single-channel microarray datasets (Bolstad et al., 2005). On the other hand, median or loess normalization are used, among others, for two-channel microarrays (Yang and Paquet, 2005). Their purpose is to standardize the expression levels within or between microarray slides. Loess (locally weighted polynomial regression) normalization is often used in microarray experiments. Here the fitted value at x_k in a scatterplot (x_i,y_i) is the value of a polynomial fit at each point in the data using weighted least squares fit (Cleveland, 1979). More weight is given to the points that are closer to the point whose response is being estimated. The process is iterative in order to achieve a robust smooth function (Cleveland, 1979).

Variance stabilizing normalization (vsn) was primarily introduced due to heteroscedasticity of log-transformed data that has been noted in microarray experiments after loess or other types of normalization. After a series of transformations of the measured intensities, the variance becomes approximately independent of the mean (Huber et al., 2002). This normalization has become widely used, especially for single-channel arrays, but can be also applied to two-channel arrays as was the case in our dataset.

Several microarrays are designed to include spots in duplicates. One can then simply average the intensity values or ratios in duplicate spots within a microarray. However, this can result in artificially higher or lower values if one of the spots was affected by mechanical damage of the microarray or other similar artifacts that might not have been detected in the preprocessing step. Furthermore, by simply averaging duplicate spots, important information about the gene's expression variability is lost (Smyth et al., 2005). Another approach is to use the correlation between duplicated spots to estimate the common correlation between all spots on a microarray and from there estimate the variance 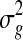of a gene in a microarray keeping the average estimator of log expression 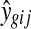unchanged. More details about the method are given in Smyth et al. (2005).

Because several preprocessing methods are available, it is sometimes difficult to choose one over another.

The second step in microarray analysis is the data analysis. Because the focus of this paper was to show the impact of preprocessing, we used linear models to find differentially expressed genes. The linear model could be expressed in the form

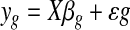(2)

where y_g is the expression of a gene g in a microarray, X is the design matrix, β_g is the matrix of linear coefficients and ɛ_g is the error. The null hypothesis that is stated in microarray experiments is H₀ : y_g = 0.

The choice of significance level α for the rejection of the null hypothesis (using a t-test or other statistical tests), determines the number of differentially expressed genes under given experimental conditions. Depending on the chosen experimental design, the significance of contrasts of interest is tested for each gene. The last step of microarray data analysis is the data visualization and the biological interpretation of the results. Various visualization tools that help the data analysts and biologists are available today, from GenMapp, Pathway Processor, and GeneXpress (reviewed in Cavalieri and De Filippo, 2005) to MapMan (Thimm et al., 2004) where large datasets are projected onto diagrams of metabolic pathways.

Studies involving influence and comparison of applying various preprocessing methods have been carried out previously for Affymetrix (i.e., single-channel) arrays (Bolstad et al., 2003; Choe et al., 2005; Cope et al., 2003; Lim et al., 2007). Furthermore, similar work has been done focusing on selection of appropriate statistical tests for determining differentially expressed genes (e.g., Vardhanabhuti et al., 2006), or even the appropriate false discovery method for determining differentially expressed proteins (Fodor et al., 2005). A study involving the influence of preprocessing for two-channel microarray data was recently published (Kerr et al., 2007), but not so extensively due to a different study goal.

In our study we investigated the effects of combinations of data preprocessing methods on the outcome of statistical data analysis. We focused on the presence of genes among differentially expressed genes and not on the mere number of genes on the list. In this way we tried to establish certain guidelines for analysis of two-channel microarray data by reducing false discovery rate. Two inhouse experiments were used, both studying the impact of biotic stress on gene expression. The system was built on the experiment studying potato–PVY interaction and further tested on experiments studying grapevine–phytoplasma interaction. A third data set (Bacac et al., 2006), dealing with mice stromal response to tumor growth, publicly available at GEO (Gene Expression Omnibus) was also used as a control of the proposed data analysis methodology. Experiments differ in type of microarrays used (cDNA vs. oligo) and experimental setup (direct comparison versus reference design).

Materials and Methods

Biological experiment and quality control

Two independent inhouse biological experiments, both dealing with plant biotic interactions, were used to test the effect of preprocessing methods.

In the case of potato microarray, a simple comparisons design was conducted using a potato cultivar, sensitive to potato virus Y (PVY^NTN). We tried to find the genes that were differentially expressed 12 h following virus inoculation in treated (virus-inoculated) compared to control (mock-inoculated) plants. Four biological replicates of the experiment were performed. Total RNA was isolated from inoculated leaves of six to eight treated or control plants and transcribed to cDNA. It was then hybridized to TIGR potato 10k microarrays (http://www.tigr.org/tdb/potato/microarray desc.shtml), versions 2 and 3, for the first two and second two biological replicates, respectively. There are 15,264 potato clones, spotted in duplicates on the microarray. Each microarray was hybridized with a virus-inoculated sample and mock-inoculated sample from the same biological replicate.

Dendrimere Cy3 and Cy5 labeling was used and dye swaps were performed between the biological replicates. Quality control of the hybridization was performed in Array Pro (Media Cybernetics, Silver Spring, MD) and low-quality spots: (1) nonuniform spots [mean (signal)/SD (signal) < 1], (2) spots with low signal/background ratio [mean (signal)/mean (background) < 1.5]) or (3) spots with low signal-to-noise ratio (SNR) < 3, and (4) empty or nonvalidated spots, were downweighted. Additionally, nonvalidated spots were downweighted.

In the case of grapevine a common reference design was used. Total RNA was isolated from the central midribs of field-grown healthy and phytoplasma-infected plants. RNA from three plants of the same disease status was pooled to pepare the sample RNA, and a part of RNA from all samples was pooled to create the reference RNA. Pooled total RNA was then transcribed to cDNA and amplified to cRNA. The amplification step included the labeling: incorporation of Cy5-UTP nucleotides (sample RNA) and Cy3-UTP nucleotides (reference RNA). Sample and reference cRNA were co-hybridized on microarrays. In this way, four microarrays (biological replicates) were prepared for healthy plants, and four microarrays were prepared for infected plants. Oligonucleotide microarrays were used (Vitis vinifera AROS 1.0, 14,562 oligoset, Operon, Alameda, CA, printed by INRA Montpellier). Each oligonucleotide was printed only once per array, with the exeption of a few genes that were used as controls. Quality control was performed manually in GenePix Pro software (Axon Instruments, Foster City, CA): (1) ununiform spots (e.g., doughnut-shaped), (2) spots that had diameter smaller than 50% of the normal spot size, and (3) spots with saturated pixels (including dust particles) were down-weighted. Gene expression data is available at GEO, accession number GSE10903 (potato) and GSE10906 (grapevine).

For the publicly available dataset on mouse tumor (Bacac et al., 2006; GEO accesision number GSE5945), changes in gene expression were monitored between invasive cancer stroma and prostate intraepithelial neoplasia (PIN). Samples from 10 mice, 6 with invasive cancer and 4 with PIN, were used. A common reference design with the reference being pooled RNA from the four PIN samples was done. Reference RNA was always labeled with Cy3-dCTP, while test RNA was labeled with Cy5-dCTP. NIA 17k microarrays were used (www.unil.ch/dafl) containing around 17,000 spotted cDNA clones. More details about the microarray experiment are given in Bacac et al., (2006).

Initially we wanted to include more different datasets, dealing also with, for example, bacterial samples, but have found that not all the criteria to include the datasets were fulfilled: (1) the results from the GEO datasets needed to be published somewhere in order for the comparison of the results to be possible; (2) in the published article or supplemental material a list of all differentially expressed genes (DEG) was considered necessary. We have found that not so many articles provide the readers with full lists of DEG, and we considered partial lists of DEG, not sufficient for our work. (3) We needed data from experiments on cDNA microarrays and not Affymetrix microarrays, which are more ubiquitous; (4) many studies, although fulfilling the above mentioned criteria, are time-course designs or were analyzed using various clustering methods. Because we did not use these methodologies, the available datasets were not suitable. (5) GAL files where gene annotation is visible is sometimes missing for the datasets. (6) Sometimes the Cy5/Cy3 ratio only was available, but we needed raw data for our work. (7) On several occasions the descriptions of the datasets in the database were incomplete; therefore, setup of statistical analysis was not possible.

Background corrections and normalizations

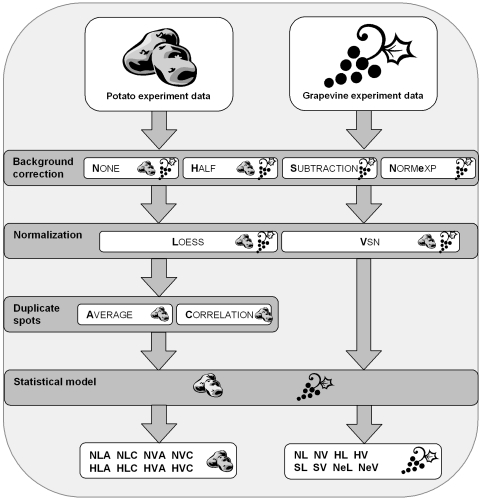
A schematic representation of the analysis can be seen in Figure 1. Data analysis was done in R computing environment (http://www.R-project.org). The R scripts for all data analysis are available from the corresponding author upon request. Background was measured locally. For both channels signal (trimmed mean of the whole variable spot area) and background (trimmed mean of the spot's local corners) intensities were calculated. Background variance was calculated for each channel and array. This, along with boxplots of background variability (Fig. 2), served us to determine the type of background correction to be used, if any. After background correction and normalization, MA plots were drawn. An MA plot depicts the relation between M values, which denote the ratio of gene intensities and are a measure of fold change in gene expression, and A values, which denote the average gene intensity (red and green channel) for a spot.

FIG. 1.

Schematic representation of data analysis conducted. Bold letters denote the method used for background correction/normalization/spot duplication used. The combination of all methods yielded in eight different data matrices for both experiments that were modeled using linear models. The data analysis scheme for the mouse data is analogous to the grape one.

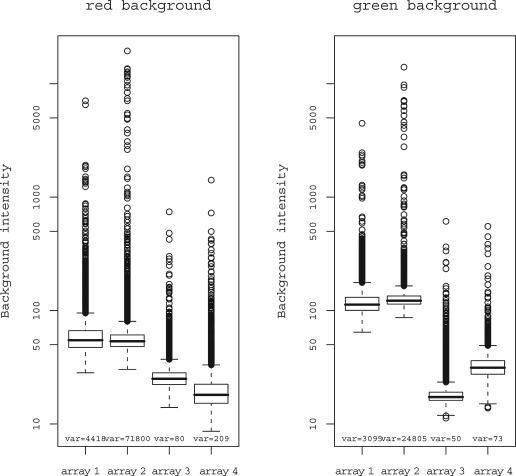
FIG. 2.

Boxplots for red and green background. Background values are plotted in log scale. Background variance is denoted at the bottom of each boxplot.

Differential expression

After normalization, duplicate spots within the potato microarrays were (1) simply averaged using the default correlation value of 0.75 or (2) averaged with the inclusion of common correlation information as described in Introduction section. In the case of the grapevine and mouse experiment, oligos/clones were printed only once per microarray, and therefore averaging or correlation between duplicated spots could not be taken into account. Eight combinations of different data preprocessing approaches (Fig. 1) were analyzed using the linear model. To assess how many genes within the top 100 differentially expressed genes (ranked first according to their p-values and, in a second instance also according to their M values) in one analysis were also present; in another, the lists of genes were compared in a pairwise manner. The analysis was repeated to compare the top 500 and top 20 differentially expressed gene lists. The choice of first 100 genes in the list was made because not all the data pre-processing combinations yielded in the same number of differentially expressed genes and, to make the comparisons equal, we chose a cutoff point.

Results

Background correction and normalization

Boxplots of background variability for all spots in the potato experiment can be seen in Figure 2. All further plots shown in this article were drawn from potato array 2, as this array showed the highest background variance. The background variance (data not shown) in grapevine experiments was lower than in the potato ones in all cases.

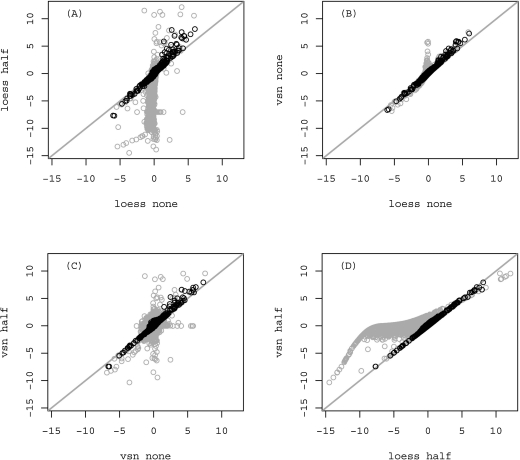
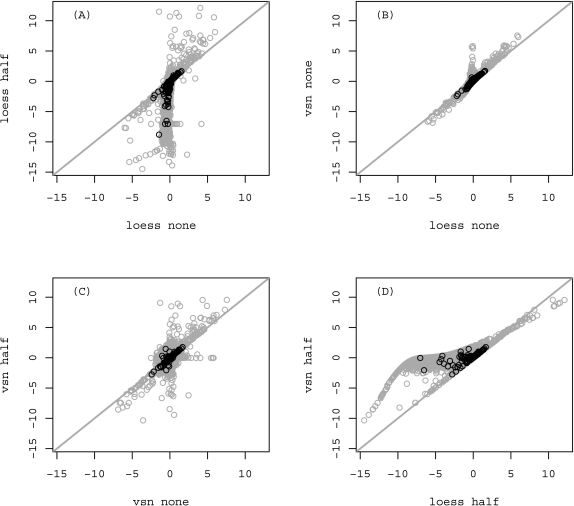
Correlations of M values within a microarray using different data analysis approaches were visually inspected (Fig. 3). From Figure 3 it can be seen that M values from spots that were weighted with 1, thus representing spots of higher quality are close to linear relation regardless of normalization or background correction method applied. In fact, the correlation between spots that were weighted with 1 was in all cases >0.96. This shows that various pre-processing methods combinations do not drastically affect the outcome, in this case the calculated M values. But the minor changes that arise between the calculated M values lead to different differentially expressed gene lists, and therefore confirm our emphasis on the fact that much attention is needed when selecting the appropriate data pre-processing. Because the influence of various preprocessing methods on spots of lower quality is much higher than on spots of good quality (seen in black on Fig. 3), it is a proof that quality control of spots is necessary. If filtering would not have been used, these spots would go to calculation of differentially expressed genes, which would introduce bias to the actual results. The linear relation is most apparent in Figure 3B), and can be ascribed to the fact that no background correction was used; therefore, the M values after normalization were not so extremely spread out.

FIG. 3.

Scatterplots of M values in the potato experiment using different normalization and background correction methods. Plots depict M values obtained after loess normalization without background correction compared with the M values obtained for the same spots after loess normalization with the background correction method half (A) or vsn normalization without background correction (B). M values after vsn normalization with background correction half are shown in relation to M values after vsn normalization with no background correction (plot C) and loess normalization with background correction half (plot D). Spots that were flagged after preprocessing are shown in gray. The gray line shows linear dependence between M values. Correlations between all spots that were weighted with 1 (and thus kept for further analysis) were in all cases >0.96.

Differential expression

Pairwise intersections from all analysis approaches in the top 100 differentially expressed genes (ranked by their respective p-values) were inspected. All p-values were <0.05, and in the range between 3.16 × 10⁻⁶ and 3.93 × 10⁻³ for potato; between 3.15 × 10⁻¹⁰ and 6.43 × 10⁻⁵ for grapevine; and between 1.25 × 10⁻⁷ and 7.43 × 10⁻⁴ for the mouse experiment. The pairwise comparison results are shown in Table 1. It can be seen that regardless of the preprocessing method used, there are >50 genes for potato, >65 genes for grapevine, and >63 genes for mouse that overlap in the list of the 100 most differentially expressed genes.

Table 1.

Pairwise Comparisons

POTATO	NLA	NLC	NVA	NVC	HLA	HLC	HVA	HVC
NLA	100	69	74	65	77	67	63	55
NLC		100	61	69	63	84	52	62
NVA			100	77	66	60	79	66
NVC				100	58	67	67	82
HLA					100	71	70	60
HLC						100	58	74
HVA							100	72
HVC								100

GRAPEVINE	NL	NV	HL	HV	SL	SV	NeL	NeV
NL	100	67	67	67	67	66	70	66
NV		100	79	89	78	89	88	89
HL			100	83	95	83	86	83
HV				100	82	92	89	92
SL					100	82	84	82
SV						100	91	100
NeL							100	91
NeV								100

MOUSE	NL	NV	HL	HV	SL	SV	NeL	NeV
NL	100	80	65	73	69	74	83	71
NV		100	63	83	70	84	64	79
HL			100	66	83	68	66	69
HV				100	75	92	64	87
SL					100	75	67	78
SV						100	68	85
NeL							100
NeV								100

Pairwise comparisons of the number of genes, present in the top 100 genes list that showed evidence for differential expression under different data analysis conditions. Combinations of all background correction (N—none, H—half and for grapevine, also S—subtract and Ne—normexp), normalization (L—loess, V—vsn) and spot averaging for potato (A—average, C—duplicate correlation) that was done are shown.

The intersection of the top 100 differentially expressed gene lists of all preprocessing combinations was also inspected. One hundred ninety-seven different genes in the potato experiment, 155 different genes in the grapevine experiment, and 183 genes in the mouse experiment were found in the top 100 differentially expressed gene lists of all eight data analysis combinations.

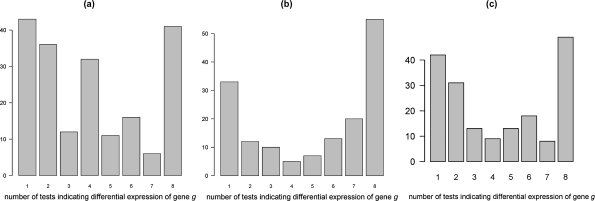
Around 40% of the genes (79 out of 197 and 73 out of 183) for potato and mouse, respectively, and around 30% of the genes (45 out of 155) in grapevine were found as the top 100 were differentially expressed in only one or two methods used (Fig. 4). Interestingly, Figure 4 shows that the percentage of common genes resulting as differentially expressed is again increased when comparing all eight data analysis methods: 21% for the potato experiment, 27% for the mouse, and 35% for the grapevine. These genes are most probably genuinely differentially expressed, and this is why they are seen as high ranking in all data analysis methods used. The difference between barplots (Fig. 4) is that for the potato dataset, which of the lowest quality out of the three, there is a high number of genes found as differentially expressed in four out of the eight preprocessing methods combinations (Fig. 4a). As four of the preprocessing methods correspond to loess normalization and the other four to vsn normalization, it is to be expected that there are some of the genes found as differentially expressed only after applying one normalization. When the data is of lower quality, this can blur the final result (higher number of differentially expressed genes) and introduce false positives in to the final result. Another point of interest in Table 1 is that the data analysis combination NL (no background correction with loess normalization) stands out when compared to other data analysis combinations for the grapevine experiment. It had the lowest number of common differentially expressed genes when compared to other analysis methods. The results were better for the method NV (no background correction with vsn normalization). This leads to the conclusion that it is not the lack of background correction per se that leads to different results in this case but also the choice of normalization method. Loess normalizes within a microarray, whereas vsn normalization is used to normalize each channel separately across all the microarays. Generally it is believed that if something is, in fact, differentially expressed it should be found as such regardless of the data analysis method used. Because the NL analysis combination deviated from the rest, this preprocessing method would not be recommended for this particular experimental dataset.

FIG. 4.

Barplot for genes that were found at least once in the top 100 differentially expressed genes for the (a) potato, (b) grapevine, and (c) mouse experiment. Numbers below lines denote the number of times gene g was found to be differentially expressed in any of eight data analysis combinations used.

Figure 5 shows pairwise comparisons of M values between sets of genes that were differentially expressed using different combinations of background corrections (none and half) and normalizations (loess and vsn). From it we conclude that (1) genes that were not differentially expressed were the ones that were the most affected by the background correction-normalization combinations; (2) generally there is good agreement between expression values obtained after different data preprocessing combinations, although substantial differences in calculated M values can be seen in some cases (e.g., loess–half combination yields expression values that are more scattered than the other combinations).

FIG. 5.

Scatterplots of M values in the potato experiment for all genes using different normalization and background correction methods. Black spots denote genes showing evidence for differential expression in two different background correction and normalization method combinations: loess normalization without background correction versus loess normalization with background correction half (A) or vsn normalization without background correction (B). M values after vsn normalization with background correction half are shown in relation with M values after vsn normalization with no background correction—(C) and loess normalization with background correction half—(D). All other genes are plotted in gray. The gray line shows linear dependance between M values.

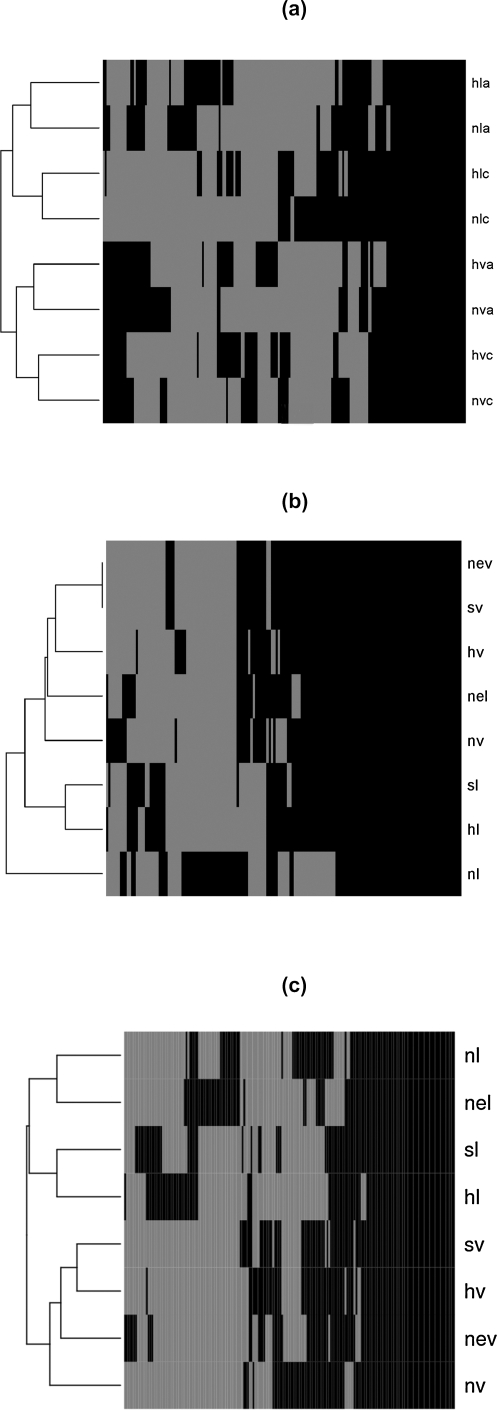
The heatmap for the 197 potato genes is shown in Figure 6a. After hierarchical clustering for the data preprocessing combinations used, it can be seen (Figure 6a)that the upper two clusters are formed depending on the type of normalization applied (loess or vsn). Clusters are further divided based on whether simple averaging or correlation information was used. Background correction has the least influence on the separation of clusters. If M values are plotted instead of depicting only presence or absence of genes in the top 100 differentially expressed genes, all genes identified as differentially expressed have |M| > 0.5 (data not shown).

FIG. 6.

Heatmaps for genes that were found in the top 100 differentially expressed genes at least for one data analysis method used. Heatmap (a) shows potato genes, while heatmaps (b) and (c) depict grapevine and mouse genes, respectively. Heatmaps show presence of top 100 differential expression gene list (in black). Genes that were not differentially expressed after applying other data analysis methods are shown in gray.

The heatmap for all the 155 grapevine genes is shown in Figure 6b. Except for the normexp background correction the respective vsn and loess normalized data group together. Unlike the potato example, it seems that the dataset that was loess-normalized without background correction yields quite different results than the other data. M values for differentially expressed genes found using various preprocessing approaches show a clear preference for |M| > 1 (data not shown). The heatmap for all 183 mouse genes is shown on Figure 6c. Again, the clusters are well separated according to the type of normalization that was used. For the vsn-normalized data, no background correction stands out compared to the other background corrections. This is somehow to be expected, as the function gives an estimate of the overall background that is subtracted within each array. Because this was the case in the mouse example, no background correction would have been advised.

In addition, the same data analysis was performed two more times, using the top 20 or top 500 differentially expressed genes ranked by their respective t-test p-values. For potato, p-values ranged from 3.16 × 10−⁶ to 0.001 for the top 20 differentially expressed genes and 0.02 for the top 500 differentially expressed genes. Using the “top 20 cutoff,” 65% of the genes were found in all eight data analysis approaches. With a “top 500” cutoff, this figure was 47%.

For grapevine, p-values ranged from 3.15 × 10⁻¹⁰ to 2.53 × 10⁻⁶ for the top 20 differentially expressed genes and to 1.71 × 10⁻³ for the top 500 differentially expressed genes.

Using the “top 20 cutoff,” 35% of the genes were found in all eight data analysis approaches. With a “top 500” cutoff, this figure was 63%.

For the mouse, p-values ranged from 1.25 × 10⁻⁷ to 1.35 × 10⁻⁴ for the top 20 differentially expressed genes and to 6.29 × 10⁻³ for the top 500 differentially expressed genes.

Using the “top 20 cutoff,” 55% of the genes were found in all eight data analysis approaches. With a “top 500” cutoff, this figure was 59%, indicating that the choice of p-value cutoff does not improve the reliability of the results by themselves.

Besides taking the first 20, 100, or 500 genes ranked by their respective p-values, we have also ranked the genes based on their |M| values. This was done primarily because, sometimes, p-values in a differentially expressed gene list can be similar or the same, and thus ranking is unstable. The results after ranking according to the |M| values were virtually the same as ranking according to the p-values.

Biological interpretation

To check the biological relevance of the results obtained, findings were assessed in view of potential gene function. Although this was not the primary purpose of this study, we thought it might serve as a general check point for the experimental results because we hypothesized that the genes that will be affected by the experimental conditions are somehow connected to the plant defense pathway. Forty-one genes out of 100 were present in all eight lists of the top 100 differentially expressed genes in the potato experiment (Fig. 4a). Functional categories were ascribed to those 41 genes, and their biological relevance was explored. The genes can be largely assigned to five functional categories: photosynthesis, signaling, regulation of transcription, protein synthesis or degradation, and genes with unknown ontology or function. Genes belonging to a certain category or subcategory were in all cases uniformly either upregulated or down-regulated. As for grapevine (Fig. 4b), 55 genes were present in all of the data analysis combinations performed. These genes can be grouped into 10 functional categories with transport, stress, miscellaneous enzyme functions, and grapevine-specific transcripts being affected most by the experimental conditions. Both results are in line with expected changes in the biological examples studied. As for the mouse experiment, 30 out of the 35 differentially expressed genes that were selected for biological interpretation and/or biological validation using real-time PCR, were found using our methodology also. This shows high reproducibility of our methodology in comparison with previously analyzed, verified, and published data. Forty-nine genes out of the first 100 were present in the list of differentially expressed genes in all of the data analysis preprocessing combinations applied (Fig. 4c).

Validation of the proposed methodology

The results of the mouse study, that is, the list of differentially expressed genes (Bacac et al., 2006) served as a control for our methodology. The validation results are shown in Table 2. Although, realistically, false positives are to be expected in the previously analyzed mouse data set, we disregarded that possibilty. Here the published results were considered as 100% correct, and served as basis for data validation. For calculation of list of differentially expressed genes, the intersection of vsn normalized and loess normalized data was taken as the final result (p < 0.01). We can see that the true positive rate (TPR) is 65% (256/396), the false positive rate (FPR) is 2% (331/17268), the false negative rate (FNR) is 0.35 (140/396).

Table 2.

Validation of the Proposed Methodology

		ACTUAL
		P	N	Σ
Predicted	P′	256	331	587
		TP	FP
	N′	140	16937
		FN	TN	17077
	Σ	396	17268	17664

Validation of the proposed methodology. Actual values are taken from list of differentially expressed gene as in Bacac et al. (2006). Predicted values are taken from list of differentially expressed genes as from our proposed methodology. P, positive; N, negative; TP, true positive; FP, false positive; FN, false negative; TN, true negative. 17664 represents the overall number of spots on the 17k microarray.

Discussion

The impact of selected preprocessing methods on the identification of differential expressed genes was assessed. The preprocessing methods and their combinations used for either of the experiments can be seen from Figure 1.

The general consensus on the choice of the preprocessing method to be used is that any method used should change the raw data as little as possible. Checking the background variance for each channel is advisable to double check the set spot quality control parameters (e.g., SNR <3). Generally, it is advised that no background correction should be used in order not to disrupt the original data. This is recommended when vsn normalization is used (as in Ritchie et al., 2007). Because we are dealing with an estimate of the true background, it is worth remembering that using a bad estimate is worse than using no estimate at all (Lee, 2004). In our case, with the potato experiment, as seen in Figure 2, a background correction was needed as the background variance from array 2 is very high and differs from the other three arrays. Figure 2 also implies the existence of two groups with different background: group one (arrays 1 and 2) with higer median background and background variance and group two (arrays 3 and 4) with lower median background and background variance. In fact, two microarray versions (version 2 for arrays 1 and 2 and version 3 for arrays 3 and 4) were used. Different array quality is a factor that can confound the results, so information concerning array version was incorporated into the statistical model to control for this. Because, when using background correction subtract, there is a risk of obtaining negative values of subtracted intensities, the use of half or normexp background correction is recommended. Only positive background corrected intensities are returned after applying either of the two methods, and, especially method half is intuitive and straightforward.

Two normalization methods that are theoretically distinct from one another were used. The difference between loess and vsn normalization is that loess normalizes log ratios (i.e., the M values) whereas vsn normalizes raw data from each channel separately. In gene expression microarray experiments we are typically interested in ratios and not in the absolute intensity values of spots. So if the absolute intensity values for technical or biological replicates of the same spot are different by orders of magnitude but the ratio remains unchanged, loess normalization would be advisable. However, improved technology is reducing such spot-to-spot variation and lower variance makes separate channel normalization like vsn the preferred option (Yang and Paquet, 2005).

Applying various types of background correction and data normalization to the same data is expected to produce different, but nevertheless comparable results. Experiments should not by default use the same preprocessing steps and the same statistical model for all analysis. Additionally, as seen from correlations on Figure 3, preprocessing affects spots of lower quality more than it does spots of good quality. Choosing the appropriate normalization method could also be design specific, as sometimes a normalization that was suitable for one experiment is inappropriate for the other.

The most common way of dealing with duplicate spots within a microarray is averaging them. A weighted average was used, so that spots with lower quality affect the averaged result less. Weights were assigned in image quality control step. It is advisable, though, to include as much information about the data as possible. Calculating correlations within duplicated spots and between microarrays is a way of including information about variance that is later used for calculating differential gene expression. That is why, when duplicate spots were present on the microarray, the actual correlation between spots was taken into account as one of the possible approaches in data analysis (Fig. 1).

After hierarchical clustering the resulting top table gene lists were well separated according to the type of normalization that was used (Fig. 6). Thus, it is important to underline that the choice of normalization method to be used has the highest impact on the results. Additionally, the genes that showed evidence for differential expression in all eight data analysis combinations had higher M values (data not shown). This confirms that the higher the M values are, the more likely it is for the gene to be differentially expressed. This is seen regardless of the data analysis method combination used. Of course, one has to bear in mind that some theoretical knowledge has to be employed when chosing the proper data analysis method(s).

Similar studies have been done previously for Affymetrix (i.e., single-channel) arrays (Bolstad et al., 2003; Cope et al., 2003; Choe et al., 2005; Lim et al., 2007). They conclude with favoring one normalization method over another or by defining the preprocessing methods most suitable for data analysis. In contrast, here we do not favor any specific normalization but are suggesting a selection of suitable methods (depending on type of array or quality control) and then applying the intersection of results for data interpretation in order to increase the robustness of results. It has been similarily shown that the identification of a feature (differentially expressed gene or protein) by more than one method increases confidence in results obtained (Fodor et al., 2005).

As typically we cannot well assess different parameters of experimental dataset, we do not know what kind of preprocessing method (especially normalization) would be the best for a specific experiment and, consequently, cannot determine the most appropriate combination of preprocessing methods in advance. The best approach would be to try several combinations as shown in this paper. That way the suitability of a specific approach is directly assessed. A simpler method is to use two preprocessing combinations as presented in a rough guideline in Figure 7. As it was shown that normalization had the highest influence on differentially expressed gene lists, we suggest the application of two theoretically distinct normalization methods (in our case loess and vsn, but other normalizations could have been used) on each set of data. Each analysis then produces its own list of potential differentially expressed genes. The intersection (overlap) of the results obtained by the two normalization methods would then give genes whose membership in the list is more robust (i.e., consisting largerly of de facto differentially expressed genes). After validation of the different analytical approaches (our methodology compared to the one in Bacac et al., 2006), TPR was lower than expected. This confirms the need of biological confirmation of results, which already is standard practice of transcriptomic analysis. FPR, also known as α (type I error) was very low (0.02), which means that only 2% of genes that were identified as differentially expressed when in fact they were not and, hence, specificity of our proposed methodology is high (1 − α = 0.98). Power of test (1 − β = 1 − FNR = 0.65) was also high, meaning that type II error of not identifying a truly differentially expressed gene was low.

FIG. 7.

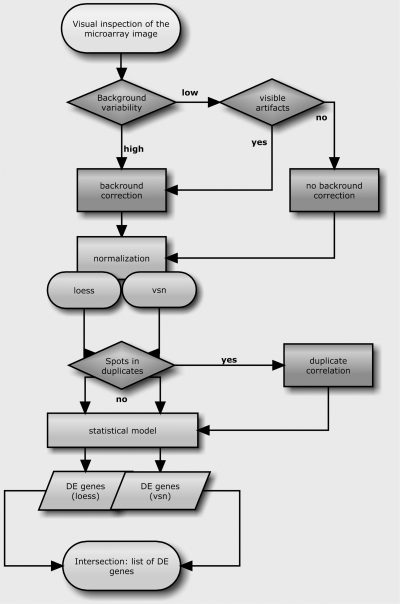
Proposed analysis scheme. The analysis should start with checking the background variability and if that is low and no spatial artifacts are present on the microarray image, no background correction is advised. Otherwise, a background correction is applied. After using two normalization methods of choice (in our case loess and vsn) and applying a statistical model, the intersection of two differentially expressed gene lists (each coming from one of the normalizations) is used to obtain more robust differentially expressed gene lists.

This analysis nicely complements a recently published discussion (Nettleton, 2006) on how microarray experimental design and analysis methods can influence the outcome of the experiment by showing that preprocessing step can also have an influence on both the obtained list of differentially expressed genes and the corresponding M values.

Acknowledgments

The authors would like to acknowledge Mike Galsworthy for carefully revising and editing the manuscript. His comments and suggestions were of great help for making the article concise and clear. The authors would also like to thank the anonymous referees for helpful suggestions on improving the paper. This work was financed by the Slovenian Research Agency (Ref. Nos. 1000-05-310172, 3311-02-831030, Z4-9697, J4-6459, P4-0165).

Author Disclosure Statement

The authors declare that there are no conflicting financial interests.