When the Tail Counts: The Advantage of Bilingualism Through the Ex-Gaussian Distribution Analysis

Abstract

Several studies have documented the advantage of bilingualism with respect to the development of the executive control (EC) system. Two effects of bilingualism have been described in conflict resolution tasks: (a) bilinguals tend to perform the tasks faster overall, and (b) bilinguals tend to experience less interference from conflicting information, compared to monolinguals. The precise way in which the bilingual advantage relies on different EC mechanisms is still not well understood. The goal of the present article is to further explore how bilingualism impacts the EC system by performing a new analysis (Ex-Gaussian) of already reported data in which bilinguals and monolinguals performed a flanker task. Ex-Gaussian distribution analysis allows us to partial out the contribution of the normal and the exponential components of the RT distribution of the two groups. The fit of the raw data to the ex-Gaussian distribution showed two main results. First, we found that the bilingualism advantage in the overall speed of processing is captured by group differences in the normal (μ) and the exponential (τ) components of the distribution. Second, the bilingual advantage in the magnitude of the conflict effect is captured by group differences only in the exponential component. The results are discussed in terms of: (a) usefulness of the ex-Gaussian analysis as a tool to better describe the RT distribution, and (b) a new approach to explore the cognitive processes purportedly involved in instantiating the bilingualism advantage with respect to EC.

Introduction

An increasing body of research indicates that bilingualism has an impact on the individual’s cognitive system beyond language processing. Perhaps the best documented of these collateral effects is the advantage exerted by bilingualism on the development of the executive control (EC) system (e.g., Bialystok et al., 2004, 2005, 2006, 2010; Colzato et al., 2008; Bialystok and Viswanathan, 2009). The hypothesis that has been driving these studies is that the continuous need of controlling two languages, both while producing and comprehending speech, involves to some extent general-domain EC mechanisms (e.g., Rodriguez-Fornells et al., 2006; Abutalebi and Green, 2008). Hence, this continuous use of EC mechanisms would lead to a more efficient EC system. But the precise way in which bilingualism affects the different EC mechanisms is still not well understood, in part due to our limited knowledge of how the EC system works.

The goal of the present article is to further explore the bilingual advantage on the EC system by, rather than introducing novel experimental evidence, performing a new analysis of already reported data. Specifically, we submit the results of two studies (Costa et al., 2008, 2009) that have explored the impact of bilingualism on conflict processing to an ex-Gaussian distribution analysis (see Matzke and Wagenmakers, 2009). As described below, this analysis allows us to partial out the contribution of different components of the RT distribution (normal and exponential components), and consequently can provide a more complete description of the RT data that will help us to better characterize the conditions in which differences between monolinguals and bilinguals are present. This in turn will hopefully lead to a better understanding of the impact of bilingualism on the EC system.

As shown elsewhere (Bialystok et al., 2004; Costa et al., 2008, 2009; Hernández et al., 2010), the performance of bilinguals and monolinguals in conflict resolution tasks depart in two main ways: (a) bilinguals tend to perform the conflict resolution task faster overall, and (b) bilinguals tend to suffer less interference from conflicting information. Let us exemplify these two effects in the context of a flanker task. In this task, participants are required to respond to a central arrow pointing to the right or to the left. The central arrow is presented with four flanker arrows that point in the same direction as the central one (congruent) or in the opposite direction (incongruent). Typically, responses tend to be slower for incongruent than for congruent trials (the conflict effect), revealing the time needed to resolve the conflict between the target and the conflicting flankers. In such a task, bilinguals have shown: (a) overall faster speed in all types of trials, and (b) a reduced conflict effect, as compared to monolinguals. Although these two effects have been widely replicated (e.g., Bialystok et al., 2004; Costa et al., 2008, 2009; Hernández et al., 2010), their functional interpretation is still open. A tentative interpretation of what these two effects may reveal about the impact of bilingualism on the EC system has been advanced in previous studies (e.g., Costa et al., 2009). Differences in overall speed would reveal differences in the functioning of monitoring mechanisms, being more efficient in the case of bilinguals. Monitoring mechanisms are referred to those processes responsible to evaluate the degree of conflict, to configure the cognitive system, and to adjust the behavior for an adequate response (e.g., Botvinick et al., 2001). Differences in the magnitude of the conflict effect would reflect differences in the way conflict resolution processes work, probably involving inhibitory control mechanisms. Note, however, that such an interpretation is just tentative, since these two effects interact in complex manners and are dissociated or not depending on the context of the experiment (see Costa et al., 2009).

Despite the empirical generalization presented above, it is important to mention that these two effects associated to bilingualism seem to be of different robustness. The advantage in the overall speed of bilinguals over monolinguals appears to be a more reliable effect, whereas in most of the studies the magnitude of the conflict effect is similar for bilinguals and monolinguals (see Costa et al., 2009). Indeed, at present, some researchers have raised their doubts about whether bilingualism actually affects the magnitude of the conflict effect (e.g., Hilchey and Klein, 2011). In the present context it is important to further explore the presence of these two effects in the different conditions that have been tested. One way to do so is to reconsider again some of the results already published and re-analyze them in a more detailed manner. All the studies that have investigated advantages of bilingualism on EC have used measures of central tendency, such as mean, to compare group performance in EC tasks. As some authors note, this strategy has some limitations when comparing the performance of groups of participants and might lead to overlook important differences between groups in the whole RT distributions (the advantages of this approach are discussed below; e.g., Heathcote et al., 1991; Van Zandt, 2000; Matzke and Wagenmakers, 2009; Balota and Yap, 2011).

Our goal here is to explore RT distributions of the two effects of bilingualism on the EC system. To do so, we make use of the data reported in two studies in which these two effects have been observed, and we re-analyze these data according to the ex-Gaussian fitting analysis. Below is a detailed explanation of how this ex-Gaussian analysis works and how it can help to better characterize the differences between monolinguals and bilinguals in EC.

The ex-gaussian analysis

Because of the nature of RT distributions (usually positively skewed) one can characterize them as the convolution of a normal and an exponential distribution. Hence, the RT distribution can be fitted to what is called an ex-Gaussian distribution, which leads to an estimation of both the normal and the exponential distribution (for the interpretation of these parameters in terms of “shape,” “scale,” and “location” of the distributions, see Jiang et al., 2004). The normal distribution is characterized by two parameters, mu (μ) and sigma (σ). μ is the mean of the fitted normal distribution, and σ corresponds to the variance. The exponential contribution is the tail of the distribution, and it is characterized by the parameter tau (τ)¹.

Along these lines, we make use of the ex-Gaussian analysis to compare RT distributions between groups. Note that this analysis has been previously applied successfully to understand differences between groups of participants. Examples of these applications come from different research contexts, such as patients with attentional disorders (e.g., Leth-Steensen et al., 2000), and aging and dementia (e.g., Spieler et al., 1996; Verhaeghen and Hoyer, 2007; Tse et al., 2010). Spieler et al. (1996) showed that older adults perform the Stroop task more slowly than young adults. Such differences between groups were present in all conditions, that is, either in conditions in which there was conflict (incongruent) or in conditions in which conflict was absent (congruent). The Ex-Gaussian analysis revealed that between-group differences in both types of trials were captured by μ, whereas group differences in the incongruent trials were also present in the exponential component of the distribution (τ). Other studies (e.g., Spieler et al., 1996; Tse et al., 2010) have shown that elderly adults and patients with dementia, who are assumed to have a diminished capacity for inhibitory control relative to young adults, showed higher τ values than young adults in Stroop or the Simon tasks.

These studies are good examples of how differences in mean RTs between groups of participants could be a result of changes in the central tendency of the distribution or/and of changes in the tail of the distribution. This suggests that it is important to examine to which extent group differences are due to changes in RTs over the whole distribution and not only to mean RTs.

Therefore, we believe that the Ex-Gaussian analysis is an interesting new approach to better understand the effects of bilingualism on the EC system. As described above, by considering a distributional analysis, this approach allows gathering more information about group differences. In particular, in the present article we compare the normal and the exponential components of the RT distributions in the bilingual and monolingual groups reported in Costa et al. (2008, 2009), where bilinguals outperformed monolinguals in both overall RTs and conflict resolution in a flanker task.

On the usefulness of the ex-gaussian distribution analysis

There are at least two independent different reasons to fit the data to an ex-Gaussian distribution: one empirical and the other one theoretical.

From the empirical point of view, the ex-Gaussian distribution analysis allows to have a more detailed description of the differences in performance between two given groups of participants. This in turn may lead to a more sensitive way to address the potential effects of bilingualism. In fact, as advanced above, beyond the excellent fit for empirically obtained RT distribution (e.g., Luce, 1986), this analysis has been shown to allow detecting differences that are not revealed by standard statistics, such as mean and variance (e.g., Heathcote et al., 1991; Van Zandt, 2000; Matzke and Wagenmakers, 2009; Balota and Yap, 2011). For example, Leth-Steensen et al. (2000) compared the performance of a group of children with attention deficit disorders with two control groups on an EC task. Mean RTs were significantly different between the group of children with attention deficits and the age-matched controls. Conversely, no RT differences were found between children with attention deficits and the younger control group. Crucially, however, the distribution analysis revealed that the two groups differed in the exponential component of the distribution (τ), suggesting differences in the performance between groups.

In the context of the bilingual research, the ex-Gaussian analysis could be a more sensitive tool to describe data on the bilingual effect on EC. This is because theoretical claims about the origin of the EC advantage are often made not only considering the conditions that lead to actual differences between the groups, but also considering those conditions in which such differences are not present. For example, in the D:Costa et al. (2009) study, monolinguals and bilinguals’ performances were compared in various versions of the flanker task that varied in the involvement of monitoring demands. One of the results was that the effect of bilingualism in overall reaction times was only present in the condition involving high-monitoring demands, leading the authors to draw conclusions about the nature of the bilingual advantage on one specific EC component (i.e., conflict monitoring). However, these results come from analyses on mean RT, and it is possible that some group differences come out when looking at the RT distribution, even in the experimental conditions that did not seem to be affected by bilingualism. Hence, a better and more sensitive description of these results by means of the ex-Gaussian distribution, where the effects on the normal and the exponential components can be partialed out, is at due.

From the theoretical point of view, this analysis might help us also to better understand the processes that might be affected by bilingualism leading to a more efficient EC. As suggested by some authors, changes in ex-Gaussian parameters could help in the interpretations of the cognitive processes involved in a specific task (e.g., Hohle, 1965; Gordon and Carson, 1990; Balota and Spieler, 1999; Kieffaber et al., 2006). As reviewed by Matzke and Wagenmakers (2009), between-group differences in the normal component of the distribution (μ) are often interpreted as revealing differences in “more automatic” processes across the whole task, whereas differences in the exponential component of the distribution (τ) are often attributed to differences for those trials or conditions in which “more controlled” processes are at play (e.g., inhibition). As it is apparent, these interpretations could be extremely helpful to characterize which components of the EC system are being affected by bilingualism. However, so far there is no converging evidence about the psychological interpretation of these parameters (Matzke and Wagenmakers, 2009). Nevertheless, even if at present it seems premature to draw specific hypotheses about how bilingualism affects these parameters we find relevant to compare the results by means of the classical approach (mean, variance) with those by means of the Ex-Gaussian distribution (we defer to the Discussion for some tentative interpretations).

Given these considerations, our main goal has an empirical nature, namely to further explore the effects of bilingualism on EC by comparing the RT distributions of monolinguals and bilinguals with an ex-Gaussian fitting. Specifically, we conducted a reanalysis of data published by Costa et al. (2008, 2009), in which the flanker task was used. In both studies, differences between bilinguals and monolinguals were present in overall RTs – either in congruent or incongruent trials. Also, under some conditions (see below) bilinguals experienced less of a conflict effect than monolinguals. We re-analyzed these two studies together (262 participants: 131 monolinguals and 131 bilinguals) to explore how the bilingual advantages in overall RTs and in the magnitude of the conflict effect are distributed over the normal (μ) and the exponential (τ) components.

We examine the ex-Gaussian parameters (μ and τ) using two strategies. First, we fit the original raw RTs to the ex-Gaussian distribution and compare bilinguals and monolinguals in μ and τ. The second strategy is to run a series of correlation analyses between the ex-Gaussian parameters and the magnitude of the conflict effect for both groups separately. The aim of this second analysis is to see if and how μ and τ capture the conflict resolution effect.

General Method

The two studies we consider in the present paper (Costa et al., 2008, 2009) investigated the bilingual advantage by means of the flanker task. Target stimuli consisted of a row of five horizontal black lines, with arrowheads pointing leftward or rightward. The target arrow was the central one. Participants were instructed to indicate the direction (left or right) of the central arrow via a button press. The target (central arrow) was presented in two main conditions: with congruent flankers (same direction as the target) and incongruent flankers (opposite direction). In one of the studies (Costa et al., 2008), a neutral condition was added, in which flankers were black lines without arrowheads.

Each target stimulus was preceded by a cue, but for the purpose of the present analyses this factor is not considered. The event presentation was as follows: (a) a fixation point (a plus sign) appeared at the center of the screen for 400 ms, (b) a cue (an asterisk) was presented for 100 ms, (c) the fixation point was again presented for 400 ms, (d) the target arrow and the flankers were presented simultaneously until participant’s response or up to 1700 ms, (e) the target and flankers disappeared after the response was given and the next trial began. The experiment consisted of three experimental blocks with 96 trials per block, presented randomly.

The task was similar in the two studies, the only difference being in the frequency of the trials requiring conflict resolution. In D:Costa et al. (2008) study, there were ∼67% of trials free of conflict (i.e., 33% neutral and 33% congruent) and 33% of trials involving conflict (i.e., incongruent trials). In D:Costa et al. (2009) study, four different versions of the task were used. For the purpose of the present analyses, we only consider the version of the task in which 75% of the trials were congruent and 25% were incongruent. We only consider this version of the task because it is the one in which bilingualism affected both the speed of processing and the magnitude of the conflict effect.

For fitting the ex-Gaussian distribution, raw data were generated from a set of 262 participants. Two hundred participants (100 Catalan–Spanish bilinguals and 100 Spanish monolinguals) took part in D:Costa et al. (2008) study. Sixty-two participants (31 Catalan–Spanish bilinguals and 31 Spanish monolinguals) took part in D:Costa et al. (2009) study.

Raw data were sorted per condition (congruent and incongruent) and per group (monolinguals and bilinguals) separately. Note that we did not consider the neutral condition of Costa et al. (2008) in order to be able to analyze the two studies together. For each condition we had 144 observations per subject (48 for each of the 3 blocks), for a total of 37,728 data points for the congruent and 37,728 for the incongruent conditions. From this set we excluded errors and RTs below 100 ms and above 3 SD, which represented the 2.3% of the observations. The analyses were performed on a set of 73,724 observations (36,808 for the monolingual group and 36,916 for the bilingual group). The parameters of the ex-Gaussian distribution (μ and τ) were obtained for each participant using the quantile maximum likelihood (QML) estimation procedure in QMPE 2.18 (Cousineau et al., 2004). The idea behind the maximum likelihood parameter estimation is to determine the parameters that maximize the probability (likelihood) of the sample data. The QML method is one of the commonly used for the fitting of raw data thanks to its good reliability in the estimation of parameters (Heathcote et al., 2002). The estimation gives us a value for each parameter (μ and τ) and for each participant per condition and per group. These values were submitted to an analysis of variance (ANOVA; see below for details). The goodness of fit of the ex-Gaussian distribution to the original data was tested using chi-squared tests.

Results

Overall analysis on the original data

Before conducting the ex-Gaussian analysis we report the analysis on the original data obtained from the two experiments together (131 monolinguals and 131 bilinguals). This will serve to assess the contribution of the normal and exponential distributions to the effects of bilingualism observed in Costa et al. (2008, 2009). We ran a repeated-measures ANOVA considering “Group” (monolinguals and bilinguals) and “Task-version” [33% (Costa et al., 2008) versus 25% (Costa et al., 2009) of trials involving conflict] as between-subject factors, and “Condition” (congruent and incongruent) as a within-subject factor.

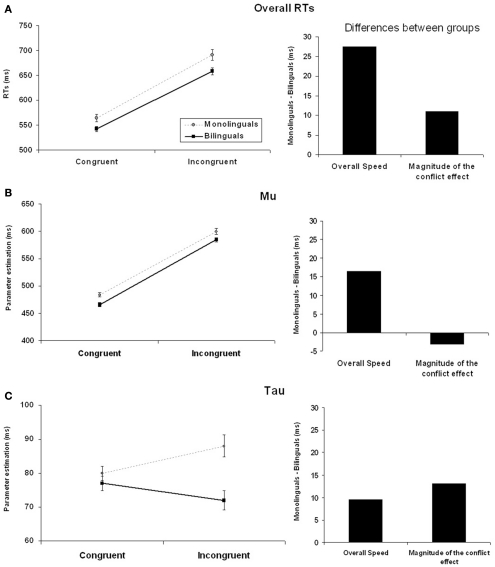
The ANOVA showed a main effect of Group [F(1,258) = 9.25, P = 0.003, ${\eta }_{\text{p}}^2=0.03$] indicating that bilinguals were faster overall (600 ms) than monolinguals (628 ms). The significant main effect of Condition [F(1,258) = 1995.89, P < 0.0001, ${\eta }_{\text{p}}^2=0.84$], indicated faster responses to congruent trials (553 ms) relative to incongruent trials (674 ms). The significant Group × Condition interaction indicated that the conflict effect (RTs of incongruent trials minus RTs of congruent trials, see Figure 1A) was different between the two groups [F(1,258) = 3.98, P = 0.05, ${\eta }_{\text{p}}^2=0.02$]. A closer look to the interaction revealed that bilinguals had a reduced conflict effect (115 ms) compared to monolinguals (126 ms).

Figure 1.

In the left column, overall reaction times (A), μ (B), and τ (C) broken by condition (congruent and incongruent) and group (monolinguals and bilinguals). In the right column, difference between monolinguals and bilinguals in overall speed of processing and in the magnitude of the conflict effect. Error bars represent the SE.

Ex-gaussian distribution fitting

The joint analysis of D:Costa et al. (2008, 2009) original data confirmed the presence of two bilingualism advantages. Bilinguals were faster overall and experienced less of a conflict effect than monolinguals. Now we move to examine how these two effects are captured by the normal and the exponential components of the distribution. The ex-Gaussian model was rejected in all the fits (all P_s > 0.05, df = 5), indicating that the model provides a good description of the original data.

We ran repeated-measures ANOVAs for μ and τ separately. In these ANOVAs we considered “Group” (monolinguals and bilinguals) and “Task-version” (33% versus 25% of trials involving conflict) as between-subject factors, and “Condition” (congruent and incongruent) as a within-subject factor.

The ANOVA for μ showed a main effect of Group [F(1,258) = 5.10, P = 0.02, ${\eta }_{\text{p}}^2=0.02$] indicating that bilinguals were faster overall (525 ms) than monolinguals (541 ms). The significant main effect of Condition [F(1,258) = 1324.72, P < 0.0001, ${\eta }_{\text{p}}^2=0.84$] indicated that responses to the congruent condition were faster (474 ms) than responses to the incongruent one (592 ms). The non-significant Group × Condition interaction [F(1,258) = 0.26, P = 0.62] indicated that the conflict effect was not different between monolinguals and bilinguals on the parameter estimate μ (see Figure 1B).

To summarize, the μ value captures the advantage of bilinguals with regard to overall speed of processing: μ was smaller for bilinguals than for monolinguals. Conversely, the μ value did not capture differences in the magnitude of the conflict effect between monolinguals and bilinguals.

The ANOVA for τ showed a main effect of Group [F(1,258) = 7.32, P = 0.007, ${\eta }_{\text{p}}^2=0.03$], indicating that the τ values were larger for monolinguals (85 ms) than for bilinguals (75 ms). The main effect of Condition was not significant [F(1,258) = 0.60, P = 0.44]. However, the significant Group × Condition interaction [F(1,258) = 5.42, P = 0.02, ${\eta }_{\text{p}}^2=0.02$] indicated that the conflict effect on τ differed between the two groups. That is, monolinguals showed an increase of τ from the congruent compared to the incongruent condition (8 ms, P = 0.03), whereas in bilinguals τ was the same in the two conditions (difference of τ between the congruent and the incongruent conditions: −4 ms, P = 0.28, see Figure 1C).

We also found a significant three-way interaction Group ×  Condition × Task. We conducted separate ANOVAs considering the Group and Condition factors, for each task separately. The analyses showed that τ significantly increased from congruent to incongruent trials only for monolinguals in the task-version with 25% of conflict trials [Group × Condition interaction: F(1, 60) = 10.38, P = 0.002, ${\eta }_{\text{p}}^2=0.15$].

To summarize, the τ value captures the overall speed of processing: τ was smaller for bilinguals than for monolinguals. The τ value also captures part of the conflict effect, but only in the monolingual group: monolinguals had a larger conflict effect on τ in the task-version with 25% conflict trials.

These results suggest that differences in the overall speed with which the task is performed are captured both by the normal component of the distribution and the exponential one, as revealed by the smaller μ and τ values of bilinguals compared with those of monolinguals.

The issue of the magnitude of the conflict effect is more complex. Similar to what happens with speed of processing, both μ and τ capture part of the conflict effect of the two groups. This is especially true for the μ value, which was significantly smaller for the congruent than the incongruent condition for both bilinguals and monolinguals. The τ values, in contrast, differed between the two groups. While τ increased from the congruent to the incongruent condition for monolinguals, it did not change for bilinguals.

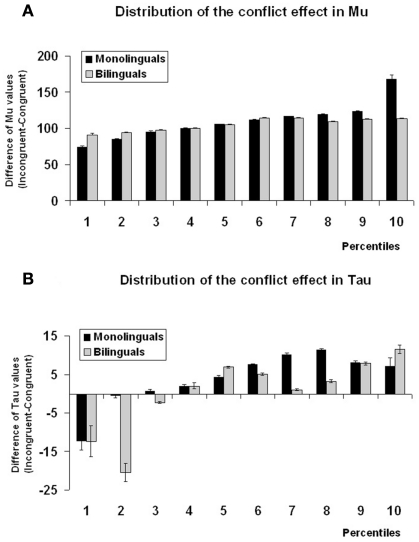
In order to explore the distribution of μ and τ, we further analyzed the data, dividing the distribution in percentiles. We divided the distribution of μ and τ according to 10 percentiles. The first percentile contained values of the parameter estimations for which participants were the fastest and the tenth percentile contained values of the parameter estimations for which they were the slowest. Then we calculated the distribution of the conflict effect in μ and τ, that is, the difference between the incongruent and the congruent conditions for each parameter in all the 10 percentiles. We performed percentile analyses to obtain converging evidence regarding the shape of the RT distributions, apart from the ex-Gaussian analyses. As proposed by other authors (e.g., Tse et al., 2010) it is important to have convergent evidence from different techniques.

We plotted the distribution of the conflict effect in μ and τ for each of the 10 percentiles for each group (see Figure 2). The magnitude of the conflict effect captured by μ for both groups was almost the same in the 10 percentiles. Only for the slowest ones the magnitude of the conflict effect was higher in monolinguals relative to bilinguals (percentiles: 8th, 9th, and 10th; P_s < 0.04). Conversely, the magnitude of the conflict effect captured by τ was higher in monolinguals relative to bilinguals in 5 out of 10 percentiles (percentiles: 2nd, 3rd, 6th, 7th, and 8th; P_s < 0.03).

Figure 2.

Percentile distribution of the magnitude of the conflict effect captured by μ (A) and τ (B), broken by group (monolinguals and bilinguals). The percentiles are based on the participants’ scores. Error bars represent the SE.

Correlations

Mu and tau parameters

In the previous analyses we found differences between monolinguals and bilinguals both for the normal component and the exponential component of the ex-Gaussian analysis. That is, monolinguals showed increased μ and τ values compared to bilinguals. These results suggested that these two parameters follow the same trend, at least in the monolingual group: longer RTs in the mean (speed of processing) correspond to longer RTs in the tail of the distribution. To verify the trend of the two parameters we ran correlation analyses between μ and τ. Positive correlations indicate that an increase in μ (the normal component) corresponds to an increase in τ (the exponential component). Negative correlations indicate that the normal and the exponential components have opposite trends, and reflect, at least to some extent, independent mechanisms.

We performed the correlations for each group separately. We found that in the monolingual group, μ and τ were positively correlated [r(129) = 0.20, P = 0.02], whereas in the bilingual group they were not [r(129) = 0.01, P = 0.92].

Mu, tau, and the conflict effect

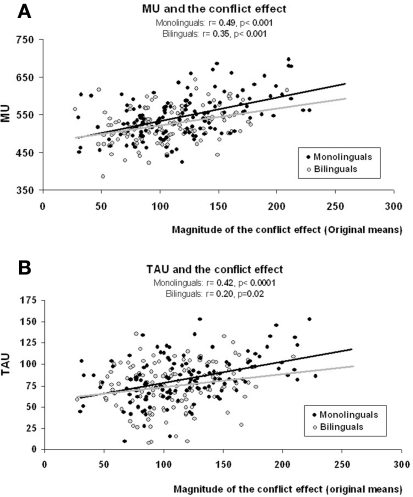
We saw in the previous correlation analyses that the μ and τ parameters are differently related in the two groups. These parameters are independent in bilinguals whereas they are dependent in monolinguals. We will now investigate how the two parameters contribute to the magnitude of the conflict effect. We will see whether an increase in the magnitude of the conflict effect is indexed by an increase in μ and/or τ values, in each of the two groups independently. We ran correlation analyses between the μ and τ parameters and the magnitude of the conflict effect (RTs of incongruent trials minus RTs of congruent trials), for each group separately. μ positively correlated with the magnitude of the conflict effect both in monolinguals [r(129) = 0.49, P > 0.001] and bilinguals [r(129) = 0.35, P > 0.001]. τ positively correlated with the magnitude of the conflict resolution effect more strongly in the monolingual [r(129) = 0.42, P > 0.001] than in the bilingual group [r(129) = 0.20, P = 0.02; See Figure 3].

Figure 3.

Correlations between the magnitude of the conflict effect and μ (A) and τ (B) in monolinguals and bilinguals respectively.

Discussion

The goal of the present article was to further explore the impact of bilingualism on EC mechanisms through ex-Gaussian distribution analyses of already reported data. We did so by reanalyzing a set of previously reported data showing that bilinguals outperformed monolinguals in: (a) speed of processing, and (b) conflict resolution. We fitted the raw data to an ex-Gaussian distribution in order to partial out the contribution of the normal and the exponential components of these two aspects of the bilingualism advantage. We examined between-group differences in the changes of these two components with the aim of providing a more complete description of the RT distributions in monolinguals and bilinguals under different experimental conditions. Below, we discuss the results considering the overall speed of processing and the conflict effect.

From an empirical point of view, the main finding is that the two effects of bilingualism on the EC system were differently captured by the group differences in the estimate parameters. First, the advantage of bilinguals with respect to overall speed of processing was captured by the normal and the exponential components of the distribution: monolinguals showed higher μ and τ values compared to those of bilinguals. Second, the difference in the magnitude of the conflict effect between groups was present in the exponential component (τ): only monolinguals showed an increase of τ from the congruent to the incongruent conditions.

We also ran correlation analyses to see how the parameter estimates captured differences in the magnitude of the conflict effect in each group. The correlations of the two parameters with the magnitude of the conflict effect indicated that the exponential and the normal components differentially predicted the conflict effect in the two groups. In bilinguals, the magnitude of the conflict effect correlated more strongly with the normal component (r = 0.35) than with the exponential one (r = 0.20). Whereas in the monolingual group the two components correlated to the same extent with the magnitude of the conflict effect (μ: r = 0.49, τ = 0.42). In monolinguals, who showed a larger conflict effect, the increase in the cost of resolving the conflict resulted in an increase in the τ values; whereas in bilinguals, the increase in the magnitude of the conflict effect resulted in small changes in the τ values. To summarize, the correlation analysis confirmed the results of the distributional analyses: that is, the exponential component captured the group differences in the conflict effect. The ex-Gaussian distribution analysis appears to be a more powerful tool for describing the impact of bilingualism on these EC control tasks.

As we argued in the Introduction, the main goal of this article was to provide a more complete description of the RT distributions in bilinguals and monolinguals, and their potential differences in EC tasks. The fact that at present the interpretation of the ex-Gaussian parameters (with respect to cognitive processes) is not yet strong, prevents us from drawing straightforward conclusions from our results (Matzke and Wagenmakers, 2009). Nevertheless, we would like to advance some tentative interpretations in line with previous studies (e.g., Spieler et al., 1996; Penner-Wilger et al., 2002; Kieffaber et al., 2006; Schmiedek et al., 2007; Rotello and Zeng, 2008). Note, however, that the main goal of this exercise is to prompt further research on the relationship between bilingualism and EC.

According to the above mentioned authors, between-group differences in the normal component of the distribution (μ) might reflect differences in more automatic processes across the whole task (e.g., overall speed of processing), whereas differences in the exponential component of the distribution (τ) might reflect differences for those trials or conditions in which more controlled processes are at play (e.g., inhibition; see for example the study by Spieler et al. (1996) described in the Introduction).

In our analysis, overall reaction time differences between monolinguals and bilinguals were captured by the changes in μ and τ. This suggests that the advantage conferred by bilingualism might have various sources, one affecting the overall speed of processing and the other affecting more controlled processes. Although at present it is difficult to be more precise about how this may take place, one could tentatively argue that speed of processing is revealing, to some extent, the better functioning of the monitoring processes. The monitoring system is continuously engaged in tasks with different types of trials, and it is in charge of signaling the need of engaging or not conflict resolution processes. Arguably, the faster this monitoring system, the faster the completion of the task, regardless of the involvement of conflict in a given trial. Consequently, differences in monitoring processes might reveal themselves in differences in speed of processing. It is even more difficult to give an interpretation of τ differences between the groups. However, and always within the present theoretical context, one could see this result as an indication of the more efficient functioning of controlled processing of bilinguals.

The second effect of bilingualism, namely the magnitude of the conflict effect, measured as the difference in RTs between the incongruent and the congruent conditions, is somewhat consistent with this interpretation. The engagement of conflict resolution processes (inhibition or other) in the incongruent trials leads to longer RTs in comparison to congruent ones. Thus, the more efficient the conflict resolution system, the smaller the difference between incongruent and congruent trials. Following this rationale, the reduced conflict effect for bilinguals has been attributed to a more efficient conflict resolution system (Bialystok et al., 2004, 2008; Costa et al., 2008; Hernández et al., 2010). Therefore, the group differences were captured by a change in the exponential component (τ).

The extent to which the exponential component captures group differences with respect to the conflict effect results from differences in efficiency when engaging inhibitory mechanisms. Thus, our results can be interpreted as evidence that the lower efficiency of monolinguals in engaging inhibitory mechanisms resulted in an increase of the τ parameter from the congruent to the incongruent condition, whereas τ did not change in bilinguals.

Another interesting result comes from the correlation analysis of μ and τ. In bilinguals the two parameters were not correlated while a positive correlation was present in monolinguals. That is, the changes in the exponential component were independent of those of the exponential one for bilinguals but not for monolinguals. This differential pattern reveals that differences between monolinguals and bilinguals appear to be more complex than previously thought, and that they cannot be attributed to a better functioning of a single component of the EC system. Rather, it appears that bilingualism may not only affect several aspects of the EC system but also how these systems interact with each other (see Costa et al., 2009 for a similar argument). Further research is needed to clarify the nature of these interactions.

To summarize, the ex-Gaussian analysis has provided a more fine-grained understanding of the bilingual effect in the flanker task. In particular, we found that the advantage of bilinguals is differentially captured by the normal and the exponential components of the distribution. On the one hand, group differences in the overall speed of processing are captured by both components. On the other hand, group differences with respect to the magnitude of the conflict effect are captured only by the exponential component of the distribution. We believe that this new approach of fitting the data to ex-Gaussian distribution is a useful descriptive analysis to look beyond the measures of central tendency, such as mean and median. Further theoretical advancements in the interpretation of the different parameters will be needed to gain better understanding of the origin of such effects.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.