An adaptation of the Wiener filter suitable for analyzing images of isolated single particles

Abstract

The Wiener filter is a standard means of optimizing the signal in sums of aligned, noisy images obtained by electron cryo-microscopy (cryo-EM). However, estimation of the resolution-dependent (“spectral”) signal-to-noise ratio (SSNR) from the input data has remained problematic, and error reduction due to specific application of the SSNR term within a Wiener filter has not been reported. Here we describe an adjustment to the Wiener filter for optimal summation of images of isolated particles surrounded by large regions of featureless background, as is typically the case in single-particle cryo-EM applications. We show that the density within the particle area can be optimized, in the least-squares sense, by scaling the SSNR term found in the conventional Wiener filter by a factor that reflects the fraction of the image field occupied by the particle. We also give related expressions that allow the SSNR to be computed for application in this new filter, by incorporating a masking step into a Fourier Ring Correlation (FRC), a standard resolution measure. Furthermore, we show that this masked FRC estimation scheme substantially improves on the accuracy of conventional SSNR estimation methods. We demonstrate the validity of our new approach in numeric tests with simulated data corresponding to realistic cryo-EM imaging conditions. This variation of the Wiener filter and accompanying derivation should prove useful for a variety of single-particle cryo-EM applications, including 3D reconstruction.

Introduction

Single-particle cryo-EM is increasingly used to produce high-resolution 2D and 3D maps of biological macromolecules. The raw data obtained by cryo-EM pose numerous technical challenges for the image processing done to obtain useful descriptions of the target molecules. Individual particle images exhibit extremely high levels of noise, owing to the extreme radiation sensitivity of biological specimens which in turn requires minimizing electron exposure in order to limit radiolysis. In addition, the image signal is itself scrambled by the microscope optics, as characterized by the Contrast Transfer Function (CTF) of the microscope, leading to partial or complete loss of the particle signal at regular intervals throughout Fourier space. Numerous techniques have been developed to address these challenges, but nevertheless the processing of cryo-EM images remains a topic of considerable research interest.

One of the early advances in single-particle cryo-EM was the application of digital signal processing theory, in order to improve estimates of the reconstructed particle density as well as to assess the quality of the reconstructions themselves (Frank, 2006). Frank and Ali described a connection between image correlation and signal-to-noise ratio (Frank and Al-Ali, 1975) that was subsequently extended to yield various resolution assessment techniques, including the Fourier Ring Correlation (FRC) for 2D projection averages, and the analogous Fourier Shell Correlation for 3D reconstructions (van Heel, 1987). Numerous approaches have been used to compensate for CTF effects and high noise levels, including phase-flipping and iterative reconstruction.

One of the methods more commonly applied in reconstruction algorithms is the Wiener filter (Wiener, 1949; Kolmogorov, 1941), which is designed to produce estimates of signal measurements having the least possible mean-squared error, given some level of prior knowledge about the system such as the signal-to-noise ratio (SNR) of the images. The benefits of the Wiener filter are widely acknowledged, and numerous applications to various single-particle applications have been described in earlier work (Tang et al., 2007; Zhang et al., 2008). However, somewhat surprisingly, the benefits of the Wiener filter are rarely if ever quantified in comparison to other image restoration techniques, leaving it an open question how beneficial this filter is in practice. Perhaps related to this issue, it is commonly considered impractical to extract useful spectral SNR (SSNR) characteristics from data sets of aligned images alone (Downing and Glaeser, 2008); instead, earlier work has suggested that additional experimental information (X-ray scattering factors, for example) is necessary to obtain useful SSNR estimates for the purpose of applying a Wiener filter (Tang et al., 2007). In the absence of accurate SSNR estimates, an arbitrary constant term is commonly substituted for the SSNR expression within the Wiener filter (Grigorieff, 2007; Zeng et al., 2007; Frank, 2006), with the result that the filter no longer minimizes the mean-squared error of the particle estimate.

Here, we present a quantitative evaluation of the Wiener filter for combining pre-aligned cryo-EM images to produce estimates of the projected density. Our results demonstrate that for images of isolated single particles, the conventionally-defined Wiener filter fails to optimize the estimate of the particle density itself, owing to the presence of a substantial signal-free solvent region in the raw data images. We address this problem by developing a modified version of the filter, which we call the single-particle Wiener filter, which is designed to optimize the density estimate within a defined mask region when the SSNR characteristics of the raw images is available. We also present a straightforward method for obtaining accurate estimates of the average SSNR characteristics from the images themselves, with no need for additional experimental information, via a masked FRC calculation. Our new treatment of the Wiener filter thus establishes a self-contained method for defining a least-squares estimate of a single-particle density map from aligned image data sets.

Theory

Wiener filter expression

We begin with the derivation of the Wiener filter expression (Saxton, 1978). We consider a series of aligned images, whose signal and noise is modeled as follows:

$$\begin{array}{c}\hfill x^{\left(i\right)}\left(\mathbf{r}\right)={\mathrm{FT}}^{-1}\left\{{\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\right\}\ast \left(m\left(\mathbf{r}\right)+n_{\text{particle}}^{\left(i\right)}\left(\mathbf{r}\right)\right)+n_{\text{image}}^{\left(i\right)}\left(\mathbf{r}\right)\left(\text{real space}\right)\hfill \\ \hfill X^{\left(i\right)}\left(\mathbf{s}\right)={\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\left(M^{\left(i\right)}\left(\mathbf{s}\right)+N_{\text{particle}}^{\left(i\right)}\left(\mathrm{s}\right)\right)+N_{\text{image}}^{\left(i\right)}\left(\mathbf{s}\right)\left(\text{Fourier space}\right)\hfill \end{array}$$ (1)

where “*” represents the convolution operator, and other terms are defined as follows. For the i’th image: x⁽ⁱ⁾ (r) is the recorded image; m(r) is the corresponding noise-free particle image; $n_{\text{particle}}^{\left(i\right)}\left(\mathbf{r}\right)$ and $n_{\text{image}}^{\left(i\right)}\left(\mathbf{r}\right)$ are specific instances of “particle” noise (i.e. signal fluctuations from the sample itself, such as embedding medium or support film) and “image” noise (from the measurement process), respectively; and CTF⁽ⁱ⁾ (s) the contrast transfer function of the microscope. The symbols r and sdenote vector coordinates in real space and Fourier space, respectively. Capitalized symbols X⁽ⁱ⁾ (s), M⁽ⁱ⁾ (s), $n_{\text{particle}}^{\left(i\right)}\left(\mathbf{s}\right)$, $n_{\text{image}}^{\left(i\right)}\left(\mathbf{s}\right)$ refer to Fourier-space equivalents of the corresponding uncapitalized symbol. Note that the CTF term here is implicitly assumed to include all transfer-function-related effects related to the imaging process, including signal attenuation due to envelope function (Glaeser, 2007).

To facilitate analysis, we will treat the noise contribution as a single term, n⁽ⁱ⁾ (r). This approximation is justified by at least two aspects of cryo-EM data: (1) when a large number of images having varying CTF functions are treated, CTF modulations of the particle noise Fourier transform will effectively disappear in the summed particle estimate, resulting in a “net particle noise” in the particle estimate whose contribution can be grouped together with the image noise contribution to yield a “net noise”; (2) the image noise is on the order of 10x larger than the particle noise in cryo-EM applications (Baxter et al., 2009).

In what follows, we will allow the Fourier equivalent of the expectation value of the noise terms $\langle {\mid N^{\left(i\right)}\left(\mathbf{s}\right)\mid }^2\rangle$ to vary as a function of resolution (thus, N⁽ⁱ⁾ (s) may be described as “colored noise”), although we will assume that, consistent with the expected behavior of cryo-EM images, the summed noise component n⁽ⁱ⁾ (r) follows an identical random distribution at every point within the real-space image. We then write an expression for the i’th image in a series of noisy image measurements:

$$X^{\left(i\right)}\left(\mathbf{s}\right)={\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)M\left(\mathbf{s}\right)+N^{\left(i\right)}\left(\mathbf{s}\right)$$ (2)

The Wiener filter is designed to give a least-squares estimate of the signal, M, from the series of N such measurements, assuming a solution of the form ${\widehat{M}}_W\left(\mathbf{s}\right)={\sum }_i{K}_w^{\left(i\right)}\left(\mathbf{s}\right)X^{\left(i\right)}\left(\mathbf{s}\right)$. The formal statement of the optimization problem is to minimize the expression:

$$\text{Error}={\mid M\left(\mathbf{s}\right)-\sum _i{K}_W^{\left(i\right)}\left(\mathbf{s}\right)X^{\left(i\right)}\left(\mathbf{s}\right)\mid }^2$$ (3)

where $K_W^{\left(i\right)}$ are the filter coefficients to be determined.

The solution to the least-squares problem in Equation (3) is (Saxton, 1978):

$$K_W^{\left(i\right)}\left(\mathbf{s}\right)=\frac{{\left\{{\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\right\}}^{\ast }}{\sum _i{\left({\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\right)}^2+\frac{\mathrm{Var}\left\{N\left(\mathbf{s}\right)\right\}}{\mathrm{Var}\left\{M\left(\mathbf{s}\right)\right\}}}\to {\widehat{M}}_W=\frac{\sum _i{\left\{{\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\right\}}^{\ast }{X}^{\left(i\right)}\left(\mathbf{s}\right)}{\sum _i{\left({\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\right)}^2+\frac{\mathrm{Var}\left\{N\left(\mathbf{s}\right)\right\}}{\mathrm{Var}\left\{M\left(\mathbf{s}\right)\right\}}}=\frac{\sum _i{\left\{{\mathrm{CTF}}^{\left(i\right)}\right\}}^{\ast }{X}^{\left(i\right)}\left(\mathbf{s}\right)}{\sum _i{\left({\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\right)}^2+1∕{\mathrm{SSNR}}_{\text{no CTF}}\left(R\right)}$$ (4)

where X* denotes the complex conjugate of X. Thus, given an estimate of the SSNR, the Wiener filter produces an optimal least-squares estimate of the entire, noise-free image field. To emphasize that “signal” in the “SSNR” term here refers to signal power prior to CTF modulation, we specifically denote this term SSNR_{no CTF}. We further note that the noise term in SSNR_{no CTF} refers to the noise power found in the raw image data, as opposed to the SSNR seen in the final, reconstructed particle (to minimize confusion, we will refer to the latter quantity as SSNR_merged).

The specific case of isolated single particles

In the case of cryo-EM images of single particles surrounded by large, featureless regions of bulk solvent, the above incarnation of the Wiener filter encounters a problem: the choice of image size in single-particle applications is essentially arbitrary, causing the overall SNR of the image to be indeterminate. Thus, for given particle size, large image sizes will contain proportionately more noise energy in the surrounding solvent region as compared to the signal energy, which remains constant regardless of image size, resulting in lower SNR estimates. Consequently, the SNR determined from the whole image field depends on the image size, and so when the Wiener filter is applied to solvent-rich particle images, the result is excessive filtering of the image and sub-optimal estimates of the particle density (see Fig. 1 below).

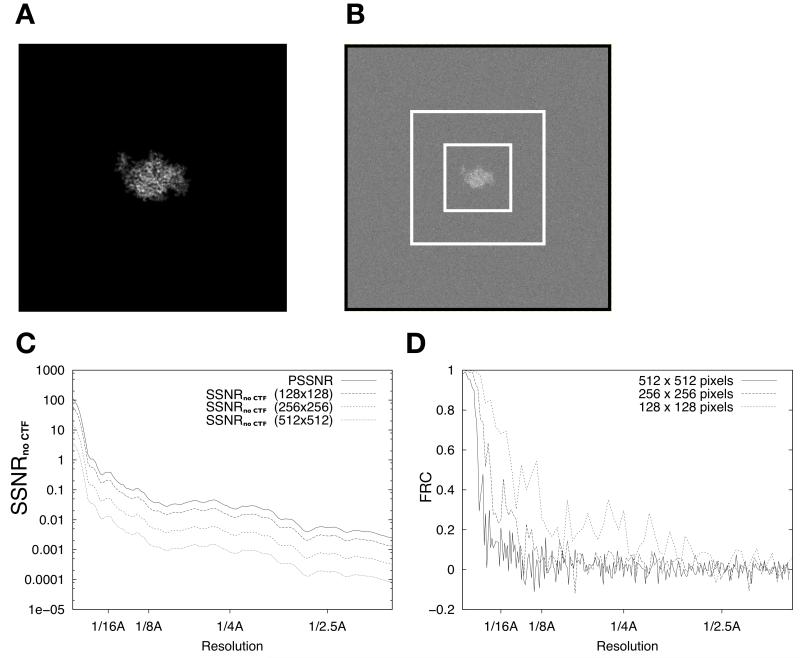
Figure 1. FRC calculations for isolated single particles depend on image size.

(A) Noise-free projection image of PDB model 1MJK (256 × 256 pixels). In this figure and all following, pixel values are scaled for maximum visual contrast within each image; these scale factors thus vary somewhat from image to image.

(B) Projection image from A with white noise subsequently added to achieve a whole-image SNR of 0.003. Image is reduced in scale relative to A, and is 512 × 512 pixels in size. Dashed rectangles indicate 256×256 and 128×128 boundary boxes.

(C) SSNR_{no CTF} characteristic of the noisy image in B, for various image sizes.

(D) Graphs of the FRC calculated between two independent straight averages of 50 noisy images (as in B). Three graphs indicate the results of the calculation for the three different image sizes shown in B.

In order to address this issue, we now recast the optimization problem using the envelope shape of the particle, which we will assume to be known (this envelope can be estimated, for example, from the previous image estimate in a refinement cycle for the image alignment parameters). We write the envelope function as env(r), defined to be 1 at locations r where particle signal is present and 0 otherwise. Then, to avoid the problem related to image size just described, we seek a new filter that optimizes the mean-squared error of the estimated density within the particle envelope only.

Modifying the Wiener filter definition above, we obtain new expressions for the error of the masked particle density (note that for compactness, below we will generally omit the vector coordinates when referring to various function symbols):

$$\begin{array}{cc}\hfill {\widehat{m}}_{\mathrm{SPW}}& =\text{env}.\sum _i{k}_{\text{SPW}}^{\left(i\right)}\ast x^{\left(i\right)}\hfill \\ \hfill \text{Error}& ={\mid \text{env}.\left(m-\sum _i\left\{k_{\mathrm{SPW}}^{\left(i\right)}\ast x^{\left(i\right)}\right\}\right)\mid }^2={\mid m-\text{env}.\sum _i\left\{k_{\mathrm{SPW}}^{\left(i\right)}\ast x^{\left(i\right)}\right\}\mid }^2\left(\text{real space}\right)\hfill \\ \hfill \text{Error}& ={\mid M-\mathrm{ENV}\ast \sum _i\left\{K_{\mathrm{SPW}}^{\left(i\right)}{X}^{\left(i\right)}\right\}\mid }^2\left(\text{Fourier space}\right)\hfill \end{array}$$ (5)

Here we have used the fact that real-space multiplication of the noise-free particle signal m by the envelope function leaves the signal unchanged. In order to apply these error expressions within the standard Wiener filter formalism, we now seek to eliminate the envelope function from the expression. This can be accomplished as follows. Expanding the above error expressions, we obtain:

$$\begin{array}{c}\hfill {\widehat{M}}_{\mathrm{SPW}}=\mathrm{ENV}\ast \sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}({\mathrm{CTF}}^{\left(i\right)}M+N^{\left(i\right)})\hfill \\ \hfill =\mathrm{ENV}\ast \left\{\sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}{\mathrm{CTF}}^{\left(i\right)}M\right\}+\mathrm{ENV}\ast \left\{\sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}{N}^{\left(i\right)}\right\}\hfill \end{array}$$ (6)

Now we consider the two terms in ${\widehat{M}}_{\mathrm{SPW}}$.

First term: summation of restored, noise-free structure measurements

The first term, $\mathrm{ENV}\ast \left\{{\sum }_i{K}_{\mathrm{SPW}}^{\left(i\right)}{\mathrm{CTF}}^{\left(i\right)}M\right\}$, represents a composite sum of noise-free measurements, first modulated by the CTF, subsequently restored by the Wiener filter operator $K_{\mathrm{SPW}}^{\left(i\right)}$, then finally multiplied (in real space) by the particle envelope. If we assume that a sufficiently large number of measurements have been collected for the Wiener filter to efficiently re-localize the particle signal (this condition is satisfied when a sufficient number of images having variable defoci are collected, see Results), the first two operations $\left\{{\sum }_i{K}_{\mathrm{SPW}}^{\left(i\right)}{\mathrm{CTF}}^{\left(i\right)}M\right\}$ will yield a relatively accurate representation of the particle, because no noise terms are present (we note, however, that the high-resolution components of M may be attenuated owing to the filter, see Results). If this correction of the delocalization is sufficiently complete, then convolving the result by the envelope Fourier transform, equivalent to multiplying the real-space object by the envelope function, will have almost no effect, and we may write:

$$\mathrm{ENV}\ast \left\{\sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}{\mathrm{CTF}}^{\left(i\right)}M\right\}\approx \left\{\sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}{\mathrm{CTF}}^{\left(i\right)}M\right\}$$ (7)

Thus, in cases where a number of images are available and there is substantial defocus variation in the images (see Fig. 4), the first term in ${\widehat{M}}_{\mathrm{SPW}}$ is effectively unaltered by the convolution with the particle envelope function ENV.

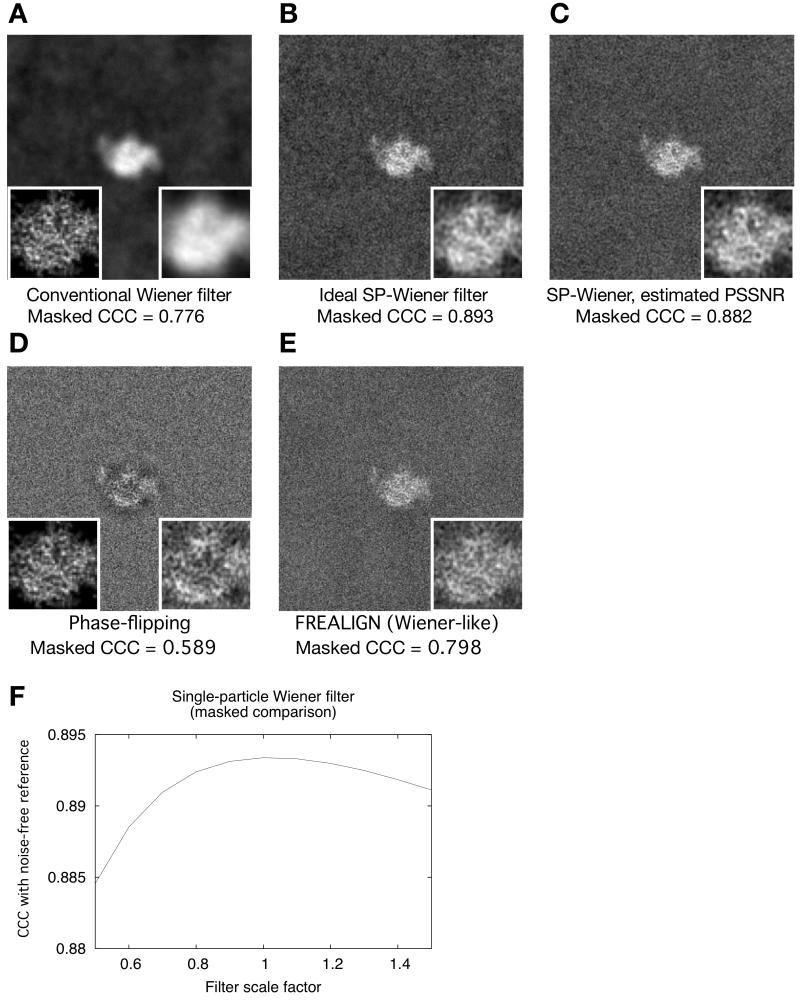
Figure 4. Image restoration using the single-particle Wiener filter.

(A) Image restoration of the CTF-corrupted 100-image series as achieved by the conventional Wiener filter; random defocus variations between 1 and 2 microns were applied to the image series.

(B) Similar to A but using the single-particle Wiener filter, applying the known PSSNR function (Fig. 1C). Insets in this and subsequent panels follow the scheme of Fig. 2.

(C) Similar to A, but using the single-particle Wiener filter, and applying the estimated PSSNR function (see Fig. 5).

(D) Similar to A, but image restoration achieved by phase-flipping.

(E) Similar to A, but image restoration achieved by dividing the noisy images by the CTF before summation.

(F) Masked cross-correlation agreement between the Wiener-filtered composite image D and the noise-free image A, for a series of modified Wiener filters where the PSSNR input to the filter was adjusted upwards or downwards by a scalar factor (x-axis). Note that in this graph, the conventional Wiener filter would correspond to a “filter scale factor” of 0.0328 (the mean squared value of the binary mask function depicted in Fig. 2A, see text). The conventional Wiener filter result is therefore off the scale in this graph; the masked correlation to the perfect image for this latter condition was 0.77.

Second term: noise attenuated by the particle envelope

The second term in our expression for ${\widehat{M}}_{SPW},\mathrm{ENV}\ast \left\{{\sum }_i{K}_{\mathrm{SPW}}^{\left(i\right)}{N}^{\left(i\right)}\right\}={\sum }_i\mathrm{ENV}\ast K_{\mathrm{SPW}}^{\left(i\right)}{N}^{\left(i\right)}$, may be reduced by the following reasoning. The convolution of a given noise term in this summation expression results in a new random noise distribution, $N^{{\left(i\right)}^{\prime }}=\mathrm{ENV}\ast \left[K_{\mathrm{SPW}}^{\left(i\right)}\cdot N^{\left(i\right)}\right]$, in which the original noise term is first filtered by the Wiener term and subsequently “spread out” in Fourier space by the convolution. The convolution introduces a correlation between neighboring points in Fourier space, and thus has the effect of smoothing out the resolution dependence of the filtered noise term $K_{\mathrm{SPW}}^{\left(i\right)}{N}^{\left(i\right)}$. However, if the particle radius is non-negligible relative to the image dimension (a condition which is almost always satisfied in cryo-EM applications), the Fourier transform of the envelope function ENV will have a relatively restricted extent in Fourier space, thus limiting the smoothing effect over two or three Fourier pixels. Moreover, we note that the original noise term N⁽ⁱ⁾ is expected to depend on spatial frequency under experimental conditions (“colored noise”), but that this dependence is relatively small in the case of cryo-EM (see Discussion). Thus, we may conclude that the spectral behavior of N^(i)’ will remain similar to N⁽ⁱ⁾ so long as the expectation value of the filtered noise term $\langle K_{\mathrm{SPW}}^{\left(i\right)}{N}^{\left(i\right)}\rangle$ does not vary too rapidly as a function of resolution. In the results section we present numerical simulations demonstrating that this assumption is appropriate for cryo-EM applications.

In contrast to the spectral behavior of N^(i)’, the net signal energy of N^(i)’ is strongly affected by the presence of the envelope function term. To derive this effect, we begin with the observation that the real-space equivalent of N^(i)’, ${\sum }_i\mathrm{env}\cdot \left(k_{\mathrm{SPW}}^{\left(i\right)}\ast n^{\left(i\right)}\right)$, is simply a uniform noise field truncated by the particle envelope; thus, the total signal energy for the summed expression = $\langle {\int }_{\mathrm{image}}{\sum }_i{\mid \mathrm{env}\cdot \left(k_{\mathrm{SPW}}^{\left(i\right)}\ast n^{\left(i\right)}\right)\mid }^{2}d\overrightarrow{r}\rangle$, is reduced by a factor of $f_{\text{particle}}={\langle {\mathrm{env}}^2\rangle }_{\text{image}}$, which may be thought of as the ratio of particle area to total image area (although this identity is only strictly true for the case of a binary mask). By Parseval’s theorem, the same result holds for the signal energy of the corresponding Fourier space noise term, ${\sum }_i\mathrm{ENV}\ast \left(K_{\mathrm{SPW}}^{\left(i\right)}\cdot N^{\left(i\right)}\right)$.

Combining the above observations, we conclude that the noise term ${\sum }_i\mathrm{ENV}\ast \left(K_{\mathrm{SPW}}^{\left(i\right)}\cdot N^{\left(i\right)}\right)$ in the presence of an envelope is expected to have similar spectral behavior as in the case where an envelope is absent $\left({\sum }_i{K}_{\mathrm{SPW}}^{\left(i\right)}{N}^{\left(i\right)}\right)$, except that the total noise amplitude will be attenuated by a factor of $\sqrt{f_{\text{particle}}}$. Therefore,

$$\sum _i\mathrm{ENV}\ast \left(K_{\mathrm{SPW}}^{\left(i\right)}{N}^{\left(i\right)}\right)\approx \sqrt{f_{\text{particle}}}\sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}\ast N^{\left(i\right)}.$$ (8)

Effective Wiener filter for the case of isolated single particles: the PSSNR

Assembling the results of the last two sections, we arrive at the following minimization condition for the new single-particle filter:

$$\begin{array}{c}\hfill {\widehat{M}}_{\mathrm{SPW}}=\mathrm{ENV}\ast \sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}\left(({\mathrm{CTF}}^{\left(i\right)}M+N^{\left(i\right)}\right)\hfill \\ \hfill \approx \sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}\left({\mathrm{CTF}}^{\left(i\right)}M+\sqrt{f_{\text{particle}}}{N}^{\left(i\right)}\right)\hfill \\ \hfill \to \text{Error}\approx {\mid M-\sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}\left({\mathrm{CTF}}^{\left(i\right)}M+\sqrt{f_{\text{particle}}}{N}^{\left(i\right)}\right)\mid }^2\hfill \\ \hfill ={\mid M-\sum _i{K}_{\mathrm{SPW}}^{\left(i\right)}\left({\mathrm{CTF}}^{\left(i\right)}M+N_{\text{effective}}^{\left(i\right)}\right)\mid }^2\hfill \end{array}$$ (9)

The above error expression is thus identical to the Wiener filter error expression for the envelope-free case, except that the noise term N⁽ⁱ⁾ is attenuated to $N_{\text{effective}}^{\left(i\right)}=\sqrt{f_{\text{particle}}}{N}^{\left(i\right)}$. Thus, the form of our new single-particle filter follows the form of the conventional Wiener filter, after substituting the new noise power $\mathrm{Var}\left(N_{\text{effective}}\right)=\langle {\mid N_{\text{effective}}\mid }^2\rangle =f_{\text{particle}}\langle {\mid N\mid }^2\rangle =f_{\text{particle}}\mathrm{Var}\left(\mathrm{N}\right):$:

$$K_{\mathrm{SPW}}^{\left(i\right)}\left(\mathbf{s}\right)=\frac{{\left({\mathrm{CTF}}^{\left(i\right)}\right)}^{\ast }}{\sum _i{\left({\mathrm{CTF}}^{\left(i\right)}\right)}^2+\frac{\mathrm{Var}\left\{N_{\text{effective}}\left(\mathbf{s}\right)\right\}}{\mathrm{Var}\left\{M\left(\mathbf{s}\right)\right\}}}\to {\widehat{M}}_{\mathrm{SPW}}\left(\mathbf{s}\right)=\frac{\sum _i{\left({\mathrm{CTF}}^{\left(i\right)}\right)}^{\ast }{X}^{\left(i\right)}}{\sum _i{\left({\mathrm{CTF}}^{\left(i\right)}\right)}^2+f_{\text{particle}}\frac{\mathrm{Var}\left\{N\left(\mathbf{s}\right)\right\}}{\mathrm{Var}\left\{M\left(\mathbf{s}\right)\right\}}}$$ (10)

The variance ratio in the denominator of the above expression is thus the inverse of the conventional, or whole-image SSNR (as found in the original Wiener filter expression), but attenuated by f_particle.

Thus, we define the “particle” SSNR, or PSSNR, as:

$$\mathrm{PSSNR}\left(\mathbf{s}\right)=\frac{1}{f_{\text{particle}}}\frac{\mathrm{Var}\left\{N\left(\mathbf{s}\right)\right\}}{\mathrm{Var}\left\{M\left(\mathbf{s}\right)\right\}}=\frac{1}{f_{\text{particle}}}{\mathrm{SSNR}}_{\text{no CTF}}\left(\mathbf{s}\right)$$ (11)

so that we may express the particle estimate as:

$${\widehat{M}}_{\mathrm{SPW}}=\frac{\sum _i{\left\{{\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\right\}}^{\ast }{X}^{\left(i\right)}\left(\mathbf{s}\right)}{\sum _i{\left({\mathrm{CTF}}^{\left(i\right)}\left(\mathbf{s}\right)\right)}^2+1∕\mathrm{PSSNR}\left(\mathbf{s}\right)}.$$ (12)

Equations (10) – (12) are a key finding of the present work, and define what we call a “single-particle” Wiener filter. The novel aspect of this filter can be understood intuitively, as follows. If one has a priori knowledge that a significant portion of the image field is free of signal (as is the case for single particles), then the performance of the Wiener filter can be improved by a simple modification in the denominator, namely by scaling the SSNR term by f_particle. In contrast to the conventional Wiener filter, the single-particle Wiener filter is expected to be largely independent of image size, because the f_particle term compensates for changes in the SSNR that result from varying amounts of signal-devoid space surrounding the particle. As we will show, this property leads to substantial gains in the performance of the new filter.

Estimating the SSNR and PSSNR via statistical analysis of the images

One strategy to obtain the SSNR from a set of raw image data is to compute the variance and other statistical quantities for each voxel in Fourier space as individual measurements are tallied during the averaging process. This approach was used by Unser et al. (1987), who derived an expression for SSNR_merged for the case of sums of aligned 2D images. We have extended this approach to account for the presence of CTF modulation during image formation (Appendix A); the result is a sequence of computations that delivers an unbiased estimate of SSNR_merged for a collection of Fourier pixels found in a given resolution shell, assuming that both the particle structure factors as well as the noise terms follow normal signal distributions within a given resolution shell. Using the above relation, this estimate can then be converted to an estimate of the PSSNR.

For convenience, we have assumed in the following computations that the average signal and noise power (Var {M(s)} and Var {N(s)}, respectively) are circularly symmetric in Fourier space, which will give a solution of the form $K_W^{\left(i\right)}\left(R\right)$, where R = |s|, the vector magnitude of s. This assumption is justified for particles that do not exhibit prominent periodic features that could give rise to significantly stronger signal in certain parts of the Fourier transform. In the case of strongly anisotropic signal distribution, the radially symmetric filter coefficients will not be optimal and a more specialized case may need to be considered. However, the formalism described here will still lead to an improvement over the conventional Wiener filter we seek to replace.

These computations can be summarized as follows:

(13)

Key differences between the above formulas and the results of Unser et al. (1987) include: (A) Our derivation estimates the quantity SSNR_{no CTF} which characterizes the raw data images, whereas the Unser derivation was for SSNR_merged of the final, averaged image; (B) CTF terms are included in our expressions for the signal estimates; (C) the bias correction for our SSNR expression, $\frac{n_R}{{\sum }_R{\sum }_{i=1}^N{\left({\mathrm{CTF}}_i\left(\overrightarrow{s}\right)\right)}^2}$, is increased in magnitude compared to the Unser bias correction (1/N if Unser’s result is adapted to compute SSNR_{no CTF}), owing to the CTF terms having magnitudes less than one.

Obtaining the PSSNR from masked FRC calculations

The above PSSNR expression suffers from at least two serious shortcomings: (1) an implicit assumption is that all signal and noise components follow normal Gaussian distributions within a single resolution shell - a condition not always met in practice; (2) the expression suffers from a relatively high statistical error at higher resolution, where accurate estimation of the PSSNR is most critical for optimal Wiener filtering (see Discussion). We therefore explored an alternative route for obtaining the PSSNR: deriving this quantity using cross-correlation comparisons of masked, half-data-set reconstructions.

We begin by modifying the FRC, a standard measure of particle resolution when two estimates are available, to include a masking step using the particle envelope function ENV defined above. The expectation value of the masked FRC is:

$$\begin{array}{cc}\hfill \langle {\mathrm{FRC}}_{mask}\left(R\right)\rangle & =\frac{\langle \sum _R[ENV\ast (M+N_1)\cdot ENV\ast (M+N_2)]\rangle }{\sqrt{{\langle \sum _{R}ENV\ast (M+N_1)\rangle }^2{\langle \sum _{R}ENV\ast (M+N_2)\rangle }^2}}\hfill \\ \hfill & =\frac{{\langle \sum _R{M}^2\rangle }_R}{{\langle \sum _R{M}^2\rangle }_R+{\langle \sum _R{\mathrm{ENV}}^2\ast N_1^2\rangle }_R}\hfill \end{array}$$ (14)

where N₁ and N₂ represent the summed noise terms from the independent half-data sets used for the two estimates to be compared and the expectation value of the N₁ and N₂ are assumed to be the same.

We note here that in practice it is necessary to replace the binary real-space envelope function env with a smoothed envelope function, env_smooth, in order to avoid artifactual high-resolution features at the boundary of the particle estimate (which could lead to inflated resolution estimates when comparing identically masked half-data set reconstructions, for example). To avoid strong artifacts, the cutoff spatial frequency for the smoothing filter for ENV_smooth should be chosen to be less than the conservative lower limit of the reconstructed particle resolution.

We now approximate the envelope-noise convolution term in the denominator of the above expression, using the same argument developed above in our derivation of the PSSNR:

$$\langle \sum _V{\mathrm{ENV}}^2\ast N_1^2\rangle \approx f_{\text{particle}}\langle \sum _i{N}_1^2\rangle$$ (15)

where $f_{\text{particle}}={\langle {\mathrm{env}}^2\rangle }_{\text{image}}$ This results in the following expression for the masked FRC:

$$\begin{array}{c}\hfill \langle {\mathrm{FRC}}_{\text{mask}}\left(R\right)\rangle =\frac{\langle \sum _R{M}^2\rangle }{\langle \sum _R{M}^2\rangle +f_{\text{particle}}\langle \sum _R{N}_1^2\rangle }\hfill \\ \hfill =\frac{\langle \sum _R{M}^2\rangle ∕\langle \sum _R{N}^2\rangle }{\langle \sum _R{M}^2\rangle ∕\langle \sum _R{N}^2\rangle +f_{\text{particle}}\langle \sum _R{N}_1^2\rangle ∕\langle \sum _R{N}^2\rangle }\hfill \\ \hfill =\frac{{\mathrm{SSNR}}_{\text{merged}}\left(R\right)∕f_{\text{particle}}}{{\mathrm{SSNR}}_{\text{merged}}\left(R\right)∕f_{\text{particle}}+2}\hfill \end{array}$$ (16)

Comparing this expression to the relation between the conventional FRC and the SSNR,

$$\mathrm{FRC}\left(R\right)=\frac{{\mathrm{SSNR}}_{\text{merged}}\left(R\right)}{{\mathrm{SSNR}}_{\text{merged}}\left(R\right)+2}$$ (17)

we see that masking causes the SSNR_merged (R) term in the FRC expression to be replaced by SSNR _merged(R)/ f_particle, if a tight binary mask is used, or by SSNR _merged(R)/ f_smooth if a smoothed mask is used (where $f_{\text{smooth}}={\langle {\mathrm{env}}_{\text{smooth}}^2\rangle }_{\text{image}}$, the mean squared envelope function computed over the image area. Thus, the whole-image SSNR for the final particle estimate is:

$${\mathrm{SSNR}}_{\text{merged}}\left(R\right)\frac{{2\mathrm{FRC}}_{\text{mask}}\left(R\right)f_{\text{smooth}}}{(1-{\mathrm{FRC}}_{\text{mask}}\left(R\right))}$$ (18)

To obtain an estimate for SSNR_{no CTF} or the PSSNR, one final step is necessary. The expected noise variance in the final estimate is reduced relative to the noise variance in the raw data, proportional to the averaged sum of squared CTF values (see Appendix A, Equation (A.4)). This yields the relation:

$${\mathrm{SSNR}}_{\text{no CTF}}\left(R\right)\approx \frac{n_R}{\sum _R\sum _{i=1}^N{\mathrm{CTF}}_i^2}{\mathrm{SSNR}}_{\text{merged}}\left(R\right)=\frac{n_R}{\sum _R\sum _{i=1}^N{\mathrm{CTF}}_i^2}\cdot \frac{{2\mathrm{FRC}}_{\text{mask}}\left(R\right)f_{\text{smooth}}}{(1-{\mathrm{FRC}}_{\text{mask}}\left(R\right))}$$

where we have used the symbol $n_R={\sum }_{R}1$ to denote the number of Fourier pixels within the resolution zone R ± dR.

Thus:

$$\begin{array}{c}\hfill \mathrm{PSSNR}\left(R\right)=\frac{1}{f_{\text{particle}}}\cdot {\mathrm{SSNR}}_{\text{no CTF}}\left(R\right)\hfill \\ \hfill \approx \frac{1}{f_{particle}}\cdot \frac{n_R}{\sum _R\sum _{i=1}^N{\mathrm{CTE}}_i^2}\cdot \frac{2f_{\text{smooth}}{\mathrm{FRC}}_{\text{mask}}\left(R\right)}{(1-{\mathrm{FRC}}_{\text{mask}}\left(R\right))}\hfill \end{array}$$ (19)

Equation (19) thus defines a close relationship between the masked FRC calculation, the SSNR, and the single-particle Wiener filter. This expression also indicates that, in typical cryo-EM applications, the PSSNR will differ substantially from conventionally obtained SSNR values, due to the f_particle term, which will be considerably less than one in practice (see Results/Discussion). As demonstrated in the Results, the Wiener filter is sensitive to differences of this magnitude in the SNR term; thus, choosing the correct SNR variant in the filter is critical for full optimization of 2D and 3D reconstruction.

Summary of the new, adapted Wiener filter

In the first step, the raw images are divided into two half-data-sets and two least-squares particle estimates are generated in the absence of SNR information. Second, the particle envelope is identified, smoothed, and used to compute a masked FRC comparison of the two initial estimates; this FRC function is subsequently converted to an estimate of SSNR_{no CTF} for the raw data images (Equation (13)). Finally, the resulting SSNR function is divided by the scalar factor f_particle (Equation (19)). The resulting scaled function, the PSSNR, is then substituted in place of the standard SSNR term in a modified Wiener filter which is applied to the full image data set.

Materials and Methods

For numerical testing purposes, we created several synthetic data sets that incorporated various combinations of key elements of the cryo-EM imaging process. The imaged particle in each data set was an identical view of a representative protein molecule (kinesin, PDB ID 1MKJ), rendered as projection image of the scattering potential as modeled by the SPIDER image processing program (Frank et al., 1996). Noisy images of known SSNR characteristic were generated by adding white noise to the perfect reference image, after an optional CTF modulation step was applied to the reference image. The modeled CTF’s were generated by the “TF C” command of SPIDER, without an envelope function, and with randomly generated defocus values uniformly distributed between 1 and 2 μm. The SSNR characteristic of the noisy images was then computed as the ratio of the rotationally averaged, squared Fourier amplitude to the white noise variance. The magnitude of the white noise variance was chosen such that a net SNR in the real-space image of 0.003 was produced in the resulting raw data images, for the image of size 256 × 256 pixels (1Å pixel size). Note, as discussed below, that cropping these images to smaller sizes substantially increases the SNR values.

Results

FRC calculations are highly sensitive to image size

We constructed several sets of noisy synthetic images (SNR = 0.003 for the “standard” image size of 256×256, see Methods), modeling various aspects of image formation in cryo-EM on a test particle generated from PDB coordinates 1MKJ. Fig. 1A shows a noise-free projection image simulating the projected Coulomb potential of the test molecule, and Fig. 1B shows the same image after adding white noise to the specified SNR level. These synthetic images were used to test various predictions of the theory developed above.

The results of Fourier Ring Correlation (FRC) analysis applied to the synthetic data sets are shown in Fig. 1. A data set of 100 raw data images was divided into two sets of 50 images and averaged separately, and the FRC was calculated between the two resulting particle estimates (this procedure was repeated for several different box sizes). For simplicity, the effects of CTF modulation were not included in the tests shown in Fig. 1, although when these tests were repeated in the presence of CTF modulation, very similar results were obtained (not shown). As shown in Fig. 1C, the SSNR of the raw synthetic images depends strongly on the dimensions of the bounding box used for analysis (three sizes were tested, as indicated by dashed boxes in Fig. 1B), owing to the inclusion of excess noise signal energy at the box boundaries as the box size increases while the total particle signal energy stays the same. Fig. 1D demonstrates that the FRC calculated between the half-data-set averages also strongly depends on the bounding box size, yielding values at an arbitrary threshold of 0.5 of ~12Å (128×128 pixel windowed image averages), ~23Å (256×256), or ~39Å (512×512). These results are consistent with the prediction of Equation (16) that as the featureless solvent region increases in size with respect to the particle region, the FRC resolution estimate correspondingly decreases owing to increased noise signal energy relative to particle signal energy.

Wiener filter behavior is highly sensitive to image size

The behavior of the conventional Wiener filter, when applied to the same set of images (no CTF applied), is shown in Fig. 2. We tested the optimality of this filter, as predicted by the theory, by comparing the filter output to a series of modified filters where the SSNR term was scaled up or down by a linear coefficient. As seen in Fig. 2A, the best agreement (as reported by the cross-correlation coefficient, or CCC) between the filtered image and the noise-free reference was achieved by a scale factor of unity, yielding a CCC of 0.853, and either increasing or decreasing the scale factor increased the mean-squared error of the image estimates. Thus, these calculations are consistent with the predicted optimality of the conventional Wiener filter.

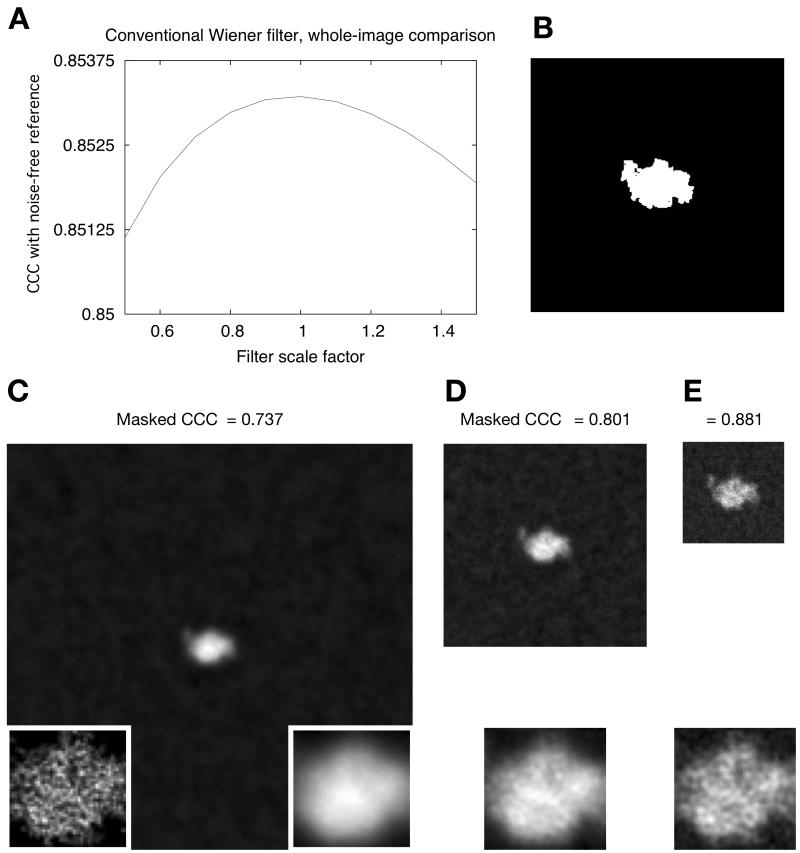
Figure 2. Image restoration of a synthetic single-particle image using a conventional Wiener filter.

(A) Results of whole-image cross-correlation comparison between the noise-free reference image (Fig. 1A) and a Wiener-filtered composite of 100 256×256-pixel noisy images, each noisy image having a SNR of 0.003 but no CTF applied (as in Fig. 1B). In this figure, the SSNR term in the Wiener filter (Equation (4) ) has been varied above and below its known value in the image data set by multiplication with a scalar factor (“filter scale factor”), such that each x-value represents a slightly different incarnation of the filter and x=1 corresponds to the “true” Wiener filter. Note that in this plot the single-particle Wiener filter would correspond to a “filter scale factor” of 1/0.0328 = 30.5, for which the masked correlation to the perfect image was found to be 0.66 (not visible on the scale shown here). Inset in the lower right corner shows a magnified view of the particle region; inset in lower left corner shows the identical view of the noise-free particle, for comparison.

(B) Tight binary envelope function generated from the noise-free image in Fig. 1A. Inset is as in A.

(C) – (E) Output of the conventional Wiener filter for sets of 100 noisy images as in Fig. 1B, for the three different box sizes. Note that CCC_mask-ref = 0.929 for the SP Wiener filter reconstruction. Inset is as in A.

The behavior of the conventional Wiener filter, however, depended strongly on the bounding box size. As shown in Fig. 2C and Fig. 2E, the estimate for the largest box is noticeably more blurred compared to the smaller box sizes. This feature of the filter comes directly from the fact that increasing the bounding box size rapidly diminishes the magnitude of the SSNR of the raw data images (Fig. 1C); this decrease in SSNR in turn generates a much stronger high-frequency attenuation by the Wiener filter, when applied to the larger boxes. For each box size tested, we repeated the scaling test of Fig. 2A and confirmed that the CCC agreement of the filtered images was maximal with respect to scaled versions of the filter (results not shown).

However, when we zeroed the solvent region of the image using a binary mask (Fig. 2B), we observed a very different behavior of the CCC. As indicated in Fig. 2C and Fig. 2E, correlation of the masked particle region to the noise-free reference drops rapidly as the box size of the filter increases, from a value of CCC_mask-ref = 0.881 for the smallest box size tested (128×128) to a value of CCC_mask-ref = 0.737 for a 512×512 pixel box. These masked CCC values were not optimal with respect to our Wiener filter scale tests; rather, we found that with appropriate scaling of the SSNR term, the conventional Wiener filter could be “tweaked” to yield a maximal value of 0.929 for the masked CCC (equivalent to the single-particle Wiener filter result, see below). Thus, these numeric experiments conclusively demonstrate that when the conventional Wiener filter is applied to images of isolated single particles, the filter neither (1) yields consistent results as the box size is varied, nor does it (2) optimize the masked CCC for the particle estimate, even for relatively small box sizes.

Validating the ‘re-localization’ assumption within the single-particle Wiener filter derivation

In the Theory section, we presented an adapted, “single-particle” Wiener filter to address the above two deficiencies of the conventional Wiener filter. One of the primary assumptions made in this adaptation of the Wiener filter is that the signal energy in the resulting filtered estimate be mostly localized within the particle envelope. Whether this re-localization condition can be satisfied depends on the nature and number of raw data images collected. For example, full re-localization is trivially satisfied in the absence of CTF modulation in the raw data images (Fig. 1 and Fig. 2); however, currently available electron microscopes generate CTF-modulated images that require CTF correction. We therefore sought to test the re-localization properties of the single-particle Wiener filter using more realistic test images.

Fig. 3 shows the noise-free signal component of a CTF-modulated particle as the data processing proceeds through various filtering and estimation steps. Note that because the Wiener filter is a linear operator, and the noise is additively combined with the signal, it is possible to consider the signal component independently of the noise. We therefore omit the noise component of the images in Fig. 3, while noting that the filters used therein are specific to the case of our 256×256 pixel, SNR = 0.003 test images. As shown in Fig. 3A, the CTF-modulated signal found in a raw data image is highly delocalized, such that more than half of the image contrast (defined as the signal magnitude squared, integrated over the total image area) lies outside the particle boundary. As shown in Fig. 3B, if this single image is corrected by phase-flipping, much of the delocalized signal energy is restored to within the particle boundary but nearly 25% of the energy remains outside the particle boundary. These observations provided a baseline for comparison with delocalization behavior of the Wiener filter.

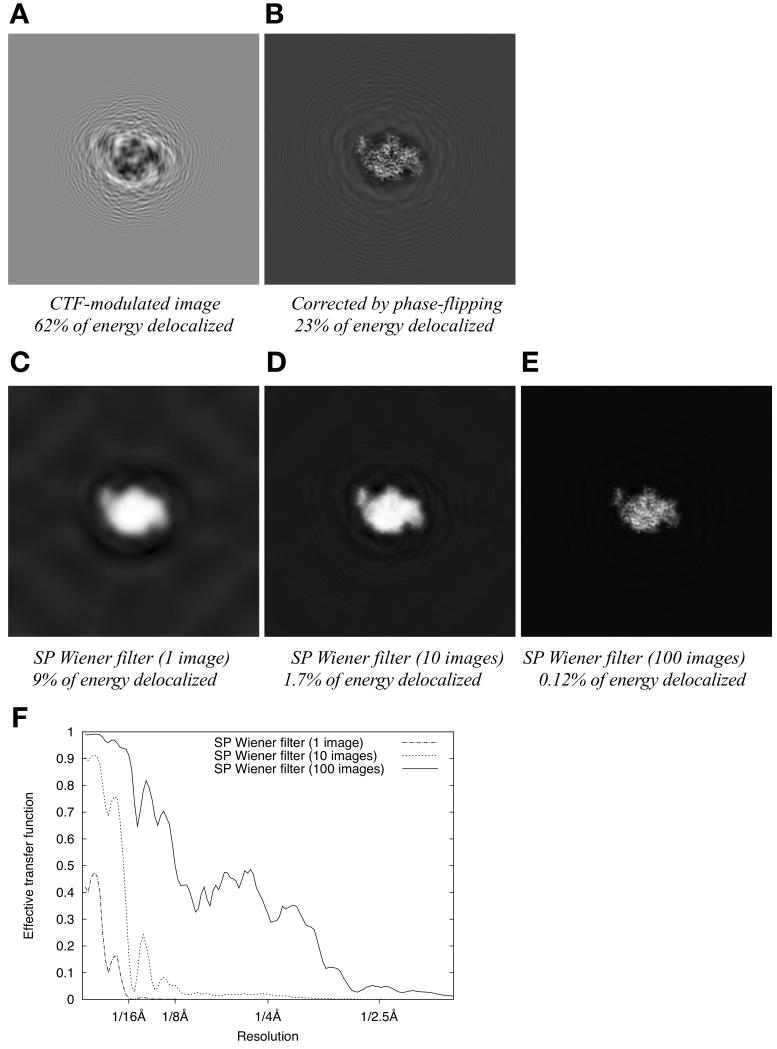
Figure 3. re-localization of signal intensity by single-particle Wiener filtering applied to a defocus series of images.

(A) Noise-free, CTF-modulated image (defocus is 1.4μm)

(B) Signal restoration achieved by phase flipping the image in B.

(C) Signal restoration achieved by applying a single-particle Wiener filter to the image in B. The Wiener filter is implemented for the specific case of white noise, added to produce a net SNR of 0.003.

(D) Signal restoration achieved by applying a single-particle Wiener filter to a series of 10 randomly defocused images as in B (defocus range 1μm to 2μm), for the same SNR condition as in D.

(E) Signal restoration as in E but for a series of 100 images.

(F) Plotted is the ratio of the squared power spectrum to the noise-free power spectrum for a series of single-particle Wiener noisy image restorations, as a function of resolution. These plots give the effective transfer function (or filtering function) that is applied to the “perfect” image signal (independent of the noise) during image restoration.

Next we analyzed the performance of a single-particle Wiener filter generated specifically for the case of a low-SNR synthetic image data set (SNR = 0.003, 256×256 images, as in Fig. 1 and Fig. 2 except with CTF modulation added). Each instance of such a Wiener filter, as defined in Equation (12), depends on the specific SSNR characteristic of the imaged particle as well as the number of images collected and their defocus characteristics. The resulting filter functions are shown in Fig. 3F for specific test data set instances containing 1, 10, and 100 images. Operating on a single image, the SP Wiener filter reduces the delocalized signal energy seen with phase-flipping correction by a factor of nearly 3, to 9% (Fig. 3C). Increasing the image data set to include multiple images, having defoci randomly distributed between 1 to 2 μm, progressively reduced the delocalization to much lower levels: to 1.7% for a 10-image data set (Fig. 3D), and to 0.12% for 100 images (Fig. 3E). These results indicate that the amount of delocalized signal present in the filtered image can be decreased to an arbitrarily low level by increasing the number of images in the data set, and that as few as 10 images yield an adequately localized signal for use with the single-particle Wiener filter.

PSSNR/Wiener filter approximates a least-squares particle density estimate

We tested the absolute performance of our single-particle adaptation of the Wiener filter on a set of 100 noisy, CTF-modulated images. In comparison to the conventional Wiener filter, the single-particle Wiener filter estimates eliminate a noticeable smoothing effect, and showed greatly reduced mean-squared error when masked CCC comparisons to the noise-free reference image were made: CCC_mask-ref = 0.776 for the conventional filter vs. CCC_mask-ref = 0.893 for the single-particle filter (Fig. 4A, 4B). In contrast, the value of CCC_mask-ref was 0.589 for a sum of phase-flipped images; and CCC_mask-ref was 0.798 for a correction scheme used by the FREALIGN package (Grigorieff, 2007), which closely resembles a Wiener filter but replaces the SSNR term with an ad hoc constant. Thus, the single-particle Wiener filter greatly improved the masked correlation relative to other available particle estimation schemes.

We also investigated the optimality of the single-particle Wiener filter by performing scaling experiments, analogous to Fig. 2A, modulating the PSSNR term within the filter (Fig. 4F). These scaling experiments demonstrated that the scaling the PSSNR function either above or below its true value (according to our derivation) increased the error in the masked CCC comparison to the noise-free reference image. These numerical tests thus indicated that our filter adequately minimizes the mean-squared error with respect to the reference particle.

In contrast to the excellent performance of the single-particle Wiener filter in the masked CCC comparison, however, the whole-image CCC to the noise-free reference yielded by this filter (Fig. 4B, CCC = 0.778) is markedly inferior to the whole-image CCC for the conventional Wiener filter (Fig. 4A, CCC = 0.861). Thus, the conventional Wiener filter and the single-particle Wiener filter have reciprocal properties: the former minimizes error in the overall image at the expense of increased error within the particle region (see Fig. 2), while the latter minimizes error in the particle region at the expense of the solvent region.

Estimating SSNR characteristics via image statistics

The above numerical experiments utilized prior knowledge of the SSNR characteristic of the synthetically generated raw data images, which allowed a “perfect” Wiener filter to be constructed. Most experimental cryo-EM images, however, are obtained in the absence of prior SSNR information. We therefore tested our above-derived relations between the masked FRC and the “particle” SSNR, for the same synthetic data sets, to determine whether the SSNR could be adequately estimated from the raw data alone.

Initial numeric tests following the “direct” SSNR calculation method of Unser et al. (1987) (Equations (13)) produced accurate estimates for the SSNR in the low-resolution regime, but rapidly became unreliable for the synthetic data sets tested here at resolutions approaching ~8Å or higher (results not shown), despite the presence of significant structure signal as indicated by masked FRC comparisons of filtered particle estimates with the noise-free reference (Fig. 5A). We attributed this issue to the presence of noise in the solvent region of the particle images, which cannot be removed by any straightforward method during the “direct” SSNR calculation scheme. We therefore tested the validity of Equation (19) in providing more accurate estimates of the SSNR and/or PSSNR.

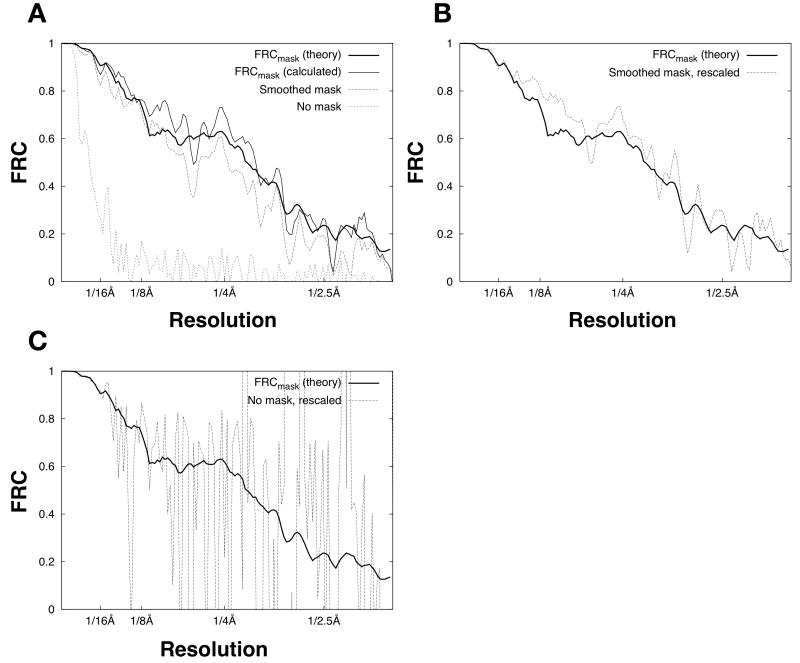
Figure 5. Estimation of the PSSNR from masked FRC calculations.

A. FRC calculations for a 100-image data set (as in Fig. 2), split into halves and averaged to produce two noisy particle estimates. In the masked FRC calculations, we applied either a binary mask (identical to Figure 3B) or a smoothed mask. The smoothed mask was obtained by expanding the border of the binary mask with a cosine-edge smoothing function (Grigorieff, 2007) such that 〈env²〉 increased by approximately 50%.

B. FRC calculations from A, but with the smoothed-mask calculation rescaled by Equation (19).

C. FRC calculations from A, but with the non-masked calculation rescaled by Equation (19).

An important result contained within Equation (19) is that the effects of masking on the FRC calculation can effectively be removed by applying a scaling factor f_smooth / f_particle at the appropriate point within the expression, where f_smooth is the average squared mask function value evaluated over the image. The resulting estimate for PSSNR is then expected to be independent of mask size (so long as the mask does not intrude on the particle density), but with varying fidelity depending on the amount of solvent noise included in the FRC calculation.

We tested the above predictions by performing FRC comparisons between a pair of noisy particle estimates, each obtained by a straight average of 50 noisy images (no CTF applied, with SNR = 0.003, as in Fig. 2). The result is shown as FRC_mask (calculated) in Fig. 5A. We also used Equation (16) to predict the expected value of the masked FRC (FRC_mask (theory) in Fig. 5A). To obtain the expected value of SSNR_merged for this latter computation, we scaled the known SSNR characteristic of the raw images (SSNR _{no CTF}) by the number N of image measurements (50 in the present calculation). Hence, SSNR _merged = N · SSNR _{no CTF}. This is equivalent to the calculation presented by Unser et al. (1987) (see Equation (7) in the Unser paper). As shown in Fig. 5A, these calculations yielded excellent agreement between predicted and calculated values for FRC_mask, as predicted by our theory. Also consistent with our predictions, a non-masked FRC calculation gives substantially lower values, when compared with FRC_mask, and a smoothed mask also shows systematically lower values in this comparison (Fig. 5A).

However, when Equation (19) is used to rescale the non-masked and smooth-mask FRC functions, compensating for the different mask sizes, the resulting estimates converge on the FRC_mask function (Fig. 5B-C). These results support the validity of assumptions used here to obtain Equation (19). We observed significantly increased random error in the rescaled FRC functions in Fig. 5B-C, however, reflecting extra solvent noise that is included when the mask size increases (see Discussion). The increased error was particularly pronounced in the absence of masking (Fig. 5C). Thus, the calculations in Fig. 5 indicate that masked FRC computations, in concert with Equation (19), provide a suitable estimate of the PSSNR for use in the single-particle Wiener filter.

Application of the estimated SSNR values in the single-particle Wiener filter

We tested the applicability of the above PSSNR estimates in the single-particle Wiener filter by repeating the numeric tests of Fig. 4, but substituting these estimated values in place of the PSSNR function previously obtained from the known SSNR characteristic (Fig. 1). These tests thus simulated a cryo-EM experiment performed on data with unknown SSNR properties. The resulting particle estimate (Fig. 4C) closely resembled the one produced using “perfect” SSNR information, yielding a masked correlation value, CCC_mask-ref, only slightly lower (0.882) than the value obtained for the ideal filter (0.893) and substantially greater than the correlations obtained with other tested CTF correction schemes (Fig. 4, panels A, D, E). These results thus demonstrate that the single-particle Wiener filter can be successfully implemented in the absence of prior knowledge of the data SSNR, yielding particle estimates that significantly reduce the mean-squared error relative to other schemes.

Discussion

Here we have shown that the Wiener filter must be modified to give consistent and suitable results when treating images of single particles. The form of the modification (Equation (10)) is straightforward, requiring only that the SSNR term in the denominator of the filter expression be scaled by f_particle, which is effectively the fraction of the image area occupied by the particle. In a related result, we have shown that a highly accurate estimate of the SSNR found in the image data set can be obtained by performing a masked FRC calculation between two half-data-set image averages (Equation (18)). Taken together, these two findings provide a practical and effective solution for finding a least-squares estimate of the particle density from a set of noisy images.

Prior applications of the Wiener filter to single-particle problems have operated under the assumption that this filter minimizes the mean-squared error of the particle. In carefully testing this assumption, the current work has revealed that it is important to distinguish between the error in the entire image, versus the error within the particle region itself. As the calculations presented in Fig. 2 show, while the Wiener filter succeeds in minimizing the overall error throughout the image, the error produced within the particle region is far from optimal (and depends on the size of the considered image field). Closely related to this issue is the property that the FRC (or analogous FSC for 3D reconstructions) for a given particle data set depends on the dimensions of the total image field, and whether the particle is masked prior to the FRC calculation. The theory presented here accounts for the effects of image size and masking, not only in the Wiener filter but also in the FRC resolution estimator.

The single-particle modification to the conventional Wiener filter is large and significant

We have shown that the SSNR of an imaged particle depends on the size of the image field, relative to the particle dimension. This property in turn means that the behavior of the Wiener filter is not unique, progressively leading to over-blurring of the particle as the image size increases. Thus, our results demonstrate that it is not sufficient to obtain the SSNR of such imaged particles, if one desires a best estimate of the particle density. Rather, the SSNR of the images must be scaled by 1/ f_particle to obtain the PSSNR, permitting application of the single-particle Wiener filter defined here.

It should be noted that our derivation of the single-particle Wiener filter relies on two specific properties of the image data set; this aspect of our theory contrasts with the conventional Wiener filter, which is more generally valid. First, the derivation requires that sufficient defocus variation is present in the data in order to counteract the delocalization effects generated by the CTF of the microscope. Our numeric tests, however, demonstrate that the single-particle Wiener filter requires relatively few images (10-100; Fig.’s 3-4) to meet this requirement, indicating that this restriction is not a serious one. A second requirement is that the noise power found in the data varies slowly with spatial frequency, compared to the Fourier transform of the particle mask function (see the discussion preceding Equation (8)). We have not investigated this aspect of noise in our numeric simulations. However, earlier work (for example, a study of purple membrane crystals by Glaeser and Downing (1992)) has indicated that cryo-EM images possess a suitably low spectral dependence for the noise, such that our theory should be generally valid. Moreover, if a pathological case of noise variability did arise, this could easily be addressed by applying a “noise-whitening” procedure to the image data (Sigworth, 2004). Thus, we anticipate that the single-particle Wiener filter is broadly applicable to cryo-EM image processing.

Many of the examples discussed here used a larger image size (256×256) than strictly necessary given the size of our test particle in combination with the modeled delocalization characteristics; this was done for illustrative purposes. However, it is important to note that the signal delocalization caused by CTF modulation, in cryo-EM applications, means that a relatively large image size must be used in order to collect all the delocalized signal information-- and this is particularly true for the highest-resolution signal components, which tend to be delocalized furthest from the particle center (Downing and Glaeser, 2008). Furthermore, many particles of interest in cryo-EM have irregular or even hollow shapes, leading to 1/ f_particle values significantly greater than 1 even when the image size is minimized relative to particle dimension. Suitable image sizes for high-resolution image processing are therefore likely to give values for 1/ f_particle of 5, 10 or greater. Moreover, if our methodology is extended to 3D reconstruction, 1/ f_particle reflects a 3D quantity rather than a 2D quantity, and is therefore increased relative to the 2D case. These qualities suggest that substantial error may commonly be introduced if the conventional Wiener filter is used in place of the single-particle Wiener filter, in high-resolution cryo-EM applications.

We note that this conclusion has apparently not been reached in earlier applications of the Wiener filter to single-particle problems. For example, Ludtke et al. (2001) applied the conventional Wiener filter within the context of a 3D reconstruction algorithm, but did not report over-filtering as our theory would predict. However, unlike the work presented here the images averaged by Ludtke et al. (2001) contained alignment errors which would have attenuated the effective SNR required for optimal Wiener filtration, relative to a perfect alignment. In contrast, the SNR estimates used by Ludtke et al. were derived using scattering profiles from X-ray experiments, which yielded the SNR of a perfectly-aligned data set. As pointed out by the authors, alignment errors would diminish the effective SNR of the data, particularly at high resolution. Thus, a Wiener filter applying the “true” SNR would be expected to under-filter the result in this case. This under-filtering would tend to compensate for the over-filtering effect that results from the use of a conventional Wiener filter rather than a “single-particle” Wiener filter, in the Ludtke et al. study.

Effect of masking on the FRC

It has been noted that the FRC (and analogously, the FSC in the 3D case) can produce unrealistically low estimates of particle resolution, and that this effect can be corrected by masking (Stewart et al., 2000; LeBarron et al., 2008). The theory presented here quantitatively explains this effect. As we have shown, masking not only reduces the amount by which the true resolution of the particle is systematically underestimated, it also reduces the amount of random error in the FRC estimate (and consequently in the resulting SSNR/PSSNR estimates, see Fig. 5). Moreover, the results presented here (equation (19) , as well as Fig. 5) demonstrate that non-masked FRC calculations can be adjusted to quantitatively correct for underestimation effects, simply by converting the FRC function to an equivalent SSNR function and subsequently multiplying by the scalar factor 1/ f_particle (defined above) that expresses the ratio of the molecular area to total image area. From the resulting PSSNR function, the particle resolution estimator FRC _particle, which will be independent of image size, can be obtained. Thus, our results make clear that, in the absence of this adjustment and/or masking, FRC calculations will underestimate the resolution of a reconstruction by a variable amount, depending on how large an image size was chosen by the user.

We note that f_particle is somewhat difficult to determine precisely. One way to estimate this quantity is to use the molecular weight of the particle, in combination with estimates of protein/DNA density (in the case of biological macromolecules) to form an estimate. This approach, however, neglects the possibility that portions of the molecule may be disordered, abnormally dense, or that an ordered solvation layer may be present. However, the theory relations presented here suggest that f_particle could also be determined experimentally from the image data set itself. Results presented in Fig. 4D indicate that there is one unique value that maximizes the masked real-space CCC agreement between the particle estimate and the true particle density map, when applied via the single-particle Wiener filter. While the true particle density map is never known experimentally, a feasible alternative is to search for the value of f_particle that maximizes the masked CCC between two half-data-set reconstructions. In this approach, the mask used for CCC comparison need not extend over the entire particle, but could be specifically designed to only include a subset of the particle region that is known to be well ordered.

A difficulty with basing resolution estimates on FRC calculations is that over-refinement of the alignment parameters can lead to noise-derived artifactual signal in the particle reconstructions, thus leading to overestimation of the resolution (Grigorieff, 2000). While the current work does not address this issue, we note that existing approaches are capable of minimizing or even eliminating such artifacts (Stewart and Grigorieff, 2004): for example, by emphasizing lower-resolution information during alignment, or by performing independent refinement of alignment parameters for half-data-set reconstructions. Combining such approaches with the resolution estimation technique proposed here thus may provide an avenue to more accurate, less-biased estimates of the particle resolution.

Disadvantage of the SSNR as a resolution estimator, when computed directly from image data

Earlier investigations of the SSNR of reconstructed single particles observed that with statistical analysis of the raw image data (via expressions similar to Equations (13)) one can in certain circumstances obtain more accurate SSNR estimates in comparison to those obtained from FRC calculations (Unser et al., 1987; Penczek, 2002). Our results and theory show, however, that for single particles this advantage is more than offset by the fact that the former method of obtaining the SSNR must necessarily include all the noise found within the solvent region of the images, leading to a significant underestimation of the resolution of the particle as well as substantially larger random fluctuations in the SSNR estimate itself. This disadvantage is particularly noteworthy for the case of cryo-EM images, where it is necessary to process images substantially larger than the particle diameter, in order to include information delocalized due to the CTF of the microscope. Thus, “raw-data” methods of estimating the SSNR can lead to unacceptably high noise levels, thus prevent the SSNR from being usefully rescaled to reflect the true particle resolution.

A second disadvantage of the SSNR approach embodied in Equations (13) is that its accuracy relies on the assumption that the Fourier pixel values of the image transform obey normal statistics. Unfortunately, molecular transforms are not guaranteed to have this property (particularly when symmetry in the particle concentrates signal power in certain regions of Fourier space). For these two reasons, masked FRC calculations should be preferred for computing SSNR characteristics of isolated single particles, under most circumstances.

Which “SSNR” to use?

We note that there is a certain ambiguity in the literature regarding the term “SSNR”. As originally introduced by Unser, the SSNR described the final reconstruction, thus qualifying as a resolution estimator (Unser et al., 1987). On the other hand, the SSNR_{no CTF} quantity required for use with the Wiener filter describes the original data and is independent of measurement conditions (for example, SSNR_{no CTF} does not depend on the CTF). Thus, the SSNR obtained by the standard relation SSNR = 2*FRC/(1-FRC) is not itself suitable for Wiener filter application, because this describes the final reconstruction. Our Equation (19) provides a way to back-calculate SSNR_{no CTF}, namely by dividing the most accurate available estimate of SSNR_merged (here obtained via masked FRC calculation) by the mean sum-of-squared CTF values per Fourier pixel.

As mentioned before, this back-calculation scheme is closely related to the relation presented by Unser (Equation (7) in Unser et al. (1987)), which using our terminology is expressed as SSNR _merged = N · SSNR _{no CTF}, where N is the number of images. In the presence of CTF modulation, which was not considered by Unser et al. (1987) the effective number of images contributing to a given Fourier pixel is reduced from N owing to attenuation of each image component, on average, by the CTF. Thus, averaging N images together (using the Wiener formula) will improve the SSNR of the final estimate (compared with a raw image) by only a factor of N〈CTF²〉 rather than N (see Appendix A). At higher resolution, when large numbers of images with a random defocus are gathered, the CTF falls between −1 and 1 in a sinusoidal distribution, causing this “improvement factor” to converge on the value N/2. This value therefore indicates that if a value SSNR_merged is measured in a given image reconstruction, SSNR_{no CTF} should be estimated as SSNR _merged = N · SSNR _{no CTF}/ 2 (rather than SSNR _merged = N · SSNR _data for the case of no CTF). We emphasize here that SSNR _{no CTF}, which refers to the signal present before CTF modulation, is the correct quantity to apply in a conventionally defined Wiener filter; in contrast, at least one prior usage of the Wiener filter incorporated a variation on the SSNR in which the signal power referred to the signal present after CTF modulation (Zeng et al., 2007).

Multiple image measurements allow the Wiener filter to fully re-localize the signal energy

A prior analysis of the Wiener filter (Downing and Glaeser, 2008) concluded that the Wiener filter fails to re-localize all signal in a CTF-modulated cryo-EM image, leading to substantial degradation in the resulting particle estimate. In that work, however, the size of the considered data set was only a single image, in contrast to the large sets of variable-defocus images considered here. As we have validated numerically (see Fig. 3), multiple image measurements on a given particle allow the Wiener filter (including our single-particle variant) to re-localize essentially all of the signal energy, resulting in a particle estimate with minimized error with respect to the true noise-free object.

A further difference between our analysis and that of Downing and Glaeser is that we apply a frequency-dependent SNR term in the Wiener filter. The analysis of Downing and Glaeser followed the assumption that the SNR was a constant term independent of resolution. This assumption is commonly made in cryo-EM applications of the Wiener filter where accurate resolution-dependent SSNR estimates have not been obtained (Grigorieff, 2007; Zeng et al., 2007; Frank, 2006) but is not accurate for imaged biological molecules (see Fig. 1C). The assumption of a constant SNR drastically changes the output characteristics of the Wiener filter, leading to over-filtering at low spatial frequencies (where the true SSNR is much higher than the average value) and under-filtering at high spatial frequencies (where the SSNR is much lower than the average value). The particle estimate thus produced will therefore have higher error relative to application of the correct, resolution-dependent SSNR term within the Wiener filter. In addition, the ability of the Wiener filter to correct CTF-driven signal delocalization is compromised by the inappropriate use of a constant SNR term, leading to significantly more delocalization in such an estimate particularly when noise levels are high, in comparison to when the correct SSNR function is used (compare Fig. 3C in Downing and Glaeser (2008) to Fig. 3C here).

We can therefore conclude that applying the Wiener filter to multiple images and utilizing a more accurate SSNR function, as done here, leads to near perfect recovery of the delocalized particle signal, in contrast to the single-image, constant-SNR scenario considered by Downing and Glaeser. It is sometimes stated that if a particle image is delocalized in a noisy image field, the particle signal is necessarily “contaminated” by extra noise due to it being spread over a larger noisy area (Downing and Glaeser, 2008; LeBarron et al., 2008). The current analysis shows that this problem is avoided when multiple images are combined using a Wiener filter, because the particle signal will be effectively re-localized, and this re-localization will occur independently of the noise component of the images (assuming linear additivity of the noise and signal components as in standard image formation models). We note, however, that CTF modulation nevertheless leads to a substantial loss in signal energy, regardless what type of reconstructing filter is applied, simply due to attenuation in the average signal amplitude; such attenuation, for example, is evident at low resolution where the CTF value approaches a minimum value near zero. Resetting the CTF of the microscope to a uniform value of one, as is the goal of recently-introduced Zernike “phase plate” correctors (Danev and Nagayama, 2010), appears to be the only feasible way of mitigating signal loss due to this latter effect.

Conclusions

We have presented a new method based on the Wiener filter for minimizing mean-squared error in single-particle reconstructions, together with a comprehensive theory connecting this filter to mask operators and resolution estimation. While we have restricted the analysis in this report to the problem of 2D images, we note that our theoretical relations may also be extended to the problem of 3D reconstruction, where a further benefit emerges: the Wiener filter can actually improve the Fourier-space statistics of a 3D reconstruction by dampening poorly-sampled regions of Fourier space. In contrast, improvements in the 2D case are limited to gains in real-space CCC statistics; in other words, the FRC is unchanged by the Wiener filter for the case where Fourier space is uniformly sampled.

Abbreviations

CCC

cross-correlation coefficient

CTF

contrast transfer function

FRC

Fourier ring correlation

PSSNR

single-particle SSNR

SNR

signal-to-noise ratio

SSNR

spectral signal-to-noise ratio