Remembering Words in Context as Predicted by an Associative Read-Out Model

Abstract

Interactive activation models (IAMs) simulate orthographic and phonological processes in implicit memory tasks, but they neither account for associative relations between words nor explicit memory performance. To overcome both limitations, we introduce the associative read-out model (AROM), an IAM extended by an associative layer implementing long-term associations between words. According to Hebbian learning, two words were defined as “associated” if they co-occurred significantly often in the sentences of a large corpus. In a study-test task, a greater amount of associated items in the stimulus set increased the “yes” response rates of non-learned and learned words. To model test-phase performance, the associative layer is initialized with greater activation for learned than for non-learned items. Because IAMs scale inhibitory activation changes by the initial activation, learned items gain a greater signal variability than non-learned items, irrespective of the choice of the free parameters. This explains why the slope of the z-transformed receiver-operating characteristics (z-ROCs) is lower one during recognition memory. When fitting the model to the empirical z-ROCs, it likewise predicted which word is recognized with which probability at the item-level. Since many of the strongest associates reflect semantic relations to the presented word (e.g., synonymy), the AROM merges form-based aspects of meaning representation with meaning relations between words.

Introduction

Interactive activation models (IAMs) have been used successfully to predict human word recognition performance, when the task implicitly requires retrieval of orthographic or phonological word forms from memory, such as perceptual identification, naming, lexical decision, or word stem completion (e.g., McClelland and Rumelhart, 1981; Grainger and Jacobs, 1996; Perry et al., 2007; Klonek et al., 2009). However, IAMs have not yet been applied to model performance in explicit memory tasks, such as the recognition of a set of studied words. Since Berry et al. (2008) propose that the same signals are detected in implicit and explicit memory, in this paper we explored the versatility of IAMs to predict explicit memory performance. This seemed like a natural extension, given that in an implicit memory task the multiple read-out model (MROM; Grainger and Jacobs, 1996) already successfully predicted receiver operation characteristics (ROCs; Jacobs et al., 2003), which are crucial for the development of formal memory theories (cf. Malmberg, 2008, for a recent overview).

A distinctive strength of IAMs is that they allow item-level predictions for various dependent variables, such as “yes” response rates, mean response times, or mean amplitudes in electrophysiological responses (e.g., Spieler and Balota, 1997; Perry et al., 2007; Hofmann et al., 2008; Rey et al., 2009). IAMs are currently able to simulate effects resulting from lexical whole word representations or from smaller, sub-lexical representations during word recognition (e.g., Perry et al., 2007; cf. Ziegler and Goswami, 2005). So far, however, they neglect the fact that words are embedded into an experimental context of other meaningful words that potentially share a common learning history with the target word. Contextual between-word associations – as for instance the semantic relation of “lung” to its hypernym “organ” – were discussed as extension possibilities for connectionist models (e.g., Rumelhart and McClelland, 1982; Seidenberg and McClelland, 1989; Coltheart et al., 2001). However, they were never used for quantitative performance predictions. Such inter-item associations are better understood in the explicit memory literature (e.g., Roediger and McDermott, 1995; Nelson et al., 1998; Kimball et al., 2007), while item-level predictions of recognition memory performance are still lacking. Therefore, the present study aimed to keep the IAMs’ quantitative strengths of z-ROC and item-level predictions, while seeking to overcome an important weakness: predicting the impact of associative relations between words in an explicit recognition memory task.

Does associative-spreading activate “false memories”?

The probably best-known associative memory phenomenon is the so-called “false memory effect” (Deese, 1959; Roediger and McDermott, 1995): learning associated items (e.g., “table,” “sit,” “legs”) to a non-learned target item (e.g., “chair”) favors its erroneous recall or recognition. Moreover, when learning “chair” in the company of such associates, its “veridical recall” is more likely (Kimball et al., 2007). These experiments rely on tediously collected free association performance to define associations in subjective terms: a target is presented and participants name the first associates coming to their minds. Learning all of the most strongly associated items increases the target’s retrieval probability in a later memory experiment. However, such an experimental design takes only a small subset of the possible associations between the items of an experiment into account (Ratcliff and McKoon, 1994). The present study tested a simple co-occurrence approach allowing to consider all associations between all items (cf. Landauer and Dumais, 1997; Bullinaria and Levy, 2007; Griffiths et al., 2007; Jones and Mewhort, 2007; Andrews et al., 2009): two words were defined as being “associated” when they occurred significantly more often together than alone in a sample of 43 million sentences (Quasthoff et al., 2006) ¹. Hebbian learning is the only assumption required for this definition: stimuli being repeatedly presented together are likely to be associated (Hebb, 1949; Rapp and Wettler, 1991).

Roediger and McDermott (1995) compared targets of which all of the most strongly associated items were learned, to targets of which no (freely) associated item occurred in the experimental context. Here, we challenged this rationale in a more fine-grained, parametric fashion. We hypothesized that the more associates occurred to a non-learned (new) target in the stimulus set, the greater is the amount of erroneous “yes” responses. Similarly, learning the most strongly associated items of an old target word should increase the tendency to freely recall it (Kimball et al., 2007). This led to the hypothesis that learned targets with more associates in the stimulus set should produce greater recognition rates. We tested these hypotheses in a study-test paradigm with the experimental factors old/new and co-occurrence level (low/high): low co-occurrence target items had less than eight significantly co-occurring items in the stimulus set, and high co-occurrence words had at least eight.

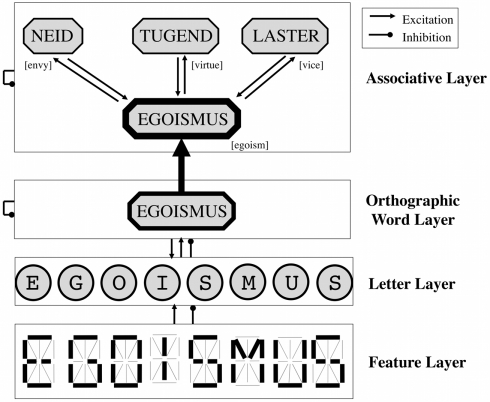
To theoretically frame these hypotheses, we extended the MROM by an associative layer (Grainger and Jacobs, 1996). The MROM consists of three layers of interacting processing units (Figure 1): the visual features of the target stimuli serve as input variables for the model’s feature layer. Feature units activate letter units, which in turn excite units of the orthographic word layer (McClelland and Rumelhart, 1981). In the associative read-out model (AROM), an associative unit for each item presented in the experiment was added. Since the process of word identification is necessary for recognizing it as learned, each association unit obtained an excitatory word identification signal from its corresponding orthographic word unit. The co-occurrence statistics implemented excitatory associative connections between the units in the associative layer. These linkages are assumed to reflect the pre-wired long-term structure of the human associative memory system that matured by experience with words (Hebb, 1949). When the target item is presented to the model, its association unit transiently activates all associated item units, which in turn activate the target unit. Thus, the greater the associative-spreading along the associative connections is (Collins and Loftus, 1975; Anderson, 1983), the greater is the activation “echo” from associated units back to the target item’s unit (Nelson et al., 1998). Since greater activation signals of IAMs typically predict a greater amount of “yes” responses (e.g., Grainger and Jacobs, 1996; Hofmann et al., 2008), the AROM allows the following hypothesis: the more associated items a target has, the larger is its associative activation. This should result in a greater amount of “yes” responses for both, new and old high co-occurrence target items. Apart from this qualitative, condition-wise prediction, we fitted the AROM to (cross-condition) ROCs, and tested whether the obtained signal strengths accounted for item-level variances.

Figure 1.

Basic architecture of the AROM. The lower three layers correspond to previous IAMs (McClelland and Rumelhart, 1981; Grainger and Jacobs, 1996). Target stimuli are presented to the feature units, which in turn activate the letter and (orthographic) word layer. The associative layer’s unit of the target receives the word identification signal from the orthographic word layer. Moreover, associated item units contained in the stimulus set are activated by the target unit, and activate the target in turn. Thus activations to item units with many associated items are greater, which predicts their higher probability of “yes” responses. Translations are bracketed.

Can each item’s signal be detected in an explicit memory task?

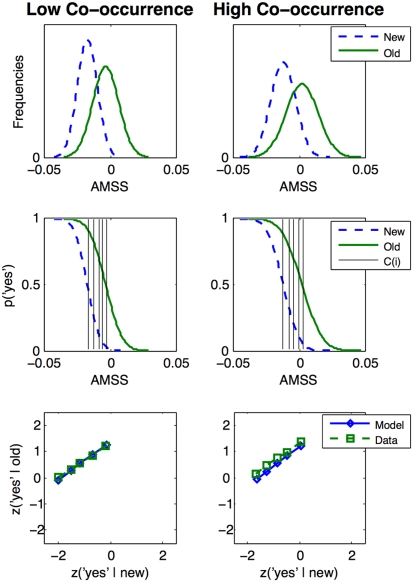
To allow for signal-detection analyses, participants in the experimental study were instructed to rate their recognition confidence on a six-point scale ranging from “sure no” (“1”) to “sure yes” (“6”). For all but the ROC analyses, “4” (“unsure yes”) to “6” counted as “yes” response. Based on these confidence ratings, the signal-detection approach (Green and Swets, 1966) allows for simulating performance from the most liberal response bias by the criterion C(1) to the most conservative bias: C(5) is prone to elicit the fewest “yes” responses by counting all “1” to “5” responses as “no.” The criteria C(i) are assumed to reflect empirical “yes” response probabilities on a bimodal Gaussian distribution of (memory) signal strength of the items: one distribution for the new target items, and another one for the old ones (cf. Figure 2, upper panels). Signal-detection theory describes episodic memory traces resulting from study-phase presentation by the ad hoc assumption of greater mean memory signal strength for old than for new items. To generate ROCs, the “yes” probabilities for all criteria (Figure 2, middle panels) are plotted for new items on the x-axis, those to old items on the y-axis. When z-normalizing these ROC probabilities (cf. Figure 2, lower panels), the so-called z-ROCs typically reveal a slope of less than one during recognition memory tasks (e.g., Ratcliff et al., 1992; Glanzer et al., 1999). Single-process signal-detection models describe this by a second ad hoc assumption: the signal strength variance is greater for old than for new items (Green and Swets, 1966). However, such an unequal variance model does not provide an answer to the question of why the variances are greater to old items (Glanzer et al., 1999). In contrast, Yonelinas (1994) dual-process model gives a simple account of the z-ROC’s tilt-down: recollection, i.e., the detailed recognition of a particular item, is a memory process only apparent for old items. One aim of the present study was to provide an explanation relying on a single signal strength variable: (associative memory) signal strength.

Figure 2.

Distributions of the AMSSs and the resulting z-ROCs for the low (left panels) and high co-occurrence conditions (right panels). The first row displays the associative memory signal strength (AMSS) distributions transformed to smoothed probability density functions for the four experimental conditions. The second row depicts these functions transformed into cumulative “yes”-response probabilities and the five response criteria C(i) for i = 1–5. The third row shows the empirical and modeled z-ROCs.

Jacobs et al. (2003) equated model activations with signal strength to predict z-ROCs from the MROM’s activations. To adopt signal-detection theory’s assumption of greater signal strengths in old items (Green and Swets, 1966), the pre-activation values were increased for association units representing learned items, in comparison to non-learned ones: this resting-level represented every memory trace which has been potentially activated before the presentation of the present test-phase trial, and will be indicated as cycle 0 (see Figure 4). Learned item units were given greater pre-activation values than non-learned ones, because they have been presented before in any case (cf. Morton, 1964, p. 217, property “P3”). In randomized stimulus sets, non-learned associates of a target item were exposed previous to that target with an average probability of 50%. Therefore, the resting-level of non-studied item units was defined to be lower than that of learned ones. Both resting levels were initialized above the activation threshold (of zero), so that all associative units were able to excite and inhibit each other in cycle 0. Due to excitation, new and old associates took an active role in contextually cueing the present item (Gillund and Shiffrin, 1984). As each active association unit inhibited each other unit (McClelland and Rumelhart, 1981), the amount of active units in the associative layer was limited. Since only about 5% of the possible unit pairs were associatively connected in an excitatory fashion (cf. Simulation Methods), the net sum of inhibition was greater than the excitation in cycle 0. When the activation change of the target item’s association unit is calculated from this net inhibition in an IAM, it is weighted by the multiplication with its present activation (McClelland and Rumelhart, 1981). As the resting level was defined to be greater for old than for new item units, greater inhibitions resulted for old item units. Therefore, the target unit’s activation variability in cycle 1 was necessarily greater for old than for new items. As a consequence, the second ad hoc assumption of unequal variance followed logically from the first assumption, when implementing it into an IAM: a greater signal strength variability for old targets items, which monotonically increased with the memory signal strength difference between old and new items.

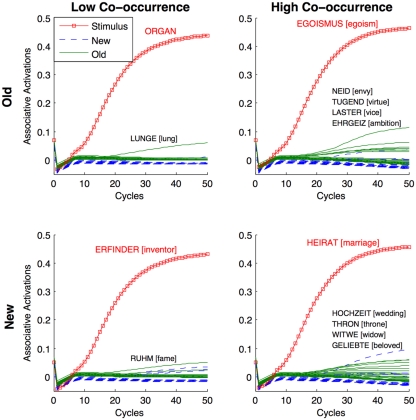
Figure 4.

Exemplary association functions for respectively one target of the four stimulus conditions. Upper panels represent old target items and the lower depict new ones. Left and right panels display low and high co-occurrence stimuli, respectively. The y-axes indicate the associative layer activations. The x-axes indicate simulation cycles. Cycle 0 activations depict resting levels for learned (ρ_old = 0.07) and non-learned stimuli (ρ_new = 0.05), implementing all events before the present trial. When associative excitation and inhibition generated the cycle 1 activations, these define the state of the cognitive system when a test–trial starts. The target items (and their association functions) are shown in (boxed) red (lines), old associates in green (solid lines), and the new associates in blue (dashed lines). Though the AMSSs as predictor variable in Figures 2 and 3 reflect mean activations across cycles 1–7, the strongest associates at cycle 50 are shown for face validity purposes (activations > ρ_new).

To predict human performance, Jacobs et al. (2003) defined signal strength as the mean activation across the first seven cycles (see also Grainger and Jacobs, 1996; Hofmann et al., 2008). Accordingly, in the AROM a target unit’s mean associative activation in cycles 1–7 is taken as its signal strength in the associative layer, henceforth called associative memory signal strength (AMSS). For cycle 1, the first assumption of signal-detection theory of greater old item variances transforms into the prediction of larger old items’ variances as compared to new items in an IAM. For AMSS, however, this prediction has to be tested within the AROM architecture across the whole parameter space, i.e., irrespective of the choice of the five free parameters: the scaling of excitation from the orthographic identification signal to the association units, the scaling of excitation and inhibition in the association layer (Figure 1), and the resting levels of old and new item units.

For obtaining signal strength distributions, the resulting AMSS values were transformed to functional forms for all four experimental conditions, i.e., the new and old low and high co-occurrence conditions. Since AMSS is conceptualized as the signal strength of the items, an additional source of variability of the items’ fixed signal strengths was required. Therefore, smoothed kernel density functions were applied for the transformation to functional forms, and the smoothing kernel factor κ was the only free parameter required for z-ROC generation. κ reflects the variability of the deterministic AMSS values of the items. The empirically obtained “yes” response probabilities were used as C(i; cf. Figure 2, second row). The parameters were optimized by fitting the model-generated z-ROCs to the empirical z-ROCs by minimizing the sum of the least squared errors of the slopes and intercepts of the low and high co-occurrence conditions (cf. Figure 2, third row). We then tested whether the z-ROC slopes of the participants deviated from those predicted by the model. These model tests were run for low and high co-occurrence conditions, separately.

Once the parameters were fixed, the AROM was challenged to account for item-level variance. Previous signal-detection-capable models of recognition memory (Malmberg, 2008) targeted the signal strengths of the items, but did not specify which particular word stimulus provides which signal strength (e.g., Glanzer et al., 1993; Murdock, 1997; Shiffrin and Steyvers, 1997; McClelland and Chappell, 1998). Instead of representing items by random variables, the AROM relies on local representation units (Grainger and Jacobs, 1998; Page, 2000). That is, visual features and letters define a particular word form (McClelland and Rumelhart, 1981; Grainger and Jacobs, 1996). In contrast to its direct precursors, the AROM additionally defines the meaning of a word by the company it kept during its learning history, i.e., co-occurrences (Hebb, 1949; Firth, 1957; Andrews et al., 2009). Because the AROM’s representation variables correspond to real-world entities, e.g., words, the face validity of its processes is testable. For instance, is it phenomenally plausible that “egoism” elicits associative activation in “vice”? We consider the transparency of such a localist approach advantageous, particularly when aiming to integrate this representational model of meaning into a processing model of recognition memory (Steyvers et al., 2006).

Simulation Methods: The AROM and Its Predictions

The feature, letter, and word layers, as well as their connections remained largely² unaltered compared to the AROM’s predecessors (McClelland and Rumelhart, 1981; Grainger and Jacobs, 1996). The added associative layer in general reflects the basic architecture of each layer of an IAM-architecture, which is described more thoroughly elsewhere (McClelland and Rumelhart, 1981; Grainger and Jacobs, 1996). The activation threshold, decay, activation minima and maxima were inherited from the word layer. The word and associative layer lexica of the model contained one unit for each of the 160 items presented in the experiment. Other assumptions critical for the present findings will be described in the following.

Word identification signals from the orthographic word layer activated the associative units (cf. Figure 1). Each Associative word unit x in cycle c obtained input activation A_x(c) by excitatory connections from the corresponding Orthographic word unit activation of the last cycle [O_x(c−1)]. Please note that only if the activation O_x(c−1) crosses the activation threshold (of zero), excitation or inhibition take place. To indicate that a variable must fulfill the logical condition of being positive, we use the subscript  ± . Thus, for instance O_x+ (c−1) = O_x(c−1) if it is positive [O_x(c−1) > 0], otherwise O_x+ (c−1) = 0. The excitation from the orthographic to the associative layer was scaled by the free excitatory parameter α_oa:

$$A_{\text{x}}\left(\text{c}\right)=O_{\text{x+ }}\left(\text{c}-1\right)*{\alpha }_{\text{oa}}$$ (1)

If a word y was significantly co-occurring to the word x (i.e., x ∧ y), an excitatory associative connection was added. It was quantified by log10-transformed χ² values of within-sentence co-occurrence statistics crossing the significance threshold of χ² = 6.63 (P < 0.01; Dunning, 1993; Quasthoff et al., 2006). The free parameter α_aa scales associative excitation of all associations. Thus, the associative excitation function can be written:

$$A_{\text{x}}\left(\text{c}\right)=A_{\text{x}}\left(\text{c}-1\right)+A_{\text{y+ }}\left(\text{c}-1\right)*log10{\chi }_{\text{x}\wedge \text{y}}^2*{\alpha }_{\text{aa}}$$ (2)

This function implements the active spreading of associative activation. Moreover, all activated words [e.g., A_y(c−1)] inhibited each other [e.g., A_x(c−1)] by an amount scaled by a free parameter γ_aa:

$$A_{\text{x}}\left(\text{c}\right)=A_{\text{x}}\left(\text{c}-1\right)-A_{\text{y + }}\left(\text{c}-1\right)*{\gamma }_{\text{aa}}$$ (3)

According to this architecture, the AROM predicts greater activations, and thus a greater amount of “yes” responses for target items with a greater amount of associated items in the stimulus set. Thus, the summed net change n_x(c) of each association unit is a function of the amount of e excitatory units (i.e., the number of significantly co-occurring items), and a function of all N neighbor units that cross the activation threshold. These are inhibiting the respective unit. Thus, the summed net change can be written as:

$$\begin{array}{ll}{n}_{\text{x}}\left(\text{c}\right)& =O_{\text{x+}}\left(\text{c}-1\right)*{\alpha }_{\text{oa}}+{\displaystyle \sum _{\text{y}=1}^{\text{e}}}\left(A_{\text{y+}}\left(\text{c}-1\right)*log10{\chi }_{\text{x}\wedge \text{y}}^2*{\alpha }_{\text{aa}}\right)\\ -{\displaystyle \sum _{\text{y}=1}^N}\left(A_{\text{y+ }}\left(\text{c}-1\right)*{\gamma }_{\text{aa}}\right)& \text{(4)}\end{array}$$

For simulating episodic memory traces, the resting levels ρ were constrained to be larger for old [ρ_old] than for new items [ρ_new, i.e., ρ_old > ρ_new]. Resting levels are referred to by cycle c = 0, i.e., A_x(0) = ρ_old for all old items, and A_x(0) = ρ_new for all new units. All units cross the activation threshold at resting level, and thus inhibit and excite other units. As each unit can be connected to each other unit, but the association of a unit to itself is set to zero, 25,440 associations between the units are possible (160²–160 items). 1,402 of these associations (i.e., significant co-occurrences) were apparent. Most of the connections are inhibitory and thus a negative net inhibition n_x(0) follows from cycle 0, i.e., n(x) is negative. To obtain non-linear dynamics, with a minimum activation m = −1, IAMs weight net inhibitory changes by the associative activation of the unit A_x(c−1) itself. The applied associative activation formula is thus finally (cf. McClelland and Rumelhart, 1981, p. 381, formula 3 and 4 while decay is zero in this case):

$$A_{\text{x}}\left(\text{c}\right)=A_{\text{x}}\left(\text{c}-1\right)-n_{\text{x}}\left(\text{c}-1\right)*\left(A_{\text{x}}\left(\text{c}-1\right)-m\right)$$ (5)

Even when the net changes would be of equal variance across n_old(0) and n_new(0), A_old(1) = ρ_old − n_old(0)^*(ρ_old − m) will produce a greater variance across all old target item units than A_new(1) = ρ_new − n_new(0)^*(ρ_new − m) for all new items, because the resting level scales the activation change by multiplication. As a consequence, activation variability must be greater when greater resting levels are assumed in learned items.

Formally, the memory signal strength of the target item’s unit is defined as AMSS (cf. Introduction):

$$\text{AMSS = }\frac{{\displaystyle \sum _{\text{c = 1}}^7}{A}_{\text{t}}\left(\text{c}\right)}{7}$$ (6)

We tested whether the old item units reveal a greater variance across these first seven cycles (AMSS) than new item units in the following parameter space, using step-sizes of 0.01: α_oa from 0.04 to 0.09, α_aa from 0.03 to 0.08, γ_aa from 0.03 to 0.08, ρ_new from 0.01 to 0.05, and ρ_old from 0.06 to 0.1. This resulted in 5400 parameter sets.

To fit the simulated to the empirical z-ROCs, we transformed the AMSSs of the four experimental conditions into smoothed density functions, using the smoothing kernel factor κ as free parameter (cf. Bowman and Azzalini, 1997; Figure 2, first row). This factor scales the width of the Gaussian smoothing kernel. When these functions are transformed to cumulative “yes” response probabilities, the empirical “yes” response probabilities of new items were used as signal-detection criteria C(i) of the model (Figure 2, second row). κ was fitted iteratively from 0 to 30 using step-sizes of 0.01, while minimizing the root mean squared differences between the modeled and the empirical z-ROC slopes and intercepts for the low and high co-occurrence conditions (Figure 2, third row). Finally, we tested whether the AMSS values of the fixed parameter set can account for a significant portion of item-level variance in new and old items.

Experimental Methods: Testing the AROM’s Predictions

Participants

The participants were 30 native German speakers (17 female, mean age: 29.5, SE: 2.39, range: 16–60) without known reading disorders. They had normal or corrected-to-normal sight, and were paid for participation or received course credits.

Corpus

Word frequency and co-occurrence measures were taken from the German corpus of the “Wortschatz” project (status: December 2006³; Quasthoff et al., 2006). They are based on 800 million tokens and 43 million sentences. The corpus is largely composed of online newspapers (1992–2006). To allow the AROM’s testability in 69 languages, corpus-size independent word frequency class measures of this cross-linguistic project were used. Therefore, a power function relates the frequency of each word to the most frequent word, i.e., “der” [the] is 2^class more frequent than the given word (cf. Adelman and Brown, 2008). Thus the lower the frequency class, the higher is the word frequency. Further, two words were defined associated if they co-occurred significantly more often within the same sentence than predicted from their single frequencies by the log-likelihood test (P ≤ 0.01, χ² ≥ 6.63; Dunning, 1993).

Stimuli

Each cell in the 2 × 2 design (factors: old/new and co-occurrence) contained 40 nouns. Stimuli of the high co-occurrence conditions had at least eight significantly co-occurring neighbors in the stimulus set, and low co-occurrence stimuli less than eight. To rule out biased effects due to confounding variables (all Fs < 0.5, cf. Table 1), we controlled for emotional valence, arousal, imageability number of orthographic neighbors (Coltheart et al., 1977) and letters (Võ et al., 2009), as well as word frequency class (cf. see Corpus). Token bigram frequencies were calculated by the SUBLEX software (Hofmann et al., 2007), using the frequency counts of the Leipzig Wortschatz project cleaned by all word forms not contained in the CELEX lexical database (Baayen et al., 1995).

Table 1.

Displays the means (SD) of the manipulated and controlled variables of the target stimuli in the four experimental conditions. Emotional valence ranges from −3 to +3. Imageability and arousal range from 0 to 5.

Factors: old/new Co-occurrence	New		Old
	Low	High	Low	High
Number of stimuli	40	40	40	40
Number of significantly co-occurring items in the stimulus set	3.85 (1.70)	13.90 (4.73)	3.80 (1.70)	13.85 (4.04)
Emotional valence	0.11 (1.31)	0.03 (1.23)	0.03 (1.09)	0.00 (1.34)
Imageability	3.89 (1.22)	3.96 (1.29)	3.94 (1.20)	4.01 (1.43)
Arousal	2.95 (0.53)	2.90 (0.58)	2.87 (0.54)	2.98 (0.64)
Word frequency class	11.65 (0.70)	11.65 (0.70)	11.68 (0.47)	11.57 (0.71)
Number of orthographic neighbors	1.57 (2.26)	1.32 (1.81)	1.57 (2.14)	1.70 (2.29)
Bigram frequency	17520 (106001)	17556 (9263)	16489 (9149)	16648 (8546)
Number of letters	6.08 (1.07)	6.12 (1.14)	6.22 (1.10)	5.97 (1.35)

Procedure

Eighty old words were presented in the study phase and all 160 words in the test phase. Participants were instructed to judge how confident they are that a target stimulus was presented in the previous study phase (“yes”), or not (“no”). Participants were informed that they receive feedback about their error scores after the test phase. Performance data were acquired using a computer mouse. Stimuli were presented by Presentation 9.9 software (Neurobehavioral Systems Inc., Canada). To familiarize the participants with the task, five practice items were presented before the study and the test phase, respectively.

Study phase

Each trial began with a fixation cross remaining on the screen for 500 ms followed by a stimulus presented for 1500 ms. Five hash marks (“#####”) appeared until a mouse button was pressed. To avoid primacy and recency effects, three filler items were presented before and after the critical stimuli.

Test phase

A fixation cross was presented for 500 ms. Target stimuli were presented for 1500 ms, followed by a blank screen of 1500 ms. A rating scale appeared on the screen, and the participants judged their recognition–confidence via mouse clicks on a six-point scale ranging from “1” (“sure no”) to “6” (“sure yes”). For a random number of participants, this assignment was reversed during the experiment, but not for the analyses. Participants were instructed to use all confidence judgments approximately equally often. A blank screen of 500 ms was presented before the next trial started with a new fixation cross. None of the filler and practice items had any significantly co-occurring item in the critical stimulus set.

Experimental and Modeling Results

A 2 × 2 repeated measures ANOVA on the percentage of “yes” responses revealed a significant old/new effect [F(1,29) = 167.77, P < 0.001, η_p² = 0.85]. Old items produced more “yes” responses. Moreover, a significant effect of co-occurrence was obtained [F(1,29) = 21.91, P < 0.001, η_p² = 0.43], but no significant interaction (F < 1). The planned comparison revealed that high co-occurrence new stimuli produced a greater “yes” response rate (M = 0.2; SE = 0.02) than low co-occurrence new stimuli [M = 0.13; SE = 0.02; t(29) = 3.80, P < 0.001]. High co-occurrence old stimuli (M = 0.76; SE = 0.04) produced more “yes” responses than low co-occurrence old stimuli (M = 0.69; SE = 0.03; t(29) = 3.02, P < 0.005]. Averaged across participants, the z-ROC slopes were 0.66 in the low co-occurrence condition and 0.70 in the high co-occurrence condition. Figure 2 displays the empirical z-ROCs with slopes smaller than 1.

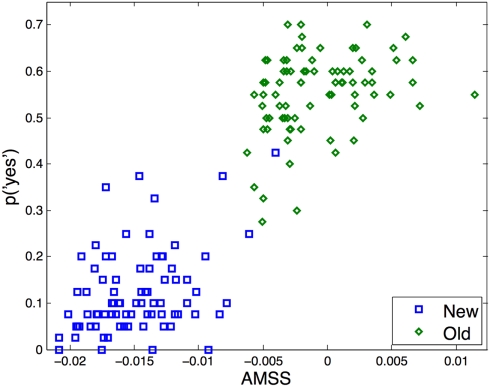
All 5400 parameter sets used for optimal parameter estimation revealed a greater AMSS variance for old than for new target items (Figure 3). The least squared differences between the modeled and the empirically obtained z-ROCs for low and high co-occurrence items were obtained for the parameters of α_oa = 0.09, α_aa = 0.03, γ_aa = 0.04, ρ_new = 0.05, ρ_old = 0.07, and κ = 10.09. The parameters were fixed at these values. Simulated z-ROC slopes were 0.75 and 0.77 for the low and high co-occurrence conditions, respectively. For both co-occurrence conditions, the modeled z-scores for the five criteria of the new and old items were tested for their capability to predict the 10 z-scores empirically obtained (cf. Jacobs et al., 2003): the model’s z-scores accounted for 99.61% of the variance of the low co-occurrence data [F(1,9) = 2044.85; P < 0.001; RMSD = 0.07], and 99.05% of the high co-occurrence z-scores [F(1,9) = 834.45, P < 0.001, RMSD = 0.10]. The behaviorally obtained z-ROC slopes of the low and high co-occurrence conditions for the individual participants did not differ significantly from the z-ROC slopes predicted by the model [t(29) = 0.17; t(29) = 1.55; Ps > 0.1]⁴. The new target items AMSS scores accounted for 14.32% of the variance of the “yes” response probabilities [F(1,79) = 13.04], and the old targets for 10.45% [F(1,79) = 9.10; Ps < 0.001; RMSDs = 0.08].

Figure 3.

AMSSs of the word units predicting the empirical “yes” response probabilities of each of the new and old items.

General Discussion

The present study provides two novel IAM features: relying on Hebb’s proposal that the repeated co-exposure of stimuli leads to their “association” (Hebb, 1949), we correctly predicted that a higher amount of associations in the stimulus set lead to higher proportions of “yes” responses to non-learned and learned items in recognition memory for words. Second, we extended a localist connectionist word recognition model by an associative layer, and showed that this AROM predicts recognition memory performance from the core cross-condition level of ROCs down to the fine-grained item-level.

The effect in non-learned items is related to “false memories” but goes beyond Roediger and McDermott (1995) seminal work. The false memory effect consisted of the comparison of target items from which either all of the most strongly associated, or no (freely) associated items were learned. The present study revealed similar effects in a recognition memory task. However, defining associations by co-occurrence statistics allowed for taking all associations between all items of the stimulus set into account. Still, when a target item contained more associations in the stimulus set, a significant effect of co-occurrence indicated more “yes” responses for new words.

For learned target items, we discovered that many associations boost recognition memory performance, as indicated by a co-occurrence effect for old words. Since the present stimulus set was carefully controlled for all kinds of psycholinguistic single-word features, we suggest that both, the co-occurrence effects to new and old items, can be attributed to the manipulation of the amount of associations of a target item.

To account for both of these findings, the co-occurrence statistics were embedded into an associative activation-spreading network (Collins and Loftus, 1975) that was added to an IAM-architecture (cf. McClelland and Rumelhart, 1981; cf. Figure 1): the MROM (Grainger and Jacobs, 1996) can account for human performance in a variety of tasks that rely on implicit mnemonic processes. As no top-down modulations from the associative to the lower layers were implemented (cf. Figure 1), the AROM in its simplest form contains an unchanged MROM. Therefore, the AROM can still account for all of its predecessor’s effects and thus has a higher level of generality than the MROM (e.g., Grainger and Jacobs, 1996). Future studies will have to show which top-down excitations or inhibitions from the associative to the lower layers would provide the best-fitting, most parsimonious and potentially also most general account on word recognition. It is likely, however, that the question of which top-down feedbacks are appropriate must be answered in a task-specific manner, because we would assume that the cognitive system is flexibly adapting to varying task demands for optimizing performance. Modeling human performance in reading aloud, for instance, might be a largely bottom-up driven process that may neglect top-down feedback for parsimony purposes (cf. Perry et al., 2007).

For extending the scope of IAMs to explicit memory processing, we implemented memory traces from the study-phase presentation according to signal-detection theory (Berry et al., 2008; cf. Morton, 1964). It assumes greater signal strengths for old than for new items (Green and Swets, 1966). Thus, the units of learned items obtained greater resting level activations in the associative layer than non-learned ones. Unequal variance analysis models require a second assumption to describe the z-ROCs tilt-down, i.e., a greater signal variance to learned items (Green and Swets, 1966; cf. DeCarlo, 2002). The present study shows that implementing the first assumption of the old items’ greater memory strength into an IAM makes the second ad hoc assumption of unequal variances redundant. An IAM explains a slope of the z-ROC smaller one based on its antecedent conditions (cf. Jacobs and Grainger, 1994): an increased signal variance for old items – critical for the z-ROC’s slope smaller than one during recognition memory – can be explained by the non-linearity assumption of connectionist models (cf. McClelland, 1993; O’Reilly, 1998): a modeling unit – mirroring a neuron or a cluster of neurons in the brain – can receive a broad range of excitatory or inhibitory signals from other neurons. To avoid catastrophic cascades of neural activation bursts that could potentially damage neurons, an IAM bounds this activation to a maximum. As the firing rate of a neuron cannot be negative, a further assumption of minimum activation is required (e.g., Bogacz et al., 2007). Connectionist models typically meet such biological constraints by modeling the activation of a unit as a non-linear function of the amount of net input (Grossberg, 1978; McClelland, 1993). Therefore, the activation change of a unit is scaled by multiplying it with its current activation in an IAM (McClelland and Rumelhart, 1981). Resulting from the activation-scaling by a unit’s resting level, which is higher for old items, incoming inhibitory signals affect the old target item units to a greater degree than units representing new items of lower resting-level activation. Therefore, the variability of the signal is greater in the old items’ units starting from cycle 1. The assumption of greater activation variance of old items was also confirmed to be true across the first seven cycles. The AMSSs are greater for old than for new items, irrespective of the choice of the free parameters explored. Accordingly, the AROM correctly predicted z-ROC slopes smaller than one, which are typically observed in the recognition memory task (Ratcliff et al., 1992; Glanzer et al., 1999). Similar to global memory models (e.g., Gillund and Shiffrin, 1984; cf. Ratcliff et al., 1992), this mechanism of the AROM predicts that the greater the resting-level difference between the old and new item’s initial memory activation, the lower should be the slope of the z-ROC. When assuming that additional study time would increase the initial memory traces and thus the resting levels, this would account for Glanzer et al.’s observation that not only accuracy would increase, but also that the z-ROC slope would decrease (Glanzer et al., 1999). We admit, however, that these changes can be small, which casts doubt on their detectability. Our simulated z-ROC slopes were close to 0.8, also questioning whether they would provide strong arguments against the “constancy of slopes” conception (Ratcliff et al., 1992). We think that this is due to the fact that the model’s necessity to produce slope changes proportional to the resting-level difference only applies to the first simulation cycle, i.e., the initial memory state in the test phases. While associative-spreading is taking place, this strong prediction can be changed. For instance, Ratcliff et al. (1992) could have concluded that the slope varies only between subjects, because for each subject a large set of stimuli has been randomly chosen from a larger corpus. As a consequence, the stimuli can be arbitrarily non-associated or strongly interconnected, which depends on the actual selection. This associative noise may cause variability minimizing the chance to detect significant slope changes. Though this untested speculation cannot yet settle the Ratcliff–Glanzer dispute (Ratcliff et al., 1992; Glanzer et al., 1999), after all the remaining assumption of greater old-item resting levels leads to a further testable AROM prediction: the higher the resting level is, the faster should be the response times in binary decisions (cf. Grainger and Jacobs, 1996), e.g., when comparing old and new items (Kuchinke et al., 2006).

Apart from these proof-of-concept explanations, the present study aimed at fitting the actual z-ROCs to low and high co-occurrence words by the AROM. Predicting z-ROCs from the AMSS of the items involves a modeling challenge well-known in recognition memory research (Gillund and Shiffrin, 1984, p. 16). The overlap between the old and new item signal distributions was too low (cf. AMSS values in Figure 3). A previous MROM-based simulation study solved this by adding noise to the criteria (Jacobs et al., 2003). In contrast, the present AMSS values were transformed into smoothed kernel density functions to obtain an estimate of the (random) signal variability of the otherwise deterministic AMSS values. Thus even “noise” was conceptualized in a fashion allowing the model to remain fully deterministic. Moreover, instead of three free parameters required for z-ROC generation in the MROM (Jacobs et al., 2003), the present study cut this number down to one, the Gaussian smoothing kernel factor κ.

In addition to the z-ROC parameter, two free parameters were necessary for the (old and new item units’) resting levels, and three scaled the excitation from the orthographic word to the associative layer, as well as excitation and inhibition within the associative layer. After fitting these free parameters, the empirically obtained z-ROC slopes and z-scores did not deviate from those predicted by the model (Figure 2).

The unequal variance signal-detection model just begged the answer to the question of why the z-ROC slope is smaller than one, by assuming greater signal strength variances of old items (Green and Swets, 1966; Glanzer et al., 1999; cf. DeCarlo, 2002). The dual-process model may, in contrast, provide an answer by conceiving of recollection as a phenomenally and neurally distinguishable process (Yonelinas, 1994; Yonelinas et al., 2005; Wixted, 2007; cf. Malmberg, 2008). The AROM’s architecture complements previous unequal-variance based models by an answer to the question of why the z-ROC slopes are smaller than one during recognition memory: these are a logical consequence of the episodic memory traces built at study itself. When many traces actively compete in memory, each representation unit obtains net inhibitory signals. As the resulting activation changes are scaled in an IAM-architecture by multiplying it with the unit’s activation, larger resting levels of old items lead to their greater signal strength variances (Squire et al., 2007).

Although the earliest associative activation-spreading models did not discuss false and veridical recognition, they can predict these effects (Roediger et al., 2001; cf. Anderson, 1983, and Collins and Loftus, 1975, and Quillian, 1967). A contemporary modeling approach can account for the build-up of associations, but it ignores the effects of pre-wired long-term associations in human memory (e.g., Danker et al., 2008). Though Ratcliff and McKoon (e.g., 1994) envisioned the predictive power of co-occurrence statistics early, Nelson et al. (1998) used free association performance to propose a pre-quantitative model, which accounted for effects of the number of associates in a stimulus set during recognition memory (cf. Thompson-Schill and Botvinick, 2006; Andrews et al., 2009). Still, a computational definition that would allow for quantitative item-level predictions was not given. For recall tasks, Kimball et al. (2007) recently proposed a computational model that quantitatively predicts false and veridical recall. However, there are substantial differences between the processes required for recall or recognition (Gillund and Shiffrin, 1984). For instance, the AROM does not require separate short-term and long-term memory stores (Norman, 1968). In contrast, transient memory activations simply spread across the long-term associative structure of human memory (Morton, 1969).

The AROM is novel in that it provides quantitative associative-spreading predictions for recognition memory performance. Neither any other spreading-activation model, nor any recognition memory model simulates word recognition with the same depth as the AROM: it predicts which word is recognized with which probability depending on the amount of its associates. The more associated items are in the stimulus set for a non-learned or learned target item, the larger is the probability to classify it as old. Thereby, the false memory logic is elevated to a level capable of making item-level predictions. For veridical memory of old items, the AROM’s item-level performance is somewhat lower than for the false memories in new items (see also Figure 2, lower right panel). This potentially results from the need to consider a second source of information for the prediction of old items (e.g., Yonelinas, 1994; DeCarlo, 2002). Moreover, we are fully aware that the AROM’s “horizontal” generality is limited (Jacobs and Grainger, 1994): other recognition memory models account for a much broader range of explicit memory phenomena (e.g., Glanzer et al., 1993; Shiffrin and Steyvers, 1997; McClelland and Chappell, 1998; Malmberg, 2008; but cf. Grainger and Jacobs, 1996, for implicit memory). In turn, the present approach “vertically” generalizes across different instances of the same data, i.e., cross-condition z-ROCs, condition-wise associative effects in new and old items, and last but not least, the AROM is the first signal-detection model of recognition memory that assigns signal strength to each particular word stimulus. This allows for predicting the percentage of participants recognizing this particular orthographic word form in the distinct associative context of other words, which extends signal-detection theory to an item-level.

The item-level variances were predicted by associative cross-trial excitation from the associative context of the experiment to the target items. The more associated items are presented before the target, the larger is its unit’s activation in cycle 1. Moreover, learned items still have a larger activation than non-learned items at this cycle. Starting at cycle 4 the visual input of the feature layer reaches the associative layer, and the identification of the stimulus begins to cue the associative memory layer (Gillund and Shiffrin, 1984; cf. Hofmann et al., 2009). Although we did not deviate from the tradition to predict item- and ROC-performance by the mean activation of the cycles 1–7 (Jacobs et al., 2003; Hofmann et al., 2008), the face validity of the model was demonstrated at cycle 50, at which the most strongly associated items emerged.

As is evident from Figure 4, the associates to a target item reflect intuitively valid associations. Moreover, the AROM can simulate semantic relations in the narrowest sense of the term, as e.g., the associate [lung] is a hyponym of the target [organ]; [vice] can be considered as a hypernym of [egoism]; [virtue] can be conceived as the antonym of [vice]; and [wedding] and [marriage] are (partial) synonyms. Why do the most strongly co-activated associates often reveal a semantic relation to the target? We think that this is because semantically related items are very likely to share many associates with the target. Consider each common associate as a common associative feature of two words (cf. e.g., Shiffrin and Steyvers, 1997). When two words share many of these contextual properties, the probability increases that they are not only related in an associative sense, because they co-occur together, but also that they will be likely to reveal a semantic relation. Moreover, as the associative layer receives input from the orthographic layer, the unique identity of a word is not only defined by its associations, but also by its orthographic form-properties.

Does the orthographic layer of the AROM account for additional item-level variance? The simplifying assumption of no top-down feedback from the associative layer allowed us to test whether not only associative, but also mere orthographic similarities between items can be accounted for by the MROM within the AROM (cf. e.g., Grainger and Jacobs, 1996; Cortese et al., 2010). Therefore, we calculated the global lexical activation (GLA) from the sum of the orthographic word unit activations across the first seven cycles (e.g., Jacobs et al., 2003; Braun et al., 2006). As the present simulations are based on “lexica” containing all items of the experiment, the GLA elicited by a stimulus can be regarded a measure of the orthographic similarity of the target item to the other items. For new items, the GLA accounted for 14.49% of the “yes” response probability variance [F(1,79) = 13.22, P < 0.001, RMSD = 3.35], and the GLA was not confounded with AMSS [F(1,79) = 2.62; P > 0.1; R² = 0.03]. For old items, in contrast, the GLA could not account for any variance (F < 0.1). So the present AROM implementation can additionally account for orthographic similarities between the new items and the remaining items in the stimulus set. It remains an issue for future research whether this second source of information can help to improve the AROM’s z-ROC predictions (cf. Yonelinas, 1994).

Finally, form-properties and semantic-associative properties of words were both proposed to be crucial for morpheme representations (e.g., Devlin et al., 2004). Reviving the early theoretical perspective of associative-spreading models, the AROM has distinct layers for lexical and semantic-associative networks (Collins and Loftus, 1975). Future studies will have to show how the AROM can account for morphemic relations between words in terms of their conjoint co-variation of orthographic and associative-semantic word features.

Form-constituents of meaning have been extensively modeled using distributed representations (e.g., Plaut et al., 1996; Harm and Seidenberg, 2004; see also Grainger and Ziegler, 2011). Rumelhart and Todd (1993) assume that (hidden) units shape associations between words, because of the repeated co-exposure of words in sentences like “a robin is a bird” (cf. Collins and Quillian, 1969; Rogers and McClelland, 2008; cf. Masson, 1991, 1995). In contrast, the AROM’s associations – implemented as two words significantly co-occurring within sentences – correspond to a mature cognitive architecture. Thus, the AROM can be considered as a first step toward a fully localist connectionist model containing an implemented semantic layer. This has been theoretically postulated for some time, but it resisted a computational implementation so far (e.g., Rumelhart and McClelland, 1982; Coltheart et al., 2001). Though we think that Rumelhart and Todd’s model (1993) and the AROM could potentially complement each other in a seamless theoretical symbiosis, it is still unclear how a Hebbian learning algorithm could quantitatively converge on the AROM’s associative connection weights. However, both types of models complement each other. The first accounts for the maturing of flexible associations, and thus reflects the plasticity of the neural system. The AROM, on the other hand, predicts human performance from activation spreading across the outlearned, stable-state associations corresponding to the long-term structure of human memory (cf. Grossberg, 1987).

Conclusion

This study introduces the AROM as a model capturing explicit memory performance for IAMs. Associative-spreading-activation inserted into the MROM can account for cross-condition z-ROCs, condition-wise effects of associations in new and old items, and item-level performance. Given that many words most strongly associated by the model reflect semantic relations (e.g., hyponomy), the AROM should be a convenient tool for future investigations of semantic effects in word recognition, particularly also for the tasks IAMs were originally designed for: implicit memory tasks.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.