Abstract
RNA thermometers are translational control elements that regulate the expression of bacterial heat shock and virulence genes. They fold into complex secondary structures that block translation at low temperatures. A temperature increase releases the ribosome binding site and thus permits translation initiation. In fourU-type RNA thermometers, the AGGA sequence of the SD region is paired with four consecutive uridines. We investigated the melting points of the wild-type and mutant sequences. It was decreased by 5°C when a stabilizing GC basepair was exchanged by an AU pair or increased by 11°C when an internal AG mismatch was converted to a GC pair, respectively. Stabilized or destabilized RNA structures are directly correlated with decreased or increased in vivo gene expression, respectively. Mg2+ also affected the melting point of the fourU thermometer. Variations of the Mg2+ concentration in the physiological range between 1 and 2 mM translated into a 2.8°C shift of the melting point. Thus, Mg2+ binding to the hairpin RNA is regulatory relevant. Applying three different NMR techniques, two Mg2+ binding sites were found in the hairpin structure. One of these binding sites could be identified as outer sphere binding site that is located within the fourU motif. Binding of the two Mg2+ ions exhibits a positive cooperativity with a Hill coefficient of 1.47. Free energy values ΔG for Mg2+ binding determined by NMR are in agreement with data determined from CD measurements.
INTRODUCTION
The maintenance of the intracellular metal ion concentration is an indispensable requirement for the viability of eukaryotic and prokaryotic cells. Cells exhibit high intracellular K+ and Mg2+ concentrations while cytosolic Na+ and especially Ca2+ concentrations are kept low (1). By varying the K+ concentration, cells adopt the intracellular to the extracellular osmolality (2). K+ acts as counterion for nucleic acids (DNA, RNA) (3,4) and has been found to stabilize the structure of cytosolic proteins. Mg2+ is prominent for binding and activating ATP (5) as well as intracellular enzymes (1). In addition to K+, it is the most important cation acting as counterion of nucleic acids (1,4). It is involved in the maintenance of the structural integrity of the plasma membrane (6) and stabilizes proteins. In gram-negative bacteria, Mg2+ binding to lipopolysaccharides stabilizes the periplasmic membrane (7). Most importantly, it is strictly required for rRNA folding, ribosome assembly and ribosome function (8,9).
The importance of Mg2+ ions for the viability of prokaryotic cells has some important implications. First, Mg2+ starvation leads to growth arrest of bacterial cultures (10). Second, although the amount of Mg2+ within a prokaryotic cell may vary by a factor of three, the RNA[kg]:Mg2+[kg] ratio (≈68) is almost constant under differing environmental conditions (10). Escherichia coli cells that enter the stationary phase reduce the concentration of ribosomes and thus reduce their Mg2+ content (11). Third, E. coli cells react on Mg2+ starvation by the synthesis of polyamines including spermidine and putrescine which are able to substitute for Mg2+ in many cases. For instance, the spermidine/Mg2+ ratio bound to the ribosomal fraction of E. coli cells reduces with increasing extracellular Mg2+ concentration (12). Due to the diversity of different Mg2+ binding partners and the multitude of different intracellular Mg2+ binding sites, most of the intracellular Mg2+ is present in a bound form, albeit transiently. E. coli cells in the exponential growth phase have a Mg2+ content of 90–110 mM (13), while only a small fraction of 1–2 mM is present in the physiologically active free form (14). In addition, most of the bound Mg2+ fraction is in fast exchange with the free Mg2+ in the cytosol (14,15) and a 20–30% loss of Mg2+ is sufficient for cell-growth arrest (14). Due to this rapid exchange between free and bound Mg2+, also the concentration of the free form has to be controlled tightly by the cell itself to assure cell viability. Indeed, Mg2+ ions have been found to be actively transported among others in E. coli (15–19), Bacillus subtilis (20) and Salmonella typhimurium (21) and the Mg2+ transport mechanisms of S. typhimurium and E. coli are equivalent to each other (1,14,18,21–25).
Ions are important for stabilizing RNA tertiary structure (3,9,26). Most often, K+ and Mg2+ cations serve this task although Mn2+ ions and polyamines such as spermidine have the potential to substitute for some of the K+ and Mg2+ binding sites. Mn2+ ions are able to substitute for 76% of the bound Mg2+ ions in E. coli without impairing viability of the cells (18). These findings provide support for using Mn2+ ions to map Mg2+ binding sites within an RNA molecule (27–30).
Due to its small size and divalent charge, the Mg2+ ion has a notably high charge density. Therefore, the first water hydration sphere is more stable than for any other physiologically relevant cation (31). Mg2+ coordinates six water molecules with octahedral geometry. Mg2+ ions are able to bind to RNA with different binding modes. Generally, ‘inner sphere’ and ‘outer sphere’ contacts can be distinguished (9). In an ‘outer sphere’ complex, water molecules of the Mg(H2O)2+6 complex but not the Mg2+ ion itself make contacts to the functional groups of the RNA. In contrast, inner sphere contacts are characterized by at least one direct contact of the Mg2+ ion to functional groups of the RNA. Inner sphere contacts can be classified by the number of inner sphere ligands other than H2O (type I, type II, type III, etc.), while ‘type 0′ is identical to an outer sphere contact (9). Klein et al. (9) modeled Mg2+ ions into the structure of the large ribosomal subunit from Haloarcula marismortui and found that 65% of the bound Mg2+ ions are outer sphere coordinated. Within the remaining inner sphere contacts, most contacts belong to the classes type I or type IIa where inner sphere ligands are orthogonally oriented to each other. Most of these Mg2+ ions (type I and type IIa) are coordinated to either one or both non-bridging oxygens of the phosphate backbone. Outer sphere coordinated Mg2+ ions are most often located within the major groove of the RNA helices and make indirect, water-mediated contacts to the heteroatoms of the nucleobases (9,27,32).
Mg2+ has a profound effect on the structure and function of riboswitches (33–35). Riboswitches are biosensors that control gene expression in response to cellular metabolites that they bind with high affinity and specificity (36,37). RNA thermometers are capable of sensing temperature. They control translation initiation of heat shock and virulence genes by sequestration of the Shine–Dalgarno (SD) sequence at low temperatures (38). At higher temperatures, the hairpin structure melts in a zipper-like manner allowing translation initiation to occur (39). Helix stability in simple synthetic RNA thermometers is directly correlated to gene expression levels of the downstream gene (40).
We recently investigated the structure, function and melting mechanism of the Salmonella fourU RNA thermometer, which controls expression of the heat shock gene agsA (39,41). In the present work, we examined the in vitro and in vivo effects of a point mutation that weakens an extraordinarily stable GC base pair, which had been shown to prevent unfolding of the wild-type RNA at lower temperatures (39) (Figure 2). Furthermore, we highlight the Mg2+ binding properties of the fourU RNA thermometer. Using NMR spectroscopy, we identified and localized two Mg2+ binding sites and determined their dissociation constants as well as the cooperativity between these binding sites. Mg2+-dependent changes in thermal stability of the fourU RNA thermometer were determined by CD spectroscopy. Our study provides first evidence for Mg2+ binding of an RNA thermometer and its relevance for RNA thermometer function.
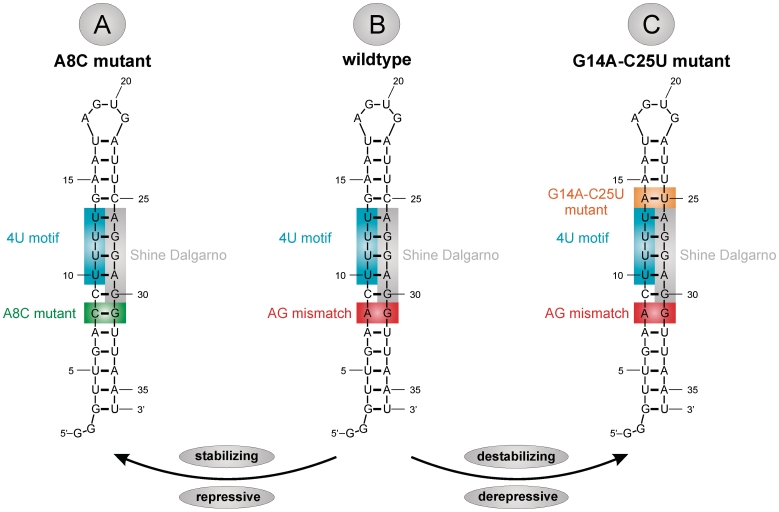
Figure 2.
Sequence and secondary structure of hairpin 2 of the Salmonella fourU RNA thermometer and mutants used in this study. (A) Secondary structure of the 4U-hp2-A8C mutant RNA. (B) Secondary structure of the 4U-hp2-wt RNA. (C) Secondary structure of the 4U-hp2-G14A-C25U mutant RNA.
MATERIALS AND METHODS
NMR spectroscopy
NMR measurements were performed on a 600 MHz (14.09 T) Bruker NMR spectrometer equipped with a 5-mm xyz-gradient probe and a 900-MHz (21.14 T) Bruker NMR spectrometer equipped with a 5-mm cryogenic HCN z-gradient probe. Spectra were recorded and processed using the Bruker TopSpin 2.0/2.1 software. Processed spectra were analyzed with Sparky 3.1.1.3.
MgCl2 titration experiments
Mg2+ titration experiments of the 4U-hp2-wt RNA were performed in NMR buffer (see RNA preparation section) at a temperature of 10°C. [1H-15N]-HSQC experiments were recorded at a B0 field strength of 900 MHz (21.14 T) using a standard pulse sequence (42) (Topspin 2.1 pulse program library: fhsqcf3gpph) with a hard Watergate pulse train for water suppression (43). Spectra were recorded with a spectral width of 30 ppm in the 15N-dimension and 22 ppm in the 1H-dimension. A total of 240 increments were recorded in the 15N-dimension and 4096 points in the 1H-dimension. [1H,15N]-HSQC spectra were recorded at the following MgCl2 concentrations: 0, 0.3, 0.5, 0.7, 1.0, 1.5, 2.0, 3, 5 and 7 mM.
Overall chemical shift perturbations (CSPs) were calculated from the CSPs of the 15N and the 1H-dimension (44) according to the following equation:
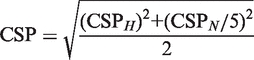 |
(1) |
Since association and dissociation of the Mg2+ ions from the target RNA are fast on the NMR timescale, CSPs can be related to the Mg2+ concentration within the sample according to the following equation:
| (2) |
Equation (2) is derived from the mass action law for an RNA/Mg2+ equilibrium with the RNA having one Mg2+ binding site. In Equation (2) f(x) is the CSP of an individual imino signal at a given x = [Mg2+]/[RNA] ratio, a is the ratio between dissociation constant (KD) and RNA concentration and b is the maximum CSP at infinite Mg2+ concentration. During the fitting procedure, the parameters a and b were allowed to adjust freely.
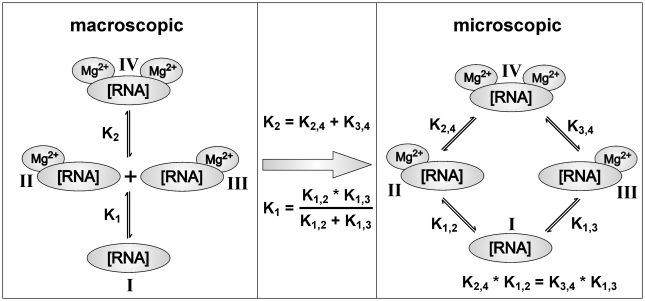
CSP curves that showed biphasic behavior and could not be fitted by Equation (2) were fitted by a model assuming two different binding sites (Figure 1). Such a model is characterized by two macroscopic (K1, K2) and four microscopic (K1,2, K1,3, K2,4, K3,4) dissociation constants that connect four different RNA states (I, II, III, IV). Considering a particular imino group, two different states with only one Mg2+ ion bound (states II and III in Figure 1) can have different or equal (degenerated) chemical shifts. Such model predicts that biphasic curves only depend on the macroscopic dissociation constants K1 and K2. Monophasic curves, in contrast, detect either macroscopic or microscopic dissociation constants, depending on which chemical shifts of the four states are degenerated for a particular imino group. Microscopic and macroscopic dissociation constants are related to each other by the equations depicted in Figure 1.
Figure 1.
Mg2+ binding model assuming two distinct Mg2+ binding sites on the RNA. The RNA can adopt four different states (I, II, III, IV). Transitions between these states are described by microscopic dissociation constants (K1,2, K1,3, K2,4, K3,4). Transitions between free RNA, binary and ternary complex are described by macroscopic dissociation constants (K1, K2). In addition, equations describing interdependencies of the different dissociation constants are given. K1 and K2 as well as K1,2, K1,3, K2,4 and K3,4 are thermodynamic constants that describe the RNA-[Mg2+]n complexes under equilibrium conditions.
Biphasic CSP curves can be fitted by Equations (3–5), if the two binary complexes have different chemical shifts.
| (3) |
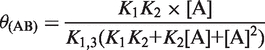 |
(4) |
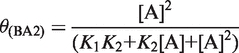 |
(5) |
Biphasic CSP curves can be fitted by Equation (5–7), if the complexes [AB] and [BA] are degenerated.
| (6) |
| (7) |
Whether chemical shifts are degenerated in the binary complexes or not, influences only the parameter b in the Equations (3) and (6). In Equations (3) and (4), the constants b and K1,3 cannot be fitted independently and can therefore be summarized to one constant.
In Equations (3)–(7), [A] is the concentration of Mg2+-ions, θ(AB) and θ(BA) are the populations of the two different binary (RNA*Mg2+)-complexes and θ(AB2) is the population of the ternary (Mg2+*RNA*Mg2+)-complex. Parameters a and b are fitting parameters that modulate the CSP amplitude. K1, K2 are the macroscopic and K1,2, K1,3, K2,4, K3,4 the microscopic dissociation constants of the Mg2+ binding model which assumes two Mg2+ binding sites (Figure 1). During the fitting procedure, the parameters a, b, K1 and K2 were allowed to adjust freely.
In some cases, three out of four RNA states have degenerated chemical shifts and only one state has a differing chemical shift. For some of these cases, this results in monophasic CSP curves. For example, if state I has a differing chemical shift, the macroscopic dissociation constant K1 is detected. If state IV has a differing chemical shift from states I, II and III, the macroscopic dissociation constant K2 is detected. In the special case of equal microscopic dissociation constants (K1,2, K1,3, K2,4, K3,4) the macroscopic dissociation constant K2 is four times larger than the macroscopic dissociation constant K1 (K2 = 4*K1).
MnCl2 PRE experiments
Paramagnetic relaxation enhancement (PRE) effects caused by paramagnetic Mn2+ ions were analyzed for the observable imino groups within the 4U-hp2-wt RNA. [1H-15N]-HSQC spectra of the imino region of a 4U-hp2-wt RNA sample were recorded in NMR buffer in the presence of 5 mM MgCl2 at MnCl2 concentrations of 0 and 4 µM. Experiments were performed at a temperature of 10°C and a B0 field strength of 900 MHz (21.14 T). The recycling delay was set to 3 s. Remaining acquisition parameters were identical to the MgCl2 titration experiments. PRE effects were quantified by intensity and line width analysis. Line width analysis was performed for the indirect 15N-dimension. Intensities and line widths were analyzed with Sparky 3.1.1.3. For the PRE analysis we plotted ln (I[0 µM]/I[4 µM]) for each observable imino signal and compared the results with the change in line width (υ[4 µM] – υ[0 µM]).
Co(NH3)3+6 NOESY experiment
To identify and localize Mg2+ outer sphere binding sites, a NOESY spectrum of a 4U-hp2-wt RNA sample in NMR buffer was recorded in the presence of 5 mM Co(NH3)3+6. Measurements were performed at a temperature of 10°C and a B0 field strength of 600 MHz (14.09 T) with a mixing time Tm of 150 ms. The spectrum was recorded with a spectral width of 15 ppm in the indirect dimension and 22 ppm in the direct dimension. A total of 896 increments were recorded in the t1 dimension and 2048 points in the t2-dimension. Each increment was recorded with 128 scans.
RNA preparation
Unlabeled and 15N-labeled RNA oligonucleotides were synthesized by in vitro transcription with T7 RNA polymerase from linearized plasmid DNA templates and purified as described previously (45). 15N-labeled nucleotides were purchased from Silantes (Munich, Germany), unlabeled nucleotides were purchased from Sigma Aldrich (St. Louis, MO, USA).
RNAs were desalted using Vivaspin 20 concentrators with a molecular weight cutoff (MWCO) of 3000 Da from Sartorius stedim biotech (Aubagne Cedex, France). RNA refolding was achieved by denaturing for 10 min at a concentration of 0.25 mM and a temperature of 95°C followed by 20-fold dilution with ice cold water and subsequent incubation at 0°C for another 30 min. RNAs were concentrated and exchanged to NMR buffer using Vivaspin 20 concentrators (MWCO = 3000 Da). The NMR buffer contained 15 mM KxHyPO4 (pH 6.5), 25 mM KCl, 90% H2O and 10% D2O. Correct RNA folding was verified by native polyacrylamide gel electrophoresis.
Native gel electrophoresis
The 5× loading buffer was composed of 87% glycerole, 0.1% (w/v) xylene cyanole FF and 0.1% (w/v) bromophenol blue. The 1× running buffer contained 50 mM Tris–acetate and 50 mM sodium phosphate (pH 8.3). Gels were cast using 15% acrylamide with an acrylamide:bisacrylamide ratio of 37.5:1. Running conditions were set as follows: U = 70 V, P < 0.5 W for 4 h, water cooling to prevent heating. Gels were stained with ethidium bromide.
CD spectroscopy
CD melting and refolding curves were recorded with a JASCO spectropolarimeter J-810 at a wavelength of 258 nm. The RNA concentration was adjusted to 25 µM. Buffer conditions: 15 mM KxHy(PO4), 25 mM KCl, pH 6.5. Melting curves were recorded with a temperature slope of 1°C/min (4U-hp2-wt: 5-90°C; 4U-hp2-G14A-C25U-mutant: 2-80°C; 4U-hp2-A8C-mutant: 10-90°C) and refolding curves with a temperature slope of −1°C/min (4U-hp2-wt: 90-5°C; 4U-hp2-G14A-C25U-mutant: 80-2°C; 4U-hp2-A8C-mutant: 90-10°C). CD melting and refolding curves were normalized according to Equation (9) and thermodynamic parameters (ΔHunf, ΔSunf, ΔGunf and Tm) were derived from Equations (10) to (12).
Assuming the RNA to be either folded or unfolded (two-state model), the fraction of unfolded RNA can be expressed by
| (8) |
The fraction of unfolded RNA α is varying with temperature. This temperature dependence of α can be determined from the temperature dependence of the ellipticity at a wavelength of 258 nm according to Equation (9)
| (9) |
In Equation (9), θ(T) is the measured temperature-dependent ellipticity, θunfolded(T) and θfolded(T) are the ellipticities of the unfolded and the folded state of the RNA, respectively. θunfolded(T) and θfolded(T) are also slightly temperature-dependent and are therefore approximated linearly. From the resulting α(T) dependence, the molar unfolding enthalpy ΔHunf can be calculated (46) according to Equation (10). The melting point Tm is defined as the temperature at which 50% of the RNA is unfolded (α = 0.5). In case of perfect sigmoidality, the slope of the α(T) curve is maximal at this temperature
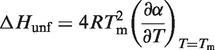 |
(10) |
In Equation (11), R is the gas constant, Tm the melting temperature, α the fraction of unfolded RNA and ΔHunf the molar unfolding enthalpy of the RNA. From ΔHunf, the molar unfolding entropy ΔSunf can be calculated according to Equation (11)
| (11) |
From the Gibbs–Helmholtz Equation (12), the molar free energy ΔGunf can be calculated, if one assumes ΔHunf and ΔSunf to be temperature-independent
| (12) |
Mg2+-dependence of the RNA melting point Tm
The RNA melting point Tm can be determined by CD spectroscopy. Assuming Tm([Mg]) to be linearly dependent on the fraction of RNA bound to Mg2+ [Equation (13)], the free energy ΔGCD of Mg2+ binding to the RNA can be calculated according to Equation (14):
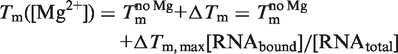 |
(13) |
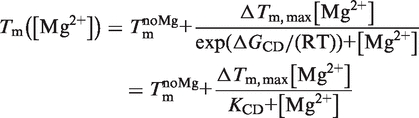 |
(14) |
In Equation (14), Tm is the melting point of the RNA, 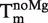 is the melting point in the absence of Mg2+ ions,
is the melting point in the absence of Mg2+ ions, 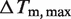 is the maximal change in Tm caused by Mg2+, [Mg2+] is the Mg2+ concentration, KCD is the RNA:Mg2+ dissociation constant and ΔGCD is the free energy of Mg2+ binding.
is the maximal change in Tm caused by Mg2+, [Mg2+] is the Mg2+ concentration, KCD is the RNA:Mg2+ dissociation constant and ΔGCD is the free energy of Mg2+ binding.
bgaB reporter gene assay
Three different translational fusion constructs have been used to study the temperature dependence of gene expression in E. coli using the ß-galactosidase gene bgaB as reporter. Constructs were designed by introducing the temperature sensitive hairpin 2 of the 5′-UTR of the Salmonella agsA gene in front of the heat stable ß-galactosidase gene bgaB utilizing an EcoRI restriction site (underlined in the sequences).
The 4U-hp2-wt construct contains the second hairpin of the fourU (4U) RNA thermometer (41) in an optimized vector. Sequence: aGCGTTGAACTTTTGAATAGTGATTCAGGAGGTTAATGATGGCAGAATTC~bgaB. The 4U-hp2-A8C-mutant construct differs from the wild-type construct by an A to C mutation (highlighted boldly). Sequence: aGCGTTGACCTTTTGAATAGTGATTCAGGAGGTTAATGATG GCAGAATTC~bgaB. In the 4U-hp2-G14A-C25U-mutant the G14-C25 base pair is exchanged to an A14-U25 base pair (highlighted boldly). Sequence: aGCGTTGAACTTTTAAATAGTGATTTAGGAGGTTAATGATGGCAGAATTC~bgaB. An amount of 25 ml LB-Amp (150 µg/ml), pre-warmed in a shaker to 30°C were inoculated with 1.5 ml over night culture (5 ml grown at 30°C) of DH5α cells containing the plasmids. Cells were grown to an optical density (OD600) of 0.5. After induction of transcripts with 25 µl l-arabinose (10%), 8 ml of the culture were shifted to two pre-warmed, shaking flasks at different temperatures, respectively. After 30 min cells were used for the enzymatic assay as described before (47). To compare the different measurements the expression value for the wt at 30°C was set to 1, respectively.
RESULTS AND DISCUSSION
Hairpin stability of the fourU thermometer inversely correlates with gene expression
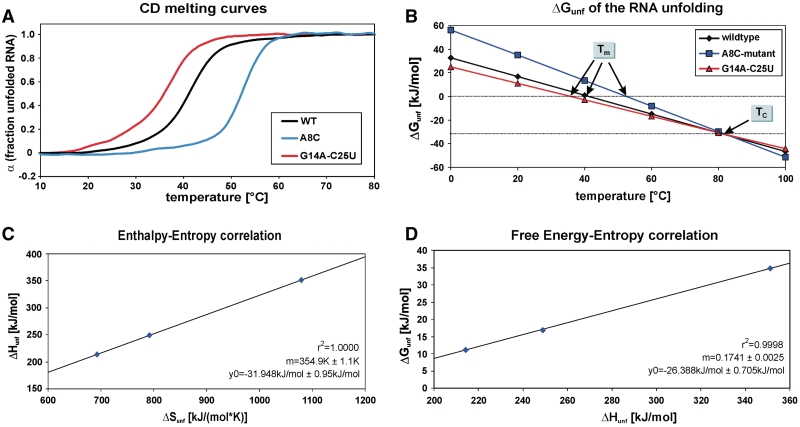
In our previous study, we determined base-pair stabilities of hairpin 2 (4U-hp2-wt, Figure 2B), which represents the temperature responsive hairpin of the Salmonella fourU thermometer, in comparison with a stabilized point mutant (4U-hp2-A8C-mutant), in which the AG mismatch of the wt structure was replaced by a CG pair (Figure 2A). From this study, we concluded that the G14–C25 base pair is by far the most stable base pair in the thermometer hairpin and has a stabilizing effect on the secondary structure of the entire RNA helix (39). Thus, substitution of this stable GC base pair into a less stable AU base pair (Figure 2C) is predicted to result in a significant reduction of the thermal stability of the 4U-hp2 RNA. CD unfolding curves recorded on the G14A–C25U double mutant indeed confirmed the expected behavior (Figure 3A). The GC to AU exchange resulted in a melting point Tm of 35.9°C, which is 5.2°C lower than the Tm value of the wild-type RNA and 16.3°C lower than the 4U-hp2-A8C mutant RNA (Figure 3A and B). Tm values for the three RNAs under investigation are given in Table 1.
Figure 3.
(A) Fraction of unfolded RNA α calculated from the CD melting curves according to Equation (9) of the 4U-hp2-wt RNA (black line), 4U-hp2-A8C mutant RNA (blue line) and the 4U-hp2-G14A-C25U double mutant RNA (red line) (B) ΔGunf(T) curves for the global unfolding of the 4U-hp2-wt RNA (black), A8C mutant RNA (blue) and the 4U-hp2-G14A-C25U double mutant RNA (red). ΔGunf(T) values were calculated from the corresponding ΔHunf and ΔSunf values (Table 1) according to the Gibbs–Helmholtz equation. Tm indicates the three different melting points (α = 0.5) of the three RNAs, respectively. Tc = 354.9 K represents the compensation temperature at which all three RNAs have the same stability. (C) Enthalpy–entropy correlation for the global RNA unfolding determined from the three 4U-hp2 RNAs under investigation. (D) Free energy–entropy correlation of the global RNA unfolding (T = 20°C) determined for the three 4U-hp2 RNAs analyzed. Linear correlations in (C) and (D) were fitted according to the linear equation f = y0 + mx. Fitting results are represented within the figures (C) and (D), respectively.
Table 1.
Thermodynamic parameters ΔHunf, ΔSunf, ΔGunf (T = 20°C) and Tm for the global unfolding of the 4U-hp2-wt, 4U-hp2-A8C-mutant and 4U-hp2-G14A-C25U-mutant RNAs
| ΔHunf (kJ/mol) | ΔSunf [J/(mol*K)] | ΔGunf (kJ/mol) (T = 20°C) | Tm (°C) | |
|---|---|---|---|---|
| Wild-type | 248.9 | 792.0 | 16.75 | 41.1 |
| G14A-C25U mutant | 214.2 | 692.9 | 11.05 | 35.9 |
| A8C mutant | 351.1 | 1079 | 34.81 | 52.2 |
Reversible melting and refolding of an RNA thermometer has recently been shown to be physiologically important for fitness of a cyanobacterium (48). CD unfolding and refolding curves demonstrated a similar full reversibility of the unfolding transition of all three fourU hairpins investigated in the current study since start and end points of unfolding and refolding curves are identical (Supplementary Figures S1–S3). However, unfolding and refolding curves slightly differ due to disturbance of the equilibrium caused by the continuous temperature change during the temperature scan. For the subsequent analysis, melting and refolding curves were averaged (the averaged curve will be referred to as unfolding curve from now on) to derive the unfolding curve under equilibrium conditions. Unfolding curves were normalized according to Equation (9) and α(T) values were determined assuming a two–state model (folded; unfolded) for RNA unfolding. The thermodynamic parameters ΔHunf, ΔSunf and ΔGunf were derived according to Equations (10–12) from the α(T) curves shown in Figure 3A. ΔHunf, ΔSunf, ΔGunf and Tm values for the three RNAs under investigation are given in Table 1.
From the ΔHunf and ΔSunf values, the corresponding ΔGunf(T) curves can be calculated according to the Gibbs–Helmholtz equation. These ΔGunf(T) curves are illustrated for the wild-type RNA and the two mutants in Figure 3B. Remarkably, all three ΔGunf(T) curves exhibit an intersection point at Tc = 81.8°C. At this temperature, the three RNAs possess the same stability ΔGunf(81.8°C) = −31.94 kJ/mol. At Tc, the unfolded RNA is almost exclusively populated since it is then much more stable than the folded conformation. The existence of an intersection point of the ΔGunf(T) curves is a consequence of the linear enthalpy–entropy correlation of the global unfolding transition which is depicted in Figure 3C. The slope of the ΔHunf(ΔSunf) correlation is equal to m = 354.9 K and the ordinate intercept was determined to be y0 = −31.95 ± 0.95 kJ/mol. Linear enthalpy–entropy correlations for global unfolding transitions have been reported earlier by Searle and Williams (49) and by Petruska (50) for DNA duplexes. There is also a strong linear correlation between ΔGunf and ΔHunf (Figure 3D) in the fourU RNA thermometer. The slope of this correlation is temperature-dependent and is illustrated for a temperature of 20°C.
Insertion of the enthalpy–entropy correlation into the Gibbs–Helmholtz equation results in the following equation:
| (15) |
At the compensation temperature (Tc = m), enthalpy and entropy contributions of the RNA-solvent interaction cancel each other and only the RNA–RNA interactions remain and equal y0.
Helix unfolding can be approximated according to Searle and Williams (49) by the following equation
| (16) |
At Tc, this leads to the following relation
| (17) |
ΔGunf(Tc) is affected by the increase in entropy upon unfolding, mainly caused by the gain of rotational freedom in the RNA backbone ΔSrotation and the loss of stacking interactions between neighboring nucleobases ΔHstacking. At the compensation temperature Tc, the absolute value of the entropy term T*ΔS exceeds by far the absolute value of the enthalpy term ΔHstacking. Thus, the RNA is almost completely unfolded at Tc (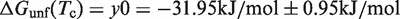 ).
).
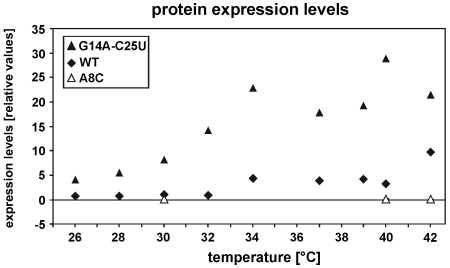
In order to test whether the in vitro observations correlate with translational control in vivo, the 4U-hp2-wt RNA, the 4U-A8C RNA and the 4U-G14A-C25U RNA were analyzed in the bgaB reporter gene assay as described previously (41). The 5′-UTRs were cloned 5′-upstream of the bgaB reporter gene downstream of an arabinose-inducible promoter and transformed into E. coli DH5α cells. Transcription was initiated with 0.01% (w/v) of l-arabinose and translation at various temperatures was followed by determination of β-galactosidase activity. Expression levels were normalized to the expression of the 4U-hp2-wt sequence at 30°C. The gene expression curves were consistent with the in vitro data in that the least stable G14A–C25U mutant led to derepressed, permanently elevated reporter gene expression even at low temperatures (Figure 4). The wild-type 5′-UTR allowed intermediate gene expression at elevated temperatures whereas the stable A8C mutant blocked gene expression completely. The combined in vivo and in vitro results show that seemingly minor mutational alterations can have a very significant effect on RNA stability and functionality of a regulatory RNA element. By switching from the stable A8C sequence to the unstable G14A–C25U sequence, gene expression levels can be increased by factors up to 150. In addition, the wild-type RNA as well as the G14A–C25U RNA are able to induce gene expression in response to a temperature shift from 30°C to 42°C by factors of 8.6 (wt) and 3.9 (mut) (Figure 4). Induction factors of at least 3.5 are described for functional thermoregulators (48,51–53) and an overall enhanced reporter gene expression for mutants with slightly destabilized structures has also been observed for the ibpA thermometer from E. coli (51). Therefore both agsA-5′-UTR-variants, wild-type and G14A–C25U, consisting only of the second hairpin of the natural occurring agsA thermometer, work well as control elements in the physiological range of living cells. We observed correlation between hairpin stability determined in vitro and gene repression levels measured in vivo. Interestingly, gene expression levels start to increase at temperatures significantly lower than the melting point determined in vitro. Apparently, translation initiation already occurs even at temperatures where only a minor fraction of RNA thermometers are unfolded.
Figure 4.
Temperature dependent expression of the agsA-(4U-hp2)-bgaB fusion in DH5α E. coli cells. Following RNA constructs were investigated: 4U-hp2-wt (filled diamonds), 4U-hp2-A8C-mutant (open triangles), 4U-hp2-G14A-C25U (filled triangles). Expression levels were referenced to the respective expression level of the 4U-hp2-wt at 30°C which was set to 1.
Curvatures of the temperature dependent gene expression curves in vivo (Figure 4) differ from the CD unfolding curves measured in vitro (Figure 3A and B). Additional effects to the accessibility of the SD sequence seem to modify the gene expression in vivo. Other possible factors like the temperature dependence of transcription, RNA degradation or translation initiation may have additional modulating effects that superimpose the initial RNA thermometer effect.
Mg2+-dependence of the melting point
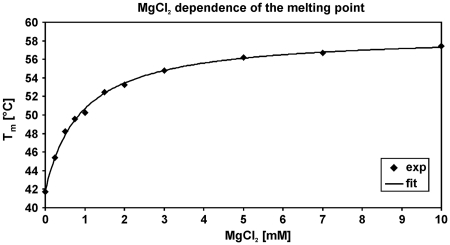
One well-known factor that contributes to folding of complex RNA structures is Mg2+. In addition, based on the sequence of the fourU thermometer, a Mg2+ binding site can be predicted (32). To examine whether this ion plays a structural and functional role in the fourU thermometer, we monitored the Mg2+ dependence of the melting point Tm of the 4U-hp2-wt RNA by CD spectroscopy. The Tm(Mg2+) dependence was fitted by Equation (14) (Figure 5) and ΔGCD, ΔTm,max and 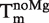 values were derived (Table 2).
values were derived (Table 2).
Figure 5.
Tm melting point dependence of the 4U-hp2-wt RNA on the MgCl2 concentration. Data points are given as filled diamonds while the fit according to Equation (14) is illustrated as continuous line.
Table 2.
Fitting results of the Tm(Mg2+) dependence of the 4U-hp2-wt RNA according to Equation (14)
| 4U-hp2-wt |
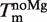 (°C) (°C) |
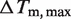 (°C) (°C) |
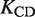 (µM) (µM) |
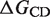 (kJ/mol) (kJ/mol) |
|---|---|---|---|---|
| 41.77 ± 0.22 | 16.93 ± 0.25 | 899a ± 47.9 | −18.860 ± 0.14 |
aKCD was calculated for a temperature of 50.24°C. Errors are derived from the fit.
The Tm(Mg2+) dependence can be described by a model which assumes only a single binding site. NMR experiments, however, provide evidence for two Mg2+ binding sites (see below). Since Mg2+ binding to these sites is cooperative (see below), the 4U-hp2-wt RNA exists most prominently in either the free form or the ternary complex ([Mg2+*RNA*Mg2+]) but rarely in one of the binary complexes ([Mg2+*RNA] or [RNA*Mg2+]). Thus, the Tm(Mg2+) curve exhibits hyperbolic shape and the ΔGCD value determined from the Tm(Mg2+)-dependence represents the free binding energy between free RNA and ternary [Mg2+*RNA*Mg2+] complex. In addition, we can show that the temperature dependence of Tm is caused by specific and not by diffuse Mg2+ binding (Supplementary Data: Evidence for defined Mg2+ binding). The fact that the temperature dependence is dominated by defined Mg2+ binding does not rule out the possibility of additional diffuse binding. However, according to our data the effects of diffuse Mg2+ binding are small in comparison to the effects caused by specific binding, at least in the concentration range observed here (0–7 mM).
The Mg2+ dependence of Tm observed in vitro indicates a potential effect of fluctuating Mg2+ concentrations within the cell on expression levels of genes under the control of the fourU RNA thermometer. According to the literature, the free intracellular Mg2+ concentration may vary between 1 and 2 mM (14,18). Such a shift in Mg2+ concentration causes a shift of the Tm value of the 4U-hp2-wt RNA by 2.8°C (Figure 5). Thus, varying Mg2+ concentration will most probably have a modulating temperature-independent effect on RNA-thermometer-controlled gene expression in vivo.
Localization of the Mg2+ binding sites
We applied different NMR methods to identify Mg2+ binding sites in the 4U-hp2-wt RNA. First, a NOESY experiment of a 4U-hp2-wt RNA sample in the presence of  ions was performed to identify and localize
ions was performed to identify and localize  binding sites.
binding sites.  ions serve as mimic for hexahydrated Mg2+ ions and therefore map binding sites for outer sphere coordinated Mg2+ ions (28,29,32). Second, we analyzed the PRE effects of the imino signals occurring upon the addition of paramagnetic Mn2+ ions to the 4U-hp2-wt RNA sample (28,29). The fact that substoichiometric amounts of Mn2+ are sufficient to cause significant line broadening of imino signals in close proximity to Mg2+ binding sites reveals that Mg2+ ions are in rapid exchange with free divalent ions. The use of Mn2+ as probe for Mg2+ is supported by the observation that 76% of the intracellular Mg2+ ions in prokaryotes (E. coli) can be substituted by Mn2+ ions without severely impairing viability of the cells (18). Third, we followed CSPs of the imino signals during Mg2+ titration experiments (28,29). Fitting of the obtained CSP curves was performed to derive KD values for Mg2+ binding. By taking the results of these three complementary techniques into account, it became possible to unravel the different effects on how Mg2+ ions interact with the 4U-hp2-wt RNA. Combination of the information yields a consistent overall picture on the effects of Mg2+ ions on the 4U-hp2-wt RNA.
ions serve as mimic for hexahydrated Mg2+ ions and therefore map binding sites for outer sphere coordinated Mg2+ ions (28,29,32). Second, we analyzed the PRE effects of the imino signals occurring upon the addition of paramagnetic Mn2+ ions to the 4U-hp2-wt RNA sample (28,29). The fact that substoichiometric amounts of Mn2+ are sufficient to cause significant line broadening of imino signals in close proximity to Mg2+ binding sites reveals that Mg2+ ions are in rapid exchange with free divalent ions. The use of Mn2+ as probe for Mg2+ is supported by the observation that 76% of the intracellular Mg2+ ions in prokaryotes (E. coli) can be substituted by Mn2+ ions without severely impairing viability of the cells (18). Third, we followed CSPs of the imino signals during Mg2+ titration experiments (28,29). Fitting of the obtained CSP curves was performed to derive KD values for Mg2+ binding. By taking the results of these three complementary techniques into account, it became possible to unravel the different effects on how Mg2+ ions interact with the 4U-hp2-wt RNA. Combination of the information yields a consistent overall picture on the effects of Mg2+ ions on the 4U-hp2-wt RNA.
The imino region of the 2D-1H-1H NOESY spectrum of the 4U-hp2-wt RNA in the presence of 5 mM  ions is given in Figure 6. Protons from
ions is given in Figure 6. Protons from  exhibit strong cross peaks to the imino protons of the nucleobases U11, U12, G27 and/or G28 and weak cross peaks to the imino protons of the adjacent nucleobases U10 and U13. Thus, a binding site for
exhibit strong cross peaks to the imino protons of the nucleobases U11, U12, G27 and/or G28 and weak cross peaks to the imino protons of the adjacent nucleobases U10 and U13. Thus, a binding site for  is located in close proximity to the nucleobases U11, U12, G27 and G28, most probably in the major groove of the RNA helix very similar to the binding site described for the structure of the P5b hairpin of the group I intron by Kieft and Tinoco (32).
is located in close proximity to the nucleobases U11, U12, G27 and G28, most probably in the major groove of the RNA helix very similar to the binding site described for the structure of the P5b hairpin of the group I intron by Kieft and Tinoco (32).
Figure 6.
Section from the 2D-1H NOESY experiment performed on a 0.9-mM 4U-hp2-wt RNA sample in the presence of 5 mM [(Co(NH3)6]3+. Assignments of cross signals between protons of the  and the imino protons of the RNA are given within the spectrum. On top of the NOESY spectrum, the corresponding imino region of the 1H-1D NMR spectrum is given. Buffer conditions: 15 mM KxHyPO4 (pH 6.5), 25 mM KCl, 90% H2O and 10% D2O.
and the imino protons of the RNA are given within the spectrum. On top of the NOESY spectrum, the corresponding imino region of the 1H-1D NMR spectrum is given. Buffer conditions: 15 mM KxHyPO4 (pH 6.5), 25 mM KCl, 90% H2O and 10% D2O.
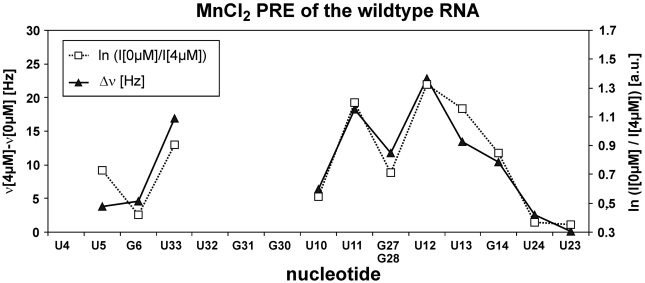
PRE effects of the imino signals caused by the addition of Mn2+ ions were analyzed in order to reveal divalent cation binding sites. For that purpose, [1H,15N]-HSQCs of the imino region of the 4U-hp2-wt RNA sample were recorded and line shapes and intensities of the imino signals were analyzed to quantify the PRE effects. Changes in line widths and signal intensities caused by the addition of 4 µM Mn2+ are given in Figure 7. Large PRE effects were observed for the nucleobases U11 and U12 within the RNA helix. In addition, the nucleobases U13, G14 and U33 also show significant PRE effects, while the imino signal of nucleobase U10 exhibits only a very weak PRE effect. Interestingly the G27/G28 double signal only shows a moderate PRE effect in comparison to U11, U12 and U13 which is consistent with binding of  in the major groove.
in the major groove.
Figure 7.
PRE of the imino resonances of the 4U-hp2-wt RNA observed upon the addition of 4 µM MnCl2. Changes in line widths Δν [Hz] in the 15N-dimension are illustrated as filled triangles (continuous line) with the corresponding scale on the left hand side of the diagram and changes in intensity (ln(I[0 µM]/I[4 µM]) [a.u.]) are illustrated as open squares (dotted line) with the corresponding scale on the right hand side. U32 and G31 do not give rise to any observable imino signals and the imino signals of G30 and U4 are too weak to be analyzed.
Taken together, the PRE analysis reveals the existence of a Mn2+ binding site within the 4U-hp2-wt RNA which is located in close proximity to the nucleobases U11, U12 and U13. This Mn2+ binding site represents a strong indication for the existence of a Mg2+ binding site at exactly the same position within the 4U-hp2-wt RNA. Furthermore, PRE analysis and  NOESY data reveal binding sites in the same region of the RNA leading to the conclusion that there is one specific outer sphere Mg2+ binding site within the fourU motif of the 4U-hp2-wt RNA. Moderate PRE effects of the nucleobases G27/G28 are in agreement with localization of this binding site within the major groove.
NOESY data reveal binding sites in the same region of the RNA leading to the conclusion that there is one specific outer sphere Mg2+ binding site within the fourU motif of the 4U-hp2-wt RNA. Moderate PRE effects of the nucleobases G27/G28 are in agreement with localization of this binding site within the major groove.
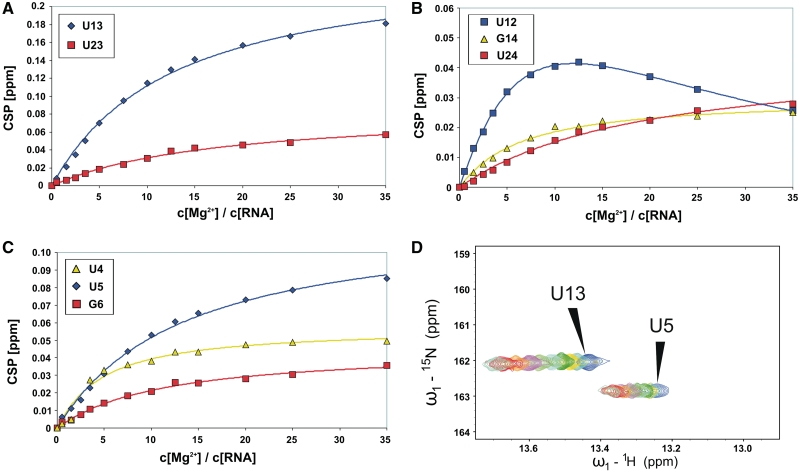
Finally, we titrated 4U-hp2-wt RNA with Mg2+ ions and analyzed the occurring CSPs of the imino group region within the [1H,15N]-HSQC spectra. CSP([Mg2+]) curves were fitted according to Equation (2) and KD values were derived. Figure 8 shows Mg2+-dependent CSPs of the imino groups with their respective fits (continuous lines). In Figure 8D, the shifting signals of the imino groups U5 and U13 within the [1H-15N]-HSQC during the titration of the RNA with MgCl2 are shown exemplarily. Fitting results are summarized in Supplementary Table S1. Interestingly, different Kdiss values are obtained for different imino signals. Lowest Kdiss values are found for U4 (0.85 ± 0.18) and G14 (1.17 ± 0.12 mM). Nucleotides U5, G6 and U13 exhibit Kdiss values of around 2.34 mM and the nucleotides U23 and U24 show Kdiss values of ~3.56 mM. U13 shows by far the largest CSPmax value (0.250 ± 0.008 ppm).
Figure 8.
(A–C) CSPs of the imino resonances of the nucleobases U13, U23, G14, U24, U4, U5 and G6 plotted against the [Mg2+]/[RNA] ratio and fitted according to Equation (2) (continuous lines). CSPs of the imino signal U12 (B) were fitted by Equation (3) (D) Mg2+-dependent changes (CSPs) of the imino groups U13 and U5 within the [1H,15N]-HSQC spectrum (titration steps: see ‘Materials and Methods’ section).
Multiple conformations of a [RNA*Mg2+]-complex assuming only a single Mg2+ binding site fail to explain the observed diversity in Kdiss values as explained in the Supplementary Data (Mg2+ binding model for one binding site but different conformations of the [RNA*Mg2+] complex).
In addition, the CSP curve of U12 shows a distinct biphasic behavior. We argue that this behavior can only be explained by two different Mg2+ binding sites. The model describing the binding properties of an RNA molecule with two different Mg2+ binding sites is given in Figure 1. The dissociation constants derived from the biphasic fit (CSP curve of U12) can be assigned to the macroscopic dissociation constants K1 (3.58 mM) and K2 (2.06 mM). Since the observed CSP curves cannot be explained by negative cooperativity (negative cooperativity would lead to negative microscopic dissociation constants), cooperativity has to be positive. In such model, the smallest dissociation constants derived by monophasic fitting have to be purely monophasic and correspond to one of the microscopic dissociation constants K2,4 and K3,4. Thus, K2,4 was set to 1.17 ± 0.12 mM (G14) and K3,4 to 0.85 ± 0.18 mM (U4) as derived from monophasic fitting of the CSP curves (Figure 8 and Supplementary Table S1). However, an assignment of the microscopic dissociation constant K2,4 (1.17 mM) or the microscopic dissociation constant K3,4 (0.89 mM) to the outer sphere Mg2+ binding site within the fourU motif is not possible. According to the equations connecting the different dissociation constants (Figure 1), the microscopic dissociation constants K1,2 and K1,3 could be derived (Table 3). Free energy values for Mg2+ binding ΔGK1 and ΔGK2 at a temperature of 10°C as well as the free energy for ternary [Mg2+*RNA*Mg2+] complex formation ΔGges are given in Table 3.
Table 3.
Thermodynamic parameters of Mg2+ binding as well as macroscopic and microscopic dissociation constants of the two-binding-site-model (Figure 1)
| Kdiss (mM) | |
|---|---|
| K1 | 3.58 ± 0.67 mM |
| K2 | 2.06 ± 0.66 mM |
| K2,4 | 1.17 ± 0.12 mM |
| K3,4 | 0.85 ± 0.12 mM |
| K1,2 | 6.31 ± 2.43 mM |
| K1,3 | 8.68 ± 3.71 mM |
| ΔGK1 (10°C) | −13.262 ± 0.446 kJ/mol |
| ΔGK2 (10°C) | −14.556 ± 0.780 kJ/mol |
| ΔGges (10°C) | −27.818 ± 0.899 kJ/mol |
| ΔGCD (50.24°C) | −18.860 ± 0.143 kJ/mol |
| ΔGges (37°C) | −21.807 ± 0.443 kJ/mol |
| ΔHges | −90.855 ± 6.469 kJ/mol |
| T*ΔSges (10°C) | −63.037 ± 6.404 kJ/mol |
ΔGK1, ΔGK2 and ΔGges were calculated for a temperature of 10°C. ΔGCD (50.24°C) was derived from CD melting studies. ΔHges, T*ΔSges and ΔGges (37°C) were calculated from the difference of ΔGges (10°C) and ΔGCD (50.24°C). Errors in K1, K2, K2,4, K3,4 and KCD (Table 2) are statistical errors resulting from the fit. Errors in K1,2, K1,3, ΔGK1 (10°C), ΔGK2 (10°C), ΔGges (10°C), ΔGCD (50.24°C), ΔHges and T*ΔSges (10°C) are Gaussian errors calculated by error propagation.
The macroscopic dissociation constant K1 is notably larger than K2 although formation of the binary complex is statistically favored over the formation of the ternary complex. The resulting microscopic dissociation constants connecting the free RNA and the binary complexes K1,2 (6.31 mM) and K1,3 (8.26 mM) are much larger than the corresponding dissociation constants K2,4 (1.17 mM) and K3,4 (0.89 mM) connecting the binary complexes with the ternary complex. In other words, binding of one Mg2+ ion promotes binding of the second Mg2+ ion (positive cooperativity). According to the determined dissociation constants (Table 3), we determine a Hill coefficient b = 1.47 (Supplementary Figure S4). This intermediate positive cooperativity is in line with positive cooperativity values for Mg2+ binding to tRNAPhe reported in the literature (b = 1.7) (54). A description how two Mg2+ binding sites may lead to the observed variety of monophasic CSP curves is given in the Supplementary Data (Qualitative explanation of the observed CSP curves using a two binding site model).
From the Mg2+ dependence of the melting point Tm determined by CD spectroscopy (Figure 5 and Table 2), the free energy for Mg2+ binding ΔGCD at a temperature of 50.24°C was determined. Assuming that Mg2+ only binds to the folded but not to the unfolded RNA ΔGCD is equal to ΔGges. From the difference of ΔGges (T = 10°C) and ΔGCD (T = 50.24°C), ΔHges and T*ΔSges (10°C) were calculated according to the Gibbs–Helmholtz equation assuming that ΔHges and ΔSges are not temperature-dependent. Results are given in Table 3.
The T*ΔSges value (−63.037 ± 6.404 kJ/mol) indicates that the Mg2+-bound state exhibits a higher degree of order than the free RNA which appears reasonable since in the ternary [Mg2+*RNA*Mg2+] complex, rotational and translational degrees of freedom of the hexahydrated Mg2+ ions are reduced. In particular, binding of two hexahydrated Mg2+ ions to the RNA molecule is accompanied by the loss of three rotational and three translational degrees of freedom per hexahydrated Mg2+ ion while the loss of one degree of freedom reduces the entropy by ½ R. However, this accounts only for 50 J/(mol*K) (2*6/2*R) which is far less than the observed change in entropy (ΔSges = 223 ± 23 J/(mol*K)). Thus, additional entropy reducing effects have to be present. Such effects might be caused by an increased conformational restriction of the RNA itself or by a higher degree of order in the water molecules involved. This energetically unfavorable entropy term is overcompensated by stabilizing ΔHges contributions (−90.855 ± 6.469 kJ/mol) which most probably result from energetically favorable Coulomb interactions.
Using ΔGCD (50.24°C) and ΔGges (10°C) values (Table 3), the free energy for Mg2+ binding ΔGges (37°C) calculates to −21.807 ± 0.443 kJ/mol. Such value indicates that most probably not more than two Mg2+ binding sites are involved since three or more Mg2+ binding sites would lead to a lower ΔGges value or to Kdiss values higher than those reported for diffuse binding (55). It may be noticed that the average ΔGges value that we obtained per magnesium binding site (−10.9 kJ/mol) is in surprisingly good agreement with the average value (~–11 kJ/mol) that can be derived from the difference in concentration of bound and free magnesium in vivo (13,14).
In summary, these results indicate the existence of two Mg2+ binding sites within the 4U-hp2-wt RNA. At least one of these binding sites is outer sphere coordinated and is located in proximity to the nucleobases U11, U12, G27 and G28 most probably within the major groove of the RNA. Although the existence of a second Mg2+ binding site is certain, it could not be localized unambiguously. PRE experiments suggest that it is near the nucleobase U33 (Figure 7). The fact that only one binding site could be located with  suggests that the second Mg2+ binding site might be inner sphere coordinated. However, it is also possible that the two binding sites are in such close proximity that they cannot be identified as two independent binding sites.
suggests that the second Mg2+ binding site might be inner sphere coordinated. However, it is also possible that the two binding sites are in such close proximity that they cannot be identified as two independent binding sites.
Using a combination of in vitro and in vivo experiments we show that fourU RNA thermometers are optimized in their sequence and Mg2+ binding properties. Two Mg2+ binding sites with positive cooperativity could be identified within the 4U-hp2-wt RNA, one of them as outer sphere binding site directly within the fourU motif as predicted from the secondary structure of this RNA (32). Mg2+ concentration has a modulating effect on the melting point of the fourU RNA thermometer and therefore most probably influences gene expression in vivo. From the in vivo experiments it became obvious that the onset of gene expression already occurs at temperatures significantly below the melting point. Apparently, a small fraction of RNA thermometers in the open conformation seems to be sufficient to efficiently permit translation initiation. In addition, the in vivo experiments reveal that already small changes in the temperature dependent stability (Tm) of the RNA thermometer lead to tremendous effects on gene expression of the downstream gene.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
State of Hesse (Center for Biomolecular Magnetic Resonance, BMRZ); DFG (priority program SPP 1258: Sensory and regulatory RNAs in prokaryotes). H.S. is member of the DFG-funded Cluster of Excellence: Macromolecular complexes. Funding for open access charge: DFG.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank one reviewer for the interesting and constructive discussions.
REFERENCES
- 1.Walker GM. The roles of magnesium in biotechnology. Crit. Rev. Biotechnol. 1994;14:311–354. doi: 10.3109/07388559409063643. [DOI] [PubMed] [Google Scholar]
- 2.Wood JM. Bacterial osmosensing transporters. Meth. Enzymol. 2007;428:77–107. doi: 10.1016/S0076-6879(07)28005-X. [DOI] [PubMed] [Google Scholar]
- 3.Shiman R, Draper DE. Stabilization of RNA tertiary structure by monovalent cations. J. Mol. Biol. 2000;302:79–91. doi: 10.1006/jmbi.2000.4031. [DOI] [PubMed] [Google Scholar]
- 4.Pyle AM. Metal ions in the structure and function of RNA. J. Biol. Inorg. Chem. 2002;7:679–690. doi: 10.1007/s00775-002-0387-6. [DOI] [PubMed] [Google Scholar]
- 5.Merlevede W, Vandenheede JR, Goris J, Yang SD. Regulation of ATP-Mg-dependent protein phosphatase. Curr. Top. Cell. Regul. 1984;23:177–215. [PubMed] [Google Scholar]
- 6.Brock TD. Effects of magnesium ion deficiency on Escherichia coli and possible relation to the mode of action of Novobiocin. J. Bacteriol. 1962;84:679–682. doi: 10.1128/jb.84.4.679-682.1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hughes MN, Poole RK. Metals and Microorganisms. London: Chapman and Hall; 1989. [Google Scholar]
- 8.Meers JL, Tempest DW. The influence of extracellular products on the behaviour of mixed microbial populations in magnesium-limited chemostat cultures. J. Gen. Microbiol. 1969;52:309–317. doi: 10.1099/00221287-52-2-309. [DOI] [PubMed] [Google Scholar]
- 9.Klein DJ, Moore PB, Steitz TA. The contribution of metal ions to the structural stability of the large ribosomal subunit. RNA. 2004;10:1366–1379. doi: 10.1261/rna.7390804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tempest DW, Strange RE. Variation in content and distribution of magnesium, and its influence on survival, in Aerobacter aerogenes grown in a chemostat. J. Gen. Microbiol. 1966;44:273–279. doi: 10.1099/00221287-44-2-273. [DOI] [PubMed] [Google Scholar]
- 11.Webb M. The influence of certain trace metals on bacterial growth and magnesium utilization. J. Gen. Microbiol. 1968;51:325–335. doi: 10.1099/00221287-51-3-325. [DOI] [PubMed] [Google Scholar]
- 12.Hurwitz C, Rosano CL. The intracellular concentration of bound and unbound magnesium ions in Escherichia coli. J. Biol. Chem. 1967;242:3719–3722. [PubMed] [Google Scholar]
- 13.Moncany ML, Kellenberger E. High magnesium content of Escherichia coli B. Experientia. 1981;37:846–847. doi: 10.1007/BF01985672. [DOI] [PubMed] [Google Scholar]
- 14.Alatossava T, Jutte H, Kuhn A, Kellenberger E. Manipulation of intracellular magnesium content in polymyxin B nonapeptide-sensitized Escherichia coli by ionophore A23187. J. Bacteriol. 1985;162:413–419. doi: 10.1128/jb.162.1.413-419.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lusk JE, Kennedy EP. Magnesium transport in Escherichia coli. J. Biol. Chem. 1969;244:1653–1655. [PubMed] [Google Scholar]
- 16.Lusk JE, Williams RJ, Kennedy EP. Magnesium and the growth of Escherichia coli. J. Biol. Chem. 1968;243:2618–2624. [PubMed] [Google Scholar]
- 17.Silver S. Active transport of magnesium in Escherichia coli. Proc. Natl Acad. Sci. USA. 1969;62:764–771. doi: 10.1073/pnas.62.3.764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Silver S, Clark D. Magnesium transport in Escherichia coli. J. Biol. Chem. 1971;246:569–576. [PubMed] [Google Scholar]
- 19.Nelson DL, Kennedy EP. Transport of magnesium by a repressible and a nonrepressible system in Escherichia coli. Proc. Natl Acad. Sci. USA. 1972;69:1091–1093. doi: 10.1073/pnas.69.5.1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Scribner H, Eisenstadt E, Silver S. Magnesium transport in Bacillus subtilis W23 during growth and sporulation. J. Bacteriol. 1974;117:1224–1230. doi: 10.1128/jb.117.3.1224-1230.1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hmiel SP, Snavely MD, Miller CG, Maguire ME. Magnesium transport in Salmonella typhimurium: characterization of magnesium influx and cloning of a transport gene. J. Bacteriol. 1986;168:1444–1450. doi: 10.1128/jb.168.3.1444-1450.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hmiel SP, Snavely MD, Florer JB, Maguire ME, Miller CG. Magnesium transport in Salmonella typhimurium: genetic characterization and cloning of three magnesium transport loci. J. Bacteriol. 1989;171:4742–4751. doi: 10.1128/jb.171.9.4742-4751.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Snavely MD, Florer JB, Miller CG, Maguire ME. Magnesium transport in Salmonella typhimurium: expression of cloned genes for three distinct Mg2+ transport systems. J. Bacteriol. 1989;171:4752–4760. doi: 10.1128/jb.171.9.4752-4760.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Snavely MD, Florer JB, Miller CG, Maguire ME. Magnesium transport in Salmonella typhimurium: 28Mg2+ transport by the CorA, MgtA, and MgtB systems. J. Bacteriol. 1989;171:4761–4766. doi: 10.1128/jb.171.9.4761-4766.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Snavely MD, Gravina SA, Cheung TT, Miller CG, Maguire ME. Magnesium transport in Salmonella typhimurium. Regulation of mgtA and mgtB expression. J. Biol. Chem. 1991;266:824–829. [PubMed] [Google Scholar]
- 26.Basu S, Rambo RP, Strauss-Soukup J, Cate JH, Ferre-D’Amare AR, Strobel SA, Doudna JA. A specific monovalent metal ion integral to the AA platform of the RNA tetraloop receptor. Nat. Struct. Biol. 1998;5:986–992. doi: 10.1038/2960. [DOI] [PubMed] [Google Scholar]
- 27.Butcher SE, Allain FH, Feigon J. Determination of metal ion binding sites within the hairpin ribozyme domains by NMR. Biochemistry. 2000;39:2174–2182. doi: 10.1021/bi9923454. [DOI] [PubMed] [Google Scholar]
- 28.Feigon J, Butcher SE, Finger LD, Hud NV. Solution nuclear magnetic resonance probing of cation binding sites on nucleic acids. Meth. Enzymol. 2001;338:400–420. doi: 10.1016/s0076-6879(02)38230-2. [DOI] [PubMed] [Google Scholar]
- 29.Gonzalez RL, Jr, Tinoco I., Jr Identification and characterization of metal ion binding sites in RNA. Meth. Enzymol. 2001;338:421–443. doi: 10.1016/s0076-6879(02)38231-4. [DOI] [PubMed] [Google Scholar]
- 30.Fürtig B, Richter C, Wöhnert J, Schwalbe H. NMR spectroscopy of RNA. Chembiochem. 2003;4:936–962. doi: 10.1002/cbic.200300700. [DOI] [PubMed] [Google Scholar]
- 31.Martin RB. In: Metal Ions in Biological Systems. Dekker M, editor. New York: 1990. [Google Scholar]
- 32.Kieft JS, TinocoI Solution structure of a metal-binding site in the major groove of RNA complexed with cobalt (III) hexammine. Structure. 1997;5:713–721. doi: 10.1016/s0969-2126(97)00225-6. [DOI] [PubMed] [Google Scholar]
- 33.Jack KD, Means JA, Hines JV. Characterizing riboswitch function: identification of Mg2+ binding site in T box antiterminator RNA. Biochem. Biophys. Res. Comm. 2008;370:306–310. doi: 10.1016/j.bbrc.2008.03.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Buck J, Noeske J, Wöhnert J, Schwalbe H. Dissecting the influence of Mg2+ on 3D architecture and ligand-binding of the guanine-sensing riboswitch aptamer domain. Nucleic Acids Res. 2010;38:4143–4153. doi: 10.1093/nar/gkq138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ramesh A, Winkler WC. Magnesium-sensing riboswitches in bacteria. RNA Biol. 2010;7:77–83. doi: 10.4161/rna.7.1.10490. [DOI] [PubMed] [Google Scholar]
- 36.Winkler WC, Breaker RR. Regulation of bacterial gene expression by riboswitches. Annu. Rev. Microbiol. 2005;59:487–517. doi: 10.1146/annurev.micro.59.030804.121336. [DOI] [PubMed] [Google Scholar]
- 37.Schwalbe H, Buck J, Fürtig B, Noeske J, Wöhnert J. Structures of RNA switches: insight into molecular recognition and tertiary structure. Angew. Chem. Int. E. Engl. 2007;46:1212–1219. doi: 10.1002/anie.200604163. [DOI] [PubMed] [Google Scholar]
- 38.Narberhaus F. Translational control of bacterial heat shock and virulence genes by temperature-sensing mRNAs. RNA Biol. 2010;7:84–89. doi: 10.4161/rna.7.1.10501. [DOI] [PubMed] [Google Scholar]
- 39.Rinnenthal J, Klinkert B, Narberhaus F, Schwalbe H. Direct observation of the temperature-induced melting process of the Salmonella fourU RNA thermometer at base-pair resolution. Nucleic Acids Res. 2010;38:3834–3847. doi: 10.1093/nar/gkq124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Neupert J, Karcher D, Bock R. Design of simple synthetic RNA thermometers for temperature-controlled gene expression in Escherichia coli. Nucleic Acids Res. 2008;36:e124. doi: 10.1093/nar/gkn545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Waldminghaus T, Heidrich N, Brantl S, Narberhaus F. FourU: a novel type of RNA thermometer in Salmonella. Mol. Microbiol. 2007;65:413–424. doi: 10.1111/j.1365-2958.2007.05794.x. [DOI] [PubMed] [Google Scholar]
- 42.Bodenhausen G, Ruben DJ. Natural abundance nitrogen-15 NMR by enhanced heteronuclear spectroscopy. Chem. Phys. Lett. 1980;69:185–189. [Google Scholar]
- 43.Sklenar V, Piotto M, Leppik R, Saudek V. Gradient-tailored water suppression for 1 H-15 N HSQC experiments optimized to retain full sensitivity. J. Magn. Reson., Series A. 1993;102:241–245. [Google Scholar]
- 44.Noeske J, Schwalbe H, Wöhnert J. Metal-ion binding and metal-ion induced folding of the adenine-sensing riboswitch aptamer domain. Nucleic Acids Res. 2007;35:5262–5273. doi: 10.1093/nar/gkm565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Stoldt M, Wöhnert J, Ohlenschläger O, Görlach M, Brown LR. The NMR structure of the 5 S rRNA E-domain-protein L25 complex shows preformed and induced recognition. EMBO J. 1999;18:6508–6521. doi: 10.1093/emboj/18.22.6508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Marky LA, Breslauer KJ. Calculating thermodynamic data for transitions of any molecularity from equilibrium melting curves. Biopolymers. 1987;26:1601–1620. doi: 10.1002/bip.360260911. [DOI] [PubMed] [Google Scholar]
- 47.Gaubig LC, Waldminghaus T, Narberhaus F. Multiple layers of control govern expression of the Escherichia coli ibpAB heat shock operon. Microbiology. 2011;157:66–76. doi: 10.1099/mic.0.043802-0. [DOI] [PubMed] [Google Scholar]
- 48.Kortmann J, Sczodrok S, Rinnenthal J, Schwalbe H, Narberhaus F. Translation on demand by a simple RNA-based thermosensor. Nucleic Acids Res. 2011;39:2855–2868. doi: 10.1093/nar/gkq1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Searle MS, Williams DH. On the stability of nucleic acid structures in solution: enthalpy-entropy compensations, internal rotations and reversibility. Nucleic Acids Res. 1993;21:2051–2056. doi: 10.1093/nar/21.9.2051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Petruska J, Goodman MF. Enthalpy-entropy compensation in DNA melting thermodynamics. J. Biol. Chem. 1995;270:746–750. doi: 10.1074/jbc.270.2.746. [DOI] [PubMed] [Google Scholar]
- 51.Waldminghaus T, Gaubig LC, Klinkert B, Narberhaus F. The Escherichia coli ibpA thermometer is comprised of stable and unstable structural elements. RNA Biol. 2009;6:455–463. doi: 10.4161/rna.6.4.9014. [DOI] [PubMed] [Google Scholar]
- 52.Morita MT, Tanaka Y, Kodama TS, Kyogoku Y, Yanagi H, Yura T. Translational induction of heat shock transcription factor sigma32: evidence for a built-in RNA thermosensor. Genes Dev. 1999;13:655–665. doi: 10.1101/gad.13.6.655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Nocker A, Hausherr T, Balsiger S, Krstulovic NP, Hennecke H, Narberhaus F. A mRNA-based thermosensor controls expression of rhizobial heat shock genes. Nucleic Acids Res. 2001;29:4800–4807. doi: 10.1093/nar/29.23.4800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Labuda D, Nicoghosian K, Cedergren R. Cooperativity in low-affinity Mg2+ binding to tRNA. J. Biol. Chem. 1985;260:1103–1107. [PubMed] [Google Scholar]
- 55.Laing LG, Gluick TC, Draper DE. Stabilization of RNA Structure by Mg Ions - Specific and Nonspecific Effects. J. Mol. Biol. 1994;237:577–587. doi: 10.1006/jmbi.1994.1256. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.