CSAR Benchmark Exercise of 2010: Combined Evaluation Across All Submitted Scoring Functions

Abstract

As part of the Community Structure-Activity Resource (CSAR) center, a set of 343 high-quality, protein–ligand crystal structures were assembled with experimentally determined K_d or K_i information from the literature. We encouraged the community to score the crystallographic poses of the complexes by any method of their choice. The goal of the exercise was to (1) evaluate the current ability of the field to predict activity from structure and (2) investigate the properties of the complexes and methods that appear to hinder scoring. A total of 19 different methods were submitted with numerous parameter variations for a total of 64 sets of scores from 16 participating groups. Linear regression and nonparametric tests were used to correlate scores to the experimental values. Correlation to experiment for the various methods ranged R² = 0.58–0.12, Spearman ρ = 0.74–0.37, Kendall τ = 0.55–0.25, and median unsigned error = 1.00–1.68 pK_d units. All types of scoring functions—force field based, knowledge based, and empirical—had examples with high and low correlation, showing no bias/advantage for any particular approach. The data across all the participants were combined to identify 63 complexes that were poorly scored across the majority of the scoring methods and 123 complexes that were scored well across the majority. The two sets were compared using a Wilcoxon rank-sum test to assess any significant difference in the distributions of >400 physicochemical properties of the ligands and the proteins. Poorly scored complexes were found to have ligands that were the same size as those in well-scored complexes, but hydrogen bonding and torsional strain were significantly different. These comparisons point to a need for CSAR to develop data sets of congeneric series with a range of hydrogen-bonding and hydrophobic characteristics and a range of rotatable bonds.

Introduction

Over the past two decades, docking has advanced from an academic exercise to a useful tool to help develop new leads in the pharmaceutical industry. Structure-based drug discovery (SBDD) methods are very successful in enriching hit rates, but it is possible that current software programs are really more effective at eliminating bad leads than identifying good ones.(1) While the ultimate goal is to properly predict tight binders, removing poor choices is valuable and focuses experiments into more fruitful chemical space.

A study by Warren et al.(2) summarizes many of the current strengths and limitations of SBDD. Many docking and scoring routines did well at binding mode prediction, reproducing ligand poses within 2 Å. Some were successful at virtual screening and yielded enrichments appropriate for lead identification, but none could rank order ligands by affinity. In general, inhibitors with nM-level affinity cannot be consistently ranked over those with μM-level binding. It is not possible to identify “activity cliffs,” small changes that result in significant increases or decreases in affinity.

Overall, there is a clear consensus that docking and scoring is a useful technique with potential to be even better, and the need for better training data is commonly identified as a limitation facing the field.(1) The aim of the Community Structure-Activity Resource (CSAR) is to gather data to help scientists improve their methods. To learn what features are most important to address first, we devised our 2010 benchmark exercise. Our exercise is intended to bring people together to compare different methods and improvements for scoring functions based on crystal structures of protein–ligand complexes (no docking was required in order to remove any limitations or biases arising from the use of different search algorithms). Our data set contains hundreds of diverse proteins and ligands of the highest quality that can be used to identify which systems are influenced by different approaches. For a detailed description of how the data set was curated and prepared for the exercise, the reader is directed to our data set paper in this same issue.(3) Most evaluations in the literature are based on a handful of targets at most, and that limited scope prevents us from properly identifying which features of targets and ligands are most difficult to treat computationally. Furthermore, it does not point toward how to improve our methods.

Here, we present an evaluation across all participants, particularly noting which protein–ligand systems are the most difficult to score and which are scored well. Our hypothesis is that sound statistical methods can be used to identify weaknesses in current scoring functions. Targets that are poorly scored across many, diverse methods point to common deficiencies in SBDD. These are the systems that call for improved approaches, departures from the status quo. For CSAR, the differences in physicochemical properties of the “universally well scored” complexes (GOODs) vs “universally poorly scored” (BADs) help to direct the kinds of data sets we curate. In this analysis, we are particularly interested in the complexes that are consistently scored well versus those that consistently scored poorly. GOOD complexes score within 1.1 pK_d of the experimental binding affinity for at least 12 of the 17 scoring functions described below, and BAD must be outliers for 12 or more of the scoring functions, see Figure 1. The BAD complexes fall into two groups: OVERs are weak binders that are consistently overscored, and UNDERs are tight binders that are consistently underscored. Differences in the physicochemical properties of GOODs versus BADs help to identify strengths and weaknesses of current approaches. Below, we show that OVERs tend to have hydrophilic ligands and binding sites, while UNDERs are typically hydrophobic. This highlights the need for efforts like CSAR to develop data sets based on congeneric series with ranging log P and hydrogen-bonding features. This is further supported by the results of three participants in the exercise who found that removing hydrogen-bonding terms and/or Coulombic energies resulted in no change in the agreement between scores and experimental affinities. In fact, the correlations significantly improved for one participant (see the papers of this special issue).

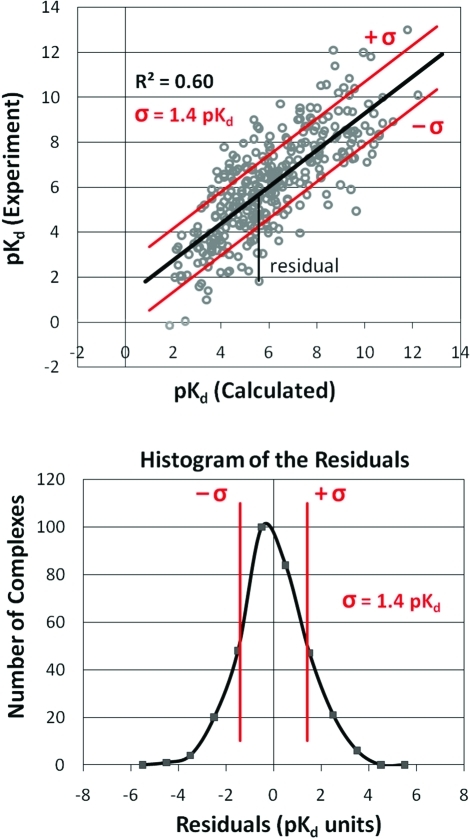
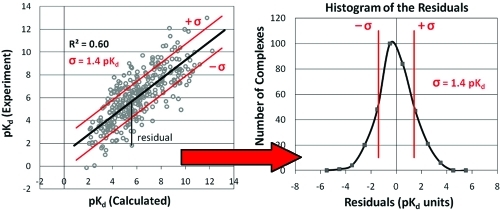
Figure 1.

Example of comparing a set of scores, pK_d (calculated), to their corresponding experimentally determined affinities. (Top) When fitting a line (black) using least-squares linear regression, the distance in the y direction between each data point and the line is its residual. (Bottom) The residuals for all the data points have a normal distribution around zero. The characteristics are well-defined, including the definition of standard deviation (σ in red, which happens to be 1.4 pK_d in this example) and the number of data points with residuals outside ± σ (15.8% in each tail). Higher correlations lead to larger R² and smaller σ; weaker correlations lead to lower R² and larger σ, but the distributions remain Gaussian in shape.

The most important aspect of this analysis is the means we use to combine the scoring functions. Improvement is regularly found by combining scores, and it is typically independent of which scoring functions are combined.(4) Research involving belief theory⁵⁻⁷ and consensus scoring^4,8−24 has focused on ways to combine data to identify potential positive outcomes, such as enrichment of hit rates. Here, we use consensus to determine which complexes are not scored well. It is very important to design the methods for combining results so that the statistical treatment makes it extremely unlikely for these choices to result from random chance or noise in the data. The equally important, subsequent task focuses on determining why these complexes are outliers.

Statistics

The methods used are straightforward and well-defined, based on linear regression. The most common assessment for a scoring function is its correlation to experimental binding data. When using a simple, least-squares linear regression to fit data points, the fit line must intersect the point (x̅, y̅), and the slope is defined to minimize the distance in the y direction between the data points and the line.(25) An underlying assumption is that the data has a normal distribution along the y axis. Indeed, the distribution of the 343 affinities in the CSAR-NRC set(3) is normally distributed about its average affinity (average pK_d/i = 6.15, median = 6.19, max = 13, min = −0.15) with the skew and kurtosis near 0 (skew = 0.06, kurtosis = −0.04). Therefore, the distribution of the residuals (errors in the y direction off any fit line) is normally distributed and centered at zero, see Figure 1. The standard deviation (σ) of the residuals is directly related to the goodness of fit of the line (smaller σ as R² approaches 1). R² is the square of the Pearson correlation coefficient which is the percentage of the total variation that can be fit by the linear relationship.

If we define an outlier as any point with an absolute error ≥1σ, then the probability of that occurrence is well-defined: 15.8% for each tail in the distribution of the residuals. This is true regardless of the R², so all fits—tighter and weaker—have the same probability of a complex having its residual in the tail regions. Below, we combine 17 scoring functions to identify common outliers or BAD complexes that are poorly scored over most methods. If a complex was poorly scored in all 17 scoring functions, then the probability of it being a random occurrence is 2 × (0.158)¹⁷ = 4.77 × 10^–14, where the factor of 2 accounts for the fact that an outlier can be either consistently above 1σ or consistently below −1σ to be a common outlier by our definition. The probability of a complex being a common outlier for 16 of 17 scores is 2 × (0.158)¹⁶ × (0.842) × 17= 4.32 × 10^–12, where the factor of 17 accounts for the number of ways that one scoring function can have an error <1σ. Following this enumeration, we can show that the probability of a complex being a common outlier for 12 or more of the 17 scoring functions due entirely to random occurrence is 1.27 × 10^–6. We would need a data set of 787 400 complexes (1/probability) to have one common outlier from random chance. That is 3 orders of magnitude larger than the CSAR-NRC data set, making it basically impossible for any of the common outliers to be due to random chance.

Our definition of ≥12 of 17 scores (at least 70% of the methods) ensures that common outliers do not occur randomly. Therefore, if a complex is a common outlier, there has to be an underlying cause. It has to represent some type of molecular recognition that most methods treat insufficiently. In order to identify the physicochemical properties that may frustrate computational methods, we compared the distribution of those properties between the BAD complexes and the set of GOOD complexes. The set of GOOD complexes was defined as those which scored within 1.1 pK_d of their experimental value (|residuals| ≤ 1.5 kcal/mol) for ≥12 of 17 scoring functions. Once these two sets were identified, two-tailed Wilcoxon rank-sum tests were used to assess statistical significance of differences in their distributions of physicochemical properties. Of course, we cannot completely rule out experimental error as a cause for an outlier. Our preparation of the data set removed all common complications, such as crystal contacts or poor electron density for the ligand, but the inherent weaknesses of using crystal structures are still there. We are not accounting for protein flexibility nor are we correcting for any differences in ions or pH between the binding assay and the crystallization conditions. There could be errors in the affinity data, particularly for very weak or very strong affinity where measurements are pushed to their limits. For all outliers, we searched the literature for updated affinity data, but none was found.

Contributors

Most of the scores were calculated by authors featured in this special issue, some by the CSAR team, and a few by participants who spoke at the ACS symposium(26) but were unable to submit papers due to various time constraints. Participants were promised anonymity to encourage submission of scores, even those with poor agreement with experiment, but attendees of the ACS symposium felt that hiding the identity of the scoring functions made it impossible to assess the results and know what inherent weaknesses might underlie the analysis. For that reason, the scoring functions are listed in the Methods Section below.

However, we stress that the list of scoring functions is ordered alphabetically, and it is not related to the ordering used in the Results and Discussion Section. In the discussions below, each scoring function is denoted with the generic term “code X”, where X = 1–17. We have chosen not to link the identity of the scoring functions with their performance to avoid trivializing this work into “winners vs losers.” This benchmark exercise is not a contest, and ranking current scoring functions was not our mission. Our goal is to combine the data across all participants and identify the most important and universal deficiencies in scoring protein–ligand binding. Only by knowing where the most significant pitfalls lie can we prioritize which data are needed most to help the community develop their new methodologies. This information has helped direct the focus of CSAR’s future data sets.

Methods

The CSAR-NRC data set(3) is 343 protein–ligand complexes with binding affinity data (K_d or K_i which we abbreviate as pK_d/i) from Binding MOAD^27,28 and PDBbind.^29,30 The challenge to participants was to calculate absolute free energies of binding over a very diverse set of proteins and small molecule ligands. The set was originally divided into two subsets so that participants could examine training and testing on related sets if they wished, but for this analysis, we are examining scoring across the full set of data.

We wanted an equivalent comparison across all the methods. To remove bias/error from different docking search routines, we asked participants to simply score poses from the crystal structures of the complex. The electron densities for ligands in the CSAR-NRC set are exceptional (RSCC ≥ 0.9 for the ligands),(3) so using poses from the crystals should be an unbiased treatment for all methods. However, we found that force field (FF)-based methods required minimization of the complexes. Small overlaps, within the error of the coordinates, were enough to create very large van der Waals (vdW) penalties. Therefore, a set of minimized structures were made available in addition to the set of crystallographic complexes. All FF methods used the same minimized structures for consistency. Though we could have asked for each FF method to use structures minimized in that FF, it would have removed the emphasis of an even comparison. The minimizations were simply meant to remove the vdW overlaps that undermined their performance. While this is not ideal, it aims to create an even basis for comparison. Participants were welcome to minimize the structures in their own FF, score again as part of their analysis, and report the results in their papers. They were also able to use crystallographic water if they chose, but none were used in the core scores below.

Sixteen groups participated in the benchmark exercise: 11 academic and 5 from the private sector, both software vendors and pharma groups. The submissions for the CSAR-NRC set included 64 variations on 19 scoring functions. Most participants submitted more than one set of scores, varying different parametric choices to determine their influence upon scoring. Two of the methods were only trained on the CSAR-NRC set and could not be included in this analysis. For each of the other 17 methods submitted, an optimal “core” score was chosen for our combined analysis across all participants. Only standard approaches were considered (only pre-existing functional choices, not functions fit to the CSAR-NRC data set). The option most appropriate to avoid artifacts was chosen. For example, FF scores require minimization of the complexes to remove the artifact of high vdW energies. Minimization was usually unnecessary for soft potentials or knowledge-based potentials, and use of the minimized structures often showed decreased agreement with experimental values. If more than one standard approach was submitted, then the option with better root-mean-square error (RMSE) or R² to the experimental data was chosen. At times, this resulted in minimized structures being used with knowledge-based or soft scoring functions. As noted above, the order below is alphabetical, but the tables, figures, and various performance metrics are ordered by correlation to the experimental values.

AutoDock 4.2.3(31)

This is a FF-based function, so scores for the minimized complexes were chosen. We also chose the scores calculated using the default charges (Gasteiger charges from AutodockTools 1.5.4.2) over using AM1-BCC charges provided with the data set because AutoDock is parametrized to use Gasteiger charges.

AutoDock Vina 1.1.1.1(32)

Standard, default scoring options were chosen, and the protein and ligand were prepared with AutodockTools 1.5.4.2. Scores calculated with the unminimized complexes were chosen because this is a knowledge-based potential.

DOCK 4.0.1(33)

This scoring function is based on the AMBER FF, so scores for the minimized complexes were chosen. Scores were submitted using both the full DOCK scoring function and the function with only the vdW terms included. The score chosen for the core set used the full scoring function.

DrugScore 1.1(34)

The default scoring parameters were used. Even though this is a knowledge-based function, scores for the minimized complexes were chosen because they had slightly better correlation with experimental affinities.

eHiTS(35)

The scores chosen for the core set were calculated with the default scoring options using the minimized set of structures. A second set of scores was also submitted with the function tuned on the entire data set. The standard score provided by eHiTS was chosen over the scores calculated from the function trained on the data set. However, the scores fit to the CSAR-NRC set were used as a type of benchmark because the large number of parameters allowed for a very tight correlation to experimental values. This was taken as a limiting case for the maximal performance possible when fitting to the data set.

FRED 2.2.5 (Chemgauss3)(36)

Standard, default scoring was chosen, calculated with the unminimized complexes because this is a soft, shape-based scoring method. The AM1-BCC charges provided with the data set were used. Scores were calculated using Shapegauss, Chemgauss3, Chemscore, OEChemscore 1.4.2, Screenscore, and PLP scoring functions with a box cutoff of 4 Å larger than the ligand. Both the minimized and unminimized structures were tested. The Chemgauss3 function using the unminimized structures was chosen because it achieved the highest R² in linear fit to experiment for the CSAR-NRC data set.

Glide 5.5 (SP)(37)

The minimized set of complexes was used because Glide is based upon the optimized potentials for liquid simulations (OPLS) FF for atom typing and charges. The grid was centered at the average ligand coordinate and the box extended 25 Å. The standard precision (SP) and the extra precision (XP) scores were calculated. SP was chosen over XP because it was able to score more of systems in the CSAR-NRC data set. Also, SP had a higher R² in linear fit to experiment for the CSAR-NRC data set.

GOLD 4.0.1 (ChemScore)^38,39

The scores of the minimized structures were chosen for the core set, since the performance based on R² was better. ChemScore was chosen over GoldScore and ASP because it had the best correlation with experiment. The binding site was defined as the region within 12 Å of the ligand’s center of mass. Non-natural amino acids and water molecules are not considered in the rescoring. GOLD used primarily knowledge-based scoring functions (or statistical potential functions), which relied only on atom typing of the ligands, so the charge information of the ligands was not used in the scoring.

ITScore 2.0(40)

Standard scoring was chosen over the new form that includes a correction for rotatable bonds in the ligand. Scores calculated for the unminimized complexes were chosen because this is a knowledge-based potential. ITScore was trained on 1152 protein–ligand complexes from PDBbind^29,30 (excluding those in the CSAR data set), to develop the pairwise statistical potentials for the scoring function.

Lead Finder(41)

Scores were based on two preparation protocols. The first used the structures provided in the CSAR-NRC set of minimized complexes. In the second, the structures were prepared using MolTech’s software Model Builder, which calculates the pK_as of the ligand to suggest proper ionization states.(42) Though the second preparation showed a slightly improved correlation to the experimental values, the scores from the first preparation were chosen for the core set for consistency with other methods.

MedusaScore(43)

The participant provided two scores based on MedusaScore and a QSAR model. MedusaScore is a FF based function, but the vdW repulsion terms are removed in order to avoid sensitivity to possible atomic clashes in the structures. MedusaScore was chosen over the QSAR approach because the latter was based on descriptors determined from the CSAR-NRC data set.

MOE 2010.10 (ASE and AffinityDG)(44)

Two scoring functions from MOE were chosen as core scores because they used fundamentally different and independent approaches. All MOE scoring functions (ASE,(45) Alpha HB, London dG, and Affinity dG) were used with their default settings and were computed on both the crystal structures and minimized structures provided. Both ASE and Alpha HB are shape-based methods, and ASE was chosen because of its better correlation with the experimental affinities. Both LondonDG and AffinityDG functions attempt to estimate the free energy of binding. Affinity DG had a lower RMSE and was chosen for the core set. The chosen core scores were calculated using the minimized data set, as it provided better agreement with experiment in both cases.

M-Score(46)

The default scoring parameters were used for this knowledge-based scoring function. The minimized structures resulted in scores with slightly better correlation to experiment and were chosen for the core set.

S2(47)

The S2 function is a linear interaction energy function based on the number of interacting types of pairs, with the weights calculated using linear regression fit to the LPDB data set. Scores for the minimized structures were chosen. The S2 function was chosen over the S1 function because the S1 function only accounts for the size of the molecule.

SIE(48)

Solvated interaction energy (SIE) scores use a FF-based method, so the minimized complexes were used. Parameters were assigned using AMBER/GAFF, but AM1-BCC charges were used for the ligand, cofactor, and any other modified residues. Two parameters of the SIE function (α and C) are fit to experimental binding free energies. The standard approach used 99 protein–ligand complexes. The α and C values were also refit using the CSAR-NRC data set. The standard scores provided from the SIE scoring function were chosen over the scores fit to our data set, to remove any bias and maintain consistent treatment across all core scores.

X-Score 2.0(49)

No special preparation was performed, and the default scoring parameters were used. X-Score reports three scores (HPScore, HMScore, and HSScore) and the average of all three. We chose the average score for the core set, based on the minimized set of structures. X-Score was developed from the PDBbind data set which has significant overlap with the CSAR-NRC set.

Caveats

Of the 17 core methods above, 12 were able to score all 343 complexes. Two methods left one complex unscored, and the other three were unable to score two, four, and five complexes, respectively. Any complex left unscored was counted as an outlier for that method. On very rare occasion, we needed to drop an individual complex from a method’s set of scores (a single complex was removed from three methods, and three complexes were removed from one method). In these cases, the complexes’ scores were well off from the rest of the set, and the residuals were greater than 3.5σ (very unlikely in a set this size). These were very likely errors in the calculation, and they greatly skewed the linear regression analysis outlined below. Of course, any removed complex was treated the same as an unscored complex.

Correlation between Scores and Experimental Binding Affinities

The statistical package “R”(50) was used to calculate Pearson’s R, Spearman ρ, and Kendall τ values. Fisher transformations coupled with standard deviations were used to determine 95% confidence intervals.(51) Every method was normalized so that the scaled scores ranged from 0 to 1 (i.e., scores were converted by first making all scores positive numbers and then scaling by [(score_i – score_min)/(score_max – score_min)]). This simply shifts the values and scales them. It does not change the value of R², but it does change any Person’s R, Spearman ρ, or Kendall τ with a negative value to its absolute value. This treatment makes it easier to compare across the methods because R, ρ, or τ of 1.0 always indicates perfect correlation and rank ordering, regardless of whether the original scores were given in positive or negative numbers.

Selecting BAD and GOOD Complexes by Linear Regression

Each method’s scores were compared to the experimental pK_d/i through least-squares linear regression analysis in JMP.(52) As noted in Figure 1, the residuals are normally distributed with σ proportional to the goodness of fit. JMP(52) was used to compare the residuals across all the fits and determine the list of BAD complexes. These BAD complexes fell into two groups. The UNDER set consisted of those complexes with residuals ≥1σ (under scored) in at least 12 of 17 functions, and the OVER set were those with residuals ≤ –1σ (over scored) in at least 12 of the 17 functions. Before progressing to the comparison of BAD and GOOD complexes, we searched the literature to identify whether any subsequent research on those targets had identified any errors in the processing or disagreements in affinity measurements. No errors in set up or changes to affinity data were found.

When identifying the GOOD structures, we wanted to remove any bias in the linear regression arising from trying to fit the BAD complexes. Therefore, the BAD structures were removed, and then the remaining complexes were fit again in JMP.(52) The set of GOOD complexes was defined as those with an absolute value of its residual less than 1.1 pK_d/i (<1.5 kcal/mol) in at least 12 of the 17 core scoring functions.

Comparison between the Physical Properties of BAD and GOOD Sets

We calculated over 400 physicochemical properties for each complex based on the ligand, the protein, and the interactions between the two. For the ligand, all two- and three-dimensional (2D and 3D) properties available in MOE(44) were calculated, except for those requiring semiempirical quantum mechanics. Energy descriptors were calculated with the MMFF94x force field in MOE. This provided 319 ligand descriptors.

The proteins, binding sites, and the protein–ligand interactions were examined in many ways. Properties describing the quality of the crystal structure included clash scores calculated by MolProbity,(53) all Z scores calculated by WhatIf,(54) DPI,(55) and the R_free and resolution reported in the original publication for each complex. The chemical interactions between the ligand and the protein were determined by the prolig_Calculate function available in MOE,(44) which yielded hydrogen-bonding, ionic, arene, and metal interactions within the binding sites. The buried and exposed molecular surface area (SA) of the binding pocket was calculated with GoCav.(56) The hydrophobic buried SA was estimated by determining which nonhydrogen atom of the protein was closest to the buried surface grid point determined by GoCav. If a carbon atom of the protein or the sulfur atom of a methionine residue was closest, then the point was considered hydrophobic. All other buried SA points were considered hydrophilic. Bridging water molecules were required to be less than 50% solvent exposed and to be within 4 Å of a nonhydrogen atom of both the ligand and the protein. Any natural amino acid, modified residue, and metal atom with a nonhydrogen atom within 4 Å of the ligand’s nonhydrogen atoms were considered part of the protein’s binding site. These contacts were determined and tallied using in-house code written in Perl. Each binding site was then described by its %amino-acid content (number of each of the 20 amino acids in the binding site divided by the total number in the binding site, where metals and modified residues were counted as a 21st residue called “other”). Then averages and standard deviations for the amino acid content of the binding sites were determined by bootstrapping for 1000 iterations, randomly combining two-thirds of the data set each time. GOOD, OVER, and UNDER complexes were each bootstrapped as separate sets.

For every physicochemical property, JMP(52) was used to compare the distribution of values for the GOOD complexes to the distribution of values for the BAD complexes. UNDER and OVER complexes were compared separately to the GOOD complexes. A nonparametric, two-tailed, Wilcoxon rank-sum test was performed to calculate the likelihood that distributions of physicochemical properties were the same. Only properties with p values ≤0.05 were considered relevant.

Results and Discussion

Factor Xa (FXa) Complexes Were Removed Early in the Analysis

The initial set of identified outliers contained several FXa structures. Each had ligands with sub-nM-level affinities, but the pockets were well exposed and the complementarity appeared poor. All FXa structures are missing an N-terminal domain, and its effect on ligand binding is unclear. In vivo, the domain is required for calcium activation of FXa, and the anticoagulant warfarin works by inhibiting the modification of this domain’s key residues that chelate calcium.(57) Therefore, we removed all 11 FXa structures from the analysis of BAD and GOOD structures.

The subsequent analysis below is based on the 332 remaining structures in the CSAR-NRC set. Note that after dropping these complexes, the characteristics of the set are basically unchanged. The maximum and minimum affinities are the same. The average and median affinities of the 332 set are 6.07 and 6.115 pK_d/i, respectively. The standard deviation is 2.20 pK_d/i, and the median unsigned error (Med |Err|) is 1.47 pK_d/i. The distribution is still Gaussian with near-zero skew and kurtosis of 0.09 and 0.04, respectively.

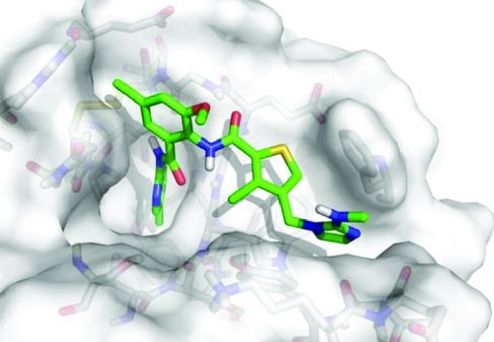
However, FXa has been a platform for successful structure-based design(58) and testing of modeling techniques.^59,60 There is a wealth of additional data on FXa in the pharmaceutical industry⁶¹⁻⁶⁹ that would help the field overcome its limitations. In fact, we are currently negotiating with two companies for FXa data. There are strong electronic influences and π–π stacking effects that can shift ligand affinities over 4 orders of magnitude. Structure 2p3t(67) (set 1, complex no. 141) is a good example of the difficulty in modeling some high-affinity inhibitors of FXa. It has a binding affinity of 5 pM but appears to have poor complementarity and is largely solvent exposed, see Figure 2. The effects of halogenation and π–π stacking provide a strong driving force for the association. Below, we show that hydrophobic interactions in tight-binding complexes are underestimated by the majority of methods examined in the benchmark exercise.

Figure 2.

Crystal structure of FXa bound with a 5 pM ligand (PDB id 2p3t). The ligand is very exposed with few hydrogen bonds to the protein.

It should be noted that several structures of HIV-1 protease were in the BAD set. At the same time, there were twice as many in the GOOD set, and the complete protein is present in the crystal structures. Therefore, we chose not to eliminate those complexes from the analysis. A table in the Supporting Information lists the proteins that have an appropriate ligand series in the data set, including FXa. Proteins were clustered at 100% sequence identity to avoid data on mutants muddling the analysis of affinities. Sixteen proteins (listed with PDB ids in the data set paper)(3) had three ligands or more, but only 10 had ligand affinities that ranged more than 1 order of magnitude. No limit was placed on chemical similarity across the ligands to define some measure of congeneric series, though some clearly are. Each code’s relative ranking of the ligand series for each of the 10 proteins is also provided in the table in the Supporting Information. A list of all protein families and their complexes has been included in the download of the data set since the project was initiated (www.CSARdock.org, accessed July 25, 2011).

Correlation between Experimental Affinities and the 17 Core Methods

Table 1 presents both parametric and nonparametric assessments of the correlation between the submitted scores and the experimental binding affinities of the 332 entries used. For methods that estimated affinities, the Med |Err| was 1.00–1.68 pK_d/i (1.4–2.3 kcal/mol), and the RMSE ranged from 1.51 to 2.99 pK_d/i (2.1–4.1 kcal/mol). Across all 17 core scores, the σ values for the residuals from the linear regression were 1.43–2.07 pK_d/i (1.9–2.9 kcal/mol). For FF-based, knowledge-based, and empirical scoring functions, all had examples with high and low correlation. There was no obvious advantage to choosing one type over another.

Table 1. Parametric and Nonparametric Measures of Correlation Between the Scores and Experimental Binding Affinities^a.

method	Pearson R	Spearman ρ	Kendall τ	R2	σb	RMSEb	Med |Err|b
code 1	0.76 (0.80–0.71)	0.74 (0.79–0.68)	0.55 (0.60–0.50)	0.58 (0.64–0.50)	1.43	1.51	1.00
code 2	0.72 (0.77–0.66)	0.73 (0.78–0.67)	0.54 (0.59–0.49)	0.52 (0.59–0.44)	1.53
code 3	0.67 (0.72–0.60)	0.68 (0.74–0.61)	0.49 (0.54–0.43)	0.45 (0.52–0.37)	1.64	1.65	1.05
code 4	0.64 (0.70–0.58)	0.64 (0.70–0.56)	0.46 (0.52–0.40)	0.42 (0.49–0.33)	1.68	2.09	1.5
code 5	0.63 (0.69–0.56)	0.64 (0.71–0.57)	0.46 (0.52–0.40)	0.40 (0.48–0.32)	1.71
code 6	0.62 (0.68–0.55)	0.61 (0.68–0.53)	0.43 (0.49–0.38)	0.39 (0.47–0.30)	1.72	1.81	1.26
code 7	0.62 (0.68–0.55)	0.61 (0.68–0.53)	0.43 (0.49–0.37)	0.38 (0.46–0.30)	1.72
code 8	0.61 (0.67–0.54)	0.59 (0.66–0.51)	0.42 (0.48–0.36)	0.37 (0.45–0.29)	1.75
code 9	0.61 (0.67–0.53)	0.60 (0.67–0.52)	0.43 (0.49–0.37)	0.37 (0.45–0.28)	1.75
code 10	0.60 (0.66–0.52)	0.60 (0.67–0.52)	0.43 (0.48–0.37)	0.36 (0.44–0.27)	1.77	2.99	1.67
code 11	0.59 (0.66–0.52)	0.57 (0.64–0.49)	0.40 (0.46–0.34)	0.35 (0.43–0.27)	1.77	1.92	1.36
code 12	0.57 (0.63–0.49)	0.57 (0.65–0.49)	0.41 (0.47–0.35)	0.32 (0.40–0.24)	1.82	2.18	1.28
code 13	0.56 (0.63–0.48)	0.60 (0.67–0.52)	0.42 (0.48–0.36)	0.32 (0.40–0.24)	1.82	2.52	1.68
code 14	0.56 (0.63–0.48)	0.54 (0.62–0.45)	0.38 (0.44–0.31)	0.32 (0.40–0.23)	1.82
code 15	0.56 (0.63–0.48)	0.56 (0.63–0.47)	0.39 (0.45–0.33)	0.31 (0.39–0.23)	1.83
code 16	0.53 (0.60–0.45)	0.53 (0.61–0.44)	0.37 (0.43–0.31)	0.28 (0.36–0.20)	1.87	1.90	1.23
code 17	0.35 (0.44–0.25)	0.37 (0.46–0.27)	0.25 (0.32–0.18)	0.12 (0.20–0.06)	2.07
Yardsticks (Maximum and “Null” Correlations)
trained on 343 setc	0.93 (0.94–0.91)	0.93 (0.94–0.90)	0.77 (0.80–0.74)	0.86 (0.89–0.83)	0.82	0.95	0.48
heavy atoms	0.51 (0.58–0.42)	0.49 (0.57–0.40)	0.35 (0.41–0.28)	0.26 (0.34–0.18)	1.90
Slog P	0.46 (0.54–0.38)	0.50 (0.58–0.41)	0.34 (0.40–0.28)	0.22 (0.30–0.14)	1.95

^aValues obtained through analysis of the set of 332 complexes (FXa structures removed from the CSAR-NRC set). 95% confidence interval in parentheses, units of pK_d for σ, RMSE, and Med |Err|.

^bMetrics appropriate for the methods that estimated absolute binding affinities, rather than relative ranking; units are pK_d.

^cOne of the 17 methods above, fit with many adjustable parameters specifically to reproduce the 343 complexes of the full CSAR-NRC set.

Modest correlations were expected because of the difficulty in predicting absolute free energies of binding, but the correlations are just as good as those for the easier problem of relative ranking to a single protein target.(2) Spearman ρ and Kendall τ are nonparametric and reflect the relative ranking across the complexes, with ρ nearly equaling the Pearson R values (0.76–0.35), while τ is less.

The R² range is 0.58–0.12 with the bulk of the methods falling between 0.4 and 0.3. Caution must be used in making a statistically significant evaluation across the codes. Though a 95% confidence interval of R² can be analytically determined,(51) the difference in the 95% confidence intervals is not the same as a 95% confidence in the difference. It is most appropriate to evaluate the statistical significance between the R² values by examining the residuals that underlie the correlation. As shown in Figure 1, residuals for all fits are normally distributed around zero, so a rank-sum test is not appropriate. Instead, the difference in the spread of the distribution can be evaluated using Levene’s F-test for the equality of variance (calculated using the “R” statistical package).(50) This is more stringent than simply comparing the confidence intervals. Codes 1 and 3 have a small overlap in their 95% confidence intervals of R², but the F-test of their residuals provides a p value of 0.015, meaning that they are statistically significant in their difference. (Levene’s tests for code 3 show it to be statistically comparable to codes 2 and 4–11, but it is a method parametrized on the PDBbind data set,^29,30 which has a great deal of overlap with the CSAR-NRC set. A “performance” comparison to other methods is not particularly meaningful.) Levene’s test for the residuals of codes 1 and 2 gives p = 0.23; therefore, the performance of codes 1 and 2 are comparable. F-test comparisons of codes 4–16 have p > 0.05, making them equivalent. The very low R² for code 17 is statistically significant in its difference to the other core methods.

Yardsticks for Linear Regression

The equivalence of the overwhelming majority of methods further underscores why the benchmark exercise is not a contest. More importantly, only codes 1–6 are statistically significant in their difference to common “null cases.” Perhaps the most appropriate null case for scoring functions is the correlation between affinity and the number of nonhydrogen atoms in the ligand,^70,71 which is R² = 0.26 for this set with a 95% confidence interval of 0.34–0.18. This is a particularly useful counter example because the additive, pairwise potentials used in most scoring functions lead to ever increasing scores as more atoms are added to the ligand.⁷⁰⁻⁷² Another null case to consider is the correlation between the affinity and the hydrophobicity of a ligand. It is well-known that adding hydrophobic moieties to a ligand will increase its affinity.⁷³⁻⁷⁵ This is a bit of a “cheat” because one is simply disfavoring the unbound state. We have used SlogP values(76) calculated with MOE to provide this null case (R² = 0.22 with a 95% confidence interval of 0.30–0.14). We should caution the reader that, unlike the count of nonhydrogen atoms, predictions of hydrophobicity are parametrized methods just like scoring functions, except that the values are independent of the protein target.

We should note that the highest correlation to experiment was obtained when the method with the most adjustable parameters was refit using the 343 CSAR-NRC complexes: R² = 0.86, R = 0.93, ρ = 0.93, and τ = 0.77. This is provided in Table 1 as an example of maximum performance possible with the data set. As our paper on the data set noted, the experimental uncertainty should limit the correlation to an R² of ∼0.83 when fitting to this data without overparameterizing.(3) Of the 64 total submissions, 4 others also fit to the whole data set, obtaining R² of 0.54–0.42, R of 0.73–0.64, ρ of 0.71–0.64, and τ of 0.52–0.46.

Identification of 63 BAD and 123 GOOD Complexes by Linear Regression and σ

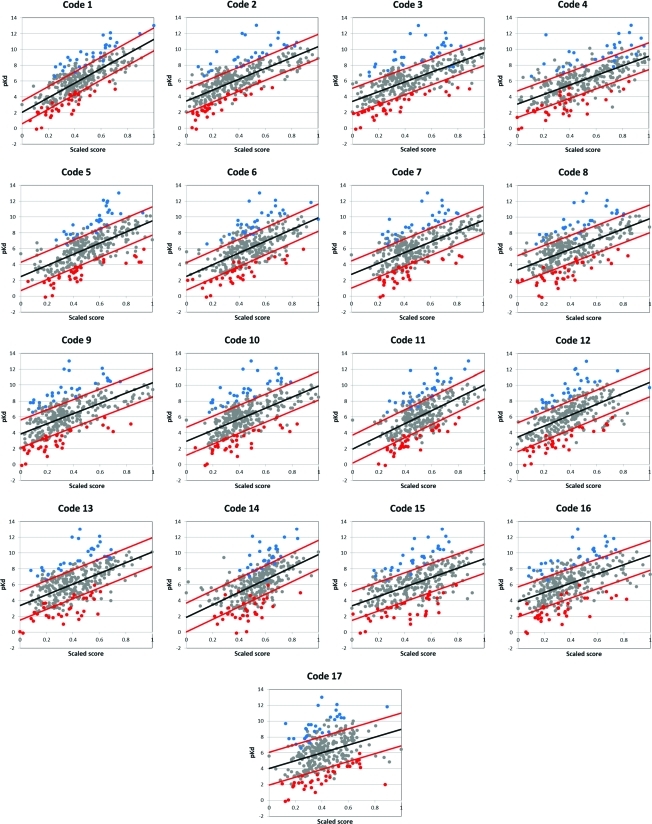
A complete list of the BAD and GOOD complexes is given in the Supporting Information. Figure 3 compares the 17 core scoring functions to the experimental affinities. The red lines highlight complexes with residuals within and outside ±1σ, where any point outside is an outlier for that individual method. The BAD complexes, defined by having residuals outside ±1σ for at least 12 of 17 methods, were composed of 34 OVER (weak binders scored too high) and 29 UNDER (strong binders scored too low). Figure 3 shows that every method may score a few BAD complexes well (red and blue data points between the red lines).

Figure 3.

Least-squares linear regression of the 17 core scoring functions. Black lines are the linear regression fit. Red lines indicate +σ and −σ, the standard deviation of the residuals. Blue points are UNDER complexes which were underscored in ≥12 of the 17 functions. The red points are OVER complexes which were overscored in ≥12 of the 17 functions.

From the linear regression of the 332 complexes, 116 had residuals within ±1.1 pK_d/i (1.5 kcal/mol) for ≥12 of 17 methods. However, it is best to keep the BAD structures from influencing the linear regression and subsequent identification of GOOD systems. Therefore, we removed the 63 BAD complexes and refit the remaining 269 complexes for each method. Based on the ≥12 of 17 requirement, the number of systems with residuals within ±1.1 pK_d/i increased to 123. The Supporting Information outlines the procedure in a figure and provides a discussion of our metrics for identifying the GOOD complexes.

Methods that Estimate Absolute Binding Affinities

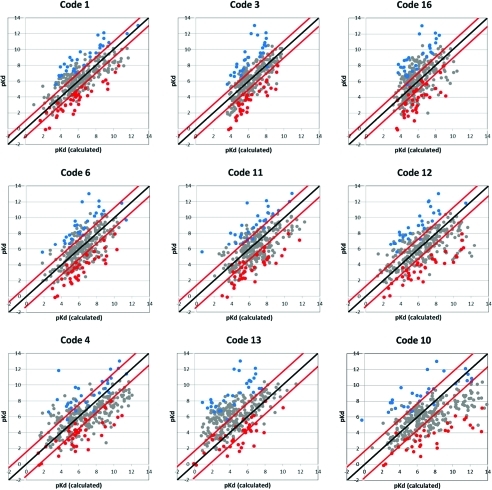
Nine of the core methods estimated binding affinities, rather than providing simple rank scores. The Med |Err| ranged from 1.00 to 1.68 pK_d/i, and the RMSE was 1.51–2.99 pK_d/i, see Table 1. The agreement with experiment ranked the codes in the order (1, 3) > (16, 6) > (11, 12, 4) > (13, 10). For this ranking, greater importance was given to Med |Err| because RMSE heavily weighs the farthest outliers. For estimates of affinities, having less error for more complexes is more important than having outliers that are closer but still quite far off.

A suggested null case is to calculate the RMSE and Med |Err| while setting every score to the average experimental value (6.07 pK_d/i). For RMSE, that simply gives the standard deviation of the data set, 2.2 pK_d/i, and the Med |Err| is 1.47 pK_d/i. Five of the 9 methods have RMSE and Med |Err| less than the null case (codes 1, 3, 16, 6, and 11). Two methods have errors less than one null metric but nearly equal to the other (codes 12 and 4). Two methods have errors in excess of the null case (codes 13 and 10). Of course, all of the methods have RMSE larger than their standard deviation from the linear regression, but it is most pronounced for codes 10 and 13 which seem to be biased to overscore and underscore, respectively, across the full range of complexes (see Figure 4). Codes 3 and 16 rank very well and have low errors, but they appear to have some bias that limits the scoring range to roughly 4–10 pK_d.

Figure 4.

Comparison of experimental and calculated values from the nine functions which predicted absolute binding affinity, listed roughly in order of increasing Med |Err| and RMSE. Black lines represent perfect agreement. The red lines indicate +Med |Err| and −Med |Err| from the black line. The blue circles denote complexes for which ≥7 of the 9 methods have consistently underestimated the affinity by at least Med |Err|, while the red circles are those where the affinity was overestimated.

Figure 4 compares the estimated affinities with the experimental values for these nine core methods, where any estimated free energies were converted to pK_d. We have identified universal outliers much as we did through linear regression. Using RMSE for a cutoff would parallel the previous analysis, but as stated above, low Med |Err| is more important in this type of scoring. OVER complexes had errors (pK_d/i^experiment – pK_d^score) less than −1 × Med |Err| in at least 7 of the 9 functions (78% of the methods, a larger percentage than the 12 of 17 requirement for the sets defined by linear regression). UNDER complexes were determined by the errors greater than 1 × Med |Err| for ≥7 of 9 methods. Again, structures were determined to be well scored if their error was <1.1 pK_d. This cutoff was maintained even if the Med |Err| was less than 1.1. This lead to 36 OVER, 28 UNDER, and 34 GOOD complexes based on Med |Err|. Unfortunately, there is no way to estimate the statistical significance of the sets determined in this manner, but the overwhelming majority of complexes are also in the sets determined by linear regression. The complexes are listed in the Supporting Information.

Comparison of the GOOD versus BAD Complexes

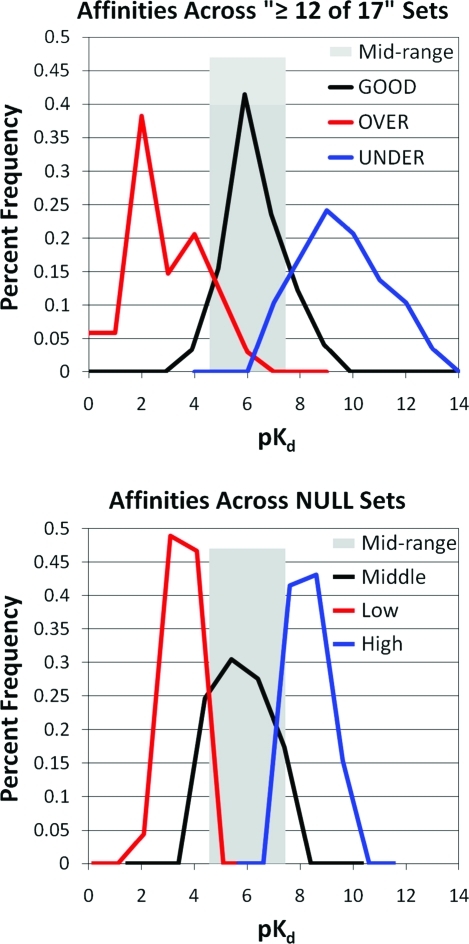
The comparison of GOOD and BAD complexes below focuses only on the sets determined through linear regression because of the solid statistics outlined in the Introduction Section. We next applied the concept of a null hypothesis to this portion of the analysis and developed a null set of complexes (NULL) to characterize a type of signal-to-noise metric. The first graph in Figure 5 shows the distribution of affinities for the GOOD, OVER, and UNDER sets. There is a large bias for OVER complexes to have low affinities, UNDER complexes to have high affinities, and GOOD complexes to lie in between. Therefore, we defined the NULL cases based on affinities and compared the characteristics of the signal to the inherent background. Within this framework, the signal is the comparison of GOOD to OVER and UNDER complexes, and the NULL sets simply compare complexes with midlevel affinity to weak binders and tight binders, respectively. First, we divided the 332 complexes into three subsets, using cutoffs of ≤50 nM and ≥50 μM, as shown in gray shading in Figure 5. We then removed any UNDER complexes from the high-affinity subset, any GOOD complexes from the midrange subset, and any OVER complexes from the low-affinity subset. The NULL set contained 179 complexes: 65 high-, 69 mid-, 45 low-affinity complexes. We would like to ensure that the differences in physical properties are not simply a reflection of affinity. Obviously, those properties are important in scoring and will be represented across the sets, but the use of a NULL set helps us identify potential bias arising from the definition of a difficult-to-score system.

Figure 5.

Distribution of binding affinities in the GOOD and BAD complexes (left) are compared to those of the NULL case (right). The NULL case is generated by the sets of all complexes with affinities ≤50 nM (high), 50 nM–50 μM (middle), and ≥50 μM (low). This midrange of affinities is highlighted with a wide, gray bar on both figures.

Our goal in this analysis is to identify the physical characteristics of the proteins and the ligands that are most difficult to model. However, we cannot base this determination solely on the properties of the BAD complexes; they must be compared to the GOOD complexes. Any properties common to both sets cannot be the root of the problem. We need to identify characteristics of difficult systems that are significantly different from the easy ones. For instance, there are studies in the literature indicating that metalloenzymes are difficult to model,⁷⁷⁻⁷⁹ and if many of the BADs contained metals in their binding sites, then it would be tempting to conclude that metals are a major stumbling block for our field. However, that would not be true if many metalloenzymes were also in the GOOD set. We can easily calculate p values for differences in the distributions of various system properties in GOOD vs OVER and GOOD vs UNDER sets. This allows us to identify statistically significant differences between the sets. In fact, we found that there is no difference between GOOD, OVER, or UNDER complexes with respect to metals in the binding sites (medians of 0 for all three sets; means of 0.32 for GOOD, 0.24 for OVER, and 0.24 for UNDER; p values of 0.85 for OVER vs GOOD and 0.79 for UNDER vs GOOD). Of course, this does not mean that metalloenzymes are easy to model; that would require a bias for metals in GOOD only. It was interesting to find that there was a statistically significant bias for metals in the binding sites of low-affinity complexes in the NULL sets (mean of 0.62 for midrange and 1.11 for low with p = 0.03). Having a bias in the NULL set that is not found in the OVER vs GOOD comparison further supports the finding that metals are not a strong influence on BAD complexes. It should be emphasized that this finding is for a general analysis over many methods, and it is still possible that an individual scoring technique could find metals to be its greatest limitation (this was the finding of one participating group that was unable to submit a paper to this special issue).

Table 2 lists the most relevant physicochemical properties of the ligands and pockets of the GOOD, UNDER, OVER, and NULL sets. Medians and p values for each property are provided.

Table 2. Comparison of the Distribution of Physicochemical Properties for UNDER, GOOD, OVER, and NULL Sets. ^a.

	≥12 of 17 UNDER vs GOOD complexes				NULL hypothesis (high vs midrange)				≥12 of 17 OVER vs GOOD complexes				NULL hypothesis (low vs midrange)
physicochemical characteristics	median (GOOD)	median (UNDER)	Δmedian (UNDER – GOOD)	p	median (middle)	median (high)	Δmedian (high – middle)	p	median (GOOD)	median (OVER)	Δmedian (OVER – GOOD)	p	median (middle)	median (low)	Δmedian (low – middle)	p
Ligand Properties
ligand heavy atoms (HA)	21	20	–1	0.63	21	36	15	<0.01	21	19.5	–1.5	0.10	21	11	–10	<0.01
calculated log S	–2.15	–3.87	–1.72	0.45	–0.70	–6.06	–5.36	<0.01	–2.15	–0.09	2.06	<0.01	–0.70	–0.20	0.50	0.02
calculated SlogP	–0.60	1.42	2.02	<0.01	–1.82	3.42	5.20	<0.01	–0.60	–2.58	–1.98	<0.01	–1.82	–2.55	–0.73	0.97
Lipinski violation	0	0	0	0.10	0	1	1	0.03	0	0	0	0.86	0	0	0	0.06
Oprea violation	1	0	–1	0.05	1	3	2	<0.01	1	0.5	–0.5	0.81	1	0	–1	0.03
Nrot	4	5	1	0.71	4	9	5	<0.01	4	4	0	0.32	4	3	–1	<0.01
Nrot/HA	0.22	0.23	0.01	0.83	0.2	0.27	0.07	<0.01	0.22	0.22	0	0.65	0.2	0.17	–0.03	0.10
Etor	8.59	2.89	–5.70	<0.01	9.64	15.67	6.03	0.10	8.59	11.18	2.59	0.11	9.64	5.94	–3.7	0.28
Etor/Nrot	1.43	0.53	–0.90	0.02	2.48	1.32	–1.16	0.06	1.43	3.07	1.64	0.02	2.48	4.30	1.82	0.22
no. oxygens	4	3	–1	0.09	4	5	1	0.88	4	6	2	0.05	4	4	0	0.20
no. oxygens/HA	0.19	0.14	–0.05	0.12	0.29	0.14	–0.15	<0.01	0.19	0.38	0.19	<0.01	0.29	0.36	0.07	0.20
no. hydrophobic	10	13	3	0.57	9	26	17	<0.01	10	8	–2	0.01	9	6	–3	<0.01
no. hydrophobic/HA	0.56	0.67	0.11	0.10	0.44	0.71	0.27	<0.01	0.56	0.43	–0.13	<0.01	0.44	0.46	0.02	0.53
no. acc + no. donors	6	5	–1	0.12	7	7	0	0.56	6	7	1	0.46	7	4	–3	0.28
(no. acc + no. don)/HA	0.24	0.23	–0.01	0.26	0.36	0.21	–0.15	<0.01	0.24	0.38	0.14	0.04	0.36	0.40	0.04	0.51
Hydrogen Bonds and Water in the Binding Pocket
protein–ligand Hbonds	9	5	–4	<0.01	8	8	0	0.15	9	9	0	0.12	8	5	–3	<0.01
pro–lig Hbonds/HAb	0.35	0.19	–0.16	0.06	0.5	0.20	–0.25	<0.01	0.35	0.59	0.24	<0.01	0.5	0.42	–0.08	0.45
pro–lig Hbonds/(lig no. acc+ no. don)	1.00	0.80	–0.20	0.13	1.05	0.94	–0.11	0.33	1.00	1.11	0.11	0.51	1.05	0.67	–0.38	<0.01
bridging H2O	5	3	–2	0.06	4	6	2	0.04	5	6	1	0.35	4	3	1	0.03
bridging H2O/HAb	0.22	0.20	–0.02	0.06	0.21	0.17	–0.04	0.06	0.22	0.31	0.09	<0.01	0.21	0.2	–0.01	0.80
total H2O in pocket	5	3	–2	0.05	5	7	2	0.04	5	6	1	0.33	5	4	–1	0.06
total H2O/HAb	0.24	0.20	–0.04	0.03	0.23	0.19	–0.04	<0.01	0.24	0.33	0.09	<0.01	0.23	0.25	0.02	0.56
Surface Properties of the Ligand and Binding Pocket
ligand vdW SA	311	300	–11	0.81	294	525	231	<0.01	311	293	–18	0.06	294	182	–102	<0.01
lig vdW SA/HA	14.9	15.2	0.3	0.09	14.6	14.7	0.1	0.62	14.9	14.5	–0.4	0.75	14.6	15.3	0.7	0.02
hydrophobic lig vdW SA	138	196	58	0.50	122	367	245	<0.01	138	112	–26	<0.01	122	85	–37	0.01
hydrophobic lig vdW SA/HA	7.69	9.49	1.80	0.05	6.28	9.87	3.59	<0.01	7.69	5.66	–2.03	<0.01	6.28	5.64	–0.64	0.65
polar lig vdW SA	71.4	52.1	–19.3	0.10	71.0	75.5	4.5	0.37	71.4	90.8	19.4	0.27	71.0	59.3	–11.7	0.02
polar lig vdW SA/HA	3.59	2.71	–0.88	0.29	4.27	1.89	–2.38	<0.01	3.59	5.05	1.46	<0.01	4.27	4.56	0.89	0.57
pocket exposed SA	83.1	34.6	–48.5	0.14	73.7	108.3	34.6	0.07	83.1	81.6	–1.5	0.70	73.7	67.9	–5.8	0.91
pocket ESA/HAb	2.93	2.20	–0.73	0.14	3.61	2.87	–0.74	0.18	2.93	3.81	0.88	0.32	3.61	5.35	1.74	0.02
pocket %ESA	0.17	0.14	–0.03	0.16	0.18	0.17	–0.01	0.30	0.17	0.19	0.02	0.47	0.18	0.25	0.07	0.11
pocket buried SA	301	278	–23	0.43	282	510	228	<0.01	301	251	–50	0.12	282	196	–86	<0.01
pocket BSA/HAb	14.2	13.8	–0.4	0.62	14.1	13.4	–0.7	0.14	14.2	15.7	1.5	0.19	14.1	16.5	2.4	<0.01
%hydrophobic pocket BSA	0.52	0.57	0.05	0.01	0.48	0.57	0.09	<0.01	0.52	0.46	–0.06	0.06	0.48	0.52	0.04	0.61
%hydrophilic pocket BSA	0.48	0.43	–0.05	0.01	0.52	0.43	–0.09	<0.01	0.48	0.54	0.06	0.06	0.52	0.48	–0.04	0.61
hydrophobic pocket BSA	167	177	10	0.69	139	287	158	<0.01	167	120	–47	0.02	139	107	–32	<0.01
hydrophobic pocket BSA/HAb	7.36	7.77	0.41	0.08	6.95	7.48	0.53	0.03	7.36	7.14	–0.22	0.80	6.95	7.59	0.64	0.16
hydrophilic pocket BSA	135	86	–49	0.03	135	205	70	<0.01	135	131	–4	0.55	135	90	–45	<0.01
hydrophilic pocket BSA/HAb	6.54	6.02	–0.52	0.03	6.69	5.81	–0.88	<0.01	6.54	7.74	1.20	<0.01	6.69	7.67	0.98	0.52

^aEntries in bold have significant p values.

^bProperties of the pocket are divided by the number of nonhydrogen atoms in the ligands, not the HA in the pocket itself.

Physicochemical Properties of GOOD versus UNDER Complexes

Very few statistically significant differences were observed between properties of the GOOD and UNDER sets. Their ligands are roughly the same size, which is in stark disagreement with the NULL case. Many physicochemical properties are proportional to size, so the fact that UNDER and GOOD ligands are similar in size makes our key comparisons between the sets more straightforward. However, comparisons to the NULL case must be done cautiously because high-affinity NULLs are much larger. Therefore, all properties were examined by the raw values and values corrected for size by dividing by the number of ligand heavy atoms (HA).

A striking difference between GOOD and UNDER ligands is the fact that both have roughly the same number of rotatable bonds (Nrot and Nrot/HA), but UNDERs have much lower torsional energies (Etor). There is less torsional strain in the UNDER ligands. Even when corrected for size (Etor/Nrot), UNDERs are less strained than the high-affinity ligands in the NULL case.

Lipinski(80) and Oprea(81) described various counts of calculated properties that aid in indentifying compounds with good oral absorption (Lipinski) and drug-like compounds (Oprea). A count of the number of ligands in each set that violate these empirical rules shows that UNDER ligands are more drug-like than the GOOD ligands and the high-affinity set in the NULL case. UNDERs are more lipophilic than GOODs (higher SlogP and lower log S), but the difference is more pronounced in the NULL case. The counts of hydrophobic and hydrogen-bonding atoms are not significantly different between UNDER and GOOD ligands, unlike the NULL case. What is most striking is that—despite the ligands being roughly the same size with the same number of hydrogen-bonding features—there are significantly fewer hydrogen bonds between the protein and the ligand in UNDER complexes. The pockets of UNDER complexes contain fewer water molecules as well. Many of the trends for hydrogen bonding indicate a more hydrophobic environment for the UNDER pockets but just miss the arbitrary cutoff of p = 0.05. There is significantly less hydrophilic buried surface area (BSA) in the UNDER pockets, which shifts the %hydrophilic and %hydrophobic BSA. It is unclear if these trends in the pocket BSA are a reflection of the NULL case because the GOOD and UNDER ligands are very similar, whereas the mid- and high-affinity sets are starkly different. In the same vein, the hydrophobic vdW surface per HA of the ligand is larger for UNDERs, but it is also similar to the value obtained for the high-affinity complexes in the NULL set.

Physicochemical Properties of GOOD versus OVER Complexes

Like the UNDERs, OVER ligands are roughly the same size as the GOOD ligands. There is a large size difference in the NULL case, but with low-affinity ligands being much smaller than the midrange, so again, comparisons to the NULL must be made cautiously.

OVER complexes have two patterns in opposition to the UNDER complexes. OVER ligands have higher Etor/Nrot, making them more strained. Also, OVER ligands are much more hydrophilic and soluble than GOOD (or UNDER) complexes. While the UNDER ligands had no differences in the count of hydrophobic and hydrophilic atoms, the OVER ligands are very different from the GOOD. There are fewer hydrophobic atoms and notably more oxygen atoms. On a per HA basis, there are more protein–ligand hydrogen bonds and more bridging water. The ligands have less hydrophobic vdW SA/HA and more polar vdW SA/HA. For the pockets, the hydrophilic BSA increases roughly the same degree as the UNDER complexes decrease, but the p value is just shy of the 0.05 cutoff.

In the NULL case of mid- vs low-affinity complexes, there are many SA properties that are significantly different, but many are due to the large size difference in the NULL case that is not seen in OVER vs GOOD complexes. There is one interesting trend in the pockets of the NULL case. The low-affinity complexes have more exposed ligands (ESA/HA). Though the OVER complexes are more exposed than the GOOD, it is not statistically significant nor is it as extreme as the trend in the NULLs.

Comparison of Amino Acids in the Binding Sites

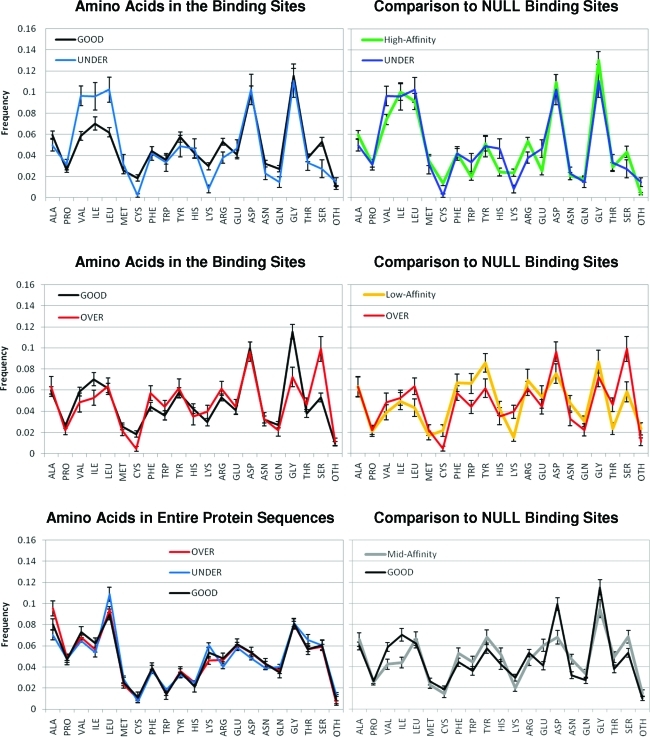
Figure 6 shows the distribution of amino acids in the binding sites of GOOD, UNDER, OVER, and NULL sets. The comparison of UNDER to GOOD binding sites shows that the increase in hydrophobic character of the pockets comes from a marked increase in the aliphatic residues Val, Ile, and Leu and not a change in the aromatic amino acids. However, large contributions from Ile and Leu are also seen in high-affinity NULLs. The decrease in hydrogen-bonding interactions and hydrophilic BSA for UNDER complexes comes from significant decreases in Lys, Arg, and Ser. It is very interesting that there is a decrease in the positively charged residues but not the presence of the acidic amino acids. While there is a decrease in Asn and Gln, this is also seen in the NULL set.

Figure 6.

Distribution of amino acids in the binding sites of the GOOD and BAD complexes meeting the ≥12 of 17 definition (left) are compared to those of the NULL case (right). The graph in the lower left provides the distribution of all amino acids in the full protein sequences to show that the important trends do not result from inherent differences in composition of the proteins (the same is true of the NULLs, data not shown). Metals and modified residues are denoted as other, “OTH”. Averages and error bars for the amino acid content were determined by bootstrapping.

The comparison between physicochemical properties of OVER and GOOD complexes revealed more hydrophilic ligands and pockets for the OVERs. However, the only significant difference in the composition of the binding sites is more Ser in the OVER pockets. There are decreases in Gly and Ile, but they are in good agreement with the content of low-affinity NULL pockets. It is possible that the similarity in the amino-acid composition may explain why the OVERs score too well. The ligands are the same size as GOOD ligands, not small like the low-affinity NULL ligands, and the pockets are more similar to GOODs than to the NULLs.

Impact on CSAR’s Future Data Sets

CSAR’s goal is to provide better, more complete data to the computational community, a widely available resource that scientists can use to improve their docking and scoring methods. This analysis across all participants in the first benchmark exercise is intended to shed light on the most pressing needs of the field as a whole. It is clear that hydrogen-bonding features should be our immediate focus, followed by rotatable bonds.

Our comparison of GOOD and BAD complexes shows that the field is underestimating the impact of hydrophobic interactions and overestimating the contribution of hydrogen bonding. This was supported by the contributions of three participants who showed that the correlation to affinity was unchanged or improved when hydrogen-bonding/Coulombic interactions were removed from their chosen scoring functions (data not shown). Scoring is usually based only on the bound complex, but binding is an equilibrium between bound and unbound states. A hydroxyl group can be added to a ligand to improve its interaction with a binding site, but experiment often shows little change in affinity.(82) The added hydrogen bonding also favors the interaction with water in the unbound state, and it is very difficult for a binding site to provide better hydrogen bonding than water. The electrostatic interactions in most scoring functions provide very favorable contributions to the estimated affinity because desolvation penalties are often overlooked. Desolvation is also an important driving force for hydrophobic association, providing a boost that simple vdW energies cannot model.

It is important that we provide data for many different protein targets. The affinities of the ligands must range at least 3 orders of magnitude so that experimental error will not limit the development of statistically meaningful models.(83) For each protein, we want to provide data on at least three congeneric series of ligands which provide the widest range of hydrogen-bonding features possible for the target. This should have a higher impact than varying size of the ligands. Of course, the data needed to tackle rotatable bonds will likely require ligand series with a range of sizes.

Our in-house efforts to enhance available data include isothermal titration calorimetry (ITC) and the determination of binding kinetics (www.CSARdock.org). These complementary techniques are independent means of determining exact binding constants, as opposed to inhibition constants or IC₅₀s. They each provide valuable insights into the contributions to binding: entropy and enthalpy for calorimetry and k_on and k_off for kinetics. These data are particularly important for understanding the hydrophobic effects and hydrogen bonding implicated here. Furthermore, ITC can be used to determine changes in protonation states upon ligand binding.(84) This complication is a factor for a few of the BAD complexes. For instance, the crystal structure 1tok(85) (set 2, complex no. 96) is aspartate transferase binding maleic acid (HOOC–HC=CH–COOH). In the binding site, both ends of the diacid are complemented by bidentate hydrogen bonding from Arg side chains, indicating that the ligand is doubly deprotonated. However, maleic acid can be singly deprotonated in solution, depending on the conditions (second pK_a of maleic acid is ∼6.3).(86)

Conclusion

The most common test to evaluate docking and scoring involves relatively ranking compounds against a single target because pharma tackles this practical challenge every day. However, the findings of those exercises are often system-dependent and cannot necessarily be extrapolated. Tackling absolute free energies of binding across diverse proteins is difficult, but we have the potential to learn something new by posing unique challenges. We have outlined a means for statistically evaluating our data set across multiple methods, emphasizing the insights possible by combining the results of many participants.

These insights help us prioritize the design of new data sets to address specific shortcomings of our methods. If the answer could be found by conducting individual, single-target studies, then the solutions would have been found long ago. It is important to keep an eye on the big picture—the global landscape of docking and scoring—to understand what model systems are most needed to improve the field.

Future benchmarks from CSAR will involve blind rankings of chosen model systems, sets of data designed to address the shortcomings we identify as a community. As always, we will strive to provide as many systems as possible to avoid system-dependent insights. Confirmed data on inactive compounds will be provided. We greatly appreciate the efforts of all of our colleagues in the pharmaceutical industry for the donation of data for these future benchmark exercises.

We thank Yu Zhou of the National Institute of Biological Sciences, Beijing for informing us that the ligand in 1x8d (set 2, no. 121) was incorrectly protonated. It is a sugar, and one of the hydroxyl groups was misinterpreted to be a ketone. As one might expect, it was indeed one of the BAD structures, improperly scored across most methods. A corrected version is available for download on the CSAR website (www.CSARdock.org, accessed August 24, 2011).

Supporting Information Available

Table of 10 proteins with ligand series and the performance of each of the 17 core codes on relative ranking, a discussion of methods and metrics for identifying the GOOD complexes, and a complete listing of GOOD and BAD complexes. This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States