Abstract
Variation among flowering seasons in the time of flowering, synchrony and length of flowering, and fluctuations in the abundance of pollinators may cause a variation in pollen dispersal distance. In this study, we analyzed the temporal variation in pollen dispersal and breeding structure in the Neotropical tree species Tabebuia aurea (Bignoniaceae) and evaluated pollen dispersal between a population inside the reserve and a patch of isolated individuals on the edge of the reserve, and tested the hypothesis that isolated individuals are sinking for pollen. All adult trees (260) within a population of 40 ha and 9 isolated individuals on the edge of the reserve were sampled, and from these adults, 21 open-pollinated progeny arrays were analyzed in 2 flowering seasons (309 seeds in 2004 and 328 in 2005). Genetic analyses were based on the polymorphism at 10 microsatellite loci. A high proportion of self-pollination found in both flowering seasons indicated a mixed-mating system. The mean pollen dispersal distance differed significantly between the two flowering seasons (307.78 m in 2004 and 396.26 m in 2005). Maximum pollen dispersal was 2608 m, but most pollination events (65%) occurred at distances <300 m. Our results also showed that isolated individuals are sinking for pollen, with high pollen flow between the population inside the reserve and individuals on the edge. These results are most likely due to the large pollinator species, which can potentially fly long distances, and also due to temporal variation in individual fecundity and contribution to pollen dispersal.
Keywords: pollen dispersal, genetic neighborhood, breeding structure, Tabebuia aurea, Bignoniaceae, cerrado
Introduction
The distribution of genetic diversity within and among populations is primarily affected by gene flow (Wright, 1940; Slatkin, 1985). In animal-pollinated species, pollen presentation and behavioral differences of animal pollinators and their flight capacity determine pollen carry-over and thus the distances over which the pollen is dispersed (Barrett and Harder, 1996; Barrett, 2003). Ecological factors, such as population spatial distribution and density and flowering phenology, may also affect the foraging behavior of pollinators, and in turn, the distance of pollen dispersal (Handel, 1983; Ghazoul, 2005). In mass-flowering species, with high synchrony of flowering of neighboring plants, pollen dispersal distance may be shorter because of the high proportion of pollination between neighbors, but the asynchrony of flowering of neighboring plants may result in a longer distance of pollen dispersal (Augspurger, 1980; White and Boshier, 2000).
Moreover, variation among flowering seasons in flowering phenology, such as time of flowering, synchrony and length of flowering, and fluctuations in the abundance of pollinators may cause a variation in pollen dispersal distance, and then in effective population size and neighborhood (Levin and Kerster, 1974; Levin, 1978). As fecundity is generally correlated with individual plant size, effective population size may be affected by differential contribution of individual plants in flowering seasons (Gottlieb, 1977; Heywood, 1986). As a consequence, populations may experience temporal variation in heterozygosity and in the evolutionary effects of genetic drift, population inbreeding and selection (Wright, 1931, 1969; Balloux and Lehmann, 2003). Therefore, the study of temporal variation in pollen dispersal distance and genetic neighborhood is highly important to conservation planning and to understand population evolution.
Forest fragmentation may also decrease effective population size and cause a disruption in ecological and genetic processes (see Ewers and Didham, 2006; Aguilar et al., 2008), negatively affecting reproductive success (see Lowe et al., 2005; Aguilar et al., 2006 for reviews). Isolated populations may receive fewer flower visitors because of the decline in the richness and abundance of pollinators, modifications in species composition and limitation in movement among patches (Cascante et al., 2002; Goverde et al., 2002; Quesada et al., 2004). However, an increased number of studies has been showing that long-distance pollen flow is common in Neotropical trees (Hamrick and Murawski, 1990; Nason et al., 1998; Latouche-Hallé et al., 2004; Dunphy and Hamrick, 2007) and also that gene flow may occur between forest fragments and isolated remnant trees (White et al., 2002, Dick et al., 2003). The range in pollen dispersal distance is very large, ranging from ∼100 to >14.5 km, most likely due to differences in species life history traits and pollinator behavior (see Ward et al., 2005; Dick et al., 2008 for reviews).
Tabebuia aurea (Manso) Benth. & Hook. f. ex S. Moore (Bignoniaceae) is a widespread Brazilian cerrado tree species with local clumped spatial distribution. It is a mass-flowering species, with big-bang flowering pattern sensu Gentry (1974) that usually lasts for <1 month in the dry season (July–August). The yellow flowers are pollinated by large bees such as carpenter bees and bumblebees and seeds are dispersed by wind (Barros, 2001). Controlled pollination experiments indicate that the species present late-acting self-incompatibility (Gibbs and Bianchi, 1993).
In this study, we studied pollen dispersal distance and breeding structure in a population of T. aurea, in an Ecological Station in Central Brazil, comparing 2 flowering seasons, based on 10 highly informative microsatellite loci previously developed for T. aurea (Braga et al., 2007). For this, we estimated pollen dispersal distance using a paternity assignment test (Marshall et al., 1998) and tested the hypothesis of differentiation in pollen dispersal distance between flowering seasons and among mother trees. Our working hypothesis was that pollen dispersal follows the distribution of nearest neighbors due to clumped distribution and mass flowering. The outcome of this prediction would be low-distance pollen dispersal, high differentiation and positive correlation between differentiation in pollen pool among mother trees and spatial distance, and also strong spatial genetic structure (SGS). To test our predictions, we compared the frequency distribution of pollen dispersal distance with nearest-neighbors distance distribution and estimated the differentiation in pollen pool (φFT) among mother trees using the method implemented in the software TWOGENER (http://poldisp.googlepages.com) (Austerlitz and Smouse, 2001, 2002). Furthermore, we tested the correlation between differentiation and distance with a Mantel test. SGS was analyzed using the method developed by Hardy and Vekemans (2002) to test the prediction of strong SGS. We also analyzed pollen dispersal between the population inside the reserve and a patch of nine isolated individuals on the edge of the reserve to verify whether fragmentation over distances of >1 km ceases the pollen dispersal in this tree species and tested the hypothesis that isolated individuals are sinking for pollen from the population inside the reserve.
Materials and methods
Study site and sampling
The study was conducted in one population of T. aurea at the Aguas Emendadas Ecological Station (15o35′04.7′′S, 47o39′59.7′′), Central Brazil, a 10 547 ha of preserved cerrado. The cerrado biome originally covered nearly 22% of the Central and Central-east Brazil, but it has been intensively fragmented in the last decades and <50% of its original area remains (Klink and Machado, 2005). The cerrado biome comprises a very heterogeneous vegetation, with seasonal savannas (cerrado), hyperseasonal savannas (vereda) on poorly drained soils, rocky savannas (campo rupestre), mesophytic evergreen forests (gallery forest) and deciduous and semi-deciduous seasonally dry forests (for a detailed description of cerrado biome, see Silva et al., 2006). In the cerrado vegetation, tree species are distributed in high-density clumps due to the patch distribution of suitable habitat or restricted seed dispersal (Hay et al., 2000).
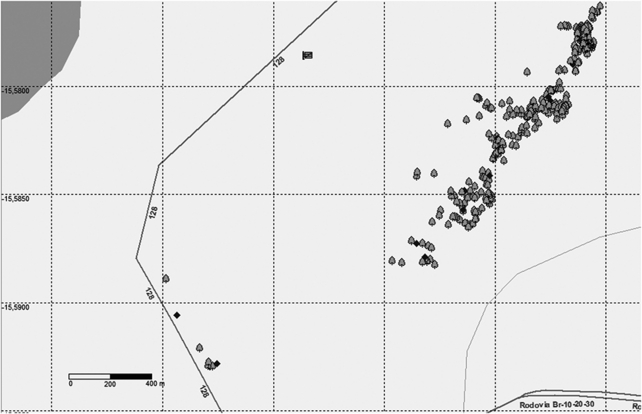
All adult individuals (260) of T. aurea in a patch of 40 ha (6.5 individuals per ha) were mapped and expanded leaves were collected (Figure 1). Nine isolated individuals on the edge of the Ecological Station were also sampled (Figure 1) to assess the effect of isolated individuals in pollen dispersal. We considered a threshold distance of 1000 m to the nearest neighbor to include individual trees in the patch.
Figure 1.
Map of 260 adult individuals in the population of Tabebuia aurea and the 9 isolated individuals sampled in the Ecological Station of Aguas Emendadas, Central Brazil. Diamonds are the mother trees for which progeny arrays were collected. The dark gray line represents the western limit of the reserve (the road DF128) and the double line (the road BR020) is the southwestern limit. The pale gray line is the Brejinho stream. Population has 40 ha and 6.3 individuals per ha. A point may represent two or more trees attributed to the small distance among individuals.
From the 260 adults, 21 trees were randomly selected (Figure 1) to sample the open-pollinated progeny arrays in the flowering seasons of 2004 and 2005. In addition, three trees from the nine isolated individuals were selected to sample progeny arrays. In all, 2–8 fruits were collected in each tree and 4–8 seeds were analyzed in each fruit (at least 10 seeds per mother tree). Genomic DNA extraction followed the CTAB (hexadecyltrimethylammonium bromide) 2% protocol (Doyle and Doyle, 1987).
Microsatellite analyses
All adults and open-pollinated progeny arrays were genotyped using 10 microsatellite loci previously developed for T. aurea (Braga et al., 2007). Primers were labeled with one of the fluorescent dyes 6-FAM, HEX or NED (Applied Biosystems, Foster City, CA, USA), and PCR amplifications were performed in 10 μl volume containing 0.5 μ of each primer, 1 Unit of Taq DNA polymerase (Phoneutria, BR), 250 μ of each dNTP, 0.25 μg of bovine serum albumin and 9 ng of template DNA. For amplifications, we used a GeneAmp PCR System 9600 (Applied Biosystems) under the following conditions: 95 °C for 5 min (1 cycle); 94 °C for 1 min, 56 °C for 1 min, 72 °C for 1 min (35 cycles); 72 °C for 30 min (1 cycle). An additional cycle of 72 °C for 1 h was added to avoid mistyping due to the non-template addition of adenine by TaqDNA polymerase (see Magnuson et al., 1996).
The amplified products were electrophoresed in the ABI 3130 XL automated DNA sequencer (Applied Biosystems). An automated genotyping system was developed for the 10 loci in the Genotyper 3.7 software (Applied Biosystems), assigning each allele to a ‘bin' based on the histogram generated by 36 randomly chosen adult individuals. The automated allele sizing successfully improves genotyping, avoiding scoring errors due to stutter band and non-template addition of adenine by TaqDNA polymerase.
Genotype errors due to stutter bands, allele dropout and null alleles were estimated using the Micro-Checker software (http://www.microchecker.hull.ac.uk/) (Oosterhout et al., 2004). Microsatellite loci were characterized based on the 260 adult individuals. The number of alleles per locus, observed and expected heterozygosity under the Hardy–Weinberg equilibrium and inbreeding coefficient (f) were estimated (Nei, 1978). Analyses were performed using FSTAT 2.9.3.2 (http://www2.unil.ch/popgen/softwares/fstat.htm) (Goudet, 2002), and randomization-based tests with Bonferroni's correction were performed to test for deviation from the Hardy–Weinberg expectation and linkage equilibrium (Goudet et al., 1996). The probability of genetic identity (I) (Chakravaratt and Li, 1983) and that of paternity exclusion (Q) (Weir, 1996) were estimated for each locus and the combined probability of paternity exclusion, QC=1−(Π(1−Qi)), and the combined probability of genetic identity, IC=Π Ii, were estimated for the overall loci.
Breeding structure and pollen dispersal
Before paternity analyses, mismatching between the mother tree and each offspring was visually inspected, and the offspring was removed when mismatching was identified to avoid error due to null alleles and dropout.
The paternity assignment test approach (Marshall et al., 1998) was used to identify the most likely pollen donor and determine the mating structure and pollen dispersal distance. The assignment test was performed using the maximum likelihood-based method implemented in CERVUS 3.0.3 software (http://helios.bto.ed.ac.uk/evolgen) (Kalinowski et al., 2007). To obtain the critical values of Δ at 99% confidence, we carried out two simulations: in the first simulation, we considered that 80% of the candidate parents were sampled, and in the second, we considered that we sampled 100% of the candidate parents. Both simulations were run with 10 000 cycles and considering 1% of genotyping error. Parentage analyses were carried out considering both simulations, but the paternity assignment did not differ between the two analyses because of the high logarithm of odds ratio score of the most likely father for all offspring; thus, we presented only the results for simulation considering 80% of candidate parents sampled, with critical Δ=2.11 at 99% confidence. Cryptic gene flow, that is, the probability that an adult matched an unrelated offspring or the chance that an offspring assigned to a parent in the population is actually the offspring of a tree outside the population, was estimated following Westneat and Webster (1994) and Dow and Ashley (1996).
To analyze the pollen dispersal distance and breeding structure, we obtained the pairwise distance between each mother tree and pollen donor to generate the frequency distributions of pollen dispersal distance, mean distance and variance. Variation in pollen dispersal distance between flowering seasons was tested with an analysis of variance for repeated measures, considering the effects of variation between flowering seasons, among progeny arrays and the interaction between these two factors (Sokal and Rohlf, 1995). Frequency distributions of pollen dispersal distances from 2004 and 2005 were compared using the Kolmogorov–Smirnov test (Sokal and Rohlf, 1995). These distributions were also compared with the frequency distribution of distance among adult plants and among the nearest neighbors in a population using the Kolmogorov–Smirnov test (Sokal and Rohlf, 1995). In addition, we estimated the differentiation of allelic frequencies among the pollen pools sampled by the females in the population, φFT (Smouse et al., 2001, Austerlitz and Smouse, 2001, 2002), using the software TWOGENER (Austerlitz and Smouse, 2001, 2002). The Mantel test was performed between pairwise φFT and spatial distance matrices to test the hypothesis that differentiation increases with distance. We also analyzed variation in proportion of self-pollination (logarithmic transformed) between flowering seasons and among mother trees using an analysis of variance for repeated measures.
The effective neighborhood pollination area (Levin, 1988), that is, a circle around flowering individuals whose radius is equivalent to the variance of the gene dispersal, was estimated for each flowering season using the equation Ae=2πσp2. The neighborhood is the area of a deme within which mating is random, considering hermaphroditic species and Poisson distribution of the number of offspring per parent (Wright, 1943, 1946). The effective size of a neighborhood (Ne) is equivalent to the number of flowering individuals within the genetic neighborhood area, Ne=Ad, where d is the density of flowering plants.
Spatial genetic structure
An autocorrelation analysis was performed to verify SGS in parental population using the software SPAGeDI (http://www.ulb.ac.be/sciences/ecoevol/spagedi.html) (Hardy and Vekemans, 2002), and to test the prediction of a strong SGS. The kinship between all pairs of adult individuals was estimated using the Nason estimator Fij (Loiselle et al., 1995). The relationship between kinship and spatial distance was analyzed by linear regression over 24 distance classes (in meters): 0–10, 10–20, 20–30, 30–40, 40–50, 50–100, 100–200, 200–300, 300–400, 400–500, 500–600, 600–700, 700–800, 800–900, 900–1000, 1000–1250, 1250–1500, 1500–1750, 1750–2000, 2000–2250, 2250–2500, 2500–2750, 2750–3000 and >3000. These distances were selected on the basis of the frequency distribution of distance among adults and the number of individuals in each distance class (at least 30 pairs) by a permutation test. Permutation tests (1000 permutations) were performed to verify the significance of kinship for each distance class and the regression. s.e. were estimated by jackknife over loci, and the intensity of the SGS was quantified using the parameter Sp=b/(F1−1), where F1 is the average kinship coefficient between individuals of the first distance class and b the slope of the regression, following Vekemans and Hardy (2004).
Results
Characterization of microsatellite loci
All pairs of loci were in linkage equilibrium (all P>0.0011, Bonferroni's adjusted value for a nominal level of 5%). The 10 microsatellite loci displayed high levels of polymorphism (Table 1). For all loci, observed heterozygosity was lower than the expected under the Hardy–Weinberg equilibrium leading to a significant inbreeding coefficient (Table 1). The analysis of raw data in the Micro-Checker software (Oosterhout et al., 2004) showed that the results were not due to genotyping errors or null alleles (results not shown). Nevertheless, the high combined paternity exclusion probability (QC=0.988923) and the low combined probability of identity (IC=1.033 × 10−37) showed that the battery of loci is suitable for parentage analyses (Table 1).
Table 1. Characterization of the 10 microsatellite loci of Tabebuia aurea based on 260 adult individuals sampled in a cerrado area of Central Brazil.
| Locus | A | He | Ho | f | Q | I |
|---|---|---|---|---|---|---|
| Tau12 | 37 | 0.968 | 0.631 | 0.349 | 0.862 | 0.008 |
| Tau13 | 27 | 0.941 | 0.698 | 0.206 | 0.873 | 0.007 |
| Tau14 | 24 | 0.913 | 0.789 | 0.134 | 0.775 | 0.024 |
| Tau15 | 33 | 0.937 | 0.761 | 0.235 | 0.811 | 0.017 |
| Tau16 | 39 | 0.951 | 0.879 | 0.072 | 0.879 | 0.007 |
| Tau17 | 45 | 0.961 | 0.911 | 0.037 | 0.865 | 0.009 |
| Tau21 | 47 | 0.958 | 0.805 | 0.116 | 0.824 | 0.015 |
| Tau24 | 26 | 0.931 | 0.733 | 0.148 | 0.753 | 0.028 |
| Tau28 | 33 | 0.953 | 0.638 | 0.288 | 0.811 | 0.017 |
| Tau31 | 42 | 0.960 | 0.805 | 0.140 | 0.718 | 0.039 |
| Overall | 36 | 0.947 | 0.765 | 0.178 | QC=0.988923 | IC=1.033 × 10−37 |
A, number of alleles; f, inbreeding coefficient (all values are significant, P<0.005, Bonferroni's adjusted P-value for a nominal level of 5%); He, expected heterozygosity; Ho, observed heterozygosity; I, probability of genetic identity; IC, combined probability of genetic identity; Q, probability of paternity exclusion; QC, combined probability of paternity exclusion.
Breeding structure and pollen dispersal
A total of 21 open-pollinated progeny arrays were analyzed in each flowering season (2004 and 2005). We sampled a total of 267 fruits and the mean number of seeds per fruit was 61.4 (s.d.=11.6 seeds per fruit). From these fruits, we analyzed 309 seeds (124 fruits) in the flowering season of 2004 and 328 seeds (143 fruits) in 2005.
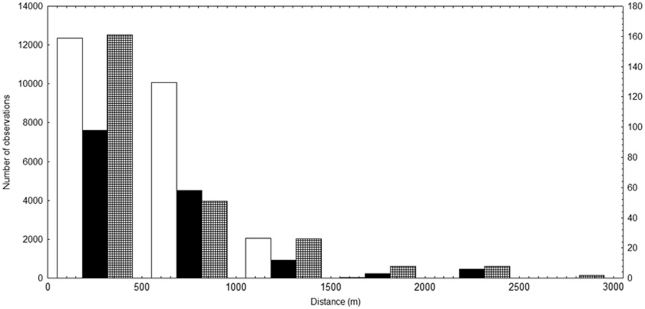
The mean distance among adult individuals in the population is 537.52 m (s.d.=308.33 m) and median is 496.28 m (Figure 2), but most individuals are distant from each other by <600 m (60%, Figure 2). The mean distance from isolated individuals and population is 1887.69 m (s.d.=435.63 m) and median is 1978.57 m.
Figure 2.
Pairwise distance frequency distribution of 260 adult individuals (white bars, primary y axis, left scale) in the population of Tabebuia aurea in a cerrado area of Central Brazil and pollen dispersal distribution based on the distance between each pollen donor assigned by CERVUS and the mother tree in the flowering season of 2004 (black bars, secondary y axis, right scale) and 2005 (cross line bars, secondary y axis, right scale).
All progeny could be assigned to paternal trees within our sample with no mismatch at 99% confidence (critical Δ=2.11). For most offspring, just one candidate father presented Δ higher than the critical Δ. When more than one candidate father was assigned, we excluded the other candidate fathers based on the mismatching among know parent, candidate 0.000026 (1–0.9999999260). Thus, the number of seeds that matched unrelated males by chance was likely to be 0.008 in 2004 (309 × 0.000026) and 0.0085 in 2005 (328 × 0.000026).
The mean pollen dispersal distance differed between the two flowering seasons (Table 2; F=5.751, df=1, P=0.017). In addition, the mean pollen dispersal distance varied significantly among mother trees (F=20.388, df=20, P<0.001), and the mother trees contribute differently in the two flowering seasons to the pollen dispersal (F=6.439, df=40, P<0.001). Effective neighborhood pollination area and effective population size were higher than census size for both flowering seasons (Table 2). In addition, both parameters were much higher in the flowering season of 2005 (Table 2) than in that of 2004.
Table 2. Temporal variation in pollen dispersal distance in a population of Tabebuia aurea in a cerrado area of Central Brazil, in two flowering seasons.
| Season | N | Mean PD (s.d.) (m) | Max PD (m) | Median PD (m) | Ne | Ae (ha) |
|---|---|---|---|---|---|---|
| 2004 | 309 | 307.78 (438.80)a | 2339 | 118.00 | 786.37 | 120.98 |
| 2005 | 328 | 396.26 (546.77)b | 2608 | 161.00 | 1220.96 | 187.84 |
Ae, effective neighborhood pollination area (hectares); N, number of seeds analyzed; ; Ne, effective population size; PD, pollen dispersal distance (meters).
The analyses were based in 21 progeny arrays.
Mean PD values were statistically different, P = 0.017.
The proportion of self-pollination varied significantly between the flowering season and the mother tree (F=5.033, df=1, P<0.001, flowering season effect; F=23,397, df=20, P<0.001, mother tree; F=7.894, df=40, P<0.001, interaction). The mean proportion of self-pollination was 42.5% in 2004 and 20% in 2005.
In the flowering season of 2004 and 2005, most pollination events occurred at a distance <300 m (65%) and 75% at distance lower than 600 m (Figure 2). The lowest distance of cross-pollination was 6.0 and 4.0 m (between nearest neighbors) in the flowering seasons of 2004 and 2005, respectively. The frequency distribution of pollen dispersal distance was significantly different from the distribution of distance among adults in population (Figure 2) for both flowering seasons (2004, Kolmogorov–Smirnov test 0.447, P<0.001; 2005, Kolmogorov–Smirnov test 0.450, P<0.001). Besides, pollen dispersal and nearest-neighbor distance frequency distributions were different (2004, Kolmogorov–Smirnov test 0.550, P<0.001; 2005, Kolmogorov–Smirnov test 0.604, P<0.001). The mean distance of nearest neighbors was 13.67 m (s.d.=15.52 m), and the maximum distance was 62.43 m but median was 10.0 m and most neighbor individuals were at distance lower than 14.00 m (60%). In addition, the distribution of pollen dispersal distance differed between flowering seasons (Kolmogorov–Smirnov test 0.374, P<0.001).
Analyses performed using TWOGENER showed a high differentiation in the pollen pool received by mother trees (pairwise φFT ranged from 0.077 to 0.337), with global φFT=0.202 and φFT=0.152, for 2004 and 2005, respectively. In addition, differentiation in the pollen pool among mother trees was significantly related to pairwise spatial distance in both seasons (2004, R=0.159, P=0.038; 2005, R=0.427, P<0.001).
Pollen donor frequency distribution was not homogeneous in both flowering seasons (Kolmogorov–Smirnov test statistic=0.235, P<0.001 for 2004; Kolmogorov–Smirnov test statistic=0.097, P=0.004, for 2005). In the flowering season of 2004, 5 trees presented higher fecundity, and each tree was responsible for ∼4% of the pollination events. However, for these 5 trees, the higher fecundity was due to self-pollination because they had >60% of seeds sired by self-pollination. If self-pollination is excluded from the analysis, other three plants presented higher fecundity, and each tree was responsible for 2.8% of the pollination events. In the flowering season of 2005, 4 other pollen donors presented higher fecundity and each one was responsible for 3.5% of the 328 pollination events analyzed. For two pollen donors, the higher fecundity was due to self-pollination (∼50% of their ripened seeds were sired by self-pollination).
From the nine isolated individuals, three were responsible for siring eight seeds from the sampled population in the reproductive season of 2004 and seven seeds in 2005 (including the event of maximum pollen dispersal distance—2608 m). Although most seeds from isolated individuals were sired by the nearest neighbors, they also received pollen from the sampled population (25% of the seeds).
Considering only the population inside the Ecological Station, the mean pollen dispersal was 266.43 m (s.d.=346.71 m) in the flowering season of 2004, and the maximum pollen dispersal was 1651 m. In the flowering season of 2005, the mean pollen dispersal distance was 388.36 m (s.d.=515.31 m) and the maximum pollen dispersal was 2484 m. Effective neighborhood pollination area and effective population size were also lower (Ne=490.95 individuals and Ae=75.53 ha, for 2004; Ne=1,084.53 individuals, Ae=166.85 ha, in 2005). The proportion of seeds sired by isolated individuals was 2.6% (8 seeds in 309) in the flowering season of 2004 and 2.1% (7 seeds in 328) in 2005. On the basis of these values, the number of immigrants per generation from the patch of isolated individuals into the population inside the reserve was directly estimated as follows (Trapnell and Hamrick, 2005): Nem=½Ne(sm/st), where sm and st are the number of seeds sired by immigrant pollen and the total number of analyzed seeds, respectively. Considering Ne estimated above, the number of immigrants per generation was 6.36 in 2004 and 11.57 in 2005.
Spatial genetic structure
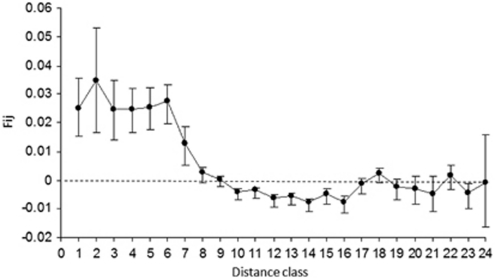
Kinship was slightly related to the spatial distance (b=−0.0059, R2=0.011, P<0.001; Figure 3) and was significant (P<0.05) until the distance class 8 (200–300 m, Figure 3). However, Fij of the first distance class was low (F1=0.0251, P=0.009), leading to a weak spatial structure (Sp=0.0061).
Figure 3.
Relationship between kinship (Fij±s.e.) and distance for 260 adult individuals in the population of Tabebuia aurea in a cerrado area of Central Brazil. Distance class are (in meters): 0–10, 10–20, 20–30, 30–40, 40–50, 50–100, 100–200, 200–300, 300–400, 400–500, 500–600, 600–700, 700–800, 800–900, 900–1000, 1000–1250, 1250–1500, 1500–1750, 1750–2000, 2000–2250, 2250–2500, 2500–2750, 2750–3000 and >3000.
Discussion
Our results showed a high temporal variation in pollen dispersal and breeding structure between flowering seasons, leading to a high variation in effective neighborhood pollination area and effective population size. The distance of pollen dispersal in the flowering season of 2004 was lower than that in 2005. In addition, the proportion of self-pollination was higher in the flowering season of 2004 (42.5% in 2004 and 20% in 2005), which probably affected the mean pollen dispersal distance and neighborhood size. Unexpectedly, this study provides a new insight into the mating system of T. aurea, acknowledged as a self-incompatible species (Gibbs and Bianchi, 1993). The authors observed pollen tube growing in pistils after controlled self-pollination but no fruit development and concluded that T. aurea is self-incompatible with late-acting mechanism. Late-acting self-incompatibility is also named ovarian self-incompatibility because self-pollen germinates and reaches the ovules, but no fruit is set (Seavey and Bawa, 1986). The existence of the Late-acting self-incompatibility mechanism is still in debate, and some authors argue that the absence of fruit set is the outcome of inbreeding depression due to self-fertilization (Waser and Price, 1991; Mahy and Jacquemart, 1999). The variation in the proportion of self-pollination among individuals and between flowering seasons in T. aurea suggest that the breeding biology of this species may be more complex or flexible than previously believed. The report of variation in self-fertility among plants in self-incompatible species suggests that pseudo-self-fertility alleles may modify the expression of the S locus (Lipow and Wyatt, 2000).
The breeding structure also differed because different individuals had higher fecundity and higher proportion of self-pollination in different flowering seasons. The pollen dispersal distance within mother trees differed between flowering seasons as well. Although the population's flowering pattern did not differ between the flowering seasons analyzed in this study (flowering time and duration), a variation in the number of flowers within individuals was observed, and usually individuals that produced high number of flowers in one flowering season presented a low number of flowers in the subsequent season (RG Collevatti, unpublished). Hence, individual fecundity and contribution to pollen dispersal may be highly heterogeneous among flowering seasons.
T. aurea presents long-distance pollen dispersal, of at least 2600 m. However, most pollination events occurred at distances lower than 300 m (65%). This may be the outcome of pollinator foraging behavior. Owing to their flight capacity, large bees may carry pollen over long distances (Goulson and Stout, 2001). In mass-flowering species, the residence time of pollinators may be greater decreasing pollen carry-over and thus effective population size (Frankie et al., 1976). Therefore, the mass-flowering pattern, with highly within individual and population synchronous flowering, high population density and clumped distribution may affect pollinator foraging behavior, increasing residence time and leading to a high proportion of low-distance pollen dispersal and self-pollination. Nevertheless, in T. aurea, the individual flowering pattern (number of flowers and distribution among branches) in each year is highly variable (RG Collevatti, unpublished), which may decrease the frequency of pollination between nearest neighbors and increase pollen dispersal distance (Kitamoto et al., 2006). In fact, our results showed that bee pollinators of T. aurea may not fly to nearest-neighbor trees, because the frequency distribution of pollen dispersal distance was different from nearest-neighbor distribution for both flowering seasons. Thus, the relationship between pollen pool differentiation among mother trees and spatial distance was not due to nearest-neighbor pollination. However, cross-pollination between nearest neighbors was observed in some individuals and it was especially frequent in isolated individuals and in some individuals on the edge of the population. For instance, from the three progeny arrays sampled from isolated trees, ∼50% of the seeds were sired by the nearest neighbors. These results also explain the weak SGS. Although a significant SGS was observed in adult population, kinship was low in all distance class (<0.035) and also declines very fast after the sixth class of distance (50–60 m). Moreover, Sp was very low and showed that SGS is weak suggesting long-distance seed dispersal (Vekemans and Hardy, 2004).
Pollen dispersal distances in the two flowering seasons were comparable with distances found for other Neotropical tree species. For instance, Dicorynia guianensis (Fabaceae) presents long-distance pollen dispersal with a neighborhood size of 560 ha and >65% of pollen dispersal at distance >700 m (Latouche-Hallé et al., 2004). Platypodium elegans (Fabaceae) also presents a high proportion of long-distance pollen dispersal over 750 m (Hamrick and Murawski, 1990). Both species are pollinated by large bee species but are low-density canopy species from Neotropical rain forest. However, Glyricidia sepium (Fabaceae), a low-density tree from Guatemala forests also pollinated by large bees, presents maximum pollen dispersal of 275 m (Dawson et al., 1997). These contrasting results show that life history traits and ecological factors other than spatial distribution and pollinator species modulate pollen dispersal. Many aspects of the pollination system such as nectar and pollen presentation may affect pollinator movement within and among flowering plants, and thus the distance of pollen dispersal (Levin and Anderson, 1970; Schmitt, 1980).
Despite variation between flowering seasons, effective neighborhood pollination area and effective population size were higher than the number of individuals and the area sampled. These results indicated that the distance of gene flow by pollen may be higher than that estimated in this study. Although the patch of nine individuals on the edge of the Ecological Station were >1.0 km distant from the last sampled individuals of the population inside the Ecological Station, our results indicated that all sampled individuals belong to the same population but pollen dispersal is asymmetrical—the isolated patch of individuals is sinking for pollen and eventually provides pollen for the population inside the park. Our results were not driven by the artifact of mismatching between unrelated father and offspring because cryptic gene flow levels were extremely low in both flowering seasons.
In conclusion, our study showed that T. aurea presents long-distance pollen dispersal and strongly supports that T. aurea has mixed-mating system and that self-pollination rate may be highly variable within population and between flowering seasons. Pollen dispersal distance, breeding structure and effective neighborhood pollination area vary greatly among flowering seasons. Thus, the maintenance of a large population for long-term species viability is required, to guarantee a higher proportion of pollen flow among unrelated individuals increasing heterozygosity and preventing inbreeding depression, and minimizing the effects of effective population size fluctuations.
Acknowledgments
This work was supported by CNPq (Brazilian Ministry of Science and Technology) by a competitive grant to RGC and a scholarship to ACB. We thank Alessandra MM Reis for the kind help in the field work, Dario Grattapaglia for the kind help with laboratory supplies, the Subject Editor and an anonymous reviewer for helpful comments on the paper.
The authors declare no conflict of interest.
References
- Aguilar R, Ashworth L, Galetto L, Aizen MA. Plant reproductive susceptibility to habitat fragmentation: review and synthesis through a meta-analysis. Ecol Lett. 2006;9:968–980. doi: 10.1111/j.1461-0248.2006.00927.x. [DOI] [PubMed] [Google Scholar]
- Aguilar R, Quesada M, Ashworth L, Herrerias-Diego Y, Lobo J. Genetic consequences of habitat fragmentation in plant populations: susceptible signals in plant traits and methodological approaches. Mol Ecol. 2008;17:5177–5188. doi: 10.1111/j.1365-294X.2008.03971.x. [DOI] [PubMed] [Google Scholar]
- Augspurger CK. Mass-flowering of a tropical shrub (Hybanthus prunifolius): influence on pollinator attraction and movement. Evolution. 1980;34:475–488. doi: 10.1111/j.1558-5646.1980.tb04837.x. [DOI] [PubMed] [Google Scholar]
- Austerlitz F, Smouse PE. Two-generation analysis of pollen flow across a landscape. II. Relation between fFT, pollen dispersal and inter-females distance. Genetics. 2001;157:851–857. doi: 10.1093/genetics/157.2.851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Austerlitz F, Smouse PE. Two-generation analysis of pollen flow across a landscape. IV. Estimating the dispersal parameter. Genetics. 2002;161:355–363. doi: 10.1093/genetics/161.1.355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balloux F, Lehmann L. Random mating with a finite number of matings. Genetics. 2003;65:313–2315. doi: 10.1093/genetics/165.4.2313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barros MG. Pollination ecology of Tabebuia aurea (Manso) Benth. & Hook. and Tabebuia ochracea (Cham.) Standl. (Bignoniaceae) in Central Brazil cerrado vegetation. Revista Brasileira de Botânica. 2001;24:255–261. [Google Scholar]
- Barrett SCH. Mating strategies in flowering plants: the outcrossing–selfing paradigm and beyond. Phil Trans R Soc Lond B. 2003;358:991–1004. doi: 10.1098/rstb.2003.1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett SCH, Harder LD. Ecology and evolution of plant mating. Trends Ecol Evol. 1996;11:73–79. doi: 10.1016/0169-5347(96)81046-9. [DOI] [PubMed] [Google Scholar]
- Braga AC, Reis AMM, Leoi LT, Pereira RW, Collevatti RG. Development and characterization of microsatellite markers for the tropical tree species Tabebuia aurea (Bignoniaceae) Mol Ecol Notes. 2007;7:53–56. [Google Scholar]
- Cascante A, Quesada M, Lobo JJ, Fuchs EA. Effects of dry tropical forest fragmentation on the reproductive success and genetic structure of the tree Samanea saman. Conserv Biol. 2002;16:137–147. doi: 10.1046/j.1523-1739.2002.00317.x. [DOI] [PubMed] [Google Scholar]
- Chakravaratt I, Li CC.1983The effect of linkage on paternity calculationsIn: Walkera RH (ed).Inclusion Probabilities in Parentage Testing American Association of Blood Banks: Arlington; 411–420. [Google Scholar]
- Dawson IK, Waugh R, Simons AJ, Powell W. Simple sequence repeats provide a direct estimate of pollen-mediated gene dispersal in the tropical tree Gliricidia sepium. Mol Ecol. 1997;6:179–183. [Google Scholar]
- Dick CW, Etechelecu G, Austerlitz F. Pollen dispersal of tropical trees (Dinizia excelsa: Fabaceae) by native insects and African honeybees in pristine and fragmented Amazonian rainforest. Mol Ecol. 2003;12:753–764. doi: 10.1046/j.1365-294x.2003.01760.x. [DOI] [PubMed] [Google Scholar]
- Dick CW, Hardy OJ, Jones FA, Petit RJ. Spatial scales of pollen and seed-mediated gene flow in tropical rain forest trees. Trop Plant Biol. 2008;1:20–33. [Google Scholar]
- Dow BD, Ashley MV. Microsatellite analysis of seed dispersal and parentage of saplings in bur oak, Quercus macrocarpa. Mol Ecol. 1996;5:615–627. [Google Scholar]
- Doyle JJ, Doyle JL. Isolation of plant DNA from fresh tissue. Focus. 1987;12:13–15. [Google Scholar]
- Dunphy BK, Hamrick JL. Estimation of gene flow into fragmented populations of Bursera simaruba (Burseraceae) in the dry-forest life zone of Puerto Rico. Am J Bot. 2007;94:1786–1794. doi: 10.3732/ajb.94.11.1786. [DOI] [PubMed] [Google Scholar]
- Ewers RM, Didham RK. Confounding factors in the detection of species responses to habitat fragmentation. Biol Rev. 2006;81:117–142. doi: 10.1017/S1464793105006949. [DOI] [PubMed] [Google Scholar]
- Frankie GW, Opler PA, Bawa KS. Foraging behavior of solitary bees: implications for outcrossing of a Neotropical forest tree species. J Ecol. 1976;64:1049–1057. [Google Scholar]
- Gentry AH. Flowering phenology and diversity in tropical Bignoniaceae. Biotropica. 1974;6:64–68. [Google Scholar]
- Ghazoul J. Pollen and seed dispersal among dispersed plants. Biol Rev. 2005;80:413–443. doi: 10.1017/s1464793105006731. [DOI] [PubMed] [Google Scholar]
- Gibbs PE, Bianchi M. Post-pollination events in species of Chorisia (Bombacaceae) and Tabebuia (Bignoniaceae) with late acting self-incompatibility. Acta Botanica Brasilica. 1993;106:64–71. [Google Scholar]
- Gottlieb LD. Genotypic similarity of large and small individuals in a natural population of the annual plant Stephanomeria exigua ssp. coronaria (Compositae) J Ecol. 1977;65:127–134. [Google Scholar]
- Goudet J.2002FSTAT, a program to estimate and test gene diversities and fixation indices (version 2.9.3.2)Free available from http://www.unil.ch/izea/softwares/fstat.html .
- Goudet J, Raymond M, Meeds T, Rousset F. Testing differentiation in diploid populations. Genetics. 1996;144:1933–1940. doi: 10.1093/genetics/144.4.1933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goulson D, Stout JC. Homing ability of the bumblebee Bombus terrestris (Hymenoptera: Apidae) Apidologie. 2001;32:105–111. [Google Scholar]
- Goverde M, Schweizer K, Baur B, Erhardt A. Small-scale habitat fragmentation effects on pollinator behavior: experimental evidence from the bumblebee Bombus veteranus on calcareous grasslands. Biol Conserv. 2002;104:293–299. [Google Scholar]
- Hamrick JL, Murawski DA. The breeding structure of tropical tree populations. Plant Species Biol. 1990;5:157–165. [Google Scholar]
- Handel SN.1983Pollination ecology, plant population structure and gene flowIn: Real L (ed).Pollination Biology Academic Press: Orlando; 163–212. [Google Scholar]
- Hardy OJ, Vekemans X. SPAGeDi: a versatile compute program to analyze spatial genetic structure at the individual or population levels. Mol Ecol Notes. 2002;2:618. [Google Scholar]
- Hay JD, Bizerril MX, Calouro AM, Costa EMN, Ferreira AA, Gastal MLA, et al. Comparação do padrão da distribuição espacial em escalas diferentes de espécies nativas do cerrado, em Brasília, DF. Revista Brasileira de Botânica. 2000;23:341–347. [Google Scholar]
- Heywood JS. The effect of plant size variation on genetic drift in populations of annuals. Am Nat. 1986;127:851–861. [Google Scholar]
- Kalinowski ST, Taper ML, Marshall TC. Revising how the computer program Cervus accommodates genotyping error increases success in paternity assignment. Mol Ecol. 2007;16:1099–1106. doi: 10.1111/j.1365-294X.2007.03089.x. [DOI] [PubMed] [Google Scholar]
- Kitamoto N, Ueno S, Takenaka A, Tsumura Y, Washitani I, Ohsawa R. Effect of flowering phenology on pollen flow distance and the consequences for spatial genetic structure within a population of Primula sieboldii (Primulaceae) Am J Bot. 2006;93:226–233. doi: 10.3732/ajb.93.2.226. [DOI] [PubMed] [Google Scholar]
- Klink CA, Machado RB. Conservation of the Brazilian cerrado. Conserv Biol. 2005;19:707–713. [Google Scholar]
- Latouche-Hallé C, Ramboer A, Bandou E, Caron H, Kremer A. Long-distance pollen flow and tolerance to selfing in a Neotropical tree species. Mol Ecol. 2004;13:1055–1064. doi: 10.1111/j.1365-294X.2004.02127.x. [DOI] [PubMed] [Google Scholar]
- Levin DA.1978Pollination behavior and the breeding structure of plant populationIn: Richard AJ (ed.).The Pollination of Flowers by Insects Academic Press: London; 133–150. [Google Scholar]
- Levin DA. The paternity pool plants. Am Nat. 1988;132:309–317. [Google Scholar]
- Levin DA, Anderson WW. Competition for pollinators between simultaneously flowering species. Am Nat. 1970;104:455–467. [Google Scholar]
- Levin DA, Kerster HW. Gene flow in seed plants. Evol Biol. 1974;7:139–220. [Google Scholar]
- Loiselle BA, Sork VL, Nason J, Graham C. Spatial genetic structure of a tropical understory shrub, Psychotria officinalis (Rubiaceae) Am J Bot. 1995;82:1420–1425. [Google Scholar]
- Lowe AJ, Boshier D, Ward M, Bacles CFE, Navarro C. Genetic resource impacts of habitat loss and degradation; reconciling empirical evidence and predicted theory for neotropical trees. Heredity. 2005;95:255–273. doi: 10.1038/sj.hdy.6800725. [DOI] [PubMed] [Google Scholar]
- Lipow SR, Wyatt R. Single gene control of postzygotic self-incompatibility in poke milkweed, Asclepias exaltata L. Genetics. 2000;154:893–907. doi: 10.1093/genetics/154.2.893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnuson VL, Ally DS, Nylund SJ, Karanjawala ZE, Rayman JB, Knapp JI, et al. Substrate nucleotide-determined non-templated addition of adenine by Taq DNA polymerase: implications for PCR-based genotyping and cloning. BioTechniques. 1996;21:700–709. doi: 10.2144/96214rr03. [DOI] [PubMed] [Google Scholar]
- Marshall TC, Slate J, Kruuk LEB, Pemberton JM. Statistical confidence for likelihood-based paternity inference in natural populations. Mol Ecol. 1998;7:639–655. doi: 10.1046/j.1365-294x.1998.00374.x. [DOI] [PubMed] [Google Scholar]
- Mahy G, Jacquemart AL. EarlyinbreedingdepressionandpollencompetitioninCalluna vulgaris (L.) Hull. Ann Bot. 1999;83:697–704. [Google Scholar]
- Nason JD, Herre EA, Hamrick JL. The breeding structure of a tropical keystone plant resource. Nature. 1998;391:685–687. [Google Scholar]
- Nei M. Estimation of average heterozygosity and genetic distance from a small number of individual. Genetics. 1978;89:583–590. doi: 10.1093/genetics/89.3.583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oosterhout CV, Hutchinson WF, Wills DPM, Shipley P. MICRO-CHECKER: software for identifying and correcting genotyping errors in microsatellite data. Mol Ecol Notes. 2004;4:535–538. [Google Scholar]
- Quesada M, Stoner KE, Lobo JA, Herrerías-Diego Y. Effects of forest fragmentation on pollinator activity and consequences for plant reproductive success and mating patterns in bat-pollinated Bombacaceous trees. Biotropica. 2004;36:131–138. [Google Scholar]
- Schmitt J. Pollinator foraging behavior and gene dispersal in Senecio (Compositae) Evolution. 1980;34:934–943. doi: 10.1111/j.1558-5646.1980.tb04031.x. [DOI] [PubMed] [Google Scholar]
- Seavey SF, Bawa KS. Late-acting self-incompatibility in angiosperms. Bot Rev. 1986;52:195–218. [Google Scholar]
- Silva JF, Fariñas MR, Felfili JM, Klink CA. Spatial heterogeneity, land use and conservation in the cerrado region of Brazil. J Biogeogr. 2006;33:536–548. [Google Scholar]
- Slatkin M. Gene flow in natural population. Annu Rev Ecol Syst. 1985;16:393–430. [Google Scholar]
- Smouse PE, Dyer RJ, Westfall RD, Sork VL. Two generation analysis of pollen flow across a landscape. I. Male gamete heterogeneity among females. Evolution. 2001;55:260–271. doi: 10.1111/j.0014-3820.2001.tb01291.x. [DOI] [PubMed] [Google Scholar]
- Sokal RR, Rohlf F.1995Biometry: The Principles and Practices of Statistics in Biological Research3rd ed.WH Freeman, and Company: New York [Google Scholar]
- Trapnell DW, Hamrick JL. Mating patterns and gene flow in the Neotropical epiphytic orchid, Laelia rubescens. Mol Ecol. 2005;14:75–84. doi: 10.1111/j.1365-294X.2004.02383.x. [DOI] [PubMed] [Google Scholar]
- Vekemans X, Hardy OJ. New insights from fine-scale spatial genetic structure analyses in plant populations. Mol Ecol. 2004;13:921–935. doi: 10.1046/j.1365-294x.2004.02076.x. [DOI] [PubMed] [Google Scholar]
- Ward M, Dick CW, Gribel R, Lowe AJ. To self, or not to self…a review of outcrossing and pollen-mediated gene flow in Neotropical trees. Heredity. 2005;95:246–254. doi: 10.1038/sj.hdy.6800712. [DOI] [PubMed] [Google Scholar]
- Waser NM, Price MV. Reproductive costs of self-pollination in Ipomopsis aggregata (Polemoniaceae): are ovules usurped. Am J Bot. 1991;78:1036–1043. [Google Scholar]
- Weir BS. Genetic Data Analysis II. Sinauer Associates: Sunderland, MA; 1996. [Google Scholar]
- Westneat DF, Webster MS.1994Molecular analysis of kinship in birds: interesting questions and useful techniquesIn: Schierwater B, Streit B, Wagner GP, DeSalle R (eds). Molecular ecology and evolution: approaches and applications. Birkhiiuser: Basel; 91–126. [Google Scholar]
- White GM, Boshier DH.2000Fragmentation in Central American dry forests: genetic impacts on Swietenia humilis (Meliaceae)In: Young AG, Clarke GM (eds).Genetics, Demography and Viability of Fragmented Populations Cambridge University Press: Cambridge, UK; 293–311. [Google Scholar]
- White GM, Boshier DH, Powell W. Increased pollen flow counteracts fragmentation in a tropical dry forest: an example from Swietenia humilis Zuccarini. Proc Natl Acad Sci USA. 2002;99:2038–2042. doi: 10.1073/pnas.042649999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Breeding structure of populations in relation to speciation. Am Nat. 1940;74:232–248. [Google Scholar]
- Wright S. Isolation by distance. Genetics. 1943;28:114–138. doi: 10.1093/genetics/28.2.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Isolation by distance under diverse system of mating. Genetics. 1946;31:39–59. doi: 10.1093/genetics/31.1.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Evolution and Genetics of Populations. IV. The Theory of Gene Frequencies. University of Chicago Press: Chicago; 1969. [Google Scholar]