Intact α_IIbβ₃ Integrin Is Extended after Activation as Measured by Solution X-ray Scattering and Electron Microscopy

Abstract

Integrins are bidirectional signaling molecules on the cell surface that have fundamental roles in regulating cell behavior and contribute to cell migration and adhesion. Understanding of the mechanism of integrin signaling and activation has been advanced with truncated ectodomain preparations; however, the nature of conformational change in the full-length intact integrin molecule remains an active area of research. Here we used small angle x-ray scattering and electron microscopy to study detergent-solubilized, intact platelet integrin α_IIbβ₃. In the resting state, the intact α_IIbβ₃ adopted a compact, bent conformation. Upon activation with Mn²⁺, the average integrin extension increased. Further activation by addition of ligand led to stabilization of the extended state and opening of the headpiece. The observed extension and conformational rearrangement upon activation are consistent with the extension and headpiece opening model of integrin activation.

Introduction

Integrins are cell adhesion receptors that transmit signals bidirectionally across the plasma membrane and are non-covalently linked heterodimers of α and β subunits (1, 2). These subunits are type I membrane glycoproteins that contain a large extracellular ligand binding domain, a single pass transmembrane domain, and a cytoplasmic domain. Conformational changes within and between these domains regulate diverse biological processes, including development, wound healing, hemostasis, and immunity (3, 4).

The human platelet integrin, α_IIbβ₃ or glycoprotein IIb/IIIa, is a model for this family of cell adhesion receptors (5). Integrin α_IIbβ₃ is highly expressed on platelets and is essential in platelet adhesion and aggregation. Regardless of the mechanism of activation, the final step for platelet aggregation is activation of α_IIbβ₃, resulting in a conformational change that enables it to bind fibrinogen and von Willebrand factor and form stable bridges between platelets (6). Regulation of integrin activity is bidirectional. For example, when platelets are stimulated, inside-out signaling causes structural rearrangements in the α_IIbβ₃ receptor to increase its affinity for ligands, including fibrinogen, von Willebrand factor, and fibronectin (7). Also, α_IIbβ₃ outside-in signaling is initiated by ligand binding that leads to kinase activation, platelet shape change, and spreading (5).

Upon activation, integrins can rapidly change from an inactive, low affinity state to an active, high affinity ligand binding state. Previous x-ray crystallography studies on the α_IIbβ₃, α_Vβ₃, and α_xβ₂ ectodomains showed that resting integrins are in a compact, bent conformation (8–10). In addition, global structural rearrangements upon activation were demonstrated by electron microscopy (EM) of soluble ectodomain truncations and supported by exposure of activation epitopes known as ligand-induced binding sites (LIBSs),³ which are not accessible in the resting state (11–15). Two distinct conformational changes are seen, extension and headpiece opening (hybrid domain swing-out), resulting in three overall conformations: bent with a closed headpiece, extended with a closed headpiece, and extended with an open headpiece that is stabilized by ligand binding (11, 16). Additionally, studies with six different function-regulating Fab fragments with α_xβ₂ (17) as well as allosteric inhibitory β₁ integrin Fab fragments (16) have shown that the bent-closed and extended-closed conformations have low affinity for ligand, and the extended-open conformation has high affinity for ligand. X-ray crystal structures of α_IIbβ₃ headpiece constructs have revealed the atomic basis for structural rearrangements upon ligand binding (8, 18, 19) and confirmed the open state in the presence of a bound ligand and the closed state in the absence of ligand (18, 20).

The extension and headpiece opening model of integrin activation has been challenged. One group reported that α_Vβ₃ could bind to ligand in the bent conformation (21), and no extension occurs on cell surfaces in the presence of ligand (22). These observations led to the dead bolt model of integrin activation in which the high affinity ligand binding state is achieved by modest quaternary changes without requiring hybrid domain swing-out or extension. However, the postulated “dead bolt” interaction that prevents integrin extension buries an insignificant surface area of only 40 Ų in α_Vβ₃ (23) and is not present in α_IIbβ₃ or α_xβ₂, and its mutation in α_Vβ₃ and α_IIbβ₃ has no effect on their ligand binding capacities (10, 24). Disulfide bonds in multiple locations to favor the bent conformation or closed headpiece and glycan wedges to stabilize extension and headpiece opening all support a requirement for integrin extension and headpiece opening for activation and the insufficiency of the bent conformation (11, 25–27).

Detergent-solubilized intact integrins are of considerable interest because they more closely represent the native state on the cell surface than integrin ectodomains. In fact, interactions between the α and β subunit transmembrane domains are important in stabilizing the resting, low affinity state (28–30). Nonetheless, results with the model integrin α_IIbβ₃ have been controversial perhaps because of the challenges of maintaining the complex between the α_IIb and β₃ subunits and a homogeneous conformational state. Detergent-solubilized α_IIbβ₃ has been reported to be in a conformation intermediate between bent and extended states based on cryo-EM (31). The possibility has been raised that this might result from averaging conformationally heterogeneous particles (32). Negative stain electron tomography of detergent-solubilized α_IIbβ₃ purified on an Arg-Gly-Asp affinity column revealed an extended conformation with 90% of particles showing an open headpiece conformation (33). Hydrodynamic studies of detergent-solubilized α_IIbβ₃ suggested an extended conformation even in the resting state (34). Cryoelectron tomography showed that purified α_IIbβ₃ reconstituted into membrane vesicles was extended and did not alter its conformation when activated by Mn²⁺ (35); however, the same group subsequently used another α_IIbβ₃ preparation and demonstrated the bent conformation in lipid nanodiscs and integrin extension induced by binding to fibrin or talin headpiece (36). Recent small angle neutron scattering studies of detergent-solubilized α_IIbβ₃ showed a bent conformation in the resting state (37).

To clarify the structure of intact, native α_IIbβ₃, here we used a combination of small angle x-ray scattering (SAXS) and EM to study the structure of detergent-solubilized α_IIbβ₃ isolated and purified from platelets. We investigated the average molecular extension of resting and activated integrins and determined the structure of resting α_IIbβ₃. We found predominantly a bent integrin conformation, that extension increased upon activation with Mn²⁺, and that ligand binding led to headpiece opening through hybrid domain swing-out in intact α_IIbβ₃.

EXPERIMENTAL PROCEDURES

Purification of Intact α_IIbβ₃ from Human Platelets

We purified intact integrin α_IIbβ₃ from human platelets by adapting a protocol described previously (38). Briefly, platelets from outdated platelet concentrate (Children's Hospital Boston, Boston, MA) were collected by centrifugation and washed in Tris-buffered saline (TBS) (10 mm Tris, pH 7.4 and 140 mm NaCl) with 1 mm CaCl₂ and 1 mm MgCl₂. The platelets were lysed by six rounds of successive freeze thawing and homogenization in $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$ of their concentrate volume using a Dounce B set. Platelet membranes were isolated on a sucrose cushion by overlaying the resuspended platelet homogenate on 25% sucrose and spinning at 200,000 × g for 1 h. Platelet membranes were collected and solubilized in a minimal volume of TBS, pH 7.4 with 1 mm CaCl₂, 1 mm MgCl₂, and 1% Triton X-100. α_IIbβ₃ was isolated by concanavalin A-Sepharose chromatography followed by Mono Q-Sepharose and Superose 6 gel filtration chromatography in TBS, pH 7.4 and a 3–5× critical micelle concentration (CMC) of the desired detergent.

ELISA Plate Assay

Outdated human platelets were solubilized in at least a 3× CMC of various detergents and incubated for 1 h at 37 °C. α_IIbβ₃ was captured onto ELISA plate wells using AP3, an anti-β₃ antibody, and then incubated with biotinylated AP5, a LIBS antibody to the plexin-semaphorin-integrin (PSI) domain, or 7E3, an anti-β₃ antibody, in TBS, pH 7.4 with a 3× CMC of the desired detergent. The amount of biotinylated AP5 or 7E3 bound was quantitated by the addition of avidin-peroxidase conjugate, and color was developed using 2,2′-azino-bis(3-ethylbenzthiazoline-6-sulfonic acid) substrate and read in an EMax plate reader (Molecular Devices, Sunnyvale, CA). Each sample was repeated four times.

Negative Stain EM

After the Superose 6 purification described above, 5–10 μg of α_IIbβ₃ from the peak fraction was incubated with 1 mm Ca²⁺ and 1 mm Mg²⁺; 1 mm Mn²⁺ and 0.1 mm Ca²⁺; or 1 mm Mn²⁺, 0.1 mm Ca²⁺, and 10 nm L-739758 (18) in a 200-μl volume for 30 min at RT. Each sample was then rerun on a Superose 6 column equilibrated with the same cations and ligands in TBS, pH 7.4 and a 1× CMC of DDM. Within 15–90 min of elution, the peak fraction was adsorbed to glow discharged carbon-coated copper grids, stained with uranyl formate, and inspected with an FEI Tecnai 12 electron microscope (Hillsboro, OR) operated at 120 kV. Images were acquired at a nominal magnification of 67,000×. Imaging plates were scanned and digitized with a DITABIS Micron Imaging Plate Scanner (DITABIS Digital Biomedical Imaging Systems AG, Pforzheim, Germany) using a step size of 15 μm, a gain setting of 20,000, and a laser power setting of 30%; and 2 × 2 pixels were averaged to yield a final pixel size of 4.48 Å at the specimen level. Between 7,000 and 12,200 particles were interactively collected, windowed into 100 × 100 pixel individual images, and subjected to 10 cycles of multireference alignment and K-means classification into 75–100 classes. Images were processed and cross-correlated using SPIDER (39) as described (40).

Synchrotron SAXS Measurements

Purified intact native α_IIbβ₃ in TBS, pH 7.4 and a 1× CMC of Triton X-100 was flash frozen and shipped to the synchrotron on dry ice. Samples were thawed on ice, passed through an Ultrafree-MC Centrifugal Filter Unit (Millipore, Billerica, MA) with a 0.22-μm pore size, and incubated with desired cations and/or ligands for 15–30 min at 20 °C before x-ray solution scattering measurements were performed on beam line 12-ID (BESSRC-XOR CAT) at the Advanced Photon Source, Argonne National Laboratory, Argonne, IL. The detector was a linear position-sensitive proportional counter capable of collecting 256 scattering intensity points along the angular region. Camera lengths, i.e. sample-to-detector distances, were 70 cm or 2 m. The individual scattering curves from different experiments for a given type of sample were normalized using their individual protein concentration to obtain the average scattering curve for that sample, which was used for further calculations. I(0) and the pair distance distribution function P(r) were calculated from the scattering intensities I(q) using the software GNOM (41). Low resolution models of the integrin were obtained from the experimental data by ab initio modeling using GASBOR (42). 20 GASBOR models were obtained and automatically averaged by the program DAMAVER (43).

RESULTS

Stabilization and Activity of Intact α_IIbβ₃ in Detergent Micelles

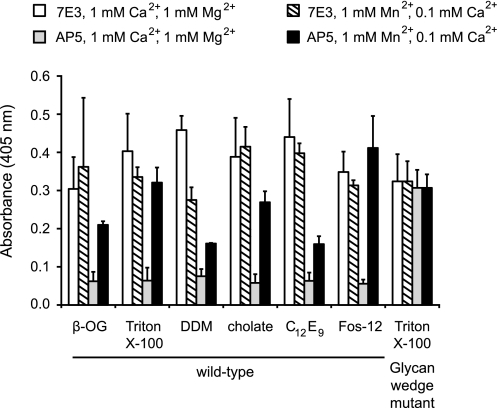
To select detergents that would stabilize α_IIbβ₃ in solution, we screened 24 detergents for their ability to extract α_IIbβ₃ from platelets in TBS and preserve antigenic activity as measured by ELISA. Our screen included nonionic detergents (Anapoes, polyoxyethylene glycols, glucosides, and maltosides), ionic detergents (cholate and LysoFos glycerols), and zwitterionic detergents (Anzergents and Fos-cholines). The top five series of detergents were Fos-cholines (Fos-12/Fos-14), maltosides (dodecyl maltoside/decyl maltoside/nonyl maltoside), polyoxyethylene glycols (C₁₂E₈ (octaethylene glycol dodecyl ether)/C₁₂E₉ (nonaethylene glycol dodecyl ether)), Tritons (X-114/X-100), and cholate. These detergents showed comparable solubilization as shown by 7E3, an anti-β₃ mAb (Fig. 1, white bars). Furthermore, most solubilized α_IIbβ₃ is in a resting state because exposure of the LIBS epitope recognized by AP5 to the β₃ plexin-semaphorin-integrin domain was increased under activating conditions in Mn²⁺ compared with resting conditions in Ca²⁺/Mg²⁺ (Fig. 1). In contrast, this epitope was basally exposed in a mutant α_IIbβ₃ in which extension and hybrid domain swing-out is favored by a glycan wedge (Fig. 1).

FIGURE 1.

Mn²⁺-induced activation increases LIBS exposure of detergent-solubilized integrin. ELISA-based assay was used to detect the amount of total and active α_IIbβ₃ in Ca²⁺/Mg²⁺ (white and gray bars) and Mn²⁺/Ca²⁺ (striped and black bars) in various detergents. α_IIbβ₃ was captured using mAb AP3 (conformation-independent anti-β₃) and assayed for the total amount of receptor using 7E3 (white and striped bars), a conformationally independent anti-β₃ mAb, and for the amount of active receptor using AP5 (gray and black bars), a LIBS mAb detecting the plexin-semaphorin-integrin domain. The high affinity, N-glycan wedge mutant that introduces an N-glycosylation site at Asn-303 was used as a control for maximum AP5 binding. Error bars are 1 S.D. with a sample size of n = 4. β-OG, octyl β-d-glucopyranoside.

Although a number of detergents appeared promising in the above assay, they had differing effects on stability and SAXS. Purified α_IIbβ₃ at 1–10 mg/ml concentrations was stable to long term storage in TBS buffer with 3–5× CMCs of polyoxyethylene glycols, maltosides, or Tritons. In our SAXS experiments, the detergent concentration was titrated to ∼1× CMC to match the x-ray scatter of TBS buffer with or without detergent. Fos-cholines and polyoxyethylene glycols at concentrations of ≥1× CMC had considerable x-ray solution scatter compared with TBS buffer. Maltosides at concentrations of ≤1× CMC had low x-ray scatter, and shorter chain maltosides (e.g. nonyl maltoside) maintained low scatter at concentrations >1× CMC. Triton X-100 at concentrations >1× CMC had no appreciable x-ray scatter over TBS buffer. Storage of α_IIbβ₃ in a 1× CMC of detergent led to protein precipitation within a day in Fos-cholines or cholate to no protein precipitation after several days in maltosides and Tritons. Based on the ability to maintain α_IIbβ₃ activity and stability during storage and compatibility with structural experimental methods, Triton X-100 and DDM were chosen for further studies.

EM of Detergent-solubilized α_IIbβ₃

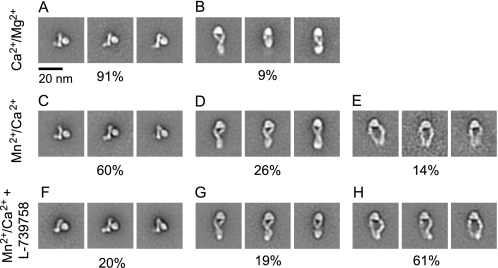
Intact α_IIbβ₃ in DDM detergent was examined by negative stain EM. In 1 mm Ca²⁺ and 1 mm Mg²⁺, 91% of α_IIbβ₃ particles were in a compact, bent conformation, and 9% were extended with a closed headpiece conformation (Fig. 2, A and B, and supplemental Fig. 1A). In 1 mm Mn²⁺ and 0.1 mm Ca²⁺, α_IIbβ₃ was a mixture of bent (60%) and extended (40%) conformations (Fig. 2, C–E, and supplemental Fig. 1B). The bent conformation had a configuration and dimensions similar to those of the α_IIbβ₃ in Ca²⁺/Mg²⁺. In Mn²⁺, extended α_IIbβ₃ was primarily in the closed headpiece conformation (26%) (Fig. 2D and supplemental Fig. 1B) with 14% that had a higher cross-correlation value to an open headpiece conformation (Fig. 2E). The longest molecular dimension increased from about 13 nm in bent particles to about 23 nm in extended particles (Table 1).

FIGURE 2.

Two-dimensional class averages of intact α_IIbβ₃. Representative class averages of DDM-solubilized α_IIbβ₃ in Ca²⁺/Mg²⁺(A and B), Mn²⁺/Ca²⁺(C–E), and Mn²⁺/Ca²⁺ with L-739758 (F–H) are shown. The percentage of the particles represented by bent (A, C, and F), extended-closed (B, D, and G), and extended-open (E and H) is shown below the panels.

TABLE 1.

Molecular extension comparison

	Ca2+/Mg2+	Mn2+/Ca2+	Mn2+/Ca2+ + L-739758
SAXS Rg from experiment (nm)	5.77 ± 0.38	6.43 ± 0.35	7.30 ± 0.59
SAXS Rg from 20 bead models (nm)	5.41 ± 0.20	7.31 ± 0.42	8.07 ± 0.42
SAXS length from 20 bead models (nm)	17.0 ± 0.7	21.1 ± 0.2	20.8 ± 0.5
EM length bent (nm)	12.5 ± 1.6	13.0 ± 1.9	12.8 ± 1.4
EM length extended (nm)	21.0 ± 2.6	22.8 ± 1.0 (closed), 23.3 ± 2.1 (open)	23.0 ± 1.2 (closed), 23.4 ± 1.5 (open)

L-739758 is a small molecule high affinity Arg-Gly-Asp mimetic that co-crystallizes with the headpiece of α_IIbβ₃ in the open conformation (18). In Mn²⁺ in the presence of L-739758, particles in the extended conformation (80%) greatly outnumbered those that were bent (20%) (Fig. 2, F–H, and supplemental Fig. 1C). The extended molecules showed both the closed (Fig. 2G and supplemental Fig. 2B) and open headpiece conformations (Fig. 2H and supplemental Fig. 2C). Thus, L-739758 stabilized integrin extension and shifted the conformational equilibrium toward an active conformation with an open headpiece and greater separation of the upper legs. The opening of the headpiece resulted in an increase in width from 11 nm for the extended-closed conformation to roughly 16 nm for the extended-open conformation (Fig. 2, G and H). At the knees, the width increased from 0 nm for the crossed leg extended-open conformation to about 14 nm for the extended-open conformation. The lengths of these two extended conformations were similar: 23.0 ± 1.2 nm for the extended-closed and 23.4 ± 1.5 nm for the extended-open conformations (Table 1).

Compared with previous class averages of α_IIbβ₃ ectodomains with an artificial coiled coil C-terminal clasp (8), the class averages of the detergent-solubilized α_IIbβ₃ were essentially identical with one exception. Additional density was present for the transmembrane domains, cytoplasmic domains, and associated detergent micelle. This density appeared in many bent integrin class averages at the C terminus of the leg density (Fig. 2, A, C, and F). It appeared to be oriented away from the head; however, this does not necessarily reflect the physiologic orientation of the TM domains, which are attached through flexible linkers (10, 29). In extended integrin class averages, extra density appeared to be present at the base of the legs opposite the head (Fig. 2, B, D, and G). In unclasped α_IIbβ₃ and α_Vβ₃ ectodomains, either the leg C termini are separated or the lower β leg is averaged out (8, 11). Throughout all conditions we tested with intact α_IIbβ₃, the bent, extended-closed, and extended-open integrin conformations had the C-terminal portions of their α_IIb and β₃ legs close together. These results suggest that the α_IIb and β₃ transmembrane domains are associated with one another.

Molecular Extension in Solution

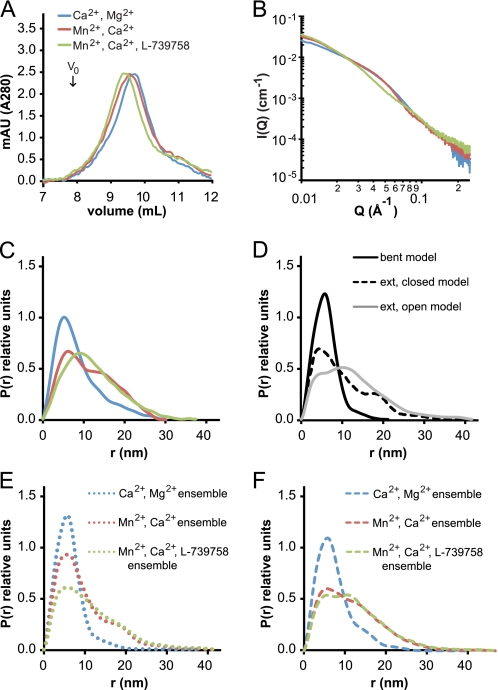
Integrin conformational changes may also be tracked by gel filtration. Intact α_IIbβ₃ in DDM had a Stokes radius (mean ± S.D.) of 6.95 ± 0.04 nm in Ca²⁺/Mg²⁺, 7.12 ± 0.06 nm in Mn²⁺, and 7.76 ± 0.37 nm in Mn²⁺ with L-739758 (Fig. 3A). The Stokes radii in Mn²⁺ and Mn²⁺ with L-739758 were significantly different from that in Ca²⁺/Mg²⁺ by t test (p < 0.05 and p < 0.002, respectively). The hydrodynamic or Stokes radius is given by the Stokes-Einstein equation and is the radius of a hard sphere that diffuses at the same rate as the hydrated, tumbling, non-spherical integrin. As a comparison, the truncated α_Vβ₃ ectodomain Stokes radius was 5.6 nm in Ca²⁺/Mg²⁺, 5.8 nm in Mn²⁺, and 6.4 nm in Mn²⁺ with a cyclic RGD peptide (11).

FIGURE 3.

Tracking α_IIbβ₃ extension by size exclusion chromatography and SAXS. Ca²⁺/Mg²⁺ buffer conditions are shown in blue, Mn²⁺/Ca²⁺ buffer conditions are shown in red, and Mn²⁺/Ca²⁺ and L-739758 buffer conditions are shown in green. A, Superdex 200 gel filtration runs of α_IIbβ₃ in TBS, pH 7.4 with a 1× CMC of DDM. Note the lack of aggregated material in the void volume (V₀). B, x-ray solution scattering curves of 2.3 mg/ml α_IIbβ₃ in TBS, pH 7.4 with a 1× CMC of Triton X-100. C, distance distribution plot of data in B. D, distance distribution plot of atomic models of α_IIbβ₃ in the bent (black line), extended-closed (dashed line), and extended-open (gray line) conformations. E, distance distribution plots of modeled ensembles of α_IIbβ₃ based on EM in Ca²⁺/Mg²⁺ with 91% bent and 9% extended-closed (blue dotted line); Mn²⁺/Ca²⁺ with 60% bent, 26% extended-closed, and 14% extended-open (red dotted line); and Mn²⁺/Ca²⁺ and L-739758 with 20% bent, 19% extended-closed, and 61% extended-open (green dotted line). F, distance distribution plots of modeled ensembles of α_IIbβ₃ by least square fitting to experimental data in Ca²⁺/Mg²⁺ with 50% bent and 50% extended-closed (blue dashed line); Mn²⁺/Ca²⁺ with 20% bent, 5% extended-closed, and 75% extended-open (red dashed line); and Mn²⁺/Ca²⁺ and L-739758 with 15% bent and 85% extended-open (green dashed line). mAU, milliabsorbance units; ext, extended.

We also assessed overall shape in solution using SAXS. Changes in the x-ray solution scattering curves demonstrated shape changes between Ca²⁺/Mg²⁺, Mn²⁺, and Mn²⁺ with L-739758 (Fig. 3B). The radius of gyration (R_g) calculated from the solution scattering curves was 5.8 nm in Ca²⁺/Mg²⁺, 6.4 nm in Mn²⁺, and 7.3 nm in Mn²⁺ with L-739758 (Table 1). The R_g is defined as the root mean square distance of the collection of atoms from their common center of gravity and is smaller than the hard sphere described by the Stokes radius. From our EM experiments, we know that under these experimental conditions α_IIbβ₃ is a mixture of bent and extended conformations. To estimate the average R_g of bent and extended α_IIbβ₃ in solution, we assumed that the fraction of bent and extended α_IIbβ₃ determined by EM (Fig. 2) approximated the conformations in solution. When comparing atomic models of α_IIbβ₃, the calculated R_g values for the extended-closed (7.4 nm) and extended-open (7.3 nm) atomic models were nearly the same (supplemental Fig. 3, B and C); for this reason, we treated the R_g values from the extended conformations as equivalent. Therefore, in Ca²⁺/Mg²⁺, the experimentally determined R_g of 5.8 nm by SAXS would be an ensemble with 91% of the R_g contributed by R_b (R_g of bent α_IIbβ₃) and 9% contributed by R_e (R_g of extended α_IIbβ₃). Similarly, in Mn²⁺, the R_g of 6.4 nm is an ensemble of 60% from R_b and 40% from R_e, and in Mn²⁺ with L-739758, the R_g of 7.3 nm is an ensemble of 20% from R_b and 80% from R_e. Solving for R_b and R_e in all three experimental conditions, we calculated that bent α_IIbβ₃ had an average R_g of 5.3 ± 0.4 nm and that extended α_IIbβ₃ had an average R_g of 7.8 ± 0.3 nm in solution (Table 2).

TABLE 2.

R_g calculation of α_IIbβ₃ based on EM and SAXS data

	Fraction benta	Fraction extendeda	Rg from SAXS experiment	Calculated Rg ensembleb,c
			nm	nm
Ca2+/Mg2+	0.91	0.09	5.77	5.60
Mn2+/Ca2+	0.60	0.40	6.43	6.45
Mn2+/Ca2+ + L-739758	0.20	0.80	7.30	7.41

^a Taken from the α_IIbβ₃ EM class averages in Fig. 2.

^b R_c² = f_b × R_b² + f_e × R_e² where R_c is calculated R_g ensemble, R_b is average R_g of bent α_IIbβ₃, R_e is average R_g of extended α_IIbβ₃, f_b is fraction bent, and f_e is fraction extended.

^c Applying the above equation in the three experimental conditions (R₁² = 0.91R_b² + 0.09R_e² = 5.77² where R₁ = R_g in Ca²⁺/Mg²⁺, R₂² = 0.60R_b² + 0.40R_e² = 6.43² where R₂ = R_g in Mn²⁺/Ca²⁺, and R₃² = 0.20R_b² + 0.80R_e² = 7.30² where R₃ = R_g in Mn²⁺/Ca²⁺ + L-739758) simplifies to R_b² = 74.81 − 43/57 × R_e² and yields an average calculated R_b of 5.33 ± 0.36 nm and R_e of 7.84 ± 0.31 nm.

Calculating a distribution of distances (Fig. 3C) is a more intuitive method for interpreting SAXS data than reporting scattering intensities (Fig. 3B) and is more informative than reporting a single R_g value. The distribution of distances under the different experimental conditions shows larger separation between the atoms of intact α_IIbβ₃ in the order Mn²⁺ with L-739758 > Mn²⁺ > Ca²⁺/Mg²⁺ (Fig. 3C). The experimental distributions were compared with distance distributions calculated from atomic models of α_IIbβ₃ (Fig. 3D and supplemental Fig. 4). The distance distribution curve in Ca²⁺/Mg²⁺ has a main population with a peak centered on 5 nm and a lagging edge gradually trailing off around 30 nm (Fig. 3C, blue line). This curve shape is similar to the atomic model of the bent integrin (Fig. 3D, black line) but is weighted toward longer distances in the experimental data. In Mn²⁺, there are two main populations of distances, the main peak centered at 6 nm and another around 15 nm (Fig. 3C, red line). The extended-closed model also has a bimodal distribution; however, the main distribution is at 5 nm with a smaller second peak at 18 nm (Fig. 3D, dashed line). Addition of L-739758 to Mn²⁺ changed the distance distribution curve to contain only one main peak around 10 nm (Fig. 3C, green line). The extended-open atomic model (Fig. 3D, gray line) is similar to the Mn²⁺ with L-739758 experimental distance distribution with a main distribution at 11 nm but contains a shoulder on the leading edge at 4 nm.

We next calculated theoretical distance distributions for ensembles using distance distribution curves from atomic models and the percentage of each conformation in the ensemble as experimentally determined by EM in Fig. 2. The modeled ensemble distance distribution curves (Fig. 3E) are similar to the experimentally collected data (Fig. 3C); however, the modeled curves are skewed more toward shorter distances. If particles in different conformational states in solution differ in their efficiency in adsorbing to EM substrates, biases could arise in the estimates from EM. Therefore, as an independent estimate, we also used least square fitting of distance distributions from atomic models of the three conformational states to determine the ratio of each conformation that best represents the SAXS data. Distance distributions in Ca²⁺/Mg²⁺ can almost entirely be accounted for by a calculated ensemble of 50% bent and 50% extended-closed α_IIbβ₃ (Fig. 3F, blue dashed line). In Mn²⁺, the bimodal distribution is best modeled with an ensemble comprising 20% bent, 5% extended-closed, and 75% extended-open (Fig. 3F, red dashed line). Similarly, the Mn²⁺ with L-739758 distance distribution is best fit by a calculated ensemble of 15% bent and 85% extended-open conformations (Fig. 3F, green dashed line). These results show the same trend as the EM results with the amount of the extended-open conformation increasing from Ca²⁺/Mg²⁺ to Mn²⁺ to Mn²⁺ with L-739758 (Fig. 2) but estimate higher proportions of extended conformations.

SAXS Solution Structures of α_IIbβ₃

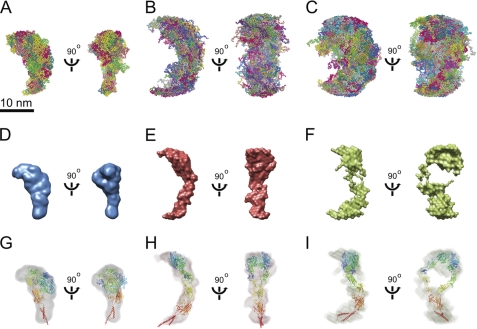
To gain further insight into the conformation of α_IIbβ₃ in solution, we used GASBOR (42), an ab initio program that minimizes a chainlike ensemble of spheres, one per residue, to the experimental data. For each of the three experimental conditions, 20 independent GASBOR models were generated, then superimposed (Fig. 4, A–C), and averaged using DAMAVER (43). The average bead model in each condition was scaled to a volume equal to the average excluded volume of all the generated models in that condition and used to create a consensus molecular envelope (Fig. 4, D–F). The envelope model calculated from α_IIbβ₃ in Ca²⁺/Mg²⁺ has a globular head with a tail roughly 3 × 6 nm and an overall shape consistent with a resting/bent conformation (Fig. 4D). The α_IIbβ₃ ectodomain crystal structure in the bent conformation with modeled transmembrane domains was docked into the SAXS envelope model by cross-correlation maximization in Chimera (44) (Fig. 4G).

FIGURE 4.

SAXS ab initio models. SAXS ab initio models of α_IIbβ₃ in Ca²⁺/Mg²⁺ (A, D, and G), Mn²⁺/Ca²⁺ (B, E, and H), and Mn²⁺/Ca²⁺ with L-739758 (C, F, and I) are shown. A–C, 20 superimposed bead models calculated by GASBOR (42). D–F, envelope models of the averaged bead models calculated by DAMAVER (43) scaled at 4 × 10⁵ ų in Chimera (44). G–I, envelope models of α_IIbβ₃ docked with atomic models by cross-correlation maximization in Chimera (44). G, the full α_IIbβ₃ ectodomain crystal structure (Protein Data Bank code 3FCS) with modeled transmembrane domains is shown in ribbon diagram. H and I, the extended atomic models were generated by manually changing the bends in the α and β subunit knees (supplemental Fig. 3, B and C) to resemble SAXS envelope models.

The extended conformation could similarly be modeled using a combination of GASBOR and DAMAVER. Although single ab initio models made from atomic models with GASBOR did not entirely replicate the extended-closed and extended-open conformations, averaging of sets of 10 ab initio models with DAMAVER was able to reproduce the main features of the starting models. Therefore, we used GASBOR to calculate 20 independent models from the experimental scattering data for intact α_IIbβ₃ in Mn²⁺ and Mn²⁺ with L-739758 (Fig. 4, B and C). Superposition of the 20 models showed that they were clearly more extended than the models in Ca²⁺/Mg²⁺ (Fig. 4, A–C). Furthermore, the models in Mn²⁺ with L-739758 showed greater width at the waist, corresponding to the integrin knee region (Fig. 4C), than the models in Mn²⁺ (Fig. 4B). Scaling of the superimposed models showed the same features; the DAMAVER model in Mn²⁺ resembled an integrin with an extended-closed headpiece (Fig. 4E), whereas the DAMAVER model in Mn²⁺ with L-739758 showed a large solvent region near its middle similar to that created by hybrid domain swing-out in headpiece opening (Fig. 4F). Reasonable docking of extended-closed and extended-open α_IIbβ₃ atomic models was achieved in the DAMAVER models by cross-correlation maximization in Chimera (44) (Fig. 4, H and I).

DISCUSSION

As visualized by EM, the purification of α_IIbβ₃ in detergent from resting platelets yielded integrins predominately in a compact, bent conformation (Fig. 2A). The overall molecular length was ∼13 nm, which is consistent with the length of the full α_IIbβ₃ ectodomain crystal structure (Protein Data Bank code 3FCS) (8) in the bent conformation with modeled transmembrane domains (supplemental Fig. 3A). This length is also similar to preparations of α_IIbβ₃ in nanodiscs that extend ∼11 nm from the nanodisc (36). The most direct comparison of our results is with the small angle neutron scattering of Triton X-100-solubilized α_IIbβ₃ in Ca²⁺ that yielded an R_g of 5.8 nm (37), which is the same value we calculated in our SAXS experiments (5.77 ± 0.38 nm). Our ab initio modeling of x-ray solution scattering curves from Triton-solubilized resting α_IIbβ₃ yielded a three-dimensional model in a compact, bent conformation (Fig. 4D) similar to the one calculated by neutron scattering (37) and in agreement with our negative stain EM experiments. Furthermore, the models from both small angle x-ray and neutron scattering are in excellent agreement with the crystal structure of the complete ectodomain of α_IIbβ₃ in the bent conformation (8). In contrast, none of these three structures agree with a cryo-EM structure of α_IIbβ₃ prepared and stored at 4 °C in 1% octyl β-d-glucopyranoside that shows a conformation intermediate between bent and extended (31). This may result from a preparation containing a higher proportion of extended particles than found here in DDM. We found that α_IIbβ₃ was more efficiently extracted with DDM than octyl β-d-glucopyranoside (supplemental Fig. 6).

Activation of detergent-solubilized α_IIbβ₃ preparations by Mn²⁺ led to an increased binding of the LIBS antibody AP5, an effect characterized previously with cell surface measurements (11, 26, 45). Mn²⁺ also increased the Stokes radius and increased the R_g from 5.8 to 6.4 nm. EM of α_IIbβ₃ in Mn²⁺ showed the majority (60%) in the bent conformation and 40% in an extended conformation consistent with the R_g reflecting an ensemble average. In contrast to the extended α_Vβ₃ ectodomain fragment in Mn²⁺ where there are classes with separation between the α_V and β₃ legs and hybrid domain swing-out as well as the closed headpiece with crossed or parallel legs (11), full-length α_IIbβ₃ in Mn²⁺ showed crossed or parallel lower legs and a headpiece in the closed conformation in most class averages.

Stabilization of an extended-open high affinity state was achieved in our experimental conditions by addition of Mn²⁺ and a high affinity Arg-Gly-Asp ligand mimetic (Merck L-739758). L-739758 and Mn²⁺ extended 80% of α_IIbβ₃ with 61% in an extended-open conformation as shown by EM. We also measured both Stokes radius from gel filtration and R_g from SAXS as other measures of integrin extension and headpiece opening. It is important to bear in mind as pointed out under “Results” that R_g measures the average position of mass from the center of mass and that the Stokes radius includes associated solvent molecules and is the radius of a hard sphere with equivalent diffusion coefficient. Thus, not only do these quantities measure different things, but they also approximate complex molecular shapes with a single number. Furthermore, gel filtration and SAXS average shape over very different time scales so that the gel filtration Stokes radius but not the SAXS R_g would likely average over interconverting conformational states. Comparisons among the three different conditions of Ca²⁺/Mg²⁺, Mn²⁺, and Mn²⁺ with L-739758 show a greater increase in Stokes radius from Mn²⁺ to Mn²⁺ with L-739758 than from Ca²⁺/Mg²⁺ to Mn²⁺, whereas SAXS shows the same trend but with less difference between the two increases. This is explicable based on the large increase in the volume of solvent between the upper α and β legs upon headpiece opening, which would differentially increase the Stokes radius compared with R_g in the presence of L-739758.

Shifts to the extended-closed and extended-open conformations were also detected here by SAXS for the first time. A previous SAXS study of the α₅β₁ headpiece in Ca²⁺ and the α₅β₁ headpiece in Mn²⁺ with a five-domain fibronectin fragment (46) reported one representative of 12 GASBOR models as opposed to averaging 20 GASBOR models here. The α₅β₁ SAXS results were complicated by the large contribution to scattering by the fibronectin fragment, which showed interdomain flexibility. The representative GASBOR model did not show hybrid domain swing-out, but support for swing-out was provided by calculations that showed, given a particular five-domain fibronectin fragment orientation, a better fit to the scattering data upon hybrid domain swing-out. Our GASBOR and DAMAVER models derived from SAXS of activated, intact α_IIbβ₃ with ligand more clearly highlight this conformational change (Fig. 4, E and F) even though only two-thirds of the sample was in an extended-open conformation as measured by EM. Activation of α_IIbβ₃ led to an extension of the longest molecular length from 17 nm in the bent conformation to about 21 nm in the extended conformation in our bead models (Table 1). Consistent with the hybrid domain swing-out model of activation, addition of ligand also led to an increase of overall width of the GASBOR models from 16.7 ± 0.7 nm in Mn²⁺ to 19.6 ± 0.6 nm in Mn²⁺ with L-739758. Moreover, the extended-open conformation is clearly visualized in the EM class averages (Fig. 2H) and the resultant SAXS envelope model of α_IIbβ₃ in Mn²⁺ with L-739758 (Fig. 4F) with a solvent-exposed area in the headpiece region.

Each structural technique has limitations. In our negative stain EM approach, an ensemble of conformations may be analyzed by sorting particles into different classes, but each class is a two-dimensional projection of the three-dimensional molecule, and the sample is prepared by adsorbing the molecules to a flat surface. The advantage of SAXS is that measurements are made in solution; however, the results average measurements over different conformational states (ensembles). The combination of these techniques in our study has the advantage that the EM results can be used to estimate the population of each conformational state in the SAXS measurements, and SAXS can be calculated from pseudoatomic models based on crystal structures and EM projections for comparison with the experimental SAXS data. This approach was carried out both at the level of R_g and distance distributions.

We correlated our experimental R_g values from our SAXS experiments with the fraction of bent and extended molecules from our EM data in each of the three experimental conditions to calculate an average R_g for bent α_IIbβ₃ of 5.3 nm and extended α_IIbβ₃ of 7.8 nm in solution (Table 2). In these calculations, we treated the extended-closed and extended-open conformations as having equivalent R_g values. As shown in our atomic models, the overall R_g values for the extended-closed and extended-open conformations are almost identical (supplemental Fig. 3, B and C). Accordingly, the R_g increase upon addition of L-739758 to Mn²⁺ can be accounted for by solely an increase of extended α_IIbβ₃; however, from our EM studies, the addition of L-739758 not only favors extension but also stabilizes the extended-open conformation. Thus, our SAXS R_g measurements are a useful tool to assay integrin extension but are not sensitive enough to investigate headpiece conformational rearrangements in intact integrins.

To further analyze the conformation of α_IIbβ₃ under resting and activating conditions, we compared distance distribution plots of our data with atomic models based upon prior structural information and our EM data (supplemental Fig. 4). For our bent atomic model, we added transmembrane domains to the crystal structure of the full ectodomain (8). In integrin extension from the bent to extended conformations, the largest changes occur at the α and β subunit knees. The extended-closed and extended-open atomic models based on EM of α_IIbβ₃ on flat grids represent maximally extended conformations. However, computational results and the model of the β knee as an entropic spring suggest a less extended conformation in solution or on cell surfaces (47) more similar to extended conformations trapped in crystals of β₂ leg fragments (48). Utilizing these β leg conformations in single extended integrin atomic models was not as effective as utilizing ensembles; however, ensembles with multiple leg conformations including such models better fit the experimental data than fully extended models (supplemental Fig. 5). The best agreement with experimental data was obtained when the percentage of extended-open conformation was increased. For Mn²⁺ and Mn^{2 +} with L-739758, increasing the extended-open conformation by at least 20% led to ensembles that more closely matched the experimental distance distributions (Fig. 3, compare F with C, and supplemental Fig. 5). This might suggest that the proportion of extended-open integrins is greater in solution than estimated by EM but also could be an artifact resulting from the limitations of simulating the ensembles in solution with atomic models. What is clearly shown by both SAXS and EM is that detergent-solubilized, intact α_IIbβ₃ extends and adopts the open headpiece in the presence of Mn²⁺ and ligand.

Several recent studies on α_IIbβ₃ integrin activation have focused on testing the extension and headpiece opening model (34–36). Based upon the full ectodomain crystal structure (8), extension translates to an increase in height of about 11 nm from the membrane bilayer in the resting state to roughly 20 nm in the activated state. Comparisons among different studies are complicated not only by the different techniques used but by differences in sample quality. Our experience demonstrates the great importance of sample preparation and storage. Integrin subunits spontaneously dissociate and aggregate during prolonged storage at 4 °C. Therefore, our preparations are stored flash frozen at −80 °C. Dissociation and aggregation are greatly enhanced by storage in Mn²⁺. Integrin α_Vβ₃ preparations dialyzed and stored at 4 °C in the presence of 0.2 mm Mn²⁺ showed substantial aggregation in EM field views (21), whereas similar views of α_Vβ₃ preparations showed no aggregation when applied to grids immediately after gel filtration in 1 mm Mn²⁺ (11). α_IIbβ₃ incubated with Mn²⁺ showed multimerization by rotary shadow EM (49). Furthermore, extensive dialysis in the presence of Mn²⁺ induced aggregation that made it impossible to obtain the conformation in Mn²⁺ of α_IIbβ₃ in Triton X-100 by small angle neutron scattering (37). In our study, incubation with Mn²⁺ or Mn²⁺ and ligand was limited to 15–30 min immediately before SAXS data collection or 15–90 min before EM grid preparation. Purification methods also influence α_IIbβ₃ conformation; isolation on RGD-Sepharose columns and elution with RGD peptides stabilize the extended open conformation as shown by tomography (33).

Our use of monomeric small molecules to activate α_IIbβ₃ shifted the equilibrium toward the extended, high affinity state, but from our EM analysis, we were able to detect multiple conformations in each condition. Although our sample conditions are homogeneous enough for reliable modeling of the resting integrin in the compact, bent conformation, there was a portion (9%) of extended-closed α_IIbβ₃ under resting conditions.

Initial studies from a group using cryoelectron tomography of α_IIbβ₃ in lipid vesicles did not show a height change with Mn²⁺ activation (35). Individual tomogram z-sections showed a single globular domain connected through a single leg to the membrane. However, the resolution of class averages was poor with only a round globular head seen and little density for a leg. Therefore, analysis was confined to measurement of the height of the globular head above the membrane in the minority of class averages for which the membrane bilayer was resolved. Subsequently, Ginsberg and co-workers (36) followed up with a negative stain EM study of α_IIbβ₃ in nanodiscs. This time, a bent conformation of α_IIbβ₃ indistinguishable from that reported here was found in the resting state. Furthermore, talin was found to induce integrin extension to a conformation with the closed headpiece and crossed legs identical to that first seen with α_Vβ₃ (11) and seen since with many integrins, including α_Xβ₃ (40) and α_IIbβ₃ here. In the second study, Mn²⁺ was not used, and discrepancies with the first study were not discussed. However, the height seen in the first study was intermediate between the bent and extended conformations (35).

In this study, integrin activation was induced by ligand binding, which has been shown not to require separation of the TM domains in the membrane in contrast to inside-out and outside-in signal transmission in integrins (50). In all conformations detected by EM and in the SAXS envelope models, the lower legs of the α_IIb and β₃ subunits are close to one another, indicating that the transmembrane domains remain associated. Furthermore, density for the TM and cytoplasmic domains in EM was particularly evident in the bent conformation and was also present in at least some extended integrin class averages. These results contrast with previous EM studies with unclasped ectodomain fragments where the lower legs are usually unassociated in the extended-closed and extended-open conformations (10, 11, 40). This demonstrates that even in Triton X-100 and DDM detergents the association between the α_IIb and β₃ TM domains is strong enough to maintain them in the same detergent micelle; otherwise, they would have been in two separate detergent micelles, and their positions would not have been correlated due to the extreme flexibility of the lower β leg (10, 11, 40). Merely demonstrating retention of association between the α_IIb and β₃ TM domains in this study is an advance. Previous EM studies of intact α_IIbβ₃ in liposomes or lipid nanodiscs were not of sufficiently high resolution to define whether the α_IIb and β₃ TM domains or the C-terminal ends of the legs were associated (35, 36). Ligand-induced extension of α_IIbβ₃ occurred upon binding to fibrin fibrils (36), but the resolution in this experiment did not enable discrimination between the closed and open headpiece.

Our studies do not address the mechanism of inside-out integrin activation. Talin binding by itself has been shown to induce 22% of integrins in lipid nanodiscs to extend; however, although not reported, all of the extended integrin class averages show a closed headpiece (36). Here we demonstrate a proportion of extended-open particles in Mn²⁺ in the absence of ligand and a preponderance of this conformation in the presence of Mn²⁺ and ligand. However, induction of the active extended-open conformation and separation of integrin TM domains have not yet been reconstituted with purified components from the pathway for inside-out activation. Additional required factors may include other integrin cytoplasmic domain-binding proteins and actin cytoskeleton translation. A previous molecular dynamics simulation on the complete α_IIbβ₃ ectodomain showed that association with the translating actin cytoskeleton during ligand binding exerts a lateral force on the β₃ leg that stabilizes the active extended-open conformation with complete separation of the α_IIb and β₃ legs in their membrane-proximal regions (8).

Our studies with SAXS and EM on activation of intact α_IIbβ₃ with external or outside-in activators substantially advance our knowledge of native integrin conformation in solution. These studies demonstrate that ensembles using only the main conformational states of bent, extended-closed, and extended-open integrins essentially describe the conformational ensembles found. Our study further extends previous EM observations on integrin ectodomain preparations by demonstrating with SAXS and native intact α_IIbβ₃ that extension and hybrid domain swing-out occur in solution upon activation with Mn²⁺ and ligand and helps resolve previous controversy on integrin conformational states.