Inadequacies of Minimum Spanning Trees in Molecular Epidemiology

Abstract

Minimum spanning trees (MSTs) are frequently used in molecular epidemiology research to estimate relationships among individual strains or isolates. Nevertheless, there are significant caveats to MST algorithms that have been largely ignored in molecular epidemiology studies and that have the potential to confound or alter the interpretation of the results of those analyses. Specifically, (i) presenting a single, arbitrarily selected MST illustrates only one of potentially many equally optimal solutions, and (ii) statistical metrics are not used to assess the credibility of MST estimations. Here, we survey published MSTs previously used to infer microbial population structure in order to determine the effect of these factors. We propose a technique to estimate the number of alternative MSTs for a data set and find that multiple MSTs exist for each case in our survey. By implementing a bootstrapping metric to evaluate the reliability of alternative MST solutions, we discover that they encompass a wide range of credibility values. On the basis of these observations, we conclude that current approaches to studying population structure using MSTs are inadequate. We instead propose a systematic approach to MST estimation that bases analyses on the optimal computation of an input distance matrix, provides information about the number and configurations of alternative MSTs, and allows identification of the most credible MST or MSTs by using a bootstrapping metric. It is our hope this algorithm will become the new “gold standard” approach for analyzing MSTs for molecular epidemiology so that this generally useful computational approach can be used informatively and to its full potential.

INTRODUCTION

Although a classic problem of academic mathematics (10), minimum spanning trees (MSTs) have become an increasingly common tool for molecular epidemiology research. With a set of pairwise distances that describe the degree of dissimilarity among individuals, an MST represents a set of edges (connections) that link together nodes (individuals) by the shortest possible distance. In molecular epidemiology, this path is interpreted as the most likely chain of pathogen transmission. Given that MSTs are calculated from simple arithmetic distance matrices, they are particularly useful for examining relationships of organisms over short time scales, such as disease outbreaks or the short-range transmission of pathogens within communities, where not enough genetic diversity has accrued to permit the use of more mathematically sophisticated algorithms for inferring population structure, such as phylogenetic analysis (20) or model-based clustering algorithms (7).

Despite their popularity, there are serious problems in applying MSTs to molecular epidemiology that are almost invariably overlooked. (i) Although a single MST is reported by virtually all algorithms, there are frequently multiple, equally optimal solutions to the MST problem. In any data set, there can exist several equally parsimonious paths if two or more edges have the same lengths. In such situations, only one of the possible shortest paths is arbitrarily selected during tree construction (10, 12, 18), which has the potential to significantly affect the structure of the tree. In light of this issue, it has been appreciated that the solution to the MST problem is better considered a minimum spanning network (MSN), in which all MST solutions are combined into a single graph that demonstrates all equally parsimonious paths (5, 6). Nevertheless, we are not aware of any published use of MSNs for molecular epidemiology other than two related studies of botanical pathogens (14, 15). (ii) For most methods of inferring population structure, statistical metrics are employed to gauge the credibility of inferences so that the overall credibility of the estimation can be ascertained and spurious relationships can be appropriately disregarded. Such quality controls are not employed in MST estimations. Common techniques for assessing the statistical robustness of population structure estimations include bootstrapping (9) or the use of Bayesian posterior probabilities (7, 20). A bootstrapping metric has recently been proposed for MSTs used in financial applications (25), yet this practice has not been adopted for molecular epidemiology.

Here, we explore the consequences of these two factors in applying MSTs to molecular epidemiology. In all previously published works that we have surveyed, we found a number of equally parsimonious alternative solutions which individually encompass a range of credibility values. We further show that taking into account these additional factors can alter the interpretation of molecular epidemiology data. In response to this alarming finding, we propose a systematic approach to MST analysis that addresses these shortcomings and allows a more objective evaluation of population structure through MST estimations.

MATERIALS AND METHODS

All functions described below have been automated through a software program, MSTgold, which is freely downloadable for academic use (with documentation) from http://bellinghamresearchinstitute.com. In the event that data sets are too complex to allow complete exploration of alternative MSTs, MSTgold incorporates three user-specified conditions that can be used to terminate estimations: (i) a maximum amount of time for the run, (ii) a maximum number of unique MSTs to be saved, or (iii) a minimum rate for the discovery of new MSTs, as measured by the ratio of alternative MSTs saved at the end of the current cycle to the total number previously saved.

Distance matrix calculation.

For sequence, spoligotype, and single nucleotide polymorphism (SNP) data, the pairwise distance between isolates was calculated such that any difference carried the same weight (equidistant method). For variable-number tandem repeat (VNTR) data, the difference between the values of two alleles was calculated as the absolute value of the arithmetic difference in the numbers of repeats, and the cumulative pairwise distance between isolates was the sum of such values across all sites (difference method). Gaps in sequence alignments were treated as missing data; if either individual had missing data at a site, that site was ignored in calculating the distance. Individuals with identical genotypes were condensed into a single entry prior to analysis.

Estimating MSTs and creating MSNs.

An MST is an acyclic graph that consists of nodes connected by edges. Edges have lengths that correspond to the distances between the two individuals represented by the nodes. MSTs were calculated by Kruskal's algorithm (12) as implemented by the Perl module Graph 0.94, available from CPAN (http://search.cpan.org/∼jhi/Graph-0.94/lib/Graph.pod). We found that the algorithm was sensitive to the order in which the nodes were listed in the input and that alternative MSTs could be computed if the node order was altered. MSTs were calculated following randomization of the node input order, and MSTs not previously encountered were stored.

The combination of all edges defined within unique MSTs constitutes the MSN. The percentage of alternative MSTs that contained a given edge in the MSN was calculated. For the purposes of data visualization, edges present in less than 50% of alternative MSTs were not displayed.

Estimation of the number of possible MSTs.

Following each interval of 100 randomizations, the Schnabel method of mark-recapture (21) was used to estimate the total number of possible MSTs according to the equation n = [(M + 1)(C + 1)]/(R + 1) − 1, where n is the total number of possible MSTs, M is the number of unique trees generated during previous intervals of randomization, C is the total number of MSTs generated during the current interval, and R is the number of trees in C that were already present among M. Overall estimates of the number of MSTs were calculated as the average of all individual estimations after discarding a “burn-in” period, prior to which individual estimations had begun to converge. For all data sets, a burn-in period of 10 cycles was used, and MSTs were generated over a period of 12 h.

Bootstrapping.

Individual MSTs were subjected to a bootstrapping procedure to establish confidence levels. For each alternative MST, 100 individual pseudoreplicates were produced from the original data by randomly sampling sites with a replacement until the pseudoreplicate contained the same number of sites as the original input. Pseudoreplicates were subjected to distance matrix computation, and a single MST was estimated for each without node order randomization. For each edge in the original alternative MST, the percentage of pseudoreplicate MSTs containing the same edge was computed. MSTs were typically bootstrapped for a period of 12 h. For analyses of DNA sequence data, only polymorphic sites were retained in the original data to increase the speed of pseudoreplicate computation.

MST and MSN visualization.

MSTs and MSNs were expressed in Dot format and visualized in Neato as implemented by GraphVIZ v2.26.3 software (4) (http://www.research.att.com/sw/tools/graphviz/). MST and MSN diagrams were edited for clarity using Adobe Illustrator 10.

RESULTS

We first explored the potential impact on molecular epidemiology studies by (i) examining the set of equally parsimonious MSTs and (ii) evaluating the credibility of those MSTs. We therefore considered data from a survey of prior publications (1, 3, 11, 13, 16, 17, 19, 22–24) where MSTs had been used to draw inferences about population structure from various data, including spoligotypes, VNTRs, DNA sequences, and multilocus sequence types (MLST).

Estimating alternative MSTs.

Given the size and complexity of most experimental data sets, it is unlikely that a singular MST exists, and it is much more likely that multiple, equally parsimonious solutions are possible.

We found that Kruskal's MST algorithm was sensitive to the order in which nodes were added; for any data set with possible alternative MSTs, the same MST was consistently calculated if the algorithm was run multiple times, but if the order in which nodes were added had been randomized prior to MST analysis, other MSTs were often calculated. Thus, to explore the realm of alternative MSTs for any data set, we iteratively randomized the order in which nodes were added prior to MST analysis. It was sometimes possible to produce the same MST configuration through different orders of data entry, and thus, particular alternative MSTs could be revisited several times during node order randomization. We therefore retained only previously unseen MSTs to populate the MSN.

The problem of estimating the number of possible MSTs by this process shares similarity with the “mark and recapture” methods used in ecology to estimate population sizes. Mark and recapture methods involve labeling a random subset of individuals, releasing them to disperse through the population, and subsequently sampling the population again to determine the fraction of marked specimens compared to the fraction of previously unseen individuals. For our application, we serially estimated the number of possible MSTs after batches of 100 node order randomizations. The unique trees generated by previous intervals of node order randomization are analogous to the marked individuals, the trees generated by the current interval are analogous to the resampled population, and the number of trees in the resampled population which have been previously encountered are analogous to the recaptured marked specimens.

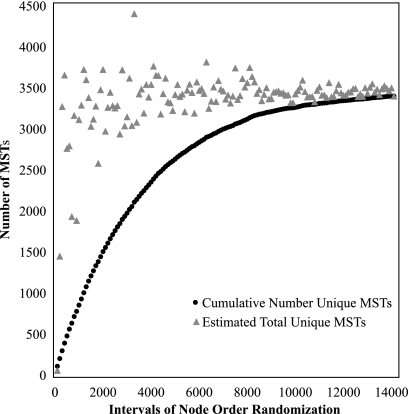
We therefore used the Schnabel method of mark-recapture (21) to estimate the total number of possible MSTs. We found that estimates of the number of possible MSTs typically fluctuated greatly among early intervals of node order randomization, when the fraction of unique trees is highest (Fig. 1). After this initial period, estimates of the true number of possible trees became increasingly concordant with the number of unique MSTs that could be obtained in practice. We concluded that the Schnabel method of mark-recapture is an appropriate equation to estimate the number of alternative MSTs and that discarding estimates from early cycles of node order randomization (generally, the first 10) permits more accurate estimation of that value.

Fig. 1.

Comparison of estimated numbers of MSTs and actual numbers of MSTs as ascertained by node order randomization. The data are a subset of VNTR strain typing data from the work of Lari et al. (13). A total of 14,100 randomizations were performed in intervals of 100 each with a burn-in period of 10 intervals. The mean estimated number of MSTs ± the standard deviation was 3,420 ± 16.7, and the mean actual number of MSTs produced was 3,391.

We estimated the number of possible MSTs for each of the studies in our survey (Table 1) and found that this value varied widely. For one data set, only 4 alternative trees were found. For several studies, there were so many alternative trees that the true number could not be estimated by our procedure; no tree was encountered twice during the cumulative cycles of node order randomization.

Table 1.

Survey of MST and bootstrap analysis in previously published studies

Reference	Organism	Data type (method)	No. of sites	No. of unique genotypes	Estimated no. of MSTsa	No. of trees bootstrapped	Minimum avg bootstrap value (%)	Maximum avg bootstrap value (%)	Difference between minimum and maximum avg bootstrap value (%)	Bootstrap difference/maximum avg bootstrap value
13	Mycobacterium bovis	VNTR (equidistant)	15	29	247,662 ± 17,533.4	1,659	18	45	27	0.6
13	Mycobacterium bovis	VNTR (difference)	15	29	7,283 ± 376.9	1,629	20	43	23	0.51
22	Bordetella pertussis	VNTR (equidistant)	6	44	Too many to estimate	1,407	21	39	18	0.46
22	Bordetella pertussis	VNTR (difference)	6	44	118,591 ± 8,161.2	1,550	19	38	19	0.5
11	Mycobacterium tuberculosis	Spoligotype	43	48	2,028 ± 36.3	1,117	27	46	19	0.41
17	Staphylococcus aureus	SNP	148	89	48 ± 0.7	48	18	26	8	0.31
16	Mycobacterium tuberculosis	Spoligotype	43	24	45 ± 0.2	8	36	46	10	0.22
23	Hepatitis C virus	Sequence	187	16	4 ± 0	4	42	47	5	0.11
19	Ixodes scapularis	Sequence	468	25	8 ± 0.2	8	24	39	15	0.38
3	Candida albicans	MLST (equidistant)	6	27	Too many to estimate	4,412	32	60	28	0.47
1	Streptococcus pneumoniae	MLST (equidistant)	7	72	Too many to estimate	523	33	47	14	0.3
1	Streptococcus pneumoniae	MLST (sequence)	2,716	72	588 ± 10.8	547	34	47	13	0.28
24	Campylobacter coli	MLST (equidistant)	6	49	Too many to estimate	2,403	20	39	19	0.49
24	Campylobacter coli	MLST (sequence)	3,309	49	445,339 ± 23,997.1	1,030	20	39	19	0.49

^aEstimate ± standard error of the mean.

The number of possible MSTs is proportional only to the number of minimal pairwise distances with equal lengths, or, in other terms, the number of connections that allow alternative paths for MSTs. Consequently, there is a relationship between the number of possible MSTs and the method used to compute the pairwise distance matrix. Distance matrices may be calculated in one of two ways: sites can be scored merely as “same” or “different,” such that any difference carries the same weight (equidistant method), or distances between sites can be calculated on the basis of the difference between the values of the two sites, such that allelic sites with similar values generate a smaller distance than allelic sites with larger differences in value (difference method). All previously published studies that we have considered in this work calculated distance matrices using the equidistant approach.

Using the equidistant distance matrix calculation, there were too many alternative trees for one of the VNTR data sets to permit estimation of their actual number, and for the other data set, a very large number of alternative MSTs were estimated (Table 1). Mutations at VNTR loci can be unpredictable, and a number of different mechanisms may operate on the same locus to alter its length by various degrees. The length of the repeat sequence itself may also have bearing on resultant polymorphisms. Despite these complexities, changes at VNTR loci often occur in small, stepwise increments of only one or two tandem repeats at a time (2). As a simplifying assumption, we therefore calculated VNTR distance matrices by the difference method, which (unlike the equidistant method) reflects the property that alleles of similar lengths are more likely to be closely related than alleles of dissimilar lengths. There were significantly fewer alternative MSTs possible when the same data were processed using the difference method of calculating distance (Table 1), presumably because that method allowed better discrimination between individuals and thus limited the number of identical pairwise distances.

There is also a relationship between the type of data used and the number of possible alternative trees. It was not possible to determine an estimate of the number of alternative MSTs for all three MLST data sets. MLST data typically involve sequencing 7 to 10 sites at which alleles are given arbitrary numbers that signify a particular genotype and which are considered to be equidistant from all other allele numbers in downstream analyses. However, those alleles reflect polymorphisms in sequence data. We therefore reasoned that better discrimination of the genetic distances separating individuals could be achieved by using the raw sequence data; if one assumes that greater than one polymorphism may distinguish MLST alleles, considering the number of polymorphisms present allows degrees of relatedness to be assessed, whereas classifying entire sequences as “same” or “different” does not. For two of the data sets (1, 24), information was available from online MLST databases to allow conversion of allele numbers into sequence data (http://spneumoniae.mlst.net and http://pubmlst.org/campylobacter/). We again estimated the number of possible MSTs using those sequence data and found that smaller estimates of the number of possible trees could be reasonably obtained (Table 1). Because using sequence data dramatically reduces the number of possible MSTs, we consider that form of information to be the preferred substrate for performing MST analysis of MLST data.

In summary, when there are limited numbers of informative sites and alleles are treated as equidistant from one another, there are many pairwise distances of the same length, and consequently, prohibitively large numbers of MSTs are often possible. Basing analyses on the arithmetic number of pairwise differences among individuals both limits the number of possible MSTs and more faithfully represents the genetic distances between individuals.

Calculating the MSN.

The MSN represents the set of all possible MSTs (5, 6) and allows exploration of the full realm of relationships defined by individual MSTs. In cases where the number of alternative MSTs was small, it was practical to calculate the entire MSN. In most cases, however, it was not feasible to generate the entire set of alternative MSTs, and the calculated MSN represents an approximation of the full MSN.

Although all alternative MSTs are equally parsimonious solutions, when a set is large, the topology of an MSN may contain so many alternative edges between nodes as to appear overwhelming and meaningless. To simplify this visualization problem, we imposed a “majority rule” in calculating MSNs. Edges that are present in a certain fraction of MSTs or more (our default is 50%) are reported as dashed lines, and edges present in all MSTs are shown as solid lines (Fig. 2C and E), limiting the complexity of the diagram. However, it should be emphasized that the fraction of MSTs containing an edge does not correlate with the credibility of that edge; edges dropped by this filtering procedure may be no less credible than the ones that are retained. Although edges present in every alternative MST are likely to be important, separate metrics of credibility are required to evaluate the reliability of inferences within MSTs.

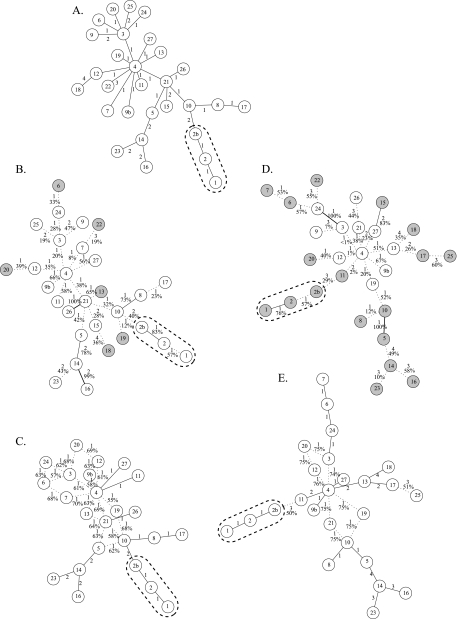
Fig. 2.

Reanalysis of a published MST. MSTs and MSNs of M. bovis strains collected by Lari et al. (13). Node designations are arbitrary. BCG-like strains (nodes 1, 2, and 2b) are enclosed by dashed lines. Individuals that are placed differently in the published tree and in the highest-credibility trees are shaded in gray on the highest-credibility trees. (A) MST published by Lari et al. (13), where different VNTR states are treated as equidistant. (B) MST with the highest bootstrap value based on an equidistant pairwise distance matrix. The lengths of the edges and their bootstrap percentages are indicated. Edges with less than 70% bootstrap support are indicated by dashed lines. (C) Fifty-percent-majority MSN based on an equidistant pairwise distance matrix. The length of each edge is indicated. The percentage of MSTs containing the edge is reported if that value is less than 100%. Edges appearing in all MSTs sampled are solid lines, and all others are dashed. (D) MST with the highest bootstrap value based on an arithmetic pairwise distance matrix. The edges are labeled as in panel B. (E) Fifty-percent-majority MSN based on an arithmetic pairwise distance matrix. The edges are labeled as in panel C.

Estimating the reliability of MSTs.

To establish measures of credibility for MSTs, we elected to use a bootstrapping approach because of its computational simplicity and its widespread use in phylogenetics (9) and because the approach has been used anecdotally with MSTs (3, 25). Bootstrapping is a method that estimates the confidence of a model through the generation of “pseudoreplicates,” which are equal in size to the original data but produced by randomly sampling those original data with replacements. The principle behind this approach is that, given enough information, there should be sufficiently redundant data that independent pseudoreplicates will yield analyses identical to that of the complete data set. Conversely, if the data are not robust, random sampling will significantly perturb the analysis, and pseudoreplicates will appear different from the original data when identically analyzed. Bootstrap values are expressed as the fraction of the pseudoreplicates that yields the same inference as the original data.

Unique MSTs were individually bootstrapped and evaluated. Bootstrap values apply to individual edges, but the average of those values over an entire MST provides a relative measure of the overall confidence in the MST. We found that within any set of alternative MSTs examined, the individual trees demonstrated a considerable range of average bootstrap values (Table 1). To investigate whether variability from the bootstrapping procedure itself could account for the range of bootstrap values observed, we repeatedly bootstrapped individual trees from several data sets. For each tree examined, we found that nearly the same average bootstrap percentage was obtained from each replicate and that the standard deviations for replicate average bootstrap values were not large enough to account for the range of bootstrap values observed across the sets of alternative MSTs. We therefore conclude that variance from the bootstrapping procedure cannot account for the much larger range of bootstrap values encompassed by those sets.

These findings imply that although all MSTs in the MSN are equally parsimonious, some tree configurations are more statistically robust, and thus more credible, than others. In some instances, there may be either a single MST with the highest bootstrap value or a number of highly similar MSTs that have equally high bootstrap values, indicating that a particular tree configuration is the most credible. In other cases, there may exist multiple dissimilar configurations with high bootstrap values that represent distinct but equally credible hypotheses about the true relationships among individuals.

Although in phylogenetic applications bootstrap probabilities of greater than 70% are typically considered trustworthy, phylogenetic trees are based on many more polymorphic sites than are available in MST analyses. As such, the bootstrapping procedure has much greater potential to perturb relationships within MSTs than it does for phylogenetic trees. For MSTs, bootstrap probabilities must be considered relative measures of reliability rather than a hard and fast cutoff of believability.

We conclude that by restricting analysis to a single, arbitrary MST, there is considerable risk in picking a tree with an inferior credibility. Conversely, by surveying and evaluating trees within the MSN, it is possible to identify those with more credible configurations. In the data sets examined here, the absolute difference between the most- and least-credible MSTs measured as much as a 28% difference in average bootstrap values (Table 1). In one case, this difference represented 60% of the maximum average bootstrap value achieved.

A systematic approach to MST estimation.

In order to permit more comprehensive and objective analysis of MSTs, we propose a rational approach for their evaluation by estimating the number of possible MSTs, calculating an MSN, and bootstrapping alternative MSTs. Combined, these functions permit an assessment of possible MST configurations, provide an estimate of the overall number of those configurations, and allow the most credible hypothesis or hypotheses that explain the underlying population structure to be identified.

For a proof of concept, we applied this approach to a representative data set from our initial analysis and compared it to the previously published MST calculation. Lari and colleagues (13) based their study on VNTR markers from 29 genotypically distinct Mycobacterium bovis strains collected from Tuscany, Italy, between 1990 and 2009 and used MST analysis to infer their population structure (Fig. 2A). Several inferences can be drawn from this MST. The most likely ancestral node, corresponding to the node with the largest number of edges, is node 4. Diversification of that clone appears to have proceeded in two major directions: toward node 3, which had the second largest number of edges, and toward node 21, which itself is closely related to two major branches, namely, that with Mycobacterium bovis BCG (bacillus Calmette-Guérin, or vaccine)-like strains and node 5 and its close relatives.

We initially calculated the most credible MST (Fig. 2B) and the MSN (Fig. 2C) from those data using an equidistant pairwise distance matrix, which Lari et al. had previously used. The major structural features of the published MST are intact in the highest-credibility MST (average bootstrap value of 45%), although 6 terminal nodes were placed in alternative locations on the MST. Most of these alternative edges have high bootstrap probabilities associated with them (especially 13 to 21, 18 to 15, and 20 to 12) and are therefore likely to be credible. Separately, node 3 has significantly fewer edges than in the original MST. The MSN accordingly reflects significant variability among the placements of individuals connected to node 3, as well as to nodes 4 and 21. The placement of node 15 was sufficiently variable that it did not have a particular connection which appeared in greater than 50% of the MSTs, and that node was consequently excluded from the final MSN.

We next calculated the most credible MST (Fig. 2D) (average bootstrap value of 43%) and the MSN (Fig. 2E) from those data using a distance matrix calculated by the difference method, which we consider to be preferred because it both limits the number of possible MSTs and may more realistically model the genetic distances among individuals. Use of that distance matrix produced a most credible MST with a substantially different topology, where 18 of the 26 individuals were placed differently than in the previously published tree. In this configuration, the major divisions of isolates are more numerous and more directly related to the inferred ancestral node (node 4). The relative relationships of the BCG-like strains and node 5 descendants are unaltered, but these groups have dramatically different progenitors than in the original tree. Once again, most of the alternative connections specified by the highest-credibility MST are statistically robust and are likely to be credible.

DISCUSSION

MSTs provide a solution to the classic computational problem of connecting individuals together by the shortest possible path. Given the general nature of this problem, MSTs have been applied to diverse applications in engineering, economics, information technology, and the sciences.

Nevertheless, there is an important distinction between using MSTs to find the optimal path for connecting physical or virtual objects, such as phone networks or financial transactions, and applying them to estimate historical lineage relationships for molecular epidemiology. In the former situation, it is important to ensure only that the chosen solution equals the minimum distance possible, and there is consequently no need to consider alternative MSTs. Yet in molecular epidemiology, every MST represents a distinct and equally valid approximation of the relationships among strains. Although it is standard practice to report a single MST in molecular epidemiology publications, it is fundamentally misleading to regard this individual hypothesis as correct. Failing to consider alternative solutions can easily mislead or confound our understanding of population structure.

A separate issue involves evaluating the reliability of MSTs. For methods of inferring population structure through phylogenetic or clustering approaches, quality metrics are incorporated to evaluate the reliability of those estimations. Partially because it has inherited the use of MSTs through other fields, molecular epidemiology has yet to adopt similar measures. Once again, this limitation has the potential to adversely affect molecular epidemiology studies by failing to identify which associations within an MST are unreliable.

Several molecular epidemiology studies are noteworthy because they have acknowledged these issues to various degrees. In reconstructing a nosocomial outbreak of the hepatitis C virus, Spada and colleagues (23) used prior knowledge about the identity of the index patient in order to limit the population of possible MSTs to only those consistent with the expected model. Schouls et al. (22) similarly limited selection of alternative MSTs to those consistent with bacterial clonal growth as modeled by the BURST method (8). Separately, Bougnoux et al. (3) employed bootstrapping to evaluate the reliability of their MST estimation of Candida albicans isolates. Despite these exceptions, MSTs have been used with increasing regularity in molecular epidemiology studies without any acknowledgment of their potential weaknesses. At least part of this problem derives from the reliance of researchers on commercial software analysis packages that similarly fail to address the inherent limitations of MST analysis.

To explore the effect of considering alternative MSTs and credibility values, we examined previously published data sets that had been analyzed and interpreted using MSTs (Table 1). For all studies considered in our survey, alternative MSTs do exist, and in most instances, we find that there are a considerable number of alternative MSTs. In some cases, this number is too high to even estimate. Among the population of equally parsimonious alternative MSTs, bootstrapping analysis reveals that there are MSTs with a range of credibility values such that some alternative MSTs are significantly more statistically robust than others. It is clear that presenting a single MST neither explores the range of alternative hypotheses nor evaluates the quality of MSTs based on their relative credibilities.

To address these problems, we propose a novel approach to MST analysis, which we have automated through the MSTgold algorithm.

1. The distance matrix that maximizes the differences between individuals is calculated. For VNTR data, a distance matrix calculated by the difference method should be used, and for MLST data, distances should be computed from the underlying DNA sequence data.

2. Instead of returning a single, arbitrarily selected MST, the MSN (representing or approximating the entire population of alternative MSTs) is reported. The total number of possible MSTs is estimated using a mark-recapture calculation (21).

3. A bootstrapping metric is employed to estimate the credibility of individual MSTs within the population of alternative solutions comprising the MSN. As many MSTs as time permits are subjected to bootstrap analysis so that the most reliable MST topology can be estimated and statistical support for particular relationships may be ascertained.

4. The most credible hypothesis or hypotheses within the larger population of MSTs are reported.

Collectively, these steps allow a more objective evaluation of population structure through MST estimations.

We have presented here a representative example where using this algorithm changes the interpretation of molecular epidemiology data (Fig. 2). Revisiting a recently published MST employed to study M. bovis strains, we found that there were about 250,000 possible alternative solutions (Table 1) with the standard equidistant distance matrix utilized by Lari et al. (13). By simply using an arithmetic distance matrix optimal for VNTRs, the number of alternative trees could be reduced to about 7,000. Thus, selecting an appropriate distance matrix is an important initial consideration in constructing MSTs. After bootstrapping within the set of alternative trees, we found a >20% difference in average bootstrap values between the most- and least-credible alternative MSTs, corresponding to over 50% of the average maximum bootstrap values encountered (Table 1). In other words, choosing an arbitrarily selected MST for presentation may be less than half as credible as some other solution. In this instance, the most-credible alternative MSTs calculated from either distance matrix exhibited significant differences from the originally published tree. Using the equidistant matrix, 23% of the nodes in the most credible MST were placed differently than in the published tree, while in the more dissimilar optimal distance matrix, more than 69% of individuals were affected. In several cases, these alterations strongly affected the inferred descent of individuals or groups of related individuals.

Given the role of molecular epidemiology in understanding, preventing, and treating human disease, we assert that the issues raised in this work must be acknowledged by researchers in that community. We recommend that the systematic approach described here, or some variant of it, be adopted as a “gold standard” by molecular epidemiologists in order to provide more adequate modeling and statistical evaluation of the possible relationships between strains through MST analysis.