Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2011 Aug 18;27(20):2866–2872. doi: 10.1093/bioinformatics/btr479

Improved quality control processing of peptide-centric LC-MS proteomics data

Melissa M Matzke 1, Katrina M Waters 1, Thomas O Metz 1, Jon M Jacobs 1, Amy C Sims 2, Ralph S Baric 2, Joel G Pounds 2, Bobbie-Jo M Webb-Robertson 1,*
PMCID: PMC3187650  PMID: 21852304

Abstract

Motivation: In the analysis of differential peptide peak intensities (i.e. abundance measures), LC-MS analyses with poor quality peptide abundance data can bias downstream statistical analyses and hence the biological interpretation for an otherwise high-quality dataset. Although considerable effort has been placed on assuring the quality of the peptide identification with respect to spectral processing, to date quality assessment of the subsequent peptide abundance data matrix has been limited to a subjective visual inspection of run-by-run correlation or individual peptide components. Identifying statistical outliers is a critical step in the processing of proteomics data as many of the downstream statistical analyses [e.g. analysis of variance (ANOVA)] rely upon accurate estimates of sample variance, and their results are influenced by extreme values.

Results: We describe a novel multivariate statistical strategy for the identification of LC-MS runs with extreme peptide abundance distributions. Comparison with current method (run-by-run correlation) demonstrates a significantly better rate of identification of outlier runs by the multivariate strategy. Simulation studies also suggest that this strategy significantly outperforms correlation alone in the identification of statistically extreme liquid chromatography-mass spectrometry (LC-MS) runs.

Availability: https://www.biopilot.org/docs/Software/RMD.php

Contact: bj@pnl.gov

Supplementary information: Supplementary material is available at Bioinformatics online.

1 INTRODUCTION

The majority of statistical strategies to assess peptide/protein differential abundances from liquid chromatography-mass spectrometry (LC-MS) proteomic experiments are based on analysis of variance (ANOVA) methodologies applied to peak intensities (i.e. abundance measures) of proteolytic peptides (Bukhman et al., 2008; Daly et al., 2008; Karpievitch et al., 2009; Oberg and Vitek, 2009; Oberg et al., 2008). However, the ANOVA approach relies upon accurate estimates of sample variance, and proteomics studies not only have inherent variability associated with the biological samples, but potentially diverse process-based sources of variability. That is, the accurate estimate of sample variances is often difficult to obtain. For example, sample preparation protocols and instrument variations associated with the LC column (particularly important for multi-column platforms) and mass spectrometer can cause variations in peak intensities, as well as peptides identified across MS analyses within an experiment. Data quality is especially important when the number of biological samples is small, often the case in proteomics experiments, and extreme values can negatively influence all subsequent data analysis outcomes.

Identification of statistical outliers in univariate data is an established but highly debated statistical topic (Barnett and Lewis, 1994; Hawkins, 1980). There are many consecutive outlier procedures, focusing on one suspect value at a time, that have been proposed and implemented across many fields of application, such as Grubbs' test and Dixon's Q-test (Dixon, 1950; Grubbs, 1950). Because these methods iteratively remove outlier points, the false positive rate (i.e. Type 1 error) is inflated (Jain, 2010). In contrast, recursive outlier detection procedures detect the presence of any number of outliers and control Type 1 errors. For example, Jain (2010) presents a recursive version of Grubbs' test and Caroni and Prescott (1992) derived a sequential application of Wilks's multivariate outlier test. There are downfalls to these recursive procedures: (i) they are designed for univariate data, and if applied to multivariate data, will likely fail to detect statistically influential extreme values, and (ii) they are negatively affected by masking (i.e. the inability to detect an outlier in the presence of another outlier) and swamping (i.e. identify non-outliers as outliers) effects.

The identification of statistical outliers in multivariate data, such as microarray and proteomic data, is non-trivial. The multiple dimensions of the data often subject outliers to masking (Filzmoser et al., 2008). The microarray community, however, has made considerable progress in applying statistical metrics to assess the quality of microarray data (Kauffmann et al., 2009; Kemmeren et al., 2005; Lee et al., 2006; Wilson and Miller, 2005). Of particular applicability to proteomics data are the ideas presented by Kauffmann et al. They note that a poor quality array will impede the statistical and biological significance of the analysis due to the added noise. This is also true for proteomics data. That is, poor quality peptide abundance data will hinder downstream statistical analysis, including normalization, and subsequent biological interpretations.

For proteomics data, a routine but non-probabilistic approach used for the identification of outlier LC-MS analyses (i.e. runs) during data preprocessing is through a correlation matrix plot (Metz et al., 2008). The sample correlation coefficient is calculated among technical replicates and biological replicates. Those runs with a relatively low correlation are removed from the dataset. The determination of ‘low’ correlation is subjective, and varies across analysts, experiments and time. Correlation may be examined via a heat map in which a color palette represents the numeric value, the color palette choice as well as the range of correlation values it covers can be highly subjective and extremely influential on the selection of which runs should be removed from the dataset. In addition, the sample correlation coefficient can only be computed across peptides with common identifications between runs (i.e. it does not account for missing data), it does not account for the multivariate nature of LC-MS runs, nor is there any statistical certainty associated with the exclusion of a run.

Advanced statistical approaches to outlier detection in proteomics data have focused either on the identification of outlier spectra maps (Rudnick et al., 2010; Schulz-Trieglaff et al., 2009) or on peptide/protein abundances independent of LC-MS run behavior (Cho et al., 2008; MacCoss et al., 2003; Xia et al., 2006). Rudnick et al. (2010) described a large set of metrics for the quantitative assessment of system performance and evaluation of technical variability among inter- and intra-laboratory LC-MS/MS proteomics experiments. However, the use of these metrics to assess the quality of an individual LC-MS/MS run is not addressed. Schulz-Trieglaff et al. (2009) applied a multivariate method to perform a quality assessment of raw LC-MS maps using 20 quality descriptors. The goal of their approach was to identify and remove outlier runs using unprocessed spectra before noise filtering, peak detection or centroiding was performed. Cho et al. (2008) presented a peptide outlier detection method using quantile regression to account for the heterogeneity of variance between replicate LC-MS/MS runs. Peptide intensity ratios were plotted on an MA plot, where M is the difference in peptide abundance values and A is the average peptide intensity value. MacCoss et al. (2003) developed a correlation algorithm to detect outlier peptides using fractional changes between sample and reference intensities. Xia et al. (2006) proposed a two-stage method, combining Dixon's Q-test and a median absolute deviation (MAD) modified z-score test, for outlier detection of peptide ratios. These latter methods focus on assessing individual peptides for extreme behavior rather than the distribution of peptide abundance values for an entire LC-MS run.

Our goal is to statistically identify runs that exhibit extreme peptide abundance distribution properties, and thus will likely impact downstream statistical analyses. Consequently, we are not focused on outliers specific to the spectral properties. We describe a statistical strategy to identify and remove extreme LC-MS runs with a high level of statistical certainty, thus removing subjectivity from the filtering process. The approach, based on a robust Mahalanobis distance (rMd), assesses the reproducibility of the distribution of peptide abundance values across replicate runs of the same biological sample as well across related biological samples. Statistical methods, which limit the influence of extreme observations, are applied to obviate assumptions about underlying probabilistic models (Hoaglin et al., 2000). We demonstrate the approach by applying it to simulated and real LC-MS datasets.

2 METHODS

Our approach to detect and ascertain if an individual LC-MS run within an experiment, is a statistical outlier with a four-step process. The algorithm was implemented in MATLAB (version 7.10.0.499, R2010a, The MathWorks Inc.: Natwick, MA, USA).

2.1 Summarize each LC-MS run as five metrics

Five statistical metrics were chosen to describe the distribution of observed peptide abundance values in a single LC-MS run. These metrics described below capture selected aspects of the peptide abundance distribution such as shape and scatter. The location of each distribution is not directly considered since it could potentially be a false indicator of outlingness. In addition, location can easily be corrected by a simple overall normalization factor. The metrics are vectorized for each run, represented as 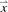Inline graphic; initially reducing the dimension of each run from p peptides to q metrics with the resulting dataset dimensionality of (n×q) where n is the number of LC-MS runs.

2.1.1 Metric 1: correlation coefficient

The sample correlation coefficient, rij, is calculated for peptide abundance values between all LC-MS runs (i=1,…, n; j=1,…, n) resulting in an n×n matrix. The correlation coefficient metric for the i-th run, Ri, which is used for the robust principal component analysis, is the average correlation within a common grouping (e.g. treatment group, G), and has dimension (n×1). For the i-th run this is computed as,

graphic file with name btr479m1.jpg (1)

where NG(i) is the total number of runs in the group associated with run i. The average correlation among biological replicates, rather than among technical replicates, is used due the small number of technical replicates, if any at all, observed in a typical LC-MS experiment.

2.1.2 Metric 2: fraction of missing peptide abundance data

The fraction of missing abundance data in the i-th (1,…, n) LC-MS run is defined as,

graphic file with name btr479m2.jpg (2)

where aij=1 if the j-th peptide abundance is absent for the i-th run; otherwise, aij=0.

2.1.3 Metric 3: median absolute deviation of peptides within a LC-MS run

The MAD (Hoaglin et al., 2000) is a robust measure of the spread of the data, and is used as an estimate of the sample standard deviation if scaled by a factor of 1.483. The MAD of the i-th LC-MS run is defined as,

graphic file with name btr479m3.jpg (3)

That is, within a run, each abundance value for peptide j is compared with the median peptide abundance values of the run i.

2.1.4 Metric 4: skew

The asymmetry of a distribution is described by skew. In our application to the i-th (1,…, n) LC-MS run, p is the number of peptides observed in the i-th run, Inline graphicis the average peptide abundance value of all peptides observed in the i-th run and S is the sample standard deviation of the i-th run.

graphic file with name btr479m4.jpg (4)

2.1.5 Metric 5: kurtosis

The peakedness, or ‘heavy-tailedness’, of a distribution is described by kurtosis. The same parameters are used as skew. Kurtosis is calculated as,

graphic file with name btr479m5.jpg (5)

2.2 Obtain a robust estimate of the covariance matrix

The purpose of robust principal component analysis (rPCA) in our method is to obtain the eigenvalues and eigenvectors to calculate a robust covariance matrix, which will be used in the calculation of the rMds. We employ a rPCA algorithm developed by Croux et al. that is based on the projection-pursuit approach to estimate the eigenvalues, and subsequent scores obtained from the projections of the metrics on the eigenvectors (Croux and Ruiz-Gazen, 2005; Li and Chen, 1985). The robust covariance estimate is defined as,

graphic file with name btr479m6.jpg (6)

for which Sn is the robust scale estimator used by the projection-pursuit index λSn,k is the k-th eigenvalue and νSn,k is the k-th eigenvector (Croux and Ruiz-Gazen, 2005). The rPCA algorithm uses the L1-median value to center the data, and (MAD*1.483) as the robust scale estimate.

2.3 Identify outlier LC-MS run(s) using the rMd

A widely accepted measure of distance in multivariate data is the Mahalanobis distance because it accounts for not only the average value, but also the covariance structure of the measured variables (Mahalanobis, 1936). The distance of an individual LC-MS run from the center of the data is measured by a rMd. For a q-dimensional multivariate vector 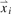Inline graphic for i=1,…, n, the rMd is defined as,

graphic file with name btr479m7.jpg (7)

where CSn, a robust estimate of the covariance matrix, is obtained from the robust principal component analysis of the n×q quality matrix, and 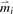Inline graphic is a vector of medians of the five metrics.

2.4 Statistical assessment of the rMds

The rMd squared values associated with the peptide abundances vector (rMd-PAV) is the score used to assess whether an individual LC-MS run is an outlier. The rMd-PAV scores are approximately chi-square distributed with q degrees of freedom (χq2). Therefore, outlier LC-MS runs are defined by a large rMd-PAV score such that the calculated squared distance exceeds a critical value of the χq2 distribution specified a priori.

2.5 Proteomics data processing

We present two independent real datasets to demonstrate the application of this outlier discovery strategy to LC-MS proteomics data. Human cell culture samples were analyzed with an Exactive mass spectrometer (Thermo Electron Corp.), and mouse plasma samples were analyzed with an LTQ-Orbitrap mass spectrometer (Thermo Electron Corp.). Nanoelectrospray ionization was used in the analysis of all samples. Spectra were collected at 400–2000 m/z with a resolution of 100 k and analyzed using the accurate mass and elution time (AMT) tag approach (Smith et al., 2002). The mass de-isotoping process was performed using Decon2LS (Jaitly et al., 2009), and the matching process was performed using VIPER (Monroe et al., 2007). Features from the LC-MS analyses were matched to AMT tags to identify peptides, using an initial tolerance of ±3 p.p.m. for mass and 2.5% for the LC normalized elution time (NET). The human cell culture peptide datasets were further processed to remove peptides identified with low confidence, using the uniqueness filter Statistical Likelihood Confidence (SLiC) (Anderson et al., 2006) score of 0.35 and a DelSLiC of 0.2. In circumstances where a peptide was identified in some LC-MS analyses, but not others, the missing data were coded as ‘NaN’. All peptide abundance values were transformed to the log10 scale. Minimum occurrence data filters were used to identify those peptides for which the amount of data present was not adequate for differential abundance analysis (Webb-Robertson et al., 2010). The sample complexity of the sham controls (SCs) in each of the designed experiments is the same with respect to original biological material.

3 RESULTS

Simulations of size 500 based on the p-variate standard normal distribution Np(0,I), and an empirically influenced p-variate normal distribution Np(μ, Σ) were performed to examine a range of outlier configurations. In addition, we assessed the performance of the multi-dimensional outlier detection method against the conventional method of using a Pearson's correlation coefficient [previously described in Section 2.1 as metric 1—Equation (1)] to ascertain whether a LC-MS run is an outlier. Simulation is useful to investigate the properties of rMd-PAV, however; since simulation of expected distribution parameters in real proteomics data is not well understood, these results are presented in Supplementary Material (Rocke et al., 2009).

The results of the multi-dimensional outlier detection analysis are displayed in a simple yet effective graphic in which rMd-PAV scores are plotted for each LC-MS run and compared with a reference line representing the χ2 critical value. For improved visualization, the rMd-PAV scores and the χ2 critical value are transformed to the log 2 scale. The red horizontal line represents the log2(χ20.9999,5) critical value. That is, at a significance level of 0.0001, a LC-MS run may be classified as a statistical outlier if the calculated test statistic ≥χ20.9999,5 critical value, or equivalently, the χ2 P≤0.0001. LC-MS runs with log2(rMd-PAV) scores above the red horizontal line are suspect and should be removed from the dataset.

3.1 Real data benchmark—expert identified outlier runs

Calu-3 cells, a human lung adenocarcinoma cell line, were infected with the severe acute respiratory syndrome coronona virus (SARS-CoV) at a multiplicity of infection of 5. Cell monolayers were inoculated with SARS for 40 min at 37○C, and sham-infected controls were inoculated with medium only. Following inoculation, monolayers were rinsed and incubated for times 0, 3, 7, 12, 24, 30, 36 and 48 h. At the indicated times post-infection, wells were washed three times with ice cold 150 mM ammonium bicarbonate buffer and cells lyzed for 5 min in ice cold 8 M urea. Samples were frozen at −80○C until assayed. Samples were analyzed in triplicate, except where noted in Supplementary Table S2, and the minimum occurrence filter returned a total of 26 776 peptides (Webb-Robertson et al., 2010).

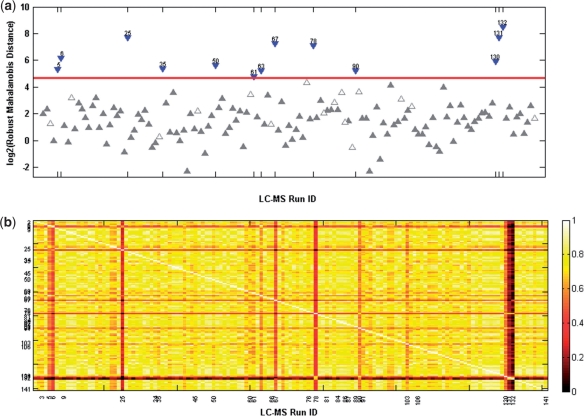
This study included three biological replicates per time point as well as a large number of LC-MS runs (n=141), thus the removal of runs with poor quality abundance data is essential to maintain statistical power in downstream analyses. An LC-MS expert at Pacific Northwest National Laboratory upon reviewing the chromatography maps for this study was able to designate 28 out of 141 (~20%) LC-MS analyses as suspect due to various reasons (e.g. electrospray instability, elution time, sample prep/collection problem). We performed the rMd-PAV analysis, and compared its performance with t correlation alone to identify statistical outliers (runs at the peptide abundance level) via a receiver operating characteristic (ROC) curve analysis.

The rMd-PAV approach identified 12 out of the 28 expert-designated suspect runs as statistical outliers at the 0.0001 significance level (Fig. 1a). Electrospray issues represent almost half (13/28) of the expert identified runs, while the statistical algorithm identified three of these runs. It is the most likely technical issue to occur and the most difficult to detect. One reason could be that the electrospray issue does not translate to a poor peptide abundance distribution, and thus an outlier. The other 15 runs identified by the MS expert are due to elution time (5/28; 4/5 identified by algorithm), chromatography (3/28; 1/3 identified by algorithm) and sample prep/collection (7/28; 4/7 identified by algorithm).

Fig. 1.

Fig. 1.

Open in a new tab

Calu-3 cell-line experiment. (a) The rMd-PAV plot of the LC-MS runs. Runs identified as outliers (blue downward triangles) sit above the red horizontal line which represents the log2 (χ0.9999,52) critical value (i.e. P=0.0001). The empty upward triangles below the red horizontal line represent runs identified as suspect by the MS expert that were not identified as statistical extreme. (b) The correlation plot of the LC-MS runs.

LC-MS runs that were expert designated as suspect, but did not exhibit different peptide abundance distributions from those runs that were not designated as suspect are identified in Figure 2a as unfilled triangles. Although the MS expert identified these runs as suspicious, the peptide abundance distributions are indistinguishable from those runs that were not designated as suspect.

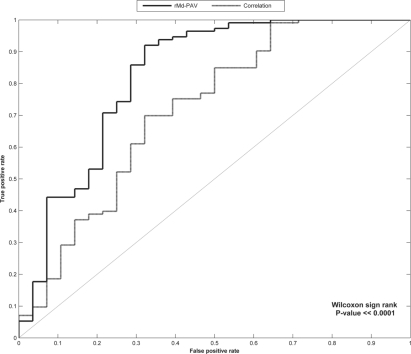
Fig. 2.

Fig. 2.

Open in a new tab

The ROC curves from the rMd-PAV and correlation alone outlier analyses of the calu-3 cell-line experiment.

In addition, we reviewed the sample correlation coefficient between all the study runs (Fig. 1b). Based on a subjective visual inspection of this graph, 6 out of the 28 expert-designated suspect LC-MS runs (#6, 25, 67, 78, 131 and 132) would have been dropped from the dataset. The rMd-PAV scores identified six additional runs as statistical outliers. This method did not identify any of the extreme runs due to electrospray issues; it did identify 3/5 runs labeled as suspect due to elution time, 1/3 suspect runs due to chromatography and 2/7 runs due to sample prep/collection issues.

A ROC analysis was completed to compare all levels of sensitivity and specificity. A comparison of the ROC curves for the rMd-PAV scores and the correlation metric alone by a Wilcoxon signed rank test results in statistically significant differences between the curves in favor of rMd-PAV (P<0.0001, Fig. 2). Therefore, for this benchmark dataset we observe that rMd-PAV scores are superior to correlation alone for the identification of statistical outlier runs in LC-MS peptide abundance data.

3.2 Case study—cigarette smoke exposure data

Groups (N=8 biological replicates) of regular weight (RW) and diet-induced obese (OB) C57BL/6 mice (15 weeks old) were exposed to either filtered air (SCs), mainstream (MS) or side stream (SS) cigarette smoke by nose-only inhalation exposure for 5 h/day for 8 days. Target cigarette smoke exposure concentrations were 250 μg wet-weight total particulate matter (WTPM)/L of air for the MS exposures and 85 μg WTPM/L for the SS exposures. RW mice are defined as those mice fed a regular diet (PMI 5002 Rodent Diet®, Richmond, IN, USA; ~5kal% fat) throughout the study. DIO mice were fed a high-calorie/high-fat diet (D12492 Rodent Diet, Research Diets Inc., New Brunswick, NJ, USA; 60kal% fat) starting at 6 weeks of age and continued throughout the study. Immediately following the last exposure, each animal was removed from the exposure unit and anesthetized. Blood was collected into tubes containing potassium ethylenediaminetetraacetic acid (EDTA) (Tyco Healthcare Group LP, Mansfield, MA, USA) and centrifuged to obtain plasma for analysis by LC-MS/MS. Samples were analyzed in duplicate, except where noted in Supplementary Table S3 and a minimum occurrence filter returned a total of 3655 peptides (Webb-Robertson et al., 2010).

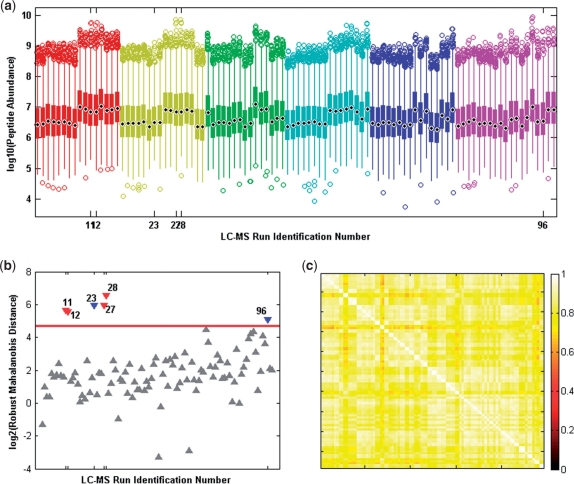
As in any data analysis problem, visual inspection of complex data before statistical analysis is vital. Box plots are a simple and statistically robust techniques that are informative concerning distributional properties (e.g. skew and kurtosis), and provide visual guidance when interpreting analysis results. Peptide abundance data for each example has been displayed versus a LC-MS run order identification number (not true LC run order) using a box plot. The box plot of the mouse plasma data (Fig. 3a) shows a fair amount of variability from run to run making visual determination of statistical outlier runs difficult.

Fig. 3.

Fig. 3.

Open in a new tab

Cigarette smoke exposure experiment. (a) Box plots of peptide abundance values observed in LC-MS runs (n=98) for the mouse plasma dataset. The color indicates experimental group membership. (b) The rMd-PAV plot of the LC-MS runs. Those runs identified as outliers sit above the red horizontal line which represents the log2 (χ0.9999,52) critical value (i.e. P≤0.0001). The downward triangles represent outlier runs—red represents all technical replicates from a biological sample, and blue represents individual technical replicates within a sample. (c) The run-by-run (rij) correlation plot of the LC-MS runs.

The rMd-PAV approach identified 6 out of the 98 LC-MS runs as statistical outliers at the 0.0001 confidence level (Fig. 3b). Singleton technical replicates were removed (run id #23 and 96), in addition to two complete biological samples (run id #11 and 12—obese SC sample; run id #27 and 28—obese MS inhalation sample). Of the six runs identified as statistical outliers, it is unlikely any would have been removed using run-by-run correlation coefficient, rij, as the median correlation of all runs is 0.86 (Fig. 3c), and ranging from 0.72 to 0.87 across the pool of identified outlier runs. Using a more reflective score of correlation, Ri, which for the i-th run is the average correlation among the biological replicates within a group, the rMd-PAV identified runs would not have been removed from the dataset as the median correlation is 0.88 ranging from 0.73 to 0.85 across the identified outlier runs.

An additional benefit of the rPCA is the ability to explore the behavior of the metrics (e.g. skew, kurtosis, fraction missing, etc.) used to describe the peptide abundance distributions for the LC-MS runs within an experiment. Explaining high-dimensional data in two or three latent variables (i.e. principal components) is highly desirable. With only a few latent variables, data can be graphically displayed and the key contributing attributes to the total explained variation is easily interpreted. The relationship among the five metrics for peptide abundance data can be understood by examining the score plots of the latent variables. In addition, the behavior of the outlier runs can be understood relative to the non-outlier runs (i.e. average).

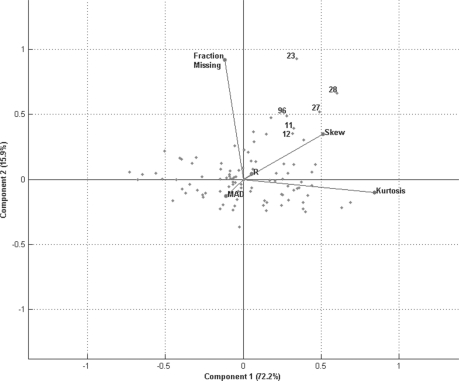
The most dominant manner in which these runs deviate is Kurtosis, Skew and Fraction Missing Data, as observed in the score plot associated with the rPCA (Fig. 4). The score plot is unique to an experiment, and thus is an excellent tool to further understand statistical differences in the peptides distributions among the LC-MS runs. The first score plot to consider is a comparison of the first two rPCA components (i.e. latent variables). In combination they account for >88% of the total variation in the data, and suggest differences among kurtosis, skew and fraction of missing abundance data explain most of the variation in the data. The plot shows the rMd-PAV identified runs located at the extreme ends of the observed data with respect to the first and second latent variables. Using the angle between vectors as a visual guide, for this data, it can be deduced the Fraction Missing Data and Skew of the peptide abundance distribution are correlated. In total, the first three components account for ~95% of the variation observed in the data. While a two-dimensional view of the data is helpful in understanding relationships among variables, outliers and non-outliers, it is the relationship among the data under the full dimensionality that is the basis for the evidence of outlier runs.

Fig. 4.

Fig. 4.

Open in a new tab

Cigarette smoke exposure experiment. The score plot of the first two latent variables resulting from the rPCA of the data. It suggests the runs labeled on the plot are outliers due to the fraction of missing peptide abundance values, and the skewness and kurtosis of the peptide abundance distribution within a run.

4 DISCUSSION

Outlier detection in multivariate data is a non-trivial statistical task often subject to the masking effect (Filzmoser et al., 2008; Rocke and Woodruff, 1996). Caution should always be taken when removing data from any dataset, large or small, and data should not be removed solely on the grounds of a statistical outlier test. Rather, the results of any statistical outlier algorithm used should always be reviewed in the context of the research goal and the experiment. Often the extreme data values are of interest and may explain technical difficulties in the process (e.g. sample preparation issues, technical difficulties with instrumentation and a mislabeling of samples). However, as with any statistical analysis and especially those dealing with small sample sizes, reviewing the outcome of the analysis is imperative. Specifically, graphical methods allow the analyst to review the analysis in a stepwise manner. For example, as our first step, we first plot the peptide abundances observed in the experiment for each LC-MS run using a box plot. Then to understand how the abundance distributions vary across the LC-MS runs we examine the scores plot resulting from the robust PCA.

5 CONCLUSION

We have presented a novel approach to the identification of statistical outliers in LC-MS proteomics peptide abundance data. The value of the multivariate outlier discovery strategy utilizing rMd-PAV scores is the use of an objective probabilistic model to assess statistical certainty of the exclusion of runs within an experiment in the context of the complete dataset. Proteomics has placed considerable effort on assuring the quality of the peptide identification with respect to spectral processing (Piening et al., 2006; Rudnick et al., 2010; Schulz-Trieglaff et al., 2009; Stead et al., 2008); however, quality assessment of the subsequent data matrix has focused on subjective visual inspection of run-by-run correlation, or individual peptide components. The quality of the LC-MS peptide abundance data matrix is essential to the identification of robust biomarkers. Moreover, statistical evaluation of the data relies upon tools often based on linear models, such as ANOVA which require accurate estimates of variance (Bukhman et al., 2008; Daly et al., 2008; Karpievitch et al., 2009; Oberg et al., 2008). Without proper identification of statistical outlier runs the estimates of variance will be inflated, which may have a considerable effect on the identification of significant peptides and proteins.

Supplementary Material

Supplementary Data
supp_27_20_2866__index.html (807B, html)

ACKNOWLEDGEMENTS

Portions of this work were performed in the Environmental Molecular Science Laboratory, Office of Biological and Environmental Research, National Scientific User Facility at Pacific Northwest National Laboratory (PNNL) in Richland, WA, a U.S. Department of Energy (DOE).

Funding: This work was supported by the National Institutes of Health, the National Institute of General Medical Sciences (R01 GM084892 to B.-J.M.W.-R.); the National Institute of Environmental Health Sciences (U54 ES 016015 to J.G.P.); and the National Institute of Allergy and Infectious Disease (HHSN272200800060C to K.M.W.). PNNL is operated by Battelle Memorial Institute for the DOE under contract number DE-AC05-76RLO1830.

Conflicts of Interest: none declared.

REFERENCES

  1. Anderson K.K., et al. Estimating probabilities of peptide database identifications to LC-FTICR-MS observations. Proteome Sci. 2006;4:1. doi: 10.1186/1477-5956-4-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barnett V., Lewis T. Outliers in Statistical Data. West Sussex, England: John Wiley & Sons; 1994. [Google Scholar]
  3. Bukhman Y.V., et al. Design and analysis of quantitative differential proteomics investigations using LC-MS technology. J. Bioinform. Comput. Biol. 2008;6:107–123. doi: 10.1142/s0219720008003321. [DOI] [PubMed] [Google Scholar]
  4. Caroni C., Prescott P. Sequential application of Wilks's multivariate outlier test. J. R. Stat. Soc. Ser. C (Appl Stat) 1992;41:355–364. [Google Scholar]
  5. Cho H, et al. OutlierD: an R package for outlier detection using quantile regression on mass spectrometry data. Bioinformatics. 2008;24:882–884. doi: 10.1093/bioinformatics/btn012. [DOI] [PubMed] [Google Scholar]
  6. Croux C., Ruiz-Gazen A. High breakdown estimators for prinicpal components: the projection-pursuit approach revisited. J. Multivariate Anal. 2005;95:206–226. [Google Scholar]
  7. Daly D.S., et al. Mixed-effects statistical model for comparative LC-MS proteomics studies. J. Proteome Res. 2008;7:1209–1217. doi: 10.1021/pr070441i. [DOI] [PubMed] [Google Scholar]
  8. Dixon W.J. Analysis of extreme values. Ann. Math. Stat. 1950;21:488–506. [Google Scholar]
  9. Filzmoser P., et al. Outlier identification in high dimensions. Comput. Stat. Data Anal. 2008;52:1694–1711. [Google Scholar]
  10. Grubbs F.E. Sample criteria for testing outlying observations. Ann. Math. Stat. 1950;21:27–58. [Google Scholar]
  11. Hawkins D.M. Identification of Outliers. New York, NY: Chapman and Hall; 1980. [Google Scholar]
  12. Hoaglin D.C., et al. Understanding Robust and Exploratory Data Analysis. New York: John Wiley & Sons, Inc.; 2000. [Google Scholar]
  13. Jain R.B. A recursive version of Grubbs' test for detecting multiple outliers in environmental and chemical data. Clin. Biochem. 2010;43:1030–1033. doi: 10.1016/j.clinbiochem.2010.04.071. [DOI] [PubMed] [Google Scholar]
  14. Jaitly N., et al. Decon2LS: An open-source software package for automated processing and visualization of high resolution mass spectrometry data. BMC Bioinformatics. 2009;10:87. doi: 10.1186/1471-2105-10-87. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Karpievitch Y., et al. A statistical framework for protein quantitation in bottom-up MS-based proteomics. Bioinformatics. 2009;25:2028–2034. doi: 10.1093/bioinformatics/btp362. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kauffmann A., et al. arrayQualityMetrics–a bioconductor package for quality assessment of microarray data. Bioinformatics. 2009;25:415–416. doi: 10.1093/bioinformatics/btn647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kemmeren P., et al. Predicting gene function through systematic analysis and quality assessment of high-throughput data. Bioinformatics. 2005;21:1644–1652. doi: 10.1093/bioinformatics/bti103. [DOI] [PubMed] [Google Scholar]
  18. Lee E.K., et al. arrayQCplot: software for checking the quality of microarray data. Bioinformatics. 2006;22:2305–2307. doi: 10.1093/bioinformatics/btl367. [DOI] [PubMed] [Google Scholar]
  19. Li G., Chen Z. Projection-pursuit approach to robust dispersion matrices and principal components: primary theory and Monte Carlo. J. Am. Stat. Assoc. 1985;80:759–766. [Google Scholar]
  20. MacCoss M.J., et al. A correlation algorithm for the automated quantitative analysis of shotgun proteomics data. Anal. Chem. 2003;75:6912–6921. doi: 10.1021/ac034790h. [DOI] [PubMed] [Google Scholar]
  21. Mahalanobis P. On the generalized distance in statistics. Proc. Indian Natl Sci. Acad. 1936;12:49–55. [Google Scholar]
  22. Metz T.O., et al. Application of proteomics in the discovery of candidate protein biomarkers in a diabetes autoantibody standardization program sample subset. J. Proteome Res. 2008;7:698–707. doi: 10.1021/pr700606w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Monroe M.E., et al. VIPER: an advanced software package to support high-throughput LC-MS peptide identification. Bioinformatics. 2007;23:2021–2023. doi: 10.1093/bioinformatics/btm281. [DOI] [PubMed] [Google Scholar]
  24. Oberg A.L., Vitek O. Statistical design of quantitative mass spectrometry-based proteomic experiments. J. Proteome Res. 2009;8:2144–2156. doi: 10.1021/pr8010099. [DOI] [PubMed] [Google Scholar]
  25. Oberg A.L., et al. Statistical analysis of relative labeled mass spectrometry data from complex samples using ANOVA. J. Proteome Res. 2008;7:225–233. doi: 10.1021/pr700734f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Piening B.D., et al. Quality control metrics for LC-MS feature detection tools demonstrated on Saccharomyces cerevisiae proteomic profiles. J. Proteome Res. 2006;5:1527–1534. doi: 10.1021/pr050436j. [DOI] [PubMed] [Google Scholar]
  27. Rocke D.M., Woodruff D.L. Identification of outliers in multivariate data. J. Am. Stat. Assoc. 1996;91:1047–1061. [Google Scholar]
  28. Rocke D., et al. Papers on normalization, variable selection, classification or clustering of microarray data. Bioinformatics. 2009;25:701–702. [Google Scholar]
  29. Rudnick P.A., et al. Performance metrics for liquid chromatography-tandem mass spectrometry systems in proteomics analyses. Mol. Cell Proteomics. 2010;9:225–241. doi: 10.1074/mcp.M900223-MCP200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Schulz-Trieglaff O., et al. Statistical quality assessment and outlier detection for liquid chromatography-mass spectrometry experiments. BioData Min. 2009;2:4. doi: 10.1186/1756-0381-2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Smith R.D., et al. An accurate mass tag strategy for quantitative and high-throughput proteome measurements. Proteomics. 2002;2:513–523. doi: 10.1002/1615-9861(200205)2:5<513::AID-PROT513>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
  32. Stead D.A., et al. Information quality in proteomics. Brief. Bioinform. 2008;9:174–188. doi: 10.1093/bib/bbn004. [DOI] [PubMed] [Google Scholar]
  33. Webb-Robertson B.M., et al. Combined statistical analysis of peptide intensities and peptide occurrences improves identification of significant peptides from MS-based proteomics data. J. Proteome Res. 2010;9:5748–5756. doi: 10.1021/pr1005247. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Wilson C.L., Miller C.J. Simpleaffy: a BioConductor package for affymetrix quality control and data analysis. Bioinformatics. 2005;21:3683–3685. doi: 10.1093/bioinformatics/bti605. [DOI] [PubMed] [Google Scholar]
  35. Xia Q., et al. Quantitative proteomics of the archaeon Methanococcus maripaludis validated by microarray analysis and real time PCR. Mol. Cell Proteomics. 2006;5:868–881. doi: 10.1074/mcp.M500369-MCP200. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_27_20_2866__index.html (807B, html)
supp_btr479_MATZKE_SupplementaryMaterial_JUN2011.pdf (747.8KB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES