Integration of SNP genotyping confidence scores in IBD inference

Abstract

Motivation: High-throughput single nucleotide polymorphism (SNP) arrays have become the standard platform for linkage and association analyses. The high SNP density of these platforms allows high-resolution identification of ancestral recombination events even for distant relatives many generations apart. However, such inference is sensitive to marker mistyping and current error detection methods rely on the genotyping of additional close relatives. Genotyping algorithms provide a confidence score for each marker call that is currently not integrated in existing methods. There is a need for a model that incorporates this prior information within the standard identical by descent (IBD) and association analyses.

Results: We propose a novel model that incorporates marker confidence scores within IBD methods based on the Lander–Green Hidden Markov Model. The novel parameter of this model is the joint distribution of confidence scores and error status per array. We estimate this probability distribution by applying a modified expectation-maximization (EM) procedure on data from nuclear families genotyped with Affymetrix 250K SNP arrays. The converged tables from two different genotyping algorithms are shown for a wide range of error rates. We demonstrate the efficacy of our method in refining the detection of IBD signals using nuclear pedigrees and distant relatives.

Availability: Plinke, a new version of Plink with an extended pairwise IBD inference model allowing per marker error probabilities is freely available at: http://bioinfo.bgu.ac.il/bsu/software/plinke.

Contact: obirk@bgu.ac.il; markusb@bgu.ac.il

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The emergence of high-throughput genotyping platforms introduces various challenges to genetic mapping. In particular, high-throughput genotyping data contain errors which even in small rates can obscure signals in genetic mapping (Akey et al., 2001; Kirk and Cardon, 2002; Pompanon et al., 2005; Sobel et al., 2002). An important analysis in genetic mapping is identical by descent (IBD) inference, which aims to detect regions inherited from a common ancestor (Bercovici et al., 2010; Kruglyak and Lander, 1995; Kruglyak et al., 1996; Purcell et al., 2007; Thompson, 2008). Merlin and Plink are examples of popular tools for IBD inference in pedigrees and distantly related individuals, respectively (Abecasis et al., 2001b; Purcell et al., 2007). These tools are based on an efficient implementation of the Lander and Green algorithm for IBD inference (Kruglyak et al., 1996). It is well recognized that IBD inference is sensitive to errors which in certain situations could result in loss of IBD signals (Abecasis et al., 2001a; Douglas et al., 2000; Gordon et al., 2000). Although not complete, error detection in pedigree data can be quite effective and cleaning processes became a routine prior to IBD analysis (Mukhopadhyay et al., 2004; O'Connell and Weeks, 1998). A major drawback of error detection methods is the need to set threshold values for flagging a mistyped genotype. These thresholds balance between false positive and false negative rates and often depend on other specific parameters such as pedigree structure, allele frequencies and error rates (Mukhopadhyay et al., 2004). Moreover, IBD mapping using distant relatives and case–control association analyses hold little or no information that facilitate error detection in individual genotypes. The alternative in these situations is to conduct strict QC procedures and re-genotype suspicious samples (McCarthy et al., 2008).

An alternative approach is to incorporate error probabilities per marker in the statistical models (Lincoln and Lander, 1992; Sobel et al., 2002). Models that deal with inconsistent markers within long, nearly identical stretches of markers were implemented for identical in state (IIS) and identical by descent (IBD) methods. For example, Purcell et al. implemented an IIS procedure for detecting runs of homozygosity allowing for a few mismatched markers within a candidate run (Purcell et al., 2007). Leutenegger et al. (2003) and Browning et al. (2010) allowed a small probability of marker error for estimating homozygosity by descent and pairwise IBD probabilities, respectively (Browning and Browning, 2010; Leutenegger et al., 2003). These models assume a predefined error rate for the entire data despite the fact that marker error probability may not be homogeneous. Error rates may vary between samples, due to sample-specific preparation details (Wellcome Trust Case Control Consortium, 2007). Marker error probabilities may also depend on specific SNP parameters. For example, markers with extreme allele frequencies are generally more challenging for genotype calling algorithms (Affymetrix Inc., 2006; Korn et al., 2008).

Both the per SNP and per array biases could be addressed via the confidence scores accompanying each marker call. Genotyping algorithms report a confidence score for each call based on the allele intensities of the measured marker relative to a reference sample. These scores are informative since they assess the confidence of each call relative to all other samples and therefore reflect the per SNP relative performance for each sample. They are also informative for a per sample quality assessment (Yeung et al., 2008). Despite the valuable knowledge embedded in confidence scores, no rigorous model has been presented to date that incorporates them in IBD analysis. Such a model is not trivial because the probability of an error given a confidence score is not known and depends on details beyond the genotyping procedure. Estimating the error probability per marker is important by itself for the analysis of unrelated individuals for which there is little or no information facilitating error detection.

In this article, we develop an extended model for IBD inference incorporating marker confidence scores. We apply a modified Lander–Green Hidden Markov Model (HMM) on nuclear families genotyped with Affymetrix 250K SNP arrays and infer both IBD status and error status for each marker. The main result is an empirical distribution of confidence scores conditioned on error status that could be used for IBD inference, error rates estimation and SNP filtering. Our model is compared with the standard approach for IBD inference using Merlin, and the results suggest a significant improvement in correct inference especially for noisy samples. In addition, we show how to incorporate our findings in the analysis of unrelated individuals. Plinke, a modified Plink code for pairwise IBD sharing that incorporates genotyping error probabilities per marker was implemented. We demonstrate using real and simulated data the efficacy of the modified algorithm in the recovery of lost IBD signals between sib-pairs and distantly related individuals. Further applications for analyzing datasets of general pedigrees and unrelated individuals are discussed.

2 METHODS

2.1 IBD inference and the Lander–Green model

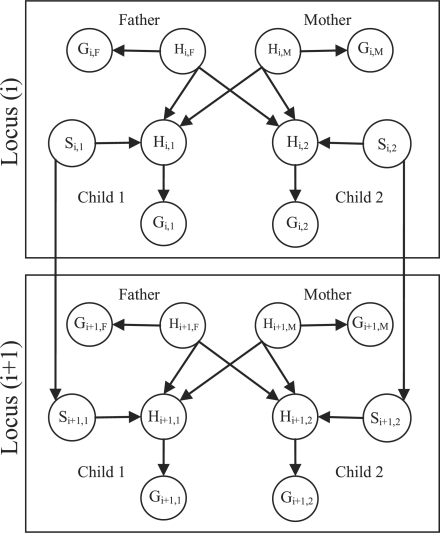
The standard approach for analyzing small pedigrees is the Lander–Green model (Lander and Green, 1987). This model could be represented as a directed acyclic graph (DAG) as indicated in Figure 1 (Fishelson and Geiger, 2002). The figure corresponds to a nuclear family of two parents and two siblings genotyped over positions (loci) along their genomes. Each locus has a representation of the entire pedigree as follows. Denote by H_ij and G_ij variables corresponding to the j-th individual at the i-th locus. G_ij is an unordered pair of measured alleles as measured for individual j at locus i (in our case, these are SNPs: AA, AB, BB or 00 for missing value). Another set of variables, H_ij, is defined to indicate the true genotype behind G_ij. H_ij is an ordered pair indicating the hidden haplotypes for individual j at locus i as follows: H_ij=(H_ij^p, H_ij^m) where p and m represent the paternal and maternal alleles, respectively. Pedigree members are connected via the variables H_ij by connecting parents with their children as depicted in Figure 1. Following Lander–Green's approach, we define selector variables: S_ij=(S_ij^p, S_ij^m) to be an ordered pair for paternal and maternal inheritance indicators: S_ij^x assumes the values 1 or 2, indicating whether a paternal or maternal allele were inherited, respectively. Adjacent loci are connected via the selectors S_ij, S_i+1,j which indicate the inheritance pattern along the loci for each individual (Lander and Green, 1987). The model depicted in Figure 1 assumes that the markers are in linkage equilibrium. Therefore, there are no edges between H_i,j and H_i+1,j (Bercovici et al., 2010). The probability table for these selectors is modeled by the recombination fraction θ between adjacent loci with the following transition matrix:

(1)

To simplify notation, locus i is represented by the following vectors for a pedigree of n individuals:

(2)

The vector of all inheritance vectors in the data is a matrix represented by the set of all vectors, one per locus: S = {S₁,S₂,…, S_L}. Similarly the matrix G = {G₁,G₂,…, G_L} denotes all measurement vectors and H = {H₁,H₂,…, H_L} denotes all hidden alleles in the data.

Fig. 1.

The Lander–Green model shown for a nuclear family having two parents and two siblings. The model is drawn for two adjacent loci assuming linkage equilibrium. G_ij indicates the measured genotype for individual j at locus i as an unordered pair. H_ij indicates the real genotype and S_ij indicates a pair of inheritance selectors with transition probabilities as indicated in Equation (1).

In IBD inference, the state space at each slot is defined to be the inheritance vector S_i. The inheritance matrix S is inferred using an HMM over adjacent loci. The conditional probability of the inheritance vector at locus i is P(S_i|G_i), where G_i represents the data at locus i. Using the forward and backward algorithms (Rabiner and Juang, 1986), the posterior probability of S_i=s given the data at all loci are calculated as follows:

(3)

The probability of the data, P(G), is calculated by iterating over all values of H_i as follows:

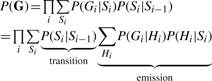(4)

The emission probability in Equation (4) for each locus can be further decomposed into two selectors. In a nuclear pedigree, the conditional probability of the hidden alleles is:

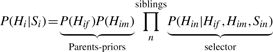The conditional probability of the measured genotype is:

The joint probability of the data and S_i is calculated in a similar manner:

(5)

where {S_i=s} is the set of all possible inheritance vectors such that S_i=s.

2.2 Incorporating confidence scores

Originally in the Lander–Green model, the data were assumed to be error free and the posterior probability for S was estimated without a measurement error model. In order to introduce an error model, we define additional variables for each measured locus. Denote by e_ij an indicator variable such that e_ij=1 whenever H_ij and G_ij are not consistent. Assuming no errors, as in the original Lander−Green model, implies P(e=1)=0. Current error models that assume a homogeneous error rate interpret the probability P(e=1) as the error rate of the data which is the same for all loci (Douglas et al., 2000). The inclusion of confidence scores for each marker in the model enables a per marker treatment.

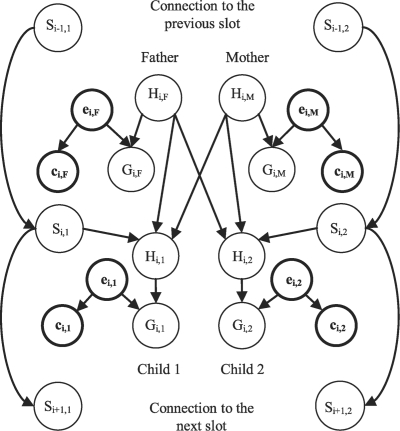
Confidence scores are introduced to our model by defining a new variable c_ij for each measured genotype, which indicates the confidence score for individual j at locus i. Consistent with Equation (2), we define the vectors e_i and c_i for locus i and the matrices e and c over all loci and individuals. Furthermore, define τ_ij=P(c_ij, e_ij) to be the joint probability distribution of marker confidence and error status for marker i of individual j. Figure 2 depicts the modified Lander–Green model with the suggested changes to each slot emphasized in thick lines.

Fig. 2.

The Lander–Green model extended with error indicators and confidence scores.

The assumptions of our model are as follows:

1. e_ik is independent of e_jk for all loci pairs i, j.

2. e_ik is independent of e_im for all individual pairs k, m.

3. The probability table τ_ij is identical for all loci of individual j. We denote τ_ij=τ_j, for all i.

These assumptions are reasonable approximations in most cases and they considerably simplify the calculation of posterior probabilities. Assumption (3) expresses the assertion that confidence scores should be calibrated per sample in order to reliably calculate marker error probabilities and maintain consistency with the definition of error rates.

The error rate for individual j is,

(6)

Under this model, the probability of the data P(G,C) takes the following form:

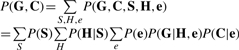(7)

Decomposing over loci, we get:

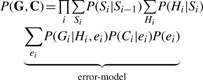(8)

Decomposing also over individuals, we get:

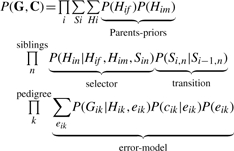(9)

In this expression, the index k is iterated over pedigree members including parents, while the index n is iterated over siblings.

The error model in Equation (9) has two components; the conditional probability of the measured genotype and the joint probability of marker error and confidence scores. The first factor, P(G_ik|H_ik, e_ik), encodes the details of the error model. We use a simple model by assuming equal probabilities to all types of genotype inconsistencies. The second factor τ_ik=P(c_ik|e_ik)P(e_ik) is unknown and in the next section we show how to estimate it from a training dataset. Inference of either IBD status, error status or both is accomplished by summing up all other hidden variables. One convenient way of accomplishing such inferences is to define the state space as composed of both the inheritance and error indicator vectors. Inference of this extended state space could be calculated by the standard HMM algorithms. The emission and transition probability matrices are given by:

In particular, the posterior probability for the error vector e_i at locus i is:

(10)

And the posterior probability of a specific error indicator e_in is:

(11)

In Equation (11), the expression e_i∈{e_in=e} indicates all error vectors for slot i for which the value of the n-th individual is fixed at e.

2.3 Parameter estimation

To enable a realization of the joint probability P(c_ij, e_ij), binning is applied on the confidence scores. Note that due to assumption (3), binning is applied per individual. Let β^M(c) = {c⁰, c¹,…, c^M} define a grid of M confidence scores so that bin m resides between c^{m − 1} and c^m. The distribution of confidence scores for each individual is estimated by a counting procedure in each bin. Define an indicator function I(x), which counts the occurrences of x: ∀x∈{0, 1}, I(x)=x. Then bin m for the confidence distribution of individual k takes the form:

(12)

The joint distribution for individual k is estimated in the same way:

(13)

The table τ_k could be estimated from two types of data. The simplest dataset for this task is a repeated measurement for the same individual. Since we propose to address this distribution per individual, there is no need for many measurements. In principle, five repeated arrays already suffice to form a consensus genotype per individual. Comparing this consensus genotype with each measured array yields the desired error indicator and the confidence scores are generated for each sample by the genotyping algorithm. However, measuring each sample several times is usually not practical. In many cases, nuclear families with parents are genotyped and could be used to estimate this table within the suggested IBD model. Since the inheritance selectors and the error selectors are conditionally dependent given the data in the proposed model, some iterative process should be applied on the desired table.

We propose to perform a modified EM algorithm to study the table for each individual in nuclear pedigrees. At each step, we evaluate the most likely error states for each individual and use these error states to estimate the corresponding probability table. Finding the most likely state sequence is a well-defined problem in Bayesian inference and requires some criterion for optimal solution (Dechter, 1999). We employ the Viterbi algorithm for finding the state sequence that maximizes the joint probability of state space and data (Rabiner and Juang, 1986). Define a state sequence to be a set of values for the state space (S_i, e_in) for each locus i and individual n. S_i corresponds to the inheritance vector of all individuals and e_in corresponds to the error state for individual n at locus i. Let the most likely state sequence for individual n be the one which maximizes the following probability:

In this expression, e(n) is the set of error indicators corresponding to individual n over all loci: e(n) = {e_1n, e_2n,… e_Ln}, and (e(n)^*, S^*) is the most likely state sequence. This expression is calculated by applying the Viterbi algorithm over the state space (S_i, e_in), i=[1, 2,…, L] (Rabiner and Juang, 1986). Since the probability P(S,e(n),G,C) is marginal, summing over error states for all other individuals in the pedigree, the time and space complexities of this calculation are held at a reasonable cost allowing it to be applied for several siblings simultaneously.

The modified EM algorithm is as follows: at iteration t, we iterate over all n individuals and calculate the most likely error sequence over all loci using the current tables for all the n individuals denoted by τ^t = {τ₁^t, τ₂^t,…, τ_n^t}. For individual n it is:

Next we estimate the new tables using these error states:

The initial table assumes that confidence and error states are independent:

2.4 Error handling in Merlin and Plink

Plink implements a simple error detection procedure by analyzing trios for Mendelian inconsistencies. A marker that is not consistent with Mendelian inheritance is removed from all individuals. This scheme is widely used in many tools prior to statistical analysis and requires no error model. However, the small detection rates and the need to genotype the parents make it inefficient for samples of unrelated individuals (Douglas et al., 2002). This means that in the general case for which there are no genotyped parents, Plink offer no error detection at all.

Merlin error detection is a multipoint extension to the simple Mendelian inconsistency procedure. It takes into account all available pedigree members and uses several linked markers simultaneously. After cleaning the data from Mendelian inconsistent markers, Merlin iterates over each marker and calculates the likelihood of the data with and without that marker. A likelihood ratio score statistics is generated for each marker which is compared with a predefined threshold for mistyping detection. We used the default error detection options in our tests, which include the removal of Mendelian inconsistent markers and markers flagged with the default threshold by Merlin.

In the following section, we present results for several error models. The standard model is represented by the analysis carried out with Merlin using the default error filtering. All other error models do not use error detection and filtering, even for Mendelian errors. Our model, designated by the marker error model, calculates a per marker error probability. The sample error rate model uses a per array error rate calculated from the joint probability P(c, e). The fixed error rate model represents current algorithms that use an error model and assume a fixed error rate. The three error models are available in Plinke for pairwise IBD inference.

3 RESULTS

3.1 Real data

We compared our model to two standard tools for IBD inference, Merlin and Plink, by analyzing real and simulated datasets. The pedigree data were taken from a recent study of Pelizaeus–Merzbacher-like disease, a rare recessive syndrome that was mapped to the gene AIMP1 using standard linkage analysis (Feinstein et al., 2010). From this pedigree, we genotyped a nuclear family of three siblings and their parents, three additional relatives and one distantly related individual. All members were genotyped with Affymetrix 250K arrays. The SNP data were processed prior to the analysis with the following filters. Non-informative SNPs and SNPs having minor allele frequency (MAF) <0.1 were filtered out. From the remaining list, SNPs were selected at random with a minimum distance of 0.1 Mb between consecutive SNPs.

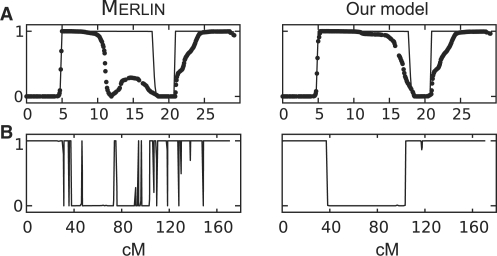
Figure 3 depicts the results of IBD inference between siblings from the nuclear family. Figure 3A shows an example of a sib-pair analysis for sharing one allele IBD with no parental information. The solid line was generated using all three siblings including their parents and represents the real IBD status. Note the dramatic recovery of the IBD status by our model, spanning 5 cM in length. Figure 3B shows an example of IBD inference including parental genotypes. These probabilities were inferred using all three siblings and parents, a situation in which Merlin is able to filter out >90% of the errors. Despite of the cleaning procedure, the figure on the left still contains many spikes. These are highly unlikely events and as depicted on the right plot, our model classifies them as errors.

Fig. 3.

Comparing sib-pair IBD inference between our model and Merlin. (A) Depicts sib-pair analysis with no parental information. Note the recovery of a 5 cM region in our model on the right. (B) Depicts IBD inference with parental genotypes. Note that the spikes generated with Merlin were classified as errors in our model.

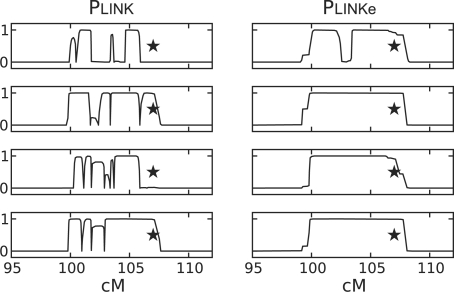
Figure 4 shows pairwise IBD probabilities between four affected members of the pedigree and a distant relative. The exact pedigree relatedness is unknown and we used Plink and Plinke to infer the probability of sharing two alleles IBD. The locus depicted in the figure was confirmed to be IBD by typing additional microsatellite markers (data not shown). The star at 107 cM marks the location of a rare causative allele of the gene AIMP1, which was found present in all affected individuals (Feinstein et al., 2010). The main concern when comparing the results of the two models at this locus is that, in some of the cases, Plink inference is fragmented into a collection of smaller segments. Typically, there is a 1 Mb threshold on region length under which the region is marked as IIS rather than IBD. In such cases, there is a high risk of false negatives (Purcell et al., 2007).

Fig. 4.

Pairwise IBD inference for distant relatives. The inference was carried out on a 7 cM region that was confirmed to be IBD between all individuals. The star indicates the locus of the causative mutation (Feinstein et al., 2010).

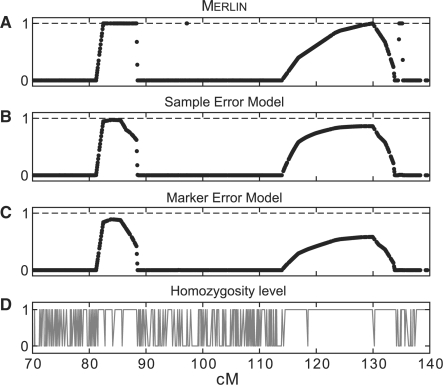
Next we demonstrate a situation which involves error in the parental data. Figure 5 depicts the probability for sharing two alleles IBD in sib-pair data that includes the parental genotypes. These probabilities were calculated using Merlin, the sample error models and the marker error model. This situation is common when searching for recessive traits and inference is considerably easier when including parental information (Kruglyak et al., 1995). The three models show two candidate places along the chromosome at which the IBD status changes from sharing one allele to two alleles. Figure 5A was generated using Merlin, Figure 5B using the sample error rate model and Figure 5C using the marker error model. Note that the IBD inference using both error models tend to be less certain of the regions than Merlin.

Fig. 5.

Comparison of sib-pair IBD inference between three models under high homozygosity level. The data includes the parental genotypes. (A), (B) and (C) depict 3 different models for inferring IBD probabilities between a pair of siblings (see main text for details). (D) Shows the homozygosity level in one of the parents. The presence of a few heterozygous SNPs within the large homozygous regions is probably due to undetected errors. Note that the marker error model is correctly less certain of these regions than the other methods.

Inspection of the parents in these regions reveals that the father is homozygous precisely along the IBD signals (Fig. 5D). Homozygous regions are not informative for IBD inference and therefore the change in IBD status from sharing one allele to two alleles does not stand on firm evidence. The fact that the standard model yields high probabilities in these regions is probably due to undetected errors in the father, which are manifested as heterozygous SNPs. A few of these markers could be seen in Figure 5D sporadically along the homozygous regions. Note that the marker error model does not infer these regions decisively. This is because the confidence scores of these heterozygous markers are poor, indicating that these markers are uncertain. In this case, the IBD signals are probably a false positive and certainly cannot be represented with high posterior probabilities.

We now present the results relating marker error status and marker confidence scores. Confidence scores occupy the range [0,1]. The confidence metric is such that lower confidence scores correspond to higher certainty in the genotyping procedure. Usually, SNPs having extremely high confidence scores are marked as ‘No-Calls’. We retained the BRLMM threshold of 0.5 above which a call would not be determined.

We analyzed eight nuclear pedigrees which include parental data and were genotyped on the same platform at various time points during the past 3 years. The results depicted in Supplementary Figure S1 suggest that under the BRLMM algorithm, the conditional probability of confidence scores is approximately uniform for the positive error status, P(c|e = 1). In a separate test (data not shown), we found that using a uniform distribution instead of the measured one for P(c|e = 1) yields a negligible difference in the posterior probabilities (99% of the difference is <0.015, averaged over all datasets). We assumed a uniform P(c|e = 1) distribution when using Plinke in Figure 4.

We also examined the confidence distributions under two different genotyping algorithms: BRLMM and Birdseed V2 (Affymetrix Inc., 2006; Korn et al., 2008). Supplementary Figure S2 shows a comparison of the distributions between these two algorithms. Note that the distribution of confidence scores is not similar between the two genotyping algorithms. In Birdseed, the distribution tends to occupy smaller confidence scores and peak steeper toward zero. Similar results for the Birdseed algorithm were obtained using our EM procedure (data not shown).

Using the eight nuclear pedigrees, we compared the performance of several types of error models with Merlin. We used the default error handling in Merlin as indicated in Section 2.4. The other three error models include a fixed error model, a sample error model and a marker error model. The first model uses a fixed error rate of 0.5%, which is the median level in our dataset. This represents current algorithms that use a fixed error rate. The second error model uses a per sample error rate as estimated from the learned joint probability table p(c, e) using Equation (6). The third model is our proposed algorithm integrating the confidence scores per marker. The result depicted in Supplementary Figure S5 and Table S1 suggests a gradual improvement in accuracy of IBD inference as a function of the error rate. Note that for error rates >2% there is a substantial difference between the fixed error rate model and the other two error models. It should be noted that the error rates depicted in this analysis correspond to one of the siblings and thus the effective error rate of the sibling pair is actually lower.

3.2 Simulated data

Using simulated data, we compared the performance of the marker error rate and sample error rate models to Merlin. We simulated the genotypes of a sib-pair over 100 chromosomes each with 6800 SNPs spanning 50 Mb in length. The simulation was carried out using SimPed (Leal et al., 2005) assuming Hardy–Weinberg equilibrium (no marker LD). Allele frequencies were taken from the HAPMAP CEU samples and confidence scores were taken from real datasets. Noise was added at random for each marker according to our model. Consistent with our finding for the BRLMM genotyping algorithm, we assumed a flat distribution of confidence scores given the positive error state (e=1). For each marker, we calculated the conditional probability of marker error given its confidence score and used it as the probability of success in a Bernoulli process for which success corresponds to the presence of an error.

Following the introduction of noise, we preprocessed the simulated data as follows:

1. Filter SNPs with MAF <0.1.

2. Select SNPs at a minimum distance of 0.1 Mb.

These filters form a reasonable strategy for analyzing real data when no LD modeling is applied. The results for sib-pair analysis with no parental information are summarized in Table 1. The table summarizes a comparison of the marker error model with the standard model using Merlin and with the sample error rate model. For each model, three error rates were tested by comparing the inferred probabilities to share 0, 1 or 2 alleles IBD (Z0, Z1 or Z2, respectively). We defined the sharing state of each locus to be 1 whenever the posterior probability was >0.5, and zero otherwise. The discrepancy column indicates the percentage of inconsistencies as the relative number of loci inconsistent between the two models being compared. Improvement was defined as the relative number of loci that were classified correctly by our model among those loci which are inconsistent. Thus for example under the 4% error rate, the sample error rate model and marker error model disagree on 4% of the loci for Z0 probabilities. Out of these 4%, 70% were classified correctly by the marker error model. Note that there is a big difference between the standard model and the marker error model especially under Z0 and Z1. Practically, all places inconsistent between the models were classified correctly by our model. The differences between the marker error model and the sample error rate model are more subtle. In this case, the marker error model classifies correctly the IBD status in 70–80% of the cases.

Table 1.

Simulation results for sib-pair analysis with no parental information comparing the standard and the per sample error models to the marker error model

The error model	Error rate (%)	Z0		Z1		Z2
		Discrepancy (%)	Relative improvement (%)	Discrepancy (%)	Relative improvement (%)	Discrepancy (%)	Relative improvement (%)
Standard model	4	28	99	33	98	12	99
	2	17	98	19	98	4	98
	1	10	97	11	96	1	97
Sample error rate	4	4	70	4	70	<0.5	–
	2	3	76	3	74	<0.5	–
	1	2	82	2	81	<0.5	–

4 DISCUSSION

In this study, we proposed a model that integrates confidence scores within the standard model for IBD inference. Confidence scores measure the amount of certainty a genotyping algorithm has in each call and therefore contain relevant information for error modeling even without pedigree data. We found that the joint distribution of confidence score and error status holds relevant information for error detection. In particular, our finding that the conditional probability distribution p(c|e = 1) is approximately uniform is surprising. In an ideal situation, a genotyping algorithm would yield an increasing distribution of confidence scores under the positive error states. The fact that there are mistyped markers even for very good confidence scores suggests that there might be two conceptually different mechanisms in the genotyping process. The first is the correct genotyping of the targeted sample which would create an increasing distribution (i.e. p(c→ 0| e=1)→0). The other process involves the genotyping of different material not relevant to the targeted DNA (contamination for example). Markers that manifest this process would generate a decreasing distribution (i.e. p(c→ 1| e = 1) → 0) similar to the overall confidence distribution. Adding these two processes together with different ratios could yield the observed distributions for both genotyping algorithms examined (see Supplementary Figs S1 and S2).

Our initial motivation for integrating confidence scores was to increase accuracy of IBD inference when no parental information is at hand. However, even when both parents are genotyped we found unlikely spikes in the standard inference that our model classifies as errors. In general, the presence of spikes becomes more prominent with increased density of the SNPs selected for the analysis. This may be important for studies on recombination hotspots for which the location of a cross-over is sought within nuclear families (Coop et al., 2008). In such studies, spikes as we observed may bias the results substantially. In sib-pair analysis with no parental information, we found discrepancies between our model and the standard model that can span a few centimorgan in length, a scale which is significant in linkage analysis (Terwilliger and Ott, 1994). Simulation suggests that for noisy datasets our model can recover up to 30% of the IBD signal, which was not inferred correctly by the standard model. As expected, these discrepancies decrease with lower noise levels to ~10% at 1% error rate.

The use of our model requires an estimation of the joint probability distribution τ(c,e) which in turn requires knowledge on the error states for each marker. Since this knowledge is not always available, we examined ways to approximate the probability table without the need to genotype additional individuals. We found that it is possible to estimate the error rates from the call rates of each array with good accuracy (Supplementary Figure S3). This result is consistent with other findings for the Affymetrix technology although it must certainly depend on other factors such as the genotyping algorithm (Saunders et al., 2007; Yeung et al., 2008). Using the per array error rate, we were able to perform nearly as good as the full model as could be seen in Table 1 and Supplementary Table S1. This suggests that the per array error rates are the most important factor in the analysis. Using a sample error rate model with the correct error rates could be considered as a smoothed version of our full model, which ignores the per marker error weights. As a second order correction, one can use an approximated distribution for p(c|e = 1) and together with the approximated error rate deduce the joint probability table p(c,e) as suggested in Methods of Supplementary Material. We found that under the BRLMM algorithm using a uniform distribution for p(c|e = 1) is practically as good as the full model.

The complexity of the Lander–Green algorithm is exponential in the number of individuals in the pedigree (Kruglyak et al., 1996). Our algorithm adds another constant factor for each genotyped individual and thus changes the overall complexity by a constant factor. However, a naïve implementation of the Lander–Green algorithm is limited to small pedigrees and current implementations use various algorithms to allow more efficient calculations. In particular, the use of sparse trees or descent graphs allows the analysis of moderate pedigrees otherwise not feasible with the naïve calculations (Abecasis et al., 2001b; Sobel and Lange, 1996). The main idea is to select a subspace of the inheritance space which is compatible with the observed data and thus reduce both time and space complexities. Once errors are incorporated to the model, all options for founder alleles are compatible with the data since we do not observe the real alleles directly (Sobel et al., 2002). Therefore, the reduction of the state space is not possible using our algorithm which means that analysis is limited to small nuclear pedigrees.

There is, however, a class of approximated models for IBD inference that can benefit from our error model without a change in the overall complexity. In this approach, the entire process from founders to the measured descendants is averaged. This replaces the Markovian inheritance process of hidden generations with a single probability table and thus does change in complexity with increasing generations. This approach has been suggested for pairwise IBD inference (Thompson, 2008), autozygosity (Leutenegger et al., 2003) and locus-specific ancestry inference (Falush et al., 2003). In particular, the Plink package implements such a method for pairwise IBD inference which we extended with our error model. The new implementation includes the three error models described in this article, the fixed error rate, the per array error rate and per marker error model.

A different application that we plan to examine is to use the joint distribution table τ(c,e) to facilitate the selection of a subset of SNPs in general pedigrees. A common practice in linkage analysis using the standard IBD models is to select a subset of markers that are in linkage equilibrium. This approach to dealing with marker LD may result in the reduction of 1–2 orders of magnitude in the number of SNPs, from 10⁶ to 10⁴. Thus, the vast majority of SNPs are filtered out and the remaining are assumed to be error free. A reasonable approach to SNP filtering would be to perform a per sample confidence cutoff depending on the corresponding error rate. Our approach in generating the reference IBD curves was to level all error rates in the data to the best performing sample as indicated in Methods of Supplementary Material. This approach minimizes the loss of knowledge while addressing the fluctuation in the quality of each sample.