Abstract
Molecular dynamics based free energy calculations allow the determination of a variety of thermodynamic quantities from computer simulations of small molecules. Thermodynamic integration (TI) calculations can suffer from instabilities during the creation or annihilation of particles. This ‘singularity’ problem can be addressed with soft-core potential functions which keep pairwise interaction energies finite for all configurations and provide smooth free energy curves. “One-step” transformations, in which electrostatic and van der Waals forces are simultaneously modified, can be simpler and less expensive than “two-step” transformations in which these properties are changed in separate calculations. Here we study solvation free energies for molecules of different hydrophobicity using both models. We provide recommended values for the two parameters αLJ and βC controlling the behaviour of the soft-core Lennard-Jones and Coulomb potentials and compare one-step and two-step transformations with regard to their suitability for numerical integration. For many types of transformations, the one-step procedure offers a convenient and accurate approach to free energy estimates.
1 Introduction
Free energy calculations aim at the rigorous computation of thermodynamic properties of molecules via the methods of statistical thermodynamics. The thermodynamic integration (TI) formalism is widely applied to compute free energy changes between chemical systems. Molecular mechanics forcefields play an important role in TI free energy calculations due to their ability to provide Boltzman-weighted conformational ensembles from molecular dynamics (MD) simulations. Their ability to provide macroscopic data from atomistic simulations makes them excellent tools to connect experimental data to molecular models. A multitude of applications exists and the technique has been extensively reviewed.1–7
The focus of this work is on the performance of single-step vs. multi-step transformation methods, as described below in more detail. Single-step transformation approaches have been studied before8–10, but the effects of different soft-core potential parameter settings have not been investigated comprehensively. Also, important sampling issues which single-step transformations may encounter have not been discussed in detail. In this work, we will investigate what values of the scaling parameters αLJ, βC and the order parameter m (see equations 3 and 5 below) result in the smoothest free energy curves for optimal numerical integration of five test compounds selected from lipophilic, polar and ionic species. Additionally, we will compare the performance of one-step transformations, i.e. those using soft-core potentials for electrostatics as well as for van der Waals interactions, with two-step transformations consisting of separate transformation steps with linearly scaled electrostatics and soft-core van der Waals potential functions, respectively.
2 Theory
The general principle is straightforwardly derived from elementary statistical thermodynamics and gives the free energy difference between two states described by two potential functions V0 and V1 as 11:
| (1) |
The two potential functions are coupled via a non-physical coordinate λ so that the coupled function V (λ) equals the initial state function V0 for λ = 0 and the end state function V1 for λ = 1. The angular brackets indicate a Boltzmann-weighted ensemble average taken at a given value of λ. Since nearly arbitrary transformations can be simulated, changing the number and types of atoms in the system, TI calculations are sometimes refered to as computational alchemy. TI calculations are normally included in thermodynamic cycles so that they can be compared to experimental values. In a typical application, the free energy cost of transforming a molecule A into B would be computed both in solution and bound to a receptor. The difference in the TI results would then equal the difference in the two molecule’s receptor binding strengths.
The integration in Equation 1 usually cannot be solved analytically. In practice, simulations are performed at various fixed values of λ and numerical integration techniques are used. In this work, numerical integration was performed by using the trapezoidal rule, i.e. linear interpolation. It is therefore desirable that the free energy curve constructed from the 〈∂V(λ)/∂λ〉-values should be as smooth as possible to limit errors in the numerical integration. In the special case of TI calculations concerned with introducing or removing van der Waals centers to or from the system, an endpoint singularity effect can occur in which the value of 〈∂V(λ)/∂λ〉 diverges for λ close to zero or one respectively12,13. The divergence can be traced back to the shape of the repulsive part of the van der Waals forces, the r−12 term in the Lennard-Jones (LJ) equation.13 The divergence is weak enough to render the total integral finite, but the singularity effect is still a problem for the subsequent integration. Several schemes have been developed to address this, among them non-linear mixing functions to construct V(λ)13–19, slow-growth methods20 or analytical fitting schemes21,22.
A widely used solution is the introduction of separation-shifted scaling, or soft-core, potentials which generally use a modified LJ equation of the form:
| (2) |
in which εi j and σi j are the common LJ equation parameters, ri j the interatomic distance, αLJ a parameter that adjusts the softness of the potential and t, s and n parameters that were set to 1,2 and 6 in the original formulation of the potential function19. For the soft-core potential suggested by Beutler et al., a value of 0.5 for αLJ was found to yield the smoothest curve shapes, but this has not been extensively tested for other values of t, s and n.
Introducing the soft-core potential for van der Waals interactions requires an additional decision about the treatment of electrostatic interactions because at low λ-values the repulsive force in Equation 2 is weakened sufficiently to allow oppositely charged particles to come too close to each other, leading to numerical instabilities in simulations. This can be prevented by (a) introducing or removing only LJ-particles of zero partial charge and computing the free energy cost of the addition or removal of their electrostatic interactions in a separate step (the two-step approach) or (b) also subjecting electrostatic interactions to a λ-dependent soft-core Coulomb potential similar to Equation 2 (the one-step approach). The former approach adds the need to conduct additional simulations and therefore adds to the necessary computation time and human workload for data evaluation. The latter approach may introduce sampling problems because of the unusual shape the pair interaction potential function takes for intermediate λ-values (see Figure 1, further details are discussed in Results).
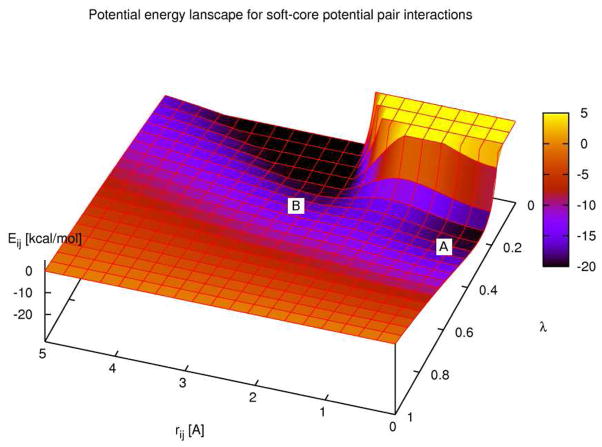
Figure 1.
The potential energy landscape of an atomic pair interaction as a function of both the inter-atomic distance ri j and λ. Both electrostatic and van der Waals soft-core potentials are used. Typical values for atomic partial charges and Lennard-Jones parameters from the Amber forcefield23,24 have been used. At regions of low λ both the strong van der Waals repulsion at small ri j and the energy minimum at the most favorable interaction distance of approximately 3 Å can be seen. Conversely, at λ-values close to one, the potential energy surface is flat. The problematic intermediate region at λ ≈ 0.3 in which the interplay of softened electrostatic and van der Waals interactions generates a potential curve with two minima (marked A and B) can be distinguished. Values for αLJ and of 0.5 and 3.5 Å were used.
A λ-dependent soft-core Coulomb potential can be designed by comparison to the functional form of the soft-core LJ potential. The Amber molecular modelling suite uses 1, 1 and 6 for t, s, and n of Equation 2.17 We will keep the t and s values unchanged in the following. This gives:
| (3) |
where
| (4) |
Equation 3 contains two important parts. First, the prefactor (1 − λ ) flattens the potential as λ approaches one. Second, the introduction of the modified LJ potential (VvdW (f(ri j))) ensures that as ri j approaches zero, the transformed distance (f(ri j)) converges to a constant value of (αLJλ)1/n σ. A soft-core Coulomb potential can be designed in a similar manner:
| (5) |
| (6) |
where
| (7) |
qi and qj are the atomic partial charges. m is an order parameter comparable to n. βC is a new parameter, the analog of αLJσn of Equation 3. This equation is not new but few combinations of the parameters have been tested intensively. Previous accounts have used m = 29,10 and m = 6.8
We will now consider appropriate ranges for these parameters. A potential energy curve of two atoms, plotted as a function of ri j, has a minimum if the atoms have no or opposite charges and no minimum if they are equally charged. The shape of the potential energy curve will vary as λ changes during the course of a TI calculation. The formation of a second minimum in the curve at a certain λ is not desirable, as it may lead to sampling problems. However, a second minimum may form for an oppositely charged atom-pair. In order to have only one or zero minima, f(ri j) should not be larger than g(ri j) at any ri j. Otherwise the repulsive term, in VvdW(ri j) may be weakened too much to still prevent numerical instabilities. To keep f(ri j) ≤ g(ri j),
| (8) |
because f (0) ≤ g(0). Secondly, n and m should be equal. If n > m, f (ri j) > g(ri j) as r → ∞. If n < m, f(ri j) > g(ri j) occurs when r roughly equals σ or greater. Therefore, potential curves with single or zero minima only are always guaranteed under the following conditions:
| (9) |
3 Computational methods
All calculations described were performed using version 10 of the Amber molecular modelling suite25 with additional modifications to implement optional soft-core potential treatments of electrostatic interactions as described above.
The test molecules were parametrized according to the general amber force field (gaff)26 and atomic partial charges were derived according to the RESP procedure27. Molecules were embedded in a box of preequilibrated water molecules so that no solute atom was closer than 12 Å to the box edges. The improved version of the TIP4P water model for simulations using an Ewald type long range electrostatics treatment was used28,29. All simulations were conducted using a 2 fs timestep while constraining bonds to hydrogen atoms via the SHAKE algorithm30. A Langevin thermostat31 was employed to constrain the system temperature to 298 K and a pressure of 1 atm was controlled by a Berendsen coupling algorithm32. The nonbonded cutoff distance was 9 Å. The Amber molecular modelling suite uses a soft-core potential function of Equation 3 with n = 6 for disappearing van der Waals particles17 and Equation 5 with m =2 or 6 for electrostatic interactions. Corresponding forms for appearing atoms are obtained by replacing λ with (1 − λ ) and vice versa. In the particle-mesh Ewald treatment of electrostatics, soft-core potentials are used only for the direct sum part, since only short range interactions give rise to the ‘singularity’ problem. The reciprocal contribution to electrostatic interactions is scaled linearly with λ. Similarly, in regular MD simulations van der Waals interactions are evaluated according to the LJ equation up to the same cutoff distance and long-range dispersion interactions beyond this cutoff are treated by an analytical isotropic long-range correction. In TI calculations, the former term makes use of the soft-core potential while the latter, which does not contribute any forces due to its isotropic nature, is linearly scaled.
4 Results
The computation of free energies of solvation was selected to test the accuracy of different TI parametrisations. Five test molecules were selected for simulations: cyclohexane, a chloride ion, ethanol, a magnesium ion and water, to cover examples of nonpolar, polar and charged species. Free energies of solvation were computed by simulating the removal of the molecule from a water filled simulation box. For onestep transformations, a single transformation was studied in which the initial state corresponded to the solvated molecule and the end state to a box of pure water (keeping the number of solvent molecules unchanged). The connection between this fixed-charge free energy change and experimental solvation free energies has been discussed elsewhere.28,29,33 For two-step transformations, the molecule first had its atomic partial charges reduced to zero by a linear scaling TI calculation, followed by removing the van der Waals interactions from the now chargeless molecule in a subsequent TI calculation using a soft-core Lennard-Jones potential.
4.1 Optimal value for the parameter αLJ in two-step transformations
To test if the value of 0.5 for αLJ suggested in Ref. 19 is suitable for a soft-core van der Waals potential of the form given in Equation 3 with n = 6, we computed the second (vdW) step contribution to the solvation free energy for the five test molecules, i.e. for the removal of the van der Waals interaction of the chargeless molecule with the solvent, while varying αLJ from 0.3 to 0.7. The calculations were conducted using 99 evenly spaced λ-windows (λ =0.01, 0.02, …, 0.99). Each window was subjected to a 1000 step steepest descent minimization to remove bad initial contacts and a 50 ps NPT heating run in which the system temperature was raised to 298 K with a target pressure of 1 bar. Equilibration was followed by a 100 ps NPT simulation for data collection. While the value of αLJ used markedly affected the shape of the free energy curves obtained (Figure 2), all simulations yielded comparable free energy estimates (Table 1).
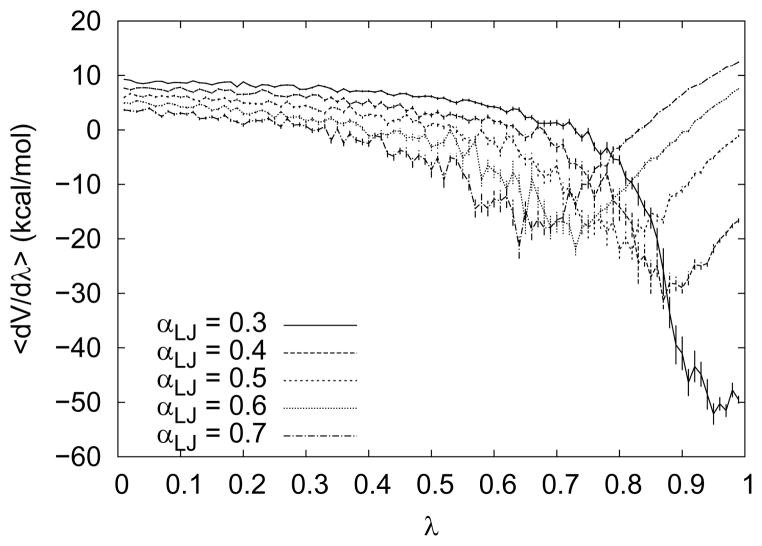
Figure 2.
Influence of αLJ on the free energy curve shape, plotted for values of 0.3, 0.4, …, 0.7. The minimum of the curve shifts to the left as αLJ increases and the value for λ → 0 becomes smaller. The curves shown are for simulations of a cyclohexane molecule, similar results were obtained for the other test compounds. For αLJ < 0.4 the curve shape begins to resemble that of a non soft-core simulation showing the singularity problem. The lowest error estimates are obtained for αLJ-values of 0.5 or larger. Error bars indicate σSEM of the individual λ-window.
Table 1.
Average free energy estimates (in kcal/mol) for the second (vdW) step of a two-step TI calculation of the solvation free energy for the five test compounds. gives the average free energy change for the five tested αLJ-values. σSEM indicates the standard error of the mean estimate (Equations 10 and 11, C indicates the average curvature acc. to Equation 12.
| Compound | αLJ | σSEM | C | ||
|---|---|---|---|---|---|
| cyclohexane | 0.3 | 2.28 | 0.106 | 0.25 | |
| 0.4 | 2.13 | 0.096 | 0.26 | ||
| 0.5 | 2.05 | 0.087 | 0.26 | ||
| 0.6 | 2.20 | 0.089 | 0.31 | ||
| 0.7 | 2.12 | 0.085 | 0.28 | ||
|
| |||||
| chloride ion | 0.3 | 4.75 | 0.052 | 0.17 | |
| 0.4 | 4.75 | 0.053 | 0.14 | ||
| 0.5 | 4.72 | 0.055 | 0.15 | ||
| 0.6 | 4.66 | 0.056 | 0.16 | ||
| 0.7 | 4.79 | 0.056 | 0.16 | ||
|
| |||||
| ethanol | 0.3 | 2.03 | 0.062 | 0.16 | |
| 0.4 | 1.90 | 0.056 | 0.19 | ||
| 0.5 | 1.98 | 0.054 | 0.16 | ||
| 0.6 | 2.01 | 0.054 | 0.17 | ||
| 0.7 | 2.01 | 0.060 | 0.19 | ||
|
| |||||
| magnesium ion | 0.3 | −0.66 | 0.018 | 0.03 | |
| 0.4 | −0.63 | 0.016 | 0.03 | ||
| 0.5 | −0.65 | 0.014 | 0.03 | ||
| 0.6 | −0.65 | 0.014 | 0.03 | ||
| 0.7 | −0.64 | 0.014 | 0.04 | ||
|
| |||||
| water | 0.3 | 2.21 | 0.030 | 0.07 | |
| 0.4 | 2.21 | 0.029 | 0.08 | ||
| 0.5 | 2.22 | 0.029 | 0.11 | ||
| 0.6 | 2.18 | 0.029 | 0.09 | ||
| 0.7 | 2.18 | 0.031 | 0.09 | ||
The effect of sampling fluctuations on a free energy calculation can be estimated from the standard error of the mean for the free energy:
| (10) |
where σi is the standard error of the mean for the ∂V/∂λ-values of the i-th window. The standard error (SEM) for each window can be estimated as:
| (11) |
where σ∂V/∂λ is the standard deviation, τ is the autocorrelation time of ∂V/∂λ and tsim is the total length of the simulation.34 Values for τ are typically in the range of 1 ps, but may depend on λ. See the Supplementary Information for details and a plot of τ vs. λ. Equation 10 does not take into account errors arising from the numerical integration step. For widely-spaced windows, errors in the numerical integration scheme may contribute to the overall uncertainty in the result. This difficulty in directly assigning uncertainties is a drawback of TI methods, but minimizing the estimated error from Equation 10, (or the curvature, which we discuss next) is still a useful goal for generating good soft-core potentials. The error estimate drops as the number of TI windows increases, both by decreasing errors in numerical integration and because errors in estimating the mean for each window should be uncorrelated and tend to cancel.
As an alternative measure of the smoothness of a free energy curve, we introduce the finite difference curvature value C:
| (12) |
where N is the number of TI simulation windows and 〈∂V/∂λ〉i is the Boltzman weighted average of the mixed potential function derivative for simulation window i. An alternative formulation for non-evenly spaced λ-windows, requiring the second λ-derivative of V, would be:
| (13) |
A smaller value for C suggests a corresponding smaller error from numerical integration. (Due to the noise of the free energy curves, we did not use the raw 〈∂V/∂λ〉-data to calculate the curvature. The curve was smoothened by 10th order B-spline and an even-spaced 100 points were collected along the new curve to calculate C.).
Generally, an optimal αLJ should yield a smooth free energy curve, a low error estimate and a small curvature. From Table 1, we see that e.g. for cyclohexane, errors get smaller with bigger values of αLJ up to a value of about 0.5. We have chosen αLJ = 0.5 for cyclohexane, αLJ = 0.4 for the chloride ion, αLJ = 0.5 for ethanol, αLJ = 0.6 for the magnesium ion, and αLJ = 0.4 for a water molecule as a best compromise value for each compound, but differences for αLJ in the range between 0.4 and 0.6 are small and differences in σSEM are probably not significant enough to unambigously indicate an optimal value in each case.
We conclude that the value of 0.5 for αLJ, which was used in e.g. Refs. 17 or 35,36 yields acceptable results for the Amber implementation of soft-core LJ potentials, but small deviations from that number represent a slight improvement in terms of estimated error of free energy for some of the test molecules. Values outside the range 0.4 to 0.6 appear to be less suitable since they tend to increase the curvatures and estimated errors.
4.2 Effect of the parameters αLJ, βC and m in one-step transformations
We now explore the effect different choices for the two softness parameters in one-step TI transformations of the five test molecules have. For m = 2 in Equation 5, higher (softer) values for αLJ require correspondingly higher values for βC, otherwise the electrostatic attraction of oppositely charged atoms can overcome the weakened van der Waals repulsion at some short distances ri j, i.e. violating the condition of Equation 8. This would correspond to forming a second minimum in the potential energy curve of oppositely charge atoms, separated from the first minimum by a high energy barrier. While this has to occur at some λ with m = 2, the energy barrier can be lowered by assigning high values on βc. On the other hand, higher values for βC lead to large changes of 〈∂V/∂λ〉 at low λ-values because the separation factor, λβC added to the interatomic distance in Equation 5 will change faster with λ. This is equivalent to a quicker decoupling of the electrostatic interactions, causing the corresponding free energy change to occur early in the transformation. This makes the free energy from the change in electrostatic interactions heavily dependent on data from the first λ-windows in case of disappearing atoms, which is undesirable in terms of optimal sampling and would prevent simulations to be conducted with fewer, wider spaced λ-windows. When m = 6 in Equation 5, an additional minimum does not form as far as Equation 9 is satisfied. Accordingly, the lower limit of βC is roughly bounded by αLJσ 6 in this case.
Since βC has units of m-th order of distance, we will use the more intuitive , which is a distance. Free energy calculations were conducted varying αLJ from 0.2 to 0.5 and from 1.5 to 5 Å to find the parameter setting resulting in the smoothest free energy curves and lowest errors for the same five test molecules used above. Free energies were evaluated with 99 TI windows (λ =0.01, 0.02, …, 0.99). Each window was minimized by 1000 steps of steepest descent method and was relaxed further by undergoing 50 ps NTP MD simulations. ∂V/∂λ was collected from the following 100 ps of NTP MD simulations. From the simulations, solvation free energies, C-values and error estimates were calculated. Optimal values for αLJ and would be found from simulations with low errors and C-values. The full data set is provided in the Supplementary Information.
The calculated solvation free energy of the nonpolar test molecule cyclohexane was not much affected by and the calculated free energy by the one-step transformation agreed well to that of the two-step transformation (compare with Table 2).
Table 2.
Solvation free energies (ΔG), in kcal/mol, of test molecules calculated by two-step transformation method. Calculations were performed using optimal αLJ parameters as determined in Table 1. Contributions from the Coulombic potential (C) and LJ potential are displayed separately. For the two larger molecules, cyclohexane and ethanol, the free energy contributions from re-appearing the charges in vacuum are also listed. This vacuum correction constitutes an implementation dependent ‘third step’ for a two-step transformation, however, it is computationally inexpensive and does not contribute much to the uncertainty of the results. Errors of the sum (σSEM (sum)) are calculated from the errors of each substep ( ).
| Molecule | σSEM (C) | σSEM (LJ) | σSEM (vac) | σSEM (sum) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cyclohexane | 0.03 | 0.000 | 2.05 | 0.087 | −0.05 | 0.00 | 2.03 | 0.087 | ||||
| chloride ion | −93.97 | 0.034 | 4.75 | 0.053 | 0.00 | 0.00 | −89.22 | 0.063 | ||||
| ethanol | −33.05 | 0.014 | 1.98 | 0.054 | 26.74 | 0.00 | −4.33 | 0.056 | ||||
| magnesium ion | −413.66 | 0.059 | −0.65 | 0.014 | 0.00 | 0.00 | −414.31 | 0.061 | ||||
| water | −9.21 | 0.019 | 2.21 | 0.029 | 0.00 | 0.00 | −7.00 | 0.034 |
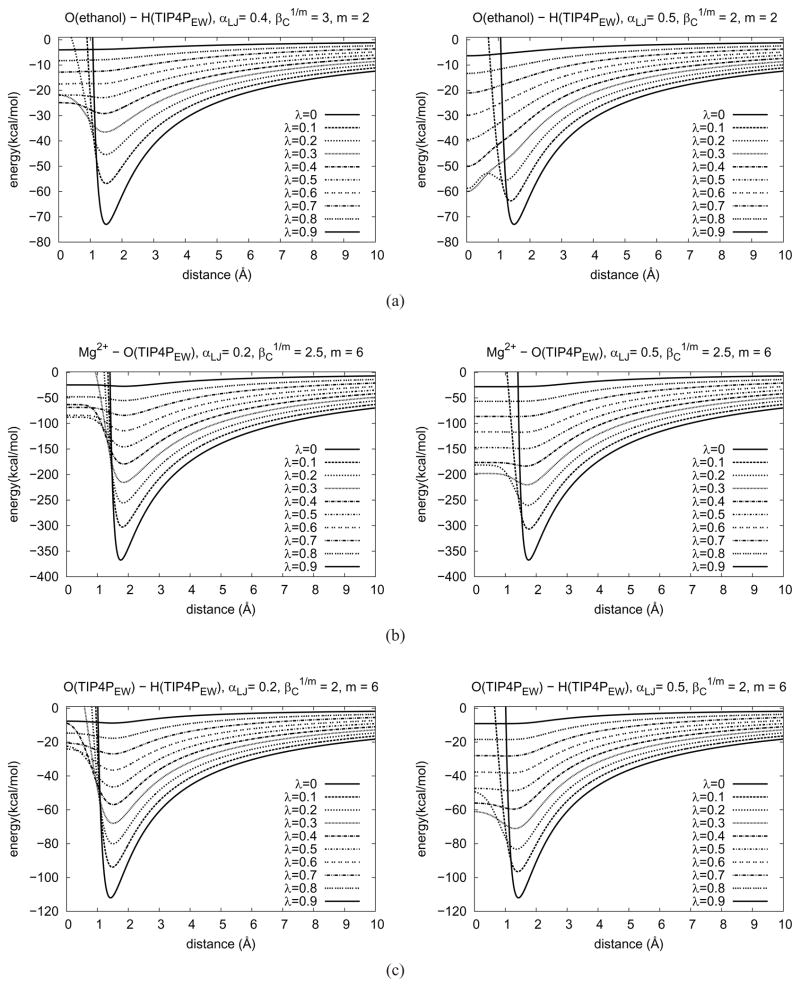
For ethanol the calculated solvation free energy deviated substantially from the result of the two-step calculation with parameters αLJ =0.4 or 0.5, and m = 2. We believe that these deviations were caused by the second minimum in the potential energy curve. At λ ≈ 0.2 the second minimum can be observed near zero distance in potential energy reference curves (right-hand side of Figure 3a). A high energy barrier between the two minima prevents efficient sampling. An improved combination of parameters (with a higher ) resolves this problem (left-hand side of Figure 3a).
Figure 3.
Soft-core pair potential energy curves between two atoms as a function of distance. The curve shape changes according to λ. The hydrogen atoms of TIP4PEW do not have a LJ potential. In this case, the LJ potential of the oxygen atom was used instead but the distance was offset by the bond length of the hydrogen and the oxygen atoms. (rs =OH-distance). (See Equation 14 and main text)
The calculated solvation free energy of the highly charged magnesium ion was strongly affected by small - and large αLJ-values, but for larger than 3.0 Å, the results converged to the corresponding value in Table 2. When m = 2, the potential energy curve between the magnesium ion and the oxygen atom of water has a second minimum at a certain range of λ (curves are not shown). The depth of the second minimum becomes deeper as decreases and this may cause the deviation of the computed ΔG. Which one of the minima is sampled depends on the initial geometry of the system. Generally it is expected that the minimum near ri j = 0 is less likely to be sampled unless the magnesium ion and a water molecule are almost in contact at the beginning of the simulation. Therefore, for m = 2, needs to be set to above a certain lower limit which is affected by αLJ. The result show that αLJ = 0.2 is optimal and the lower limit for was about 3.0 Å in this case. However, for m = 6, an even smaller could be used.
This second minimum should not occur with m = 6 as far as Equation 9 is obeyed. Nevertheless, the calculated solvation free energies were still strongly affected by even when setting m = 6. The results differed by up to 8 kcal/mol, beyond the range of σSEM. To understand the reason of the discrepancy better, 〈∂V/∂λ〉 vs λ was plotted for the two cases. (Figure 4) In these specific cases, we noticed that there is a kink at λ ≈ 0.6 for αLJ = 0.5. The point λ = 0.6 is roughly the point where the exclusive volume of the test molecule completely collapses (see right-hand side of Figure 3b) because the potential energy curve becomes almost flat at short distances at λ ≥ 0.6 (e.g. the energy changes only by 0.6 kcal/mol for distances between 0 and 1.1 Å where the minimum is located) and the minimum moves to zero distance for λ-values higher than this. Therefore, one can expect that the magnesium ion will most of the time have a water molecule on top of it at higher λ-values. While this collapse of the molecule’s solvent exclusion volume has to occur at some point during the simulation, the effect should be spread out over as wide a λ-range as possible, to ensure better sampling.
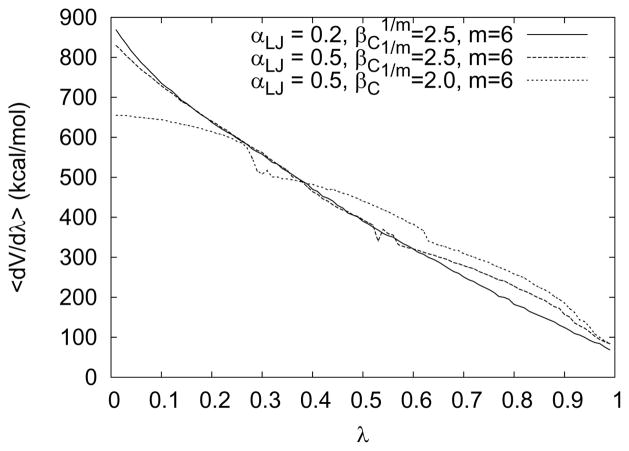
Figure 4.
Some soft-core parameters produce kinks in the curve of 〈∂V/∂λ〉. Sometimes dramatic geometrical change may occur around the kinks, leading to bad sampling and therefore, avoiding them is recommended. This chart shows three 〈∂V/∂λ〉 curves of one-step transformations for a magnesium ion. A kink is noticeable around λ = 0.6 when the parameter set is αLJ = 0.5, , m = 6. With a shorter , the kink becomes even more pronounced. Error bars for individual windows would not be visible on the scale drawn, since they are all much smaller than 1 kcal/mol. See the main text for details.
However, stable close contacts between the ion and solvent may also occur at λ < 0.6. At λ = 0.5, the core repulsive potential has not yet spontaneously completely collapsed, but we intentionally moved one water molecule near the magnesium ion for a second simulation and collected ∂V/∂λ-values (Figure 5). The magnesium ion and the water were very close (< 0.2 Å) during the whole simulation time (100 ps). Figure 5 shows that ∂V/∂λ-values can fluctuate in different ranges depending on the initial geometry. This implies that the contact geometry is trapped in a deeper potential well, which cannot be intuitively predicted by the pair potential of magnesium ion and water. These sorts of alternative conformations were not easily interconverted by thermal fluctuations. It can be interpreted that the early collapse of exclusive volume is the primary reason of the problem. In other words, when it collapsed, the core potential (VSC(ri j = 0)) was still too negative (about −40 kcal/mol). To confirm this assumption, a ‘harder’ core potential was used (αLJ = 0.2), making the core potential about −20 kcal/mol when the exclusive volume collapses (left-had side of Figure 3b). Now, the calculated free energy agreed with that from the two-step simulation.
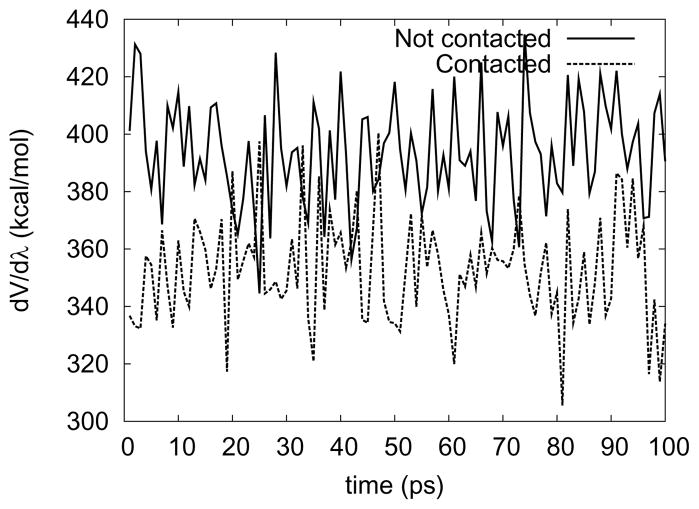
Figure 5.
Fluctuations of ∂V/∂λ can depend on the initial geometry when there are several local minima. In the process of decoupling a magnesium ion from solvent water (αLJ = 0.5, , m = 6), ∂V/∂λ was collected at λ = 0.5. Two different initial geometries were tested: 1) The magnesium ion and the oxygen atom of a water molecule were placed less than 0.1 Å apart (Contacted) 2) The magnesium ion was located further than 1 Å away from the nearest water molecule (Not contacted). The ranges of ∂V/∂λ are clearly separable, fluctuating around different averages, which means each geometry is trapped in its own minimum state.
The appearance of a deep second minimum in the potential function where, as in our example, a water molecule can become trapped is a case to be avoided in simulations. At that point, the system has entered a state were barriers exist that are too high to be overcome during any reasonable simulation time. As Figure 4 shows, standard error calculations can significantly underestimate the actual problem, since a large part of the conformational ensemble is not sampled. The autocorrelation time computed for a finite sample remains small but the system properties actually strongly depend on a conformational change that is unlikely to ever be observed in the simulation. Sudden kinks in the free energy curve (resulting from neighboring windows exploring different conformational ensembles) therefore point to possible problems in simulation convergence. It should be noted however, that the molecule studied here, the small, highly charged Mg2+ ion, arguably represents a worst case scenario for one-step TI transformations.
To compute the solvation free energy of water, a relatively hard core potential (αLJ = 0.2) also turned out to be optimal. If the core of the water molecule is too soft, the repulsive potential cannot efficiently cover the hydrogen atom and the same problem as seen in the case of magnesium ion can occur. With a softer LJ potential (αLJ = 0.5), the repulsive core of the molecule collapses at around λ = 0.5 and its core potential is about −50 kcal/mol, but with a harder core potential (αLJ = 0.2), the core collapses at around λ = 0.85 and its core potential is about −10 kcal/mol. (Figure 3c). The corresponding free energies showed a significant discrepancy (−10.82 kcal/mol for αLJ = 0.5 and −7.0 kcal/mol for αLJ = 0.2) and only the one with the harder core was comparable with the calculation for the two-step transformation.
To predict the appearance of additional minima in the pair potential curve, one additional complication must be adressed: Most commonly used water models have only one center for their van der Waals potential, which is usually located close to or at the center of the oxygen atom. The hydrogen atoms then have no LJ interactions. The single-minimum condition (Equation 9) for the pair potential between such a hydrogen atom and any negatively charged atom needs modification: In this case f(ri j) ≤ g(ri j) becomes:
| (14) |
Here, rs indicates the offset distance of the LJ potential center, projected onto the pair interaction axis. This value will change dynamically depending on water model, geometry and λ. To simplify, we consider the case of n = m = 6 and ri j = 0 only, where:
| (15) |
Here, rs will not go to zero due to the fixed distance between the oxygen and hydrogen atoms of water molecule. Therefore, as λ goes to 0, lhs of Equation 15 can be larger than rhs and consequently, f (0) > g(0). As the result, a new minimum in the potential curve can appear when λ is near zero. Although the contribution of the minimum may be small, this is an apparant limitation of the current single step soft-core method. Some water molecules like TIP4PEW additionally separate the center for Coulombic interaction and van der Waals interaction on the oxygen atom. Accordingly, the same type of minimum can also appear between a positively charged atom and the negative charge of a water molecule oxygen atom. However, using optimal parameter sets, our results show the effect of the new minimum on the computed solvation free energy to be apparently negligible, since both the one-step and two-step transformations converged to almost equal results.
4.3 Optimal values for αLJ, βC and m in one-step transformations
Summarizing these results, for m = 2, a range from 2.5 to 3.5 Å is appropriate for and when m = 6, a range from 2.0 to 2.5 Å is suitable. However, determining αLJ can be more difficult. Qualitatively we see that the core potential should not be too negative when the core collapse occurs, but the potential should be soft enough to prevent ‘origin singularity’-like curve shapes. Plotting potential energy curves as shown in Figure 3 is helpful in making a choice for αLJ.
As a general rule of thumb, we suggest m = 6, αLJ = 0.5 and for most molecules, unless they have large local charges, in which case a smaller αLJ of 0.2–0.3 seems to work better. For molecules that contain zero-vdW radius atoms or off-center partial charges, like the TIPXP or SPC water models, αLJ < 0.5 is also recommended. Should simulation instabilities or odd curve shapes be observed, αLJ can be systematically reduced or increased until smooth, integratable curves are obtained. Alternatively, a way of more carefully determining settings for αLJ and βC, based on the optimal parameter sets (Table 3) is outlined in the Appendix.
Table 3.
Single step transformation solvation free energies ( ), error estimates (σSEM) and curvatures (C) of the optimal parameter set for each test compound. Optimal parameter sets were determined for the two conditions m = 6 and m = 2. Generally, lower estimated errors and lower curvatures are obtained in the m = 6 case.
| αLJ | m | σSEM | C | |||||
|---|---|---|---|---|---|---|---|---|
| cyclohexane | 0.5 | 1.5 | 6 | 2.06 | 0.082 | 0.22 | ||
| 0.5 | 4.0 | 2 | 2.02 | 0.086 | 0.26 | |||
| chloride ion | 0.4 | 2.5 | 6 | −89.23 | 0.036 | 0.21 | ||
| 0.4 | 3.0 | 2 | −89.06 | 0.040 | 0.33 | |||
| ethanol | 0.5 | 2.0 | 6 | −4.45 | 0.040 | 0.20 | ||
| 0.5 | 3.0 | 2 | −4.67 | 0.041 | 0.32 | |||
| magnesium | 0.2 | 2.4 | 6 | −414.06 | 0.061 | 0.78 | ||
| 0.2 | 3.0 | 2 | −414.65 | 0.061 | 1.26 | |||
| water | 0.3 | 2.0 | 6 | −6.98 | 0.023 | 0.26 | ||
| 0.2 | 2.5 | 2 | −7.06 | 0.032 | 0.19 |
4.4 Comparison of one-step and two-step transformations
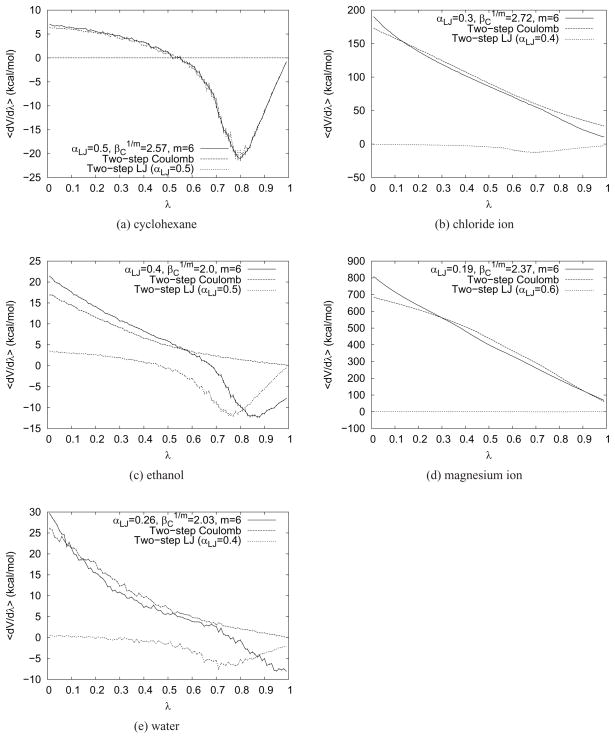
To compare the accuracy of one-step and two-step transformations, we first conducted extensive sampling benchmark calculations to obtain a ‘best estimate’ free energy result. These were conducted using 99 λ-windows, using the same equilibration protocol as above, but with a 1 ns length data collection phase. Simulation parameter values determined as outlined in the Appendix with m = 6 were used for each calculation (summarized in Table 4). Using the parameter settings from Table 3 instead did not change the results significantly (data not shown). For all compounds, almost identical free energies of solvation were calculated with one- or two-step transformations, with very similar overall σSEM (Table 4). All calculations resulted in very smooth free energy curves (Figure 6).
Table 4.
Solvation free energies of test compounds measured by one-step (first line) and two-step (second line) transformations. Free energies obtained from the two methods were almost identical. Corresponding error estimates were also similar. Curvatures of the two-step calculations are from the steps of removing Coulomb and removing LJ potential, respectively.
| molecules | transformation | σSEM | C | ||
|---|---|---|---|---|---|
| cyclohexane | αLJ = 0.5, , m = 6 | 2.01 | 0.028 | 0.11 | |
| Two-step (αLJ = 0.5) | 2.16 | 0.027 | 0.00, 0.12 | ||
|
| |||||
| chloride ion | αLJ = 0.3, , m = 6 | −89.20 | 0.020 | 0.19 | |
| Two-step (αLJ = 0.4) | −89.24 | 0.024 | 0.11, 0.05 | ||
|
| |||||
| ethanol | αLJ = 0.4, , m = 6 | −4.33 | 0.018 | 0.07 | |
| Two-step (αLJ = 0.5) | −4.32 | 0.019 | 0.03, 0.07 | ||
|
| |||||
| magnesium ion | αLJ = 0.19, , m = 6 | −414.21 | 0.035 | 0.62 | |
| Two-step (αLJ = 0.6) | −414.28 | 0.035 | 0.42, 0.01 | ||
|
| |||||
| water | αLJ = 0.26, , m = 6 | −7.04 | 0.012 | 0.12 | |
| Two-step (αLJ = 0.4) | −7.00 | 0.013 | 0.04, 0.03 | ||
Figure 6.
〈∂V/∂λ〉 curves for the five test compounds from TI calculations. The curves for one-step transformations and both the electrostatic and van der Waals substeps of two-step transformations are plotted. Optimized parameters from Table 4 were used. Error bars indicate σSEM, but are too small to be visible in plots (b) and (d).
Starting from the high precision values from the benchmark calculations, we subsequently reduced the number of λ-windows used in computing the free energy, to get results as they would have been obtained from a more typically applied TI calculation using many fewer windows, e.g. 24, 14, 9 or 6. The results (Table 5) show that even for 6 λ-windows, the deviations between the one- and two-step approaches are below 1 kcal/mol except in the case of the magnesium ion. Its solvation free energy is much more negative than the other test molecules and the error estimate was quite large. Longer simulations might be needed for the magnesium ion to obtain more accurate results with less number of λ-windows.
Table 5.
Influence of the number of λ-windows per step on the free energy result in units of kcal/mol. λ-values used were: 0.01, 0.02, …, 0.99 for 99 windows, 0.04, 0.08, …, 0.96 for 24 windows, 0.07, 0.14, …, 0.98 for 14 windows, 0.1, 0.2, …, 0.9 for 9 windows and 0.01, 0.2, 0.4, 0.6, 0.8, 0.99 for 6 windows. “average deviation” gives the difference to the 99 window result.
| number of λ-windows | ||||||
|---|---|---|---|---|---|---|
| 99 | 24 | 14 | 9 | 6 | ||
| cyclohexane | one-step | 2.01 | 2.07 | 1.94 | 2.01 | 2.04 |
| two-step | 2.16 | 2.11 | 2.06 | 1.99 | 2.12 | |
|
| ||||||
| chloride ion | one-step | −89.2 | −89.2 | −89.1 | −88.7 | −90.2 |
| two-step | −89.2 | −89.2 | −89.3 | −89.1 | −89.6 | |
|
| ||||||
| ethanol | one-step | −4.33 | −4.29 | −4.40 | −4.06 | −4.48 |
| two-step | −4.32 | −4.34 | −4.31 | −4.42 | −4.65 | |
|
| ||||||
| magnesium ion | one-step | −414.2 | −414.2 | −413.8 | −413.4 | −415.9 |
| two-step | −414.3 | −414.2 | −414.3 | −413.6 | −413.0 | |
|
| ||||||
| water | one-step | −7.04 | −7.14 | −7.15 | −7.05 | −7.37 |
| two-step | −7.00 | −7.02 | −7.14 | −7.03 | −7.38 | |
|
| ||||||
| average deviation | 0.04 | 0.11 | 0.27 | 0.57 | ||
In comparison to the high precision results, reducing the number of λ windows to 24 or 14 typically resulted in deviations of less than 0.2 kcal/mol and even the results with only 6 λ-windows tend to lie within 1 kcal/mol of the 99 λ ones. The largest contribution to the deviation comes from the magnesium case. The thermodynamic integration results turn out to be fairly robust with respect to reducing the number of substeps, both for the one- and two-step approach. Still, errors from numerical integration appear larger than the σSEM calculated above.
4.5 Solvation free energies of amino acid side chain residues
Having derived optimal settings for the soft-core parameters in the previous sections, we now turn to testing these parameters in other typical applications. A common test case for precise calculations of solvation free energies are amino acid side chain residues, built from amino acid residues by replacing the protein backbone part with a hydrogen atom. To test the performance of one-step vs. two-step TI transformations on larger and biochemically more relevant test molecules than the ones discussed above, we have calculated the solvation free energies of the side chains of tyrosine, histidine and glutamine (para-methyl phenol, 4-methyl imidazole and propionamide). The molecules were built as described in the work of Shirts et al.35 and solvated using the TIP4PEW water model, to stay consistent with the calculations described so far. The histidine molecule was set to be the ε-protonated tautomer. Simulations were performed using the same protocol as in the previous section, but with an extended 2 ns length data collection phase, using parameters of αLJ = 0.6 for two-step and for one-step transformations. m = 2 was used to allow a comparison to previously published work. The results are summarized in Table 6. For all three amino acid side chain analogues, free energies of solvation are computed in excellent agreement with previous results.
Table 6.
Free energies of solvation for three amino acid side chain analogues from one- and two-step transformations, compared to previous (two-step) simulations for the same force field (Amber ff99 plus TIP4PEW water).
| sidechain | ||||
|---|---|---|---|---|
| one-step | two-step | literature, Ref.37 | ||
| tyrosine | −3.92 ± 0.02 | −3.85 ± 0.02 | −4.0 | |
| histidine | −9.14 ± 0.02 | −9.16 ± 0.02 | −9.1 | |
| glutamine | −10.18 ± 0.02 | −10.25 ± 0.02 | −10.1 | |
5 Conclusion
We present here optimized parameter settings for a widely used implementation of soft-core potential functions for TI calculations. It is advisable to use the same value for the order parameter m for the Coulomb potential as the order parameter n for the LJ potential. In this work, we showed that n = m = 6 performs well. Optimal range for turned out to be from 2.0 to 2.5 Å. While the ideal value for the αLJ-parameter is 0.5 in the second (vdW) step of two-step TI transformations of chargeless molecules, it can be lowered to ~0.2 for one-step transformations of compounds with moderately large partial charges.
Both one-step as well as two-step TI calculations resulted in very similar and precise free energy results as far as correct soft-core parameters are used. One-step transformations gave free energy curves of approximately the same average curvature as two-step transformations, indicating that in most cases, TI calculations can be performed in a single transformation step without a loss of precision. However, care must be taken when performing one-step transformations, in case kinks in the curve of 〈∂V/∂λ〉 as seen in Figure 4 occur. Preliminary short calculations to obtain an estimate of the free energy curve shape for a selected set of parameters could be used to identify such problems.
Although the calculations used here employed the thermodynamic integration scheme, the parameters for soft-core potentials should also be of use with other free energy approaches, such as free-energy perturbation theory or Bennett acceptance ratio calculations38,39. In all such calculations, having smooth behavior as a function of λ, avoiding multiple minima, and preventing premature “collapse” of interactions (in the one-step transformations) are important to obtain reliable free energy estimates with minimal sampling requirements.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge fruitful discussions with the Amber developer community as well as financial support from a DFG return fellowship and NIH grant GM57513.
Appendix: Optimizing soft-core parameters
The “rule of thumb” given in Section 4.3 has worked for us in many examples, but the parameters for new compounds can alternatively be optimized by an analysis of important pair potentials, as desribed here:
First, a representative pair potential is chosen that is dominantly affecting the interaction free energy. For example, we will consider the pair potential between a magnesium ion and an oxygen atom of water to be the most important interaction for the calculation of the solvation free energy of a magnesium ion.
Second, is taken to be the distance where the depth of the pair-potential is 80% of its minimum value, to the right of the minimum distance. E.g., the lowest potential energy of Mg2+-O(TIP4PEW) is about −367.4 kcal/mol. At the distance of 2.37 Å, the potential energy reaches about 80% of this value. Therefore, can be set to 2.37 Å.
Third, if the maximum depth of the potential energy is shallower than −18 kcal/mol, αLJ = 0.5 is a good starting point to try. Otherwise αLJ should be adjusted to set the core potential (V (ri j = 0, λ )) to −18 kcal/mol when the exclusive volume is collapsed. Taking the magnesium ion as an example again: When αLJ = 0.19, the core potential becomes −18 kcal/mol at λ = 0.93 and the lowest potential becomes −19.8 kcal/mol. Assuming the thermal fluctuation is about 1.8 kcal/mol (aqueous solution at 298 K), it can be assumed that the exclusive volume is collapsed at this λ. Therefore, αLJ = 0.19 can be used for magnesium ion.
Note that in the limit of extensive sampling, the choice of does not affect the accuracy of the calculated free energy. In practice however, the suggest value for helps reduce errors because, with the suggested value, the potential well-depth almost linearly decays at early stage of perturbation (low λ) and thus errors are distributed evenly over the broad range of λ. Plots like those in Figure 3 aid in determining .
Also, the choice of αLJ is important not only to have low errors but also to avoid the problems mentioned in Figure 5. Even if the collapsed core potential is above −18 kcal/mol, it may not necessarily cause a problem, but estimated errors may increase. The not-so-obvious second minimum (for example, ‘Not contacted’ status of Figure 5) is caused by the repulsion of solvent molecules around the solute. The value of −18 kcal/mol mentioned here has been empirically determined and will probably not be optimal for every case. The number will dependent on the various conditions, e.g. temperature, pressure, solvent composition and more complex molecular structures.
We chose major pair potentials to determine parameters in this way for the rest of the four test compounds: H(c-hexane)-H(TIP4PEW), Cl−-H(TIP4PEW), O(ethanol)-H(TIP4PEW) and O(TIP4PEW)-H(TIP4PEW). New parameters were determined and their instrinsic errors and curvature-values of the calculation of free energy was measured in the same way as above. We obtained for cyclohexane, αLJ = 0.30, for chloride ion, αLJ = 0.38, for ethanol, αLJ = 0.19, for magnesium ion, and αLJ = 0.26, for TIP4PEW. Note that these sets are generally close to the previous best sets listed in Table 3.
References
- 1.Kollman P. Chem Rev. 1993;93:2395–2417. [Google Scholar]
- 2.Reddy M, Erion M, Agarwal A. Rev Comp Chem. 2000;16:217–304. [Google Scholar]
- 3.Wang W, Donini O, Reyes C, Kollman P. Ann Rev Biophy Biomol Struct. 2001;30:211–243. doi: 10.1146/annurev.biophys.30.1.211. [DOI] [PubMed] [Google Scholar]
- 4.Lazaridis T. Curr Org Chem. 2002;6:1319–1332. [Google Scholar]
- 5.Foloppe N, Hubbard R. Curr Med Chem. 2006;13:3583–3608. doi: 10.2174/092986706779026165. [DOI] [PubMed] [Google Scholar]
- 6.Simonson T. Free energy calculations. In: Becker O, MacKerell A, Roux B, Watanabe M, editors. Computational Biochemistry and Biophysics. Marcel Dekker; New York: 2001. [Google Scholar]
- 7.Brandsdal B, Osterberg F, Almlof M, Feierberg I, Luzhkov V, Åqvist J. Free energy calculations and ligand binding. Vol. 66. Academic Press Inc; San Diego: 2003. [DOI] [PubMed] [Google Scholar]
- 8.Özal T, Peter C, Hess B, van der Vegt N. Macromolecules. 2008;41:5055–5061. [Google Scholar]
- 9.Pitera J, van Gunsteren W. J Phys Chem B. 2001;105:11264–11274. [Google Scholar]
- 10.Hritz J, Oostenbrink C. J Chem Phys. 2008;128:144121. doi: 10.1063/1.2888998. [DOI] [PubMed] [Google Scholar]
- 11.Kirkwood J. J Chem Phys. 1935;3:300–313. [Google Scholar]
- 12.Valleau J, Torrie G. Modern Theoretical Chemistry. In: Berne B, editor. Statistical Mechanics, Part A. Vol. 5. Plenum Press; New York: 1977. [Google Scholar]
- 13.Simonson T. Mol Phys. 1993;80:441–447. [Google Scholar]
- 14.Maye P, Mezei M. THEOCHEM. 1996;362:317–324. [Google Scholar]
- 15.Mezei M. J Comp Chem. 1992;13:651–656. [Google Scholar]
- 16.Resat H, Mezei M. J Chem Phys. 1993;99:6052–6061. [Google Scholar]
- 17.Steinbrecher T, Mobley D, Case D. J Chem Phys. 2007;127:214108. doi: 10.1063/1.2799191. [DOI] [PubMed] [Google Scholar]
- 18.Pitera J, van Gunsteren W. Mol Sim. 2002;28:45–65. [Google Scholar]
- 19.Beutler T, Mark A, van Schaik R, Gerber P, van Gunsteren W. Chem Phys Lett. 1994;222:529–539. [Google Scholar]
- 20.Pearlman D, Kollman P. J Chem Phys. 1989;90:2460–2470. [Google Scholar]
- 21.Lin C, Wood R. J Comp Chem. 1994;15:149–154. [Google Scholar]
- 22.Postma J, Berendsen H, Haak J. Far Symp Chem Soc. 1982;17:55–67. [Google Scholar]
- 23.Cornell W, Cieplak P, Bayly C, Gould I, Merz K, Jr, Ferguson D, Spellmeyer D, Fox T, Caldwell J, Kollman P. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 24.Duan Y, Wu C, Chowdhury S, Lee M, Xiong G, Zhang W, Yang R, Cieplak P, Luo R, Lee T. J Comp Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 25.Case D, Darden T, Cheatham T, III, Simmerling C, Wang J, Duke R, Luo R, Crowley M, Walker R, Zhang W, Merz K, Wang B, Hayik S, Roitberg A, Seabra G, Kolossvary I, Wong K, Paesani F, Vanicek J, Wu X, Brozell S, Steinbrecher T, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Mathews D, Seetin M, Sagui C, Babin V, Kollman P. AMBER10. University of California; San Francisco: 2008. [Google Scholar]
- 26.Wang J, Wolf R, Caldwell J, Kollman P, Case D. J Comp Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 27.Bayly C, Cieplak P, Cornell W, Kollman P. J Phys Chem. 1993;97:10269. [Google Scholar]
- 28.Horn H, Swope W, Pitera J, Madura J, Dick T, Hura G, Head-Gordon T. J Chem Phys. 2004;120:9665–9678. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 29.Horn H, Swope W, Pitera J. J Chem Phys. 2005;123:194504. doi: 10.1063/1.2085031. [DOI] [PubMed] [Google Scholar]
- 30.Ryckaert J, Ciccotti G, Berendsen H. J Comp Phys. 1977;23:327–341. [Google Scholar]
- 31.Chandrasekhar S. Rev Mod Phys. 1943;15:1–89. [Google Scholar]
- 32.Berendsen H, Postma J, van Gunsteren W, DiNola A, Haak J. J Chem Phys. 1984;81:3684–3690. [Google Scholar]
- 33.Swope W, Horn H, Rice J. J Phys Chem B. 2010;114:8621–8630. doi: 10.1021/jp911699p. [DOI] [PubMed] [Google Scholar]
- 34.Straatsma T, Berendsen H, Stam A. Mol Phys. 1986;57:89–95. [Google Scholar]
- 35.Shirts M, Pitera J, Swope W, Pande V. J Chem Phys. 2003;119:5740–5761. [Google Scholar]
- 36.Shirts M, Pande V. J Chem Phys. 2005;122:134508. doi: 10.1063/1.1877132. [DOI] [PubMed] [Google Scholar]
- 37.Hess B, van der Vegt N. J Phys Chem B. 2006;110:17616–17626. doi: 10.1021/jp0641029. [DOI] [PubMed] [Google Scholar]
- 38.Bennett C. J Comp Phys. 1976;22:245–268. [Google Scholar]
- 39.Shirts M, Chodera J. J Chem Phys. 2008;129:124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.