Onset and Offset Phonation Threshold Flow in Excised Canine Larynges

Abstract

Objectives/Hypothesis

This study examined the hypothesis that the minimum flow required for phonation onset, the onset phonation threshold flow (PTF), is greater than the minimum flow to sustain phonation, the offset PTF. This study also explored the hypothesis that the ratio of these two (PTF offset divided by PTF onset) falls within [0.707, 1.0].

Study Design

This was a methodological study to measure onset and offset PTFs in 10 excised canine larynges, whose ratio was predicted to fall in a specific domain.

Method

The onset and offset PTF and phonation threshold pressure (PTP) values were observed using ten excised canine larynges mounted on a bench apparatus. The subglottal flow was increased until phonation was observed, and then decreased until phonation ceased; airflow and pressure measurements at critical conditions of phonation were observed as the PTF and PTP. Larynges with elongated vocal folds were then tested to observe PTF and determine if the hypothesis was observed in pathological-like larynges.

Results

The offset PTF was always less than the onset PTF (p<<0.0001) and 80.0% of the observed onset-offset PTF ratios were bound by [0.707, 1.0].

Conclusions

PTF onset or offset could be a useful diagnostic parameter of the voice, particularly when used in conjunction with PTP to describe laryngeal resistance and aerodynamic power. Further exploration of the relationship between onset and offset PTF values could augment clinical diagnostic ability and advance current theories on the physics of phonation.

INTRODUCTION

Phonation threshold flow (PTF), defined as the minimum glottal airflow required to initiate vocal fold vibration, has been studied recently because it could provide information about speech system dysfunctions (1). It is theorized that PTF is sensitive to changes in tissue viscosity, mucosal wave velocity, vocal fold thickness, and prephonatory glottal area. Recently, by comparing PTF and phonation threshold pressure (PTP) in excised canine larynges with varying degrees of posterior glottal width, Hottinger et al. observed that PTF is more sensitive to posterior glottal width changes than PTP (2). Theoretical analysis on a modified one-mass model confirmed that this higher sensitivity of PTF compared to PTP could be a consequence of the pressure recovery effect at the glottal exit (3). These experimental and theoretical results suggested that contrary to PTP, PTF may be an aerodynamic parameter of the voice useful for indicating pathological conditions in which the incomplete glottal gap is often seen. Moreover, in comparison with PTP, PTF may be more practical for clinical vocal health assessment because unlike subglottal pressure, glottal airflow can be easily, directly, and noninvasively measured extraorally using a circumferentially vented pneumotachograph mask. Before this new aerodynamic parameter can be employed in routine clinical assessment, deeper experimental and theoretical insight is necessary.

For years it has been known that the vocal fold vibration system is nonlinear and that the hysteresis phenomenon could occur in this nonlinear system (4–6). This means that the critical condition of phonation onset is usually measurably different from that of the phonation offset (7–10). Lucero predicted that the offset PTP is about 50%–100% of the onset PTP by using a oscillation hysteresis model (5,11), which agrees with measurements of the onset and offset PTP (7–10). Plant et al, however, could neither confirm nor deny the existence of hysteresis in direct measurements of PTP in normal subjects (12). As with pressure, we can expect that the minimum airflow for phonation onset (onset PTF) and the minimum airflow to sustain phonation (offset PTF) could also be different due to the hysteresis phenomenon. The maximum airflow resulting in vocal fold oscillation offset may be important in clinical evaluation of laryngeal health in addition to the minimum airflow for oscillation onset, particularly when the onset minimum flow cannot accurately be measured. However, the previous theoretical study on PTF is based on linear assumptions and the previous experiments on PTF only measure the minimum airflow to elicit phonation onset (1–3). To our knowledge, no studies have been published exploring the maximum glottal airflow to initiate oscillation offset.

This study investigated the critical airflows at vocal fold oscillation onset and offset. The hysteresis phenomenon of a one-mass model of vocal folds was reviewed (5,8), and based on the analysis of this one-mass model we defined the offset phonation threshold flow as the minimum glottal airflow to sustain phonation, whereas the onset phonation threshold flow, which was defined previously, is the minimum glottal airflow to initiate phonation (1). An excised larynx setup was used to experimentally investigate the onset and offset PTF in a canine larynx model. Because the circulatory, neural, and homeostatic in vivo properties of the larynx are absent in an ex vivo experiment, an excised larynx experiment using a bench apparatus as described by Jiang et al. is well-suited to studying the aerodynamic properties of phonation (13). We hypothesize that the onset PTF is greater than the offset PTF and that the ratio of offset to onset PTF values is bound by a finite domain, [0.707, 1.0].

MATERIALS AND METHODS

Laryngeal Modeling

Ten canine larynges were harvested immediately postmortem from mongrel dogs (25–30 kg) not sacrificed for this study. They were inspected to exclude pathologies or trauma and then stored in 0.9% saline solution and frozen until use. The cuneiform cartilage, epiglottis, and lateral posterosuperior portions of the thyroid cartilage were dissected away to expose the muscular process of the arytenoids. The ventricular folds were dissected away immediately before experimentation to reduce dehydration and damage to the true vocal folds while mounting the larynx.

Apparatus

The larynx was mounted on a bench apparatus as described by Jiang et al. (13). A metal pull clamp was used to fasten the trachea to the pseudolung, which was used to simulate the human pulmonary system as described in Jiang et al. (13), and two three-pronged micrometers were inserted into the arytenoids for lateral stabilization and adduction (Figure 1). Tension was applied to the vocal folds by suturing the thyroid cartilage at the laryngeal prominence to an anterior micrometer. Pressurized airflow was channeled through two Concha Therm III humidifiers (Fisher & Paykel Healthcare Inc., Laguna Hills, CA) in series and an Omega airflow meter (model FMA-1601A; Omega Engineering Inc., Stamford, CT) to collect airflow measurements. Pressure was measured directly below the larynx using a Heise digital pressure meter (901 series; Ashcroft Inc., Stratford, CT). Acoustic data were collected via a Sony microphone (model ECM-88; Sony Electronics Inc., New York, NY) positioned at a 45° angle to the vocal tract axis and 10.0 cm from the glottis to reduce acoustic noise caused by airflow. The acoustic signal was amplified using a Symetrix pre-amplifier (model 302; Symetrix Inc., Mountlake Terrace, WA). Airflow, pressure, and acoustic signals were recorded on a personal computer using a National Instruments data acquisition board (model AT-MIO-16; National Instruments Corp., Austin, TX) and customized LabVIEW 8.2.1 software (National Instruments Corp.). The entire experimental bench apparatus was enclosed in a triple-walled sound proof room to reduce noise pollution in the acoustic recordings and maintain constant temperature and humidity.

Figure 1.

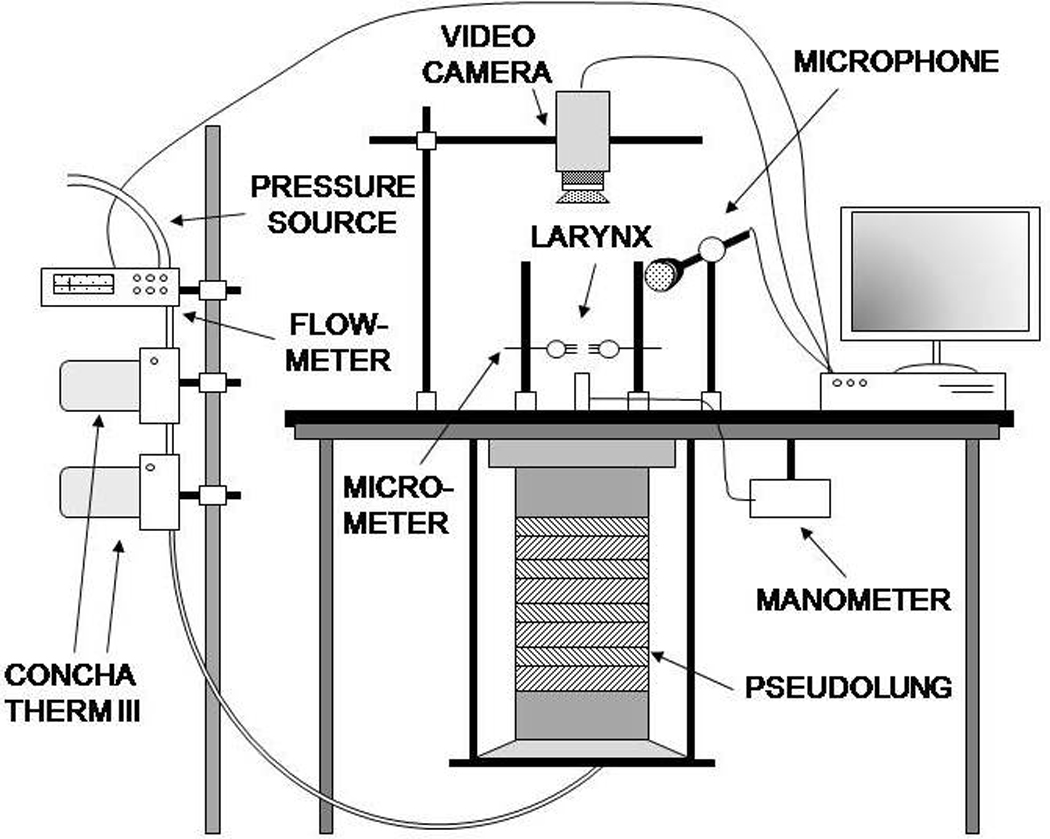
Diagram of the experimental bench apparatus used to mount larynges. All measurements are recorded digitally on a PC.

Data collection

With the larynx fastened to the bench apparatus and physiologic tension applied to the vocal folds, airflow was increased slowly and consistently until phonation occurred. Once phonation was observed, the airflow was decreased slowly and consistently until phonation ceased. The values of airflow and pressure at the phonation onset time index were recorded as the onset PTF and onset PTP, respectively (Figure 2). Likewise, the values of airflow and pressure at the phonation offset time index were recorded as the offset PTF and offset PTP, respectively (Figure 2). Subsequent trials were performed on the same larynx but with elongated vocal folds. The vocal folds were elongated by measuring the physiologically normal vocal edge length and increasing it by 5%, 10%, and 15%, adjusting the anterior micrometer slowly to achieve precise elongations. The elongation measurements were performed using a Fowler digital micrometer (Newton, MA). Three trials were conducted for each elongation state, including normal elongation. The mean onset and offset PTF values were calculated for each elongation state of all ten larynges.

Figure 2.

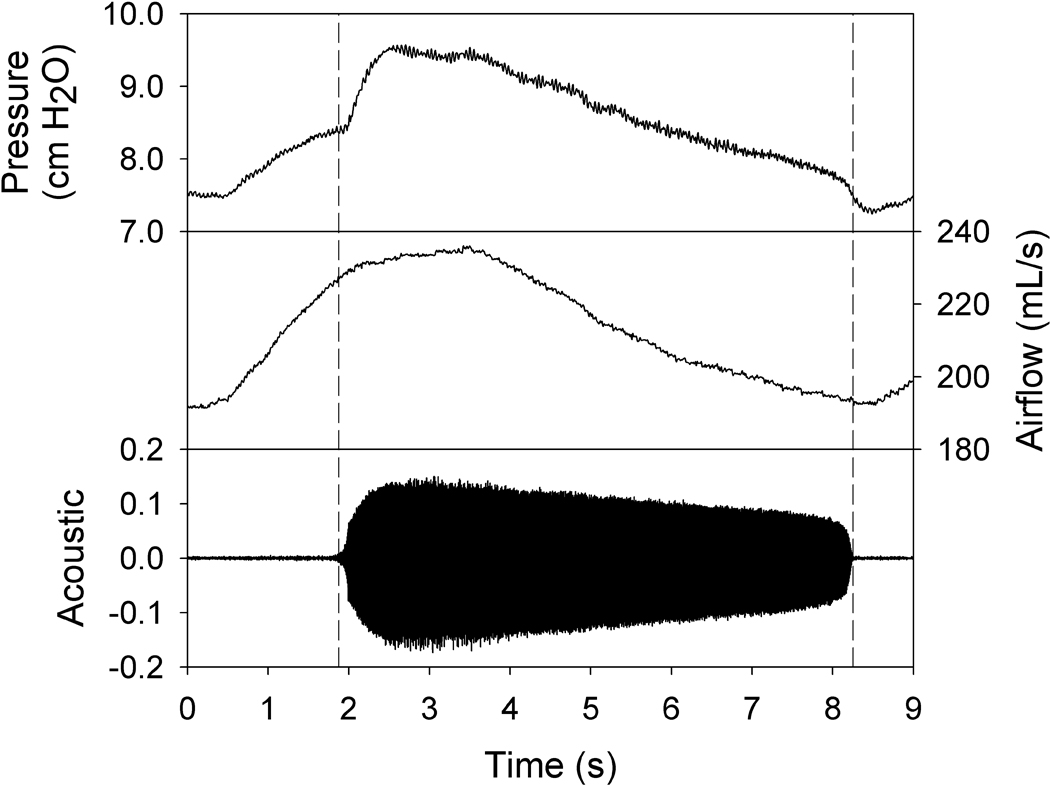
Example graphs of acoustic, airflow, and pressure measurements obtained from larynx 9 at normal elongation. Airflow was increased until the phonation onset occurred (left vertical line), at which point the computer recorded the onset phonation threshold acoustic, airflow, and pressure data. Airflow was then gradually decreased until the phonation offset occurred (right vertical line), at which point the computer recorded the offset phonation threshold acoustic, airflow, and pressure data.

Data analysis

A paired t-test with a directional alternative hypothesis was performed on the aggregate onset and offset PTF and PTP data. Onset was hypothesized to be greater than offset due to hysteresis. The onset-offset ratio, offset PTF divided by onset PTF, was calculated for each trial and the mean and standard deviation were determined.

RESULTS

Mean onset and offset PTF values for each elongation level are recorded in Table 1. A directional paired t-test was performed on the aggregate data to test the hypothesis that onset was greater than offset. For all PTF data, p << 0.0001, providing statistical significance to the hypothesis. The onset-offset PTF ratio, R_PTF, defined as

$$R_{\mathit{\text{PTF}}}=\frac{U_{\mathit{\text{offset}}}}{U_{\mathit{\text{onset}}}},$$

was calculated for each trial of phonation, with a mean of 0.795 ± 0.116. All of the data were bound by [0.515, 0.972]. Approximately 80.0% of the observed data fell within the expected R_PTF domain [0.707, 1]. The measured R_PTF data passed a Kolmogorov-Smirnov normality test and a normal probability distribution was written to determine the probability that using our experimental setup the onset-offset ratio occurs within the domain predicted by theory:

$$P\{0.707<R_{\mathit{\text{PTF}}}<1\}={\displaystyle {\int }_{0.707}^1}[\frac{1}{0.1163\sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{Q-0.7953}{0.1163}\right)}^2}]{\mathit{\text{dR}}}_{\mathit{\text{PTF}}}=0.737$$

Table 1.

Mean onset and offset phonation threshold flow and R_PTF in all larynges according to elongation group. For each elongation group, mean onset PTF was greater than mean offset PTF, and the onset-offset ratio (R_PTF) was bound by the theoretically predicted range [0.707, 1.0].

Elongation Level	Mean Onset PTF	Mean Offset PTF	Mean RPTF
+0%	344.14 mL/s	287.34 mL/s	0.835 ± 0.137
+5%	222.78 mL/s	182.02 mL/s	0.817 ± 0.146
+10%	363.11 mL/s	276.57 mL/s	0.762 ± 0.0869
+15%	505.24 mL/s	379.75 mL/s	0.752 ± 0.0987

In addition to testing the hysteresis in PTF, a directional paired t-test demonstrated that PTP onset was greater than PTP offset (p << 0.0001, α = 0.05). The mean PTP hysteresis ratio was 0.876 ± 0.0752.

DISCUSSION

In order to understand the difference in airflow values from oscillation onset to offset, we reviewed the hysteresis phenomenon as it presents in vocal fold oscillation (5). Based on the theoretical analysis of a one-mass model of the vocal folds, the onset and offset PTF are derived from the flow-pressure relationship in the glottis.

Titze proved that the minimum lung pressure to initiate vocal fold oscillation is P_onset = k_tBcx₀/T, where k_t is an empirical coefficient of pressure losses related to turbulent flow and glottal viscous resistance, B is the damping coefficient of tissue viscosity, c is the mucosal wave velocity, x₀ is the neutral glottal width, and T is the thickness of the vocal folds (14). This critical pressure value represents the onset PTP. However, Baer observed that the minimum pressure required to sustain oscillation after the onset of phonation is lower than the predicted theoretical onset PTP value (7). Lucero theoretically determined that the minimum lung pressure necessary to sustain the oscillation, the offset PTP, is

$$P_{\mathit{\text{offset}}}=\frac{k_t{\mathit{\text{Bcx}}}_0}{T}\left(\frac{1+\sqrt{1-a^2}}{2}\right),$$ [1]

where a = A/x₀ is the normalized oscillation amplitude and A is the oscillation amplitude (5). Because 0 < a < 1, it was shown that 0.5 < P_offset/ P_onset < 1.0.

Jiang and Tao defined the onset phonation threshold flow (U_onset) as the minimum airflow to initiate vocal fold oscillation (1). It was shown that U_onset can be related to glottal configuration and tissue properties by the relationship $U_{\mathit{\text{onset}}}=\sqrt{8{\mathit{\text{BcL}}}^2{x}_0^3/T\rho }$, where L is the vocal fold length and ρ is the glottal airflow density. Through analysis of the oscillation hysteresis phenomenon as done by Lucero, the offset PTF can likewise be determined (5). Because a relationship between the glottal airflow and the subglottal pressure exists, P_s ≈k_t(ρ/2)(U̅/2Lx₀)² (1,14), the offset PTF can be determined by substituting the above flow-pressure relationship into Eq. [1],

$$U_{\mathit{\text{offset}}}=\sqrt{\frac{8{\mathit{\text{BcL}}}^2{x}_0^3}{T\rho }}\times \sqrt{\frac{1+\sqrt{1-a^2}}{2}}=U_{\mathit{\text{onset}}}=\sqrt{\frac{1+\sqrt{1-a^2}}{2}}$$ [2]

Because a is defined such that 0 < a < 1, substitution of these limits of a into the above equation yields 0.707 < U_offset/ U_onset < 1.0. This is the theoretically derived basis of our hypothesis.

With consideration to the limitations inherent in excised larynx experiments, the fidelity of the data to the hypothesis was good. In all trials, PTF (Figure 3) and PTP (Figure 4) onset values were observed to be greater than their respective offset values, providing evidence of the hysteresis phenomenon and affirming that the experimental setup was appropriate in all trials. The mean PTF hysteresis ratio was 0.795 ± 0.116 and 80.0% of the data were bound by the expected domain (Figure 5). A normal probability distribution was written on the aggregate onset-offset PTF ratio data, and an integral suggested that there was a probability of 73.7% that additional trials would be observed to fall in this domain. 20.0% of all onset-offset PTF ratio trials were bound by the domain (0.515, 0.707), suggesting that in the excised experimentation setup, offset may have been observed to be lower or onset higher than theoretically expected (Figure 5). Confounding variables of the excised experimentation setup, such as dehydration, and inherent simplification of the theoretical model may have exacerbated the hysteresis phenomenon in the isolated trials that did not agree with the hypothesis.

Figure 3.

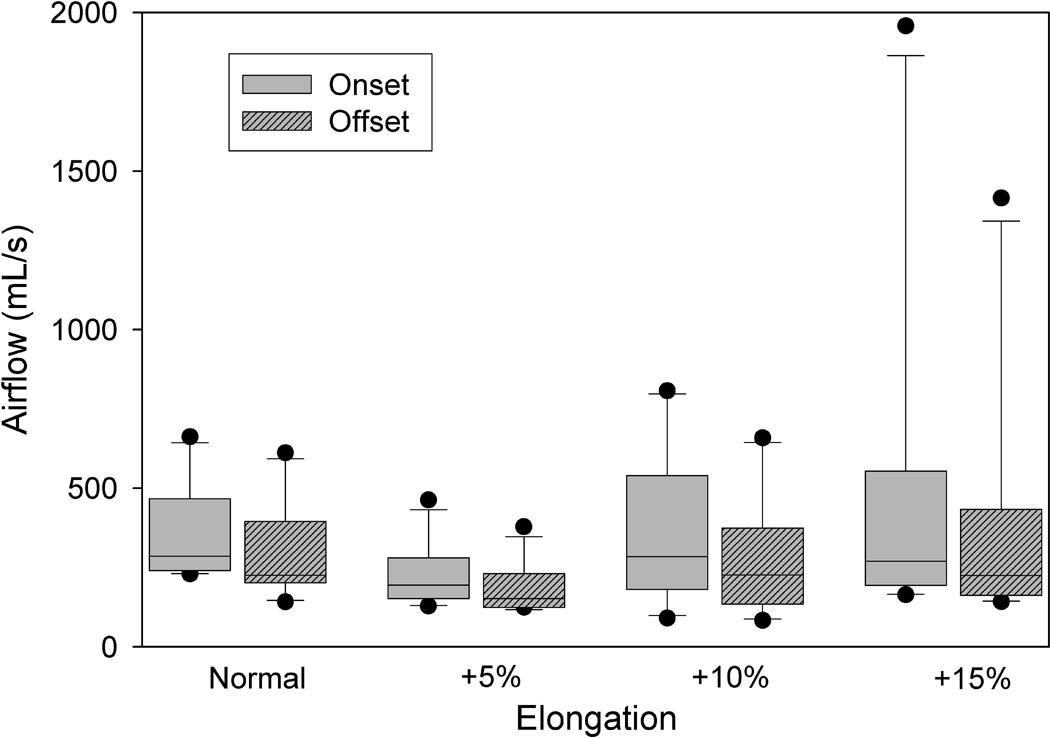
Aggregate PTF data for phonation onset and offset in excised canine larynges with elongated vocal folds. The upper and lower edges of the box represent the 75th and 25th percentile, respectively, and a line within each box marks the median PTF for the given elongation level. Whiskers above and below each box represent the 90^th and 10^th percentiles, respectively. Statistical outliers are graphed as points. PTF onset is consistently greater than PTF offset.

Figure 4.

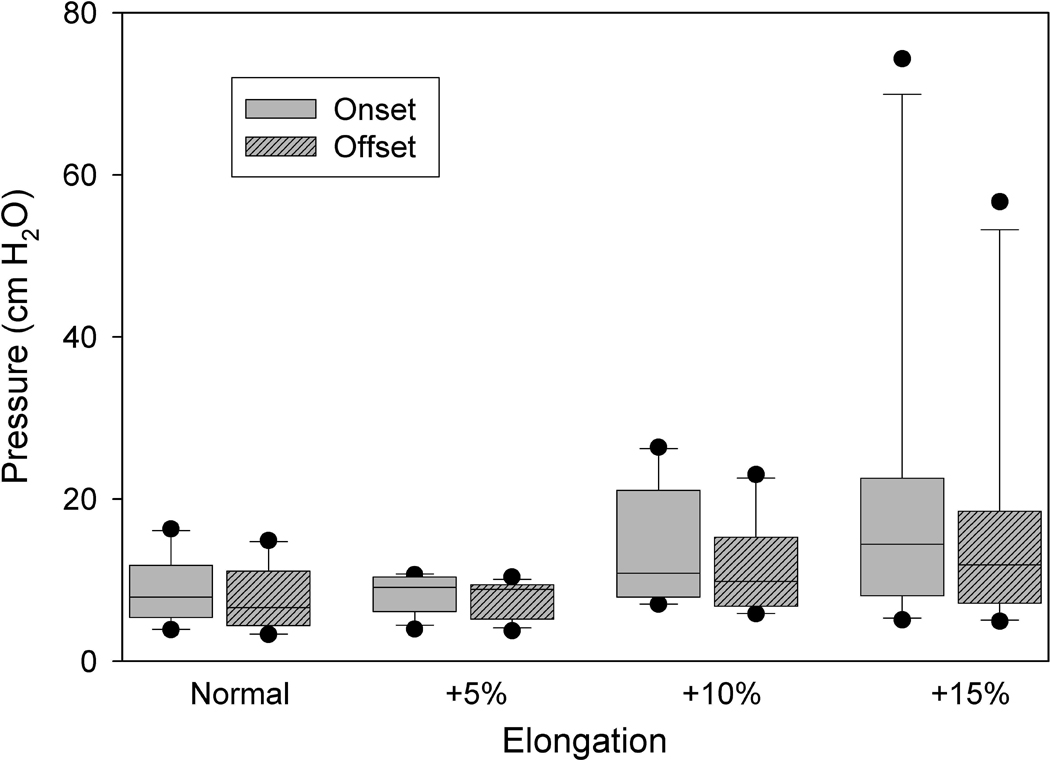
Aggregate PTP data for phonation onset and offset in excised canine larynges with elongated vocal folds. The upper and lower edges of the box represent the 75th and 25th percentile, respectively, and a line within each box marks the median PTF for the given elongation level. Whiskers above and below each box represent the 90^th and 10^th percentiles, respectively. Statistical outliers are graphed as points. PTP onset is consistently greater then PTP offset.

Figure 5.

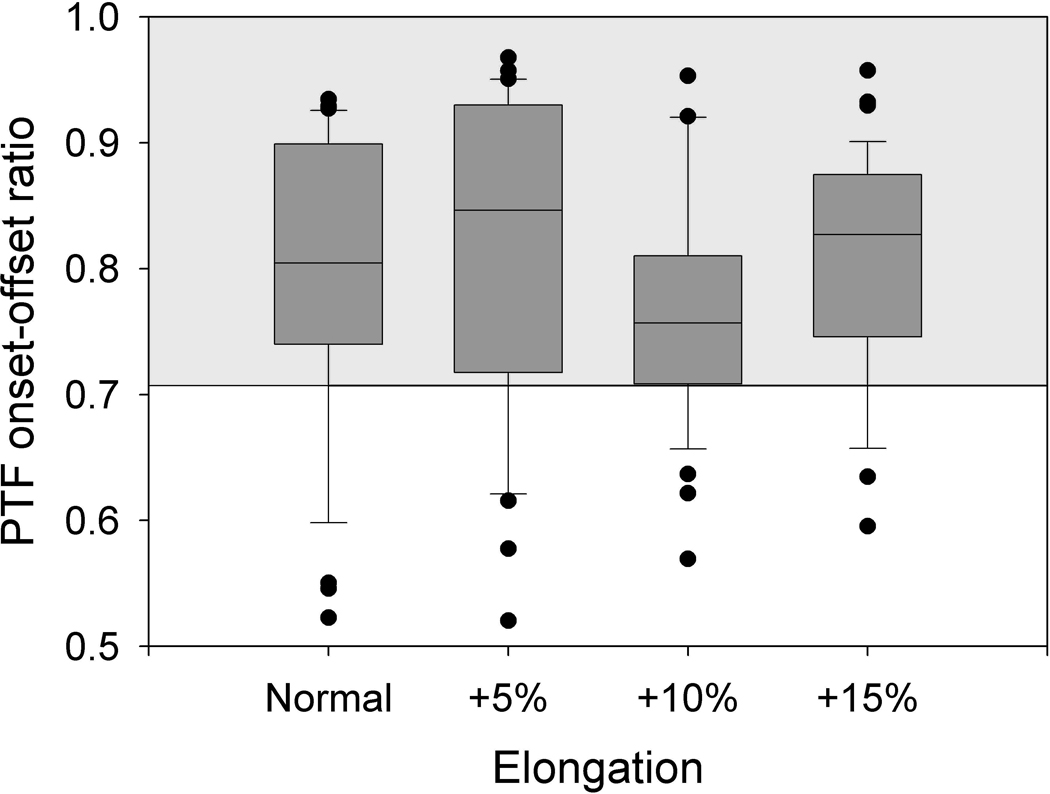
PTF onset-offset ratios for each elongation level. The upper and lower edges of the box represent the 75th and 25th percentile, respectively, and a line within each box marks the median PTF for the given elongation level. Whiskers above and below each box represent the 90^th and 10^th percentiles, respectively. Statistical outliers are graphed as points. The horizontal lines at 0.707 and 1.0 indicate the theoretically expected lower and upper bounds of the data. The majority of the data (80.0% of all data points) fell within the theoretically expected range (shaded).

Determining the offset PTF value and its relationship with the onset PTF value is clinically significant. The results show that both offset and onset PTF are affected by and can be used to indicate abnormal tensions due to elongation, which could be symptomatic of vocal fold pathologies. Therefore, it can be expected that just as the onset PTF could be an indicator of laryngeal health (1,2), the offset PTF could as well, particularly in instances when the onset PTF cannot be easily measured. Subglottal pressure or glottal airflow itself can only reflect one aspect of glottal aerodynamics (2,15); therefore, the values of PTP and PTF together could provide a more robust indicator of glottal aerodynamic characteristics and related laryngeal disease. Current noninvasive measurement of the aerodynamic parameters of the voice use phonation interruption techniques to measure PTP at offset (16,17). Therefore, by adding to the offset PTP measurements an offset PTF value as proposed in this study, clinicians can complement known diagnostic information and provide additional diagnostic information such as airflow channel resistance (defined as pressure/airflow) and aerodynamic power (defined as pressure × airflow) (1,15). This additional information could be helpful in providing more accurate clinical assessment of laryngeal health.

Determining the offset PTF value and its relationship with the onset PTF value is important to advance current theory on the physics of phonation, and determining this offset-onset relationship would verify current theories. Understanding the hysteresis phenomenon as it presents in the aerodynamics of the human voice is essential to a more comprehensive understanding of how biomechanical and clinically observable parameters of the vocal folds affect voice. Future studies should further elucidate the PTF hysteresis phenomenon and explore PTF as a diagnostic parameter. Controlled excised larynx experiments may help determine if dehydration or tissue fatigue exacerbate the hysteresis effect. Direct measurement of PTF onset and offset values in tracheotomy patients may help substantiate current theory with data from human larynges and provide in vivo experimental evidence of the diagnostic value of PTF.

CONCLUSION

This study examined the onset and offset phonation threshold flows due to the hysteresis phenomenon of vocal fold oscillation. Theoretical models predict that the onset-offset PTF ratio, the offset PTF divided by onset PTF, is bound by the domain [0.707, 1.0]. The experimental data suggested the offset PTF is lower than the onset PTF (p << 0.0001, α = 0.05) and 80.0% of the observed onset-offset PTF ratios was bound by [0.707, 1.0]. These experimental data support our hypothesis and theory. Exploring the relationship between offset and onset PTF values could be important in augmenting clinical diagnostic ability and advancing current theories on the physics of phonation.