Abstract
The myelin water fraction (MWF) has been used as a quantitative measure of the amount of myelin present in tissue. However, recent work has suggested that inter-compartmental exchange of water between myelin and non-myelin compartments may cause the MWF to underestimate the true myelin content of tissue. In this work, multi-exponential T2 experiments were performed in-vivo within the rat spinal cord, and a wide variation of the MWF (10–35%) was measured within four rat spinal cord tracts with similar myelin content. A numerical simulation based upon segmented histology images was used to quantitatively account for T2 variations between tracts. The model predicts that a difference in exchange between the four spinal cord tracts, mediated by a difference in the average axon radius and myelin thickness, is sufficient to account for the variation in MWF measured in-vivo.
Keywords: MRI, exchange, multi-exponential T2, myelin water fraction
Introduction
The water proton NMR signal from white matter is known to exhibit two T2 components—a fast-relaxing component that is believed to originate from the water within myelin, and a slow-relaxing component that is believed to originate from water in both the extra-and intra-axonal spaces (1,2). The myelin water fraction (MWF), defined as the fraction of water signal associated with the fast-relaxing T2 component, has been found to decrease in demyelinating and dysmyelinating lesions in both white matter (3) & peripheral nerve (4) and found to correlate with optical densitometry of luxol fast blue stained white matter (5). These findings support the interpretation that MWF is a quantitative measure of myelin content in tissue, and has been used to surmise differences in myelin content in different white matter tracts of the human brain (6). A recent study in excised rat spinal cord, which showed MWF to vary substantially between spinal cord tracts with similar myelin volume fractions (vm) (7), has raised questions about the interpretation of MWF in white matter. The proposed explanation for this lack of correlation between MWF and vm was a variation in rate of water exchange between myelin and non-myelin tissue volumes across tracts, dictated by variation in axon radius and myelin thickness. This study, however, was not performed in-vivo and no quantitative model was presented to explain the postulated exchange-mediated changes in multi-exponential T2 (MET2) relaxation. The present work revisits MET2 in the rat spinal cord and interprets in-vivo data with a histology-based quantitative model of water proton relaxation and diffusion.
Many previous computational models of MET2 in tissue have been based on a finite number of discrete compartments (8–10) with exchange effects described by the Bloch-McConnell equations (11). One assumption in these models is that each compartment is instantaneously well mixed (i.e., that water diffusion is large enough to keep each pool in equilibrium with itself). Biases may exist in these compartmental models if diffusion is slow enough to keep compartments from being well mixed. Compartmental models also (typically) neglect the intrinsic heterogeneity of tissue, using only enough discrete compartments to account for the number of distinct tissue components and not factoring in variations in the sizes or shapes of these physical compartments throughout the volume of tissue being modeled. Finite difference and Monte-Carlo models, like those previously used in diffusion studies (12–14), do not require the assumption of well mixed compartments, and are naturally well-suited to account for variation in the shape and dimensions of tissue components, such as variation in axon radius and myelin thickness. The present study uses histology of the rat spinal cord to define a finite difference model of water proton exchange and transverse relaxation, and fits model parameters to explain the in-vivo observations of MET2 relaxation in four spinal tracts of the rat spinal cord.
Methods
Histology
Histology sections stained with Toluidine blue were taken from a previous study of rat spinal cord (7). Within this analysis, effects of sample shrinkage due during fixation (4% gluteraldehyde, 0.5% paraformaldehyde), secondary fixation (osmium) and embedding (epoxy) were neglected; however, previous studies have shown less than a 10% decrease in cross-sectional area with this protocol (15,16). From the histology sections, digital images were acquired using oil immersion light microscopy (LM) at 75 nm × 75 nm resolution (higher resolution than in the previous study). LM images were collected from four spinal white matter tracts — vestibulospinal (VST), rubrospinal (RST), funiculus gracilis (FG), and dorsal corticospinal (dCST) tracts. Images were enhanced with an adaptive histogram equalization algorithm and smoothed with an edge preserving anisotropic diffusion filter. Anatomical boundaries were then defined by local curvature, and images were manually segmented into regions of myelin, intra-axonal space, and extra-axonal space. From each tract vm, average myelin thickness, represented as , and average axon radius, r̄i, were calculated, where the axon radius was measured inside the myelin. Also, since the signal from water is proportional to the axon area, an area-weighted average axon radius, 〈ri〉A, was also calculated as
| [1] |
where rin is the radius inside the myelin sheath of the nth axon. An area-weighted myelin thickness, 〈ro−ri〉A, was calculated by
| [2] |
where ron is the radius outside the myelin sheath of the nth axon.
Magnetic Resonance Imaging
Animal studies were completed in accordance with the Vanderbilt University Institutional Animal Care and Use Committee. Five female Sprague Dawley rats (226 – 266 g) were anesthetized with isoflurane and imaged with a 9.4 Tesla 31-cm horizontal bore Varian (Palo Alto, CA) DirectDrive scanner, using a 38 mm Litz quadrature coil (Doty Scientific, Columbia SC) for RF transmission and reception. An external heater was used to maintain body temperature. A 1.5 mm thick slice transverse to the long axis of the rat cervical spinal cord was selected from scout images. Using an inversion-recovery prepared multiple spin echo imaging sequence, a total of 32 echoes were acquired with the first echo time at 7.4 ms, echo spacing of 9 ms through the first 24 echoes (optimized following methods in (17)) and 50 ms echo spacing for the final 8 echoes (18). Images were encoded using a 128 × 128 sampling over a 25.6 × 25.6 mm2 field of view then zero-filled to 256 × 256 prior to reconstruction, resulting a nominal in-plane resolution of 100 μm in each direction. Inversion and refocusing were achieved with 500 μs duration 90x-180y-90x composite hard pulses, with each refocussing pulse surrounded by a pair of amplitude-modulated spoiler gradients to remove signal from unwanted coherence pathways (19). Phase encoding for all echoes was achieved with one gradient pulse prior to the first echo. An inversion recovery time (TI) equal to 2 s resulted in the effective nulling of cerebrospinal fluid signal, which was necessary to avoid flow-induced ghosts of substantial magnitude in the late echo images. The repetition time (TR) was 6 s and 8 excitations were averaged, resulting in a total acquisition time of approximately 100 min and a mean signal-to-noise ratio (SNR) in the spinal white matter of 217 +/− 21 (first echo magnitude divided by the standard deviation of the background noise, where the standard deviation of the noise, σ, was estimated by the mean of the background signal divided by (π/2)1/2).
Finite Difference (FD) Model
The Bloch-Torrey equations (20) classically describe the diffusion and relaxation of magnetization
| [3] |
where X=M(r,t)/M0 is the mole fraction of water magnetization on the transverse plane, D is the diffusion coefficient, T2 is a relaxation time constant, the magnetization, M, is the volume density of the net magnetic moment on the transverse plane, and M0 is the volume density of the net magnetic moment in the longitudinal direction at thermal equilibrium, which is proportional to the proton density. Using standard approximations to differentiation
| [4] |
and discretizing X in space (by Δx) and time (by Δt), the numerical solution of [3] (in one spatial dimension) can be found explicitly using Euler’s forward approximation at spatial index, j, and temporal index, n+1, by
| [5] |
where cj⃗j+1 is the jump probability from the spatial grid-point j to j+1. The jump probability is
| [6] |
where PB is the compartment boundary permeability of water. If the neighboring grid-point is in the same compartment, the jump probability is simply
| [7] |
where i, e and m designate the tissue compartment (i.e. intracellular, extracellular, or myelin). The MRI signal at a given echo time is given by
| [8] |
where gn is a scaling factor related to coil sensitivity at the nth spinal cord tract. The grid spacing, Δx, is chosen to resolve the simulation geometry. The time step, Δt, is then subject to the constraints
| [9] |
| [10] |
This 1-dimensional case is easily generalizable into multiple dimensions. Note that the 1/2 factor in [9] changes to 1/4 and 1/6 in 2- and 3-dimensions, respectively.
The segmented LM images of each white matter tract were used to define the geometry of the finite difference model. By constraining the geometry, the model was defined by 10 parameters: intrinsic water diffusion coefficient (Di,e,m), transverse relaxation time constant (T2i,e,m), equilibrium magnetization (M0i,e,m), and compartment boundary permeability coefficient of water (PB). For the purposes if this work, water diffusion coefficients of the intra- and extra-axonal compartments were fixed at Di = 2.5 μm2/ms and De = 3.0 μm2/ms (large enough to make in intra- and extra-axonal space well mixed within the T2-timescale). All tissue parameters were defined identically across spinal cord tracts, making the underlying geometry derived from the LM the only source of inter-tract signal variation.
Since each segmented LM image contains more than 100 axons, the LM images were deemed to be representative of axonal characteristics within the tract, and all boundaries of the geometry were made reflective. The finite difference calculations were implemented in C and CUDA, run on a Linux system with two NVIDIA GeForce GTX 295 dual GPU cards, which allowed simulation of transverse relaxation with the Bloch-Torrey equations from all four tracts in ≈ 60 seconds.
Bloch -McConnell (BM) Model
Transverse relaxation was also simulated by calculation of the Bloch-McConnell equations (11) for a three-compartment system. In matrix form,
| [11] |
where
| [12] |
| [13] |
where Mi,e,m is the magnetization within each compartment, and kim, kmi, kem, and kme are first order exchange rate constants between intra-axonal and myelin, and between extra-axonal and myelin compartments. Note that there is no direct exchange term between the intra- and extra-axonal compartments. Like the FD model, the BM model neglects any susceptibility differences between tissue compartments. The general solution for [11] is
| [14] |
where vi,e,m is the compartmental volume fraction assuming hexagonal axon packing, exp is the matrix exponential function, and M0 is the equilibrium magnetization from a uniform volume element. The detectable MRI signal from nth tract is then
| [15] |
where once again gn is related to coil sensitivity. The BM model was implemented in MATLAB (The Mathworks, Natick MA).
Since we are attempting to model the role of exchange in MET2 analysis, we must constrain the exchange rate constants within the spinal cord tracts analyzed. Hence, the exchange rate constants were defined as a function of water compartmental boundary permeability
| [16] |
| [17] |
where the surface area to volume ratio of the inner myelin barrier is
| [18] |
That of the outer myelin barrier is
| [19] |
and 〈ri〉A & 〈ro−ri〉A are taken from equations [1] and [2]. Exchange rate constants between the intra- & extra-axonal compartments and myelin are then
| [20] |
| [21] |
Note that, consistent with the FD model, M0 is defined as a density within a uniform volume, and therefore this notation (Eqns. [11–21]) differs from the standard notation used to describe the BM model, which normally defines M and M0 without assuming specific spatial volumes to which the signal is compartmented. The initial conditions (Eqn. [14]) and the relationship between exchange rates (Eqn. [20–21]) reflect that vxMx is proportional to the amount of signal within the x compartment.
Data Analysis
From each rat MRI image set, regions of interest (ROIs) were manually defined in the four spinal white matter tracts identified previously. To minimize bias due to Rician noise, the mean echo magnitudes were estimated from each ROI by maximum likelihood estimation of the signal magnitude (see eqn. [12] in (21)). These echo magnitudes were then fitted to the sum of 200 decaying exponential functions with time constants spaced logarithmically between 7 and 1000 ms, resulting in an estimated T2 spectrum for each tract and each rat for in-vivo measurements. The fitting was implemented with a non-negative least squares algorithm with the addition of a minimum-curvature regularization (22). In order to compare similarly-smoothed spectra across tracts, the regularization parameter was set to the average of the regularization parameter values determined from preliminary fittings of the in-vivo measurements with regularization adjusted using the generalized cross-validation method (23).
From each in-vivo T2 spectrum, the so-called myelin and other (intra- and extra-axonal) water components were distinguished by the local minimum between the two dominant T2 spectral components, and three metrics were extracted. The MWF from each spectrum was calculated as the fraction of signal within the myelin water peak, the myelin water T2 (MWT2) and other water T2 (OWT2) were calculated as the first moment of their respective T2 peaks. These metrics were tabulated (mean and standard deviation (SD)) across animals for each tract.
Following empirical evaluation of the T2 spectra, the echo magnitudes were then also fitted to the FD and BM models of transverse relaxation. For each animal and model, three T2 time constants (T2i, T2e, T2m, constant across tracts), the scaling factor for each tract (gn) and, for some models, an exchange-related parameter (Dm or PB, also constant across tracts) were fitted by non-linear regression of the observed signal magnitudes to the model predictions for all four tracts simultaneously. The Bloch-McConnell simulations used PB to dictate water exchange. For all simulations the compartmental equilibrium magnetizations were fixed at M0m/M0i = M0m/M0e = 0.5 (24). The finite difference simulation was run for all tracts in one of three conditions: i) no inter-compartmental water exchange, dictated by constraining Dm = 0 μm2/ms and PB = 0 μm/ms (referred to as FD + NE); ii) diffusion-limited exchange, dictated by constraining PB = 1 μm/ms (effectively infinite for the compartment geometries studied) and fitting for Dm (referred to as FD + Dm); iii) permeability-limited exchange, dictated by constraining Dm = 3.0 μm2/ms (large enough to allow rapid mixing of the myelin water for all tracts) and fitting for PB (referred to as FD + PB).
The reduced chi-square statistic (χ2) was computed for each fit as
| [22] |
where S is the observed signal, Ŝ is the modeled signal, σ2 is the noise variance, d is the degrees of freedom (total number of echoes from all four tracts minus the number of fitted parameters), and the sum is taken over the signal from each echo and each spinal cord tract. For each fit, this statistic was tested against a chi-square distribution to assess goodness-of-fit. In order to compare goodness-of-fit between the pth and qth models, an f-statistic was defined as
| [23] |
The qth model was deemed significantly better than the pth model if the values of f from all 5 rats were greater than some cutoff value, fc, such that the joint probability of this statistic was ≤ 0.05. That is,
| [24] |
where fn indicates the f-statistic in Eq [23] evaluated for the nth animal, and Ff(fc) is the cumulative distribution of this statistic at critical value fc.
Results
The segmented images from each tract are shown in Fig. 1 where white, gray and black represent the intra-axonal, extra-axonal, and myelin compartments, respectively. These images served as the basis of the tissue geometry used for the finite difference simulations. The myelin and axon characteristics derived from these images are summarized in Table 1 for each tract. The average myelin thickness and axon radius are presented as the intra-sample mean and standard deviation (SD), while vm, 〈ro−ri〉A, and 〈ri〉A, which are whole-tract measures, are presented without uncertainty, but we note that the inter-sample coefficient of variation within the rat population for histology-derived metrics of our previous study was <≈ 10% (7). It is clear from these data that while vm was relatively constant across tracts, the axon radius and myelin thicknesses varied considerably.
Figure 1.

Segmented light microscopy images from four white matter tracts within the rat spinal cord: Vestibulospinal (VST), Rubrospinal (RST), Funiculus Gracilis (FG), and dorsal corticospinal (dCST). Scale bars = 10 μm, white = intra-axonal space, gray = extra-axonal space, black = myelin.
Table 1.
Quantitative axon tract characteristics derived from segmented light microscopy images. Results are given as mean (±SD, where applicable) within the axon population of the light microscopy images. Myelin volume fraction (vm), mean myelin thickness ( ), mean axon radius (r̄i), area-weighted mean myelin thickness (〈ro−ri〉A), and area-weighted mean axon radius (〈ri〉A).
| Tract | vm | (μm) | r̄i (μm) | 〈ro−ri〉A (μm) | 〈ri〉A (μm) |
|---|---|---|---|---|---|
| VST | 0.54 | 1.25 (0.52) | 1.37 (0.94) | 1.49 | 2.63 |
| RST | 0.55 | 0.84 (0.33) | 0.99 (0.52) | 1.02 | 1.51 |
| FG | 0.54 | 0.59 (0.21) | 0.87 (0.30) | 0.69 | 1.07 |
| dCST | 0.51 | 0.38 (0.14) | 0.56 (0.21) | 0.43 | 0.72 |
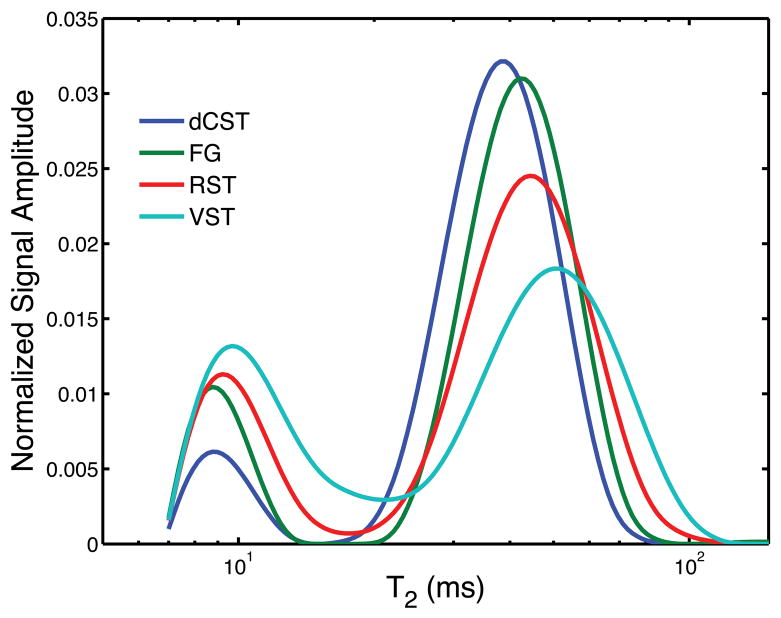
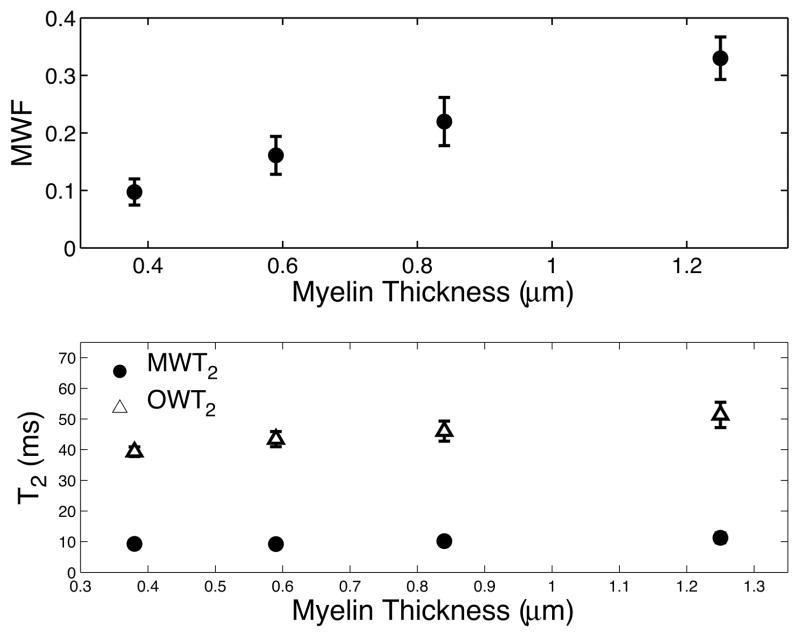
An example T2-weighted image (TE = 7.4 ms) is shown in Fig. 2 cropped to a size just larger than the spinal cord. Example ROIs corresponding to four white matter tracts are overlaid on the image: dCST = blue, FG = green, RST = red, and VST = teal. Fig. 3 shows the T2 spectrum within each tract averaged across all 5 animals, where each color corresponds to a tract as indicated in Fig. 2. In contrast to the roughly constant vm across these regions (Table 1 and (7,13)), the MWF varied from ≈10% to ≈35%. Fig. 4 shows the MWF (top panel), MWT2 (lower panel, blue circles), and OWT2 (lower panel, red triangles) (inter-sample mean ± SD) vs. myelin thickness across tracts. Consistent with our previous study of excised and fixed rat spinal cord (7), the MWF, MWT2, and OWT2 all tended to increase with myelin thickness. As apparent from Table 1, the same trends were present with respect to axon radius and area-weighted axon radius.
Figure 2.
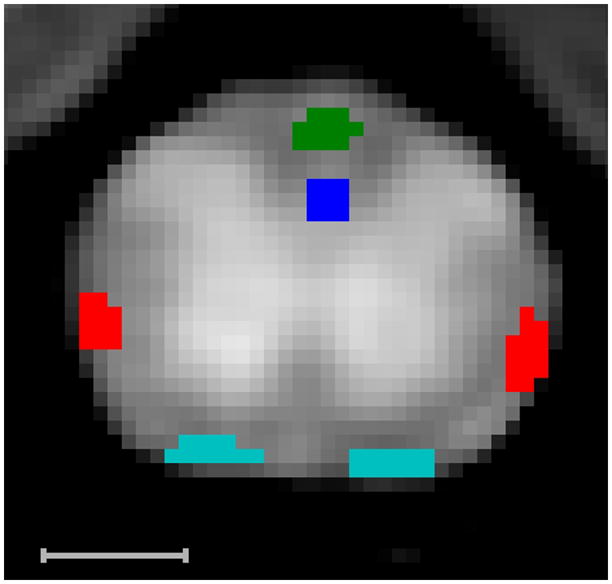
Example T2 weighted image (TR=6 s, TI = 2 s, TE = 7.2 ms) cropped to view the spinal cord. The bright butterfly-shaped region is gray matter, and the surrounding darker region is the white matter in which example ROIs of four tracts are drawn: dCST = blue, FG = green, RST = red, VST = teal. Scale bar = 1 mm.
Figure 3.
Population averaged T2 spectra for the four spinal cord tracts indicated in Figure 2. There are large variations in the fractional area of the short-lived T2 peak (i.e. myelin water).
Figure 4.
MWF as well as myelin water T2 (MWT2) and other water T2 (OWT2) values +/− SD plotted vs. the average myelin thickness within each spinal cord tract. The MWF, OWT2 and MWT2 tend to increase with increasing myelin thickness.
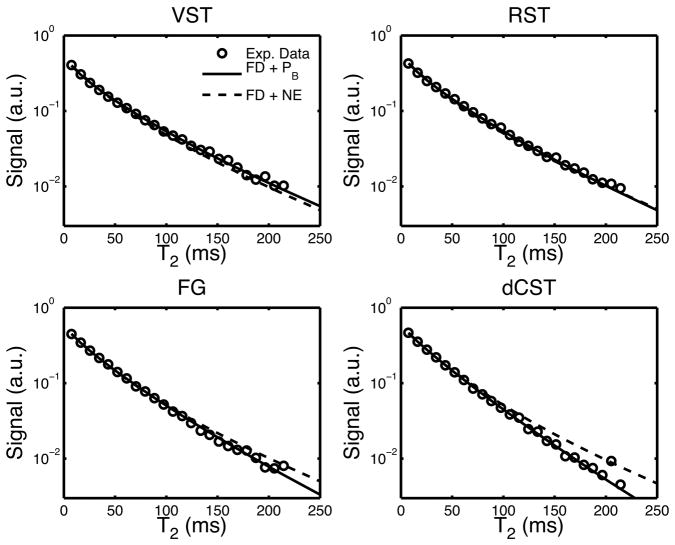
Fitted parameters (inter-sample mean ± SD) from each of the four simulation scenarios are given in Table 2 and two example fits are given in Fig. 5, cropped for ease of view to the first 24 echoes. As expected, all fits to the FD+NE model (no water exchange) failed the chi-square goodness-of-fit test at the 95% confidence level, while all other models exhibited a mix(across animals) of fits above and below the 95% confidence level. Comparing models by joint f-statistic test (described above) demonstrated that the FD models with exchange (FD+Dm and FD+PB) were fitted significantly better than the BM model, which incorporated water exchange but not intra-compartment diffusion or intra-tract variation in axon/myelin dimensions. All of the models predicted a significant difference in T2i and T2e, but there was not a statistical difference in fits between FD-models with T2i < T2e compared with T2i > T2e.
Table 2.
Numerical fitting results and reduced chi-square error (χ2), given as mean (standard deviation) within the animal population. Two of the models (FD + Dm & FD + PB) had two minima, distinguished by the compartment with long- vs. intermediate-lived T2s, that were not statistically differentiable.
| Model | T2i (ms) | T2e (ms) | T2m (ms) | Dm (μm2/ms) | PB (μm/ms) | χ2 |
|---|---|---|---|---|---|---|
| FD + NE | 39.7 (2.4) | 77.9 (4.2) | 20.2 (1.0) | 0.0* | 0.0* | 2.87 (1.25)a |
| FD + Dm | 81.5 (5.6) | 35.5 (4.0) | 10.9 (1.2) | 0.0012 (0.0002) | 1.0* | 1.18 (0.40) |
| 40.7 (3.2) | 102.6 (12.5) | 14.7 (1.5) | 0.0005 (0.0002) | 1.0* | 0.98 (0.25) | |
| FD + PB | 87.6 (7.0) | 34.3 (3.8) | 8.9 (1.5) | 3.0* | 0.0071 (0.0006) | 1.43 (0.52)c |
| 38.2 (3.0) | 127.0 (23.9) | 14.3 (1.8) | 3.0* | 0.0040 (0.0012) | 0.99 (0.28) | |
| BM | 67.2 (5.4) | 43.9 (6.8) | 14.0 (1.2) | n/a | 0.0038 (0.0011) | 1.51 (0.51)b |
Fixed model parameters: M0m/M0e = M0m/M0i = 0.5, for the FD based models De = 3.0 μm2/ms and Di = 2.5 μm2/ms;
indicates additional fixed parameters; significant difference in pair-wise comparisons (joint f-test, P<0.05) of χ2 of
FD + NE vs. all other fits,
BM vs. all FD + exchange model fits, and
FD + PB (T2i>T2e) vs. FD + Dm (T2i<T2e).
Figure 5.
Raw signal decay (circles) and two example fits: the finite difference model with exchange mediated by membrane permeability (FD + PB, line), and a finite difference model with no exchange (FD + NE, dashed line). The plot was cropped to the first 24 echoes to magnify the difference in fit between the two models. Fitted parameters are given in Table 2.
Discussion
A recent study of water proton transverse relaxation in excised and chemically fixed rat spinal cord revealed a substantial variation in T2 spectra between different white matter tracts with similar myelin content (7). By comparing observed T2 spectra with histology, it was inferred by the authors that the variation in T2 spectra was mediated by varying effects of water exchange between myelin and both axonal and extra-axonal spaces. It was further postulated that a similar effect could be expected in-vivo. Thus, the primary observation of this follow-up work is a similar variation between white matter tracts of T2 spectral characteristics measured in-vivo. Indeed, Fig. 3, which shows the population-average in-vivo T2 spectra from four spinal WM tracts, and Fig. 4, which shows MWF, MWT2 and OWT2 vs. mean myelin thickness, compare well qualitatively with a similar figures (cf 4 and 5, (7)) from excised spinal cord. As in the previous study, tracts with smaller axons and thinner myelin showed T2 spectra shifted with peaks at lower apparent T2s and with a smaller MWF, which is consistent with a greater effect of inter-compartmental water exchange on transverse relaxation. Quantitatively, the effect was even greater in the present study, with MWF as low as ≈0.10 in the dCST, compared to 0.19 in the dCST of excised spinal cord. The natural conclusion is that water exchange plays an even greater role in transverse relaxation in-vivo than in the previous study, which consequently indicates that the lower temperature of the ex-vivo work (≈18°C) reduced water exchange to a greater extent than it was increased by chemical fixation (25).
The relationship between these observations and the role of inter-compartmental water exchange in the transverse relaxation of water in cerebral white matter remains unclear. A previous study in human corpus callosum, which contains axons with sizes similar to the dCST (26), reported MWFs between 10–13% (6). While similar with the average MWF measured within the dCST in this work, ~10%, the corpus callosum is also thought to have lower myelin content than the spinal cord (27,28). Therefore, exchange properties of myelin water may be different within the brain. Future studies are being planned to explore the effects water exchange in cerebral white matter.
Computational Modeling
Given the known micro-anatomies of spinal WM tracts, computational models were employed in an attempt to quantitatively account for the T2 variations with a physically realistic model of water diffusion and transverse relaxation. Two-dimensional models of WM micro-anatomy were built using a representative set of light microscopy images for each tract. Fig. 5 and Table 2 indicate that if intrinsic T2 and diffusion characteristics for each tissue compartment are constant across tracts, a model without exchange does not predict the observed variations in T2 across tracts. This is not surprising given the large variation of MWF observed across tracts in comparison to the relatively small variation in vm. However, if water exchange is incorporated into the model, mediated either through a finite diffusion coefficient in the myelin compartment (FD+Dm model) or by defining a finite permeability at each compartment boundary (FD+PB and BM models), reasonable model parameters can be found that predict the observed T2 variation. The myelin water lifetimes, τm = 1/kmi + 1/kme,varied significantly between the tracks investigated in this work. Calculated based upon the mean PB fit in Table 2 and area-weighted axon and myelin dimensions given in Table 1 with hexagonal packing, the myelin water lifetimes are 43, 69, 100, and 150 ms for the dCST, FG, RST, and VST, respectively.
The BM model, like the FD+PB model, assumes boundary-mediated water exchange, but did not fit the data as well as the FD+PB model, indicating that the intra-tract tissue heterogeneity accounted for in the FD models (but not the BM model) is a significant factor in the observed transverse relaxation. In comparing the FD+Dm and FD+PB models, the lack of a significant difference in fits dictates that this study cannot distinguish whether water exchange in spinal white matter is mediated at the boundary of myelin or by the rate of water diffusion within the myelin. However, experiments in peripheral nerve, which has thicker myelin, may be more sensitive to this type of comparison. The permeability of water through a myelin boundary estimated from both the FD+PB and BM fitting, PB ≈ 0.004 – 0.007 μm/ms, is consistent with plasma membrane permeabilities estimated in previous studies, and is within the range believed to physiological relevant (29–32).
Myelin Water Diffusion
The value of Dm estimated in this work is more than three orders of magnitude smaller than the diffusion coefficient of water at body temperature (33), and two orders of magnitude smaller than the apparent diffusion coefficient (ADC) of myelin water previously estimated perpendicular to the axon orientation (34). However, this previously measured ADC originates from a combination of water diffusing in normal and tangential directions to membrane layers in myelin. In a circular axon, the myelin water ADC measured with low b-value can be shown equal the arithmetic mean of the water ADCs in the normal and tangential directions. In this work, Dm is the myelin water ADC normal to the myelin membranes, since it is in the normal direction that water must diffuse to enter or leave the myelin compartment. The value of Dm estimated in this work (0.005–0.0012 μm2/ms) corresponds reasonably with the diffusion coefficient of water measured through stacks of synthetic lipid bilayer near body temperature, ≈ 0.0017 μm2/ms (35).
Given Dm, it is possible to estimate the permeability of the lipid bilayers constituting the myelin. Extending the formula given of Tanner (36) used to calculate the effective diffusion coefficient across permeable barriers to one that accounts for a finite barrier thickness (35), one gets
| [25] |
where PL is the permeability coefficient of water across the lipid bilayer, a is the spacing between the membranes, and L is the thickness of the bilayer. With Dm = 0.0009 μm2/ms (the mean of the two Dm values estimated in this work), the permeability of the individual lipid bilayers constituting myelin would be between 0.006 – 0.044 μm/ms, depending upon the value of the average membrane thickness and membrane spacing used in the calculation (37). This is within this range of membrane permeability believed to be physiologically relevant for a cellular lipid bilayer (29–32).
Three T2 Components
All of the models predict a difference between the T2 of the intra- and extra-axonal spaces. Within these models, no minima were found near T2i ≈ T2e. The compartmental T2 values estimated within these models correspond well with the three T2 components observed in peripheral nerve (38), where axons are much larger and myelin is much thicker thereby allowing for less water exchange between compartments. The observed short-, intermediate- and long-lived T2 components within peripheral nerve are thought to originate from water within myelin, extra-, and intra-axonal space, respectively (39–41). A few studies have even hypothesized a difference in the T2 of intracellular and extracellular space in gray matter (32,42). There is no direct evidence for a difference in the intra- and extra-axonal T2 in white matter. Still, intrinsic differences in the compartmental T2 may be present within white matter, since exchange and/or inadequate SNR could make these peaks indistinguishable under MET2 analysis. When using the generalized cross-validation approach utilized in this work for regularization of T2 spectra, simulations (not shown) indicated that a SNR of greater than 2000 would be required to distinguish the 3 components predicted by the finite difference model.
Conclusion
This study reports a variation of the MWF measured in-vivo between rat spinal cord tracts with a similar underlying myelin content. Further, numerical simulation suggests that exchange between underlying tissue compartments, mediated by a difference in the axon size and myelin thickness, plays a role in determining white matter T2 characteristics and, in particular, the MWF. Within the model used, both exchange and anatomical heterogeneity was necessary to account for the variation of the observed MWF between white matter tracts in the rat spinal cord.
Acknowledgments
This work was supported by NIH grant EB001744, NSF career award 0448915, and by NCRR instrument grant 1S10 RR17799.
References
- 1.Menon RS, Rusinko MS, Allen PS. Proton relaxation studies of water compartmentalization in a model neurological system. Magn Reson Med. 1992;28(2):264–274. doi: 10.1002/mrm.1910280208. [DOI] [PubMed] [Google Scholar]
- 2.MacKay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magn Reson Med. 1994;31(6):673–677. doi: 10.1002/mrm.1910310614. [DOI] [PubMed] [Google Scholar]
- 3.Stewart WA, MacKay AL, Whittall KP, Moore GR, Paty DW. Spin-spin relaxation in experimental allergic encephalomyelitis. Analysis of CPMG data using a non-linear least squares method and linear inverse theory. Magn Reson Med. 1993;29(6):767–775. doi: 10.1002/mrm.1910290608. [DOI] [PubMed] [Google Scholar]
- 4.Does MD, Snyder RE. Multiexponential T2 relaxation in degenerating peripheral nerve. Magn Reson Med. 1996;35(2):207–213. doi: 10.1002/mrm.1910350212. [DOI] [PubMed] [Google Scholar]
- 5.Laule C, Vavasour IM, Paty D, Li D, Arnold D, MacKay A. Correlation between magnetization transfer and myelin water content in normal white matter and MS lesions. Honolulu, HI: 2002. p. 182. [Google Scholar]
- 6.Whittall KP, MacKay AL, Graeb DA, Nugent RA, Li DK, Paty DW. In vivo measurement of T2 distributions and water contents in normal human brain. Magn Reson Med. 1997;37(1):34–43. doi: 10.1002/mrm.1910370107. [DOI] [PubMed] [Google Scholar]
- 7.Dula AN, Gotchberg DF, Valentine HL, Valentine WM, Does MD. Multi-Exponential T2, Magnetization Transfer and Quantitative Histology in White Matter Tracts of Rat Spinal Cord. Magn Reson Med. 2010;63(4):902–909. doi: 10.1002/mrm.22267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Levesque IR, Pike GB. Characterizing healthy and diseased white matter using quantitative magnetization transfer and multicomponent T(2) relaxometry: A unified view via a four-pool model. Magn Reson Med. 2009;62(6):1487–1496. doi: 10.1002/mrm.22131. [DOI] [PubMed] [Google Scholar]
- 9.Stanisz GJ, Kecojevic A, Bronskill MJ, Henkelman RM. Characterizing white matter with magnetization transfer and T(2) Magn Reson Med. 1999;42(6):1128–1136. doi: 10.1002/(sici)1522-2594(199912)42:6<1128::aid-mrm18>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- 10.Zimmerman JR, Brittin WE. Nuclear Magnetic Resonance Studies in Multiple Phase Systems: Lifetime of a Water Molecule in an Adsorbing Phase on Silica Gel. The Journal of Physical Chemistry. 1957;61(10):1328–1333. [Google Scholar]
- 11.McConnell HM. Reaction Rates by Nuclear Magnetic Resonance. The Journal of Chemical Physics. 1958;28(3):430–431. [Google Scholar]
- 12.Szafer A, Zhong J, Gore JC. Theoretical Model for Water Diffusion in Tissues. Magnetic Resonance in Medicine. 1995;33(5):697–712. doi: 10.1002/mrm.1910330516. [DOI] [PubMed] [Google Scholar]
- 13.Chin C-L, Wehrli FW, Fan Y, Hwang SN, Schwartz ED, Nissanov J, Hackney DB. Assessment of axonal fiber tract architecture in excised rat spinal cord by localized NMR q-space imaging: Simulations and experimental studies. Magnetic Resonance in Medicine. 2004;52(4):733–740. doi: 10.1002/mrm.20223. [DOI] [PubMed] [Google Scholar]
- 14.Harkins KD, Galons JP, Secomb TW, Trouard TP. Assessment of the effects of cellular tissue properties on ADC measurements by numerical simulation of water diffusion. Magn Reson Med. 2009;62(6):1414–1422. doi: 10.1002/mrm.22155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tang Y, Nyengaard JR. A stereological method for estimating the total length and size of myelin fibers in human brain white matter. J Neurosci Methods. 1997;73(2):193–200. doi: 10.1016/s0165-0270(97)02228-0. [DOI] [PubMed] [Google Scholar]
- 16.Denef JF, Cordier AC, Mesquita M, Haumont S. The influence of fixation procedure, embedding medium and section thickness on morphometric data in thyroid gland. Histochemistry. 1979;63(2):163–171. doi: 10.1007/BF00644538. [DOI] [PubMed] [Google Scholar]
- 17.Dula AN, Gochberg DF, Does MD. Optimal echo spacing for multi-echo imaging measurements of Bi-exponential T2 relaxation. J Magn Reson. 2009;196(2):149–156. doi: 10.1016/j.jmr.2008.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Skinner MG, Kolind SH, MacKay AL. The effect of varying echo spacing within a multiecho acquisition: better characterization of long T2 components. Magn Reson Imaging. 2007;25(6):840–847. doi: 10.1016/j.mri.2006.09.046. [DOI] [PubMed] [Google Scholar]
- 19.Poon CS, Henkelman RM. Practical T2 quantitation for clinical applications. J Magn Reson Imaging. 1992;2(5):541–553. doi: 10.1002/jmri.1880020512. [DOI] [PubMed] [Google Scholar]
- 20.Torrey HC. Bloch Equations with Diffusion Terms. Physical Review. 1956;104(3):563. [Google Scholar]
- 21.Bonny JM, Renou JP, Zanca M. Optimal Measurement of Magnitude and Phase from MR Data. J Magn Reson B. 1996;113(2):136–144. doi: 10.1006/jmrb.1996.0166. [DOI] [PubMed] [Google Scholar]
- 22.Whittall KP, Mackay AL. Quantitative Interpretation of Nmr Relaxation Data. Journal of Magnetic Resonance. 1989;84(1):134–152. [Google Scholar]
- 23.Golub GH, Heath M, Wahba G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter. Technometrics. 1979;21(2):215–223. [Google Scholar]
- 24.Knaap MSvd, Valk J. Magnetic Resonance of Myelination and Myelin Disorders. Berlin, New York: Springer; 2005. p. 1084. [Google Scholar]
- 25.Shepherd TM, Thelwall PE, Stanisz GJ, Blackband SJ. Aldehyde fixative solutions alter the water relaxation and diffusion properties of nervous tissue. Magn Reson Med. 2009;62(1):26–34. doi: 10.1002/mrm.21977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Aboitiz F, Scheibel AB, Fisher RS, Zaidel E. Fiber composition of the human corpus callosum. Brain Res. 1992;598(1–2):143–153. doi: 10.1016/0006-8993(92)90178-c. [DOI] [PubMed] [Google Scholar]
- 27.Laule C, Vavasour IM, Moore GR, Oger J, Li DK, Paty DW, MacKay AL. Water content and myelin water fraction in multiple sclerosis. A T2 relaxation study. J Neurol. 2004;251(3):284–293. doi: 10.1007/s00415-004-0306-6. [DOI] [PubMed] [Google Scholar]
- 28.Jito J, Nakasu S, Ito R, Fukami T, Morikawa S, Inubushi T. Maturational changes in diffusion anisotropy in the rat corpus callosum: comparison with quantitative histological evaluation. J Magn Reson Imaging. 2008;28(4):847–854. doi: 10.1002/jmri.21496. [DOI] [PubMed] [Google Scholar]
- 29.Finkelstein A. Water Movement Through Lipid Bilayers, Pores, and Plasma Membranes: Theory and Reality. John Wiley & Sons Inc; 1987. [Google Scholar]
- 30.Latour LL, Svoboda K, Mitra PP, Sotak CH. Time-Dependent Diffusion of Water in a Biological Model System. Proceedings of the National Academy of Sciences of the United States of America. 1994;91(4):1229–1233. doi: 10.1073/pnas.91.4.1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Stanisz GJ, Wright GA, Henkelman RM, Szafer A. An analytical model of restricted diffusion in bovine optic nerve. Magnetic Resonance in Medicine. 1997;37(1):103–111. doi: 10.1002/mrm.1910370115. [DOI] [PubMed] [Google Scholar]
- 32.Vestergaard-Poulsen P, Hansen B, Østergaard L, Jakobsen R. Microstructural changes in ischemic cortical gray matter predicted by a model of diffusion-weighted MRI. Journal of Magnetic Resonance Imaging. 2007;26(3):529–540. doi: 10.1002/jmri.21030. [DOI] [PubMed] [Google Scholar]
- 33.Mills R. Self-diffusion in normal and heavy water in the range 1–45. deg J Phys Chem. 1973;77(5):685–688. [Google Scholar]
- 34.Andrews TJ, Osborne MT, Does MD. Diffusion of myelin water. Magn Reson Med. 2006;56(2):381–385. doi: 10.1002/mrm.20945. [DOI] [PubMed] [Google Scholar]
- 35.Khakimova AM, Rudakova MA, Doroginitskii MM, Filippov AV. An NMR study of the temperature dependence of the coefficient of water self-diffusion through lipid bilayer membranes. Biofizika. 2008;53(2):271–280. [PubMed] [Google Scholar]
- 36.Tanner JE. Transient Diffusion in a System Partitioned by Permeable Barriers -Application to Nmr Measurements with a Pulsed Field Gradient. Journal of Chemical Physics. 1978;69(4):1748–1754. [Google Scholar]
- 37.Lazzarini RA. Myelin Biology and Disorders. Academic Press; 2004. [Google Scholar]
- 38.Vasilescu V, Katona E, Simplaceanu V, Demco D. Water compartments in the myelinated nerve. III. Pulsed NMR results. Experientia. 1978;34(11):1443–1444. doi: 10.1007/BF01932339. [DOI] [PubMed] [Google Scholar]
- 39.Peled S, Cory DG, Raymond SA, Kirschner DA, Jolesz FA. Water diffusion, T(2), and compartmentation in frog sciatic nerve. Magn Reson Med. 1999;42(5):911–918. doi: 10.1002/(sici)1522-2594(199911)42:5<911::aid-mrm11>3.0.co;2-j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wachowicz K, Snyder RE. Assignment of the T(2) components of amphibian peripheral nerve to their microanatomical compartments. Magn Reson Med. 2002;47(2):239–245. doi: 10.1002/mrm.10053. [DOI] [PubMed] [Google Scholar]
- 41.Dortch RD, Apker GA, Valentine WM, Lai B, Does MD. Compartment-specific enhancement of white matter and nerve ex vivo using chromium. Magnetic Resonance in Medicine in early view. doi: 10.1002/mrm.22460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Buckley DL, Bui JD, Phillips MI, Zelles T, Inglis BA, Plant HD, Blackband SJ. The effect of ouabain on water diffusion in the rat hippocampal slice measured by high resolution NMR imaging. Magnetic Resonance in Medicine. 1999;41(1):137–142. doi: 10.1002/(sici)1522-2594(199901)41:1<137::aid-mrm19>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]