Revisiting United States Valuation of EQ-5D States

Abstract

In the original US valuation study of EQ-5D states, all worse-than-dead time trade-off responses (26% of the sample) were divided by 39 to increase the QALY estimates. This transformation has no theoretical justification and motivates this re-examination. Using the publically available dataset, we compared three alternative random utility models: instant (IRUM), angular (ARUM), and episodic (ERUM) models. Each leads to a distinct econometric estimator: mean ratio, ratio of means, and coefficient, respectively. IRUM suggests that 203 of the 243 EQ-5D states are worse-than-dead, which has little face validity compared to ARUM and ERUM (42 and 3 WTD states). ARUM and ERUM estimates are proportionally related such that losses in QALYs are approximately 37% larger under ARUM than ERUM. Compared to ERUM, economic evaluations using ARUM estimates emphasize quality of life, and this difference may influence policy decisions. Either ERUM or ARUM values sets are recommended over the original, transformed set.

Survival may be the most fundamental health outcome in economics, epidemiology and comparative effectiveness research; nevertheless, it is far from a sufficient measure of health. An array of patient-report outcomes (PRO) instruments, such as the EQ-5D, have been developed as measures of health-related quality of life (HRQoL). PRO evidence complements evidence on mortality and longevity by capturing the experiences of the living. For decades, health economists have struggled to summarize quality and quantity of life evidence into a unitary measure of health utility to guide medical decision-making and public policy. As a summary unit of health utility, a quality-adjusted life year (QALY; i.e., 1 year of life in optimal health) combines quality and quantity of life evidence, improving upon survival measures. While it has its limitations (e.g., constant proportionality assumption), it has served as the primary benchmark in cost-utility analysis since their inception. The primary purpose of a health valuation study is to estimate decrements in quality of life, as described by PRO instruments, on a QALY scale (e.g., 2 years in poor health equals 1 QALY). In this paper, we re-examine health utility estimates for EQ-5D decrements using data from a US valuation study.

In 2002, the seminal Measurement and Valuation of Health (MVH) study conducted in the United Kingdom (UK) by Williams and colleagues (Williams 1995) was replicated in the United States (US) by Coons and colleagues (Coons, Johnson et al. 2005; Shaw, Johnson et al. 2005b). Both massive studies marked a scientific milestone, integrating state-of-the-art technology with a large, logistic effort and making the outcomes easily accessible for end users. While the methods for conducting the interview survey and collecting the time trade-off (TTO) responses still remain modern up until this day, we put forth that the estimation methods need to be revisited. Prior to the original analysis, all worse-than-dead (WTD) TTO responses (26% of the sample) were divided by 39 to increase QALY estimates. This arbitrary transformation of the lower quartile motivates this re-examination of US EQ-5D values.

During the advent of the trade-off techniques, Torrence and colleagues transformed TTO responses into ratios (i.e., dividing years in optimal health by years in non-optimal health; y_i/x_i) (Torrance, Thomas et al. 1972; Torrance 1976). Even then, it was well-known that ratios can behave badly, particularly as the denominator, x_i, approaches zero (Drummond 2005). In the US study, TTO ratios ranged from −39 to 1, and 26% of the TTO ratios were negative. At the time of the analysis, Torrance had already suggested that the negative values be bounded at −1. Shaw and colleagues followed this advice and divided all negative ratios by 39, changing the lower quartile of the sample and increasing all mean ratio estimates above negative 1. This linear data transformation was considered novel at the time and was clearly described in their paper. To justify the transformation, the authors wrote that “values for WTD states are conventionally transformed so as to be bounded by 0 and −1” and that they selected a “linear transformation due to its greater consistency with expected utility theory.” As stated in subsequent publications, division of responses by 39 is arbitrary and seems to contradict utility theory (Charro, Busschbach et al. 2005; Lamers 2007; Craig and Busschbach 2009; Craig, Busschbach et al. 2009). This shortcoming brings into question the scientific credibility of existing cost-utility analyses based on the original US EQ-5D values.

The primary purpose of this paper is to address the shortcomings in the original estimates and provide possible alternative US value sets for the 243 EQ-5D health states. Using the unaltered TTO responses, the values are re-estimated under three alternative random utility models: the instant, episodic, and angular random utility models (IRUM, ERUM, and ARUM) (Craig and Busschbach 2009; Craig and Oppe 2009). These alternative models and their econometric specifications (mean ratio, coefficient, and ratio of means, respectively) have been previously introduced and exemplified using UK TTO responses; however, this is the first head-to-head comparison. The original data of US data are publically available from the granting institution (Coons, Johnson et al. 2005) and we provide the Stata code online (StataCorp 2008) (plus url for data and stata code). Therefore, all results shown in this paper can be independently replicated to aid in the discussion of comparative modeling and estimator transparency in health valuation. Furthermore, we illustrate the implications of the original and revised predictions by plotting the association between respondent age and their QALY predictions.

METHODS

The original US valuation study applied a multi-stage probability sampling design with over-sampling of Hispanics and Black adults. A complete description of this nationally representative interview survey can be found elsewhere (Coons, Johnson et al. 2005; Shaw, Johnson et al. 2005b). Five respondents with no TTO responses were excluded from this analysis (N=4,043).

Health Valuation and TTO

During the interview, each respondent rated 1 randomly assigned set of 14 out of 43 EQ-5D health states, including full health (Shaw, Johnson et al. 2005b). Respondents began by ranking the 14 scenarios from best to worst. Each scenario described a 10-year episode in 1 of 14 different EQ-5D health states, plus the scenario of “immediate death.” After ranking was completed, respondents were asked to locate each scenario on the EQ-VAS, a visual analogue scale bounded by 0 (worst imaginable heath state) and 100 (best imaginable health state). Subsequent to the VAS task, the 13 non-optimal EQ-5D states were valued using the same TTO props as used in the original UK MVH study. Optimal health and “immediate death” were excluded from the TTO task, because their values anchor the QALY scale.

For each of the 13 non-optimal states in the TTO task, the respondent was asked whether 10 years in the non-optimal state was better than or worse than “immediate death.” If better than dead (BTD), the respondent was offered 5 years in optimal health (y = 5), which was increased or decreased until the respondent was indifferent between the optimal scenario and 10 years in a non-optimal state (x = 10).

In Figure 1, the x-axis represents the years in non-optimal health and the y-axis represents years in optimal health, such that the respondent is indifferent. The upper half of Figure 1 illustrates the potential BTD responses. For all states regarded as BTD, the x-values are fixed at 10 years by design. For example, a respondent might give a BTD response: 8 years in optimal health is equal to 10 years in non-optimal health, which yields the point labeled A in Figure 1, located at (10,8). Thus, all BTD responses fall on the vertical dotted line.

Figure 1.

Time Trade-off Responses

The bars illustrate the frequency of the TTO responses for unconscious. Each response represents a unique slope reflecting health utility on a QALY scale.

A: The TTO response that 8 years in optimal health equals 10 years in non-optimal health implies that 1 year in the non-optimal health equals 0.8 QALYs (8/10).

B: The TTO response that 9.75 years in optimal health followed by 0.25 years in non-optimal health equals immediate death implies that 0.25 years in non-optimal health equals −9.75 QALYs or that 1 year equals −39 QALYs (−9.75/0.25).

If the respondent considered 10 years in non-optimal health to be worse than “immediate death,” the worse-than-dead (WTD) response would lie below the x-axis. For example, respondents may consider a scenario of 3 months in severe pain followed by 9.75 years in optimal health to be equal to “immediate death.” In this case, 9.75 years in optimal health exactly compensates the burden of 3 months in severe pain, yielding the point labeled B in Figure 1, located at (0.25,−9.75). Thus, all WTD TTO responses fall on the skewed dotted line.

In 1972, Torrance was one of the first to describe TTO responses (x, y) as ratios, y/x (Torrance, Thomas et al. 1972; Torrance 1976). The arrow from the origin (0, 0) to the response (8, 10) in Figure 1 has a slope of 0.8 or 8/10. For every TTO response, there is a unique TTO ratio (or slope), and vice versa. TTO responses also have a one-to-one correspondence with angles, θ_i = arctan(y_i/x_i) and with years in optimal health, y (i.e., QALYs). The ratios or angles represent the marginal utility with respect to time in a health state, and years in optimal health reflect the utility of an episode of time in a health states. The primary difference between the 3 random utility models is whether error is placed on the TTO ratio, y/x; TTO angle, arctan(y/x); or QALYs, y.

Three alternative estimators and their theoretical bases

The purpose of a health state valuation study is to estimate health state values, β_h, on a QALY scale. Under all three alternative random utility models, change in utility with respect to time is assumed to be invariant with time (i.e., QALY = β_h*year). This is known as the constant proportionality assumption (CP-TTO) and is commonplace in economic evaluations of health outcomes (Doctor and Miyamoto 2003). Craig and Busschbach introduced the instant random utility model (IRUM) as a theoretical interpretation of the mean ratio estimator of health state values (Craig and Busschbach 2009). Under IRUM, a health state value, β_h, depends on additive individual (i) variability: β_h,i = β_h + ε_i. Therefore, QALY_i = (β_h + ε_i)*years, and QALY_i/years = β_h + ε_i. Using the TTO responses (y, x), the econometric specification is y_i/x_i = β_h + ε_i. When estimating β_h over individuals, Torrence suggested to first calculate the individual TTO ratios (β_h,i) and, then, take the average of these ratios: ${\widehat{\beta }}_h=\frac{1}{N}\sum y_i∕x_i$ (Torrance 1976).

When years in non-optimal health, x_i, vary, TTO ratios may become very large. Under the MVH protocol for BTD TTO responses, x_i was constrained to 10 years, and y_i varies from 0 to 10 years. Therefore, BTD TTO ratios ranged from 0 to 1. For WTD TTO responses, x_i varies from 3 months to 10 years, causing instability in the TTO ratio, which range from −39 to 0. For instance, a respondent may make an error of 6 months (0.5 year) in a WTD response. A downward error of y = −0.5 to y = −1.0 would cause a relatively minor change, from −0.5/9.5 = −0.053 to −1/9 = −0.11, in the WTD TTO ratio; however, a same error of −7.5 to −8 changes the ratio from −3 to −4. In this latter case, the error leads to a loss of 1 QALY, equivalent to a year in optimal health. Small response errors, therefore, can produce large deviations in a WTD TTO ratio.

Furthermore, large negative ratios have a disproportionate influence on the mean values. For instance, one ratio of −39 plus 39 responses near optimal health equates to 40 responses of “immediate death.” Extreme ratios and their interpretation have been a topic of a heated debate and ad hoc solutions since TTO introduction (Patrick, Starks et al. 1994; Charro, Busschbach et al. 2005).

Likewise, criticism of ratio statistics as the primary measure for the statistic of central tendency has been previously noted and cautioned against in economic evaluations. In their prominent text, Drummond and colleagues recommend against the use of ratio statistics in the estimation of incremental cost-effectiveness ratios (ICERs) (Drummond 2005). If effectiveness is zero (e.g., some cost, no effects) for any patient in the ICER calculation, the ICER ratio statistic becomes infinite. The results for these infinitely cost-ineffective patients dominate the cost effectiveness of all other patients. Instead of using the mean of the individual ICER ratios, the conventional ICER estimator is mean cost divided by mean effectiveness, which is identical to the angular estimator put forth by Craig and Oppe (Stinnett and Paltiel 1997; Cook and Heyse 2000; Drummond 2005).

Recognizing the limitations of ratios and ratio statistics, Craig and Oppe introduced a directional interpretation of TTO responses (Craig and Oppe 2009). Each ratio, y_i/x_i, is also an angle, θ_i = arctan(y_i/x_i), and angles are better behaved that ratios. When x approaches zero and the WTD TTO ratio goes to negative infinity, the angle approaches −90 degrees. Individual variability may be expressed according to additive angular error, arctan(QALY_i/years) = arctan(β_h) + ε_i. This angular random utility model (ARUM) is nearly identical to the IRUM except for a change in error specification, arctan(y_i/x_i) = arctan(β_h) + ε_i, and may be estimated by minimizing circular variance, a directional loss function analogous to ordinary least squares. When the radius is incorporated into the estimator as a sampling weight, the estimator favors larger trade-offs over smaller trade-offs. Craig and Oppe showed that the tangent of a radially weighted mean angle is the ratio of two means, ${\widehat{\beta }}_h=\sum y_i∕\sum x_i$. Unlike the mean of a ratio, a ratio of means is robust to small x_i. Extreme negative ratios still influence this angular estimator, but extreme values are only possible when there is a large consensus among responders (i.e., a low variance between responders) that the health state has an extreme negative value. Individual extreme responses (outliers) have limited influence on the ratio of means.

As an alternative to IRUM and ARUM, Craig and Busschbach put forth a third random utility model based on a probit model (Craig and Busschbach 2009). The episodic random utility model (ERUM) is nearly identical to that of Torrence and colleagues (Torrance, Thomas et al. 1972; Craig and Busschbach 2009), but avoids the use of ratio statistics by placing an additive error on the utility of an episode (QALY_i = β_h*years + ε_i), not on the marginal utility, β_h. The econometric specification, y_i = β_h*x_i + ε_i, may be estimated using ordinary least squares, and the health state value estimator, ${\widehat{\beta }}_h=\sum x_i{y}_i∕\sum {x_i}^2$, is a coefficient, similar to a ratio of means. Coefficients are robust to individual-level variability in x_i, because small x values near the origin have limited influences on the mean of x².

In comparison, the three alternative estimators for β_h are special cases of a weighted mean ratio, $\frac{1}{N}\sum w_i(y_i∕x_i)$, For a mean ratio (IRUM), $\frac{1}{N}\sum y_i∕x_i$ the weight, w_i, is 1. For a ratio of means (ARUM), $\Sigma y_i∕\Sigma x_i$, the weight, w_i, is x_i/x̄. For a coefficient (ERUM), $\Sigma x_i{y}_i∕\Sigma {x_i}^2$, the weight, w_i, is x_i²/x². If x_i is constant, the three weights are identical and the estimators produce the same health state values (e.g., the absence of WTD TTO responses). If x_i varies, the 3 estimators are ordered by construction (mean ratio < ratio of means < coefficient).

Arbitrary Replacement of WTD Responses

The original motivation to bound TTO ratios at −1 may have been an initial reaction to the mean ratio estimates. The disproportionate influence of low responses and the extreme variances of mean ratios led the investigators of the original UK MVH study to replace WTD TTO ratios, y_i/x_i, with the years in optimal health divided by 10, y_i/10 (Dolan 1997). In the US analysis, Shaw and colleagues, instead, changed the WTD ratios by dividing them by the absolute value of the largest possible ratio, 39 (Shaw, Johnson et al. 2005b). Both replacement methods inherently produce more robust estimates by limiting the range of the adjusted dependent variable to −1.

These replacement methods are arbitrary in three aspects: Firstly, the boundary of −1 has no justification other than being a mirror image of the top boundary of +1 (Patrick, Starks et al. 1994; Craig and Busschbach 2009). Secondly, the functional form of the transformation, linear in the US and convex in the UK, is not justified and not clearly superior to any other possible form. Thirdly, by transforming the scale below zero, but not the scale above zero, the units of the full scale are no longer the same above and below zero, which complicates interpretation and casts doubt on whether BTD and WTD responses can be combined under IRUM.

Multi-attribute Utility Model and the EQ-5D Descriptive System

The EQ-5D is a descriptive system of health states that includes five domains (mobility, self-care, usual activities, pain/discomfort, and anxiety/depression). Each domain can take one of three levels (no problems, some problems, or extreme problems), rendering 243 or 3⁵ possible health states. A vector of these five scores may be used as shorthand in identifying specific health states. For instance, a health state with some problems in walking, no problems with self-care, no problems with performing usual activities, moderate pain, and moderate anxiety is abbreviated to 21122.

Health valuation studies typically elicit direct values for a subset of health states and predict the values of out-of-sample states through extrapolation based on a multi-attribute utility (MAU) model, β_h = δZ_h, where Z_h is a vector of variables characterizing the attribute levels for state h, and δ is a vector of coefficients. By estimating δ, the values of all 242 non-optimal EQ-5D states can be predicted on the QALY scale.

The MAU model is a regression without a constant term composed of 11 indicator variables, Z_h: five for the second-level domains, five for the third-level domains, and one for unconscious. Shaw and colleagues excluded the indicator for unconscious and introduced four additional variables due to their statistical significance (D1, I2-squared, I3, and I3 squared) (Shaw, Johnson et al. 2005b). To facilitate interpretation, the coefficients, δ, are shown in terms of decrements from optimal health (1.00) on a QALY scale. For each coefficient, 95% confidence intervals were estimated using the percentile bootstrap method with replacement resampling of respondent clusters (Efron and Tibshirani 1993). The statistical analyses were conducted using Stata MP 10.1 (StataCorp 2008) and code is available online.

Sample Selection and Weights

Studies of US societal preferences face the added challenge of attempting to represent its diverse and wide-spread citizenry. The Healthcare Research and Quality Act of 1999 “designated priority populations that have been underserved by the US health care system, or are noteworthy for their unique health care needs, specifically racial and ethnic minorities, women, children, elderly, residents of rural areas, low income groups, and individuals with special needs” (US Congress 1999). The US valuation study was sponsored by the Agency for Healthcare Research and Quality (AHRQ) and, in concordance with the institution’s mission, the survey over-sampled Hispanic and Black, non-Hispanic adults (Coons, Johnson et al. 2005).

To better represent the US, the original valuation study incorporated sampling weights, which adjusted for the oversampling of minorities. However, these weights do not account for possible sampling disparities related to age, socioeconomics, or rural residency (Shaw, Iannacchione et al. 2005a). Differences between the observable sample characteristics and the 2000 US census are described in Table 1. Due to the known issues with the construction of these sampling weights, the weights were not used in this analysis and are not recommended for any further study.

Table 1.

Sample Characteristics and United States Census

	2002 US Valuation Study				2000 US Census (in millions)
	Adults (18+)	White or Other Race	Black, Non- Hispanic	Hispanic	Adults (18+)	White or Other Race	Black, Non- Hispanic	Hispanic
Sample Size	4,048	1,709	1,123	1,216	208.6	162.8	23.3	23.0
Age
18-24	14%	11%	13%	19%	13%	11%	16%	21%
25-34	24%	19%	24%	30%	19%	17%	22%	28%
35-44	22%	21%	23%	23%	22%	21%	23%	22%
45-54	17%	18%	18%	13%	18%	19%	17%	14%
55-64	10%	13%	11%	7%	12%	12%	10%	7%
65+	13%	17%	10%	8%	17%	19%	12%	8%
Gender
Female	58%	55%	63%	57%	52%	52%	54%	48%
Male	42%	45%	37%	43%	48%	48%	46%	52%
Residence
Non-Metropolitan	7%	10%	4%	6%	17%	20%	12%	7%
Metropolitan	93%	90%	96%	94%	83%	80%	88%	93%
Census Division
New England	3%	3%	3%	2%	5%	6%	2%	2%
Middle Atlantic	10%	12%	9%	10%	14%	14%	15%	13%
East North Central	15%	15%	16%	13%	16%	17%	16%	7%
West North Central	4%	4%	4%	5%	7%	8%	3%	2%
South Atlantic	19%	15%	35%	11%	19%	18%	32%	13%
East South Central	6%	9%	8%	0%	6%	6%	10%	1%
West South Central	15%	10%	15%	23%	11%	9%	13%	20%
Mountain	9%	13%	3%	7%	6%	7%	1%	10%
Pacific	19%	20%	7%	29%	16%	15%	7%	32%

RESULTS

According to the 2000 US Census, Hispanic and Black, non-Hispanic adults compose 10.7% and 10.9% of all adults in the US; however, these sub-populations compose 30% and 27.7% of the sample respectively (Table 1) (Coons, Johnson et al. 2005). In addition to over-sampling these two sub-populations, the sample differs from the US population by age, sex, and rural residence, which may be attributed to the design of the household interview survey. Average age of a male respondent is 42.76 and average age of a female respondent is 43.2, which are younger than the census estimates (43.94 and 46.32, respectively). Female respondents compose 58% of the sample and 52% of the US adult population. Lastly, respondents who reside in Metropolitan areas, as measured through county-specific Beale codes, compose 93% of the sample and 83% of the US adult population (Parker 2005). In summary, the US valuation sample has a disproportionate number of young, female, and minority respondents who reside in metropolitan areas; however, it is unclear whether this selection bias influenced the value estimates.

Before reviewing the EQ-5D results, the QALY calculations for unconscious are described to illustrate the simplicity of each specification. As shown in Figure 1, the US valuation study has 3,903 TTO responses for unconscious, describing its value in terms of years in optimal health (Y) and years unconscious (X). Based on these responses, mean(Y/X) is −4.25, mean(XY) is −5.61, mean(XX) is 57.35, mean(Y) is −2.99 and mean(X) is 6.65. Based on these means, we can calculate the health utility of unconscious on a QALY scale for each specification: −4.25 IRUM QALYs, −0.10 ERUM QALYs (−5.61/57.35), and −0.43 ARUM QALYs (−2.99/6.65). The original analysis would have arbitrarily divided all negative TTO ratios, Y/X, by 39 and estimated the mean adjusted ratio (i.e., −0.74 Shaw QALYs). Each calculation is simple to perform and renders a different QALY estimate for unconscious.

Table 2 provides three sets of MAU model estimates for the three alternative specifications. Using the levels within the EQ-5D descriptive system, we assess the logical consistency of these estimates. Each coefficient represents a decrement in health. ARUM and ERUM results have face validity in that the estimated decrements in health have all positive confidence intervals, and all second-level decrements are significantly smaller than their third-level counterparts. The IRUM estimates do not all have positive confidence intervals, and only 40 out of the 243 EQ-5D states are valued BTD. The number of states WTD is 42 under ARUM (17%) and 3 under ERUM (1%). Based on poor face validity and concerns about the robustness of ratio statistics, IRUM is an unlikely choice for EQ-5D values on a QALY scale.

Table 2.

Multi-attribute Utility (MAU) Model Estimates

EQ-5D Domains and Levels	IRUM (Mean Ratio)			ERUM (Coefficient)			ARUM (Ratio of Means)
	Coef.*	95% CI		Coef.*	95% CI		Coef.*	95% CI
Mobility, ≥2	0.083	−0.018	0.190	0.048	0.041	0.054	0.054	0.046	0.061
Self-Care, ≥2	1.712	1.523	1.920	0.202	0.189	0.215	0.362	0.342	0.381
Usual Activity, ≥2	0.214	0.093	0.341	0.091	0.083	0.099	0.101	0.092	0.110
Pain/Discomfort, ≥2	1.073	0.867	1.282	0.116	0.104	0.127	0.190	0.173	0.206
Anxiety/Depression, ≥2	0.044	−0.053	0.140	0.068	0.060	0.075	0.071	0.063	0.078
Mobility, 3	0.589	0.424	0.746	0.103	0.093	0.113	0.131	0.120	0.144
Self-Care, 3	0.204	0.073	0.333	0.076	0.067	0.086	0.084	0.073	0.094
Usual Activity, 3	1.535	1.357	1.709	0.206	0.196	0.216	0.342	0.326	0.358
Pain/Discomfort, 3	0.229	0.136	0.323	0.092	0.084	0.100	0.105	0.096	0.114
Anxiety/Depression, 3	0.959	0.827	1.112	0.112	0.102	0.122	0.185	0.172	0.198
Unconscious	4.481	4.176	4.815	0.724	0.707	0.741	1.035	1.006	1.065

^*Each coefficient represents a decrement in health. For example, the ERUM QALY prediction for 21111 is 0.952 (i.e., 1.0 - 0.048).

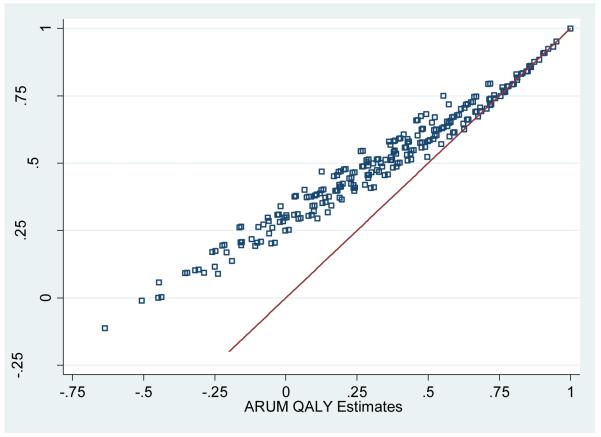
ARUM and ERUM exhibit identical parameter ranks. The decrement representing some problems in mobility is smallest; yet, having severe problems in mobility (i.e., “being confined to bed”) produces the second largest decrement. The primary difference is that the parameters of ARUM are larger than those of ERUM as was predicted in the methods section. Figure 2 illustrates the association between ERUM and ARUM values for the 242 EQ-5D states. The largest difference is in the value of the worst possible EQ-5D state (i.e., 33333 or “pit-state”): −0.113 QALYs under ERUM and −0.624 QALYs under ARUM. The difference in value attenuates as health improves. Based on the proportional patterns and the average value of pits under ERUM and ARUM, a simple rule of thumb is that QALY losses under ARUM are 37% larger than losses under ERUM (i.e., (1-0.321)/(1-0.504)-1).

Figure 2.

Revised ERUM and ARUM QALY Estimates for 243 EQ-5D States*

*Line reflects equivalence between ERUM and ARUM estimates, and illustrates how the difference between estimates attenuates as health improves.

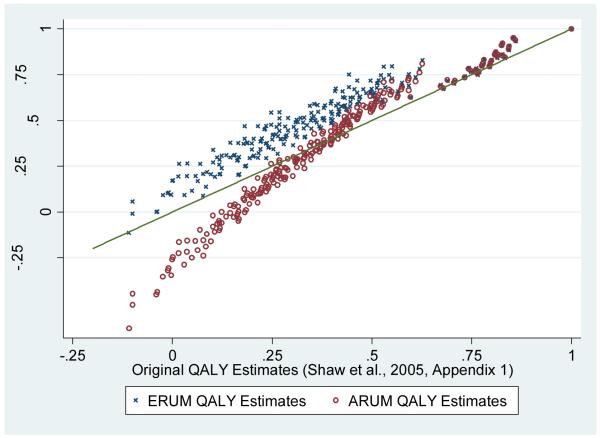
Figure 3 compares the ARUM and ERUM values with published values from the original US valuation study. The original values have a similar range as ERUM values (ERUM pits = −0.113 and Shaw pits = −0.109), but their average value (0.369) is more similar to ARUM (0.321) than to ERUM (0.504). An additional difference between the revised and published values is that the original value set has a bimodal distribution with a gap (where no state resides) between 0.626 and 0.672 QALYs, and the revised values have unimodel continuous distributions. The gap at 0.66 QALYs in the original study is an artifact of the data transformation when dividing negative values by 39. Because states with values above 0.66 had few WTD responses, these “healthy” states were largely unaffected by the transformation, causing the discontinuity in value distribution.

Figure 3.

Original and Revised QALY Estimates for 243 EQ-5D States

* Line reflects equivalence between the original and revised estimates.

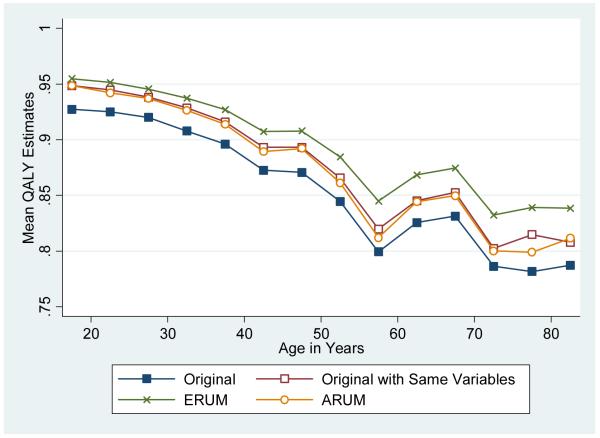
After removing 70 respondents with incomplete EQ-5D responses, we predicted the QALY values for each respondent (N=3,973) using ERUM and ARUM estimates as well as the original values. In addition, we repeated the original analysis using the same variables (excluding D1, I2-squared, I3, and I3 squared) and sample as the revised estimations. Its controlled predictions allow us to assess whether the differences in mean are due to the differences in specification or differences in sampling and MAU regressions. Figure 4 illustrates the mean values by 5-year age group. The patterns are similar across specifications, characterized by a decline with age and a bump around the median retirement age. The means of original estimates are the lowest and the means of ERUM estimates are the highest across all age groups. The means of the ARUM and original specification are nearly identical when the original analysis is repeated using the same variables and sample as the ARUM specification.

Figure 4.

Mean QALY Estimates by 5-year Age Groups*

* Final age group is 80 years and older.

DISCUSSION

In this paper, we respond to repeated criticisms of the original US valuation study and its ad hoc adjustment of WTD TTO responses by re-estimating EQ-5D health state values under three alternative random utility models. The IRUM, ARUM, and ERUM provide theoretical support for three distinct econometric estimators (mean of ratios, ratio of means, and coefficient), none of which involve the arbitrary transformation of WTD responses or the bounding of health state values above −1. IRUM values seem to lack face validity, characterizing 83% of EQ-5D states as WTD. ARUM and ERUM are reasonable alternatives. As a rule of thumb, QALY losses are 37% larger under ARUM than ERUM. Therefore, incorporating ARUM QALYs into cost-effectiveness studies may magnify estimated gains (or losses) in quality of life relative to ERUM QALYs. Whether this difference alters resource allocation decisions awaits further review; however, both sets are recommended over the original value set, or IRUM.

To further clarify the difference between ARUM and ERUM, we draw attention to the randomness term, ε_i. It is unclear whether randomness is a consequence of differences in individual preferences, response error, or both. The ERUM coefficient estimator controls for randomness in y_i, similar to response error (Craig and Busschbach 2009). The ARUM estimator, ratio of means, is identical to a Wald estimator, which was developed to control for error in both the dependent and independent variables (Wald 1940). For BTD responses, x_i is constant and y_i varies, favoring ERUM, while both vary for WTD responses, which favors ARUM. Future study may avoid this dilemma by forgoing the two-scale valuation techniques.

Under the MVH TTO protocol, BTD and WTD responses are placed on separated scales, which may introduce response biases (Gudex 1994). Two scales may impose differential cognitive challenges (e.g., respondents may simply misinterpret the WTD questions). The scales may also induce differential ceiling and floor effects (i.e., non-optimal gap) or reflect intervals, not cardinal numbers (Craig, Busschbach et al. 2009). The task is based on repeated choice, which may compound errors under its adaptive survey design. If a respondent errors in the initial question (Is the health state BTD or WTD?), this error affects the down-stream equivalence statement.

Aside from issues with scales and trade-off responses, each random utility model assumes constant proportionality between utility and time (CP-TTO). CP-TTO is a restrictive and potentially incomplete relationship. If the trade-off responses had been collected in a manner such that duration and preferences were independent, years squared may have been included in the ERUM model (QALY_i = β_h*years + α_h*years² + ε_i) or the IRUM model (QALY_i = (β_h+ α_h*years + ε_i)*years) to test constant proportionality. Nevertheless, CP-TTO remains commonplace in cost-utility analyses and still warrants further empirical investigation (Bleichrodt 2002; Craig 2009).

Aside from the transformation of WTD responses under the IRUM specification, the original analysis applied a more restrictive set of sample selection criteria, sampling weights, and multiplicative attribute variables (Shaw, Johnson et al. 2005b). More respondents (275 or 6.7%) were excluded in the original analysis than in the revised analysis (5 or 0.1%). Reasons for exclusion in the original analysis are poor logical consistency or fewer than 12 responses. To adjust for this bias, the original analysis applied sampling weights adjusted for housing unit occupancy, household zip code, gender, and race/ethnicity, but did not adjust for respondent age, residency in a rural area, or socioeconomic characteristics (Shaw, Iannacchione et al. 2005a). The revised analysis did not incorporate sampling weights, because it is unclear whether they would attenuate or magnify sampling bias. The original MAU regression includes four additional attribute variables (D1, I2-squared, I3, and I3 squared) selected on the basis of statistical significance. These variables may capture multiplicative effects; however, no theoretical justification is provided for their inclusion, and their statistical significance may be attributable to experimental design (e.g. the selection of hypothesized states) or the arbitrary data transformation.

Once we accounted for differences in sample and removed the multiplicative attribute variables, the original specification rendered QALY predictions similar to the ARUM estimates. While the practice of data manipulation should not be tolerated, the estimates from the original QALY estimation may be interpreted a proxy for the ARUM estimates. Still, the choice between the ARUM and ERUM estimates remains unclear. Although ARUM and ERUM differ in their strategy to minimize randomness, both represent reasonable approaches to US values based on a nationally representative interview survey. They have the necessary level of transparency for legitimate use in public policy (i.e., data and code are provided). The selection between these models is arbitrary; however, this choice seems to be an order of magnitude less subjective than the choice to divide the lower quartile of the TTO ratios by 39.