Abstract
An adaptive Cartesian grid (ACG) concept is presented for the fast and robust numerical solution of the 3D Poisson-Boltzmann Equation (PBE) governing the electrostatic interactions of large-scale biomolecules and highly charged multi-biomolecular assemblies such as ribosomes and viruses. The ACG offers numerous advantages over competing grid topologies such as regular 3D lattices and unstructured grids. For very large biological molecules and multi-biomolecule assemblies, the total number of grid-points is several orders of magnitude less than that required in a conventional lattice grid used in the current PBE solvers thus allowing the end user to obtain accurate and stable nonlinear PBE solutions on a desktop computer. Compared to tetrahedral-based unstructured grids, ACG offers a simpler hierarchical grid structure, which is naturally suited to multigrid, relieves indirect addressing requirements and uses fewer neighboring nodes in the finite difference stencils. Construction of the ACG and determination of the dielectric/ionic maps are straightforward, fast and require minimal user intervention. Charge singularities are eliminated by reformulating the problem to produce the reaction field potential in the molecular interior and the total electrostatic potential in the exterior ionic solvent region. This approach minimizes grid-dependency and alleviates the need for fine grid spacing near atomic charge sites. The technical portion of this paper contains three parts. First, the ACG and its construction for general biomolecular geometries are described. Next, a discrete approximation to the PBE upon this mesh is derived. Finally, the overall solution procedure and multigrid implementation are summarized. Results obtained with the ACG-based PBE solver are presented for: (i) a low dielectric spherical cavity, containing interior point charges, embedded in a high dielectric ionic solvent – analytical solutions are available for this case, thus allowing rigorous assessment of the solution accuracy; (ii) a pair of low dielectric charged spheres embedded in a ionic solvent to compute electrostatic interaction free energies as a function of the distance between sphere centers; (iii) surface potentials of proteins, nucleic acids and their larger-scale assemblies such as ribosomes; and (iv) electrostatic solvation free energies and their salt sensitivities – obtained with both linear and nonlinear Poisson-Boltzmann equation – for a large set of proteins. These latter results along with timings can serve as benchmarks for comparing the performance of different PBE solvers.
Keywords: Poisson-Boltzmann equation, biomolecular electrostatics, implicit solvent model, algorithm, finite difference methods, Cartesian grid, adaptive, electrostatic potential
Introduction
The efficient and accurate implicit solvent-based electrostatic modeling of large complex and highly charged biomolecules in aqueous electrolyte solution at finite ionic strengths remains an important and difficult challenge in computational molecular biophysics. Considerable success in modeling the long-range and nonspecific electrostatic interactions of biomolecules in ionic solution has been achieved on the basis of the Poisson-Boltzmann equation (PBE), which provides the electrostatic potential and other important derived quantities (e.g., electrostatic solvation free energies, electrostatic binding free energies, forces and pK shifts) at varying ionic conditions1. Nevertheless, two challenges persist in the numerical calculation of such systems. First, for large molecules the mesh topologies used to date – regular lattices and unstructured tetrahedral grids – are subject to various inefficiencies and/or mesh generation challenges that can be improved upon by considering an alternate mesh structure as well as selecting a representation of the solution that reduces the mesh resolution demands. In the current development the PBE is solved upon a hierarchical mesh structure variously referred to as an adaptive Cartesian grid (ACG), or octree or simply a Cartesian mesh. The ACG terminology is adopted here to distinguish it from regular lattices which are also commonly called Cartesian grids. The second challenge is achieving reliable and rapid solution convergence for highly charged biomolecular systems. The current article describes a methodology that addresses both challenges resulting in a robust nonlinear PBE analysis capable of properly modeling salt-mediated and non-specific electrostatic effects in nucleic acids and their associations with charged ligands such as cationic drugs, peptides and larger proteins.
One goal of the ACG-based PBE solver is to facilitate computation of electrostatic properties for large-scale biomolecular systems at the atomic level of detail using readily accessible computational resources. For example, a recent experimental study suggests that the electrostatic interactions in the ribosomal exit tunnel can modulate the elongation rates of nascent peptides2. For such large-scale ribosomal systems, most Poisson-Boltzmann studies have necessarily been based on coarse-grained molecular models due to memory constraints and convergence issues3. The PBE solver described here provides the variable mesh spacing necessary to efficiently accommodate such nanoscale biomolecular assemblies. Moreover, it contains robust iterative procedures that reliably converges the electrostatic solution at comparable rates for both the linear and nonlinear PBE of highly charged complex biomolecular systems such as ribosomes. This property is used to obtain a high resolution (0.3 Å) surface potential map of the highly charged large 50S ribosomal subunit. To the best of our knowledge, nonlinear PBE calculations for such a highly charged and large biomolecular system have not been previously performed on a serial platform – at least at such a fine grid resolution. Moreover, with the computational tools developed here, nonlinear PB calculations can be conducted in nearly the same computer times as linear ones as borne out in the Supplementary Materials that provide such timings for a collection of proteins.
Solution Methods for the PBE
Numerical solutions to the PBE can be obtained using either finite difference (FD) techniques, which here includes finite element (e.g., unstructured tetrahedral meshes) and finite volume-based discretizations, or boundary element methods (BEM). Each approach has inherent advantages as reviewed in 1, 4. Briefly, when solving the linear PBE using the BEM: (i) only a surface mesh is required since the solution is expressed entirely in terms of surface distributions; (ii) far-field boundary conditions are automatically satisfied; (iii) the constraints upon the electrostatic potential and its normal gradient at the molecular surface are explicitly imposed; (iv) the potential fields associated with point charges are expressed analytically, thereby circumventing problems relating to representing singular solutions upon grids; and (v) the interactions between distant elements are evaluated using the exact expressions thus conferring high accuracy. With the introduction of fast multipole methods, computational costs have been reduced from O(N2) to O(NlogN) (N being the number of boundary elements), thus allowing much larger problems to be addressed. The first PBE solvers utilizing fast multipole-accelerated BEM were limited to zero salt conditions5–7. The extension to finite salt concentrations was first achieved by Boschitsch & Fenley4, 8 and subsequently by Lu and co-workers using a different form of the fast multipole expansion9, 10.
A major limitation of BEM-based approaches is the forfeiture of a pure surface-based solution representation and the attendant increase in computational effort when solving the nonlinear form of the PBE. Our experience11 has consistently shown that even for very simple cases, computation times can easily increase by O(10)-(100) when using the BEM for the linear part and nonlinear terms expressed as source distributions, where the latter appear as volume integrals over the entire computational domain. Hybrid schemes offer one venue for retaining the advantages of a BEM while allowing the nonlinear PBE to be addressed11.
In the FD method, the differential form of the equations is solved on a volume mesh that fills the region of interest. The discrete equations can be derived according to variational principles which underlie the finite element (FE) method or by classical finite difference schemes based on the Taylor series expansions about a given mesh point. The FE method provides a general and systematic approach for developing the discrete model upon a variety of meshes including unstructured (tetrahedral) and curvilinear grids. In some instances however, the FD method offers a more efficient approximation. For example, when adopting a regular lattice mesh the FD approximation to the Laplacian operator at a mesh point is both second order accurate and involves only six neighboring mesh points whereas a FE model is only first order accurate (at least in the most common implementations12, 13 using linear order tetrahedral elements) and involves all 26 neighboring mesh points thus increasing computational requirements.
The mesh structure employed in a FD method directly influences the performance and the quality of the results obtained. Historically, FD-based PBE modeling has employed two basic grid structures:
Regular 3D lattice
This is the grid arrangement adopted in the popular PBE solvers such as APBS14, UHBD15, PBEQ16, MEAD17, ZAP18, DelPhi19 and the PBSA-Amber20–22 and consists of a uniformly spaced rectangular grid superimposed over the biomolecule of interest. While no attempt is made to align the mesh with the molecular surface, good estimates of the electrostatic potential solution are nevertheless obtained because this solution is continuous across the surface. Regular lattices allow one to readily develop a simple and efficient discretization of the differential operators and to implement effective multigrid procedures. However, the lack of a variable or adaptive grid spacing capability leads to a restrictive tradeoff between accuracy and storage constraints as larger biomolecules are considered. Furthermore, to minimize errors generated at the outer boundary of the grid (such errors introduce biases in computed electrostatic potential and energies), the grid must be extended sufficiently far from the molecule so that the potential at the outer boundaries is negligible. Nonlinear PBE calculations of highly charged biomolecular systems are especially challenging in this regard since consistent outer boundary treatments for the nonlinear PBE have only recently become available 23. To reduce calculation effort and maintain good accuracy, the focusing24 procedure is invoked where the solution obtained on a global mesh with large mesh spacing is interpolated onto a collection of finer, localized grids. This approach improves local accuracy, but entails multiple PBE calculations for a given molecular configuration.
Unstructured Grids
To address the shortcomings of regular lattice grids, efforts have been directed at the use of unstructured tetrahedral grids for biomolecules [e.g., 25]. Such grids can achieve good resolution over a wide range of length scales and also offer the opportunity for solution-dependent mesh adaptation. Unstructured grids have been used in the finite element solution of the PBE to produce accurate predictions of biomolecular electrostatic properties12, 13, 25. A useful feature of unstructured grids is the ability to conform to the molecular surface so that no edges or elements intersect the surface. This allows for inherently more accurate estimates of surface properties, particularly the electrostatic field which is essential for reliable prediction of electrostatic PBE forces. On the other hand, unstructured meshes are subject to several limitations: (i) The generation of good quality meshes is complex and time consuming especially for grids that conform to the molecular boundary; however active research in this area is expected to reduce the associated computation times26. (ii) Neighboring nodes must be explicitly identified thus increasing storage costs (each node has approximately 14 neighbors, compared to 6 on a regular lattice grid). (iii) Mesh adaptation procedures are complex and expensive due to the large number of refinement possibilities in 3D. (iv) Multigrid implementation is challenging because defining coarser level meshes and linear order accurate (the minimum order needed for second order PDEs) interpolation procedures between multigrid levels, are non-trivial. (v) The discrete approximation to the PBE equation generally has first order errors (errors are O(h) where h is the local mesh spacing) compared to the approximation on a regular lattice which is second order accurate (errors are O(h2)) so that slower convergence with mesh spacing is obtained.
Herein an alternate grid structure is proposed that combines the adaptation and variable resolution features of unstructured grids with the simple cube geometry and multigrid capabilities enjoyed by regular lattice methods. This mesh, referred to here as an adaptive Cartesian grid, derives from the hierarchical decomposition of the computational domain known as an octree27 which is obtained by recursive and selective subdivision of a cube into smaller nested cubes (e.g., see for example Figure 2). It is noted that an article utilizing the ACG concept to solve the nonlinear PBE has recently appeared 28 to model supercapacitor behavior of porous electrodes. Their approach embodies several of the same methodology details described below including the derivation of the finite difference formulae. Their applications do not appear to call for a decomposition of the solution to eliminate singular behavior at charge sites and applications were limited to comparatively simple geometries. ACG has been widely used in fluid mechanics applications to model flows about complex geometries29, 30. Often, the most time-consuming and challenging task in such applications is constructing a good quality mesh (for a complex geometry, this can require several man-months) and ACGs were developed in response to the need for a fast and fully automated grid-generation capability31–33. Like unstructured grids, the ACG allows the analysis to ‘zoom’ in to regions where the solution is varying rapidly – e.g., near the molecular surface. Elsewhere, where variations are more gradual, fewer, larger cells may be used for optimal computational efficiency. Outer boundaries can be placed far from the molecular boundary to minimize the influence of boundary errors without incurring appreciable computational cost. Compared to unstructured grids, the ACG generation and adaptation procedures are both simpler and less expensive computationally (for example, a mesh containing a million nodes is easily generated in under a minute using standard non-optimized code on a readily accessible PC hardware). Finally, ACG facilitates implementation of multigrid schemes since the underlying octree data structure already prescribes a complete hierarchy of coarser level meshes and linearly accurate interpolation between levels is readily achieved.
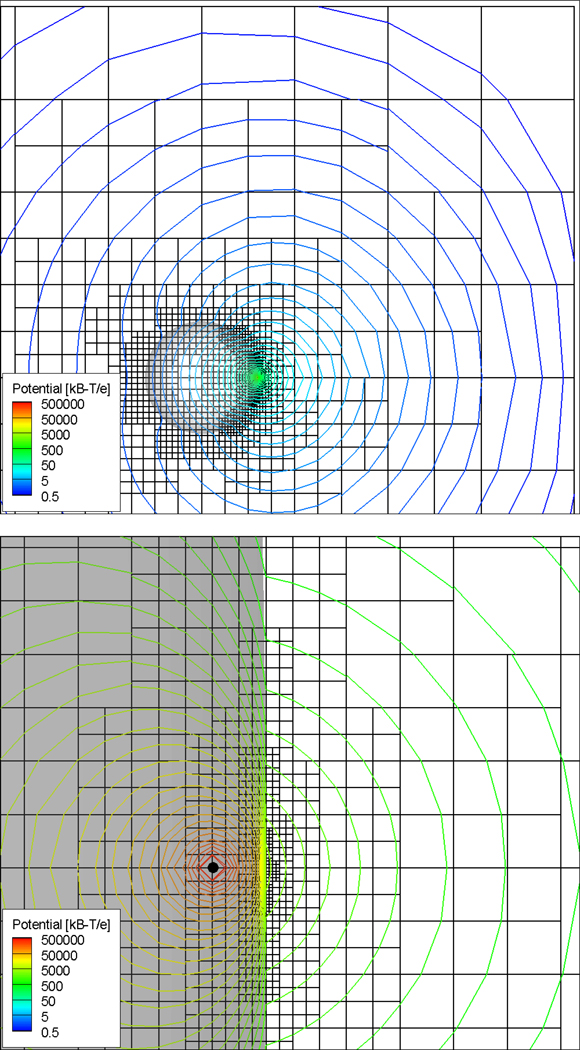
Figure 2.
Cut through ACG for unit charge placed at ρ=0.9969i inside a low dielectric spherical cavity. The lower graph provides a close-up of the mesh and solution near the charge site inside the low dielectric spherical cavity.
In addition to using an ACG, the PBE solution methodology presented here adopts a decomposition of the electrostatic potential field similar to that in 34 to eliminate the singularities at fixed atomic charge sites. In the exterior regions the usual total electrostatic potential is computed. Inside the molecule one develops the reaction field potential which contains no singularities and so is accurately resolved on a mesh. The interior and exterior solutions are connected by calculating the Coulombic potential for nodes near the molecular boundary using fast multipole acceleration methods8. By eliminating the singularities, this decomposition: (i) increases overall accuracy, and reduces sensitivity to grid translations/rotations; (ii) alleviates mesh spacing requirements (no refinement near charge sites is required); and (iii) allows one to directly and accurately compute total electrostatic free energies (the grid-dependent self-energies35 are completely absent) and forces. An interesting consequence of (i) is that the regions where the computed solution varies most rapidly are at the molecular surface rather than at atomic charge sites. This implies that the finest mesh spacing is warranted at the surface and coarser elements can be employed away from the surface.
The sections below describe the generation of the ACG mesh; the discrete approximation of the Poisson-Boltzmann equation on this grid including the decomposition of the solution into the full and reaction field potentials and the imposition of outer boundary conditions; the solution procedure using Gauss-Seidel iteration and multigrid; and post-processing operations. Results are obtained using the ACG-based PBE solver for classical idealized problems involving one and two low dielectric spheres, containing interior charges to affirm the overall accuracy of the method; high resolution calculations of the electrostatic potential and other important derived electrostatic properties for medium-size biomolecules; and demonstration calculations for a selected large-scale and highly charged ribosome. In the Supplementary Materials ACG-PB predictions of electrostatic solvation free energies are provided for a variety of proteins with varying size, shape and charge density along with timing information for both linear and nonlinear PB solutions.
Methodology
Generation of the ACG
Generation of the ACG grid for a given molecular structure presumes availability of the atomic coordinates (ρk), radii (σk) and partial charges (Qk). The atomic coordinates can be obtained from structural biology databases such as the RCSB Protein Data Bank (PDB files) or Nucleic Acid Database (NDB files). The atomic radii can be assigned using one of many available atomic radii sets (e.g., Bondi36). Assigning atomic charges is more involved especially when proper protonation state assignment is required, but typically either a formal charge set is adopted or partial atomic charges derived from molecular mechanics force fields, such as AMBER37 or CHARMM38, are used in this study. In addition to this structural description, a molecular surface definition must also be specified. Common surface definitions available in the ACG generation software include the van der Waals (vdW) surface, which is the exposed surface of the collection of overlapping spheres and solvent excluded (SE) surface (also commonly referred to as the molecular or Connolly surface) is obtained by rolling a probe sphere of radius, rprobe (usually, rprobe=1.4Å for water), over the van der Waals surface and identifying the points which can be reached by the probe (exterior points) and which ones can’t (interior). Other surface definitions, such as various Gaussian function-based descriptions (e.g., 39), can also be used and are available in the ACG software. Developing the ACG and assigning the dielectric map to the resulting mesh nodes requires the ability to determine whether a given point lies within the molecular surface. For the vdW surface, this determination is straightforward using an inside-sphere test. For the SE surface, the test is somewhat more involved – here, the procedures described by Chan et al40 are employed.
The ACG generation process begins by placing an initial cube over the entire molecule. This initial cube is sized to be several times larger than the maximum dimension of the molecule so that the boundary condition at the outer boundary can be accurately imposed (see below). The cube is then uniformly subdivided a fixed number of times, L, to produce a uniform lattice starting mesh containing (2L+1)3 nodes (or 8L cube-shaped cells).
Recursive adaptation of this initial mesh then proceeds by identifying which individual mesh cells intersect the molecular surface. Each intersected cell is tested to determine whether one of the following refinement criteria is satisfied:
The user-specified finest mesh spacing, Δmin, is reached or
The intersected cell lies more than a prescribed distance from the nearest atomic charge site.
Each intersected cell that does not meet either of these criteria is uniformly subdivided into eight smaller cells. The resulting ACG is then again subjected to these mesh intersection and refinement tests and the grid generation process continued. The refinement process naturally terminates since eventually all intersected cells meet the refinement criteria (i) or (ii).
To prevent excessive cell size variation that can be detrimental to solutions accuracy, the ACG is smoothed by requiring that no terminal cell (a cell that has not been refined into smaller ones) be larger than twice any of its neighbors. This requirement also facilitates development of the finite difference procedures and implementation of multigrid. If requested, a Stern or ion exclusion layer of specified thickness, t, is defined by appropriately marking all nodes that are outside the molecule and less than a distance, t, away from the nearest interior node.
When conducting electrostatic interaction or binding energy calculations where the electrostatic energy of, say, a charged ligand-nucleic acid complex is subtracted from the electrostatic energies of the charged ligand and nucleic acid considered in isolation, all three calculations (charged ligand, nucleic acid and charged ligand-nucleic acid pair) are conducted on the same mesh. This is because the electrostatic interaction or binding energy is often several orders of magnitude smaller than the individual electrostatic energy contributions so that small errors (e.g., due to finite mesh size) in the individual electrostatic energies appear large relative to the electrostatic interaction energy. In such calculations, the ACG is generated with respect to all three geometries as if the molecule actually consisted of the superposition of all three molecular surfaces. The same mesh is then employed for all three energy calculations using the respective dielectric maps.
Finite Differencing on the ACG
The ACG contains 'hanging' nodes which are nodes that neighbor an element but are not a vertex of that element (for example, a node that lies on a mid-edge or the face of an element). The presence of hanging nodes complicates application of a variational or finite element framework for deriving the governing equations (specifically, compatibility between different size elements is not easily enforced). For this reason a finite difference approach is adopted to obtain a discrete expression of the PBE on the ACG. In developing a FD approximation to the weighted Laplacian, ∇·(ε∇Φ), it is desirable to simultaneously achieve the following properties: (i) Compactness - to ensure robust convergence and numerical stability, the formula should be compact (i.e., only involve immediately neighboring nodes). (ii) Consistency – as mesh spacing is reduced, the difference formula should converge to the exact analytical result. (iii) Positive weights – the final expression relates the potential at a point, i, to the weighted sum of the neighboring node potentials; ensuring that the associated weights are positive is important for stable convergence and conformance with maximum principles for elliptic PDEs41. An additional consideration for continuum electrostatic modeling is that the dielectric ‘constant’ changes discontinuously at the molecular surface (MS). This makes it difficult to develop formally consistent FD rules. However, the errors committed in applying the FD formulae near the MS can be viewed as perturbations of the surface geometry. Also, the success of FD applied upon regular lattices indicates that good PBE predictions can be obtained with simple interpolation of the dielectric/ionic map (e.g., as currently done in any of the lattice code such as APBS). Here we will adopt such interpolation schemes and confirm their effectiveness by subsequent numerical studies. Current work is being directed at addressing accurate interpolation at the surface.
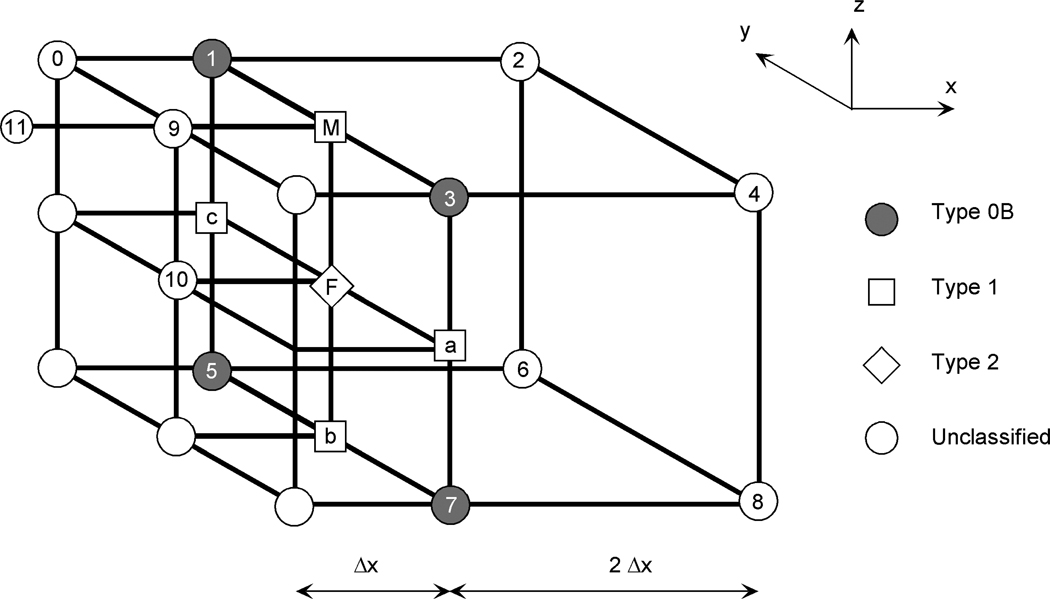
The FD method begins by distinguishing between various types of nodes. Denoting the collection of terminal octree cells, ib, that touch a node, i, by: {Ni}={ib: ib incident to node, i} (this implies that node i lies on the surface of ib), then three types of mesh nodes can be distinguished.
| Type 0 | Node i is a vertex of all terminal cells, ib ∈ {Ni}, which implies that it is not a hanging node. Type 0 nodes are further distinguished into two sub-types: | |
| Type 0A | All ib ∈ {Ni} are of equal size. | |
| Type 0B | The members ib ∈ {Ni} differ in size. | |
| Type 1 | The node lies on the mid-edge of at least one terminal cell, ib ∈ {Ni}. | |
| Type 2 | The node lies on the center of a terminal cell face of exactly one terminal cell, ib∈ {Ni}. |
|
Examples of these nodes are shown in Figure 1. Note that Type 1 and 2 nodes are necessarily adjacent to cells of differing size. Also, in all cases, the members of {Ni} differ by no more than a factor of two in size. Finally, each node can only be of one type (e.g., it cannot simultaneously lie on a mid-edge and a face center). This is a result of the size constraint between neighboring cells. Under these constraints, the finite difference expressions for the differential operator, , are now developed for each of the node types.
Figure 1.
ACG nodes lying on the interface between two different sized cells.
The finite differencing expression for type 0A nodes is the same as that used on a regular lattice. Along the x-direction, the contribution to ∇·(ε∇ϕ) is:
| (1) |
where Ri is the position of node, i, ϕi=ϕ(Ri), Ri±1=Ri ± î (Δx), î is the unit vector along x and Δx is the size of the surrounding cells. The second order error estimate, O(Δx2), formally only applies when the dielectric constant is not changing which is the case away from the molecular surface. The dielectric constant, ε̅i,i+1, is evaluated at the connecting edge mid-point.
Referring to Figure 1, the unique consistent finite difference formula at a type 0B node involving the triplet of collinear nodes, {0, 1, 2}, is:
| (2) |
where Φi is the value of Φ at the indicated vertex. Note that the formula is only first order accurate.
The FD formulas for type 1 and type 2 nodes are developed by identifying the neighboring nodes, developing Taylor series expansions for these nodes and then considering how to combine these series so that only the desired second order derivatives remain. For type 1 nodes such as node M in Figure 1, this process leads to the first order formula:
| (3) |
where the center of the face formed from nodes 1-2-3-4,
| (4) |
For a type 2 node such as node F in Figure 1, one obtains the first order accurate formula:
| (5) |
where the cell center,
| (6) |
and the central difference approximation to ∂Φ/∂x at Rc2 is:
| (7) |
This form is preferred over other options since it promotes positive weights in the final assembled Laplacian approximation (8).
Summary of the FD Formulae
The FD formulae are first order accurate (errors are of O(Δx)) for other than type 0A nodes. It is possible to extend them to higher order by including additional nearby points, but this invites other problems such as non-positive weights and numerical instability associated with the stronger influence from the more distant neighbors. The finite element method applied using linear elements is also first order accurate (this is easily demonstrated in 1D when computing ∂2Φ/∂x2 upon an unevenly spaced grid), whereas the regular lattice methods are second order accurate. The ACG-based FD method offers intermediate accuracy since, depending upon the degree of smoothing, the grid is populated mostly with type 0A nodes. Hence, the discretization is second order accurate over most of the mesh and thus approaches the order of accuracy of a regular lattice.
The FD approximations to the second order derivatives in the x-direction, extend naturally to the y- and z-derivatives which, when assembled, yield the discrete approximation to ∇·(ε∇Φ). At a node, i, this approximation can be cast in the form of a weighted sum:
| (8) |
where ωij are the weights. For regions where the dielectric is constant, ωij>0. Across the surface where dielectric changes however, some weights for type 1 and type 2 nodes at the molecular surface may become negative, but no convergence issues have occurred in our PBE calculations to date. It is easy to show that this discrete approximation of ∇·(ε∇Φ) upon the ACG is: compact, consistent, satisfies a discrete maximum principle (all weights, ωij , are positive42), and reverts to the classical finite difference expressions when implemented upon a regular lattice.
Application to the Poisson-Boltzmann Equation
The PBE is expressed over three distinct regions: (i) the molecular interior or solute region, Ω1, which contains the atomic point charges, has a low dielectric constant, ε1, and is enclosed by the molecular surface defined previously; (ii) the exterior or ionic solvent region, Ω2 , which has a high dielectric constant, ε2, and contains the dissolved ions, and (iii) a charge-free Stern layer (or ion exclusion region where no mobile ions are present), Ω3, of specified thickness about the molecular surface with dielectric constant ε3=ε2. The Stern layer can be used to account for the ion size and its thickness corresponds roughly to the hydrated radius of the ion. In all PB calculations below the Stern layer thickness is set to zero.
The reduced (or dimensionless) electrostatic potential of any arbitrary 3D complex-shaped biopolyelectrolyte, Φ, at location R in the computational domain, is governed by:
| (9) |
where the volume charge density in the different regions is given by:
| (10a) |
| (10b) |
| (10c) |
Note that the expression for ρm(R) in (10b) pertains to a 1:1 electrolyte solvent (e.g., NaCl) which is assumed here for ease of presentation. The extension to more general salt environments is straightforward and the ACG-based PBE solver currently accommodates mixtures of 1:1 and 2:1 salts11, 43 and asymmetric salts.
Introducing the Debye-Hückel screening parameter, κ, as:
| (11) |
allows one to rewrite the PBE in the exterior domain, Ω2 , as:
| (12) |
The linearized form of (12), valid for small electrostatic potentials, Ф≪1, is obtained by setting, f(Ф)≈fL(Ф)=ε2κ2Ф.
In the ACG-based FD implementation, a discrete approximation of (9) is solved at every mesh node. The discretization of the dielectric-weighted Laplacian, ∇·(ε∇Ф) is given by (8). For nodes outside the molecule (in Ω2 and Ω3 ), evaluation of the charge density in (9) according to (10b) or (10c) is straightforward. However, evaluation of the charge density within the molecular interior presents numerical difficulties because the potential becomes singular at the fixed solute charge sites (i.e., atomic centers), ρk. To eliminate this singular behavior, an alternate representation of the interior potential field is adopted.
Representation of the Interior Electrostatic Potential
The interior total electrostatic potential can be expressed as the sum, Φ=Φrf+Φc, where Φrf is the reaction field potential satisfying:
| (13) |
and Φc is the singular Coulombic potential given by,
| (14) |
Here, the reduced charge centered at position ρk is qk=(4πe/ε1kBT)Qk. The reaction field potential contains no singularities and therefore can be accurately resolved on the ACG. Thus, at all interior points the analysis solves for Φrf governed by (13) rather than, Φ. This approach closely resembles the one implemented by Zhou35 upon a regular lattice. In the exterior region, Ω2∪Ω3, the full electrostatic potential, Φ, is retained and (9) is solved.
To connect these two representations, Φrf and Φ, at the dielectric interface first distinguish between the following four possible arrangements for a grid point, i, and its neighbors, j:
The point, i, and all of its neighbors, j, lie inside the molecular interior, Ω1.
The point, i, and all of its neighbors, j, lie inside the molecular exterior, Ω2∪Ω3.
Point, i, lies in the exterior region, Ω2∪Ω3, but at least one of its neighbors lies inside the molecule in Ω1.
Point, i, lies inside Ω1, but at least one of its neighbors lies outside the molecule in Ω2∪Ω3.
Cases (a) and (b) pose no difficulty since the discrete approximation (8) can be directly applied without modification. In Case (c) one solves (9) and thus seeks to evaluate, ∇·(ε∇Ф). Here, the total electrostatic potential is available at node, i, and all neighbors lying in the exterior domain. However, for those neighbors located inside the interior region, Ω1, one has only the reaction field potential. Hence, the Coulombic potential, evaluated according to (14) must be added to these interior grid points before evaluating the weighted Laplacian. Thus, (8), is modified to:
| (15) |
Case (d) is treated similarly. One can solve (13) and subtract Φc from all exterior neighbors, j. This option requires evaluating the Coulombic potential at exterior grid points. Alternatively, if both i and its neighbors, j, are sufficiently distant from the nearest charge, then one can instead solve the equation for the full potential, ∇·(ε∇Ф)=0. Then, as for Case (c), the Coulombic potential must be added to each of the interior nodes (including node, i) before evaluating the weighted Laplacian.
All cases can be expressed in terms of the generalized potential,
| (16) |
which is the discontinuous quantity actually represented upon the ACG mesh. The evaluation of the Laplacian can then be expressed as a weighted summation over all neighbors (without distinction as to whether they lie inside or outside the molecule):
| (17) |
where σi represents the source terms originating from the Coulombic potentials at neighboring interior points such as those appearing in (15). Note that the source term is only non-zero for points having one neighbor across the molecular surface. Thus the Coulombic potential need only be evaluated at interior points lying adjacent to the molecular surface thereby minimizing the number of Coulombic potential evaluations. To further expedite the computation, Φc is evaluated using the fast multipole acceleration method4, 8, 44.
After including the ionic source contributions from the PBE in the exterior region, the final discrete form of the PBE can be written,
| (18) |
where at interior points since one is solving for the reaction field potential there.
Outer Boundary Conditions
The governing equations are closed by specifying the potential at the outer boundary. One option is to set Φ=0 at the outer boundary and place the outer boundary sufficiently far away to minimize the effects of outer boundary errors – this can be accomplished more readily with the variable mesh spacing features of the ACG. Another option is to evaluate the outer boundary potential using the Debye-Hückel approximation:
| (19) |
which is useful when solving the linear PBE. Solutions to the nonlinear PBE however, generally decay more quickly away from the surface (where, |Φ|>1) than their linear counterparts. Thus, when considering the nonlinear PBE, (19) tends to overestimate the boundary potentials which introduces a bias into the computed solution.
The approach23 adopted here is to approximate the electrostatic potential outside the computational domain by the approximate monopole formula, Φb=Be−κ(r−h)/r where the constant, B, is determined from electroneutrality conditions and 2h is the side length of the overall grid. This approach is equally valid for both the linear and nonlinear forms of the PBE and requires only that the magnitude of the potential at the outer boundaries, |Φ|≪1. An explicit expression for B is given elsewhere23.
Iterative Solution Scheme
The discrete system (18) comprises a sparse algebraic set of coupled equations to be solved for the potentials, . For large numbers of nodes, direct inversion of the equation system is not feasible and an iterative inversion method must be used. The choice of iteration method has direct bearing upon the robustness and rate of solution convergence. Here, a standard Gauss-Seidel iteration method and multigrid are combined to achieve the good convergence. Gauss-Seidel iteration usually results in an initially rapid, but then slowed convergence rate. This slackening in convergence is due to the persistence of long wavelength errors. Like most simple iteration schemes, Gauss-Seidel updating effectively eliminates short wavelength errors that fluctuate most rapidly between grid-points, but is less efficient at removing long wavelength components. To promote faster convergence at moderate computational expense (storage and CPU), multigrid acceleration is employed in the ACG-based PBE solver.
Multigrid methods exploit the error smoothing properties of the Gauss-Seidel iteration process. After several Gauss-Seidel iterations, the short wavelength errors are mostly eliminated and only long wavelength errors remain. These errors can therefore be accurately resolved upon a coarser grid. Moreover, because the mesh spacing is larger, the errors fluctuate more rapidly between grid points on the coarser mesh. Therefore, Gauss-Seidel applied on the coarser level is more effective at eliminating those errors. This basic insight motivates the multigrid concept which attempts to eliminate errors over all wavelengths by projecting the solution onto a hierarchy of increasingly coarser meshes. Descriptions of the multigrid method are available elsewhere45 (including applications to the PBE46, 47). Therefore, only a brief description of the overall method is presented here with emphasis reserved for those implementation details that are specific to the use of an ACG.
The multigrid algorithm begins by defining a sequence of nested meshes, {Mℓ: ℓ=0, nlev} where M0 is the finest level mesh. Next, interpolation procedures for transferring solutions and errors between successive levels are defined. In multigrid terminology, these are referred to as ‘restriction’ (transferring a solution from the finer grid, Mℓ−1, to the coarser level mesh, Mℓ) and ‘prolongation’ (transferring from Mℓ to Mℓ−1) operators. Here bilinear interpolation is employed for the prolongation step and its adjoint operator (full weighting45) used for restriction.
In a two-level multigrid implementation the solution process begins by conducting a series of single level Gauss-Seidel iterations on the finest level, M0. The errors (or residuals), λi from (18) are then evaluated and restricted to the next coarser level, ℓ=1, using full weighted averaging. A discrete approximation to the PBE is then developed on this coarser level. However, the Coulombic source terms, σi, on this coarser level are set to zero and replaced everywhere by the restricted errors which now 'drive' the coarser level solution. Gauss-Seidel iteration is then conducted on this coarser level to obtain a correction potential on this level, {Φ1}. The final step is to linearly interpolate the corrections to the finer level, ℓ=0, and add them to the existing solution, {Φ0}={Φg}. The extension to multiple levels is straightforward and explained elsewhere45–47.
Post-Processing
The total electrostatic free energy expression is taken from Eq. 8 of 48. After integration by parts of the last term and substituting using the governing equation (9) one obtains the total electrostatic free energy, Gel , in kBT units11:
| (20) |
where,
| (21a) |
| (21b) |
| (21c) |
and the conversion factor to express the energies in kBT units is:
| (22) |
Here Gf is the energy due to fixed charges and Gm and ΔΠ are the electrostatic stress and excess osmotic pressure terms, respectively. The excess osmotic pressure contribution has special significance when assessing salt dependencies of the electrostatic free energies since one can show 49, 50,
| (23) |
It is also useful to define the reaction field energy,
| (24) |
which is the difference between Gf and the Coulombic energy.
For interior points in Ω1 (e.g., the charge sites, ρk), Φ=Φc+Φg, is obtained by interpolating the reaction field potential from the ACG and adding the Coulombic potential, Φc from (14). The electrostatic energy contribution from the interior region, Gf, is computed by summing the product of charge times the electrostatic potential at the fixed charge sites. The volume integrals over the exterior region, Ω2, are evaluated by looping over the cubic cells, ib, of the ACG and approximating the volume integral of any function, g(Φ), by:
| (25) |
where the sum is taken over the exterior forming nodes, k, of cell, ib, and Φk is the potential at forming node, k. In addition, a correction term is added to the volume integrals to account for the contribution outside the computational domain. This correction term is based on the same monopole approximation used for the outer boundary treatment and is developed fully in 23.
Results
The results presented here serve two main objectives. The first is to assess error by comparing ACG PBE predictions against analytical solutions or results obtained by alternate highly accurate means11. In these studies, simple model geometries involving one or two low dielectric spherical cavities, containing charges, embedded in a high dielectric ionic solvent medium are considered. The second goal is to demonstrate the effectiveness of the ACG-based PBE solver as a practical tool for modeling high resolution medium- and large-scale biomolecules ranging from proteins to more highly charged nucleic acids and its large and complex multi-molecular assemblies for which numerous X-ray crystal structures are now available. This second goal is accomplished by computing the electrostatic potential maps. Calculations were performed on a Dell Precision M2300 laptop (3GHz with 4 GB of installed memory) or a dual-processor Intel Xeon Linux workstation (3 GHz with 1 GB of memory).
In addition to the results below, the Supplementary Materials contain the computed electrostatic (solvation) energies, timings and scaling with system size for proteins with varying charge densities, shape and size and modeled both with the linear and the nonlinear PBE. Those results show that for the same system the computation time to solve nonlinear PBE is, on average, 6% more than that for the linear PBE.
Linear PBE Solved for a Low Dielectric Spherical Cavity with a Unit Charge Embedded in a High Dielectric Ionic Solvent
The first model configuration studied solves the linear PBE for a unit radius low dielectric spherical cavity, containing a single interior charge, embedded in 0M, 0.1M and 5M salt solutions. The dielectric constants are set to ε1=2 and ε2=80, and the temperature set to T=298.15K. No ion exclusion or Stern layer is modeled in this or subsequent PBE calculations presented here. Since analytical expressions, developed by Kirkwood51, for the solution of the linear Poisson-Boltzmann equation are available for all κ>051, 52 this case constitutes a useful benchmark for establishing the overall accuracy of the ACG-PB solver. The computational domain extends over four radii and the mesh is generated by requiring that any surface-intersected cell whose size is larger than 0.125 times the distance to the nearest charge, is subdivided. As the charge is displaced towards the surface, this subdivision criterion produces an increasingly finer mesh about the surface point closest to the unit charge (see Figure 2). The time to complete the calculation for all 15 charge locations was 105 s on the PC laptop machine.
The mesh and contours of constant electrostatic potential for the case where the charge is closest to the surface (1−ρ=3.125×10−3 Å so that the distance from the surface is 0.3% of the atom radius) are shown in Figure 2. With the variable mesh spacing capability the full mesh involves only approximately 115K mesh points (a comparable resolution calculation on a regular 3D lattice would entail over a trillion points). Note that the finest resolution provided by the ACG PB solver is at the surface nearest the charge, not at the charge itself. This is where the exterior full electrostatic potential and the interior reaction field electrostatic potential vary most rapidly. The rapid variation in the solution about the charge reflected in the contours is due to the analytically evaluated Coulombic potential contribution. Both outside and inside the molecule the potential maps are smooth and well behaved including near the unit charge placed inside the low dielectric sphere.
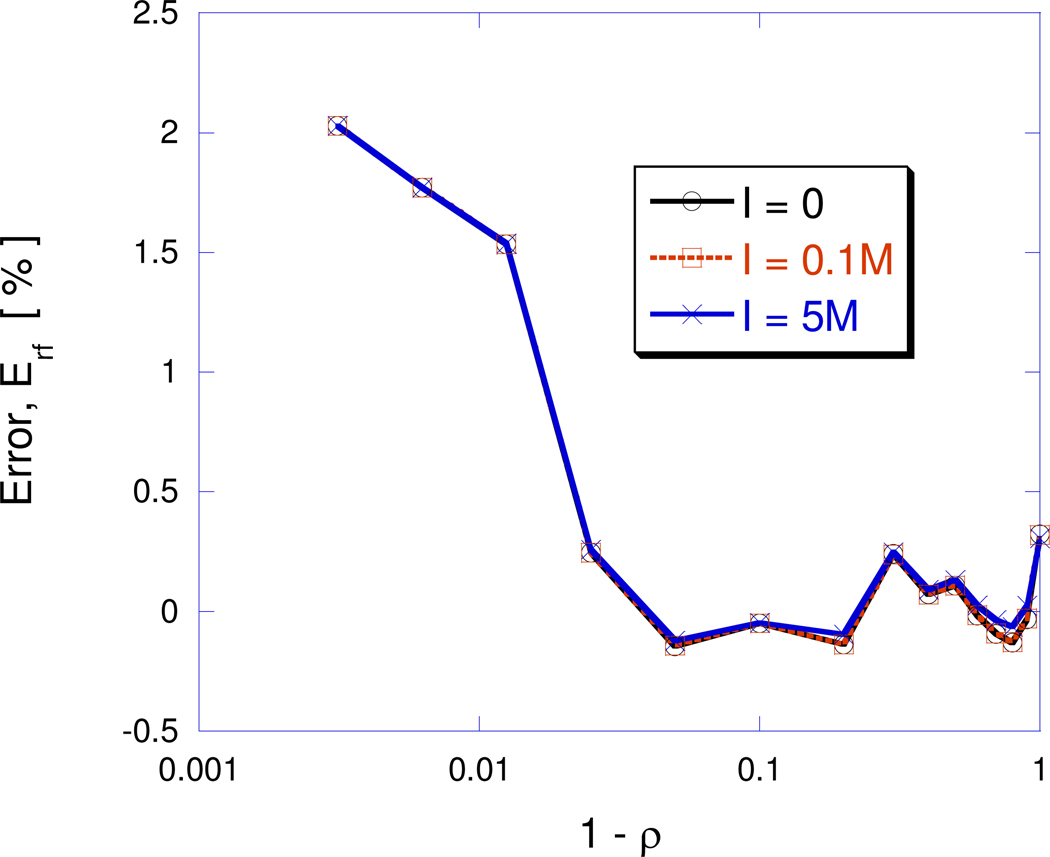
The numerical error defined as given by is plotted as a function of distance below the surface in Figure 3 and shows that the error remains small even when the charge comes very close to the surface. For charges located within 99% of the spherical cavity radius, errors remain 1% or less.
Figure 3.
Error, , plotted as a function of the distance of the interior unit charge, from the surface of the sphere. The linear PBE is solved over a unit radius spherical cavity with ε1=2 and ε2=80 at three different salt conditions: I1:1=0, 0.1M and 5.0M corresponding to Debye-Hückel screening parameters, κ=0, 0.103Å−1 and 0.728Å−1, respectively.
Nonlinear PBE for a Low Dielectric Spherical Cavity of Varying Central Charge in a Salt Solution
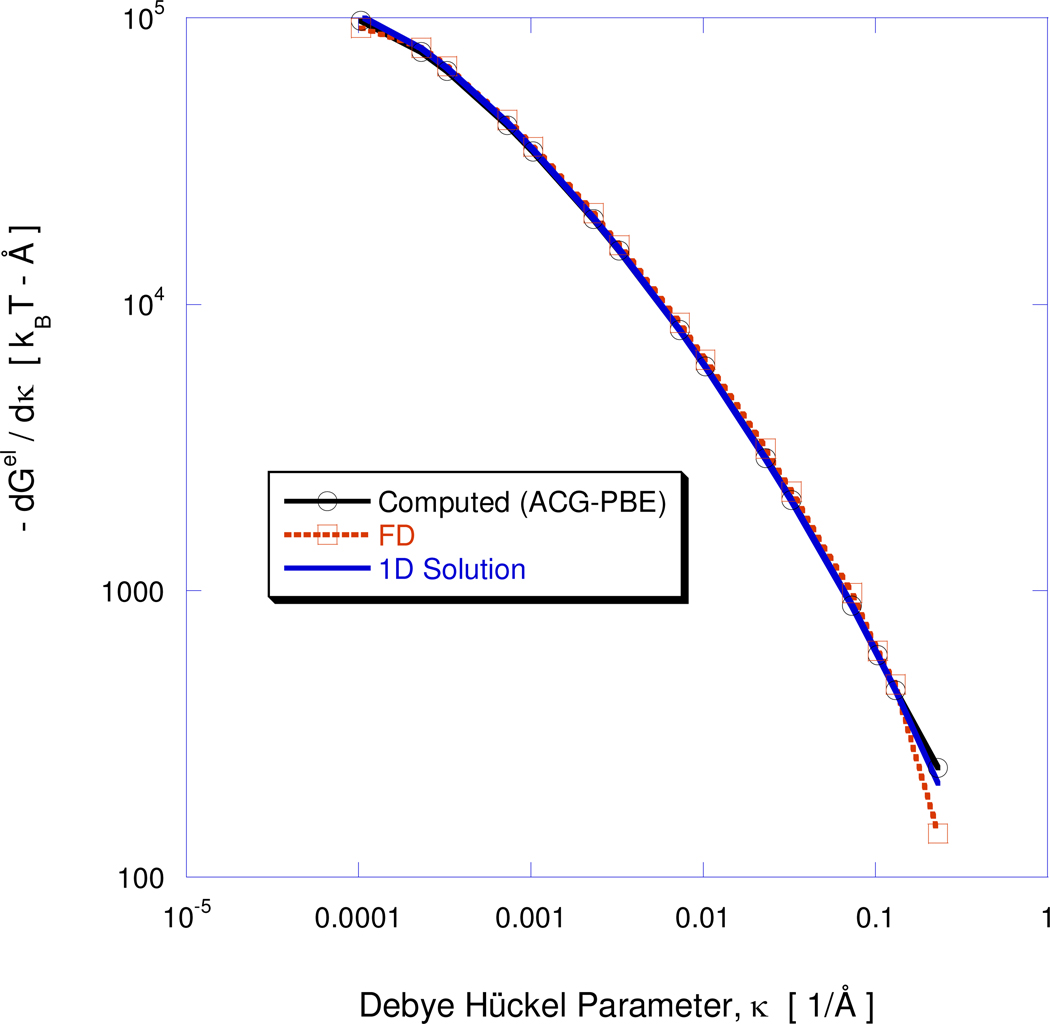
The nonlinear behavior of a spherical cavity containing a centrally located charge is considered to verify accurate recovery of nonlinear solutions and demonstrate stable convergence at high net charge values. The governing PBE in this case reduces to a second order ordinary differential equation (ODE) that can be solved by alternative means (e.g., Appendix A of11). Two cases are considered in this study. In the first, a centrally located 50e charge is placed inside a 20 Å radius sphere and the 1:1 salt concentration varied. The dielectric constant inside and outside the sphere are 4 and 78.5, respectively, and the temperature of the salt solution, T=300K. This case was examined by Zhou53 and his results closely agree with the ones obtained here. The variation of the total electrostatic free energy, Gel as a function of 1:1 salt concentration is also considered in Figure 4. According to (23) the slope of the Gel vs. κ curve is related to the excess osmotic pressure energy contribution. This relationship thus constitutes an internal consistency check valid for general molecular geometries. The plot compares three different predictions of this electrostatic energy slope: (i) the right hand side of (23) where the excess osmotic pressure, ΔΠ, is obtained using ACG-PBE; (ii) differentiation of a piecewise quadratic fit to the Gel ~κ curve where Gel is obtained from ACG-PBE; and (iii) the excess osmotic pressure predicted using the 1D analysis11. Close agreement is established over the entire 1:1 salt concentration range. The minor departure at the highest salt concentration appears to be due to the finite differencing algorithm, the excess osmotic pressure energy contributions obtained with the 1D solver and ACG-PBE remaining in close agreement.
Figure 4.
Comparison of salt sensitivity, ∂Gel/∂κ, obtained from: (i) the osmotic pressure, ΔΠ, computed with the ACG-PBE solver and relation (23)); (ii) finite differencing of the Gel vs. κ curve obtained with the ACG-PBE solver and (iii) a 1D high resolution calculation. Nonlinear energy contributions as a function of the Debye-Hückel parameter, κ, for the single centrally located charge of 50e inside a 20 Å radius sphere. The dielectric constants are ε1=4 and ε2=78.5.
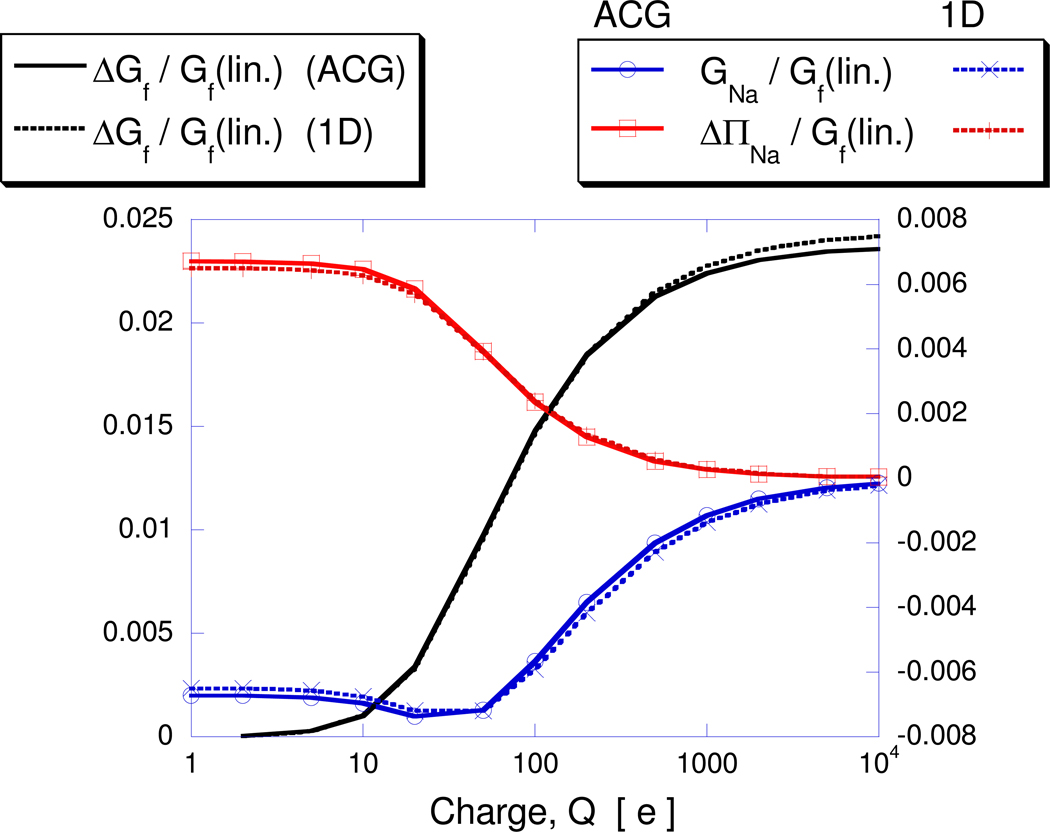
Next, the net charge is increased from 1e, where the PBE solution is essentially linear, to 10,000e where nonlinear behavior dominates and the ability of the ACG solver to converge the solution in a robust manner is put to the test. In all cases, the number of multigrid cycles required to converge the solution ranged between 40 and 60. Figure 5 records the electrostatic free energy contributions, normalized by Gf for the linear problem, Gf(lin.). Note that Gf(lin.) can be expressed analytically and the resulting values are in close agreement with the numerical predictions. Normalizing the electrostatic free energy contributions this way highlights the relative importance of the various nonlinear contributions. Again, good agreement between the 1D and ACG PB results are obtained. The change in normalized fixed charge energy, ΔGf/Gf(lin.) (here ΔGf=Gf−Gf(lin.) and Gf=Grf), is seen to be negligible at small charge values, but to dominate the nonlinear contributions at higher charge values. Also, ΔGf/Gf(lin.) seems to asymptote to a constant value at very high net charges. The opposite trend holds for the other two normalized electrostatic free energy contributions, GNa/Gf(lin.) and ΔΠNa/Gf(lin.) which individually contribute a fixed fraction of total electrostatic energy at the low charge range. As net charge increases however, their relative contributions diminish to zero. Also, since these two electrostatic free energy terms have opposite sign their combined contribution is quite small over the entire charge range.
Figure 5.
Charge dependence of electrostatic free energy ratios for I=0.03M. Results are obtained using the ACG scheme and the 1D finite element solution for the case of a spherical cavity with centrally located charge. The plotted electrostatic free energies, ΔGf=Gf−Gf(lin.)), GNa and ΔΠNa, are normalized by the fixed charge energy obtained from the linear PBE, Gf(lin.). In this case this equals the reaction field energy, Grf, since the Coulombic energy is zero.
Electrostatic Interaction Free Energies For Two Low Dielectric Charged Spherical Cavities Embedded in an Aqueous Salt Medium
The long-range and non-specific electrostatic interactions can modulate the kinetic rates of association of protein-protein and protein-nucleic acid association processes54. For instance, changes in the ionic conditions and charge distribution of the binding partners have a significant impact on the kinetic association rates of various biomolecular complexes55, 56. The quantity of interest here is the electrostatic interaction free energy which is the difference between the total electrostatic free energy of the complex and the summed total electrostatic energies of the individual molecules considered in isolation. Simple model two low dielectric spherical cavity systems have been studied previously using semi-analytical treatments and are useful for validation purposes57. Electrostatic interaction or binding free energies can be difficult to calculate because they are usually much smaller in magnitude than the quantities being differenced. Therefore, the effects of truncation and other discretization errors upon the electrostatic interaction energy may be much more pronounced than for the total electrostatic energies of the two interacting partners.
Accurate electrostatic binding free energies for realistic and large-scale biomolecular systems are given below and elsewhere using the ACG PBE solver58–62. Here the electrostatic interaction between a pair of low dielectric spherical cavities, containing interior charges is considered as a model problem for verifying the ability to accurately calculate these interaction energies. The first sphere has radius 14Å and contains three interior charges, {Qi}={−2.29, +8, +2.29}e, distributed along the x-axis at locations, xi={−7.8, 0, +7.8}Å, relative to the center. The second sphere has radius 21Å and also contains three interior charges, {Qi}={−2.21, −12, +2.21}e, distributed along the x axis at locations, xi={X2−11.7, X2, X2 +11.7}Å, where the separation, X2, is the x-location of the second sphere center. The dielectric constants chosen for this example are εin=4 and εout=78.5. The Debye-Hückel screening parameter, κ=0.1316Å−1.
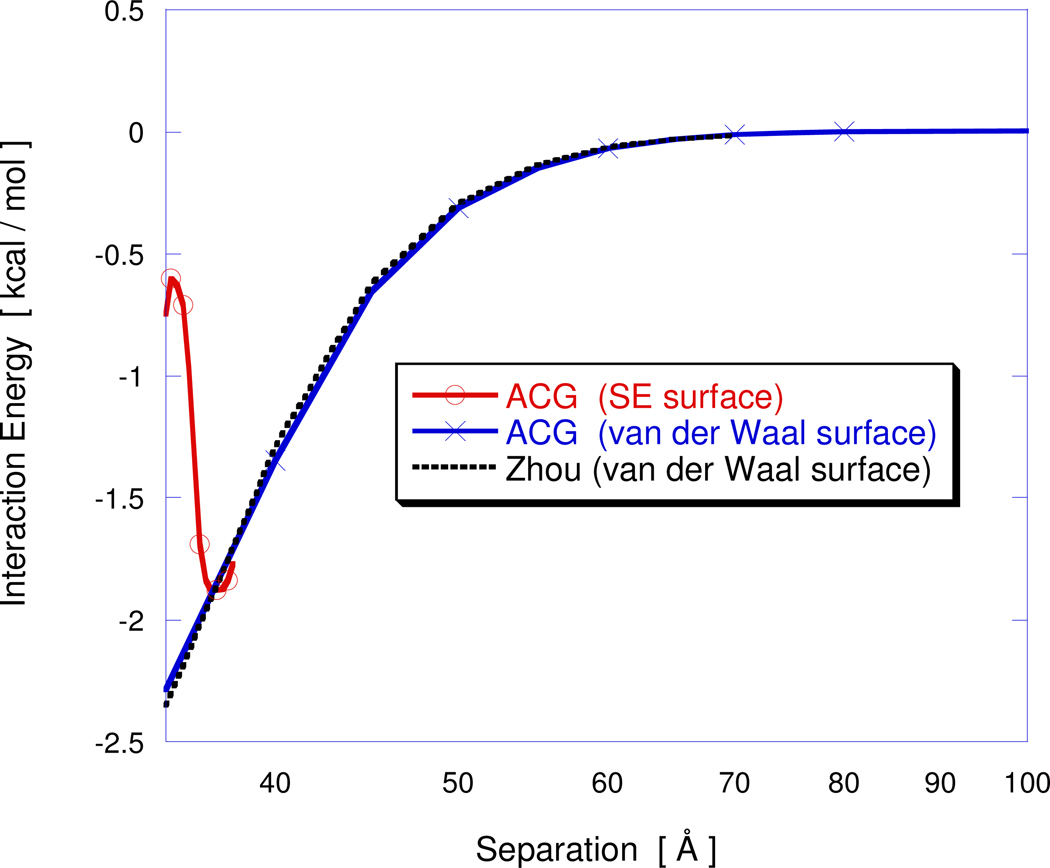
Figure 6 compares the electrostatic interaction free energy obtained using the ACG PBE solver with semi-analytical predictions57 demonstrating excellent agreement when the same (van der Waals) surface is used to define the solute boundary that separates the interior and exterior dielectric regions. The total electrostatic free energies of the isolated 14Å and 21Å low dielectric charged spheres are −199.3 kcal/mol and −283.2 kcal/mol, respectively. Hence, the electrostatic interaction free energy is two orders of magnitude smaller than the individual electrostatic free energies. As one would expect, the choice of molecular surface affects the computed electrostatic interaction energy when spheres are closer than the solvent probe diameter (2.8Å). Figure 6 also compares the electrostatic interaction energy obtained using the solvent excluded molecular surface. The resulting curve deviates significantly from the one using the van der Waals surface with a factor of four difference being obtained at the 35Å separation.
Figure 6.
Electrostatic interaction energy for two low dielectric spherical cavities with interior charges embedded in a high dielectric ionic solvent, as a function of separation distance between the centers of the charged spherical cavities.
High Resolution Surface Potential Maps of Nucleic Acids and Their Binding Partners
Surface potential maps are now routinely used to identify potential binding or recognition sites on biomolecules at atomic resolution. For example, unique recognition or ion binding sites in irregular RNA structures, that contain noncanonical base pairs (e.g., GU wobble base pairs) and/or extruded (non)canonical bases, have been identified using the hybrid boundary element and finite difference nonlinear PB solver11 and confirmed using the ACG-PB technology63, 64. Obtaining such quantitative or high resolution electrostatic potential maps of large-scale biomolecules – especially highly charged ones like nucleic acids and its complexes with various charged binding partners – is very challenging for any PB solver. Surface potential maps are generated for three configurations: a small low charge RNA binding protein along with it’s a single stranded (ss) RNA binding partner, and a more highly charged noncanonical DNA structure using the nonlinear form of the PBE. The first case examines the binding of the cationic Fox-1 protein (net charge =+3e) to the RNA element UGCAUG (PDB id: 2err, model 1), where the latter is a simple single-stranded RNA structure. The solute boundary is modeled using the solvent excluded surface with atomic radii and charges specified using the CHARMM27 force field parameters38. As previously, the ion exclusion region is omitted; also T=298K, ε1=2 and ε2=80. The surface mesh spacing resolution is set to 0.3 Å and the outer boundary set to approximately three times the largest molecule dimension. In this study the first model of the NMR ensemble was employed to assess the error incurred in electrostatic potential calculations. The histidine residues were considered unprotonated while other charged residues were assigned protonation states based on a physiological pH value of 7. Thus, the Asp and Glu residues had a charge of −1e whereas a charge of +1e was assigned to the Lys and Arg residues. The 1:1 (i.e., NaCl) salt concentration was fixed at 0.1 M.
The surface maps are obtained by first identifying the mesh edges intersected by the surface (i.e., those edges with an end point in the interior and exterior domains) and then calculating the intersection points. A triangulation of the intersection points is then developed and the potentials at the intersection points developed by extrapolating the ACG solution to the surface using the nearest exterior mesh nodes. All surface potential maps are produced using the commercial program, TecPlot.
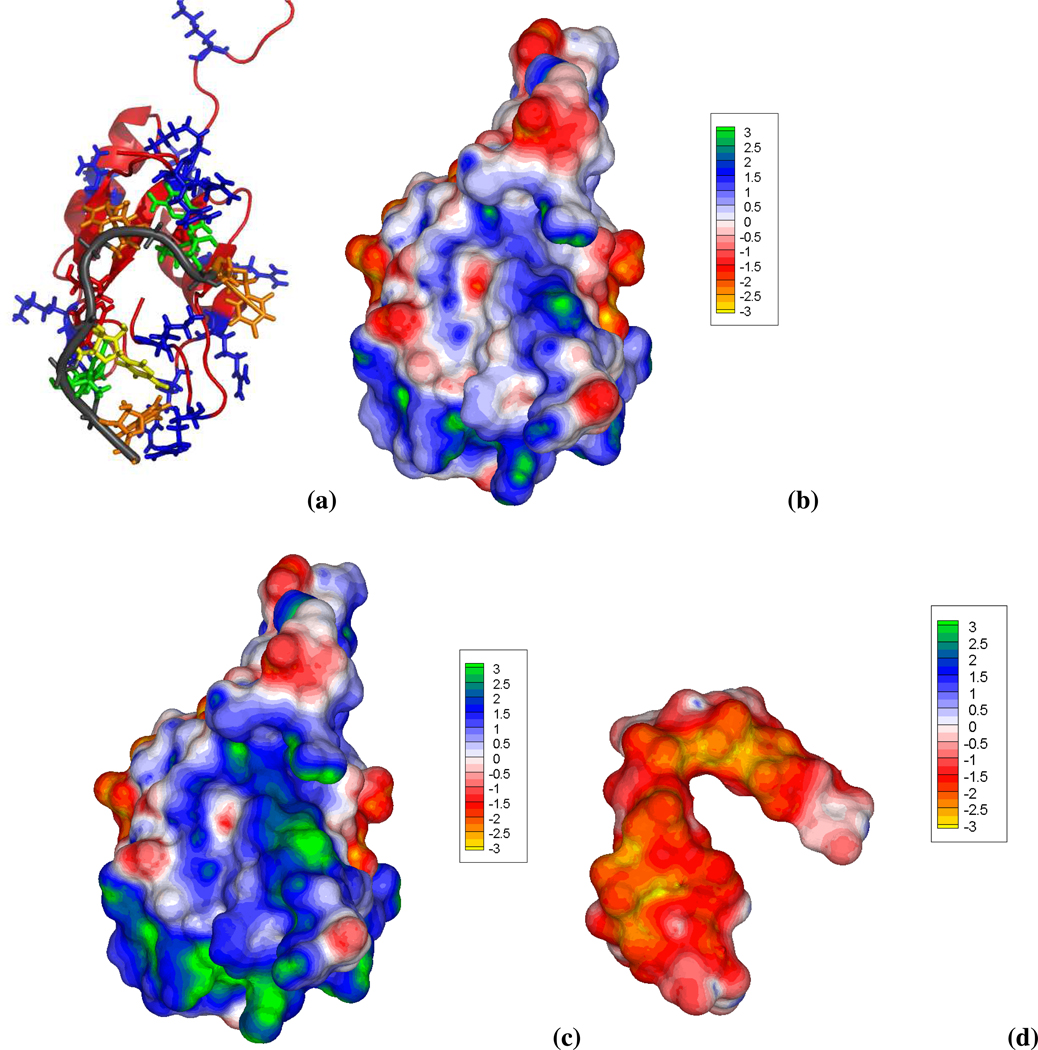
As evident from Figure 7a, b the single RNA element lies in a distinct pocket of very positive electrostatic potential on the RNA binding domain of Fox-1 protein. It has been previously reported65, 66 – on the basis of linear PBE evaluations that the surface potential in the RNA binding site of this protein is neutral. However, this is not borne out by the results obtained here with the nonlinear PBE (Figure 7b), thus highlighting the drawbacks of forming conclusions on the basis of linear PBE calculations. Predictions using the linear ACG-PB solver also show a significantly different surface potential distribution for the protein RNA binding domain of Fox-1 relative to the nonlinear one (see Figure 7b and 7c). The electrostatic potential of the ssRNA is negative over most of its surface (Figure 7d), whereas the negative potential regions of the RNA are attenuated with the presence of the cationic protein (results not shown).
Figure 7.
Different depictions of the NMR structure of RNA binding domain (RBD) of Fox-1 in complex with the single-stranded UGCAUGU RNA element (PDB id: 2err, model 1). (a) RNA phosphate backbone depicted by the dark gray ribbon and the different bases colored as: adenine= red, uracil=orange, guanine=green and cytosine=yellow. The protein peptide backbone adopts an orange ribbon representation with positively and negatively charged side chains shown as blue and red sticks, respectively. This view emphasizes the clustering of various cationic protein residues at the RNA binding interface. (b) Surface electrostatic potential (in kcal/mol/e) and overall shape of the RBD of Fox-1. A well defined and concave region of positive potential, generated by the cationic protein residues and traced by the bent RNA structure, is clearly shown when the nonlinear PBE solution is employed. This cationic protein (net charge=+3e) follows the electrostatic pattern of other RNA binding proteins that have a distinct positive potential patch on their binding interface78. Thus, the RNA fills most of concave blue/green protein surface to which it is complementary in both shape and electrostatic potential. (c) Same view and color map as (b), but using the linear PBE. The positive electrostatic potential is now overestimated and the positive region much broader than in (b). (d) Electrostatic potential of the single-stranded bent and overall negatively charged RNA structure. As expected an overall negative potential covers most of the RNA surface due to the presence of the anionic phosphate groups.
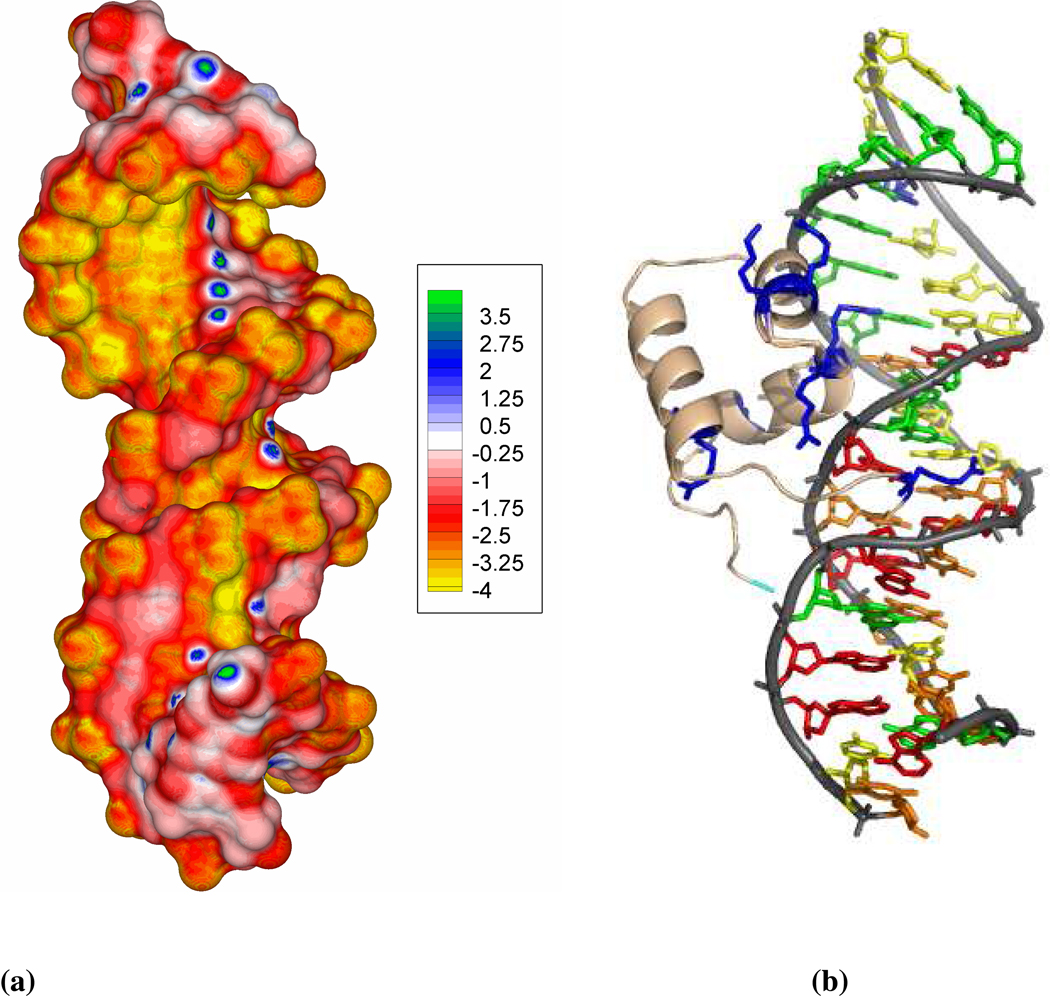
The second example is the deformed and nonlinear DNA structure in association with the Tc3 transposase protein (PDB id: 1tc3). Charges and radii are assigned using the AMBER force field37 and the solute boundary is represented using the solvent excluded molecular surface. Also, T=298K, ε1=2 and ε2=80. The 1:1 salt concentration is set to 0.1 M. It is desirable that the electrostatic potential maps for nucleic acids capture unique local sequence dependent features and the intricate phosphate charge distribution (e.g., close clustering of phosphate groups that occurs at helical junctions in RNA and DNA structures). Here high resolution surface potential maps capturing these features are produced. As portrayed in Figure 8a the G-stretch of the major groove side of the DNA structure and its locally narrowed minor groove have a deep negative potential67. The extensive region of negative potential along the G-stretch of the major groove is mostly due to the deformation of the DNA structure. Figure 8b shows how the protein Tc3 transposase positions several positively charged side chains along one side of the major groove and in the narrow minor groove, forming numerous hydrogen bonds and salt bridges in these grooves. The linear PB solution produces much larger and more negative potential patches on the grooves (results not shown).
Figure 8.
(a) The surface potential of the deformed and non-linear DNA. Radii and atomic charges are assigned using the Amber force field. This unique A/B junction DNA structure generates a surface potential map with characteristics of an A-DNA major groove and B-DNA minor groove. A continuous high negative potential band along the G-stretch along with electropositive spots due to amino groups of cytosine is observed for this nonlinear DNA structure. The electrostatic potential is given in units of kcal/mol/e. (b) The N-terminal DNA-binding domain of Tc3 transposase bound to the DNA (PDB id: 1TC3). The ribbon or tube-like representation of the DNA phosphate backbone is shown in light gray and that of the peptide backbone in gold. The cationic residues that penetrate in the narrow minor groove or face the G-stretch side of the major groove are shown in blue stick representation.
High Resolution Surface Electrostatic Potential Maps of Large-Scale Biomolecular Assemblies: Ribosomes
Due to the large-scale and highly charged nature of biomolecular assemblies such as ribosomes, which can contain more than a million atoms, it is very challenging to obtain stable and accurate electrostatic properties with standard 3D lattice nonlinear PB solvers. To date, these calculations require access to supercomputers and special techniques such as parallel focusing14, 68. Moreover, these calculations often encounter convergence issues when using the nonlinear PBE necessary to properly model these highly charged systems at the all-atom level and for resolutions finer than 0.6 Å69–72.
The computation of the surface potential can be computationally demanding for the large-scale biomolecular assemblies here considered, making such computations inaccessible to desktop computers and even large clusters. Thus, to the best of our knowledge the results here shown represent the first nonlinear PB calculation done on a serial platform for such a large-scale biomolecular system at a level of fine grid resolution of 0.3 Å using an all-atom model of a ribosomal subunit. All other reported surface potential maps of large-scale biomolecular assemblies, such as the small 30S ribosomal subunit or viruses, that were done using serial computers were obtained with the linear PBE solution, coarser grid resolutions or more approximate generalized Born-based approaches3, 69–76.
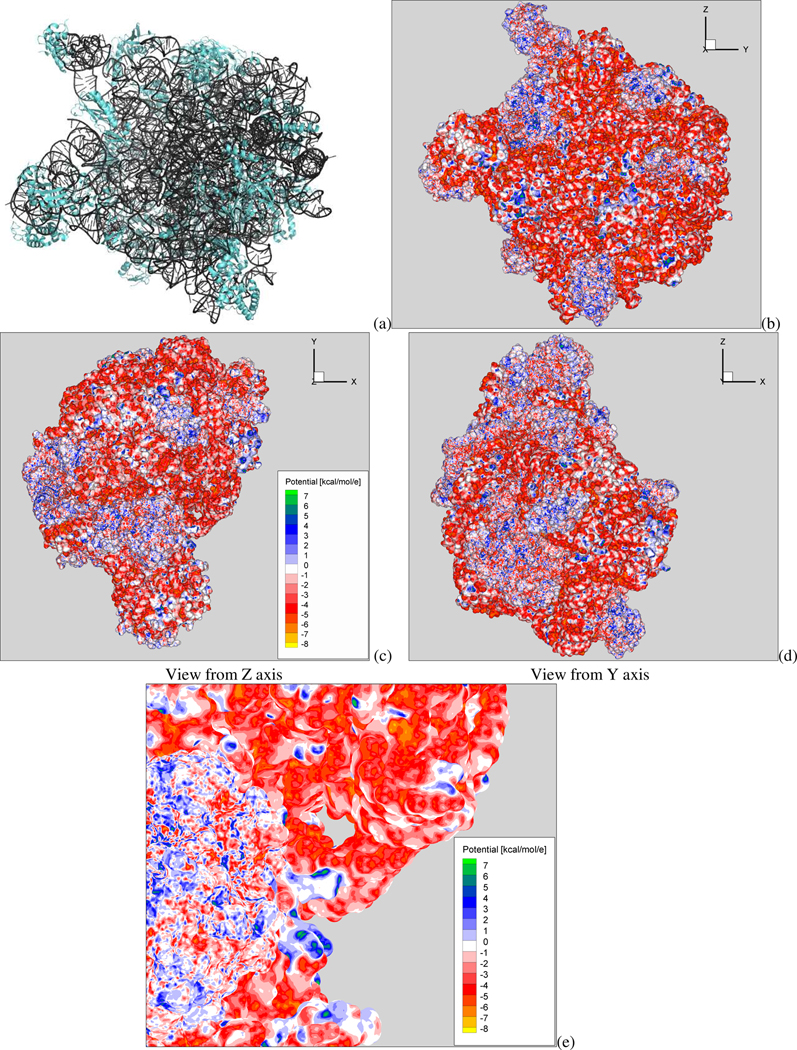
Here a high resolution electrostatic potential map of the large 50S ribosomal subunit structure from H. marismortui (PDB id: 3cc4) was computed using the nonlinear PBE. This large ribosomal subunit consists of 5S and 23S RNAs and numerous proteins with 150970 atoms and has a net charge of −2949e (see Figure 9a). The co-crystal structure of anisomycin bound to the 50S ribosomal subunit was taken from the RCSB PDB Databank. All co-factors including metals and drug were removed from the structure, and only the protein and RNA chains retained. The CHARMM38 force field atomic radii and charges were used for these PB calculations after the missing hydrogen atoms were added to the structure using the pdb2pqr server77. The solvent excluded molecular surface was, the 1:1 salt concentration was 0.1M (κ=0.1030Å−1) and the dielectric constants, ε1=2 and ε2=80.
Figure 9.
(a), Ribbon representation of the 50S ribosomal subunit (PDB id:3cc4; net charge: −2949e; 150970 atoms). The protein and rRNA molecules are shown in cyan and dark gray, respectively. (b)–(d) Different views of the surface potential (in kcal/mol/e) of the whole 50S ribosomal subunit. Note that the red and blue patches correspond to regions where the RNA and protein lie, respectively. (e) Close up view of a particular intricate region of the complex 50S subunit showing the high quality of the generated surface potential map using the ACG nonlinear PB solver at the required mesh spacing to resolve the surface geometry.
Using a finest mesh spacing of 0.3Å results in an ACG mesh with a total of 52.5 million nodes. Meshing the minimum enclosing box using a regular lattice grid with the same finest spacing would require 354 million nodes. Here the outer boundary side length is three times larger than the longest molecular dimension and thus the complete mesh spans 1228 Å. Solving the nonlinear PBE for this configuration produces stable and converged results within 170 iterations. With the ACG-based PBE solver the nonlinear PBE solution for this large-scale and highly charged biomolecular assembly took 13.5 hours using a 10-node 64-bit SGI Altix workstation. Machines of this caliber are widespread in university research departments and small businesses conducting computational biophysics research.
Figure 9b–d shows the electrostatic potential maps for the 50S ribosomal subunit (PDB id: 1CC4) and viewed from z-, y- and x-axes. The regions of positive and negative potential on the molecular surface correspond to the locations of the proteins and RNA, respectively. The presence of the proteins is essential in order to neutralize the close repulsive phosphate-phosphate interactions and thus help stabilize this intricate large-scale protein-RNA complex. A close up of a portion of the surface potential in Figure 9e reveals the resolution and attendant quality of the surface potential map. The linear PB solution provides a different potential distribution on the surface of this highly charged biomolecular entity (results not shown). Thus, the nonlinear Poisson-Boltzmann solution should be used when modeling nonspecific electrostatic interactions of the ribosome, its assembly process and associations with charged drug ligands.
Concluding Remarks and Future Directions
A finite difference method to solve the linear/nonlinear Poisson-Boltzmann equation has been formulated and implemented on a new grid structure known as an adaptive Cartesian mesh or octree. The generation of the mesh about a biomolecular structure, the construction of the finite difference operators upon the mesh, the representation of the electrostatic potential inside and outside the molecular surface, and preliminary computational results have been presented in this paper. Properties and advantages of the ACG-based PBE approach include:
Fast mesh generation due to the simple fundamental shape of the ACG cells.
Optimized grid spacing where fine cells are used where the potential gradients are changing most rapidly (i.e., at the surface) and coarser elements used elsewhere.
Use of compact finite difference formulas to evaluate the dielectric-weighted Laplacian and tailored for implementation on the ACG
A representation of the potential (total potential in the outside the molecule and reaction field potential inside) which completely eliminates charge singularities and numerically induced self-charging energies.
A robust multigrid-accelerated convergence scheme.
The incorporation of a recently developed outer boundary treatment to estimate the boundary potential and provide first order (i.e., based on a monopole approximation) corrections to computed energies.
Application of the method to idealized configurations involving charged and low dielectric spheres embedded in high dielectric ionic solvent has confirmed that the method successfully maintains high accuracy as a charge is placed near the surface, properly predicts the electrostatic interaction energies for a pair of charged spheres, and reliably converges solutions for very highly charged systems. Comparisons with semi-analytical solutions to the nonlinear PBE have verified that the ACG-based method accurately reproduces the salt-dependent behavior highly charged spheres immersed in 1:1 salt solutions. PB calculations involving very complex biomolecular systems involving highly charged nucleic acid assemblies including the 50S ribosomal subunit have also been carried out successfully. The ACG-PB solver in conjuction with molecular dynamics or Brownian dynamics techniques should allow more careful and systematic studies of the role of nonspecific electrostatic interactions on the binding of various antibacterial drugs to the ribosome, and ribosome and virus assembly processes at atomic resolution. An assessment of the performance of the nonlinear and linear PB predictions of electrostatic solvation free energies for a test set of 55 proteins – that vary in size, shape and charge distribution – are also provided in order to establish benchmark test cases for comparisons with other PB solvers.
Ongoing activity in the development of the ACG-based PBE solver includes: improved treatment of the solution near the dielectric interface to obtain more accurate predictions of the surface potential and normal gradients, and hence forces; incorporation of nonuniform ion size effects, the calculation of electrostatic interaction energies between the two molecules where the bound and unbound states differ, and validation/testing of all the above new ACG-PB features for a variety of biomolecular systems.
Supplementary Material
Acknowledgements
This work has been supported by the NIH under Grant numbers 5 R44 GM57764-03 and 5R44GM073391-03 with technical monitor, Dr. Janna Wehrle. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health. One of the authors (MOF) acknowledges the support from NIH-GM07838-01 (PI: Dr. Michael S. Chapman, OHSU, Co-PI: Dr. Marcia O. Fenley). One of the authors (MOF) would like to thank Dr. Cristina Russo, Mr. Travis Mackoy and Mr. Robert Harris for help in preparing structures, figures and some PB calculations.
Nomenclature
- C
energy conversion factor, as defined in (22)
- e
protonic charge
- f(Φ)
mobile ion charge function, as defined in (12)
- Gel
total electrostatic free energy, as defined in (20)
- Gf
fixed charged energy contribution, as defined in (21a)
- Gm
dielectric stress energy contribution, as defined in (21b)
- Grf
reaction field energy, as defined in (24)
- i, j, k
unit vectors along x, y and z, respectively
- I1:1
ionic strength of the 1:1 (monovalent) salt
- kB
Boltzmann constant
- Mℓ
ℓ-th level mesh in multigrid scheme (M0 is the finest level mesh)
- qk
normalized charge, qk=(4πe/ε1kBT)Qk, where ε1 is the interior dielectric constant
- Qk
value of the k-th charge, in units of e (electron charge)
- Ri
position of the i-th node in the ACG mesh
- t
Stern layer or ion-exclusion thickness, in Å
- T
absolute temperature of the aqueous salt solution, in K
- δ(r)
3D Dirac delta function centered at r
- Δi
size (side length) of the i-th mesh cell
- ΔΠ
excess osmotic pressure energy, as defined in (21c)
- ε
dielectric constant
- ε1, ε2
dielectric constant in the interior (Ω1 ) and exterior (Ω2 and Ω3 ) regions, respectively
- Φ
reduced (or dimensionless) total electrostatic potential
- Φc
Coulombic potential, as defined in (14)
- Φg
potential field computed on the ACG grid and defined in (16)
- Φrf
reaction field potential, Φrf=Φ − Φc
- κ
Debye-Hückel screening parameter, as defined in (11), in Å−1
- λi
residual, as defined in (18)
- ρ
charge density, in e/Å3
- ρf
contribution of fixed solute charges to the total charge density, in e/Å3
- ρm
contribution of mobile ions to the total charge density, in e/Å3
- ρk
position of k-th charge
- σi
Coulombic source term
- ωij
weights in the discrete approximation to the weighted Laplacian, e.g., (17)
- Ωi
volume domains corresponding to the molecule interior (Ω1), the Stern layer (Ω3) and the remaining exterior region, Ω2=R3−Ω1−Ω3
- ACG
Adaptive Cartesian Grid
- ACG-PBE
ACG-based PBE solver
- BEM
Boundary Element Method
- FD
Finite Difference
- FE
Finite Element
- PBE
Poisson-Boltzmann Equation
- PDB
rotein Data Bank
- PDE
Partial Differential Equation
- SA
Solvent Accessible (surface)
- SE
Solvent Excluded (surface)
- vdW
van der Waals (surface)
References
- 1.Lu B, Zhou YC, Holst MJ, McCammon JA. Recent progress in numerical methods for the Poisson-Boltzmann equation in biophysical applications. Commun. Comput. Phys. 2008;3:973–1009. [Google Scholar]
- 2.Lu J, Deutsch C. Electrostatics in the Ribosomal Tunnel Modulate Chain Elongation Rates. J. Mol. Biol. 2008;384:73–86. doi: 10.1016/j.jmb.2008.08.089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhang D, Konecny R, Baker NA, McCammon JA. Electrostatic interaction between RNA and protein capsid in cowpea chlorotic mottle virus simulated by a coarse-grain RNA model and a Monte Carlo approach. Biopolymers. 2004;75:325–337. doi: 10.1002/bip.20120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Boschitsch AH, Fenley MO, Zhou H-X. Fast Boundary Element Method for the Linear Poisson-Boltzmann Equation. J. Phys. Chem. B. 2002;106:2741–2754. [Google Scholar]
- 5.Bharadwaj R, Windemuth A, Sridharan S, Honig B, Nicholls A. The Fast Multipole Boundary Element Method for Molecular Electrostatics: An Optimal Approach for Large Systems. J. Comput. Chem. 1995;16:898–913. [Google Scholar]
- 6.Purisima EO. Fast Summation Boundary Element Method for Calculating Solvation Free Energies of Macromolecules. J. Comput. Chem. 1998;19:1494–1504. [Google Scholar]
- 7.Zauhar RJ, Varnek A. A Fast and Space Efficient Boundary Element Method for Computing Electrostatic and Hydration Effects in Large Molecules. J. Comput. Chem. 1996;17:864–877. [Google Scholar]
- 8.Boschitsch AH, Fenley MO, Olson WK. A Fast Adaptive Multipole Algorithm for Calculating Screened Coulomb (Yukawa) Interactions. J. Comput. Phys. 1999;151:212–241. [Google Scholar]
- 9.Lu B, Cheng X, Huang J, McCammon JA. Order N algorithm for computation of electrostatic interactions in biomolecular systems. Proc. Natl. Acad. Sci. USA. 2006;103:19314–19319. doi: 10.1073/pnas.0605166103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lu B, Cheng X, McCammon JA. "New-version-fast-multipole-method" accelerated electrostatic calculations in biomolecular systems. J. Comput. Phys. 2007;226:1348–1366. doi: 10.1016/j.jcp.2007.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Boschitsch AH, Fenley MO. Hybrid Boundary Element and Finite Difference Method for Solving the Nonlinear Poisson–Boltzmann Equation. J. Comput. Chem. 2004;25:935–955. doi: 10.1002/jcc.20000. [DOI] [PubMed] [Google Scholar]
- 12.Baker NA, Holst MJ, Wang F. Adaptive Multilevel Finite Element Solution of the Poisson-Boltzmann Equation II. Refinement at Solvent-Accessible surfaces in Biomolecular Systems. J. Comput. Chem. 2000;21:1343–1352. [Google Scholar]
- 13.Holst M, Baker N, Wang F. Adaptive Multilevel Finite Element Solution of the Poisson-Boltzmann Equation I: Algorithms and Examples. J. Comput. Chem. 2000;21:1319–1342. [Google Scholar]
- 14.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of Nanosystems: Application to Microtubules and the Ribosome. Proc. Natl. Acad. Sci. USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Madura JD, Briggs JM, Wade RC, Davis ME, Luty BA, Ilin A, Antosiewicz J, Gilson MK, Bagheri B, Scott LR, McCammon JA. Electrostatics and Diffusion of Molecules in Solution: Simulations with the University of Houston Brownian Dynamics Program. Comp. Phys. Commun. 1995;91:57–95. [Google Scholar]
- 16.Jo S, Vargyas M, Vasko-Szedlar M, Roux B, Im B. PBEQ-Solver for online visualization of electrostatic potential of biomolecules. Nucl. Acids Res. 2008;36:W270–W275. doi: 10.1093/nar/gkn314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bashford D, Gerwert K. Electrostatic Calculations of the pKa Values of Ionizable Groups in Bacteriorhodopsin. J. Mol. Biol. 1992;224:473–486. doi: 10.1016/0022-2836(92)91009-e. [DOI] [PubMed] [Google Scholar]
- 18.Grant JA, Pickup BT, Nicholls A. A smooth permittivity function for Poisson-Boltzmann solvation methods. J. Comput. Chem. 2001;22:608–640. [Google Scholar]
- 19.Gilson MK, Sharp K, Honig B. Calculating the electrostatic potential of molecules in solution: Method and error assessment. J. Comput. Chem. 1987;9:327–335. [Google Scholar]
- 20.Cai Q, Hsieh M-J, Wang J, Luo R. Performance of Nonlinear Finite-Difference Poisson-Boltzmann Solvers. J. Chem. Theory Comput. 2010;6:203–211. doi: 10.1021/ct900381r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Luo R, David L, Gilson MK. Accelerated Poisson-Boltzmann calculations for static and dynamic systems. J. Comput. Chem. 2002;23:1244–1253. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 22.Wang J, Luo R. Assessment of Linear Finite-Difference Poisson-Boltzmann Solvers. J. Comput. Chem. 2010;31:1689–1698. doi: 10.1002/jcc.21456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Boschitsch A, Fenley M. A New Outer Boundary Formulation and Energy Corrections for the Nonlinear Poisson–Boltzmann Equation. J. Comput. Chem. 2007;28:909–921. doi: 10.1002/jcc.20565. [DOI] [PubMed] [Google Scholar]
- 24.Gilson MK, Sharp KA, Honig B. Calculating electrostatic interactions in biomolecules: method and error assessment. J. Comput. Chem. 1988;9:327–335. [Google Scholar]
- 25.Cortis CM, Friesner RA. An Automatic Three-Dimensional Finite Element Mesh Generation System for the Poisson-Boltzmann Equation. J. Comput. Chem. 1997;18:1570–1590. [Google Scholar]
- 26.Bajaj CL, Xu G, Zhang Q. A Fast Variational Method for the Construction of Resolution Adaptive C2-Smooth Molecular Surfaces. Comput. Methods Appl. Mech. Eng. 2009;198:1684–1690. doi: 10.1016/j.cma.2008.12.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Samet H. The Design and Analysis of Spatial Structures. Addison-Wesley Publishing Company, Inc; 1990. p. 510. [Google Scholar]
- 28.Mirzadeh M, Theillard M, Gibou F. A second-order discretization of the nonlinear Poisson–Boltzmann equation over irregular geometries using non-graded adaptive Cartesian grids. J. Comput. Phys. 2011;230:2125–2140. [Google Scholar]
- 29.Aftosmis MJ, Berger MJ, Melton JE. Robust and Efficient Cartesian Mesh Generation for Component-Based Geometry. AIAA Journal. 1998;36:952–960. [Google Scholar]
- 30.Murman SM, Aftosmis MJ, Berger MJ. Simulations of Store Separation from an F/A-18 with a Cartesian Method. J. Aircraft. 2004;41(4) [Google Scholar]
- 31.Aftosmis MJ. Solution Adaptive Cartesian Grid Methods for Aerodynamic Flows with Complex Geometries. Von Karman Institute for Fluid Dynamics; 1997. Mar., Lecture Notes 1997-02. [Google Scholar]
- 32.Aftosmis MJ, Berger MJ, Melton JE. Robust and Efficient Cartesian Mesh Generation for Component-Based Geometry; 1997; 35th AIAA Aerospace Sciences Meeting & Exhibit; AIAA-97-0196, Ed. Reno, NV. [Google Scholar]
- 33.Berger MJ, LeVeque RJ. An Adaptive Cartesian Mesh Algorithm for the Euler Equations in Arbitrary Geometries; 1989; 89-1930-CP; A.; Ed. [Google Scholar]
- 34.Wang J, Cai Q, Li Z-L, Zhao H-K, Luo R. Achieving energy conservation in Poisson–Boltzmann molecular dynamics: Accuracy and precision with finite-difference algorithms. Chem. Phys. Lett. 2009;468:112–118. doi: 10.1016/j.cplett.2008.12.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhou Z, Payne P, Vasquez M, Kuhn N, Levitt M. Finite-Difference Solution of the Poisson-Boltzmann Equation: Complete Elimination of Self-Energy. J. Comput. Chem. 1996;11:1344–1351. doi: 10.1002/(SICI)1096-987X(199608)17:11<1344::AID-JCC7>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 36.Bondi A. Van der Waals Volumes and Radii. J. Phys. Chem. 1964;68:441–451. [Google Scholar]
- 37.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz K, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A 2nd generation force-field for simulation of proteins, nucleic-acids, and organic-molecules. J. Am. Chem. Soc. 1995;117:11946–11975. [Google Scholar]
- 38.Foloppe N, MacKerell ADJ. All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000;21:86–104. [Google Scholar]
- 39.Friedrichs M, Zhou R, Edinger SR, Friesner RA. Poisson-Boltzmann Analytical Gradients for Molecular Modeling Calculations. J. Phys. Chem. B. 1999;103:3057–3061. [Google Scholar]
- 40.Chan SL, Purisima EO. Molecular surface generation using marching tetrahedra. J. Comput. Chem. 1998;19:1268–1277. [Google Scholar]
- 41.Protter M, Weinberger HF. Maximum Principles in Differential Equations. Englewood Cliffs, NJ: Prentice Hall (reprint by Springer-Verlag 1984; 1967. [Google Scholar]
- 42.Barth TJ. Numerical Aspects of Computing Viscous High Reynolds Number Flows on Unstructured Meshes; 29th Aerospace Sciences Meeting; AIAA-91-0721, Ed. Reno, NV. 1991. [Google Scholar]
- 43.Chen SWW, Honig B. Monovalent and Divalent Salt Effects on Electrostatic Free Energies Defined by the Nonlinear Poisson-Boltzmann Equation: Application to DNA Binding Reactions. J. Phys. Chem. B. 1997;101:9113–9118. [Google Scholar]
- 44.Greengard L, Huang J. A New Version of the Fast Multipole Method for Screened Coulomb Interactions in Three Dimensions. New York: Courant Mathematics and Computing Laboratory, Courant Institute; 2001. p. 18. 01-002; 05-01-2001. [Google Scholar]
- 45.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes. 2 ed. Cambridge University Press; 1992. p. 960. [Google Scholar]
- 46.Holst M, Saied F. Multigrid Solution of the Poisson-Boltzmann Equation. J. Comput. Chem. 1993;14:105–113. [Google Scholar]
- 47.Oberoi H, Allewell NM. Multigrid Solution of the Nonlinear Poisson-Boltzmann Equation and Calculation of Titration Curves. Biophys. J. 1993;65:48–55. doi: 10.1016/S0006-3495(93)81032-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sharp K, Honig B. Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equation. J. Phys. Chem. 1990;94:7684–7692. [Google Scholar]
- 49.Sharp KA. Polyelectrolyte Electrostatics: Salt Dependence, Entropic, and Enthalpic Contributions to Free Energy in the Nonlinear Poisson-Boltzmann Model. Biopolymers. 1995;36:227–243. [Google Scholar]
- 50.Sharp KA, Friedman RA, Misra V, Hecht J, Honig B. Salt Effects on Polyelectrolyte-Ligand Binding: Comparison of Poisson-Boltzmann, and Limiting Law/Counterion Binding Models. Biopolymers. 1995;36:245–262. doi: 10.1002/bip.360360211. [DOI] [PubMed] [Google Scholar]
- 51.Kirkwood JG. Theory of Solutions of Molecules Containing Widely Separated Charges with Special Applications to Zwitterions. J. Chem. Phys. 1934;2:351–361. [Google Scholar]
- 52.Sader JE, Lenhoff AM. Electrical Double-Layer Interaction between Heterogeneously Charged Colloidal Particles: A Superposition Formulation. J. Colloid Interface Sci. 1998;201:233–243. [Google Scholar]
- 53.Zhou H-X. Macromolecular Electrostatic Energy Within the Nonlinear Poisson-Boltzmann Equation. J. Chem. Phys. 1994;100:3152–3162. [Google Scholar]
- 54.Schreiber G, Haran G, Zhou H-X. Fundamental aspects of protein-protein association kinetics. Chem. Rev. 2009;109:839–860. doi: 10.1021/cr800373w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Getzoff ED, Cabelli DE, Fisher CL, Parge HE, Viezzoli MS, Banci L, Hallewell RA. Faster superoxide dismutase mutants designed by enhancing electrostatic guidance. Nature. 1992;358:347–351. doi: 10.1038/358347a0. [DOI] [PubMed] [Google Scholar]
- 56.Lago H, Parrott AM, Moss T, Stonehouse NJ, Stockley PG. Probing the kinetics of formation of the bacteriophage MS2 translational operator complex: identification of a protein conformer unable to bind RNA. J Mol Biol. 2001;305:1131–1144. doi: 10.1006/jmbi.2000.4355. [DOI] [PubMed] [Google Scholar]
- 57.Zhou H-X. Boundary Element Solution to Macromolecular Electrostatics: Interaction energy between two proteins. Biophys. J. 1993;65:955–963. doi: 10.1016/S0006-3495(93)81094-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bredenberg J, Boschitsch AH, Fenley MO. The role of anionic protein residues on the salt dependence of the binding of aminoacyl-tRNA synthetases to tRNA: A Poisson-Boltzmann analysis. Commun. Comput. Phys. 2008;3:1051–1070. [Google Scholar]
- 59.Bredenberg JH, Russo C, Fenley MO. Salt-mediated electrostatics in the association of TATA binding proteins to DNA: A combined molecular mechanics/Poisson-Boltzmann study. Biophys. J. 2008;94:4634–4645. doi: 10.1529/biophysj.107.125609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bredenberg JH, Fenley MO. Salt dependent association of novel mutants of TATA-binding proteins to DNA: Predictions from theory and experiments. Commun. Comput. Phys. 2008;3:1132–1153. [Google Scholar]
- 61.Fenley MO, Harris RC, Jayaram B, Boschitsch AH. Revisiting the association of cationic groove-binding drugs to DNA using a Poisson-Boltzmann approach. Biophys. J. 2010;99:879–886. doi: 10.1016/j.bpj.2010.04.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Harris RC, Bredenberg JH, Silalahi ARJ, Boschitsch AH. Understanding the physical basis of the salt dependencd of the electrostatic binding free energy of mutated charged ligand-nucleic acid complexes. Biophys. Chem. 2011 doi: 10.1016/j.bpc.2011.02.010. appeared online. [DOI] [PubMed] [Google Scholar]
- 63.Xu D, Greenbaum NL, Fenley MO. Recognition of the spliceosomal branch site RNA helix on the basis of surface and electrostatic features. Nucleic Acids Res. 2005;33:1154–1161. doi: 10.1093/nar/gki249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Xu D, Landon T, Greenbaum NL, Fenley MO. The electrostatic characteristics of G·U wobble base pairs. Nucleic Acids Res. 2007;35:3836–3847. doi: 10.1093/nar/gkm274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Auweter SD, Fasan R, Reymond L, Underwood JG, Black DL, Pitsch S, Allain FH-T. Molecular Basis of RNA Recognition by the Human Alternative Splicing Factor Fox-1. EMBO J. 2006;25:163–173. doi: 10.1038/sj.emboj.7600918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Auweter SD, Oberstrass FC, Allain FH-T. Sequence-specific Binding of Single-stranded RNA: Is there a Code for Recognition? Nucleic Acids Res. 2006;34:4943–4959. doi: 10.1093/nar/gkl620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Xu D. Electrostatics of Nucleic Acids and Hydration Properties of the Pseudouridine Dependent Spliceosomal Branch Site Helix. Tallahassee: Florida State University; 2007. [Google Scholar]
- 68.Sayyed-Ahmad A, Miao Y, Ortoleva P. Poisson-Boltzmann theory of bionanosystems. Commun. Comput. Phys. 2008;3:1100–1116. [Google Scholar]
- 69.Trylska J, Konecny R, Tama F, Brooks CLI, McCammon JA. Ribosome motions modulate electrostatic properties. Biopolymers. 2004;74:423–431. doi: 10.1002/bip.20093. [DOI] [PubMed] [Google Scholar]
- 70.Trylska J, McCammon JA, Brooks CLI. Exploring Assembly Energetics of the 30S Ribosomal Subunit Using an Implicit Solvent Approach. J. Am. Chem. Soc. 2005;127:11125–11133. doi: 10.1021/ja052639e. [DOI] [PubMed] [Google Scholar]
- 71.Devkota B, Petrov A, Lemieux S, Bpz MB, Tang L, Schneemann A, Jonhson JE, Harvey SC. Structural and Electrostatic Characterization of Pariacoto Virus: Implications for Viral Assembly. Biopolymers. 2009;91:530–538. doi: 10.1002/bip.21168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Dlugosz M, Trylska J. Aminoglycoside association pathways with the 30S ribosomal subunit. J. Phys. Chem. B. 2009;113:7322–7330. doi: 10.1021/jp8112914. [DOI] [PubMed] [Google Scholar]
- 73.Qin S, Zhou H-X. Dissection of the High Rate Constant for the Binding of a Ribotoxin to the Ribosome. Proc. Natl. Acad. Sci. USA. 2009;106:6974–6979. doi: 10.1073/pnas.0900291106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Lu B, Cheng X, Huang J, McCammon JA. An Adaptive Fast Multipole Boundary Element Method for Poisson-Boltzmann Electrostatics. J. Chem. Theory Comput. 2009;5:1692–1699. doi: 10.1021/ct900083k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Gordon JC, Fenley AT, Onufriev A. An Analytical Approach to Computing Biomolecular Electrostatic Potential. II. Validation and Applications. J. Chem. Phys. 2008;129 doi: 10.1063/1.2956499. 075102-1-075102-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Pacios LF, Garcia-Arenal F. Comparison of Properties of particles of Cucumber mosaic virus and Tomato aspermy virus based on the analysis of molecular surfaces of capsids. J. Gen. Virol. 2006;87:2073–2083. doi: 10.1099/vir.0.81621-0. [DOI] [PubMed] [Google Scholar]
- 77.Dolinsky TJ, Nielsen JE, McCammon JA, Baker NA. PDB2PQR: an automated pipeline for the setup, execution, and analysis of Poisson-Boltzmann electrostatics calculations. Nucleic Acids Res. 2004;32:W665–W667. doi: 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Bahadur RP, Zacharias M, Janin J. Dissecting Protein-RNA Recognition Sites. Nucleic Acids Res. 2008;36:2705–2716. doi: 10.1093/nar/gkn102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.