Prediction of functionally important residues in globular proteins from unusual central distances of amino acids

Abstract

Background

Well-performing automated protein function recognition approaches usually comprise several complementary techniques. Beside constructing better consensus, their predictive power can be improved by either adding or refining independent modules that explore orthogonal features of proteins. In this work, we demonstrated how the exploration of global atomic distributions can be used to indicate functionally important residues.

Results

Using a set of carefully selected globular proteins, we parametrized continuous probability density functions describing preferred central distances of individual protein atoms. Relative preferred burials were estimated using mixture models of radial density functions dependent on the amino acid composition of a protein under consideration. The unexpectedness of extraordinary locations of atoms was evaluated in the information-theoretic manner and used directly for the identification of key amino acids. In the validation study, we tested capabilities of a tool built upon our approach, called SurpResi, by searching for binding sites interacting with ligands. The tool indicated multiple candidate sites achieving success rates comparable to several geometric methods. We also showed that the unexpectedness is a property of regions involved in protein-protein interactions, and thus can be used for the ranking of protein docking predictions. The computational approach implemented in this work is freely available via a Web interface at http://www.bioinformatics.org/surpresi.

Conclusions

Probabilistic analysis of atomic central distances in globular proteins is capable of capturing distinct orientational preferences of amino acids as resulting from different sizes, charges and hydrophobic characters of their side chains. When idealized spatial preferences can be inferred from the sole amino acid composition of a protein, residues located in hydrophobically unfavorable environments can be easily detected. Such residues turn out to be often directly involved in binding ligands or interfacing with other proteins.

Background

The task of assigning a function to each new protein structure resulting from high-throughput structural genomics experiments requires reliable computational annotation methods. Identified functionally important amino acids can provide preliminary clues on the co-evolution and molecular workings of proteins. Such information is crucial for the site-directed mutational engineering and de novo protein design. The integration of knowledge of the locations of binding sites with ligand screening or docking protocols improves initial stages of the rational drug design [1]. Also, when putative residues responsible for the complex formation are identified, protein-protein interaction interfaces can be characterized in silico [2].

Currently, due to the availability of 3D data, the exploration of properties embedded in the structure of proteins prevails over the traditional motif recognition and sequence comparison (that may turn out to be surprisingly ambiguous [3]). For close homologs, the knowledge-based approaches transfer functional annotations from proteins with already known structure and function [4-8]. Their average effectiveness is inherently limited by the availability of solved and annotated structures, so more generic methods are still desirable. Numerous pure geometry-based methods search locally for clefts and pockets in the molecular surface by employing computational geometry algorithms [9-16]. The spatial neighborhood of residues is used to characterize local environments in methods that take into account additional factors such as the flexibility of residues [17], electrostatic potential [18,19] or overall interaction energy [20], excess or deficiency of the hydrophobicity [21], hydrophobic potential around a protein [22] or a multitude of other, predominantly physicochemical, residue properties [23-27].

Interestingly, indications based on diverse descriptions are usually not correlated [28]; nor can they be used for the prediction of both protein-ligand and protein-protein interaction sites [29]. As a consequence, well-performing present-day approaches use combinations of complementary characteristics, for example the electrostatics and geometric properties [30] or the geometry and conservation [31-33]. Metaservers offer combinations of several independent fully-fledged methods in order to compensate for the shortcomings of some methods with capabilities of others [34,35]. As the compositions of distinct binding site prediction methods achieve better success rates than constituent techniques applied solo, it is still valuable not only to provide fine-tuned variations of heterogeneous approaches, but also to search for assorted methods that could complement existing ones by the exploration of specific orthogonal features.

Contrary to the majority of approaches that characterize fragments of proteins locally and with a considerable degree of detail, Brylinski et al. [21,36] showed that the rough analysis of the global spatial distribution of amino acids with respect to their hydrophobicity is capable of localizing ligation sites. They did not follow usual hydrophobicity quantifications such as the average solvent-accessible surface area or number of contacts [37], but rather measured the discrepancy between idealized and observed hydrophobicity within the fuzzy oil drop model [38], where the trivariate Gaussian distribution is used to express the idealized protein hydrophobicity (maximum value in the protein core, smoothly approaching 0 about and beyond the perimeter). It turned out that amino acids of high discrepancy (unexpectedly high hydrophobicity in relation to their peripheral position) often occur in function-related areas of proteins.

This observation is fundamental to the current work, where we devised and validated a method for the identification of function-related residues based on the probabilistic description of atomic burials originating from the conceptual framework of Gomes et al. [39]. We collected necessary statistics from a selection of globular proteins and, as opposed to the original application of the framework, we used a radial probability density function to describe preferred central distances of individual atoms of types defined within amino acids. In this view, proteins are treated as mixtures of amino acids where restraints resulting from their covalent connectivity are ignored (except for cysteines). Any deviations from the spherical shape of the macromolecule, intrinsic rigidness imposed by the presence of secondary structures and local interactions are neglected: proteins are treated as compact solid-like bodies of atoms, where the isotropic hydrophobic segregation and packing are considered to be the dominant driving forces conferring spatial organization of residues [40-42].

The classic analysis of just several protein structures suggested that the sole orientational preferences of side chains can be a criterion for the hydrophobic or hydrophilic character [43]. Therefore, although a multitude of hydrophobicity scales or burial indices are available for (whole) amino acids and many knowledge-based pair-potentials are constructed for (united) residue side chains [44], we decided to act on the per-atom rather than per-residue basis in order to account for (radial) orientational preferences of residues. The actual amino acid composition of a protein influences its native structure topology [45,46], folding type [47,48] and interactions [49]. In our statistical model, for a protein with a known amino acid abundance we assume that the relative probabilities are directly proportional to the stoichiometry. In our approach to the function prediction, every heavy atom in every amino acid of the protein considered has the measure of its unexpectedness estimated with respect to all possible atom types in a given point of space. The measure depends solely on the distance from the geometric center of the polymer. Typically, residues that place their atoms in the least probable central distances appear to contribute to the creation of ligand binding sites (including active sites of enzymes) or protein-protein binding interfaces.

Methods

Extraction of a non-redundant set of globular proteins

We examined a total of 172 265 protein chains as deposited in RCSB PDB [50] in January 2011 and excluded structures of high asymmetry or in other aspects irregular. Two geometric descriptors were used discriminatively: asphericity, calculated as the normalized sum of squared differences of the eigenvalues of the gyration tensor (according to [51]), was required to be smaller than 0.1 and compactness to be at least 0.5; the latter value was calculated as the ratio of the solvent accessible surface area of the (ideal) sphere of the volume of a considered protein to its actual solvent accessible surface area (this is a more intuitive inverse of the fraction introduced by Galzitskaya et al. [52]). Chains of sequence lengths smaller than 100 amino acids were excluded due to strong geometric constraints. Proteins that fulfill all the aforementioned conditions are denoted as globular in this paper.

Furthermore, it was required that every solved structure should contain no discontinuities, be determined with an experimental method to a resolution better than 2 Å, contain only a single domain (according to both SCOP [53] and CATH [54] classifications) and must not create multi-chain complexes, even transiently (determined on the basis of biological units assemblies available from PDB). A total of 2953 proteins were extracted for further considerations (1.71% of the whole PDB).

In the last step, in order to reduce sequence redundancy, precomputed clustering results available from the PDB, generated by the Cd-hit program [55] that grouped sequences of at least 90% of sequence identity in clusters, were used to select a single protein per every cluster. Finally, the learning data set comprised 775 high-resolution single-domain globular chains (26.2% of previously selected chains). The full list of PDB ids is available in Additional file 1 Table S1.

Compactness and asphericity of proteins in the set turned out to be only weakly interdependent (correlation coefficient, CC, -0.14). Longer chains were characterized by lower compactness (CC = -0.45) but not necessarily higher asphericity (CC = -0.06). Distributions and dependencies of geometric descriptors are presented in the Additional file 2 Figure S1.

Probabilistic description of atomic burials

Geometric centers and radii of gyration were calculated for every chain in the learning set. Distances to the geometric center of a chain of every heavy atom, r, were divided by the radius of gyration of the whole chain, r_g, enabling a uniform view of globular proteins of various sizes [43]. Histograms of such normalized distances, R = r/r_g, were collected for every amino acid-dependent atom type denoted by τ. Three types of cysteines were considered separately: generic Cys (irrespective of the presence or absence of SS bonding), Cys creating (intra-chain) disulfide bridges (denoted CSS, nearly 40% of all Cys) and Cys reduced and not involved in SS bridging (C_SH). A total of 170 histograms for different τ were obtained.

A continuous "mass" function derived by Gomes et al. [39] to describe burials of whole residues was considered for fitting. The original function expresses the quadratic increase of the volume when moving away from the core of a protein and sigmoidal decrease (Fermi function) of the atomic density in the rim as dependent on the normalized radius, R:

$$p_{\alpha }\left(R;\tau \right)=\frac{A_{\tau }{R}^2}{1+exp\left({\beta }_{\tau }\left(R^{{\alpha }_{\tau }}-{\mu }_{\tau }\right)\right)}\mathrm{\text{.}}$$ (1)

After applying the direct least-squares method for fitting individual histograms, obtained fits yielded unsatisfactory sums of the squared residuals (SSR) for atoms in hydrophilic residues, where the expression overestimated their propensity to occur in the protein core. To account for this observation, the assumption of the strictly quadratic increase was abandoned and an additional tunable parameter, γ_τ, was introduced while α_τ was set to 1 (see Additional file 3 Figure S2). The following form was finally used:

$$p\left(R;\tau \right)=\frac{A_{\tau }{R}^{{\gamma }_{\tau }}}{1+exp\left({\beta }_{\tau }\left(R-{\mu }_{\tau }\right)\right)}$$ (2)

for fitting. Parameter A_τ provides normalization, μ_τ principally determines location, β_τ influences the width of the distribution and γ_τ controls convexity of the left ridge. The goodness-of-fit of distributions of the latter form was better for 124 of 170 fits (in terms of SSR) in comparison to the original distribution function with variable α (Equation 1) and for 130 of 170 fits (F-test with p-value < 0.000001) in comparison to the original distribution function with α = 1.

Expected atomic burials in proteins

Densities of atoms are characterized globally in the environment of the protein itself in the common and reduced coordinate space. Thus, assuming the lack of void spaces inside, in a given point in space, located in the normalized distance R from the geometric center of the protein, one can estimate the expected chance of occurrence of an atom τ by relating its probability, p(R; τ), to probabilities of occurrences of all atoms, Σ_τ∈T p(R;τ), where T is the complete set of 170 atomic types. As we consider concrete protein species, probabilities depend effectively on the number of atoms τ (equal to the number of amino acids of a concrete type) present in the whole protein, n(τ). Only their relative fractions are important so we can use them directly for weighting in the expression similar to the posterior distribution of component membership in mixture models. The equation

$$\overline{p}\left(R;\tau \right)=\frac{n\left(\tau \right)p\left(R;\tau \right)}{{\sum }_{{\tau }^{\prime }\in T}n\left({\tau }^{\prime }\right)p\left(R;{\tau }^{\prime }\right)}$$ (3)

is used for the estimation of expected atomic central distances in proteins with known amino acid composition. The variability of preferred atoms in a given point in space is measured in bits as the entropy of expected burials:

$$S\left(R\right)=-\sum _{\tau \in T}\overline{p}\left(R;\tau \right){log}_2\overline{p}\left(R;\tau \right).$$ (4)

Prediction of functionally important residues

In search of residues employed directly in performing the function, we follow the crucial observation by Brylinski et al. [56] that irregularities in the global distribution of hydrophobicity often indicate function-related areas. We follow this principle in our probabilistic approach by searching for atoms of the relatively least probable central distances, $\overline{p}\left(R;\tau \right)$. Residues with such atoms are usually the hydrophobic amino acids exposed to the solvent or hydrophilic amino acids located close to the protein core. The unexpectedness of a central distance can be converted into a simple free energy-like term by the following equation:

$$Unexpectedness\left(R;\tau \right)=-{log}_2\overline{p}\left(R;\tau \right),$$ (5)

which gives estimates in bits.

Prediction of ligand binding sites

As for compact structures it holds that r_g is roughly proportional to (sequence length)^1/3 [57] and as in the task of binding sites recognition one is interested primarily in non-buried residues on the surface, the area of which is proportional to $r_g^2$, as a rule of thumb, $⌊\frac{1}{4}\cdot {\left(\text{sequence length}\right)}^{2∕3}⌋$ residues containing the most unexpected atoms are initially selected. (However, assuming the general spatial character of the statistical model, no additional factors such as estimates of solvent accessibility are taken into account.) Selected residues are weighted proportionally to the maximum value of unexpectedness among values assigned to constituent atoms and then clustered hierarchically using the pairwise average-linkage method. In search for ligand binding sites, the hierarchy of residues is partitioned into clusters separated by more than 7 Å (average Euclidean distance) that indicate (possibly multiple) putative sites. Positions of cluster centroids are computed in a weighted manner and located closer to the most unexpected atoms. Putative sites are ranked according to the proximity of their predicted centroids to the geometric center of the whole protein.

Prediction of protein-protein interfaces

Contrary to the development of the complete algorithm for the prediction of binding sites of (small) ligands, we do not attempt to create a new protein-protein docking method but rather to provide a simple unexpectedness-based scoring function for the ranking of docking predictions. Heavy atoms of one protein located within a distance of 10 Å from the other have their unexpectedness calculated and a maximum value of unexpectedness is found in this way for both macromolecules of a docked assembly. A docking prediction is then scored using the average of the highest values of unexpectedness in two interfaces.

Evaluation of predictions

The evaluation of the method based on the introduced characteristics was performed separately for the task of predicting binding sites of small ligands and for the prediction of regions creating interfaces to other proteins. In both cases, if a test data set allowed, predictions were made for unbound structures; after the assignment, the apo form was superimposed onto the holo form so that intermolecular distances were measured between the unbound structure and ligand/another macromolecule as located in the structure of the complex.

For the prediction of ligand binding sites, a set of 48 pairs of unbound/bound structures and a set of 210 bound structures, which were already employed for the benchmarking of other methods (LigSite^csc [32] and IBIS [8]), were used for the comparison with already measured success rates of the state of the art geometry-based methods: SURFNET [9], PASS [10] and LigSite [12]. The former set, further referred to as the LB₄₈ test set, includes 38 enzymes that cover 39 diverse enzymatic activities according to the EC annotations from the Catalytic Sites Atlas version 2.2.12 [58] and 10 proteins that bind compounds in their non-active sites. The latter set, referred to as the LB₂₁₀ test set, enabled large-scale benchmarking.

In order to juxtapose the results of our approach and similar fuzzy oil drop-based method (FOD), which assign prediction scores to clusters of atoms, with pocket identification methods, which indicate geometric centers of pockets located over the molecular surface, we used MSMS [59] and projected coordinates of centroids of putative binding sites onto the solvent-excluded molecular surface. Then, in order to apply the cut-off value of 4 Å used in pocket prediction benchmarks, we displaced surface-projected coordinates by 1 Å in the direction of the vector normal to the surface and 1 Å outwards from the geometric center of the protein. As the points do not always lie the space in the pocket, additionally we used the cut-off of 6 Å. We examined whether any atom of the ligand is located within the cut-off distance and reported success rates for the best ranked (Top 1) and 3 highest ranked (Top 3) candidate sites.

In order to show, preliminarily, that the unexpectedness is a property of protein-protein interfaces, we used the latest and most extensive docking benchmark (version 4.0) [60], further referred to as the PPI₁₇₆ test set. Residues of two macromolecules were considered as interfacing if they were separated by at most 4 Å. In the case of protein-protein binding interfaces, unexpected residues are usually isolated, so we did not cluster them, but rather reported the average unexpectedness in binding/non-binding protein regions.

Eventually, the capability of appropriate ranking of protein-protein docking predictions was compared to that of one of the best performing docking algorithms, ZDock [61], optionally amended with ZRank [62], and two other methods, recent ASP-Dock [63] and older FTDock [64]. The methods have their success rates already measured over the complete protein docking benchmark version 3.0 [65], so this set (referred to as the PPI₁₂₄ test set) was used to estimate the capacity of our approach. The unexpectedness-based score assessed 54,000 docking poses of a decoy generated by ZDock 3.0 operating at the rotational scanning interval of 6°. A successful prediction was defined as a docking solution of ligand C^α RMSD < 10 Å.

Comparison with other characteristics

A direct evaluation of the current method was performed in parallel with the fuzzy oil drop (FOD) method [21] using the LB₄₈ test set. The same clustering and ranking methods were used for residues with the highest unexpectedness and for residues of the highest observed vs. theoretical hydrophobicity discrepancy, $\Delta \tilde{H}$ (FOD). For the detailed comparison with other explorable characteristics, useful for the prediction of (small) ligand binding sites, the evolutionary conservation scores were assigned to residues according to the multiple-sequence alignment-based ConSurf-DB [66]; only residues of the highest conservation score (i.e. 9) are indicated in this paper. Independently, the clusters of ionisable residues with anomalous predicted titration behaviour, identified with the finite difference Poisson-Boltzmann-based technique, Thematics [25], were included in the comparison.

Results

Orientational preferences of amino acids

Parameters of probability distribution functions given by Equation 2, A_τ , μ_τ β_τ and γ_τ, were determined independently for every amino acid-dependent atom type, τ, allowing to capture the specific radial orientational propensities of amino acids. The full list of 170 sets of parameters for atomic distribution functions derived from the obtained learning set can be found in the Additional file 4 Table S2. Since the structure of side chains allows to single out the atom most distant from the C^α atom, it is possible to capture and demonstrate preferred orientations using a less redundant description. We decided to evaluate unexpectedness of every atom uniformly motivated by the fact that among 83 distributions of all side chain heavy atom types as many as 58 were statistically significantly different than distributions of relevant C^α atoms (Kolmogorov-Smirnov tests with p-value < 0.000001; see Additional file 4 Table S2 for details).

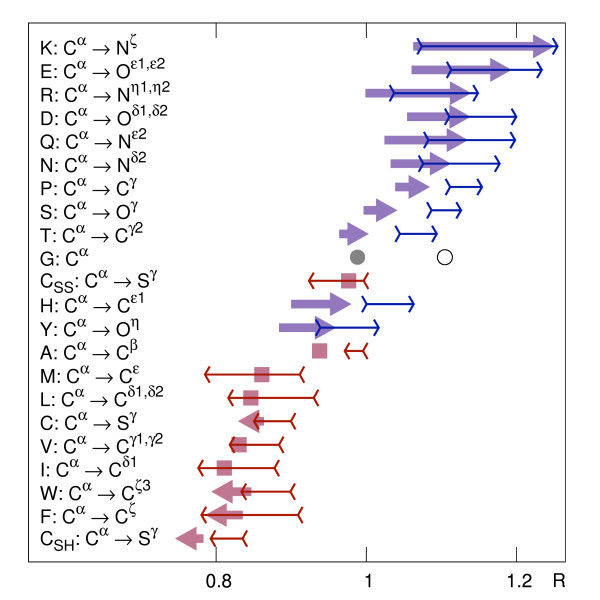
Resulting probability density functions have nonzero skewness, so in order to portray synthetically the orientational preferences, we use both differences between mean values and between maxima of distributions of C^α and distal atoms (Figure 1). The arrows can be interpreted as expressing global hydrophobic moments of (amphiphilic) residues defined in the environment of the protein itself (analogous to [67]). In this view, the two amino acids of the most prominent opposite orientational preferences are Lys and Phe (Figure 2).

Figure 1.

Orientational preferences of amino acids in globular proteins. Locations of mean and maximum values of probability density functions for C^α and most distant side chain atoms for all amino acids. Thick arrows connect means; thin arrows span between maxima of distributions. All arrows point towards the most distal atom in the side chain (except for Gly) according to the labels on the left. The arrows that would be shorter than their heads are replaced by squares.

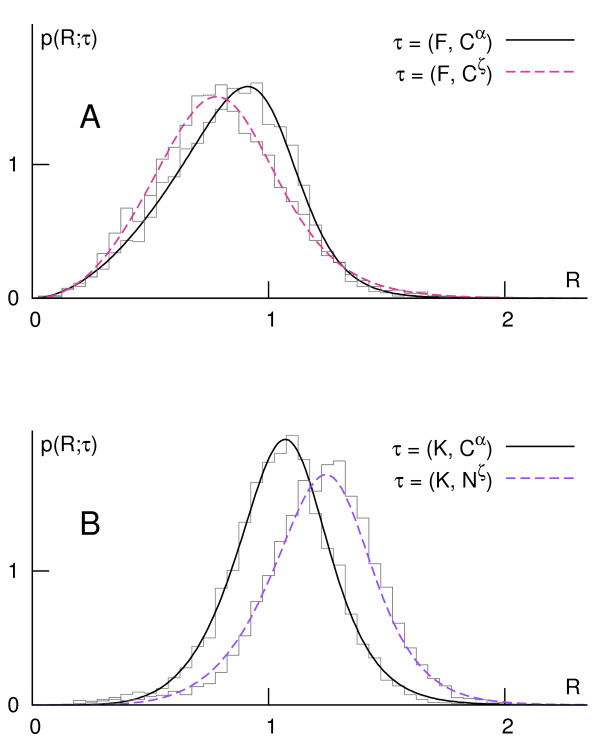
Figure 2.

Probability densities of C^α and of the most distal side chain atom in Phe and Lys. The two amino acids exhibit the most prominent (the largest separation of the means) and opposite (centripetal, A, vs. centrifugal, B) orientational preferences.

Although side chains determine the hydrophobic/hydrophilic character of amino acids, they influence considerably probabilities of spatial occurrence of (chemically equivalent across amino acid types) C^α atoms. In the synthetic picture of atomic densities (Figure 1 and Additional file 5 Figure S3), hydrophobic propensities of amino acids in the body of a protein are modulated by their sizes: broad distributions of Gly and Ala atoms are shifted from those of other hydrophobic types; distributions of large amino acids, such as Trp or Arg, are less dispersed around their maxima; the broad distribution of His can be explained by diverse possible protonation states and the ambivalent distribution of Tyr - by mixed aromatic/polar character of its side chain.

The analysis of the intriguing case of Cys reveals that, although their orientation does not depend on the possible disulfide bonding, the non-bridging cysteines prevail as the most buried residues, while those constituting cystines occur more often on the protein surface (Figure 1; Additional file 6 Figure S4). Cysteines are relatively frequently found in active sites [68]; supposedly, the evolution may easily redefine the function of a protein by tailoring the state of cysteines and adjusting their positions [69].

Distribution of unexpectedness

The mean central reduced distances of distal site chain atoms are in agreement with known hydrophobicity scales, especially those empirical ones based on the surface accessibility. Several theoretical and one experimental scale, along with similarities expressed in terms of the correlation coefficient, are listed in Table 1.

Table 1.

Correlations of mean values of distal side chain atom distributions to other characteristics

CC	Description of the characteristics	Reference
-0.984	Mean fractional area loss upon folding	[88]
-0.974	Solvent accessibility based on self-information [16% accessibility]	[89]
-0.971	Information value for accessibility [average fraction 35%]	[90]
+0.961	Normalized eigenvector of the Sweet & Eisenberg scale	[91]
-0.951	Mean combined polarity calculated from distributions of residues in proteins	[92]
+0.897	Hydrophobicity coefficient in RP-HPLC [C4 with 0.1%TFA/MeCN/H2O]	[93]

Similarities of 5 theoretical (top) and 1 experimental (bottom) single-value amino acid characteristics are expressed in terms of the correlation coefficient, CC. (For Cys, the distribution of reduced S^γ was used.)

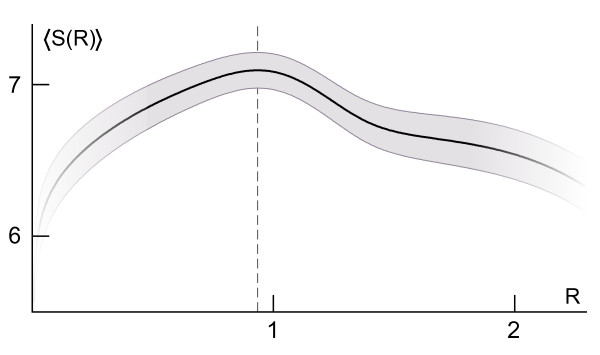
The statistical model applied to globular proteins from the learning set reveals a critical value of about 0.93 · r_g, where the average entropy, calculated according to the Equation 4 and interpreted as the lack of preference for particular atomic types, has the highest value (Figure 3). The value marks clearly the hydrophobic-hydrophilic transition on the protein surface, usually covered by a patchwork of hydrophobic and hydrophilic areas [70,71]. Although it was observed in larger proteins that the degree of hydrophobicity is constant for R <0.7 [72], according to the model the protein interior is not a volume of uniform preferences, but rather it visibly exhibits a gradually increasing preference for some apolar atomic types (decreasing entropy) when moving towards the centroid.

Figure 3.

Entropy of expected reduced central distances in globular proteins. The entropy, S(R), of $\overline{p}\left(R;\tau \right)$ was averaged over all proteins from the learning set and is expressed in bits (black line; gray band - standard deviation of the mean entropy; dashed line - location of the maximum). "Twilight zones" mark regions where the entropy was calculated using tails of distributions.

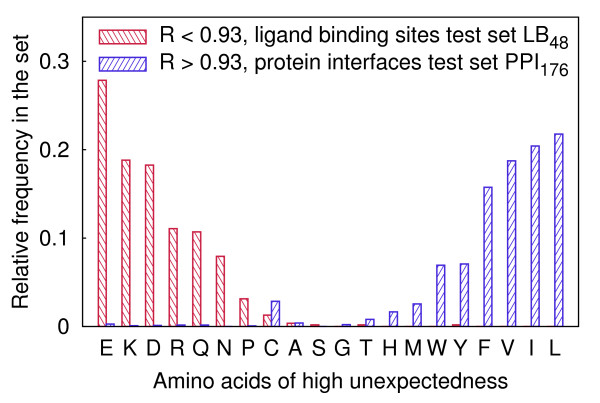
Types of the most unexpected amino acids (i.e. amino acids comprising most unexpected atoms) were determined in the LB₄₈ test set and in the PPI₁₇₆ test set separately (Figure 4). In the former set, the additional requirement of R <0.93 and in the latter the requirement of R >0.93 were imposed, because several proteins in the LB₄₈ test set create complexes with other proteins and proteins in the PPI₁₇₆ test set contain ligand binding pockets. According to the model, the most unexpected residues lying within the radius of gyration are those charged or ionizable, such as Glu, Asp, Lys and Arg, which are known to play essential functional roles in the enzymatic active sites. Amino acids with branching aliphatic side chains, Leu, Val and Ile, are properly assessed as being rarely exposed to the solvent. Unfortunately, broad distributions of central distances of His and Tyr cause them to be hardly ever indicated as unexpected. Also, due to the specific structural roles of Pro and Cys, such residues tend to be rated as unexpected despite the possible lack of any direct relation to the function.

Figure 4.

Relative frequencies of amino acids characterized by high unexpectedness. Residues lying within 0.93 · r_g in proteins from a set used for the ligand binding site prediction and residues of central distances greater than 0.93 · r_g from a set used for the protein-protein interface prediction are presented separately.

Prediction of ligand binding sites

Clusters of unexpected residues turn out to be located on the surface of proteins, very often inside clefts and pockets, where ligand compounds are bound. Geometric centroids of such clusters designate candidate ligand binding sites with the success rate similar to that of the fuzzy oil drop-based method in the LB₄₈ test set and only slightly worse in the LB₂₁₀ test set (see Table 2). For the cut-off value of 6 Å of the distance to a ligand, considered as enabling the comparison, the performance of both global hydrophobicity distribution-based strategies is similar or even marginally better than that of three state of the art methods, PASS, LIGSITE and SURFNET, which distinguish clefts or cavities based solely on the local geometry (Table 2).

Table 2.

Benchmarks of several ligand binding site prediction methods

	LB48 test set		LB210 test set
Method	Top 1	Top 3	Top 1	Top 3
PASS	60*	71*	54*	79*
LIGSITE	58*	75*	65*	85*
SURFNET	52*	75*	42*	56*
FOD	56 (71)	60 (81)	55 (68)	72 (83)
Unexpectedness	48 (69)	63 (83)	53 (65)	67 (80)

The comparison of ligand binding site prediction success rates of the current approach (Unexpectedness), a global hydrophobicity-based method (FOD) and several non-hybrid pocket-searching state of the art methods for 48 unbound molecules from the LB₄₈ test set. The cut-off distances are 4 Å and 6 Å (success rates for the latter value are in parentheses). Results marked with stars were reported in [32].

The relations to other characteristics frequently exploited for the localization of binding sites, viz., conservation and electrostatics, were examined for residues in properly indicated Top 3 clusters (Table 3). There are no clusters with active site residues displaying neither conservation nor the indicative anomalous ionisable behavior - in fact, in most cases there is a significant overlap between the unexpectedness and two other attributes; in remaining cases the three features may be seen as complementing one another (especially for residues that are nonionizable or bind with low specificity).

Table 3.

Residues in correctly predicted 3 top-ranked clusters

Structure	Function	Cluster
1ahc A	(RNA) glycosidase	$\underset{¯}{\text{R}},\underset{¯}{\ddot{\text{E}}},\ddot{\mathsf{\text{E}}},\underset{¯}{\mathsf{\text{Q}}}$
1bbs A	proteinase	$\underset{¯}{\ddot{\text{D}}},\underset{¯}{\ddot{\text{D}}}$
1bya A	O-glycosidase	$\underset{¯}{\ddot{\text{E}}},\underset{¯}{\mathsf{\text{R}}},\underset{¯}{\ddot{\mathsf{\text{E}}}},\mathsf{\text{P}}$
1cge A	metalloproteinase	$\underset{¯}{\ddot{\text{E}}}$
1djb A	hydrolase (β-lactamase)	$\underset{¯}{\text{K}},\underset{¯}{\text{E}}$
1hsi A	protease (HIV-2 retropepsin)	$\underset{¯}{\mathsf{\text{I}}}\left(\mathsf{\text{flaps}}\right)$
1hxf H	(serine) protease	$\underset{¯}{\ddot{\text{D}}}$
1ifb A	fatty acid binding	$\ddot{\text{R}},\text{E}$
1ime A	(inositol) phosphatase	$\underset{¯}{\ddot{\text{D}}},\underset{¯}{\ddot{\text{D}}},\underset{¯}{\ddot{\text{D}}}$
1krn A	hydrolase (fibrinolysin)	$\ddot{\text{K}}$
1l3f E	proteolysin	$\underset{¯}{\text{E}}$
1nna A	O-glycosidase	$\underset{¯}{\ddot{\text{K}}},\underset{¯}{\ddot{\text{E}}},\underset{¯}{\text{R}},\underset{¯}{\ddot{\text{E}}},\underset{¯}{\text{Q}}$
1npc A	(metallo)protease	$\underset{¯}{\text{E}},\underset{¯}{\mathsf{\text{E}}}$
1pdy A	enolase	$\underset{¯}{\text{K}},\underset{¯}{\mathsf{\text{R}}},\underset{¯}{\mathsf{\text{Q}}}$
1psn A	(acid) proteinase	$\underset{¯}{\ddot{\text{D}}},\underset{¯}{\ddot{\text{D}}}$
1pts A	azobenzoic acid binding	$\underset{¯}{\mathsf{\text{D}}}$
1qif A	(acetylcholin)esterase	$\underset{¯}{\ddot{\mathsf{\text{E}}}}$
1stn A	(phosphodi)esterase	$\underset{¯}{\text{R}},\underset{¯}{\ddot{\text{D}}}$
1ypi A	(triosephosphate) isomerase	$\underset{¯}{\text{K}},\underset{¯}{\mathsf{\text{E}}}$
2cba A	lyase (anhydrase)	$\underset{¯}{\ddot{\mathsf{\text{E}}}},\underset{¯}{\ddot{\text{E}}}$
2ctb A	hydrolase (carboxypeptidase)	$\underset{¯}{\text{E}}$
2fbp B	(fructose bis)phosphatase	$\underset{¯}{\text{K}},\underset{¯}{\ddot{\text{E}}},\underset{¯}{\text{D}},\underset{¯}{\ddot{\text{D}}},\underset{¯}{\ddot{\text{E}}}$
2sil A	hydrolase (neuraminidase)	$\ddot{\mathsf{\text{E}}},\text{Q},\text{Q},\underset{¯}{\ddot{\text{R}}},\underset{¯}{\ddot{\text{R}}}$
3app A	(acid) proteinase	$\underset{¯}{\ddot{\text{D}}}$
3p2p A	(carboxyl)esterase	$\mathsf{\text{R}},\underset{¯}{\text{D}}$
3ptn A	hydrolase (tripsin)	$\underset{¯}{\text{D}}$
3tms A	(methyl)transferase	$\underset{¯}{\ddot{\text{E}}},\underset{¯}{\text{N}},\underset{¯}{\mathsf{\text{Q}}}$
5dfr A	(folic acid) reductase	$\underset{¯}{\text{D}}$
8adh A	dehydrogenase	$\underset{¯}{\text{E}},\underset{¯}{\ddot{\text{D}}}$
8rat A	hydrolase (ribonuclease)	$\underset{¯}{\ddot{\text{K}}},\text{Q}$

Residues are sorted in rows according to decreasing unexpectedness. Residues of the highest evolutionary conservation scores according to the ConSurf-DB [66] are underlined; residues indicated as functional by Thematics [25] have overbars; bold residues are annotated as catalytic in the Catalytic Sites Atlas (CSA) [58]. (Two chains of non-enzymatic functions are unannotated in the CSA.)

Among the proteins annotated with EC numbers in the LB₄₈ test set, 35 out of 38 enzymes have their active sites recognized in Top 3 clusters (31/38 in Top 1). Notwithstanding, out of 10 proteins that exhibit no enzymatic activity and bind ligands in their non-active sites, binding sites are properly recognized in only 5 cases, mainly because of their eccentric locations (see Additional file 7 Table S3 for details).

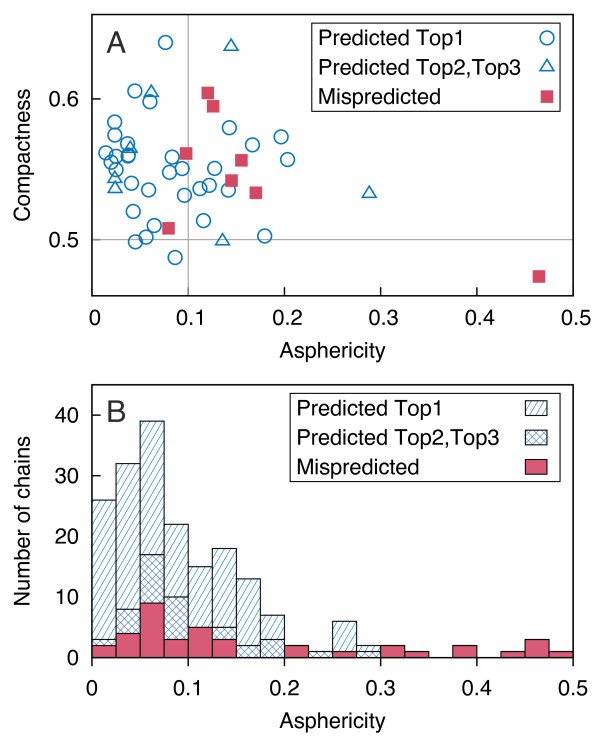
The predictive power of our approach decreases moderately for more aspherical proteins. The quality of cluster rankings seems to be independent of the asphericity (Figure 5).

Figure 5.

Dependence of the prediction success on geometric characteristics. Predictions for apoproteins from the LB₄₈ test set (A) and holoproteins from the LB₂₁₀ test set (B) are shown (cut-off 6 Å). Two perpendicular thin gray lines correspond to the geometric requirements imposed on proteins in the learning set.

Ranking of protein-protein docking results

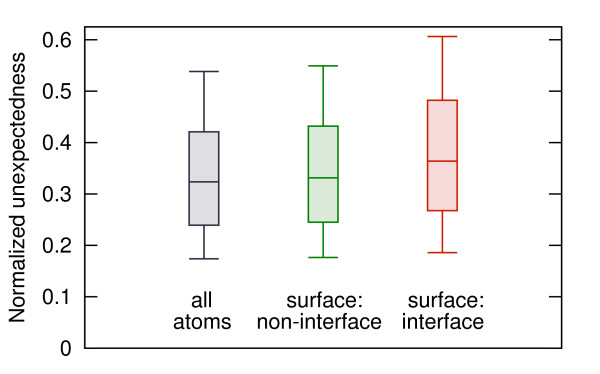
The unexpectedness was employed to characterize the protein-protein interfaces in the PPI₁₇₆ test set, where the majority of structures have the asphericity higher than 0.1. Despite this difficulty, the median unexpectedness of interacting residues turns out to be clearly higher than the median unexpectedness of all surfaces residues (Figure 6). When a subset of more globular proteins is examined, the difference is even more salient (not shown).

Figure 6.

Unexpectedness of atoms in protein interfaces. Normalized values of unexpectedness for all atoms and atoms belonging to residues exposed to the solvent (residue solvent-accessible area >10 Ų), subdivided into these creating and not creating protein-protein interfaces. Whiskers represent the 9^th and the 91^st percentile.

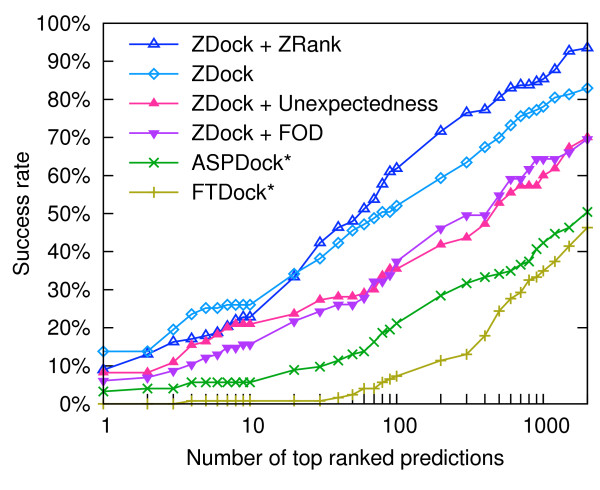
Scoring of interfaces based on the unexpectedness yields consistently better results than an analogous FOD-based scoring for 100 top-ranked solutions (Figure 7). For 10 top-ranked docking solutions success rates of our approach are nearly comparable to that of the ZRank, indicating that our score can properly account for desolvation and electrostatics-related properties used (in addition to van der Waals interactions) by ZRank.

Figure 7.

Effectiveness of rankings of docking solutions. Decoys generated and ranked by ZDock were reranked using ZRank, $\Delta \tilde{H}$ (FOD) and the unexpectedness. Success rates of two independent docking approaches, FTDock and ASPDock, marked with stars, are displayed as reported in [63].

Comparison to the fuzzy oil drop model

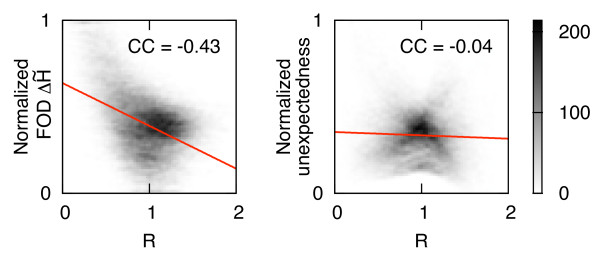
Ranking clusters according to the most unexpected atoms turned out to be less specific than the ordering based on the FOD-based discrepancy between theoretical and empirical hydrophobicity, $\Delta \tilde{H}$. Searching for the reason of disadvantageous cluster rankings we found that the FOD method not only quantifies the hydrophobicity discrepancy, but primarily indicates residues in the proximity to the molecular centroid (Figure 8). Visibly, the fuzzy oil drop model inadequately overestimates the hydrophobicity in protein cores. The satisfactory predictive capability and advantageous ranking of the FOD-based method can be explained by the observation that the distance to the centroid can be used autonomously for the detection of active sites and enzyme-ligand interfaces [73]. In our probabilistic approach, unexpectedness of atoms is virtually independent of their central distances.

Figure 8.

Dependence of $\Delta \tilde{H}$ and unexpectedness on reduced central distances. Two normalized global estimators of hydrophobic excess or deficiency, $\Delta \tilde{H}$ (according to the fuzzy oil drop model) and the unexpectedness, vs. reduced distance from the geometric center of a protein, R. Linear fits and correlation coefficients (CC) for 2D histograms were calculated for all atoms of unbound proteins from the LB₄₈ test set.

Availability

We developed a web server SurpResi for the prediction of functionally important sites based on the unusual central distances of atoms. The input of SurpResi server is a Protein Data Bank (PDB) file or user file in the PDB format. The output is a downloadable PDB file where the column of beta factors is replaced by the unexpectedness and the occupancy is replaced by the same value normalized to the range [0,1] over all protein atoms. In the header section, the file contains detailed information about clustering and ranking of clusters. The web server and source code are freely available at http://www.bioinformatics.org/surpresi.

Discussion

The presented approach quantifies polar and directional propensities of amino acids using the partition in the knowledge-based continuous gradient of hydrophobicity generated by the protein itself. It yields a middle level of description of hydrophobic preferences between (coarse-grained) scales of hydrophobicity and (fine-grained) residue-residue contact matrices, where more specific local effects such as homophilic, counterion or phenyl rings interactions can be expressed explicitly [74]. It has been already demonstrated that reduced representations and global geometric potentials are capable of a quantitative description of protein-ligand binding sites [75,76].

The adopted view concentrates on the characterization of proteins not assuming any specific chemical properties of ligands. Although based on a statistical model parametrized assuming spherical shapes of proteins (resembling the assumption behind the generalized Born solvation model), the method works well for moderately aspherical macromolecules, allowing for not only descriptive but also predictive applications. We do not incorporate into the identification method any additional features, such as the solvent accessible area or evolutionary conservation; the direct distance to the centroid was used only for the ranking in order to enable fair comparison with the FOD method; our measure is assigned homogeneously and isotropically in the whole protein volume, thus allowing for the examination of the predictive potential of the sole unexpectedness.

Favorable outcomes of our approach, especially when applied to enzymatic active sites, can be explained by analyzing the consequences of the requirement of the precise and resolute positioning of a ligand (as the prerequisite for chemical specificity), which can be best fulfilled by the creation of a binding pocket [77]. The burial of (still accessible) charged amino acids or the exposure of (partially unburied) conjugated aromatic ones, which are essential from the point of view of the mechanisms of the catalytic reactions, are not commensurate with their general expected radial positions in the bulk protein body. Frequently, despite their indented locations, pocket residues cannot be predominantly apolar as well, because of the need for the presence of bound water molecules assisting the catalysis (involved in, e.g., nucleophilic attack).

The most unexpected atoms are usually found in the deep-set parts of the pockets. The atomic depth has been found to be correlated with residue conservation [78,79] (more conserved amino acids create more contacts), which provides the explanation for the overlap between the sets of unexpected and conserved residues. It has been found, based on electrostatics, that functional sites comprise the most destabilizing residues [18]. Similarly, the unexpected amino acids are those introducing a local hydrophobic mismatch, plausibly counterbalanced by the formation of salt bridges and hydrogen bonding. The relation of the unexpectedness to the electrostatics is not, however, as simple as in the case of the conservation: buried charged residues can be encountered occasionally. It has been also demonstrated that electrostatic and hydrophobic interactions may compete [80]. This interplay is important with respect to the desolvation energy. The ease of desolvation is strongly predictive of protein-binding interfaces [29] and influences intricately ligand binding affinities [81]. As the hydrophobic interactions are dominant at protein interfaces [82], indicated scattered residues at the surface likely coincide with the view of the small fraction of hot-spots, which account for the majority of the binding energy [83].

Our approach yielded sets of parameters for every atom in an amino acid of a given type that is similar to the construction of a hydrophobicity scale, because the amount of information needed to characterize a protein is linearly proportional to the length of its sequence. The introduction of information-theoretic interpretation of hydrophobicity distributions may lead to valuable insights [84]. One result of the meeting of hydrophobicity and information theory, especially noteworthy in this context, supports our approach by demonstrating improvements in contact potentials tailored to the compositional properties of the sequences of interest [85].

The "mixture model" used in Equation 3 may be tuned via the expectation-maximization procedure to better fit the idealized distribution of the mass in individual proteins. However, we observed no improvement in the performance of the predictions for tuned forms, probably due to the already balanced composition of hydrophobic and polar amino acids in proteins selected by nature [86]. In this view, it would be interesting to check whether sequences of disordered or unfoldable structures give "mixture models" that deviate significantly from compact atomic distributions. It seems to be possible to apply the method from the smoothed surface towards the protein interior to some depth, and in this way cover proteins of more irregular shapes, consequently surpassing the most severe limitation of the approach. The attempt would require, however, the inquiry into the structure of hydrophobic cores in elongated or bent proteins.

The method is expected to be applicable for the functional annotation of low resolution structures, e.g., those resulting from mature homology modeling pipelines. Crude estimates of unexpectedness may be advantageous over computational geometry-based methods requiring precise atomic coordinates of active sites, where residues or even whole loops undergo significant displacements, not obeying the classic lock-and-key model [87].

Conclusion

We present an approach that captures orientational propensities of amino acids in globular proteins and offers a balanced description of their hydrophobic preferences. The description is created at the granularity of individual (amino acid-dependent types of) atoms but does not enumerate explicitly all possible interactions between them.

The approach is useful for the construction of a generic method that quantifies the unexpectedness of occurrences of individual atoms in a given distance from the geometric center of a protein. It turns out that the characteristics can be applied to the recognition of binding sites of both small ligands (enzymatic active sites) and other proteins (protein-protein interfaces).

Authors' contributions

MK conceived of the study, implemented the method, carried out computations, analyzed results and wrote the manuscript.

Supplementary Material

Additional file 1

Protein chains in the learning set.

Additional file 2

Geometric characteristics of the learning set and their dependencies.

Additional file 3

The plot of the probability density function used in this work.

Additional file 4

Parameters of atomic distributions.

Additional file 5

Probability densities of C^α and distal side chain atoms of 20 amino acids.

Additional file 6

Probability densities of C^α and distal side chain atoms of Cys.

Additional file 7

Details on the efficiency of the SurpResi applied to the LB₄₈ test set.

Acknowledgements

The author would like to thank prof. I. Roterman for reading a preliminary version of the manuscript and dr. K. Prymula for discussions. A computational grant from the Academic Computer Center (ACK) CYFRONET AGH (MNiSW/IBM_BC_HS21/UJ/049/2009) is acknowledged.