Parallel fuzzy connected image segmentation on GPU

Abstract

Purpose: Image segmentation techniques using fuzzy connectedness (FC) principles have shown their effectiveness in segmenting a variety of objects in several large applications. However, one challenge in these algorithms has been their excessive computational requirements when processing large image datasets. Nowadays, commodity graphics hardware provides a highly parallel computing environment. In this paper, the authors present a parallel fuzzy connected image segmentation algorithm implementation on NVIDIA’s compute unified device Architecture (cuda) platform for segmenting medical image data sets.

Methods: In the FC algorithm, there are two major computational tasks: (i) computing the fuzzy affinity relations and (ii) computing the fuzzy connectedness relations. These two tasks are implemented as cuda kernels and executed on GPU. A dramatic improvement in speed for both tasks is achieved as a result.

Results: Our experiments based on three data sets of small, medium, and large data size demonstrate the efficiency of the parallel algorithm, which achieves a speed-up factor of 24.4x, 18.1x, and 10.3x, correspondingly, for the three data sets on the NVIDIA Tesla C1060 over the implementation of the algorithm on CPU, and takes 0.25, 0.72, and 15.04 s, correspondingly, for the three data sets.

Conclusions: The authors developed a parallel algorithm of the widely used fuzzy connected image segmentation method on the NVIDIA GPUs, which are far more cost- and speed-effective than both cluster of workstations and multiprocessing systems. A near-interactive speed of segmentation has been achieved, even for the large data set.

INTRODUCTION

Image segmentation is the process of identifying and delineating objects in images. It is the most crucial of all computerized operations done on acquired images. Even seemingly unrelated operations, like image (gray-scale/color) display, 3D visualization, interpolation, filtering, and registration depend, to some extent, on image segmentation; since they all would need some object information for their optimum performance. In spite of several decades of research,^{1, 2} segmentation remains a challenging problem in both image processing and computer vision.

The fuzzy connectedness (FC) framework and its extensions^{3, 4, 5, 6, 7, 8} have been extensively utilized in many medical applications, including multiple sclerosis (MS) lesion detection and quantification via MR imaging,⁹ upper airway segmentation in children via MRI for studying obstructive sleep apnea,¹⁰ electron tomography segmentation,¹¹ abdominal segmentation,¹² automatic brain tissue segmentation⁸ in MRI images, clutter-free volume rendering and artery–vein separation in MR angiography,¹³ in brain tumor delineation via MR imaging,¹⁴ and automatic breast density estimation via digitized mammograms for breast cancer risk assessment.¹⁵ High segmentation accuracies of the FC algorithms have been achieved in these clinical applications, such as true positive volume fraction of more than 96% in brain tissue segmentation,⁸ false negative volume fraction of 1.3% in MS lesion detection and quantification,⁹ an accuracy of 97% in upper airway segmentation.¹⁰ New imaging technologies are capable of producing increasingly larger image data sets, and newer and advanced applications in quantitative radiology call for real-time or interactive segmentation methodologies. One problem with the FC image segmentation algorithms has been their high computational requirements for processing large image data sets.¹⁶

Several parallel implementations have been developed to improve the efficiency of the fuzzy connectedness algorithms. A parallel implementation of the scale-based FC algorithm has been developed for implementation on a cluster of workstations (COWs) by using the message passing interface (MPI) parallel-processing standard.¹⁶ A manager-worker scheme has been used in this implementation. The manager processor keeps a watch on the worker processors as to whose queues become empty and who, therefore, may become idle. A worker processor may be activated because there are chunks (subsets) of image data, whose queues are still not empty. The entire segmentation process stops at the point when all queues maintained by all processors (the workers) become empty. A speed-up factor of approximately three has been achieved on a COW with six workstations. An OpenMP-based parallel implementation of the fuzzy connectedness algorithm has been reported recently.¹⁷ This algorithm has been adapted to a distributed-processing scheme.⁷ This scheme also works using manager-worker paradigm in which there are several processors (the workers) handling subsets of the data set and a special processor (the manager) that controls how the other processors carry out the segmentation of their corresponding subset. A speed increase of approximately five has been achieved related to the sequential implementation. OpenMP requires special compilers that recognize directives embedded in the source code which control parallelism. Typically, OpenMP systems are expensive, tightly coupled, shared memory multiprocessor systems (MPS), such as the SGI Altix 4700, which is the hardware being used in Ref. 17. The lower boost factor achieved in Ref. 16 compared to Ref. 17 might be due to the very fast FC algorithm employed¹⁸ to begin with and due to the differences in image data, objects segmented, and the computing platforms used.

The aim of this study is to describe a parallel implementation of the FC algorithm using less expensive hardware, which can achieve vastly higher speed-up factors than both the COW and MPS systems. Toward this goal, we chose massively parallel graphics processing units (GPU) to accelerate the FC algorithms, mainly because the GPU has substantial arithmetic and memory bandwidth capabilities. Coupled with its recent addition of user programmability, it has permitted general-purpose computation on graphics hardware (GPGPU).¹⁹ Moreover, the GPU has very low cost, is wide available, and can be used on a normal desktop PC.

The use of GPU as a hardware accelerator has attracted much recent attention and has proved to be an effective approach in the domain of high performance scientific computation.²⁰ Since medical imaging applications intrinsically have data-level parallelism with high compute requirements, they are highly suitable for implementation on the GPU. Several studies of medical imaging applications on GPU have been reported recently, such as in deformable image registration,²¹ Monte Carlo-based dose calculation in radiotherapy,²² and image segmentation.^{23, 24, 25, 26} An interactive, GPU-based level set segmentation tool called GIST has been developed for 3D medical images in Ref. 23. A sparse level set solver has been implemented on the GPU. An improvement of the GPUs narrow band algorithm has been proposed.²⁴ The communication latency between the GPU and CPU that exists²³ has been avoided by traversing the domain of active tiles in parallel on the GPU. Thus, the computational efficiency has been dramatically improved. A GPU-based random walker method has been presented for interactive organ segmentation in 2D and 3D medical images.²⁵ It is implemented on an ATI Radeon X800 XT graphics card by using a graph cuts interface. The computation time has been reduced in excess of an order of magnitude, compared with the CPU version. A fast graph cut method on the NVIDIA’s GPU using the compute unified device architecture (cuda) framework has also been proposed.²⁶ The performance of over 60 graph cuts per second on 1024 × 1024 2D images and over 150 graph cuts per second on 640 × 480 2D images on an Nvidia 8800 GTX have been reported.

Theoretical and algorithmic studies of the similarities among FC, level set, graph cut, and watershed families of methods are recently emerging,^{27, 28, 29} which also demonstrate their differences in computational efficiencies. While comparative analysis of the GPU implementations of these frameworks will be worthwhile, their individual GPU implementations have to be developed first. Since such implementations do not exist for FC, and with this goal in mind, in this paper, we present a parallel FC image segmentation algorithm implemented on GPU by using cuda to achieve nearly interactive speed when segmenting large medical image data sets. We emphasize that our focus in this paper is algorithmic speed. The accuracy of the parallel FC algorithm implemented on GPU is the same as that of the sequential algorithm on CPU. We do not undertake any application-specific evaluation of the parallel FC algorithm in this paper. In Sec. 2, we first briefly present the basic FC principles and its sequential algorithm that is chosen for parallel GPU implementation; we then describe the NVIDIA GPU architecture and the cuda programming model, and explain the parallelized version of this algorithm and its implementation by using cuda. The experimental results are presented in Sec. 3. Finally, a discussion and our concluding remarks are presented in Sec. 4. An early version of this paper was presented at the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society, whose proceedings contained an abbreviated version of this paper.³⁰

MATERIALS AND METHODS

Fuzzy connectedness principles and sequential algorithm

We chose to parallelize and implement on GPU the first FC segmentation algorithm reported in Ref. 3. Although several advanced versions of FC algorithms have been reported (see Ref. 31 for a recent review), such as scale-based FC, relative FC, and iterative relative FC, we chose the absolute FC of Ref. 3 since this algorithm forms the basic building block of all other algorithms. The lessons learned from its implementation are more fundamental and can directly lead us to the realization of other algorithms on GPU.

The characteristics of both the algorithm and the GPU platform play a crucial role in determining the final speed-up factor. We briefly describe the concepts related to FC in this section to make this paper self-contained. Please see the original papers for more details.^{3, 4}

We refer to a volume image as a scene and represent it by a pair C = (C, f), where C is a rectangular array of cuboidal volume elements, usually referred to as voxels, and f is the scene intensity function which assigns to every voxel c ∈ C an integer called the intensity of c in C in a range [L, H].

Fuzzy adjacency and affinity

Independent of any image data, we think of the digital grid system defined by the voxels as having a fuzzy adjacency relation. This relation assigns to every pair (c,d) of voxels a value between zero and one. The closer c and d are spatially to each other, the greater is this number. This is intended to be a “local” phenomenon. How local it ought to be should depend on the blurring property of the imaging device. We denote the fuzzy adjacency relation by α and the degree of adjacency assigned to any voxels (c,d) by μ_α(c,d).

Now, consider the voxels as having scene intensities assigned to them. We define another local fuzzy relation called affinity on voxels denoted by κ. The strength of this relation between any voxels c and d, denoted μ_κ(c,d), lies between zero and one, and indicates how the voxels “hang together” locally in the scene. μ_κ(c,d) depends on μ_α(c,d), as well as on how similar are the intensities or intensity-based properties at c and d. The properties of fuzzy affinity relations are studied extensively and a guidance as to how to set up fuzzy affinities in practical applications is given in Refs. ⁴ and 32. In this paper, the following functional form for μ_κ:

$${\mu }_{\kappa }(c,d)={\mu }_{\alpha }(c,d)\sqrt{g_1(f(c),f(d))g_2(f(c),f(d))},$$ (1)

is used, where g₁ and g₂ are Gaussian functions of [f(c) + f(d)]/2 and [f(c) − f(d)]/2, respectively. The mean and variance of g₁ are related to the mean and variance of the intensity of the object that we wish to define in the scene. That is, this component of affinity takes on a high value when c and d are both close to an expected intensity value for the object. g₂ is a zero-mean Gaussian, the underlying idea being to capture the degree of local hanging togetherness of c and d based on intensity homogeneity.

Fuzzy connectedness and fuzzy objects

The aim in FC is to capture the global phenomenon of hanging togetherness in a global fuzzy relation on voxels called fuzzy connectedness, denoted κ. The strength of this relation μ_K(c,d) between any voxels c and d, indicating the strength of their connectedness, lies between zero and one, and is determined as follows: There are numerous possible “paths” within the scene domain C between c and d. Each path for our purposes is a sequence of voxels, starting from c and ending in d, with the successive voxels being nearby. We think of each pair of successive voxels as constituting a link and the whole path to be a chain of links. We assign a strength (between zero and one) to every path, which is simply the smallest pairwise voxel affinity along the path. Finally, the strength of connectedness between c and d is the strength associated with the strongest of all paths between c and d.

Let θ be any number in [0,1], a fuzzy connected object O in C of strength θ, and containing a voxel o, consists of a pool O ⊂ C of voxels together with a value indicating “objectness” assigned to every voxel. O is such that o ∈ O, and for any voxels c ∈ O and d ∈ O, the strength of connectedness between them μ_K(c,d) ≥ θ, and for any voxel c∈O and e ∉ O, the strength μ_K(c,e) < θ.

The absolute FC algorithm is presented below for segmenting an object O in C. For any voxel affinity κ in C = (C,f), we define the κ-connectivity scene of C with respect to a voxel o ∈ C by C_Ko = (C,f_Ko), where, for any c ∈ C, f_Ko = μ_K(o,c). The algorithm uses Dijkstra’s implementation of dynamic programming to find the best path from o to each voxel in C.

Algorithm κ FOE (Ref. ³)

Input: C = (C, f), any o∈C, fuzzy affinity κ.

Output: A κ-connectivity scene C_Ko = (C, f_Ko) of C with respect to o.

Auxiliary Data Structures: 3D array representing the connectivity scene C_Ko = (C, f_Ko) and a queue Q containing voxels to be processed. We refer to the array itself by C_Ko for the purpose of the algorithm.

Begin

• 1.set all voxels of C_Ko to 0 except o which is set to 1;
• 2.push o to Q;
• 3.whileQ is not empty do
• 4. remove a voxel c from Q for which f_Ko(c) is maximal;
• 5. for each voxel e such that μ_κ(c,e)>0 do
• 6.  set f_min = min{ f_Ko(c), μ_κ(c,e)};
• 7.  iff_min > f_Ko(e) then
• 8.   set f_Ko(e) = f_min;
• 9.   ife is already in Qthen
• 10.    update the location of e in Q;

•    else

• 12.    push (e) in Q;

End

Parallel implementation

In this section, we first briefly describe the NVIDIA GPU hardware architecture and the cuda programming model. For a full description on NVIDIA GPU and cuda, readers are referred to the cuda programming guide.³³ We then describe how we implement the FC algorithm using cuda.

NVIDIA GPU architecture and programming model

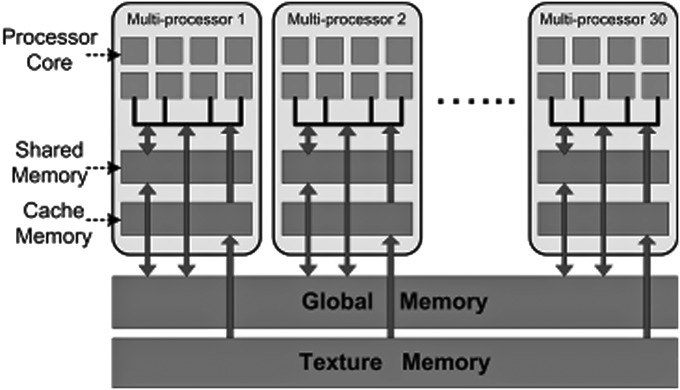
The underlying hardware architecture of a NVIDIA GPU is illustrated in Fig. 1. The NVIDIA Tesla C1060 GPU is used as an example to provide a brief overview of the architecture. The Tesla C1060 GPU has 240 processing cores with a clock rate of 1.3 GHz for each core, delivering nearly one Tera FLOPS of computational power. To support an intuitive and flexible programming environment to access such computing power, NIVIDA provides cuda framework,³³ which is based on a c-language model. cuda enables generation and management of a massive number of processing threads, which can be executed in parallel on GPU cores with efficient hardware scheduling.

Figure 1.

NVIDIA GPU hardware architecture.

The 240 cores of Tesla C1060 GPU are grouped into 30 multiprocessors. Each multiprocessor has eight processing cores, organized in a SIMD (single instruction multiple data) fashion. Each core has its own register file and arithmetic logic unit, which allows it to accomplish a specific computational task. The Tesla C1060 has 4 GB of on-board device memory, which can be used as read-only texture memory or read-write global memory. The GPU device memory features have very high bandwidth, recorded at 102 GB s⁻¹, but it suffers from high access latency. In each multiprocessor unit, there is 16 KB of user-controlled L1 cache, called shared memory. If it is used efficiently, it can be employed to hide the latency in global memory access.

The cuda programming model is based on concurrently executed threads. cuda manages threads in a hierarchical structure. Threads are grouped into a thread block, and thread blocks are grouped into a grid. All threads in one grid share the same functionality, as they are executing the same kernel code. Each thread block is mapped on to one multiprocessor unit, and threads in each block are scheduled to run on eight processing cores of the multiprocessor unit, using a scheduling unit of 32-thread warp. Since the threads in a block are executed on the same multiprocessor, they can use the same shared memory space for data communication. On the other hand, the threads between different blocks can communicate only through the low-speed global memory.

CUDA implementation

In cuda, programs are expressed as kernels. In order to map a sequential algorithm to the cuda programming environment, developers should identify data-parallel portions of the application and isolate them as cuda kernels. In the FC algorithm, there are two major computational tasks: (i) computing the fuzzy affinity relations and (ii) computing the fuzzy connectedness relations. We shall refer to (i) as “affinity computation” and (ii) as “tracking” a fuzzy object. These two tasks are implemented as cuda kernels, and a dramatic improvement in speed for both tasks is achieved as a result.

• (1)Affinity computation kernel: The cuda implementation of fuzzy affinity computation is straightforward. The fuzzy affinity computation of every pair (c,d) of voxels where μ_α(c,d) is greater than zero is totally independent of other pair of voxels. Thus for the pair (c,d), one thread is assigned to compute corresponding g₁(c,d) and g₂(c,d) in Eq. 1, and the fuzzy affinity μ_κ(c,d) result is written to the specific allocated GPU device memory. For computational simplicity, we use the six-adjacency relation for α.
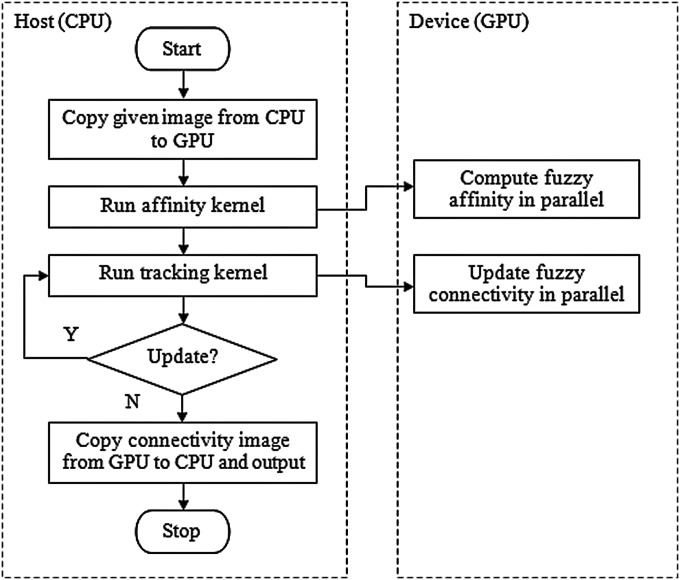
• (2)Tracking kernel: Computing the fuzzy connectedness values for a fuzzy object is a variation of the single-source-shortest-path (SSSP) problem. Dijkstra’s algorithm is an optimal sequential solution to the SSSP problem. Parallel implementation of the Dijkstra’s SSSP algorithm is quite challenging.³⁴ As far as is known, there is no efficient parallel algorithm for the SSSP problem in a SIMD model. Harish and Narayanan³⁵ proposed the use of cuda to accelerate large graph algorithms (including those for the SSSP problem) on the GPU; however, they implemented only a very basic version and did not gain much performance improvement. We use a similar scheme, but take advantage of a newer version of cuda hardware, which supports atomic read∕write operations in the device global memory. The flow chart of our cuda implementation is illustrated in Fig. 2, and the algorithm is presented below.

Figure 2.

The flow chart of the proposed cuda implementation.

Algorithm CUDA-FOE

Input: C = (C,f), any o∈C, the functional form of κ.

Output: A κ-connectivity scene C_Ko = (C,f_Ko) of C with respect to o.

Auxiliary Data Structures: Two 3D arrays representing binary scenes C _m1 = (C,f_m1) and C _m2 = (C,f_m2). We refer to the arrays themselves by C _m1 and C _m2 for the purpose of the algorithm.

Begin

• 1.set all voxels of C _Ko and C='fraktur'>C _m1 to 0 except o which is set to 1;
• 2.Invoke AFFINITY-KERNEL on grid to compute fuzzy affinity μ_κ.
• 3.whileC _m1 is not all zero do
• 4. set all voxels of C _m2 to 0;
• 5.  Invoke TRACKING-KERNEL(C_Ko,C_m1,C_m2,μ_κ) on grid;
• 6. Copy C_m2 to C_m1;

End

The above algorithm is executed on the host (CPU) side while the kernels are executed on the device (GPU) side, as shown in Fig. 2. The different threads operate on voxels for updating connectivity information simultaneously. In one invocation, they all update connectivity information as much as they can on the voxels in their purview. The CPU determines if any updating has been done in the last invocation of the tracking kernel. If so, the kernel is invoked again with updated information on the voxels (in C _m2) where connectivity needs to be further updated. The CPU terminates the run of the algorithm where no more updates are presented by the tracking kernel. The affinity kernel and the tracking kernel algorithms are presented below.

AFFINITY-KERNEL

Begin

• 1.compute thread index t(id);
• 2.for each voxel c processed by t(id) do
• 3.  for each voxel d adjacent to cdo
• 4.   compute affinity μ_κ(c,d) using Equation 1;
• 5.   write μ_κ(c,d) to corresponding GPU memory;

End

TRACKING-KERNEL (C_Ko,C_m1,C_m2,μ_κ)

Begin

• 1.compute thread index t(id);
• 2.for each voxel c processed by t(id) do
• 3.if f_m1 (c) = 1 then
• 4. for each voxel e such that μ_κ(c,e)>0 do
• 5.  set  f _min = min{ f_Ko(c), μ_κ(c,e)};
• 6.  iff_min > f_Ko(e) then
• 7.   set f_Ko(e) = f_min;
• 8.   set f_m2(e) = 1;

End

The algorithm cuda-FOE is an iterative procedure. At the first iteration, only one thread which processes the voxel o is active. TRACKING-KERNEL is called to update the connectivity scene C_Ko and the binary scene C _m2. More threads will be involved and become active for the connectivity update at the successive iteration. Because of the limited communication capability among threads from different blocks, the CPU side needs to collect connectivity update information from each thread on GPU, and decides when to terminate calling the TRACKING-KERNEL. Each thread checks the flag of each voxel under its control to see if it is 1 in the binary array C _m1. If yes (which means the connectivity of that voxel has been updated during the last iteration, thus the connectivity values of its neighboring voxels might need to be updated in current iteration), it fetches its connectivity value f_Ko(c) from the connectivity array C_Ko and the affinities μ_κ(c,e) between voxel c and its adjacent voxel e. Then the connectivity value of voxel e is updated if the minimum of μ_κ(c,e) and f_Ko(c) is greater than its original connectivity value f_Ko(e). Note in line 7 of the Algorithm TRACKING-KERNEL, atomic operation was used for consistency, because update operations for one voxel by multiple threads might happen simultaneously. The two binary arrays C_m1 and C_m2 are used to avoid inconsistency. When voxel c has been processed by one thread, whether or not it needs to be further processed in the next iteration depends on the processing results of its adjacent voxels. The algorithm cuda-FOE terminates when there is no connectivity update from any of the threads.

RESULTS

In this section, the running times of our GPU and CPU implementations of the FC algorithm are compared for image data of different sizes. The CPU version of FC is implemented in c ++ . The computer used is a DELL PRECISION T7400 with a quad-core 2.66 GHz Intel Xeon CPU. It runs Windows XP and has 2 GB of main memory. The GPU used is the NVIDIA Tesla C1060 with 240 processing cores and 4 GB device memory. cuda SDK 2.3 is used in our GPU implementation. Three image data sets—small, medium, and large—are utilized to test the performance of the GPU and CPU implementations. Table TABLE I. lists the image data set information and shows the performance of the GPU implementation versus the CPU implementation. A speed-up factor of 24.4x, 18.1x, and 10.3x, respectively, has been achieved, for the three data sets over the CPU implementation. It is noted that the segmentation results produced from both GPU and CPU implementations are identical. Here, the speed-up factor is defined as t_s/t_p, where t_s and t_p are the times taken for the sequential and parallel implementations, respectively. It seems that the larger the size of the testing data set, the less speed-up we achieved. This is mainly because for larger data sets, the affinity and tracking kernels require much more device global memory access, which has high latency.

TABLE I.

Data set information and performance of the GPU implementation with respect to the optimal CPU implementation.

Dataset	Small	Medium	Large
Protocol	PD MRI	T1 MRI	CT torso
Scene domain	256 × 256 × 46	256 × 256 × 124	512 × 512 × 459
Voxel size(mm3)	0.98 × 0.98 × 3.0	0.94 × 0.94 × 1.5	0.68 × 0.68 × 1.5
CPU time (s)	6.09	13.01	155.53
GPU time (s)	0.25	0.72	15.04
Speed-up	24.4	18.1	10.3

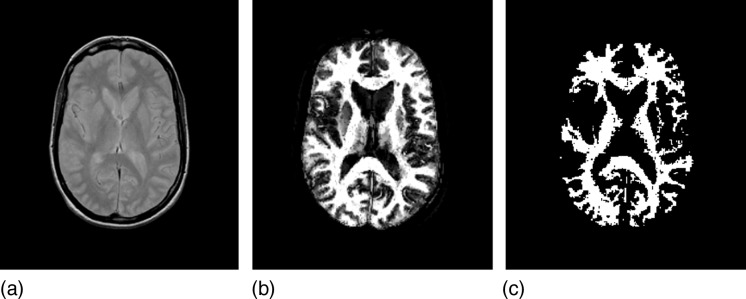
Figure 3 shows the example of the small data set, which comes from MRI of the head of a clinically normal human subject. A fast spin-echo dual-echo protocol is used. Figure 3a shows one slice of the original PD-weighted scene, Figs. 3b, 3c show corresponding slices depicting connectedness values, and the final hard segmented white matter object.

Figure 3.

A slice of the PD-weighted MRI scene from the small data set (a), the corresponding slices of the scenes depicting the connectedness values (b), and the final hard segmented white matter (c).

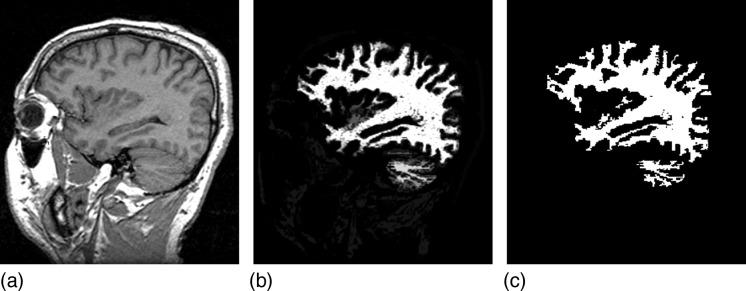
Figure 4 shows the example of the medium data set, which is a T1-weighted MRI scene of the head of a clinically normal human subject. The spoiled gradient recalled (SPGR) acquisition was used. This data set were obtained from the web site of National Alliance for Medical Image Computing.³⁶ Figure 4a shows one slice of the original scene, and Figs. 4b, 4c show corresponding slices depicting the connectedness values, and the final hard segmented white matter object.

Figure 4.

A slice of the T1-weighted MRI scene from the medium data set (a), the corresponding slices of the scenes depicting the connectedness values (b), and the final hard segmented white matter (c).

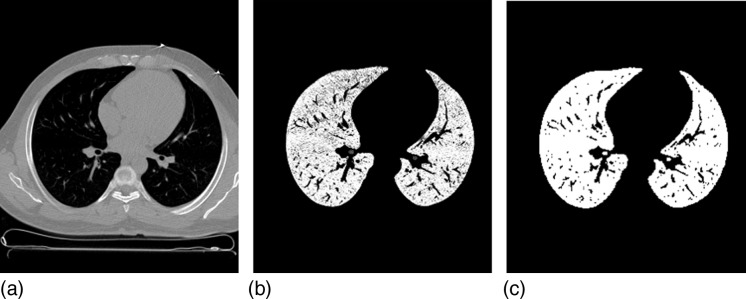
Figure 5 shows the example of the large data set, which is a CT scene of the torso. Figure 5a shows one slice of the original scene, and Figs. 5b, 5c show corresponding slices depicting the connectedness values, and the final hard segmented lung mask without pulmonary vessels.

Figure 5.

A slice of the CT scene of the torso from the large data set (a), the corresponding slices of the scenes depicting the connectedness values (b), and the final hard object (c).

DISCUSSION AND CONCLUDING REMARKS

Recently, clinical radiological research and practice are becoming increasingly quantitative. Further, images continue to increase in size and volume. For quantitative radiology to become practical, it is crucial that image segmentation algorithms and their implementations are rapid and yield practical run time on very large data sets. This paper describes an example of practical and cost-effective solutions to the problem.

We developed a parallel algorithm of the widely used fuzzy connected image segmentation method on the NVIDIA GPUs, which are far more cost- and speed-effective than both COWs and multiprocessing systems. The parallel implementation achieves speed increases by factors ranging from 10.3x to 24.4x on Tesla C1060 GPU over an optimized CPU implementation for three image data sets with a wide range of sizes, and takes 0.25, 0.72, and 15.04 s, correspondingly, for the three image data sets. The performance of the parallel implementation could be further improved by taking advantage of fast GPU shared memory. A near-interactive speed of segmentation has been achieved, even for the large data set. For some specific applications, several free parameters (e.g., fuzzy affinity parameter, threshold value for the fuzzy object) in fuzzy connected image segmentation might be difficult to optimize.⁸ The interactive speed of segmentation could give users immediate feedback on parameter settings; thus allowing them to fine-tune free parameters and produce more accurate segmentation results. Future work will also include the development of more advanced FC algorithms such as the scale-based relative FC (Ref. ⁵) and iterative relative FC (Ref. ³¹) on the GPU.